Analysis of the Applicability of the Yukawa Model and Chapman–Enskog Approach for Heated Beryllium at Metallic Density Using Quantum Molecular Dynamics

Abstract

We conducted a comprehensive analysis of quantum molecular dynamics (QMD) simulation results for beryllium (Be) at metallic density and temperatures up to 32,000 K. Using the QMD results for the radial distribution function (RDF), velocity autocorrelation function (VACF), mean-squared displacement (MSD), and the diffusion coefficient of ions, we confidently assess the effectiveness of the Yukawa one-component plasma model in describing ion structure and transport properties. Additionally, we analyzed the applicability and accuracy of the Chapman–Enskog method for calculating the diffusion coefficient. We found that Yukawa model-based molecular dynamics (MD) simulations accurately capture ion dynamics, as evidenced by the VACF and MSD, when the Yukawa potential parameters are correctly chosen. Through our comparative analysis of the QMD, Yukawa–MD, and Chapman–Enskog methods, we clearly identified the effective coupling parameter values at which the Chapman–Enskog method maintains its accuracy. Importantly, while a model that reproduces the RDF of ions may not guarantee precise transport properties, our findings underscore the necessity of benchmarking plasma models against QMD results from real materials to validate their applicability and efficacy.

1. Introduction

Warm dense matter (WDM) is being studied intensively through both experimental and theoretical approaches. At high temperatures and pressures, strong correlations, quantum degeneracy, and thermal excitation effects require careful analysis of the traditional theoretical models developed for liquids, gases, solids, and plasmas [1,2,3]. The WDM regime is often characterized by a liquid-like structure of ions, but the distances between particles are much smaller than those in traditional liquids, along with the quantum degeneracy of electrons.

A heated dense substance can be generated in various ways—such as electrical explosion of conductors—in solids and metal clusters subjected to laser pulses or powerful particle beams, and in shock wave experiments [4,5,6]. The transport parameters of a nonideal plasma are crucial for developing models of inertial thermonuclear fusion, understanding the behavior of astrophysical objects such as white dwarfs and the internal structure of giant planets. An experimental study of WDM has been performed at laser facilities such as the National Ignition Facility (NIF) [7], the European XFEL [8], and OMEGA [9]. The interpretation of the observations from these high-pressure experiments requires theoretical models of the states of matter under extreme conditions [10,11,12,13,14,15].

Theoretical approaches to studying heated dense matter must account for strong interparticle interactions and quantum degeneracy within the framework of quantum many-body theory. Numerous results related to heated dense substances have been obtained using quantum molecular dynamics (QMD), where the behavior of ions is governed by classical equations of motion while electrons are treated quantum mechanically through density functional theory (DFT) [16,17,18,19]. In fact, DFT is the most widely used ab initio modeling method for describing the electronic structure and related physical properties of heated dense substances. DFT calculations help determine the distribution of electron density in a quantum system at equilibrium, where free energy is minimized [20,21,22,23]. Furthermore, DFT can be utilized to derive various physical properties of heated dense substances, such as the density of electronic states, bulk modulus, dielectric constant, electrical conductivity, and more.

Modeling the transport properties using DFT is computationally expensive. Therefore, to calculate various transport coefficients, such as ion diffusion and viscosity, across different density and temperature regimes, effective one-component plasma models are often used in conjunction with the Chapman–Enskog approach for the Coulomb logarithm or classical MD of ions [24,25,26,27,28,29,30,31,32,33]. In these models, the effect of electrons is incorporated into an ion–ion pair potential. The often-used ion–ion interaction model is a Yukawa-type screened potential [34,35,36,37,38,39,40]. More accurate potential can be generated using logarithm of the ion–ion pair correlation function [24,25,26,27], e.g., from the hypernetted chain approximation. One advantage of effective one-component plasma models is their universal dependence on a few dimensionless parameters, typically describing coupling and screening, across a wide range of temperatures and densities.

Among various materials, the WDM state of beryllium (Be) has attracted significant interest since Be is one of the capsule ablator materials used in inertial confinement fusion experiments. Therefore, the thermodynamic and transport properties of beryllium under the extreme conditions of high density and temperature have been the subject of active experimental and theoretical studies in recent times [7,41,42,43].

Here, we present a QMD-based analysis of effective one-component plasma models, focusing on ion diffusion and the velocity autocorrelation function. Our study examines solid-density beryllium (Be) at temperatures reaching up to 32,000 K. The QMD simulations were conducted using an orbital-free density functional theory (OFDFT) approach combined with MD simulations of ions. We compare the results from the QMD simulations with data from MD simulations that employ a screened Yukawa ion–ion potential. In these MD simulations, the coupling and screening parameters are adjusted to reproduce accurately the ion pair correlation function derived from the QMD calculations. Additionally, we analyze the results for the diffusion coefficient calculated using the Chapman–Enskog approach, in which the ion–ion pair correlation function obtained from the QMD data is used to define an effective ion–ion potential.

2. Materials and Methods

The QMD simulations of dense Be were performed using the OFDFT to model the electronic component and MD method to drive ionic dynamics in the Born-Oppenheimer approximation. In addition, we performed the MD simulation of the Yukawa one-component plasma (Yukawa–MD). In the OFDFT simulations, the Wang–Teter (WT) kinetic energy functional [44] was used. The WT kinetic energy functional is fully non-local, takes into account density gradient effects, and also correctly describes the delocalised electronic structure characteristic for metals [45,46]. The exchange-correlation functional was set to Perdew-Zunger local density approximation [47]. Simulations were performed in DFTpy [48] and ASE [49,50] packages with a simulation step of 2 femtoseconds in MD. The electron–ion interaction was defined using optimized local pseudopotential [51]. The kinetic energy cutoff was set to 600 eV. The corresponding spacing separating the nearest real space grid points is 0.47 Bohr. The number of particles in the system is $N=864$ for the main results. A self-written C++ code was used for the Yukawa–MD, and integration of the equations of motion was performed using the Velocity Verlet method. The Yukawa potential $\mathsf{\Phi }\left(r^{\ast }\right)=\mathsf{\Gamma }/r^{\ast }exp(-\kappa r^{\ast })$ is fully defined by the coupling parameter $\mathsf{\Gamma }$ and the screening parameter $\kappa$ (here $r^{\ast }=r/a$, with a being the mean interparticle distance). The Yukawa potential parameters ($\mathsf{\Gamma },\kappa$) were chosen manually to match the OFDFT results. Periodic boundary conditions in MD simulations were applied. The simulations were carried out in two stages: first 200 steps in NVT ensemble with Langevin thermostat (with the friction parameter in ASE set to $\gamma =0.5$), then 300 steps in NVE ensemble without thermostat. Thermalization in the first step allowed the system to reach an equilibrium state and establish the correct particle velocity distribution. The transition to NVE ensured natural particle dynamics, eliminating the effect of the thermostat on transport properties such as diffusion and velocity autocorrelation. Test calculations with different numbers of particles were performed to ensure that the presented results are independent of system size. The parameter $\gamma$ in the Langevin equation of motion is the friction coefficient, which determines the interaction force between the particle and the heat bath. At $\gamma =0.5$, the balance between energy dissipation and random thermal perturbations is preserved, providing the correct establishment of the temperature in the system. To obtain statistically reliable values, 10 independent simulations were performed for each temperature value. All obtained data were averaged over these independent simulations.

2.1. Methods for Calculating the Diffusion Coefficient from the MD Trajectories of Ions

The diffusion coefficients D from the QMD and Yukawa–MD simulations were computed using the Einstein relation and the Green–Kubo relation.

2.2. Einstein Relation

The Einstein relation allows for determining the diffusion coefficient from the mean-square displacement (MSD) of ions. The diffusion coefficient is calculated from the long-time limit of the MSD using the following expression [52]:

$$D={\displaystyle \frac{\langle r^2\left(t\right)\rangle }{6t}},$$

(1)

where $\langle r^2\left(t\right)\rangle$ is the MSD, calculated as follows:

$$\langle r^2\left(t\right)\rangle ={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left|{\mathbf{r}}_i\left(t\right)-{\mathbf{r}}_i\left(0\right)\right|}^2.$$

(2)

Here, N is the number of particles, ${\mathbf{r}}_i\left(t\right)$ is the coordinate of the i-th particle at time t, and ${\mathbf{r}}_i\left(0\right)$ is its initial coordinate. The linear behavior of $\langle r^2\left(t\right)\rangle$ at large times allows us to determine the diffusion coefficient from the slope of the graph of dependence of $\langle r^2\left(t\right)\rangle$ on t.

2.3. Green–Kubo Relation

An alternative approach is to use the Green–Kubo relation, which allows for computation of the diffusion coefficient from the velocity autocorrelation function (VACF) of ions. The VACF describes how much the velocity of a particle at time t is correlated with its initial velocity:

$$C_v\left(t\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\langle {\mathbf{v}}_i\left(t\right)·{\mathbf{v}}_i\left(0\right)\rangle .$$

(3)

The diffusion coefficient in this case is defined through the integral of the VACF [52]:

$$D={\displaystyle \frac{1}{3}}{\int }_0^{\infty }{C}_v\left(t\right)dt.$$

(4)

Both methods give equivalent results with sufficiently long simulation times and proper statistics. The MSD method is more intuitive and widely used in molecular dynamics, but, in the context of our analysis, the VACF method provides an additional test for analyzing the dynamic properties of the system because it gives direct information on the time evolution of the particle velocity.

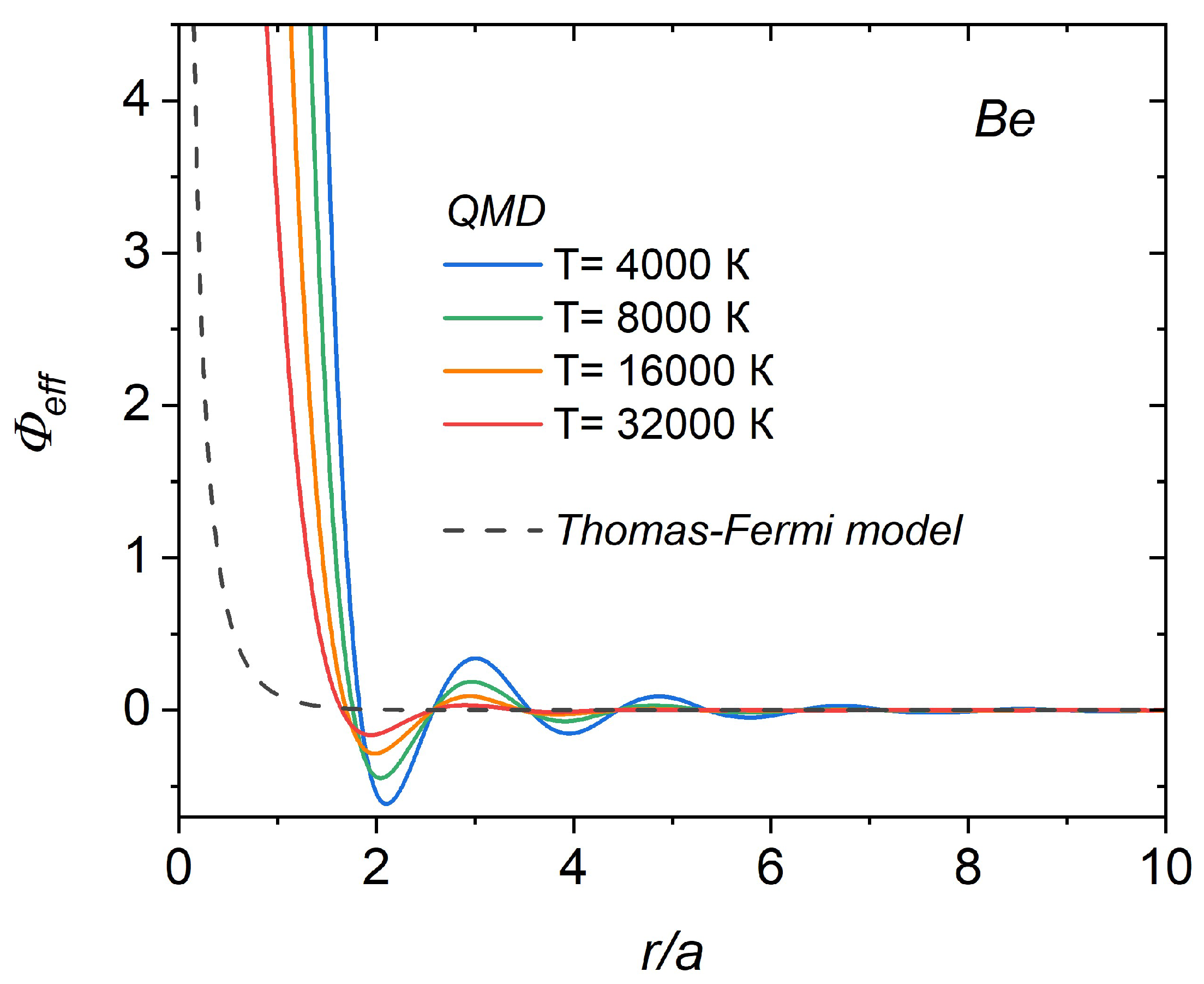
2.4. Chapman–Enskog Approach Using Effective Ion–Ion Potential

Using the data for the diffusion coefficient form the QMD simulations, we tested the accuracy of the Chapman–Enskog approach using the effective ion–ion potential [24,25,26,27,28,29,30]. The idea of this approach is to describe ion–ion collisions using the effective field ${\mathsf{\Phi }}_{\mathrm{eff}}\left(r\right)$ defined by the two particle radial distribution function $g\left(r\right)$ (RDF):

$${\mathsf{\Phi }}_{\mathrm{eff}}\left(r\right)=-k_{B}Tlng\left(r\right).$$

(5)

The effective potential (5) is used to compute the classical center-of-mass scattering angle of two colliding particles:

$${\theta }_c(b,\upsilon )=\pi -2b{\int }_{r_0}^{\infty }{\displaystyle \frac{dr}{r^2}}{\left(1-{\displaystyle \frac{2{\mathsf{\Phi }}_{\mathrm{eff}}\left(r\right)}{\mu {\upsilon }^2}}-{\displaystyle \frac{b^2}{r^2}}\right)}^{-1/2},$$

(6)

here $\mu =m_i/2$ is the reduced mass of an ion.

In Equation (6), $r_0$ is the distance of the closest approach for a given impact parameter b defined as the solution of the following equation:

$$1-{\displaystyle \frac{2{\mathsf{\Phi }}_{\mathrm{eff}}\left(r_0\right)}{\mu {\upsilon }^2}}-{\displaystyle \frac{b^2}{r_0^2}}=0.$$

(7)

Next, the scattering angle ${\theta }_c(b,\upsilon )$ is used to compute the Coulomb logarithm:

$$ln\mathsf{\Lambda }={\displaystyle \frac{1}{b_{\perp }^2}}{\int }_0^{\infty }{sin}^2\left({\displaystyle \frac{{\theta }_c}{2}}\right)bdb,$$

(8)

where $b_{\perp }=Z^2/\left(\mu {\upsilon }^2\right)$.

The Coulomb logarithm defines the first-order collision integral [34]:

$${\mathsf{\Omega }}^{(1,1)}={\displaystyle \frac{\sqrt{\pi }{Z}^4{e}^4}{2\sqrt{2\mu T^3}}}ln\mathsf{\Lambda },$$

(9)

where, in our case for Be, we set the charge to the number of valence electrons per atom $Z=2$.

Using the collision integral ${\mathsf{\Omega }}^{(1,1)}$, the diffusion coefficient is computed as

$$D={\displaystyle \frac{3T}{8n{m}_i{\mathsf{\Omega }}^{(1,1)}}},$$

(10)

with n being the number density of ions and $m_i$ being the ion mass.

In practice, $g\left(r\right)$ is approximated or supplied as an input from other methods, such as the hypernetted chain approximation. Here, for benchmarking purposes, we use $g\left(r\right)$ from QMD to test if the Chapman–Enskog method can reproduce the diffusion coefficient from QMD. In Figure 1, we show the Coulomb logarithm computed using the RDF $g\left(r\right)$ from QMD calculations and provide comparison with the Coulomb logarithm computed using classical Debye plasma model [26,28,34,53,54] and using a screened potential with the screening length computed according to the Thomas–Fermi approximation [35]. The effective potential of ion–ion interaction derived using the RDF from the QMD simulations are shown in Figure 2, where we also compare the QMD data with the Thomas–Fermi approximation For illustration, from Figure 1, we see that the QMD result for the Coulomb logarithm of warm dense matter can significantly differ from the results of the traditional Debye plasma model. Additionally, as shown in Figure 1, the Thomas–Fermi approximation aligns much better with the QMC results than the Debye plasma model does. However, as we will demonstrate shortly, there is still a significant discrepancy between the Thomas–Fermi approximation and the QMC results when it comes to the diffusion coefficient.

3. Results and Discussions

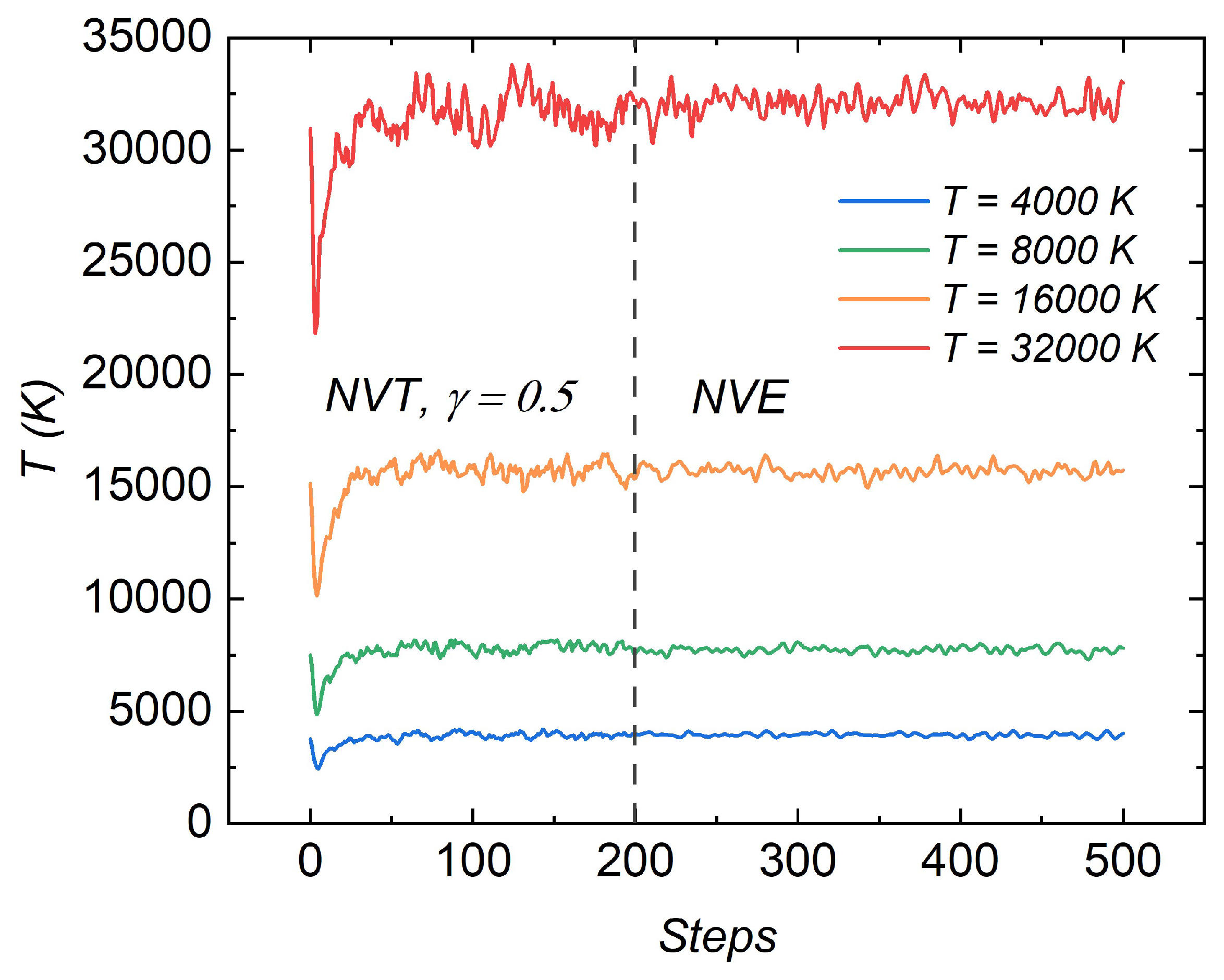
3.1. Temperature Evolution in the Simulation

Figure 3 shows the temperature evolution of the system during the simulation at different target temperatures ($T=4000$ K, 8000 K, 16,000 K, 32,000 K). The modeling was conducted in two stages: (1) a thermalization stage in the NVT ensemble using Langevin dynamics, and (2) ion dynamics in the NVE ensemble, during which physical observables were computed.

At the initial moment, the system, as a rule, is not in an equilibrium state, i.e., the temperatures of individual particles do not correspond to a target temperature. To bring the system to thermodynamic equilibrium, Langevin equations of motion are applied:

$$m{\displaystyle \frac{d\mathbf{v}}{dt}}=-\gamma m\mathbf{v}+\mathbf{R}\left(t\right),$$

(11)

where m is the mass of the particle, $\gamma$ is the coefficient of friction, which determines the rate of thermal exchange with the virtual heat bath, $\mathbf{R}\left(t\right)$—random force modeling thermal fluctuations in the system. The MD simulations were performed using ASE, where the value of $\gamma =0.5$ was used. This corresponds to a balanced regime where the particles do not lose too much energy (as in the case of high friction) and do not remain too ‘heated’ (as in the case of low friction). In 200 simulation steps, the temperature is stabilized at a level corresponding to the target value.

After reaching the equilibrium state, the thermostat is switched off, and the system switches to the NVE ensemble. In this mode, the system temperature is maintained naturally by the conservation of the total energy of the system:

$$E_{\mathrm{total}}=K+U=\mathrm{const},$$

(12)

where K is the kinetic energy, U is the potential energy of the interatomic interaction. Smooth temperature fluctuations around the stationary level confirm the correctness of the chosen modeling time step and the adequacy of the used method of integration of the equations of motion (Velocity Verlet).

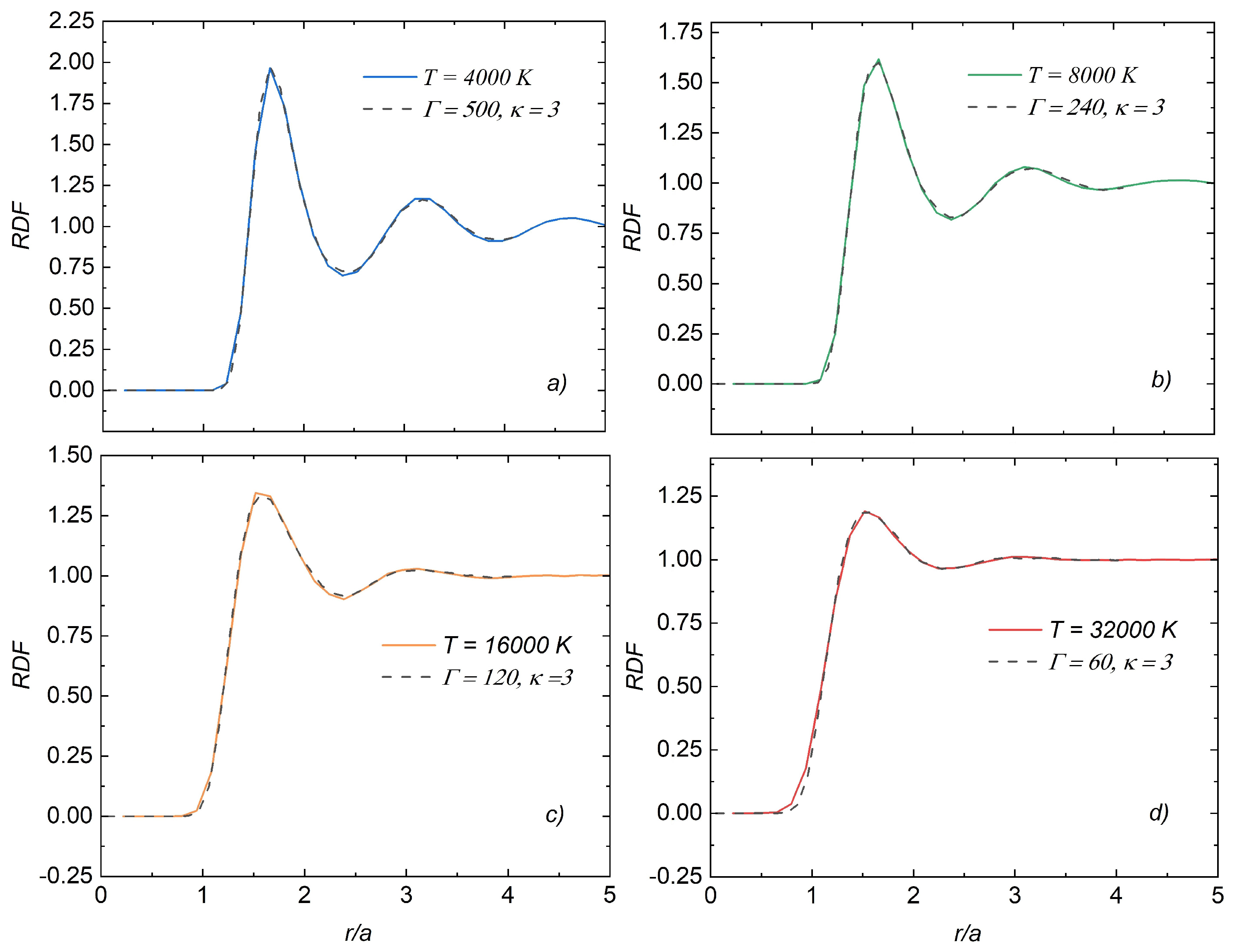
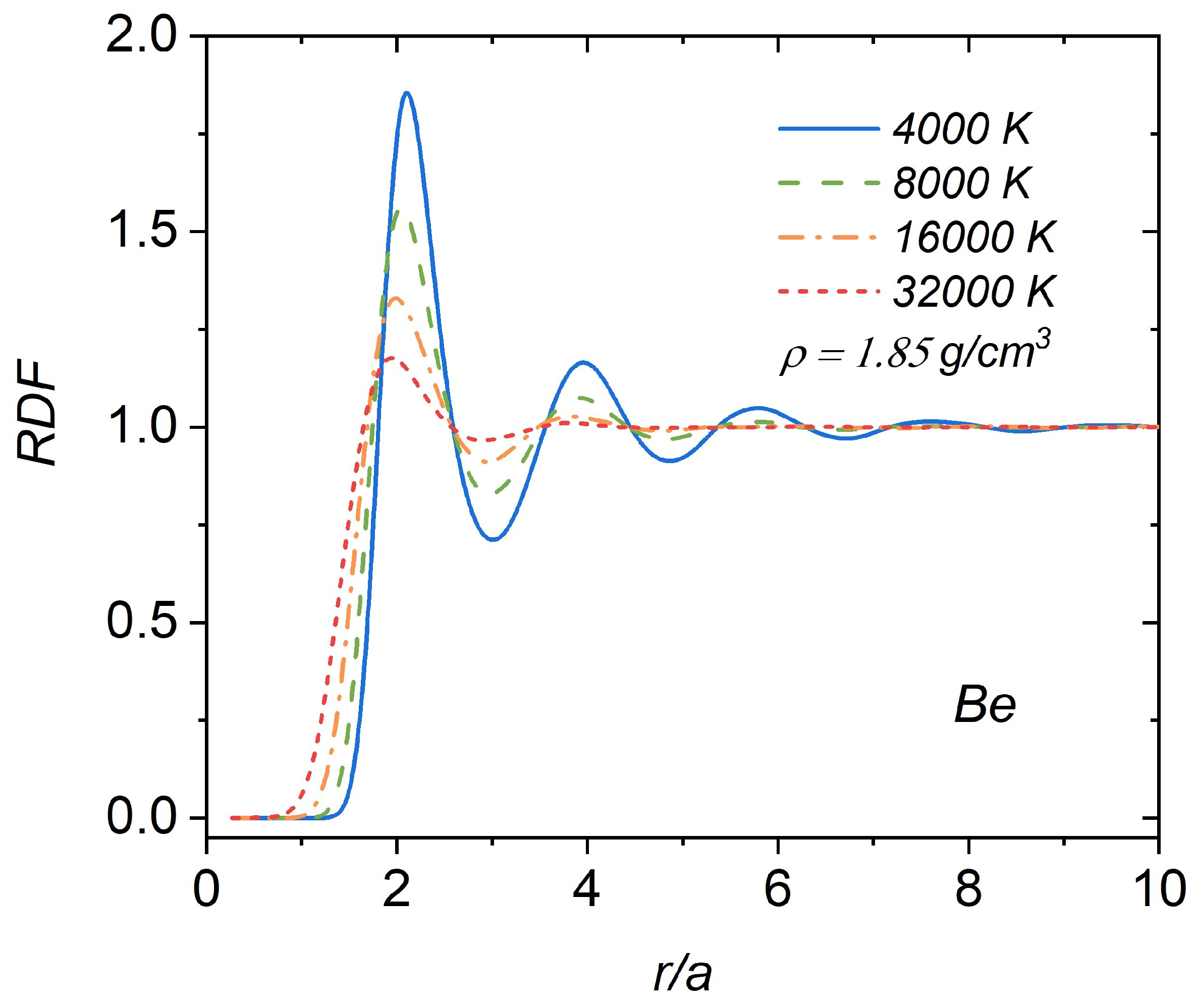
3.2. Radial Distribution Function (RDF) for Dense Beryllium

Figure 4 shows the variation of the radial distribution function (RDF) with increasing temperature. At low temperatures, the RDF has pronounced peaks indicating near-order in the system, but they smooth out with heating due to thermal motion induced disorder and decreasing interparticle correlations. At high temperatures, the RDF approaches unity, indicating a transition towards a more chaotic state characteristic of the gas phase.

Figure 5 shows the comparison between the RDF of dense beryllium calculated by the QMD method and the corresponding RDF from the Yukawa–MD simulations. To achieve a match, the parameters of the Yukawa potential ($\mathsf{\Gamma }$ and $\kappa$) were selected so as to reproduce the inter-ion correlations in beryllium. The almost identical RDF shapes from the QMD and Yukawa–MD confirm that the effective Yukawa potential is able to describe the structure of dense beryllium adequately. This indicates that the system with screened Coulomb interactions can serve as a good model to reproduce the structural properties of a metallic dense matter under similar thermodynamic conditions.

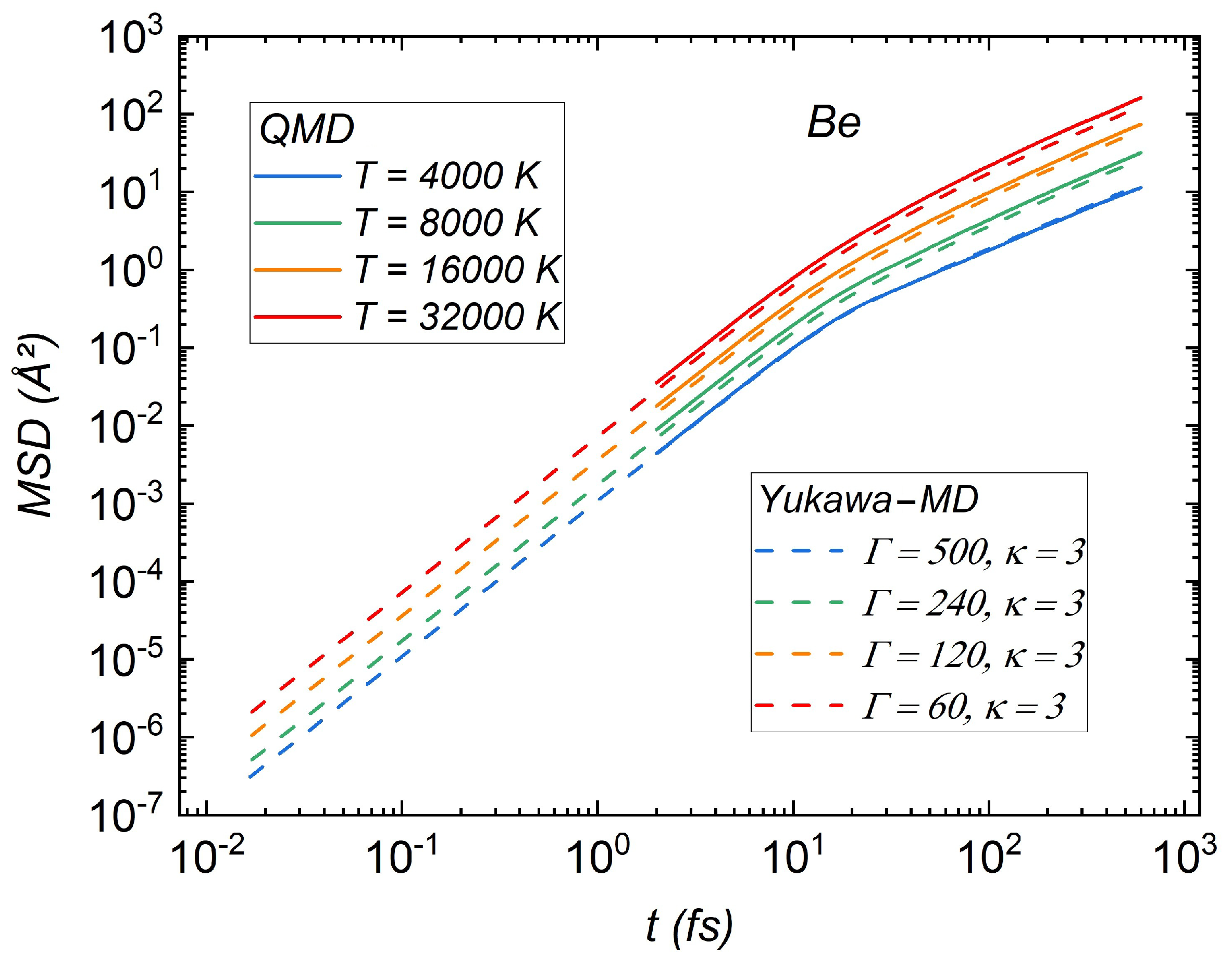
3.3. Mean-Squared Displacement (MSD) as a Function of Time

The mean-square displacement (MSD) characterizes the dynamic behavior of particles by showing how far, on average, they move from their initial position in a given time. At sufficiently large times, the MSD has linear dependence on time, indicating the establishment of a diffusion mode of particle motion (Figure 6).

At low temperatures ($\mathsf{\Gamma }$ is large), the MSD of dense beryllium calculated by the QMD method and the MSD of the Yukawa system practically coincide. In this regime, the system remains sufficiently correlated, and interatomic interactions play a dominant role. The Yukawa model reproduces the structure of the system well, indicating that the Yukawa one-component plasma model is an accurate approximation of the forces acting between beryllium ions.

Figure 5. Comparison of the radial distribution function (RDF) for dense beryllium from the QMD simulations (solid lines) and the Yukawa–MD calculations (dashed lines) at different temperatures: (a) $T=4000$ K, $\mathsf{\Gamma }=500$, $\kappa =3$; (b) $T=8000$ K, $\mathsf{\Gamma }=240$, $\kappa =3$; (c) $T=$ 16,000 K, $\mathsf{\Gamma }=120$, $\kappa =3$; (d) $T=$ 32,000 K, $\mathsf{\Gamma }=60$, $\kappa =3$.

Figure 5. Comparison of the radial distribution function (RDF) for dense beryllium from the QMD simulations (solid lines) and the Yukawa–MD calculations (dashed lines) at different temperatures: (a) $T=4000$ K, $\mathsf{\Gamma }=500$, $\kappa =3$; (b) $T=8000$ K, $\mathsf{\Gamma }=240$, $\kappa =3$; (c) $T=$ 16,000 K, $\mathsf{\Gamma }=120$, $\kappa =3$; (d) $T=$ 32,000 K, $\mathsf{\Gamma }=60$, $\kappa =3$.

Figure 6. Mean-squared displacement (MSD) for dense beryllium from the QMD and Yukawa–MD simulations at different temperatures.

Figure 6. Mean-squared displacement (MSD) for dense beryllium from the QMD and Yukawa–MD simulations at different temperatures.

As the temperature increases ($\mathsf{\Gamma }$ decreases), the kinetic energy of the particles begins to dominate over the interparticle forces, which leads to a change in their trajectories. In this regime, the MSD discrepancy between the models becomes noticeable, which is due to the simplification of interactions in the Yukawa potential. In real dense beryllium, the interaction of ions is determined not only by the screened Coulomb forces but also by more complex electronic structure effects, which are not taken into account in the Yukawa model. This leads to the fact that in the QMD simulations, the particles can show a somewhat different diffusion character than in the Yukawa model.

Nevertheless, despite these differences, the QMD and Yukawa–MD results for the MSD show similar trends and are in overall good agreement, which confirms the adequacy of using the Yukawa model as an approximate but sufficiently accurate method to describe the dynamic properties of dense beryllium in the considered temperature range.

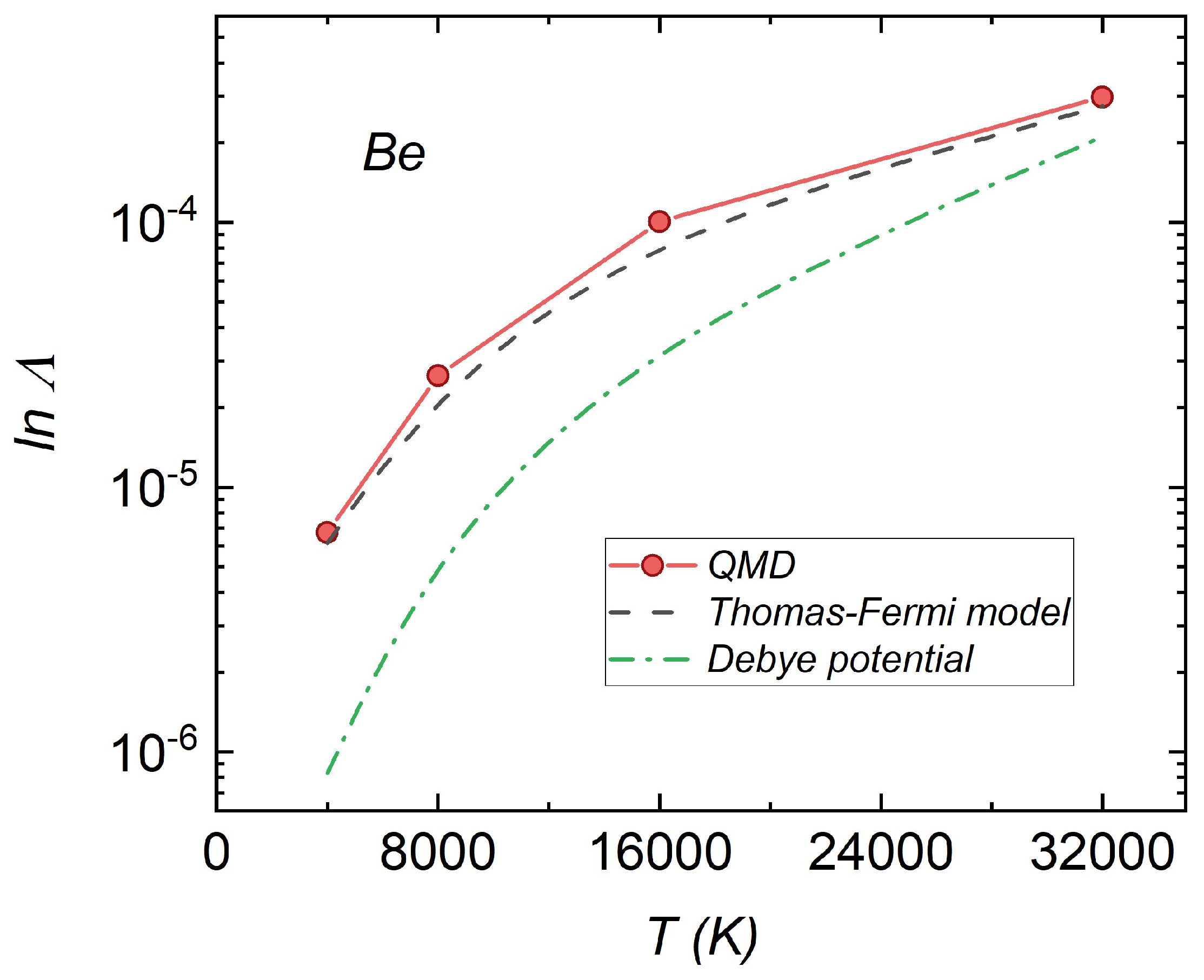
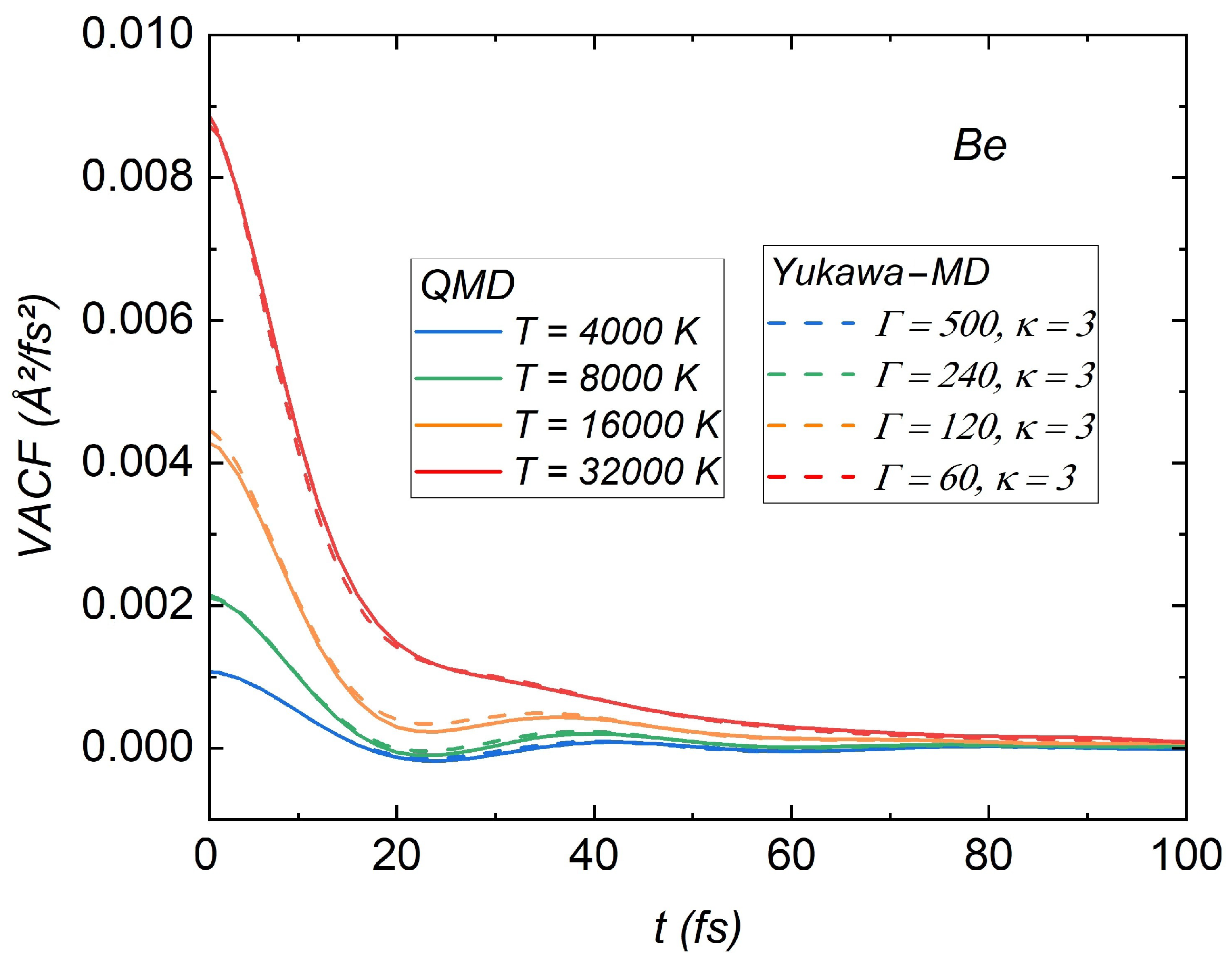
3.4. Velocity Autocorrelation Function (VACF)

The velocity autocorrelation function (VACF) allows us to characterize the extent to which the velocity of a particle at time t remains correlated (on average) with its initial velocity. In this regard, velocity correlations decay with time due to interparticle collisions.

Figure 7 shows the VACF for dense beryllium calculated by the QMD method and the corresponding results for the Yukawa system at different temperatures. It can be seen that the characteristic correlation time decreases with increasing temperature. At low temperatures ($T=4000$ K), the velocity correlations decay more slowly, which is due to the pronounced near-order in the structure of ions. At high temperatures ($T=$ 32,000 K), the velocity-velocity correlations decay much faster as thermal energy dominates the interatomic interactions, strengthening the chaotic motion of particles.

The comparison of the QMD and Yukawa–MD results, as shown in Figure 7, demonstrates a good agreement between the two methods. This confirms that the particle velocity dynamics are equivalent in both the QMD and Yukawa–MD simulations. Consequently, Figure 7 indicates that the Yukawa model accurately describes the dynamics of particles in dense beryllium at the temperatures considered.

3.5. Diffusion Coefficient

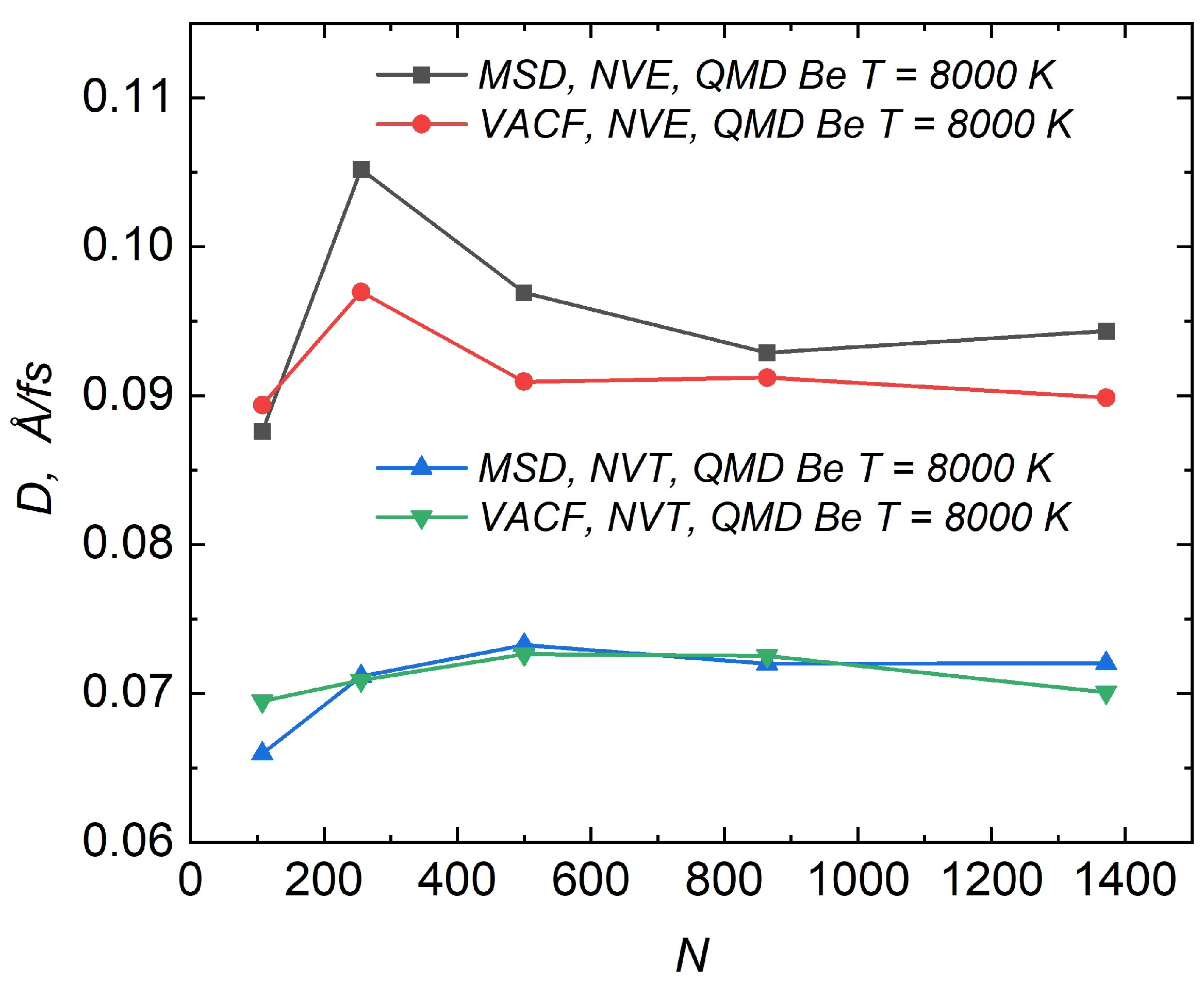
3.5.1. Dependence of the Diffusion Coefficient on the Number of Particles

The dependence of the diffusion coefficient D on the number of particles N for the dense beryllium and Yukawa system at 8000 K is shown in Figure 8, where we also compare the results computed using the NVT and NVE ensembles. It can be seen that in the NVT ensemble the diffusion coefficient is systematically lower than that from the NVE ensemble. This is due to the effect of the thermostat limiting the particle velocity fluctuations. This clearly indicates that the transport properties must be computed using the NVE ensemble to avoid the effects of a thermostat. These results also confirm that the correct calculation of the diffusion coefficient requires the scheme NVT → NVE, at which the system is first brought to equilibrium by the thermostat and then freely evolves without artificial temperature control.

From the dependence of the diffusion coefficient on the number of particles presented in Figure 8, we see that the effect of a finite number of ions in the main simulation cell becomes minor at $N>800$.

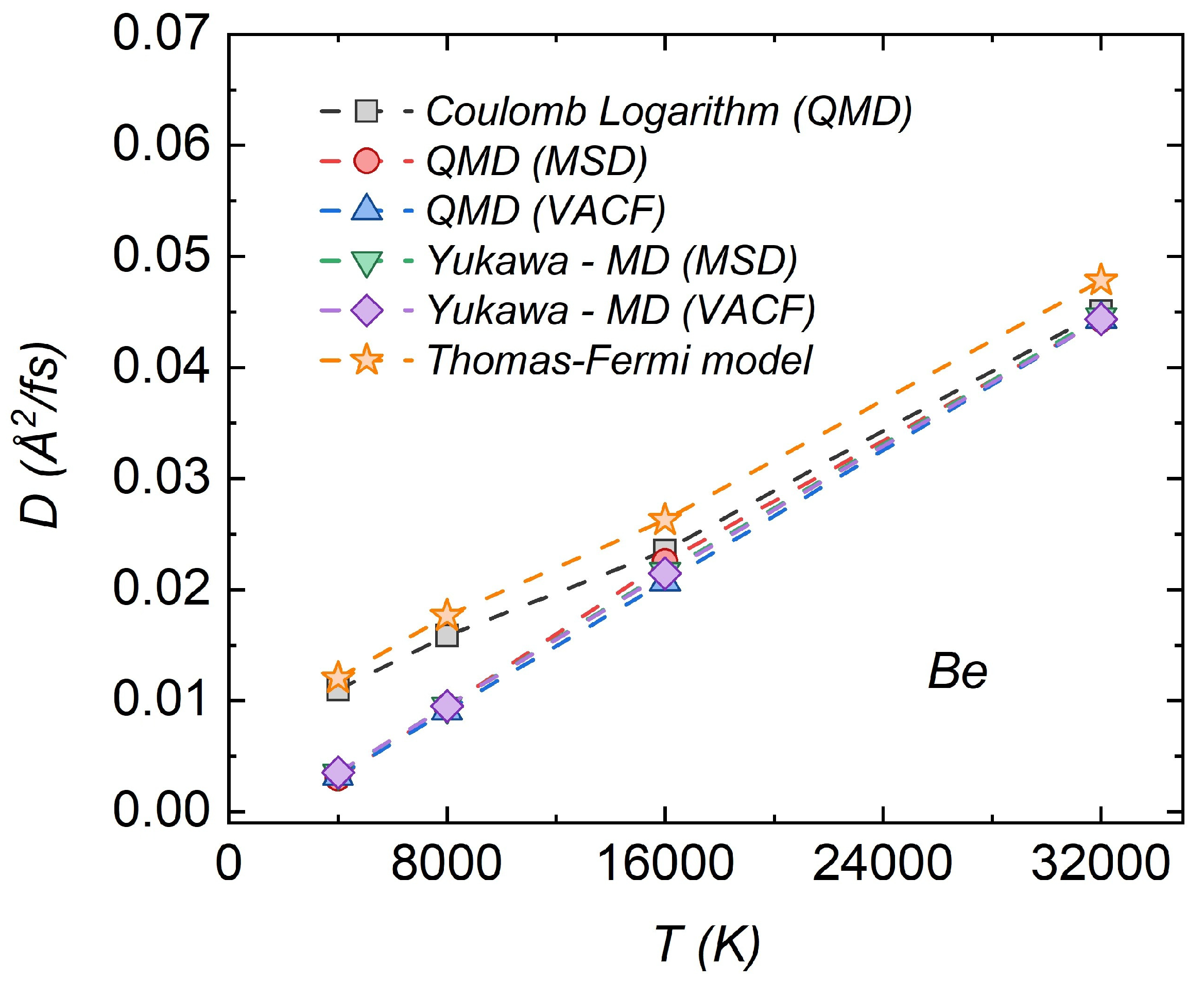
3.5.2. Diffusion Coefficient Dependence on Temperature

Figure 9 shows the dependence of the diffusion coefficient D on temperature T, where D values are calculated using the MDS in Equation (1) and the VACF in Equation (4). We compare the results from the QMD simulations with the data computed using the Yukawa–MD calculations and with the results obtained using the Coulomb logarithm (as described in Section 2.4). It can be seen that the diffusion coefficients calculated using the QMD method and the Yukawa model show good agreement with each other. This confirms that if the Yukawa model provides accurate structural properties, it can also adequately describe ion transport properties.

In Figure 9, the relationship between $D\left(T\right)$ and temperature exhibits a nearly linear behavior, which aligns with the expected physical principles. As temperature rises, the kinetic energy of the particles increases, resulting in a decrease in interatomic correlations and an increase in the mean free path length of particles. Consequently, particles can more easily overcome the barriers in the potential energy landscape created by interatomic forces.

Finally, in Figure 9, a comparison of the results obtained using the Chapman–Enskog approach (which incorporates the Coulomb logarithm) and data from molecular dynamics simulations reveals that the Chapman–Enskog method significantly overestimates the diffusion coefficient at temperatures below $16,000\mathrm{K}$. However, it provides accurate results at higher temperatures. To understand this, we note that the Chapman–Enskog method relies on the idea of pair collisions, as evidenced by the use of pair-collision cross sections. This simplification is only valid when the correlation between particles is sufficiently weak. We can illustrate this by comparing the RDF curves at different temperatures, as shown in Figure 5. At temperatures $T\ge$ 16,000 $\mathrm{K}$, the RDF displays only one dominant peak. Thus, on the example of dense Be, we can confirm that the Chapman–Enskog approach is highly effective in regimes where ion–ion coupling is relatively weak, resulting in an RDF with fewer than two main peaks. Furthermore, in Figure 9 we see that the Thomas–Fermi potential-based results overestimate the diffusion coefficient and become more accurate with increasing temperature. As expected, we see that the ion–ion correlations (nonideality) lead to a reduction in the diffusion coefficient.

Now, based on the QMD data, using the observation that the Yukawa model provides an adequate description of ion dynamics, we can define the general condition for the parameters at which the Chapman–Enskog method can be used. For that, we recall that the RDF of the Yukawa system can be uniquely defined by an effective coupling parameter in the entire liquid regime. We use the expression for the effective coupling parameter proposed in Ref. [55]:

$${\mathsf{\Gamma }}_{\mathrm{eff}}(\kappa ,\mathsf{\Gamma })=f\left(\kappa \right)\mathsf{\Gamma },$$

(13)

where

$$f\left(\kappa \right)=1-0.309{\kappa }^2+0.0800{\kappa }^3.$$

(14)

By utilizing the effective coupling parameter and observing the RDF features at temperatures where the results from the Chapman–Enskog method aligns with the data from the QMD simulations for ion diffusion in dense beryllium (Be), we conclude that the Chapman–Enskog method can accurately describe the system when ${\mathsf{\Gamma }}_{\mathrm{eff}}<50$. We expect that this conclusion will generally hold true for dense disordered metallic systems at high temperatures.

4. Conclusions

Using the QMD simulation results for dense beryllium (Be), we conducted a comparative analysis to evaluate the accuracy and applicability of the Yukawa one-component plasma model in describing the ion structure and transport properties. Our analysis considered the radial distribution function, the velocity autocorrelation function, mean-squared displacement, and the diffusion coefficient of ions. Additionally, we examined the applicability of the Chapman–Enskog method for calculating the diffusion coefficient at temperatures up to 32 000 K. The results clearly indicate that the Yukawa model-based molecular dynamics simulations can accurately capture the dynamics of ions, as demonstrated by the VACF and MSD, provided that the Yukawa potential parameters are appropriately selected. Our comparative analysis of the QMD, Yukawa–MD, and Chapman–Enskog methods allowed us to quantify the values of the effective coupling parameter at which the pair-collision model used in the Chapman–Enskog method remains accurate. These conclusions are also expected to apply to other transport properties due to the same underlying mechanism of particle dynamics. Generally, it is not guaranteed that an effective potential model reproducing the correct RDF of ions will also provide adequate transport properties. Thus, validating and determining the applicability range of plasma models requires benchmarking them against results from QMD simulations of real materials.