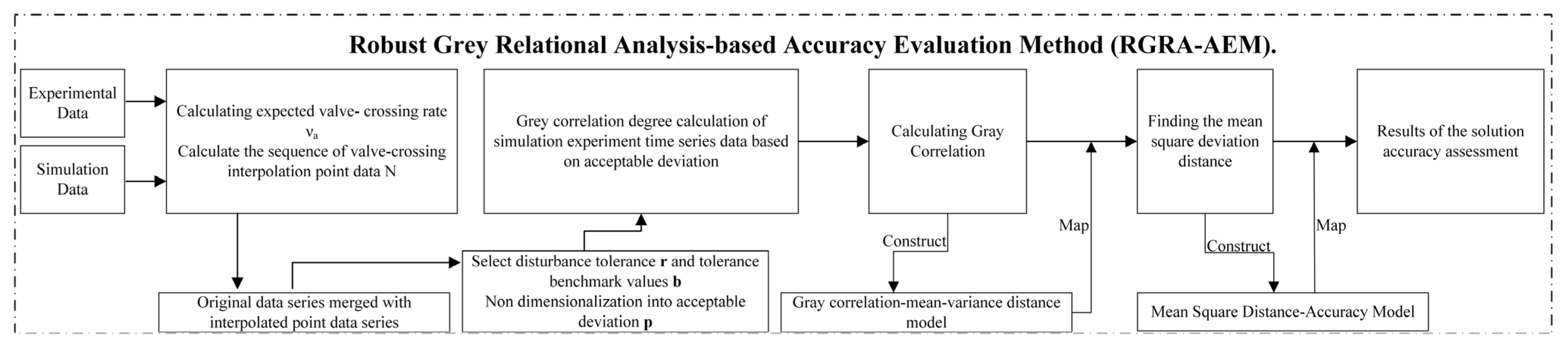
Robust Grey Relational Analysis-Based Accuracy Evaluation Method
Abstract
1. Introduction
2. Accuracy Assessment Based on GRA
2.1. Calculation of Grey Relational Degrees and Mean Square Deviation Distances
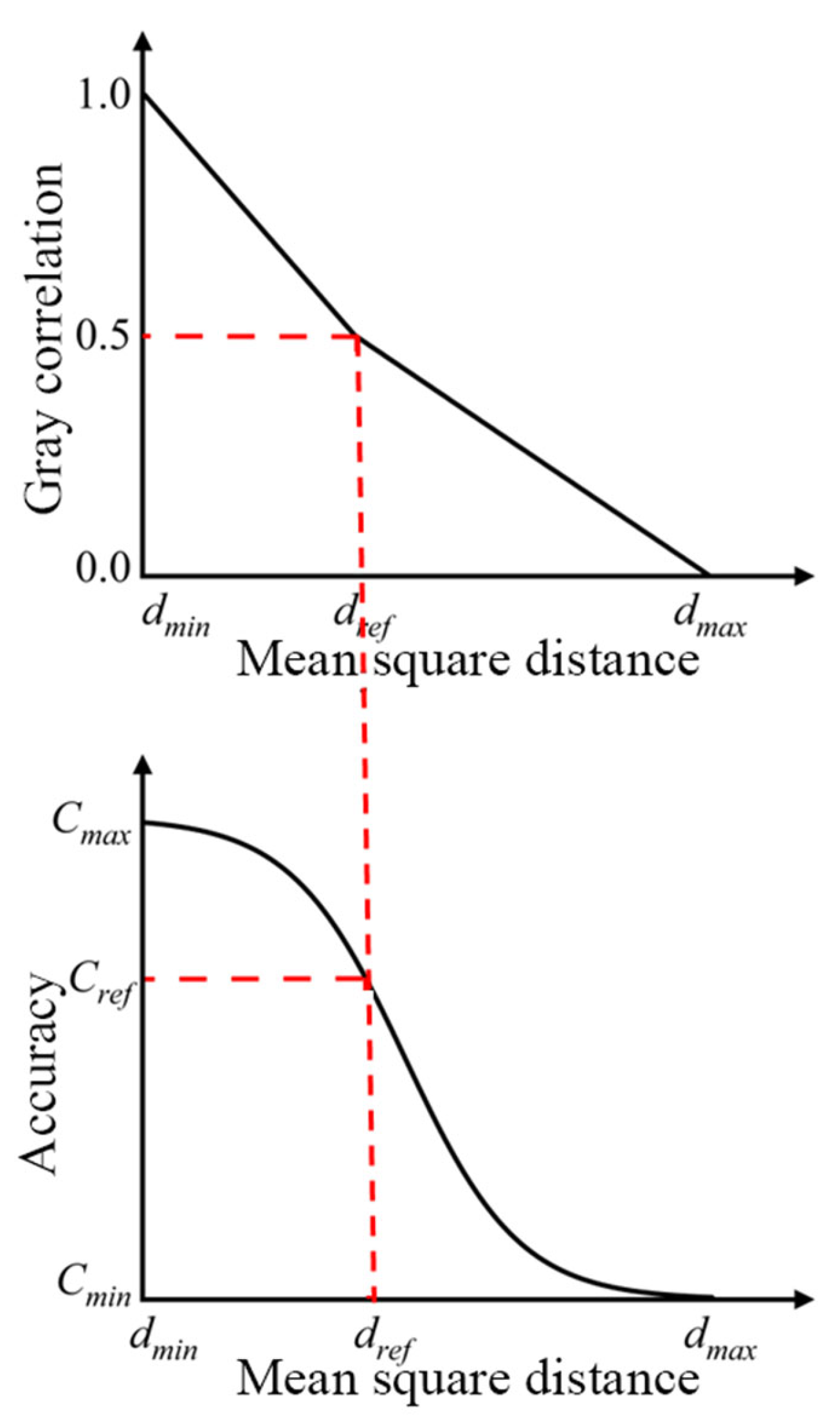
2.2. Grey Relational Degree-Mean Square Deviation Distance Model
2.3. The Mean Square Deviation Distance–Accuracy Model
3. Robust Grey Relational Analysis-Based Accuracy Evaluation Method
- (1)
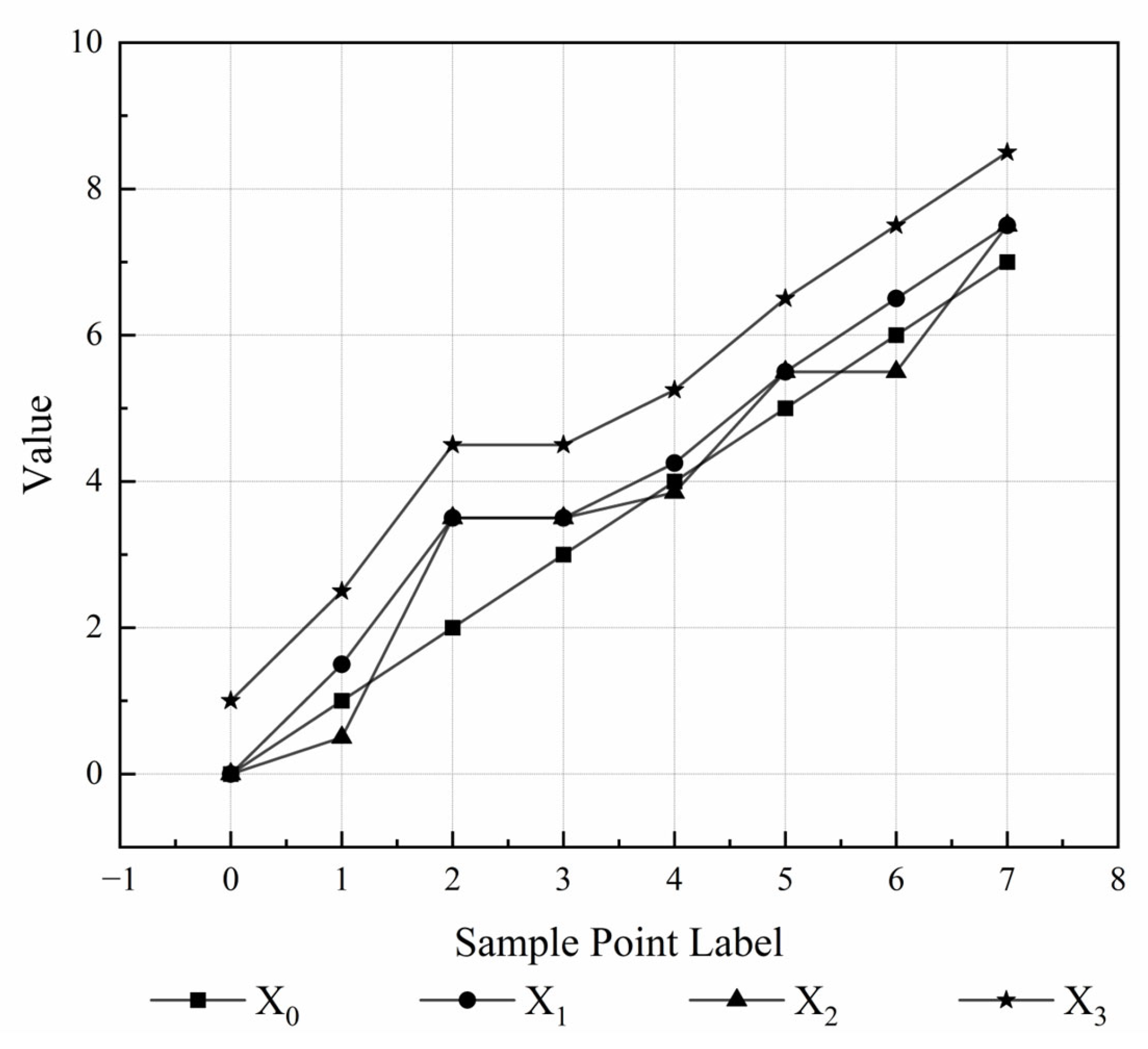
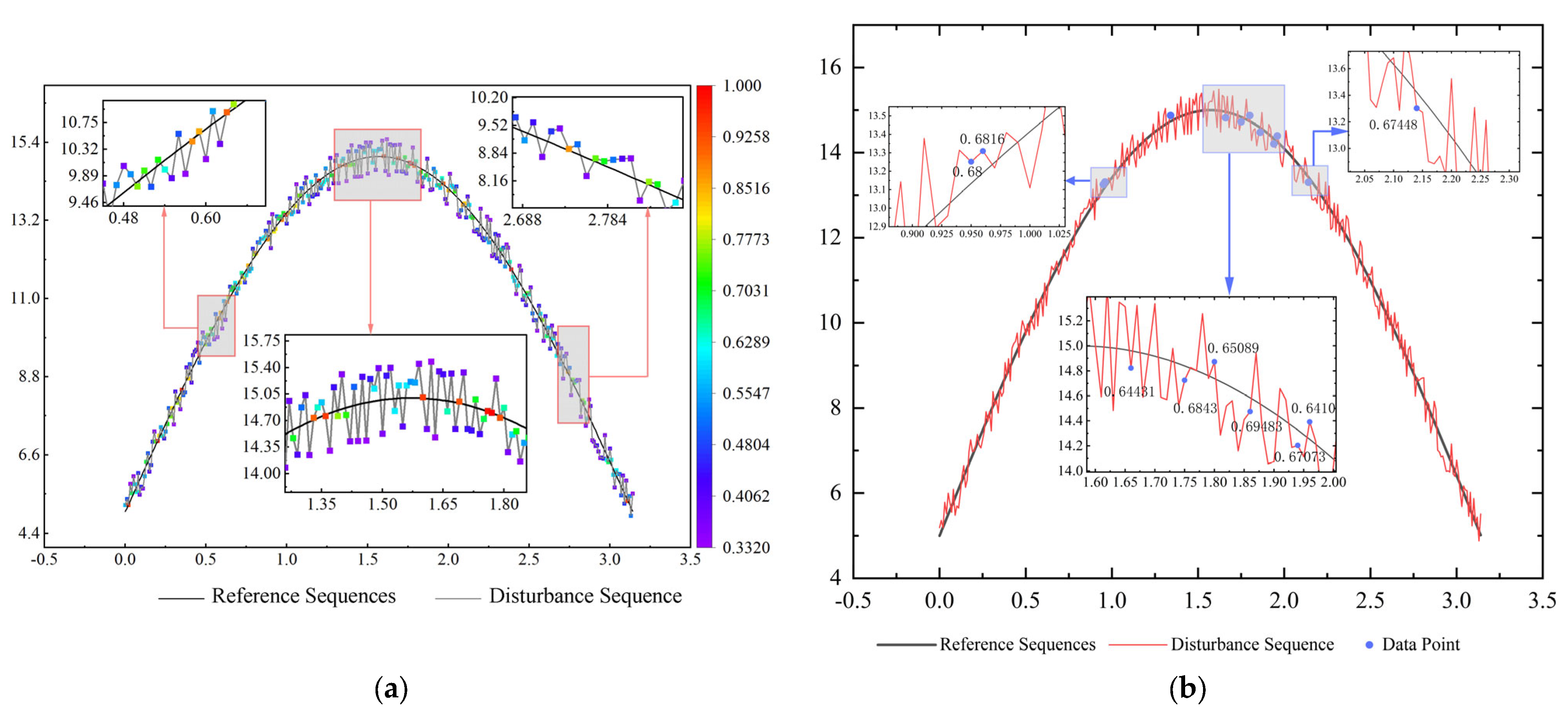
- Intuitively, when comparing the consistency of sequences and with sequence , it can be observed that sequence should exhibit better consistency with than with . This leads to . However, in the case where the differences between the data points of sequences and and the reference sequence are equal or opposite values, the traditional grey relational analysis (GRA) yields , which contradicts the actual observation.
- (2)
- For sequences and that exhibit a parallel trend, where the displacement difference at each sampling point is a constant, the minimum differences and maximum differences between the two sequences are equal. In this scenario, the traditional grey relational analysis (GRA) method yields , which fails to account for the relative distances between the sequences, leading to a result that does not align with the actual observations.
- (3)
- There are cases where the data points of the sequences are relatively close to each other; however, due to the significant difference in the range (the difference between the maximum and minimum values) of the sequences, the grey relational coefficient is low, which, in turn, results in a low overall grey relational degree.
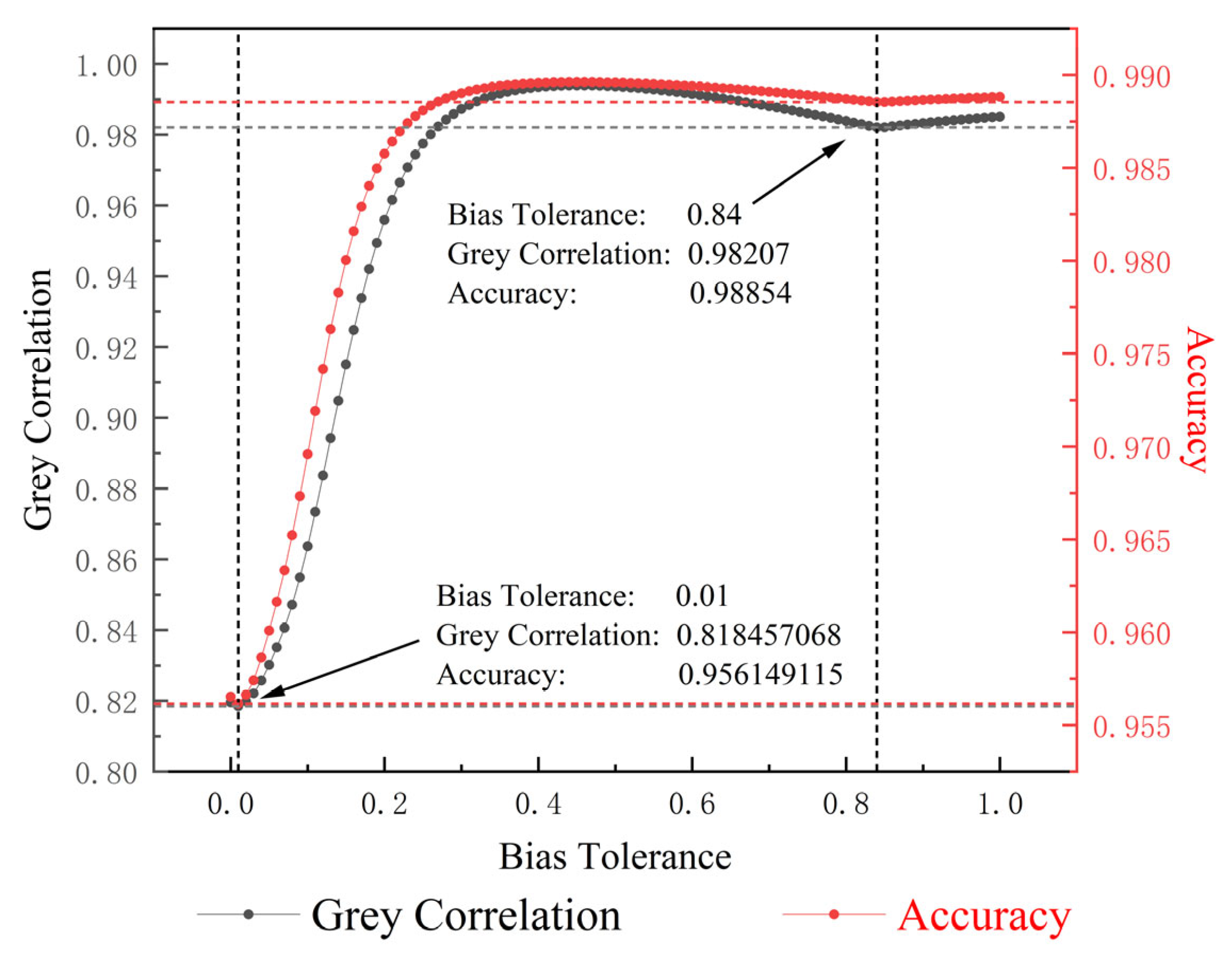
3.1. Expected Valve Crossing Rate
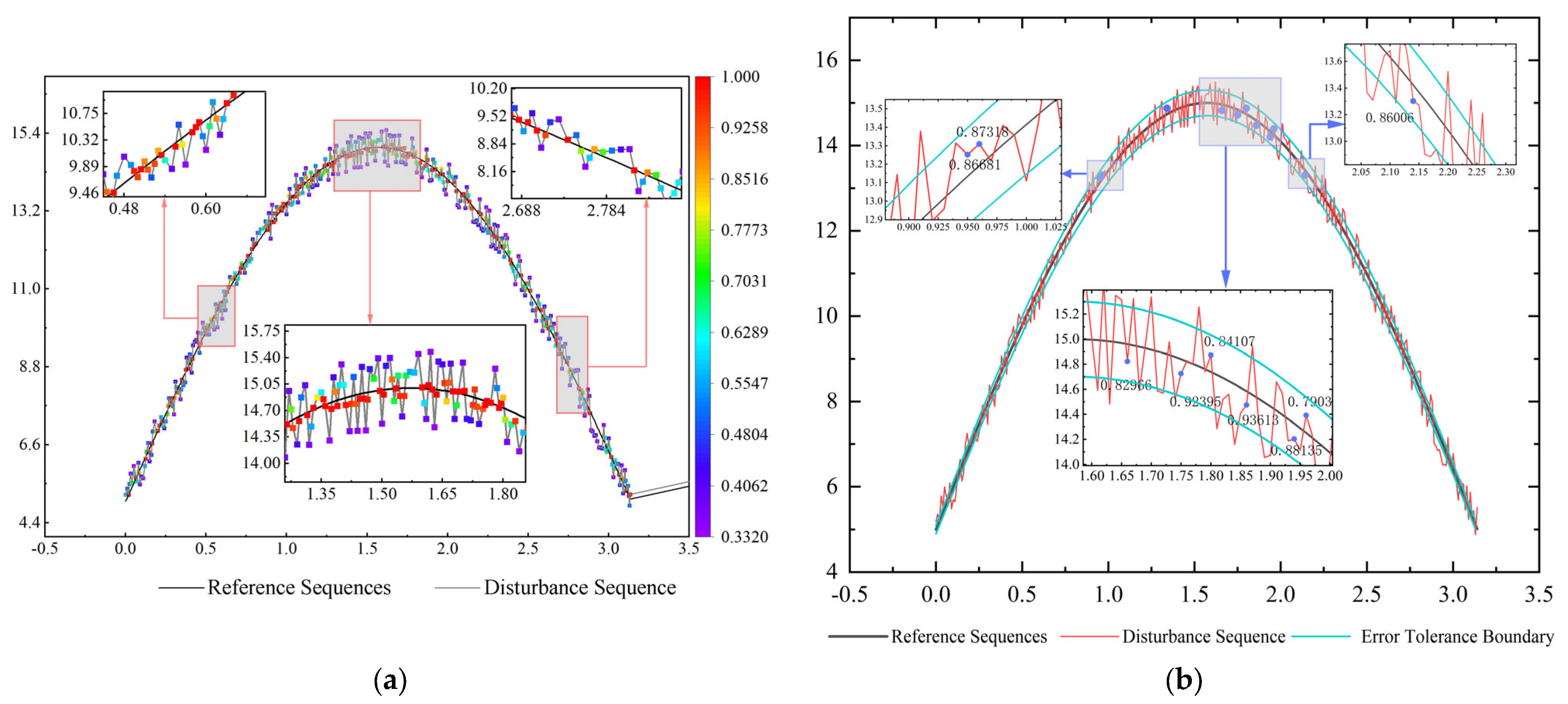
3.2. Bias Tolerance
3.3. Accuracy Assessment Process Based on Strong Robust Grey Correlation Analysis
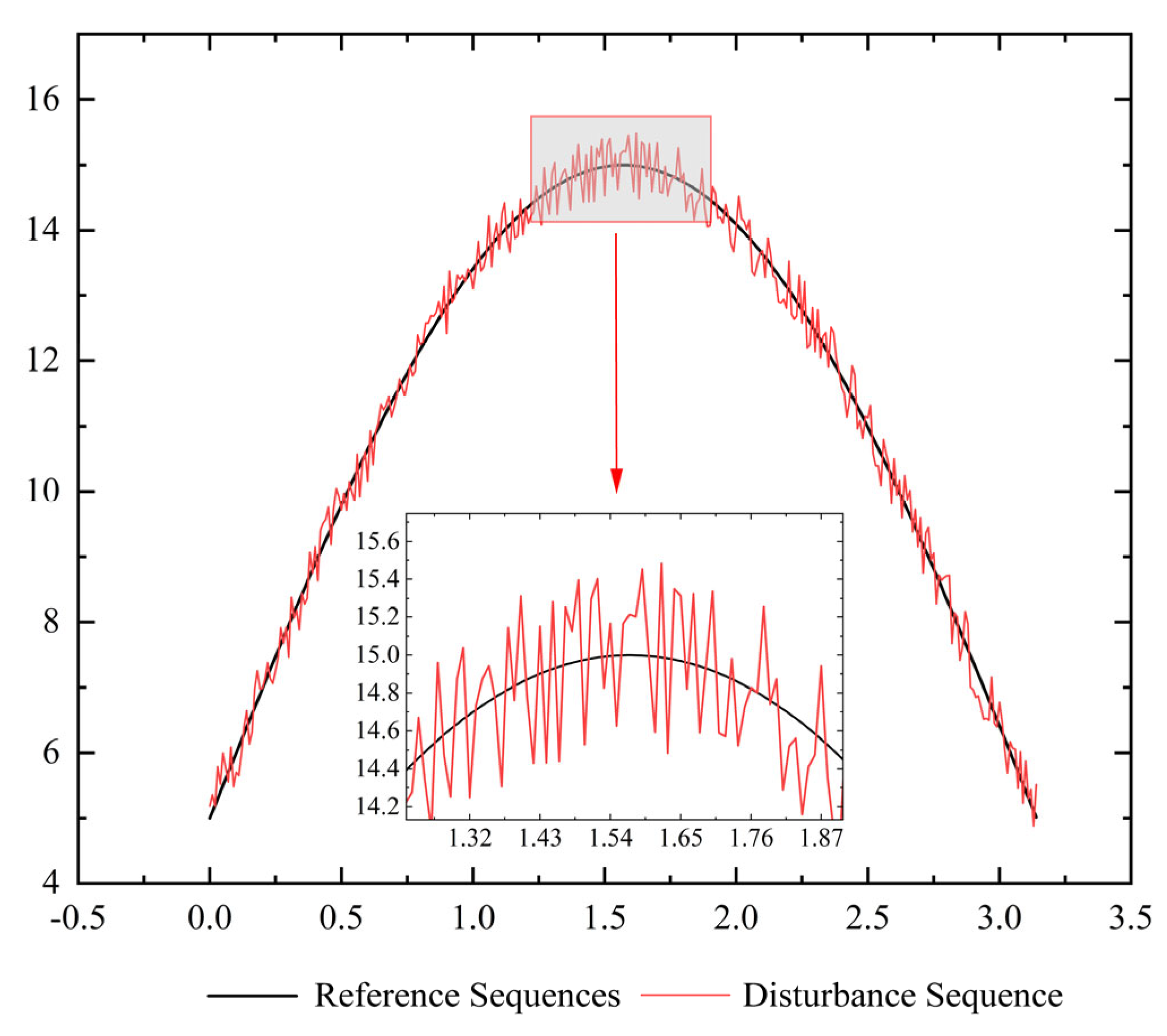
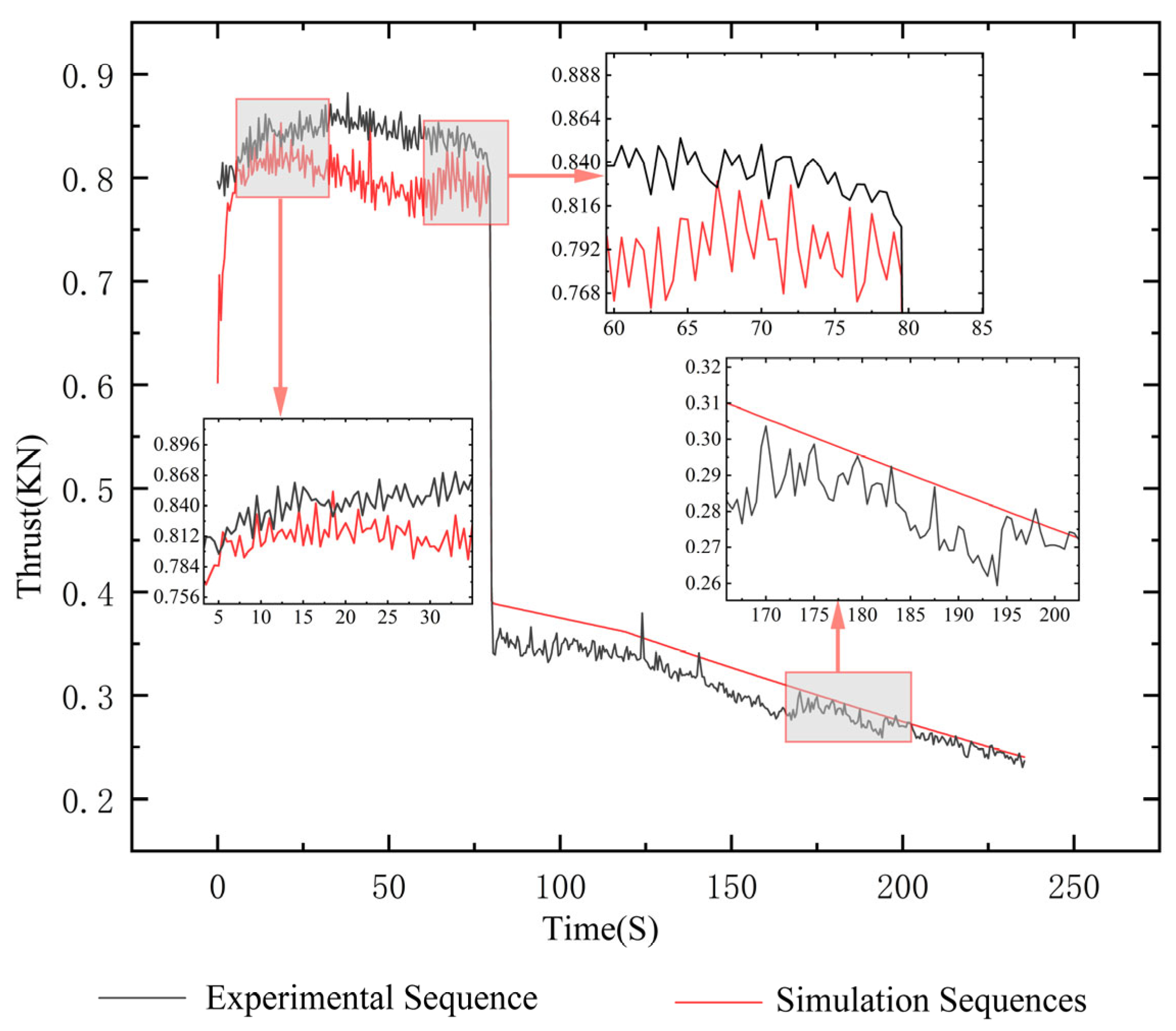
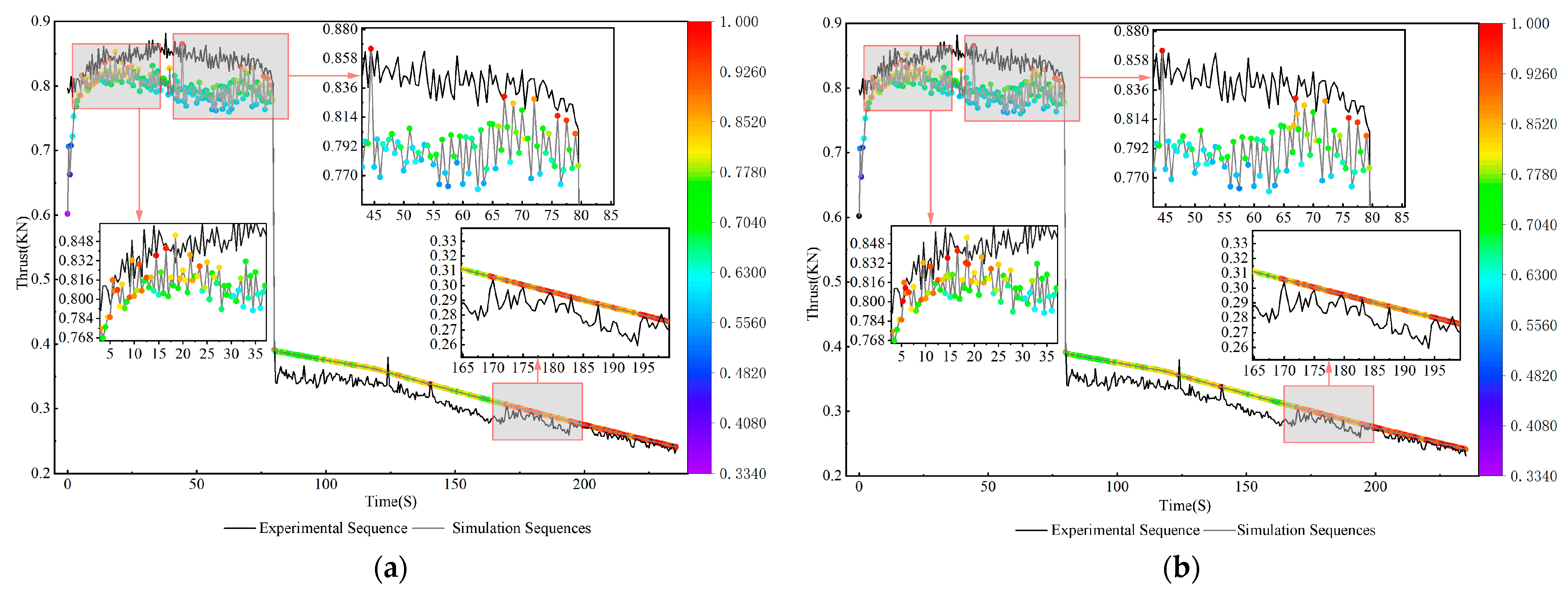
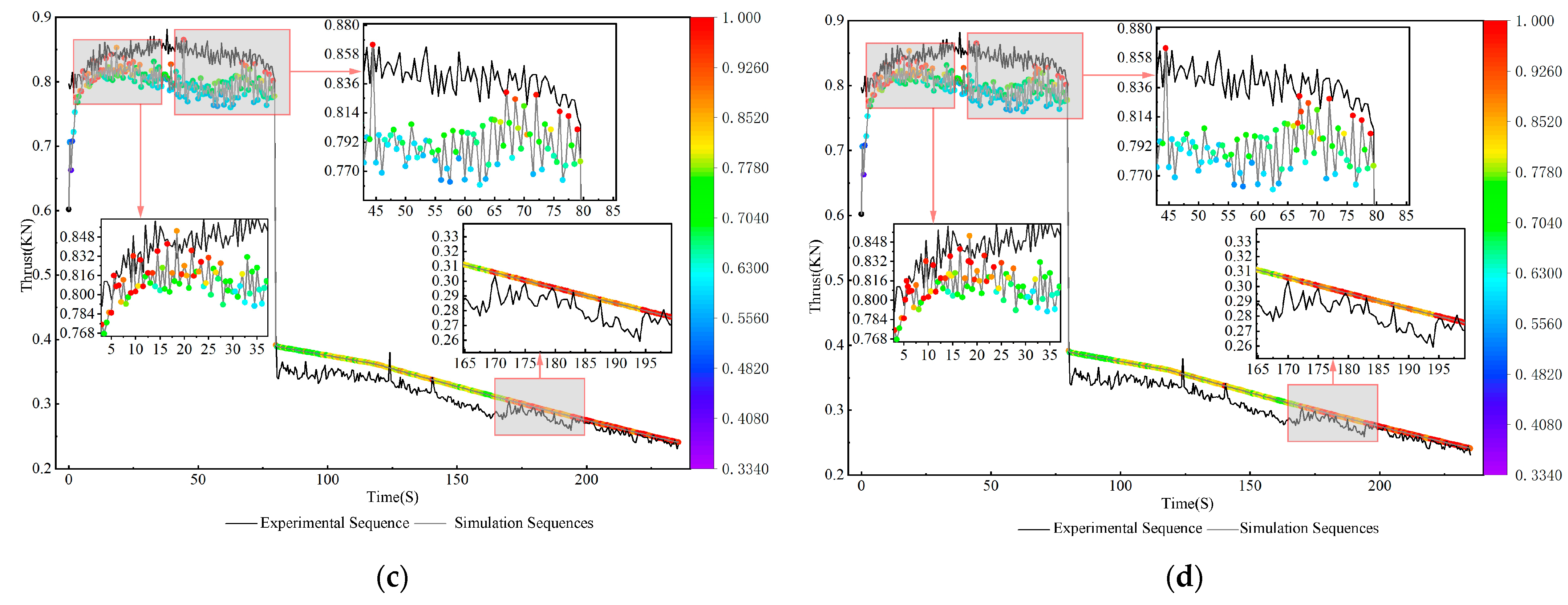
4. Instance Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, J.; Zhou, C. Sufficient condition for stability of grey systems and its application in the analysis of stability of linear time-varying systems. Inf. Control 1987, 4, 24–27. [Google Scholar]
- Deng, J. Introduction to gray system theory. Inn. Mong. Power 1993, 3, 51–52. (In Chinese) [Google Scholar]
- Tian, M.; Liu, S.; Bu, Z. A review of research on grey correlation algorithm modeling. Stat. Decis.-Mak. 2008, 1, 24–27. (In Chinese) [Google Scholar]
- Zhou, W.; Zeng, B. A research review of grey relational degree model. Stat. Decis. 2020, 36, 29–34. [Google Scholar]
- Wei, H.; Li, Z. Grey relational analysis and its application to the validation of computer simulation models for missile systems. Syst. Eng. Electron. 1997, 2, 55–61. [Google Scholar]
- Ning, X.; Wu, Y.; Chen, Z. Study on validation of simulation models based on improved grey relational analysis. Comput. Simul. 2015, 32, 259–263. [Google Scholar]
- Ning, X.; Wu, Y.; Yu, T.; Chen, W.; Shan, B.; Zhang, Y. Research on comprehensive validation of simulation models based on improved grey relational analysis. Acta Armamentarii 2016, 37, 338–347. [Google Scholar]
- Wu, J.; Wu, X.; Chen, Y.; Teng, J. Validation of simulation models based on improved grey relational analysis. Syst. Eng. Electron. 2010, 32, 1677–1679. [Google Scholar]
- Zhang, Y.; Shang, K. Evaluation of mine ecological environment based on fuzzy hierarchical analysis and grey relational degree. Environ. Res. 2024, 257, 119370. [Google Scholar] [CrossRef]
- Mei, Z. The concept and computation method of grey absolute correlation degree. Syst. Eng. 1992, 5, 43–44+72. [Google Scholar]
- Tang, W. Some shortcomings of grey absolute correlation degree. J. Syst. Eng. 1994, 5, 59–62. [Google Scholar]
- Tang, W. The concept and the computation method of t’s correlation degree. J. Appl. Stat. Manag. 1995, 1, 34–37+33. [Google Scholar]
- Shen, M.; Hu, B. The modified t’s correlative degree and its application in the securities business. Syst. Eng. Theory Pract. 2003, 5, 36–40. [Google Scholar]
- Prakash, J.U.; Sivaprakasam, P.; Juliyana, S.J.; Ananth, C.; Rubi, C.S.; Sadhana, A.D. Multi-objective optimization using grey relational analysis for wire EDM of aluminium matrix composites. Mater. Today Proc. 2023, 72, 2395–2401. [Google Scholar] [CrossRef]
- Ben Taher, M.A.; Pelay, U.; Russeil, S.; Bougeard, D. A novel design to optimize the optical performances of parabolic trough collector using Taguchi, ANOVA and grey relational analysis methods. Renew. Energy 2023, 216, 119105. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, H.; Fan, L.; Yi, J.; Junyan, Y. Dynamic modulus prediction model and analysis of factors influencing asphalt mixtures using gray relational analysis methods. J. Mater. Res. Technol. 2022, 19, 1312–1321. [Google Scholar] [CrossRef]
- Gao, S.; Zhi, Y.; Zhang, P.; Zuo, X. Consistency validation method of simulation results based on improved grey relational analysis for aerospace product performance prototype. Syst. Eng. Electron. 2023, 45, 2777–2783. [Google Scholar]
- Liu, Z.; Xie, Y.; Dang, Y. Characteristic test method of matrix grey incidence degree and its application. Oper. Res. Manag. Sci. 2020, 29, 131–138. [Google Scholar]
- Hu, A.; Xie, N. Construction and application of a novel grey relational analysis model considering factor coupling relationship. Grey Syst. Theory Appl. 2025, 15, 1–20. [Google Scholar] [CrossRef]
- Wang, R.; Xu, Y.; Yang, Q. A new adaptive grey seasonal model for time series forecasting tasks. Grey Syst. Theory Appl. 2024, 14, 360–373. [Google Scholar] [CrossRef]
- Li, X. Research on the computation model of grey interconnet degree. Syst. Eng. 1995, 6, 58–61. [Google Scholar]
- Liu, S.; Cai, H.; Ying, Y.; Yang, Y. Advance in grey incidence analysis modeling. Syst. Eng.-Theory Pract. 2013, 33, 2041–2046. [Google Scholar]
- Nowak, M.; Pawłowska-Nowak, M.; Kokocińska, M.; Kułyk, P. The evaluation of grey relative incidence. Grey Syst. Theory Appl. 2024, 14, 263–282. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, X.; He, Q.; Li, T. A novel unbiased multi-variable grey model. Grey Syst. Theory Appl. 2025, 15, 209–238. [Google Scholar] [CrossRef]
- Lu, F. Research on the identification coefficient of relational grade for grey system. Syst. Eng.-Theory Pract. 1997, 6, 50–55. [Google Scholar]
- Sun, Y. Research on Grey Incidence Analysis and Its Application; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2009. [Google Scholar]
- Li, Y. Research on Simulation Model Validation Methods and Assistant Tool Based on Grey Relational Analysis; Harbin Institute of Technology: Harbin, China, 2015. [Google Scholar]
- Zhou, Y. Research on Validation Method for Complex Simulation Model; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Middleton, D. An Introduction to Statistical Communication Theory; McGrawHill: New York, NY, USA, 1960. [Google Scholar]
- Gramacy, R.B.; Lee, H.K. Cases for the nugget in modeling computer experiments. Stat. Comput. 2012, 22, 713–722. [Google Scholar] [CrossRef]
- Tan, G.; Tian, H.; Wang, Z.; Guo, Z.; Gao, J.; Zhang, Y.; Cai, G. Experimental investigation into closed-loop control for htpb-based hybrid rocket motors. Aerospace 2023, 10, 421. [Google Scholar] [CrossRef]
- Tian, H.; Meng, X.; Zhu, H.; Li, C.; He, L.; Cai, G. Dynamic numerical simulation of hybrid rocket motor with htpb-based fuel with 58% aluminum additives. Aerospace 2022, 9, 727. [Google Scholar] [CrossRef]
- Meng, X.; Tian, H.; Niu, X.; Zhu, H.; Gao, J.; Cai, G. Long-duration dynamic numerical simulation of combustion and flow in hybrid rocket motors considering nozzle erosion. Aerospace 2024, 11, 318. [Google Scholar] [CrossRef]
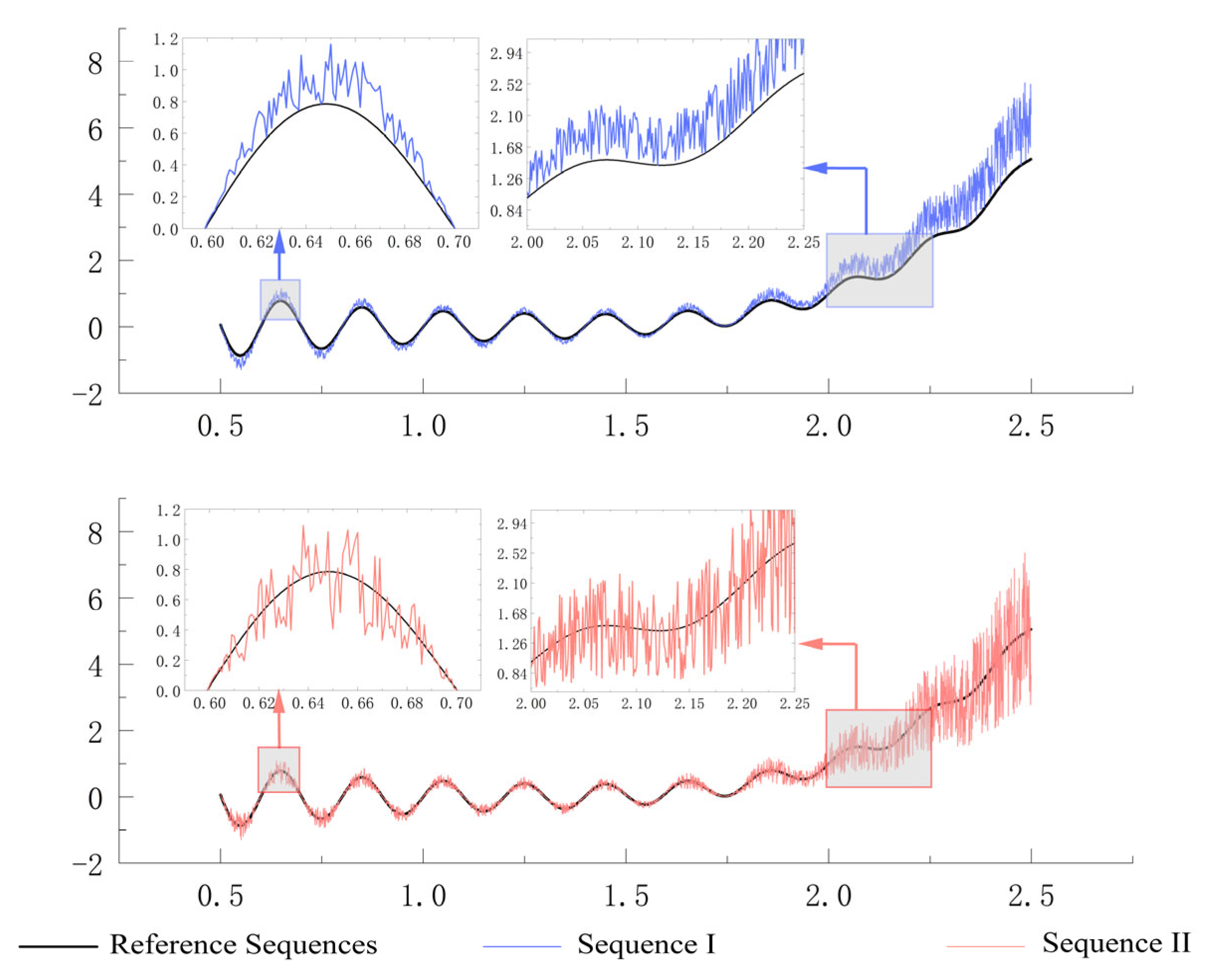


| Statistical Indicators | Traditional Method | RGRA-AEM | ||
|---|---|---|---|---|
| Sequence I | Sequence II | Sequence I | Sequence II | |
| Grey Correlation/(%) | 87.3134 | 87.3134 | 87.1090 | 89.7850 |
| Accuracy/(%) | 97.1851 | 97.1851 | 97.1377 | 97.7010 |
| Statistical Indicators | Traditional Method | RGRA-AEM | ||
|---|---|---|---|---|
| No Additional Interpolation Points Through the Valve | No Additional Interpolation Points Through the Valve | Increase Penetration Valve Interpolation Points | ||
| No Increase in Bias Tolerance | Increase in Bias Tolerance by 2% | No Increase in Bias Tolerance | Increase in Bias Tolerance by 2% | |
| Grey Correlation/(%) | 54.315 | 58.0955 | 62.048 | 68.439 |
| Accuracy/(%) | 68.312 | 74.760 | 80.504 | 87.602 |
| Statistical Indicators | Traditional Method | → | RGRA-AEM | |
|---|---|---|---|---|
| No Additional Interpolation Points Through the Valve | Only Increase Penetration Valve Interpolation Points | Only Increase in Bias Tolerance by 5% | Increase Penetration Valve Interpolation Points | |
| No Increase in Bias Tolerance | Increase in Bias Tolerance by 5% | |||
| Total number of positions | 472 | 589 | 472 | 598 |
| Number of data points corrected | 0 | 126 | 200 | 326 |
| Grey Correlation/(%) | 80.4016 | 81.8313 | 81.3763 | 83.0590 |
| Accuracy/(%) | 95.0768 | 95.6098 | 95.4465 | 96.0231 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, K.; Fang, J.; Li, J.; Shi, H.; Xu, Y.; Li, R.; Xie, R.; Cai, G. Robust Grey Relational Analysis-Based Accuracy Evaluation Method. Appl. Sci. 2025, 15, 4926. https://doi.org/10.3390/app15094926
Zheng K, Fang J, Li J, Shi H, Xu Y, Li R, Xie R, Cai G. Robust Grey Relational Analysis-Based Accuracy Evaluation Method. Applied Sciences. 2025; 15(9):4926. https://doi.org/10.3390/app15094926
Chicago/Turabian StyleZheng, Kang, Jie Fang, Jieqi Li, Haoran Shi, Yufan Xu, Rui Li, Ruihang Xie, and Guobiao Cai. 2025. "Robust Grey Relational Analysis-Based Accuracy Evaluation Method" Applied Sciences 15, no. 9: 4926. https://doi.org/10.3390/app15094926
APA StyleZheng, K., Fang, J., Li, J., Shi, H., Xu, Y., Li, R., Xie, R., & Cai, G. (2025). Robust Grey Relational Analysis-Based Accuracy Evaluation Method. Applied Sciences, 15(9), 4926. https://doi.org/10.3390/app15094926






