Study on the Impact of Ventilation Methods on Droplet Nuclei Transmission in Subway Carriages
Abstract
1. Introduction
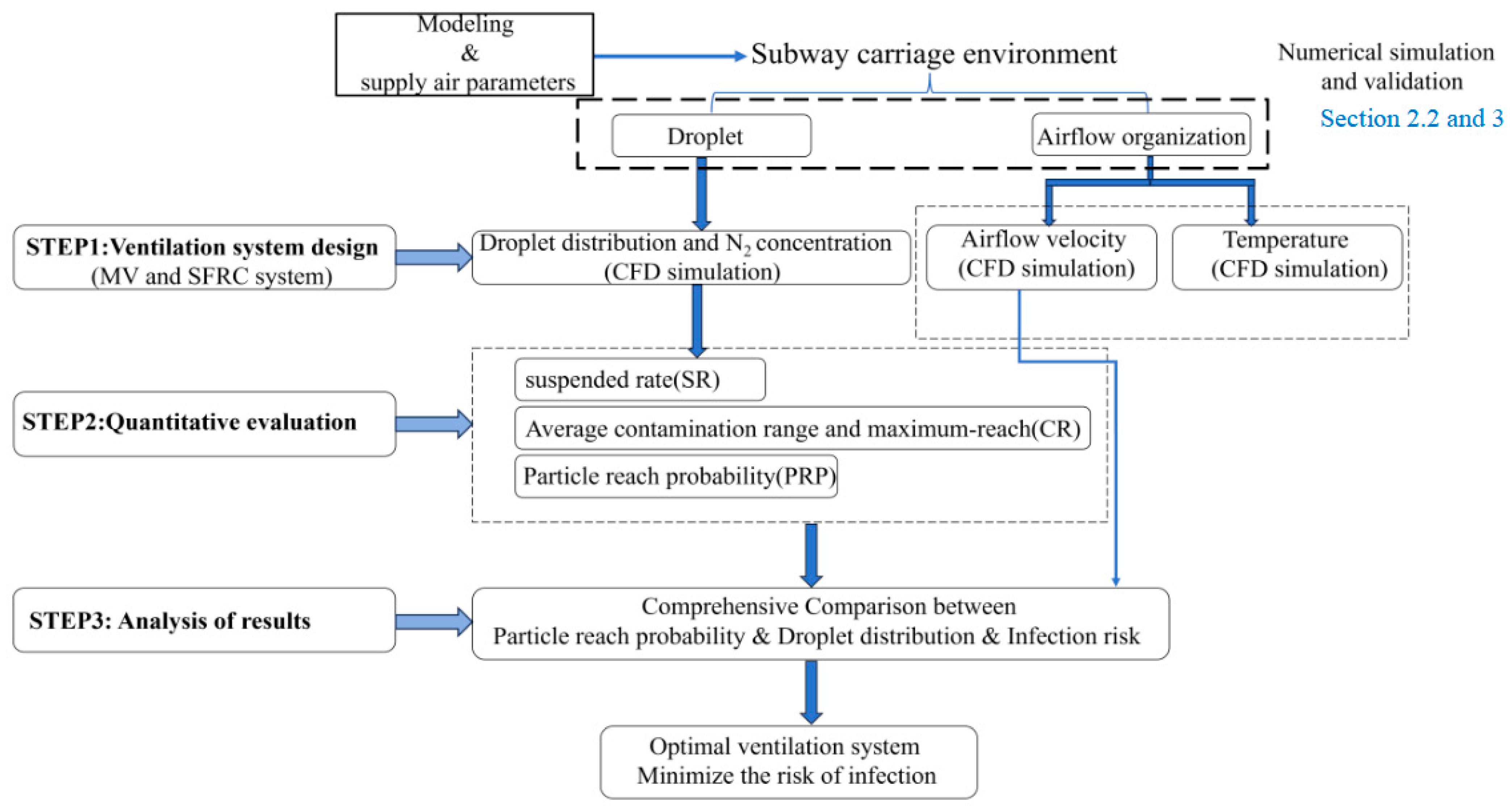
2. Materials and Methods
2.1. Numerical Models
2.2. Model Description and Mesh
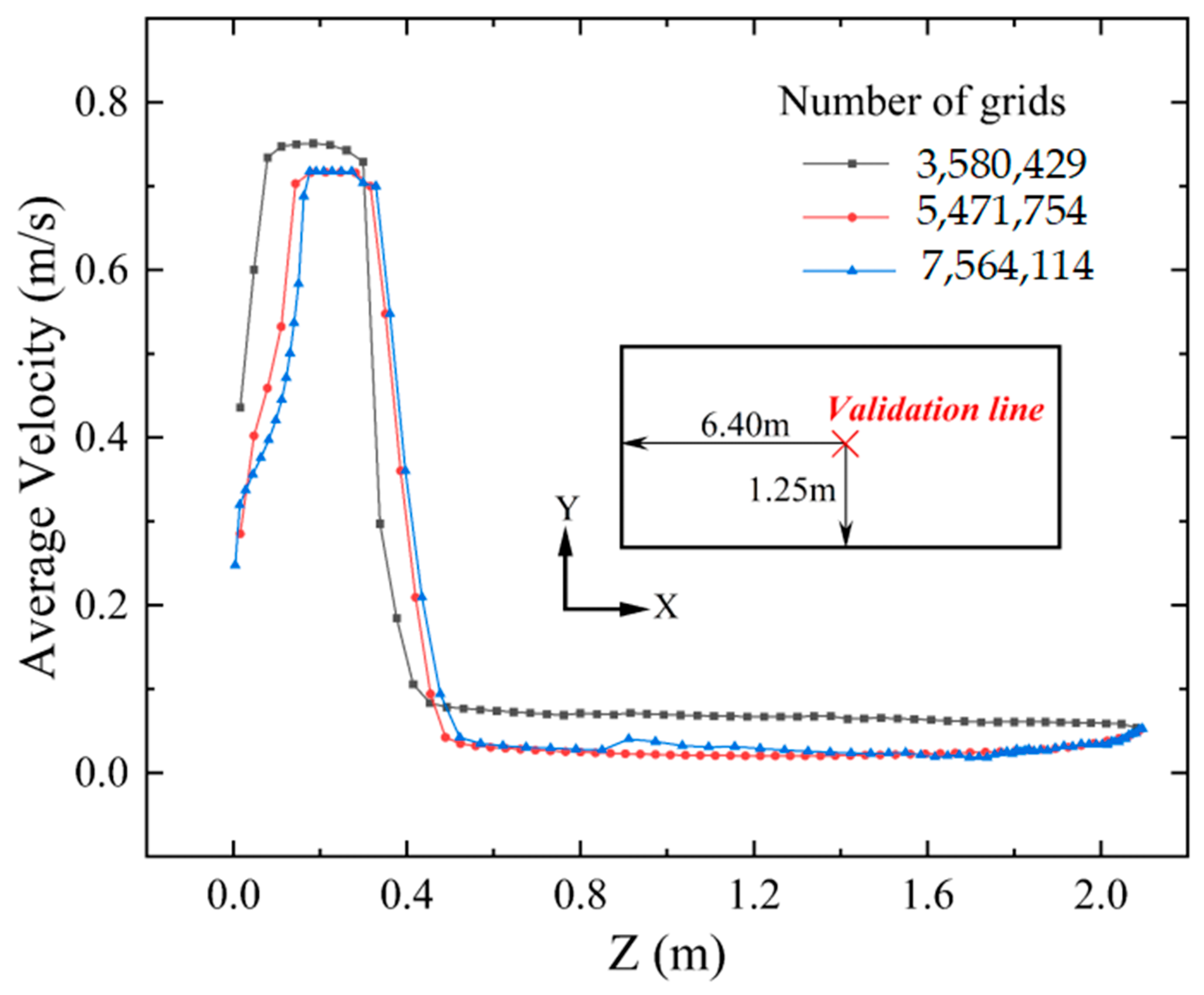
2.3. Grid Independence Test
2.4. Boundary Conditions
2.5. Evaluation Criteria
3. Results
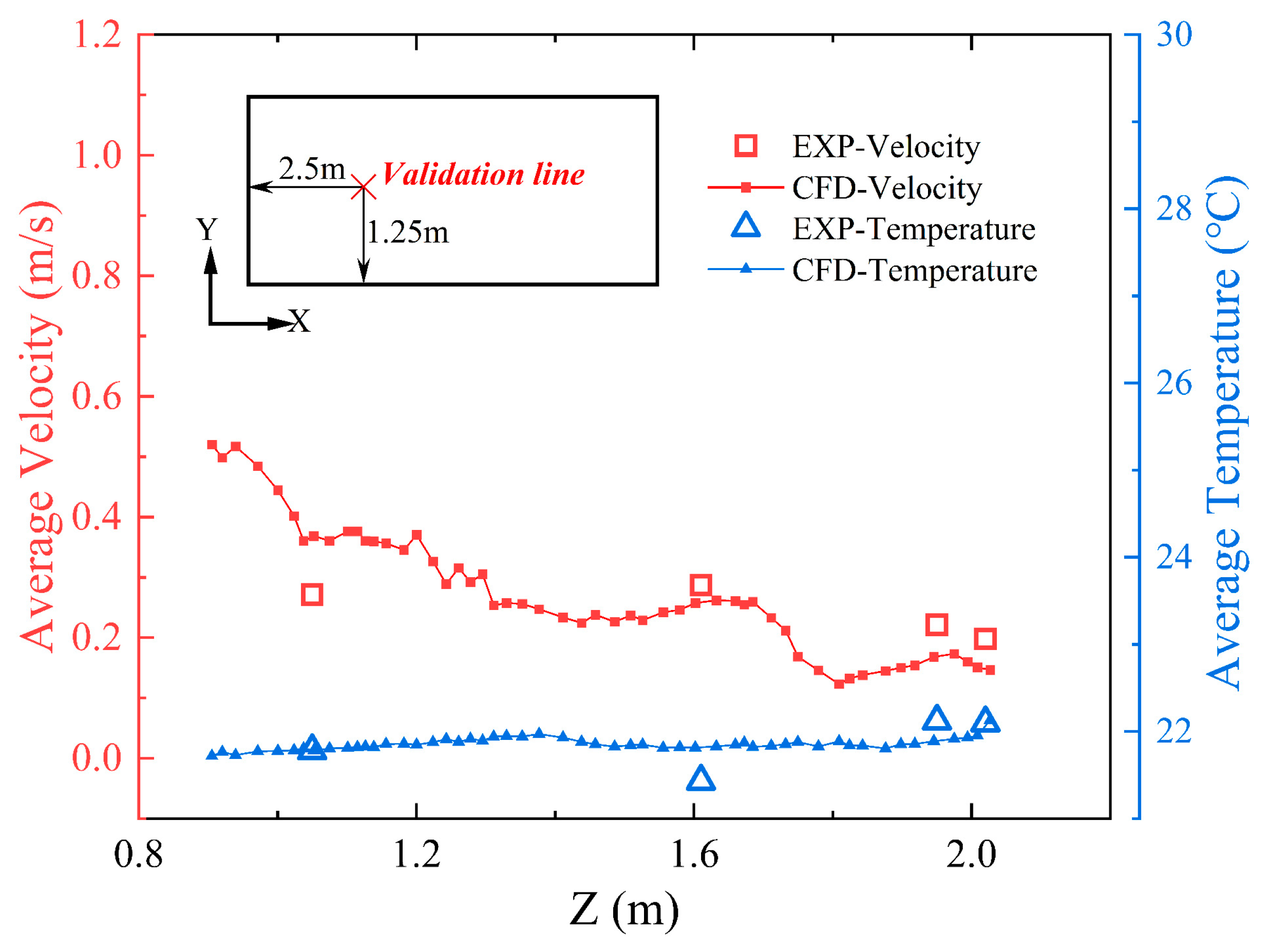
3.1. Model Validation
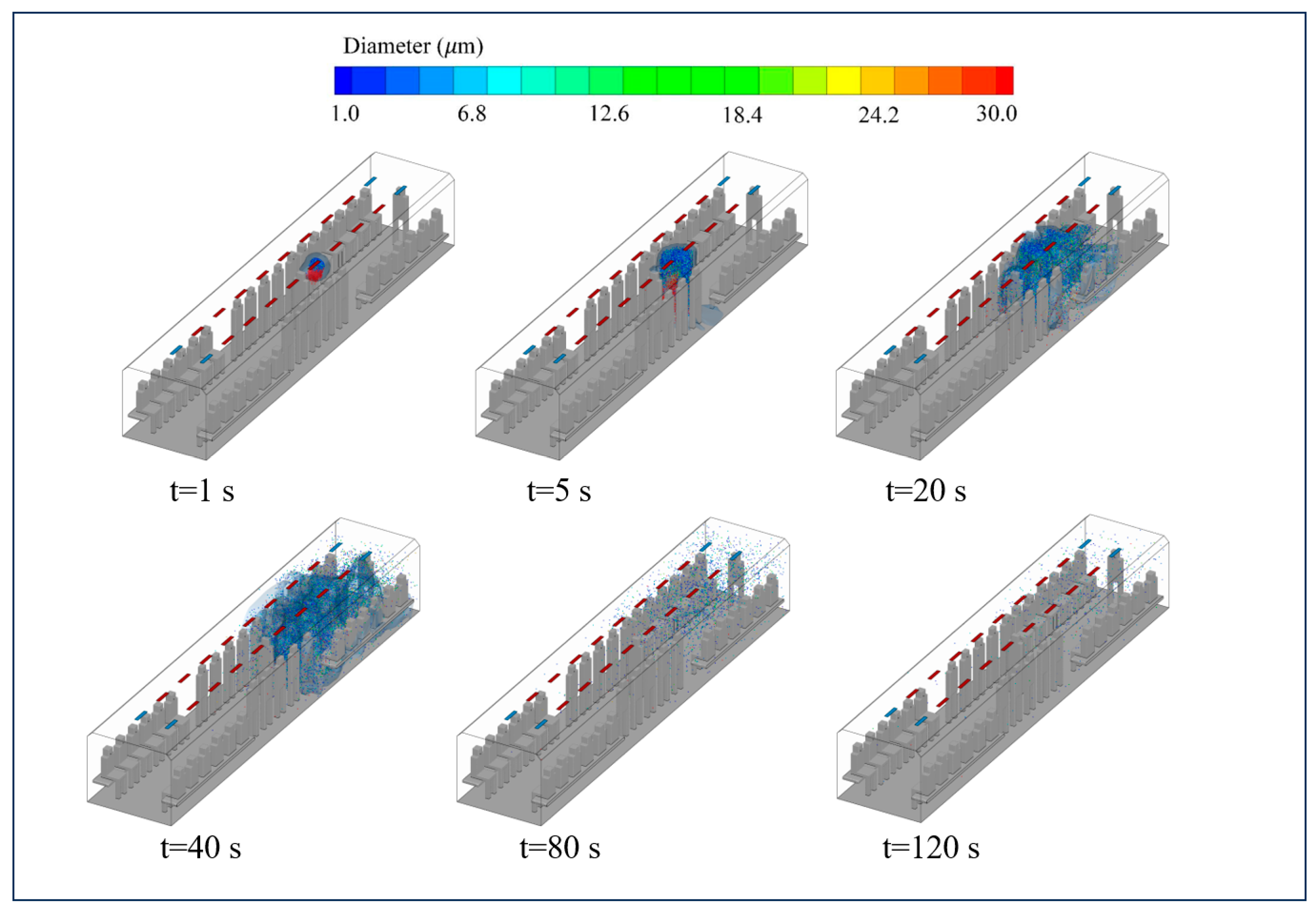
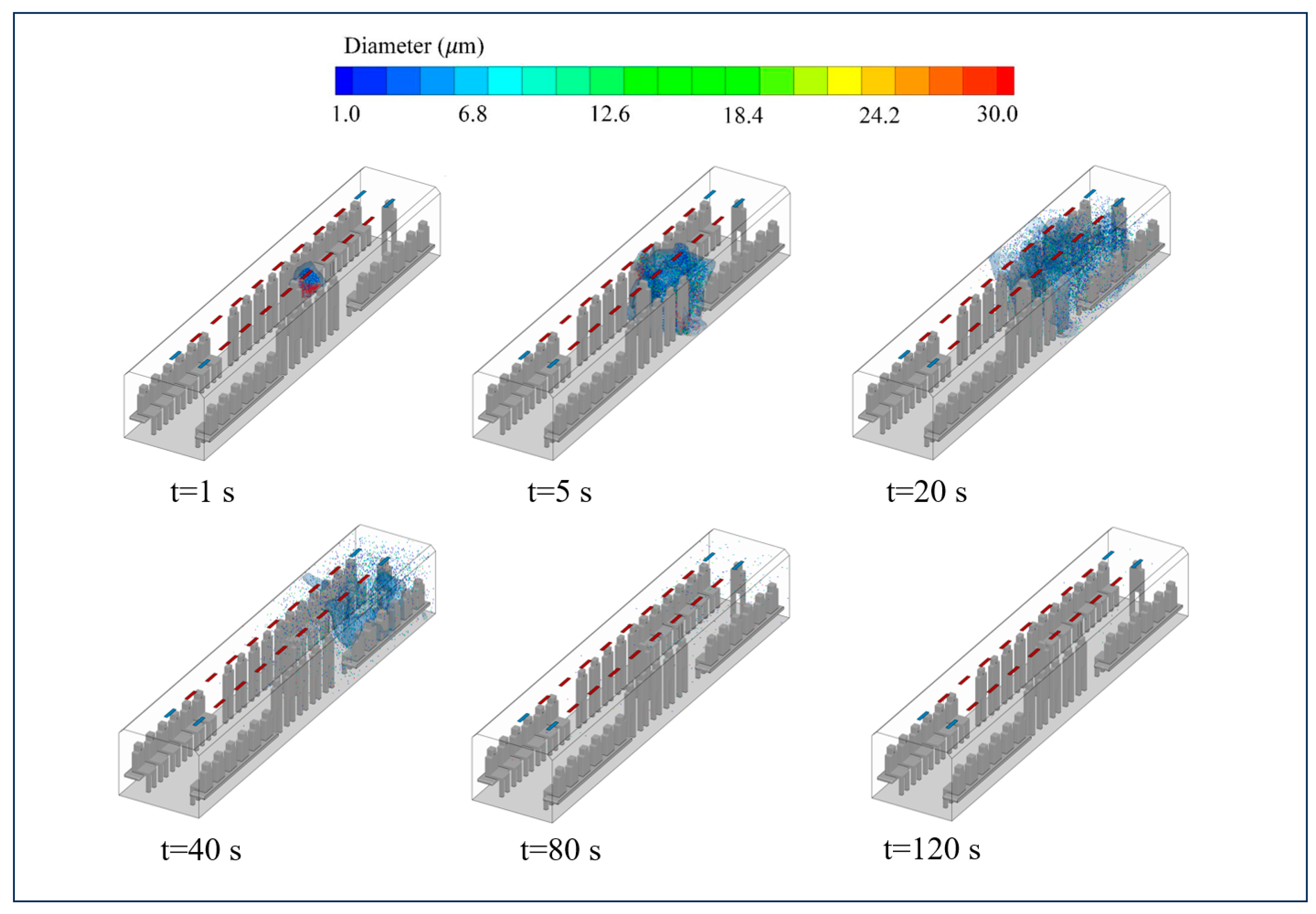
3.2. Spatiotemporal Distribution of Cough Droplets Under the MV System
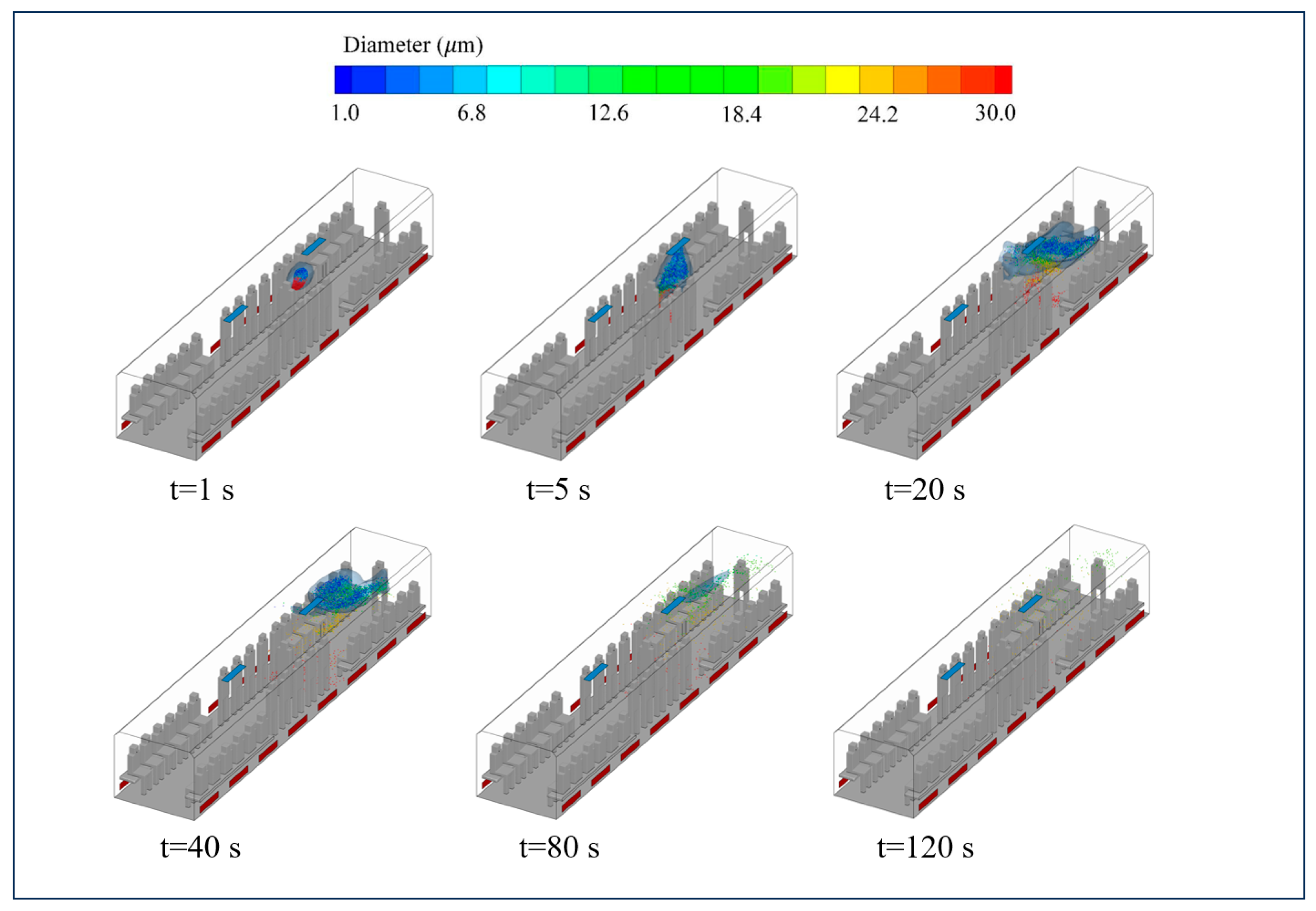
3.3. Spatiotemporal Distribution of Cough Droplets Under the SFRC System
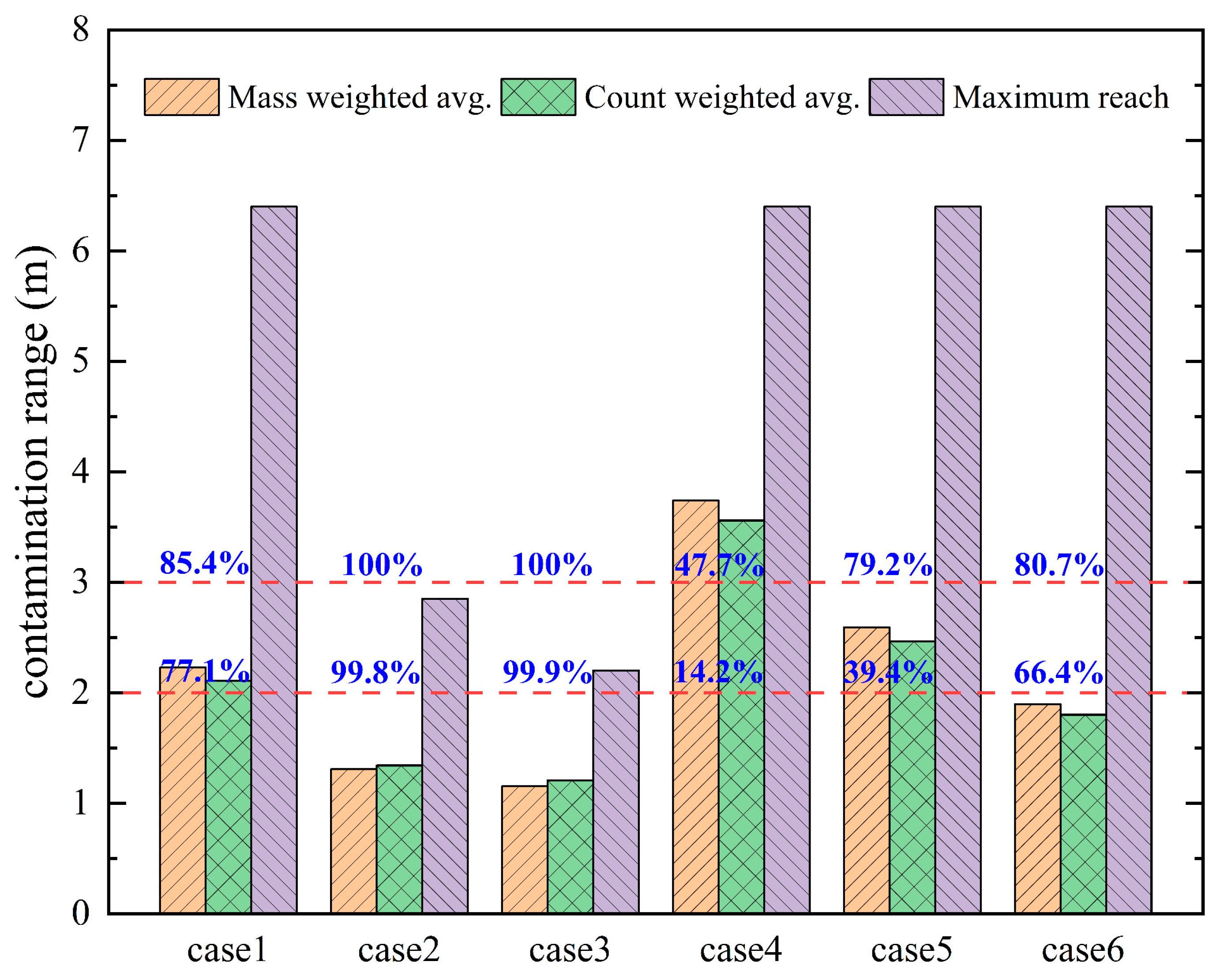
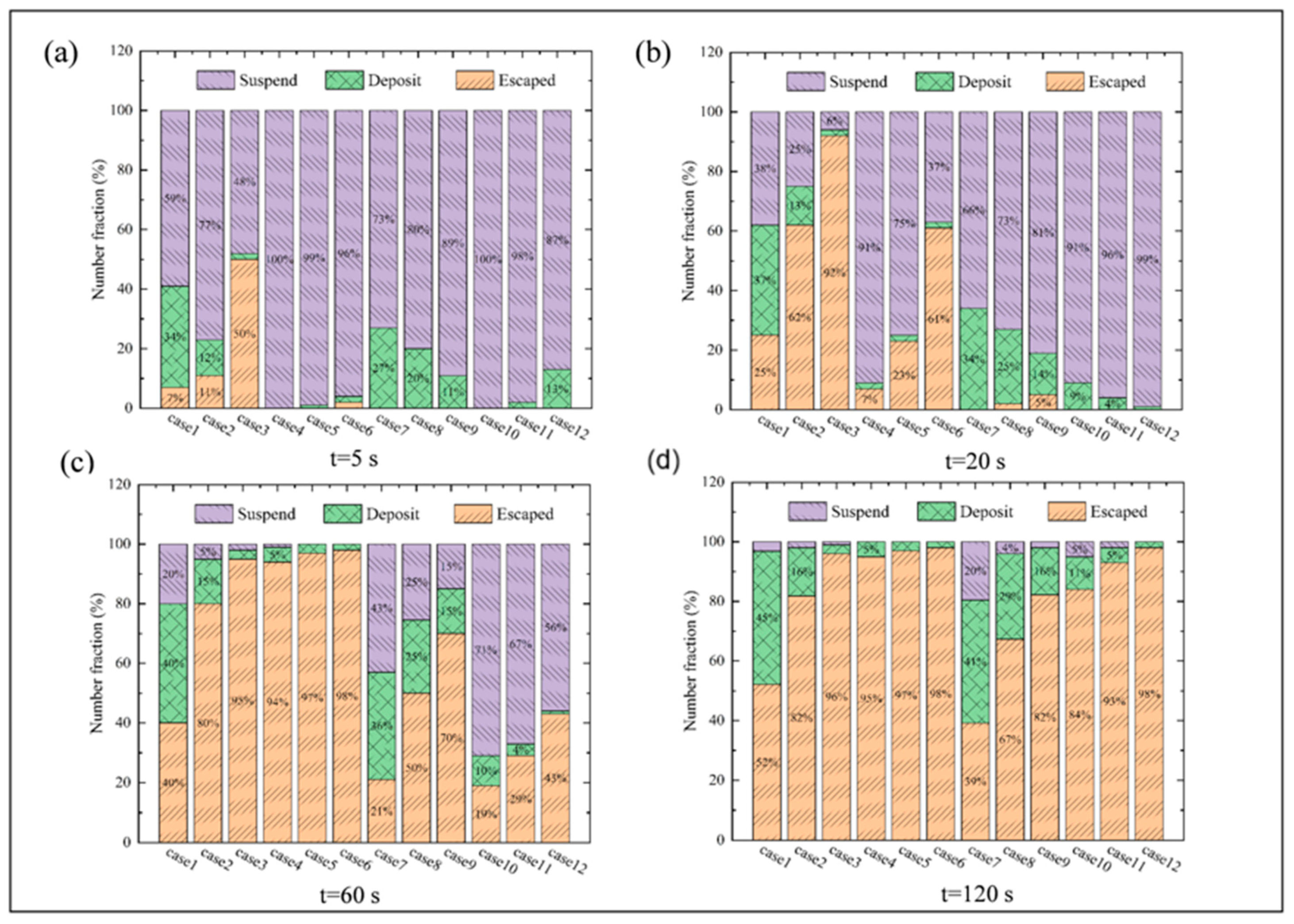
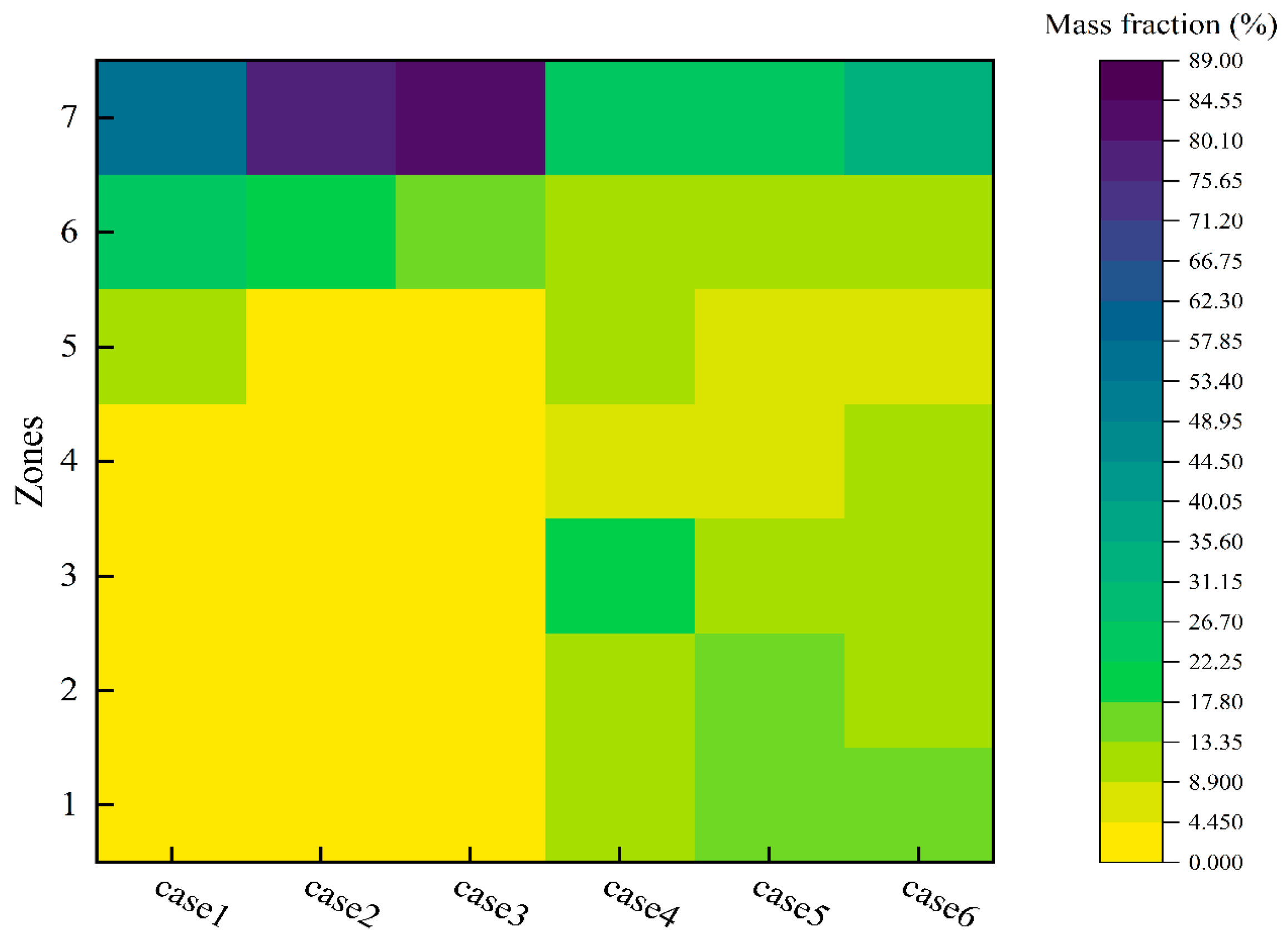
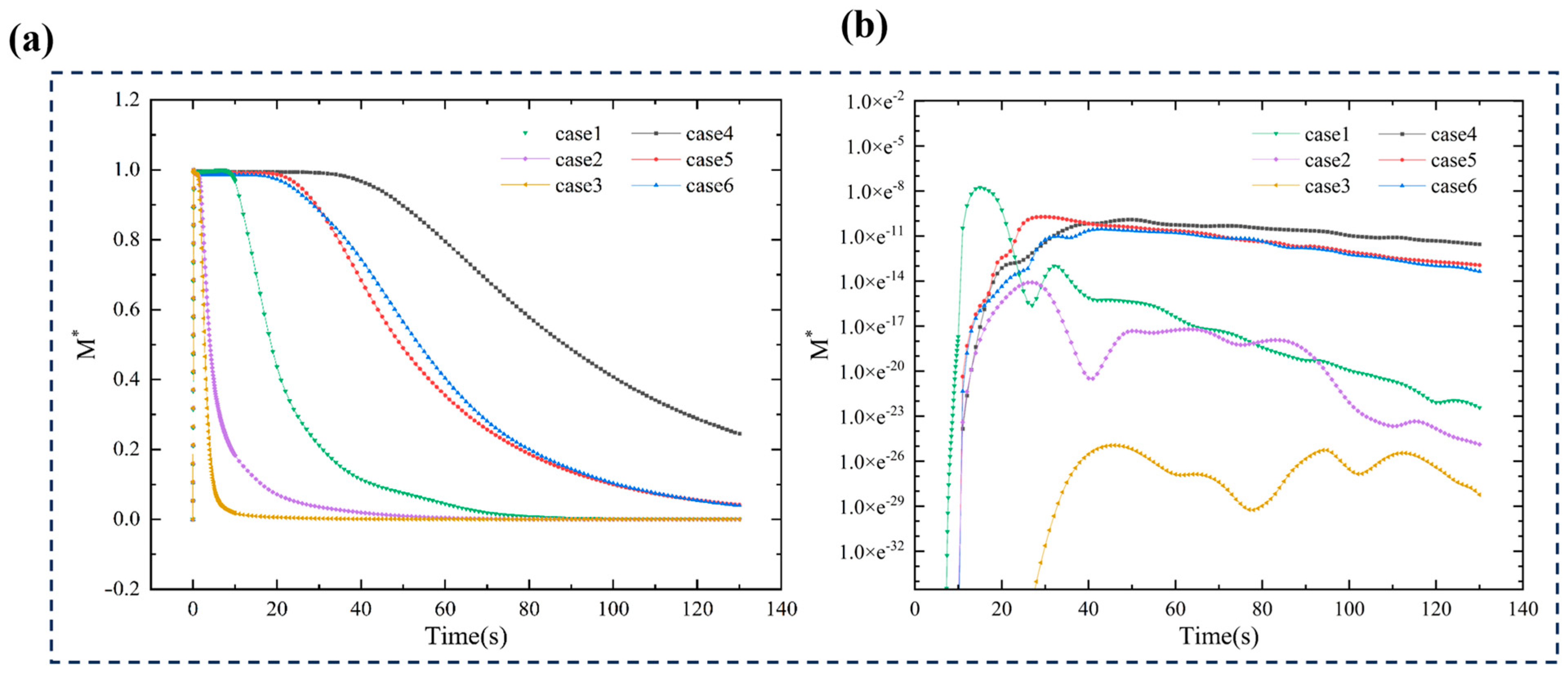
3.4. Average Contamination Range and Maximum Reach
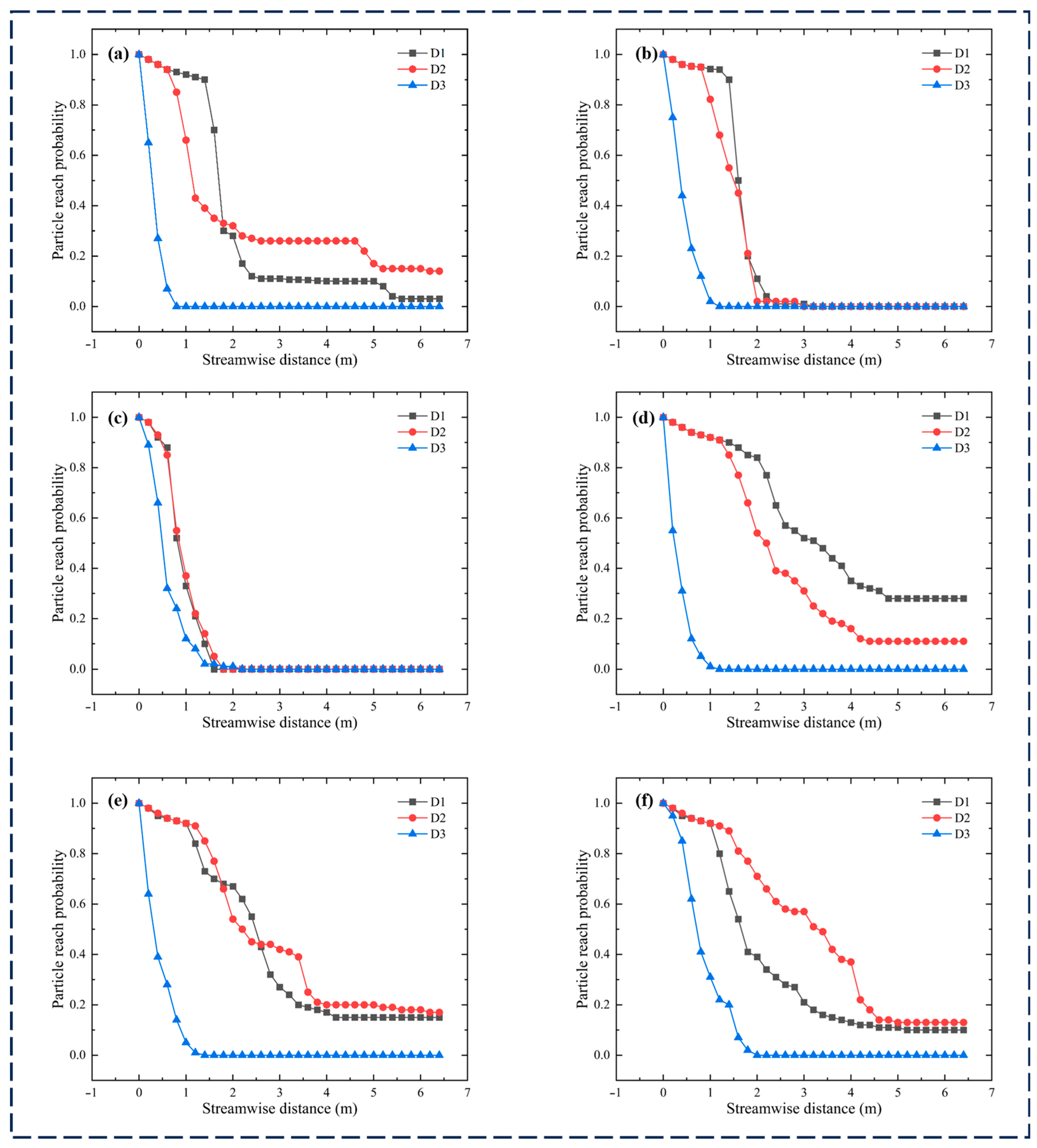
3.5. Particle Reach Probability
3.6. Characteristics of Air Supply Velocity on the Deposition, Suspension, and Expulsion of Cough Droplets from Patient
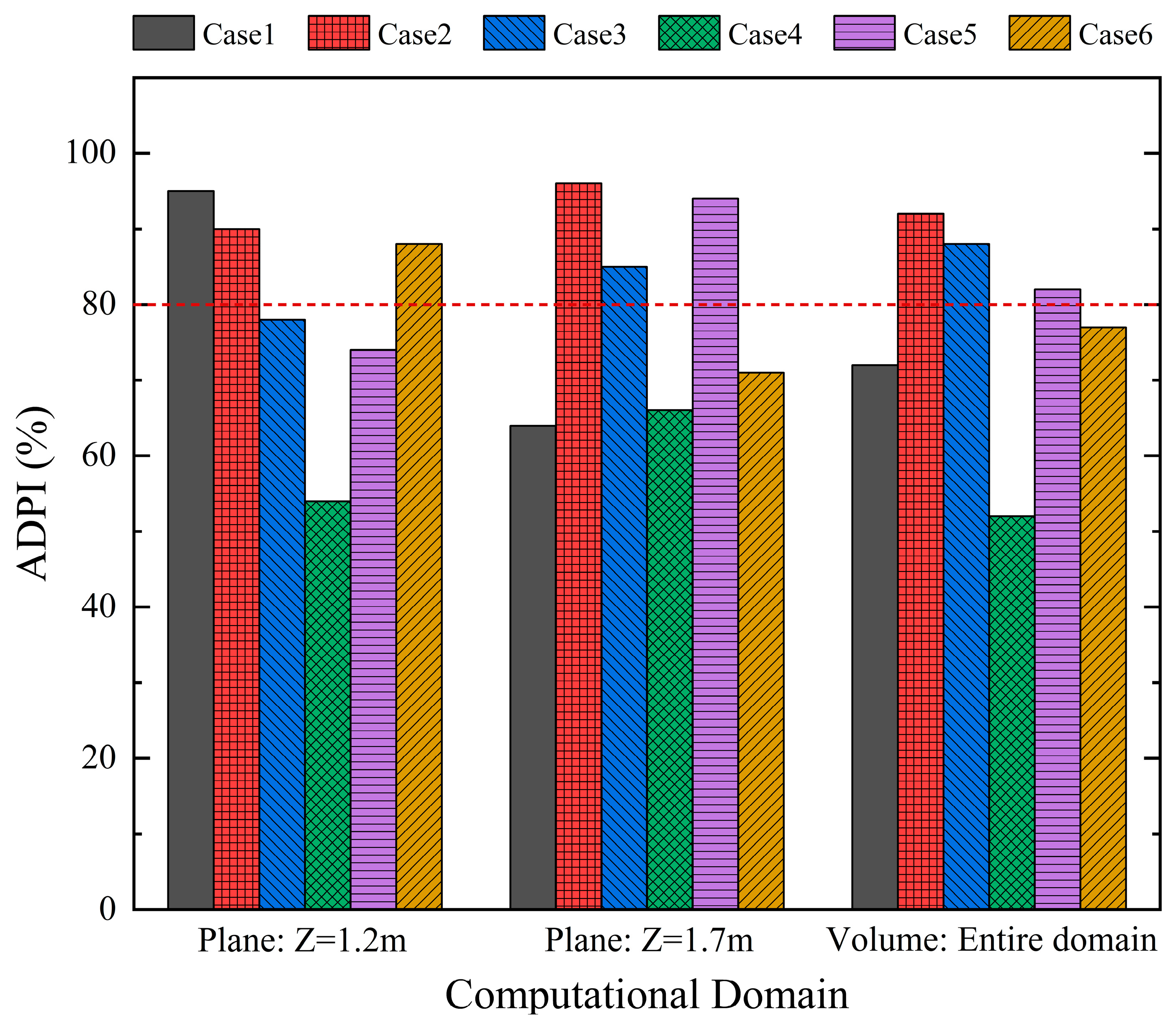
3.7. Analysis of Energy Consumption and Comfort in Different Ventilation Systems
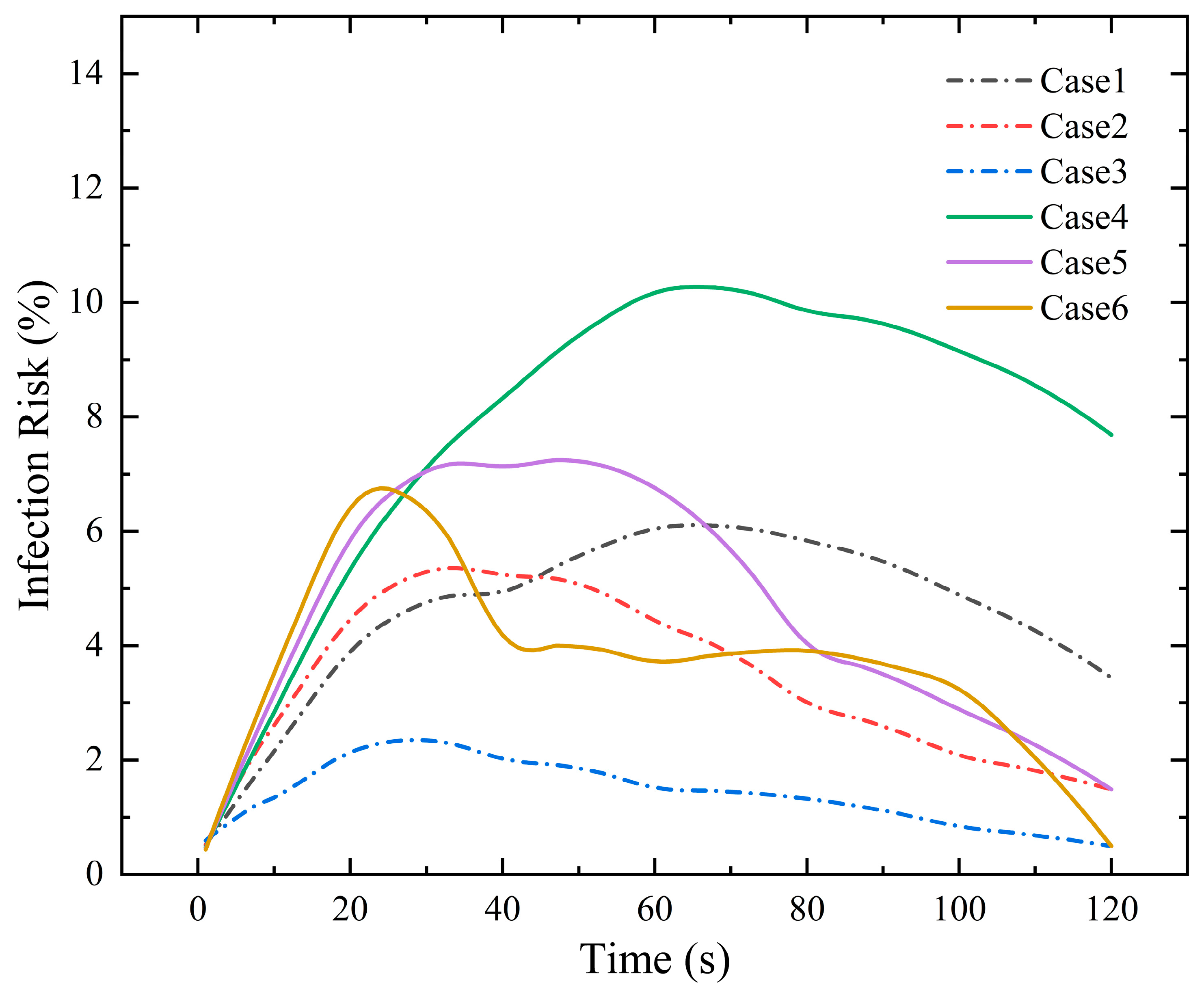
3.8. Analysis of the Infection Risk Prediction Model
4. Discussion
4.1. Analysis of Particle Behavior in the MV and SFRC Systems
4.2. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mao, Y.H.; Ma, J.L.; Wang, S.X.; Liang, J.D.; Liang, J.Z. A stratum ventilation system for pollutants and an improved prediction model for infection in subway cars. Atmos. Pollut. Res. 2022, 13, 101354. [Google Scholar] [CrossRef]
- Morawska, L.; Milton, D.K. It is Time to Address Airborne Transmission of COVID-19. Clin. Infect. Dis. 2020, 71, 2311–2313. [Google Scholar] [CrossRef]
- Peng, N.N.; Chow, K.W.; Liu, C.H. Computational study on the transmission of the SARS-CoV-2 virus through aerosol in an elevator cabin: Effect of the ventilation system. Phys. Fluids 2021, 33, 103325. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ning, Z.; Chen, Y.; Guo, M.; Liu, Y.; Gali, N.K.; Sun, L.; Duan, Y.; Cai, J.; Westerdahl, D.; et al. Aerodynamic analysis of SARS-CoV-2 in two Wuhan hospitals. Nature 2020, 582, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Cao, J. Airborne transmission of SARS-CoV-2: The world should face the reality. Environ. Int. 2020, 139, 105730. [Google Scholar] [CrossRef]
- Shin, H.W.; Kang, D.H. Estimation of airborne infection risk in a school classroom according to operation of a floor-standing type ventilation system. J. Build. Eng. 2023, 78, 107649. [Google Scholar] [CrossRef]
- Zhou, Y.; Ji, S. Experimental and numerical study on the transport of droplet aerosols generated by occupants in a fever clinic. Build. Environ. 2021, 187, 107402. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, T.T.; You, R.; Chen, Q. Evaluation of infection probability of Covid-19 in different types of airliner cabins. Build. Environ. 2023, 234, 110159. [Google Scholar] [CrossRef]
- Gralton, J.; Tovey, E.; McLaws, M.-L.; Rawlinson, W.D. The role of particle size in aerosolised pathogen transmission: A review. J. Infect. 2011, 62, 1–13. [Google Scholar] [CrossRef]
- Zayas, G.; Chiang, M.C.; Wong, E.; MacDonald, F.; Lange, C.F.; Senthilselvan, A.; King, M. Cough aerosol in healthy participants: Fundamental knowledge to optimize droplet-spread infectious respiratory disease management. BMC Pulm. Med. 2012, 12, 11. [Google Scholar] [CrossRef]
- Chao, C.Y.H.; Wan, M.P.; Morawska, L.; Johnson, G.R.; Ristovski, Z.D.; Hargreaves, M.; Mengersen, K.; Corbett, S.; Li, Y.; Xie, X.; et al. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009, 40, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Li, Y. Airborne spread of infectious agents in the indoor environment. Am. J. Infect. Control 2016, 44, S102–S108. [Google Scholar] [CrossRef]
- Han, M.; Ooka, R.; Kikumoto, H.; Oh, W.; Bu, Y.; Hu, S. Measurements of exhaled airflow velocity through human coughs using particle image velocimetry. Build. Environ. 2021, 202, 108020. [Google Scholar] [CrossRef]
- Kwon, S.-B.; Park, J.; Jang, J.; Cho, Y.; Park, D.-S.; Kim, C.; Bae, G.-N.; Jang, A. Study on the initial velocity distribution of exhaled air from coughing and speaking. Chemosphere 2012, 87, 1260–1264. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Kato, S.; Yang, J.-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build. Environ. 2006, 41, 1691–1702. [Google Scholar] [CrossRef]
- Fabian, P.; McDevitt, J.J.; DeHaan, W.H.; Fung, R.O.P.; Cowling, B.J.; Chan, K.H.; Leung, G.; Milton, D.K. Influenza virus in human exhaled breath: An observational study. PLoS ONE 2008, 3, e2691. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.W.; Nicolle, A.D.; Klettner, C.A.; Pantelic, J.; Wang, L.; Suhaimi, A.B.; Tan, A.Y.L.; Ong, G.W.X.; Su, R.; Sekhar, C.; et al. Airflow dynamics of human jets: Sneezing and breathing—Potential sources of infectious aerosols. PLoS ONE 2013, 8, e59970. [Google Scholar] [CrossRef]
- Liu, Z.J.; Di, Y.; Hu, L.N.; He, J.Z.; Cao, G.Q. Bacteria-carrying particles diffusion in the operating room due to the interaction between human thermal plume and ventilation systems: An experimental-numerical simulation study. Energy Build. 2022, 270, 112277. [Google Scholar] [CrossRef]
- Luo, Q.Q.; Ou, C.Y.; Hang, J.; Luo, Z.W.; Yang, H.Y.; Yang, X.; Zhang, X.L.; Li, Y.G.; Fan, X.D. Role of pathogen-laden expiratory droplet dispersion and natural ventilation explaining a COVID-19 outbreak in a coach bus. Build. Environ. 2022, 220, 109160. [Google Scholar] [CrossRef]
- Liu, Z.; Chu, J.; Li, H.; Huang, Z.; Liu, H.; Jiang, C.; Sun, T.; Xiao, X.; He, J. Evaluation of different computational methods for numerical simulation of aerosol distribution in the operating room. J. Build. Eng. 2024, 96, 110575. [Google Scholar] [CrossRef]
- Luo, X.L.; Huang, X.Y.; Feng, Z.B.; Li, J.; Gu, Z.L. Influence of air inlet/outlet arrangement of displacement ventilation on local environment control forum earthed relics within site museum. Energy Build. 2021, 246, 111116. [Google Scholar] [CrossRef]
- Wu, F.; Yu, C.; Xu, R.; Li, H. Numerical Simulation of Droplet Dispersion and Passenger Infection Risk Assessment in a Subway Carriage. Appl. Sci. 2024, 14, 590. [Google Scholar] [CrossRef]
- Zee, M.; Davis, A.C.; Clark, A.D. Computational fluid dynamics modeling of cough transport in an aircraft cabin. Sci. Rep. 2021, 11, 23329. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Fan, M.; Liu, S. Impact of Seat Inclination and Misalignment on Airborne Pollutant Transport in a Single-Aisle Aircraft Cabin. Appl. Sci. 2022, 12, 4538. [Google Scholar] [CrossRef]
- Dao, H.T.; Kim, K.S. Behavior of cough droplets emitted from Covid-19 patient in hospital isolation room with different ventilation configurations. Build. Environ. 2022, 209, 108649. [Google Scholar] [CrossRef]
- Castellini, J.E.; Faulkner, C.A.; Zuo, W.; Lorenzetti, D.M.; Sohn, M.D. Assessing the use of portable air cleaners for reducing exposure to airborne diseases in a conference room with thermal stratification. Build. Environ. 2022, 207, 108441. [Google Scholar] [CrossRef]
- Su, W.; Yang, B.; Melikov, A.; Liang, C.; Lu, Y.; Wang, F.; Li, A.; Lin, Z.; Li, X.; Cao, G.; et al. Infection probability under different air distribution patterns. Build. Environ. 2022, 207, 108555. [Google Scholar] [CrossRef]
- Li, K.; Kang, L.; Guo, K.; Song, L.; Zhang, X.; Xu, W. Risk assessment of respiratory droplet infections caused by coughing in various indoor dynamic environments. J. Build. Eng. 2023, 80, 108116. [Google Scholar] [CrossRef]
- Ye, J.; Ai, Z.; Zhang, C. A new possible route of airborne transmission caused by the use of a physical partition. J. Build. Eng. 2021, 44, 103420. [Google Scholar] [CrossRef]
- Wang, C.; Holmberg, S.; Sadrizadeh, S. Impact of door opening on the risk of surgical site infections in an operating room with mixing ventilation. Indoor Built Environ. 2021, 30, 166–179. [Google Scholar] [CrossRef]
- Romano, F.; Marocco, L.; Gusten, J.; Joppolo, C.M. Numerical and experimental analysis of airborne particles control in an operating theater. Build. Environ. 2015, 89, 369–379. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, B. Some questions on dispersion of human exhaled droplets in ventilation room: Answers from numerical investigation. Indoor Air 2010, 20, 95–111. [Google Scholar] [CrossRef] [PubMed]
- GB 50157-2013; Code for Design Metro. Beijing Urban Construction Design and Research Institute: Beijing, China, 2013.
- de Dear, R.J.; Arens, E.; Hui, Z.; Oguro, M. Convective and radiative heat transfer coefficients for individual human body segments. Int. Biometeorol. 1997, 40, 141–156. [Google Scholar] [CrossRef]
- Licina, D.; Pantelic, J.; Melikov, A.; Sekhar, C.; Tham, K.W. Experimental investigation of the human convective boundary layer in a quiescent indoor environment. Build. Environ. 2014, 75, 79–91. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Yan, Y.; Tu, J. Effects of cough-jet on airflow and contaminant transport in an airliner cabin section. Comput. Multiph. Flows 2017, 10, 72–82. [Google Scholar] [CrossRef]
- Duguid, J.P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiology Infect. 1946, 44, 471–479. [Google Scholar] [CrossRef]
- Chen, R.; Haofu, C.; Junqi, W. Ventilation impacts on infection risk mitigation, improvement of environmental quality and energy efficiency for subway carriages. Build. Environ. 2022, 222, 109358. [Google Scholar] [CrossRef]
- GB50736-2012; Design Code for Heating Ventilation and Air Conditioning of Civil Buildings. China Academy of Building Science: Beijing, China, 2012.
- GB50189-2015; Design Standard for Energy Efficiency of Public Buildings. China Academy of Building Science: Beijing, China, 2015.
- Wang, J.; Huang, J.; Feng, Z.; Cao, S.J.; Haghighat, F. Occupant-density detection based energy efficient ventilation system: Prevention of infection transmission. Energy Build. 2021, 240, 110883. [Google Scholar] [CrossRef]
- Ren, C.; Xi, C.; Wang, J.; Feng, Z.; Nasiri, F.; Cao, S.-J.; Haghighat, F. Mitigating COVID-19 infection disease transmission in indoor environment using physical barriers. Sustain. Cities Soc. 2021, 74, 103175. [Google Scholar] [CrossRef]
- Ridouane, E.H. Evaluation of Air Mixing and Thermal Comfort from High Sidewall Supply Air Jets; Technical Report; NREL/TP-5500-48664; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2011. [Google Scholar]
- Wang, H.; Wang, J.; Feng, Z.; Haghighat, F.; Cao, S.-J. Intelligent anti-infection ventilation strategy based on computer audition: Towards healthy built environment and low carbon emission. Sustain. Cities Soc. 2023, 99, 104888. [Google Scholar] [CrossRef]


| Ventilation Modes | Inlet Size (m) | Inlet Number | Outlet Size (m) | Outlet Number | Mesh Grids |
|---|---|---|---|---|---|
| MV | 0.5 × 0.1 | 16 | 0.5 × 0.1 | 4 | 5,471,754 |
| SFRC | 1.0 × 0.2 | 16 | 1.0 × 0.2 | 2 | 5,504,214 |
| Name | Type | Parameters |
|---|---|---|
| Air supply Diffuser Exhaust louver | Velocity inlet Outflow | Turbulence intensity = 5% DPM: reflect Mass fraction of H2O: 0.7% Mass fraction of air: 99.3% Mass fraction of N2: 100% DPM: escape |
| Mouth (patient) Mouth (passenger) Occupant Lateral wall Ceiling | Velocity inlet Mass flow outlet Wall Wall | UDF 310 K DPM: reflect Mass flux = 0.001715 Kg/s DPM: escape Stationary wall 30 W/m2 DPM: trap Density: 2200 Kg/m3 Specific heat: 830 J/(kg·K) 0.025 m Density: 2200 Kg/m3 Specific heat: 830 J/(kg·K) Thermal conductivity: 0.11 W/(m·K) DPM: trap 6 W/(m2·K) 0.025 m |
| Case No. | Supply Air Temperature (°C) | Supply Air Velocity (m/s) | Ventilation Method |
|---|---|---|---|
| Case 1 | 25 | 0.2 | SFRC |
| Case 2 | 25 | 0.3 | SFRC |
| Case 3 | 25 | 0.4 | SFRC |
| Case 4 | 25 | 0.8 | MV |
| Case 5 | 25 | 1.2 | MV |
| Case 6 | 25 | 1.6 | MV |
| Parameter | Value | Unit | Explanation |
|---|---|---|---|
| COP | 4.2 | According to the relevant standard China Academy of Building Science (2015) [40] | |
| Cp | 1.013 | kJ/(kg·°C) | Corresponding to dry air at 25 °C |
| ρ | 1.169 | kg/m3 | Corresponding to dry air at 25 °C |
| Ti | 25 | °C | According to the relevant standard China Academy of Building Science (2012) [39] |
| To | 34.8 | °C | According to the relevant standard China Academy of Building Science (2012) |
| k | 0.8 | kJ·s2/m9 | According to the relevant literature Wang et al. (2021) [41] |
| Case No. | Energy Consumption of the Ventilation System (Kw) | Energy Required for Air Transport (kW) | Total Energy Consumption (kW) | Comparative Energy-Saving Rate (%) |
|---|---|---|---|---|
| Case 1 | 0.21 | 2.95 | 3.16 | 50.31 |
| Case 2 | 0.71 | 3.43 | 4.14 | 34.91 |
| Case 3 | 1.68 | 4.07 | 5.75 | 9.59 |
| Case 4 | 0.21 | 2.95 | 3.16 | 50.31 |
| Case 5 | 0.71 | 3.87 | 4.58 | 27.99 |
| Case 6 | 1.68 | 4.68 | 6.36 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Ling, R.; Wan, X.; Ren, H.; Jing, X.; Feng, G. Study on the Impact of Ventilation Methods on Droplet Nuclei Transmission in Subway Carriages. Appl. Sci. 2025, 15, 4919. https://doi.org/10.3390/app15094919
Wu X, Ling R, Wan X, Ren H, Jing X, Feng G. Study on the Impact of Ventilation Methods on Droplet Nuclei Transmission in Subway Carriages. Applied Sciences. 2025; 15(9):4919. https://doi.org/10.3390/app15094919
Chicago/Turabian StyleWu, Xinkai, Rui Ling, Xingyu Wan, Haihua Ren, Xuerun Jing, and Guozeng Feng. 2025. "Study on the Impact of Ventilation Methods on Droplet Nuclei Transmission in Subway Carriages" Applied Sciences 15, no. 9: 4919. https://doi.org/10.3390/app15094919
APA StyleWu, X., Ling, R., Wan, X., Ren, H., Jing, X., & Feng, G. (2025). Study on the Impact of Ventilation Methods on Droplet Nuclei Transmission in Subway Carriages. Applied Sciences, 15(9), 4919. https://doi.org/10.3390/app15094919





