Semi-Analytical Solutions for One-Dimensional Consolidation of Viscoelastic Unsaturated Soils Considering Variable Permeability Coefficient

Abstract

This paper proposes a semi-analytical solution for one-dimensional consolidation of viscoelastic unsaturated soil considering a variable permeability coefficient under exponential loading. The governing equations of excess pore air pressure (EPAP) and excess pore water pressure (EPWP) were acquired by introducing the Merchant viscoelastic model. By employing Lee’s correspondence principle and the Laplace transform, the solutions for EPAP and EPWP were derived under the boundary conditions of the permeable top surface and impermeable bottom surface. Crump’s method was then used to execute the inverse Laplace transform, yielding a semi-analytical solution in the time domain. Through typical examples, the dissipation of EPAP and EPWP and the change of the average degree of consolidation over time under the influence of different elastic moduli, viscoelastic coefficients, and air-to-water permeability ratios were studied. The variation of the permeability coefficient and its influence on consolidation were also analyzed. The findings of this research show that the consolidation rate of viscoelastic unsaturated soil is slower than that of elastic unsaturated soil; however, an acceleration in the consolidation of the soil is observed when changes in the permeability coefficient are considered. These discoveries enhance our comprehension of the consolidation behaviors exhibited by viscoelastic unsaturated soil, thereby enriching the knowledge base on its consolidation traits.

1. Introduction

Unsaturated soils are prevalent across the Earth’s surface, and their consolidation, a recurrent concern in geotechnical engineering, has garnered growing interest from researchers. With the development of soil mechanics, numerous researchers have undertaken a multitude of investigations into the consolidation processes of unsaturated soils in recent decades, leading to substantial advancements in this field. Biot [1] first proposed a general consolidation theory for unsaturated soils containing closed air bubbles in the 1940s. Bishop [2] introduced the effective stress parameter χ and established the effective stress principle for unsaturated soils in 1959. Blight [3] proposed the consolidation equation of air phases for dry and unsaturated soils in 1961. Additionally, Scott [4] first analyzed the consolidation of unsaturated soil considering entrapped air pockets. Barden [5] first proposed several independent one-dimensional (1D) consolidation equations for soils of varying saturation levels in 1965. Based on prior studies, Fredlund and Hasan [6], building on the constitutive relations for unsaturated soils proposed by Fredlund and Morgenstern [7], introduced two independent stress state variables (net normal stress and matric suction) and established the widely applied 1D consolidation theory for unsaturated soils in 1979. The research presented in this paper builds upon the 1D consolidation theory of Fredlund and Hasan.

In recent years, scholars have conducted extensive research on the 1D consolidation of unsaturated soils. Ausilio and Conte [8] established a connection between the settlement rate of unsaturated soils and the mean degree of consolidation for both air and water phases in 1999. They proposed an equation capable of predicting the time-dependent settlement behavior of foundations. Ausilio et al. [9] analyzed the 1D consolidation of unsaturated soils under external loads and increasing matric suction. Qin et al. [10] acquired the analytical solution for 1D consolidation of unsaturated soils with instantaneous uniform loading and homogeneous boundary conditions using the Laplace transform, Cayley–Hamilton principle, and inverse Laplace transform. Considering instantaneous uniform loading, Shan et al. [11,12] applied the method of separation of variables to acquire analytical solutions for 1D consolidation of unsaturated soil foundations under one-sided drainage, two-sided drainage, and mixed boundary conditions. Ho et al. [13] utilized the eigenfunction expansion method to find a semi-analytical solution for one-dimensional consolidation of unsaturated soils under one- and two-sided permeability boundary conditions considering initial excess pore pressures uniformly distributed or linearly varying along depth. Additionally, some scholars [14,15,16,17,18,19,20,21] extended the research for instantaneous uniform loading to time-varying loads, obtaining analytical or semi-analytical solutions under different boundaries and initial conditions. However, these analytical or semi-analytical solutions assumed that unsaturated soils are linearly elastic, which cannot explain certain consolidation problems accurately in the case of viscoelastic unsaturated soil. In addition, they neglect the change of the permeability coefficient during consolidation progress.

In actual engineering, the soil not only exhibits elasticity but also viscosity after being subjected to stress. The Kelvin–Voigt, Maxwell, and Merchant models have been used to illustrate the consolidation characteristics of viscoelastic soils [22]. Tan [23] analyzed the consolidation characteristics of saturated soils by employing the viscoelastic constitutive model in the 1950s. Afterward, Lo [24] and Xie and Liu [25] extended the consolidation of viscoelastic saturated soils. However, they all have a common shortcoming in that they are limited to saturated soils only [26,27,28]. In the aspect of unsaturated soil, the consolidation properties of viscoelastic unsaturated soils under instantaneous uniform loading and assuming constant permeability coefficient have been investigated only by Qin et al. [29] in the current published literature [30,31].

In most previous studies of unsaturated soil consolidation, the permeability coefficient is normally supposed to be constant during the solving process. Although this assumption has been accepted in preliminary studies of unsaturated soil consolidation, it is undeniable that the supposition of the permeability coefficient being approximated to be the same during the consolidation of unsaturated soils is a special case in practical engineering. During the consolidation process, the permeability coefficients of the air and water phases in the soil exhibit nonlinear variations in response to alterations of saturation and porosity. Some scholars, for example, Zhuang et al. [32], Qin and Zhang [33], and Qin et al. [34], have studied the effect of permeability coefficient variation on consolidation [35,36]. However, their studies were limited to saturated or linearly elastic unsaturated soils. Therefore, studying the impact of permeability coefficient variation on the consolidation of viscoelastic unsaturated soils is significant and imperative.

In this paper, the nonlinear variation of the permeability coefficient was considered, and the semi-analytical solution for 1D consolidation of viscoelastic unsaturated soil under exponential loading was acquired. Firstly, based on the Merchant model, the 1D consolidation controlling equations for viscoelastic unsaturated soil were obtained, employing Lee’s correspondence principle. Then, the solution was obtained via the Laplace transform. Moreover, the correlation between the permeability coefficient and matric suction was applied to derive the final solution, considering the alteration of the permeability coefficient. The numerical inverse Laplace transform was applied using Crump’s method to acquire the semi-analytical solution in the time domain. Finally, the consolidation behavior of viscoelastic unsaturated soils was analyzed using the examples of the air permeability ratio, elastic modulus ratio, and varying permeability coefficient.

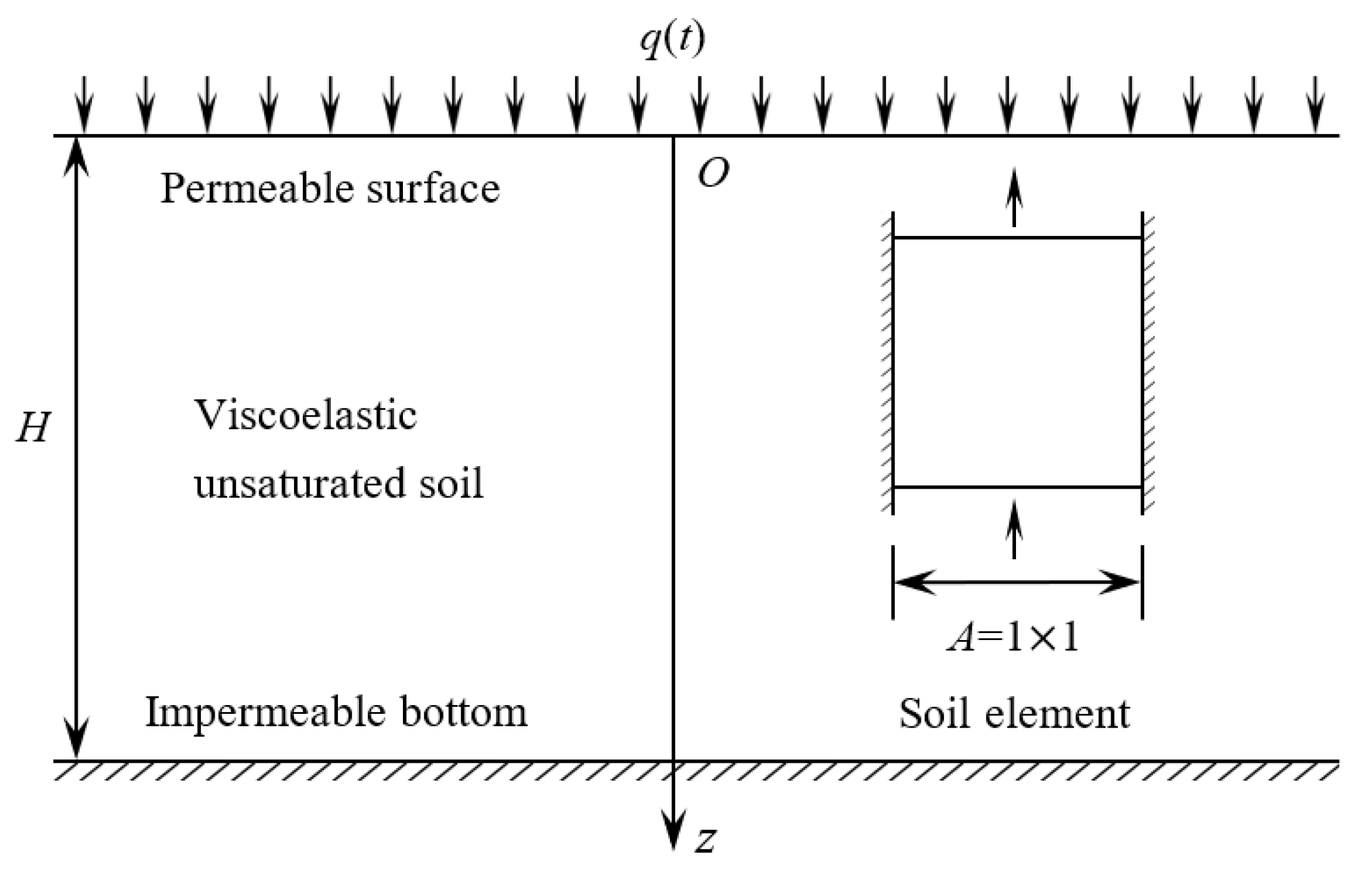
2. Governing Equations

2.1. Mathematical Modeling

In this study, a viscoelastic unsaturated soil layer of thickness H with a permeable surface which was subjected to an exponential loading $q(t)=q_0(1-{\mathrm{e}}^{-bt})$ and an impermeable bottom was adopted, where q₀ and b were the loading parameters determined by the actual loading conditions. As shown in Figure 1, a typical soil element of volume $\mathrm{d}V=1\times 1\times \mathrm{d}z$ with the 1D flow of water and air phases in the z direction was investigated in a simplified mathematical model.

As shown in Figure 2, the Merchant model with elastomer L₀ used in this paper consists of a Kelvin body alongside an elastomer L₁ and a viscous body N.

The constitutive equation of the Merchant model can be presented as follows [29]:

$$\sigma +{\displaystyle \frac{\eta }{E_0+E_1}}{\displaystyle \frac{\mathrm{d}\sigma }{\mathrm{d}t}}={\displaystyle \frac{E_0{E}_1}{E_0+E_1}}\epsilon +{\displaystyle \frac{\eta E_0}{E_0+E_1}}{\displaystyle \frac{\mathrm{d}\epsilon }{\mathrm{d}t}}$$

(1)

where σ is the stress; ε is the strain; E₀ and E₁ are the stiffness coefficients of the elastic bodies L₀ and L₁, respectively; and η is the viscous coefficients of the dashpot N.

Applying the Laplace transform to Equation (1) gives

$$V(s)={\displaystyle \frac{\tilde{\epsilon }(s)}{\tilde{\sigma }(s)}}={\displaystyle \frac{1}{E_0}}+{\displaystyle \frac{1}{E_1+\eta s}}$$

(2)

where s represents the Laplace transform of the conjugate variable of t.

According to Lee’s correspondence principle [37], the solution of the corresponding viscoelastic body can be obtained by using V(s) instead of the constant 1/E (where E represents the modulus of elasticity) in the solution of the linearly elastic body.

2.2. Laplace Transform and Governing Equations

Implementing the Laplace transforms to Fick’s law and Darcy’s law leads to

$${\displaystyle \frac{\partial {\tilde{u}}_{\mathrm{a}}}{\partial z}}=-{\displaystyle \frac{g}{k_{\mathrm{a}}}}{\tilde{J}}_{\mathrm{a}}$$

(3)

$${\displaystyle \frac{\partial {\tilde{u}}_{\mathrm{w}}}{\partial z}}=-{\displaystyle \frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{w}}}}{\tilde{v}}_{\mathrm{w}}$$

(4)

where $J_{\mathrm{a}}$ is the air flow rate in the z direction for the unit area; ${\nu }_{\mathrm{w}}$ is the water flow rate in the z direction for the unit area; ${\tilde{J}}_{\mathrm{a}}$ and ${\tilde{v}}_{\mathrm{w}}$ are the Laplace transforms of $J_{\mathrm{a}}$ and $v_{\mathrm{w}}$, respectively; $u_{\mathrm{a}}$ and ${\tilde{u}}_{\mathrm{a}}$ are EPAP and the Laplace transforms of EPWP, respectively; $u_{\mathrm{w}}$ and ${\tilde{u}}_{\mathrm{w}}$ are EPWP and the Laplace transforms of EPWP, respectively; $k_{\mathrm{a}}$ and $k_{\mathrm{w}}$ are the permeability coefficients of air and water phases in unsaturated soils; and ${\gamma }_{\mathrm{w}}$ is the unit weight of water phase.

The governing equation of the air phase for 1D consolidation in unsaturated soils under exponential loading [38] is as follows:

$${\displaystyle \frac{\partial u_{\mathrm{a}}}{\partial t}}=-C_{\mathrm{a}}{\displaystyle \frac{\partial u_{\mathrm{a}}}{\partial t}}-C_{\mathrm{v}}^{\mathrm{a}}{\displaystyle \frac{{\partial }^2{u}_{\mathrm{a}}}{\partial z^2}}+D_{\mathrm{a}}^{-bt}$$

(5)

Applying the Laplace transform and Lee’s correspondence principle to Equation (5) gives the following equation (the details are shown in Qin et al.’s study [29]):

$$s{\tilde{u}}_{\mathrm{a}}-u_{\mathrm{a}}^0=-s{\tilde{C}}_{\mathrm{a}}{\tilde{u}}_{\mathrm{w}}+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0-{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}{\displaystyle \frac{{\partial }^2{\tilde{u}}_{\mathrm{a}}}{\partial z^2}}+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}$$

(6)

Substituting Equation (3) into Equation (6) results in

$${\displaystyle \frac{\partial {\tilde{J}}_{\mathrm{a}}}{\partial z}}=s{\displaystyle \frac{k_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}g}}{\tilde{u}}_{\mathrm{a}}+s{\displaystyle \frac{k_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}g}}{\tilde{C}}_{\mathrm{a}}{\tilde{u}}_{\mathrm{w}}-{\displaystyle \frac{k_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}g}}\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)$$

(7)

where ${\tilde{C}}_{\mathrm{a}}={\tilde{m}}_2^{\mathrm{a}}/\left[{\tilde{m}}_{1\mathrm{k}}^{\mathrm{a}}-{\tilde{m}}_2^{\mathrm{a}}-u_{\mathrm{atm}}{n}_0\left(1-S_{\mathrm{r}0}\right)/{\left({\overline{u}}_{\mathrm{a}}^0\right)}^2\right]$;

$${\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}=k_{\mathrm{a}}RT/\left\{g{\overline{u}}_{\mathrm{a}}^{0}M\left[{\tilde{m}}_{1\mathrm{k}}^{\mathrm{a}}-{\tilde{m}}_2^{\mathrm{a}}-u_{\mathrm{atm}}{n}_0\left(1-S_{\mathrm{r}0}\right)/{\left({\overline{u}}_{\mathrm{a}}^0\right)}^2\right]\right\};$$

$${\tilde{D}}_{\mathrm{a}}=m_{1\mathrm{k}}^{\mathrm{a}}{q}_{0}b/\left[{\tilde{m}}_{1\mathrm{k}}^{\mathrm{a}}-{\tilde{m}}_2^{\mathrm{a}}-u_{\mathrm{atm}}{n}_0\left(1-S_{\mathrm{r}0}\right)/{\left({\overline{u}}_{\mathrm{a}}^0\right)}^2\right];$$

$$\mathrm{and}{\tilde{m}}_{1\mathrm{k}}^{\mathrm{a}}=-1/E_{0\mathrm{n}}^{\mathrm{a}}-1/\left(E_{1\mathrm{n}}^{\mathrm{a}}+{\eta }_{\mathrm{n}}^{\mathrm{a}}s\right),{\tilde{m}}_2^{\mathrm{a}}=-1/E_{0\mathrm{s}}^{\mathrm{a}}-1/\left(E_{1\mathrm{s}}^{\mathrm{a}}+{\eta }_{\mathrm{s}}^{\mathrm{a}}s\right).$$

In the above equations, ${\tilde{C}}_{\mathrm{a}}$ is the interaction constant related to the air phase in viscoelastic foundation; ${\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}$ is the consolidation coefficient associated with air phase in viscoelastic foundation; ${\tilde{m}}_{1\mathrm{k}}^{\mathrm{a}}$ is the volume change coefficient of the air phase skeleton corresponding to the net normal stress ($\sigma -u_a$) when the viscoelastic foundation $K_0$ is loaded; ${\tilde{m}}_2^{\mathrm{a}}$ is the air phase volume change coefficient corresponding to matric suction ($u_{\mathrm{a}}-u_{\mathrm{w}}$) when loaded on the viscoelastic foundation $K_0$; R represents the universal air constant, and R = 8.314 J/(mol·K); $u_{\mathrm{atm}}$ represents the atmospheric pressure; $n_0$ represents the incipient porosity and $S_{\mathrm{r}0}$ is the incipient degree of saturation; ${\eta }_{\mathrm{n}}^{\mathrm{a}}$ and ${\eta }_{\mathrm{s}}^{\mathrm{a}}$ represent the viscous coefficients of the air phase accounting for variations in net normal stress and matric suction; T represents the absolute temperature; $E_{1j}^{\mathrm{a}}/E_{0j}^{\mathrm{a}}$ are the stiffness coefficients of air phase; and the subscript j (=n or s) represents the net normal stress or matric suction, respectively. In addition, the subscripts 0 and 1 of $E_{1j}^{\mathrm{a}}/E_{0j}^{\mathrm{a}}$ represent the elastic body $L_0$ and Kelvin body, respectively.

Moreover, considering exponential loading, the governing equation of the water phase for 1D consolidation of unsaturated soils [38] can be formulated as detailed below:

$${\displaystyle \frac{\partial u_{\mathrm{w}}}{\partial t}}=-C_{\mathrm{w}}{\displaystyle \frac{\partial u_{\mathrm{a}}}{\partial t}}-C_{\mathrm{v}}^{\mathrm{w}}{\displaystyle \frac{{\partial }^2{u}_{\mathrm{w}}}{\partial z^2}}+D_{\mathrm{w}}{\mathrm{e}}^{-bt}$$

(8)

Implementing the Laplace transform and Lee’s correspondence principle in Equation (8) leads to the following equation (the details are shown in Qin et al.’s study [29]):

$$s{\tilde{u}}_{\mathrm{w}}-u_{\mathrm{w}}^0=-s{C}_{\mathrm{w}}{\tilde{u}}_{\mathrm{a}}+C_{\mathrm{w}}{u}_{\mathrm{a}}^0-C_{\mathrm{v}}^{\mathrm{w}}{\displaystyle \frac{{\partial }^2{\tilde{u}}_{\mathrm{w}}}{\partial z^2}}+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}$$

(9)

Substituting Equation (4) into Equation (9) gives

$${\displaystyle \frac{\partial {\tilde{v}}_{\mathrm{w}}}{\partial z}}=s{\displaystyle \frac{k_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\gamma }_{\mathrm{w}}}}{\tilde{C}}_{\mathrm{w}}{\tilde{u}}_{\mathrm{a}}+s{\displaystyle \frac{k_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\gamma }_{\mathrm{w}}}}{\tilde{u}}_{\mathrm{w}}-{\displaystyle \frac{k_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\gamma }_{\mathrm{w}}}}\left(u_{\mathrm{w}}^0+{\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)$$

(10)

where ${\tilde{C}}_w=\left({\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}-{\tilde{m}}_2^{\mathrm{w}}\right)/{\tilde{m}}_2^{\mathrm{w}}=\left(1-{\tilde{m}}_2^{\mathrm{w}}/{\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}\right)/\left({\tilde{m}}_2^{\mathrm{w}}/{\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}\right)$; ${\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}=k_{\mathrm{w}}/{\gamma }_{\mathrm{w}}{\tilde{m}}_2^{\mathrm{w}}$; ${\tilde{D}}_{\mathrm{w}}={\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}{q}_{0}b/{\tilde{m}}_2^{\mathrm{w}}$; ${\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}=-1/E_{0\mathrm{n}}^{\mathrm{w}}-1/\left(E_{1\mathrm{n}}^{\mathrm{w}}+{\eta }_{\mathrm{n}}^{\mathrm{w}}s\right)$; ${\tilde{m}}_2^{\mathrm{w}}=-1/E_{0\mathrm{s}}^{\mathrm{w}}-1/\left(E_{1\mathrm{s}}^{\mathrm{w}}+{\eta }_{\mathrm{s}}^{\mathrm{w}}s\right)$.

In the above equations, ${\tilde{C}}_{\mathrm{w}}$ is the interaction constant related to the water phase in viscoelastic foundation; ${\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}$ is the consolidation coefficient related to water phase in viscoelastic foundation; ${\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}$ is the volume change coefficient of the water phase skeleton corresponding to net normal stress when loaded on viscoelastic foundation $K_0$; ${\tilde{m}}_2^{\mathrm{w}}$ is the water phase volume change coefficient corresponding to matric suction when loaded on viscoelastic foundation $K_0$; $E_{1j}^{\mathrm{w}}/E_{0j}^{\mathrm{w}}$ are the stiffness coefficients of the water phase; ${\eta }_{\mathrm{n}}^{\mathrm{w}}$ and ${\eta }_{\mathrm{s}}^{\mathrm{w}}$ are the viscous coefficients of water phase; and the meanings of the subscripts 0, 1, subscript n, s are the same as those for the air phase.

3. Derivations of the Solutions

3.1. Semi-Analytical Solutions

According to Equations (3), (4), (7), and (10), the governing equations can be expressed in the following matric expression:

$${\displaystyle \frac{\partial \tilde{X}}{\partial z}}=A\tilde{X}+B$$

(11)

where

$$\tilde{X}(z,s)={\left[{\tilde{u}}_{\mathrm{a}}(z,s),{\tilde{u}}_{\mathrm{w}}(z,s),{\tilde{J}}_{\mathrm{a}}(z,s),{\tilde{v}}_{\mathrm{w}}(z,s)\right]}^{\mathrm{T}},$$

$$A=\left(\begin{array}{cccc}0& 0& -{\displaystyle \frac{g}{k_{\mathrm{a}}}}& 0\\ 0& 0& 0& -{\displaystyle \frac{{\gamma }_{\mathrm{w}}}{k_{\mathrm{w}}}}\\ s{\displaystyle \frac{k_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}g}}& s{\displaystyle \frac{k_{\mathrm{a}}{\tilde{C}}_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}g}}& 0& 0\\ s{\displaystyle \frac{k_{\mathrm{w}}{\tilde{C}}_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\gamma }_{\mathrm{w}}}}& s{\displaystyle \frac{k_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\gamma }_{\mathrm{w}}}}& 0& 0\end{array}\right),B=\left[\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\\ -{\displaystyle \frac{k_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}g}}\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+C}}\right)\\ -{\displaystyle \frac{k_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}g}}\left(u_{\mathrm{w}}^0+{\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+C}}\right)\end{array}\right].$$

It is supposed that the boundary conditions are permeable on the top surface and impermeable on the bottom surface to the air and water phases. The specifics are outlined as follows:

Boundary at z = 0:

$$u_{\mathrm{a}}(0,t)=u_{\mathrm{w}}(0,t)=0$$

(12a)

Boundary at z = H:

$${\displaystyle \frac{\partial u_{\mathrm{a}}(H,t)}{\partial z}}={\displaystyle \frac{\partial u_{\mathrm{w}}(H,t)}{\partial z}}=0$$

(12b)

The solutions in the Laplace domain of EPAP, EPWP, and normalized settlement can be obtained by using the same method described after bringing in the boundary conditions and initial conditions:

$$\begin{array}{l}{\tilde{u}}_{\mathrm{a}}(z,s)={\displaystyle \frac{1}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}({\xi }^2-{\eta }^2)}}\left\{-{\displaystyle \frac{\mathrm{ch}\left[\xi (H-z)\right]}{{\xi }^2\mathrm{ch}(\xi H)}}\left[\left({\eta }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\right)\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)+{\displaystyle \frac{s{\tilde{C}}_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\left({\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+u_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)\right]\right.\\ +{\displaystyle \frac{\mathrm{ch}\left[\eta (H-z)\right]}{{\eta }^2\mathrm{ch}(\eta H)}}\left.\left[\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)\right]\left({\xi }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\right)+{\displaystyle \frac{s{\tilde{C}}_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\left({\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+u_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)\right\}+{\displaystyle \frac{u_{\mathrm{a}}^0}{s}}+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}-{\tilde{C}}_{\mathrm{a}}{\tilde{D}}_{\mathrm{w}}}{s(1-{\tilde{C}}_{\mathrm{a}}{\tilde{C}}_{\mathrm{w}})(s+b)}}\end{array}$$

(13)

$$\begin{array}{l}{\tilde{u}}_{\mathrm{w}}(z,s)={\displaystyle \frac{1}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}({\xi }^2-{\eta }^2)}}\left\{-{\displaystyle \frac{\mathrm{ch}\left[\xi (H-z)\right]}{{\xi }^2\mathrm{ch}(\xi H)}}\right.\left[{\displaystyle \frac{s{\tilde{C}}_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)+\left({\eta }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\right)\left({\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+u_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)\right]\\ \left.+{\displaystyle \frac{\mathrm{ch}\left[\eta (H-z)\right]}{{\eta }^2\mathrm{ch}(\eta H)}}\left[{\displaystyle \frac{s{\tilde{C}}_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)+\left({\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+u_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)\left({\xi }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\right)\right]\right\}+{\displaystyle \frac{u_{\mathrm{w}}^0}{s}}+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}-{\tilde{C}}_{\mathrm{a}}{\tilde{D}}_{\mathrm{w}}}{s(1-{\tilde{C}}_{\mathrm{a}}{\tilde{C}}_{\mathrm{w}})(s+b)}}\end{array}$$

(14)

$$\begin{array}{l}\tilde{w}(s)=-{\displaystyle \frac{\mathrm{sh}(\xi H)}{{\xi }^3({\xi }^2-{\eta }^2)\mathrm{ch}(\xi H)}}\left\{{\displaystyle \frac{1}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\left[\left({\tilde{m}}_2-{\tilde{m}}_{1\mathrm{k}}\right)\left({\eta }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\right)-{\tilde{m}}_2{\displaystyle \frac{s{\tilde{C}}_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\right]\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)\right.\\ +{\displaystyle \frac{1}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\left[\left({\tilde{m}}_2-{\tilde{m}}_{1\mathrm{k}}\right){\displaystyle \frac{s{\tilde{C}}_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}-{\tilde{m}}_2\left({\eta }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\right)\right]\left.\left({\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+u_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)\right\}+{\displaystyle \frac{({\tilde{m}}_2-{\tilde{m}}_{1\mathrm{k}})({\tilde{D}}_{\mathrm{a}}-{\tilde{C}}_{\mathrm{a}}{\tilde{D}}_{\mathrm{w}})H}{s(1-{\tilde{C}}_{\mathrm{a}}{\tilde{C}}_{\mathrm{w}})(s+b)}}\\ +{\displaystyle \frac{\mathrm{sh}(\eta H)}{{\eta }^3({\xi }^2-{\eta }^2)\mathrm{ch}(\eta H)}}\left\{{\displaystyle \frac{1}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\left[\left({\tilde{m}}_2-{\tilde{m}}_{1\mathrm{k}}\right)\left({\xi }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\right)-{\tilde{m}}_2{\displaystyle \frac{s{\tilde{C}}_{\mathrm{w}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\right]\left(u_{\mathrm{a}}^0+{\tilde{C}}_{\mathrm{a}}{u}_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{a}}}{s+b}}\right)\right.\\ +{\displaystyle \frac{1}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\left[\left({\tilde{m}}_2-{\tilde{m}}_{1\mathrm{k}}\right){\displaystyle \frac{s{\tilde{C}}_{\mathrm{a}}}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}-{\tilde{m}}_2\left({\xi }^2+{\displaystyle \frac{s}{{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}}}\right)\right]\left.\left({\tilde{C}}_{\mathrm{w}}{u}_{\mathrm{a}}^0+u_{\mathrm{w}}^0+{\displaystyle \frac{{\tilde{D}}_{\mathrm{w}}}{s+b}}\right)\right\}-{\displaystyle \frac{{\tilde{m}}_2({\tilde{D}}_{\mathrm{w}}-{\tilde{C}}_{\mathrm{w}}{\tilde{D}}_{\mathrm{a}})H}{s(1-{\tilde{C}}_{\mathrm{a}}{\tilde{C}}_{\mathrm{w}})(s+b)}}+{\displaystyle \frac{{\tilde{m}}_{1\mathrm{k}}^{\mathrm{s}}{q}_{0}bH}{s(s+b)}}\end{array}$$

(15)

where, ${\tilde{m}}_{1\mathrm{k}}={\tilde{m}}_{1\mathrm{k}}^{\mathrm{w}}+{\tilde{m}}_{1\mathrm{k}}^{\mathrm{a}}$, ${\tilde{m}}_2={\tilde{m}}_2^{\mathrm{w}}+{\tilde{m}}_2^{\mathrm{a}}$;

$$\xi ={\left[{\displaystyle \frac{\sqrt{{\left({\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}-{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}\right)}^2+4{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}{\tilde{C}}_{\mathrm{a}}{\tilde{C}}_{\mathrm{w}}}-\left({\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}+{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}\right)}{2{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\right]}^{{\displaystyle \frac{1}{2}}}\sqrt{s};$$

$$\eta ={\left[{\displaystyle \frac{-\sqrt{{\left({\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}-{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}\right)}^2+4{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}{\tilde{C}}_{\mathrm{a}}{\tilde{C}}_{\mathrm{w}}}-\left({\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}+{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}\right)}{2{\tilde{C}}_{\mathrm{v}}^{\mathrm{w}}{\tilde{C}}_{\mathrm{v}}^{\mathrm{a}}}}\right]}^{{\displaystyle \frac{1}{2}}}\sqrt{s}.$$

The numerical inverse Laplace transform of Equations (14)–(16) are performed by introducing Crump’s method because of its accuracy, efficiency, and stability when it comes to the problems of soil consolidation [39]; the semi-analytical solutions of EPAP, EPWP, and normalized settlement can be acquired in the time domain.

3.2. Considering Variable Permeability Coefficient

The equations that relate the permeability coefficient to the matric suction proposed by Brooks and Corey [40] were used to consider the variation in the permeability coefficient during the consolidation of unsaturated soils.

When $(u_{\mathrm{a}}-u_{\mathrm{w}})\le {(u_{\mathrm{a}}-u_{\mathrm{w}})}_{\mathrm{b}}$, $k_{\mathrm{w}}=k_{\mathrm{s}}$, $k_{\mathrm{a}}=0$;

When $(u_{\mathrm{a}}-u_{\mathrm{w}})>{(u_{\mathrm{a}}-u_{\mathrm{w}})}_{\mathrm{b}}$,

$$k_{\mathrm{a}}=k_{\mathrm{d}}{\left\{1-{\left[{\displaystyle \frac{{(u_{\mathrm{a}}-u_{\mathrm{w}})}_{\mathrm{b}}}{(u_{\mathrm{a}}-u_{\mathrm{w}})}}\right]}^{\lambda }\right\}}^2\left\{1-{\left[{\displaystyle \frac{{(u_{\mathrm{a}}-u_{\mathrm{w}})}_{\mathrm{b}}}{(u_{\mathrm{a}}-u_{\mathrm{w}})}}\right]}^{2+\lambda }\right\}$$

(16a)

$$k_{\mathrm{w}}=k_{\mathrm{s}}{\left[{\displaystyle \frac{{(u_{\mathrm{a}}-u_{\mathrm{w}})}_{\mathrm{b}}}{(u_{\mathrm{a}}-u_{\mathrm{w}})}}\right]}^{\mathsf{\mu }}.$$

(16b)

Here, $k_{\mathrm{d}}$ represents the permeability coefficient of the air phase in the dry state, $k_{\mathrm{s}}$ represents the permeability coefficient of the water phase in the saturated state, ${(u_{\mathrm{a}}-u_{\mathrm{w}})}_{\mathrm{b}}$ represents an air entry value, and $\lambda$ and $\mu$ are empirical constants.

In this paper, it is supposed that the permeability coefficients of the water and air phases remain unchanged if the suction change is small enough ($(\Delta u_{\mathrm{a}}-\Delta u_{\mathrm{w}})/\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)<{10}^{-8}$). On the other hand, the permeability coefficient will be recalculated cyclically until the consolidation is completed if $(\Delta u_{\mathrm{a}}-\Delta u_{\mathrm{w}})/\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)>{10}^{-8}$. This method is simple, and the alteration of the permeability coefficient follows the actual situation. Figure 3 shows this general process.

Moreover, the impact of the permeability coefficient variation on the consolidation is analyzed according to three scenarios, that is, where both $k_{\mathrm{a}}$ and $k_{\mathrm{w}}$ change, only $k_{\mathrm{w}}$ changes, and $k_{\mathrm{a}}$ and $k_{\mathrm{w}}$ are both constant.

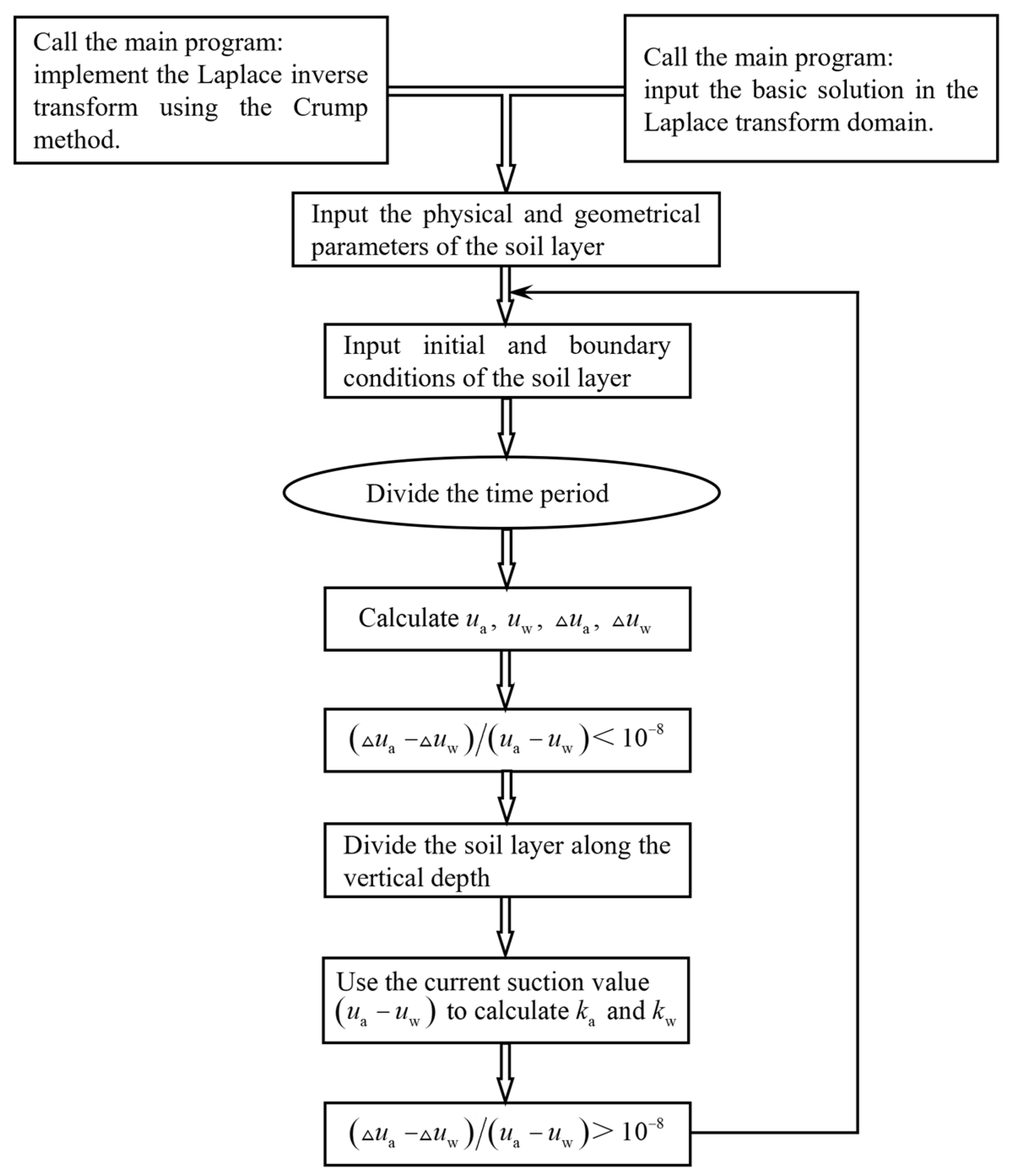
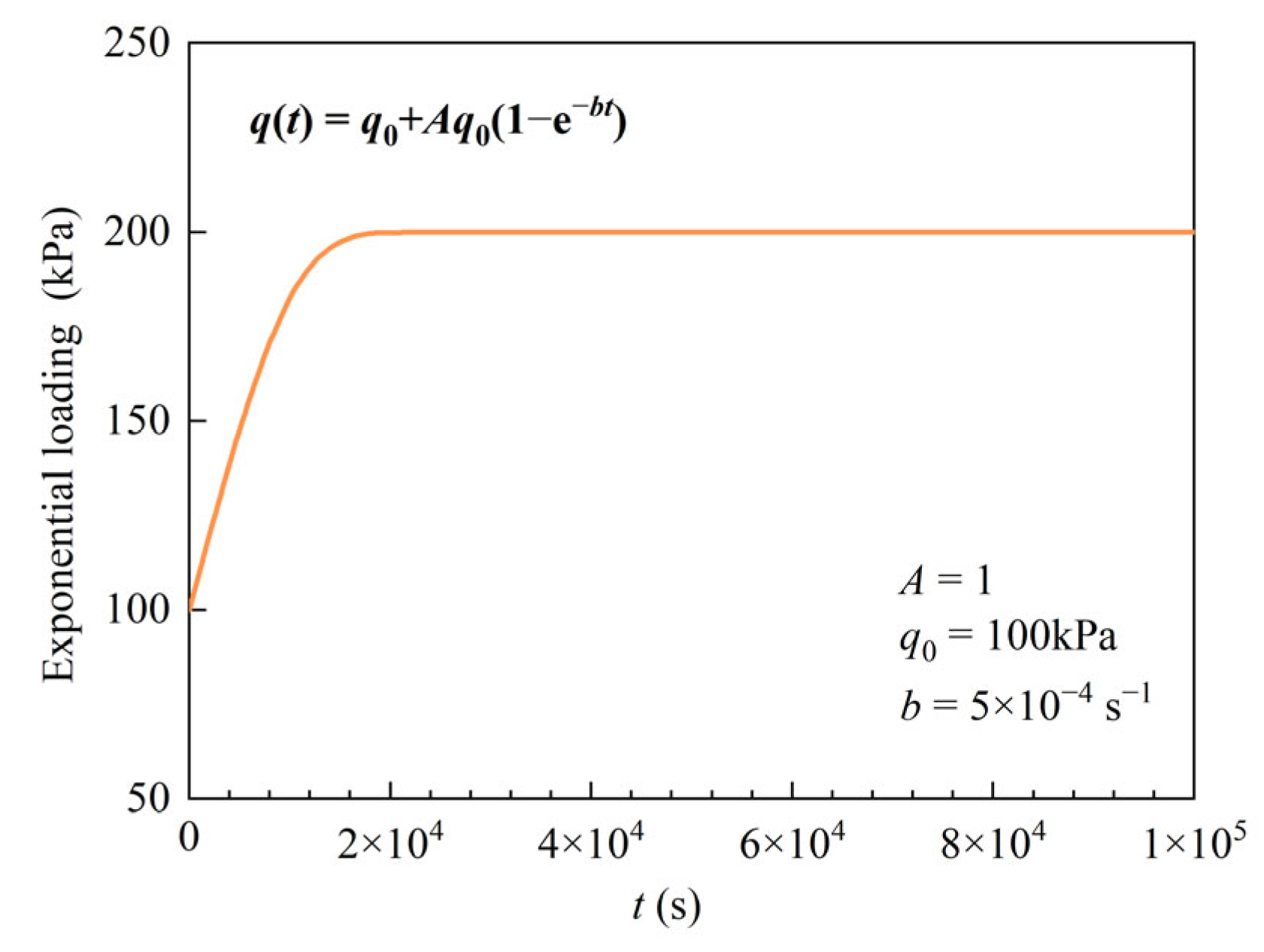
4. Verifications and Examples

4.1. Verification

In this study, the nonlinear variation of permeability coefficients during consolidation was considered by initially using the assumption of its constancy to derive a semi-analytical solution, which was then calculated by the numerical method shown in Figure 3. Therefore, it is not feasible to verify the results through another numerical model. Moreover, it is extremely difficult to measure the evolving permeability in real time during consolidation in laboratory or field conditions. Therefore, at this stage, this paper performs a degradation-based validation (a common method used in the theoretical study of unsaturated soil consolidation) [13,16,41] using analytical results from the literature [41] when unsaturated soils are assumed to be elastic and the permeability coefficient is assumed to be constant during consolidation, confirming the correctness and consistency of the model and solutions. The parameters used for the analysis are identical to those in the literature [41], and the results obtained are shown in Figure 4. The agreement between the two proves the reliability of the model and the solutions obtained in this paper.

4.2. Influence of $k_{\mathrm{a}}/k_{\mathrm{w}}$ on Consolidation

According to Figure 1, mathematical modeling is adopted to explore the consolidation behavior of the viscoelastic unsaturated soils subjected to exponential loading. The initial EPAP $u_{\mathrm{a}}^0=5\mathrm{kPa}$ and the initial EPWP $u_{\mathrm{w}}^0=40\mathrm{kPa}$ can be determined according to the method given by Fredlund and Hasan [6]. The following are the other parameters displayed: $H=10\mathrm{m}$, $S_{\mathrm{r}0}=80\%$, $k_{\mathrm{w}}={10}^{-10} \mathrm{m}/\mathrm{s}$, $n_0=50\%$. (The other parameters are as follows in Figure 5; $k_{\mathrm{a}}/k_{\mathrm{w}}=10$ and other parameters are as follows in

Table 1. Example parameters.

Parameter	Value	Unit	Parameter	Value	Unit
$E_{0\mathrm{n}}^{\mathrm{a}}=E_{1\mathrm{n}}^{\mathrm{a}}$	5 × 103	kPa	$E_{0\mathrm{n}}^{\mathrm{w}}=E_{1\mathrm{n}}^{\mathrm{w}}$	1 × 103	kPa
$E_{0\mathrm{s}}^{\mathrm{a}}=E_{1\mathrm{s}}^{\mathrm{a}}$	1.25 × 103	kPa	$E_{0\mathrm{s}}^{\mathrm{w}}=E_{1\mathrm{s}}^{\mathrm{w}}$	2.5 × 103	kPa
${\eta }_{\mathrm{n}}^{\mathrm{a}}$	5 × 10	kPa·s	${\eta }_{\mathrm{n}}^{\mathrm{w}}$	1 × 10	kPa·s
${\eta }_{\mathrm{s}}^{\mathrm{a}}$	1.25 × 10	kPa·s	${\eta }_{\mathrm{s}}^{\mathrm{w}}$	2.5 × 10	kPa·s

[26,29], except the analytical parameters in Figure 5, Figure 6, Figure 7 and Figure 8).

Exponential loading $q(t)=q_0+A{q}_0\left(1-{\mathrm{e}}^{-bt}\right)$ is exerted on the unsaturated soil layer as shown in Figure 5. Here, $q_0$ represents the incipient surcharge, A represents the loading constant, and b represents the nonlinear rate of exponential loading. ${\mathrm{U}}_{\mathrm{s}}$ is the degree of consolidation, ${\mathrm{U}}_{\mathrm{s}}=w(t)/w(\infty )$.

In this study, $q_0=100\mathrm{kPa}$, A = 1, and $b=5\times {10}^{-4}$ s⁻¹ were chosen to conduct research on the consolidation behavior of viscoelastic unsaturated soils under exponential loading.

Figure 6 shows the variations of EPAP, EPWP, and ${\mathrm{U}}_{\mathrm{S}}$ at different values of $k_{\mathrm{a}}/k_{\mathrm{w}}$. It is shown that the larger $k_{\mathrm{a}}/k_{\mathrm{w}}$ is, the faster the excess pore pressures dissipate. There are two periods (i.e., the prior and latter periods) of EPAP and three periods (i.e., the prior, intermediate, and latter periods) of EPWP in the dissipation process. It can be found from Figure 6a that the EPAP starts to dissipate at the end of the prior period when the load reached its maximum except when $k_{\mathrm{a}}/k_{\mathrm{w}}=100$. This is because the dissipation rate of EPAP is greater than the increasing rate of the loading when $k_{\mathrm{a}}/k_{\mathrm{w}}=100$. Figure 6b shows that the prior and intermediate dissipation periods of EPWP are similar to the whole dissipation process of EPAP. The main reason for this is that the permeability coefficient of EPAP is bigger than that of EPWP in practice; thus, the water phase begins to flow when the air phase flows to termination. In the latter period, the dissipation curves of EPWP at varying values tend to become the same, as the EPAP has been fully dissipated. The dissipation curves of EPWP shown in Figure 6 are roughly double-S-typed, and there is a steady period in these curves. When the EPAP dissipates to zero, it is just the beginning of the steady period. Figure 6c shows the variation in the average ${\mathrm{U}}_{\mathrm{S}}$ with time at different values of $k_{\mathrm{a}}/k_{\mathrm{w}}$. The larger $k_{\mathrm{a}}/k_{\mathrm{w}}$, the earlier the soil begins to be consolidated. In the latter period, the dissipation curves of the average ${\mathrm{U}}_{\mathrm{S}}$ with different values of $k_{\mathrm{a}}/k_{\mathrm{w}}$ tend towards the same. This indicates that the consolidation of unsaturated soils is primarily triggered by the dissipation of the EPAP in the prior period, and by the dissipation of the EPWP in the latter period.

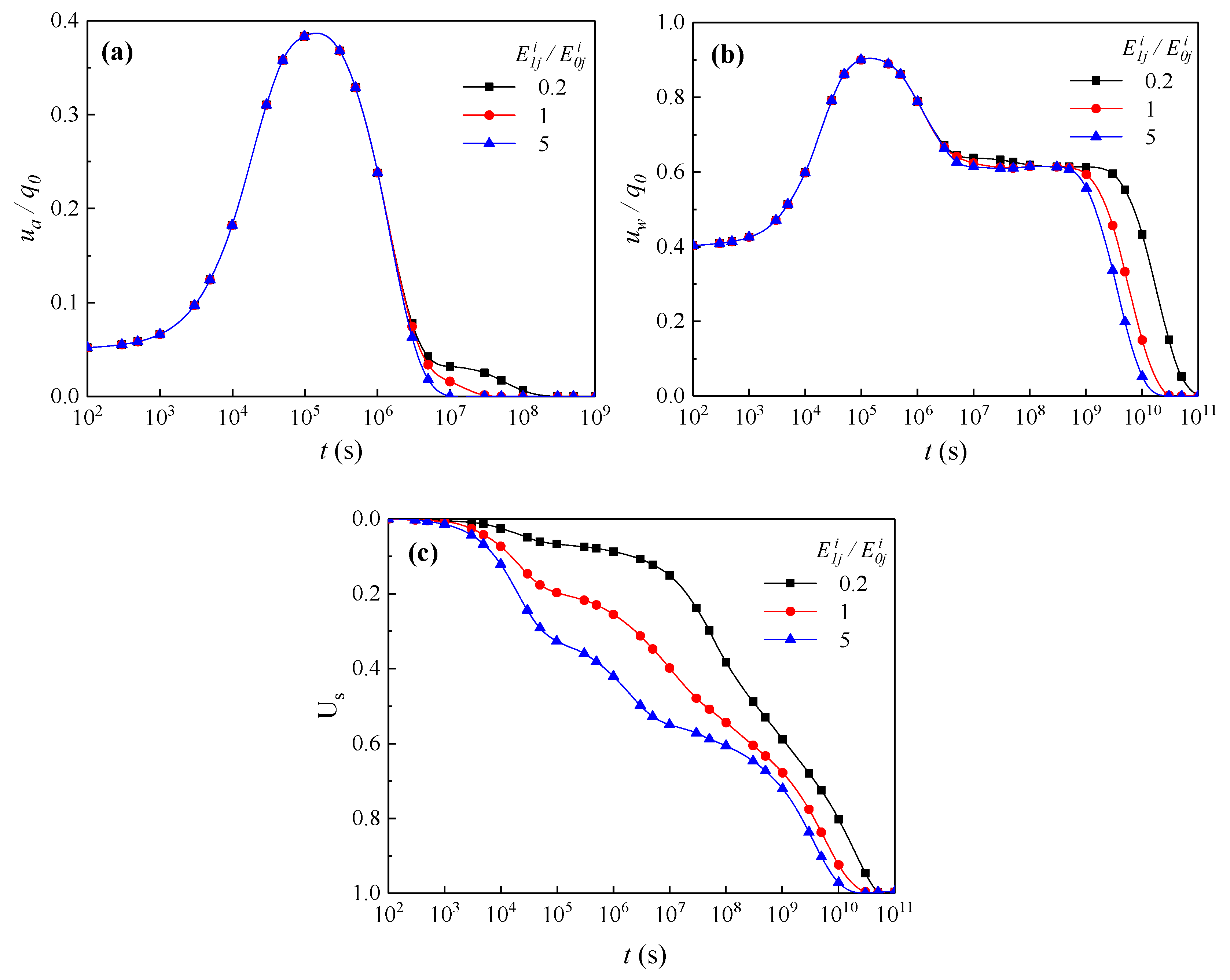
4.3. Influence of $E_{1j}^i/E_{0j}^i$ on Consolidation

Figure 7 depicts the changes in the EPAP, EPWP, and ${\mathrm{U}}_{\mathrm{S}}$ at different ratios of elastic modulus $E_{1j}^i/E_{0j}^i$, where i denotes a (air) or w (water) and j denotes n (net normal tress) or s (suction); the subscripts 0 and 1 represent the same meaning as before. It can be found that the value of $E_{1j}^i/E_{0j}^i$ has no effect on the prior dissipation of EPAP and EPWP but affects the ${\mathrm{U}}_{\mathrm{S}}$ in the prior period. The reason for this is that the degree of consolidation of viscoelastic unsaturated soils is not only determined by the dissipation of EPAP and EPWP, but also by the coefficient of volume change. Figure 7c indicates the variation curves of the average ${\mathrm{U}}_{\mathrm{S}}$ with time appear anti-S-typed when $E_{1j}^i<E_{0j}^i$. When $E_{1j}^i>E_{0j}^i$, the variation curves of the average ${\mathrm{U}}_{\mathrm{S}}$ along time appear double-S-typed. And the larger $E_{1j}^i/E_{0j}^i$ is, the earlier and the faster the consolidation takes place. This is because the elasticity modulus is a key parameter that characterizes the ability of soil to resist elastic deformation. A higher modulus (with a higher coefficient of consolidation) results in smaller soil deformation under the same stress, which leads to a faster rate of consolidation.

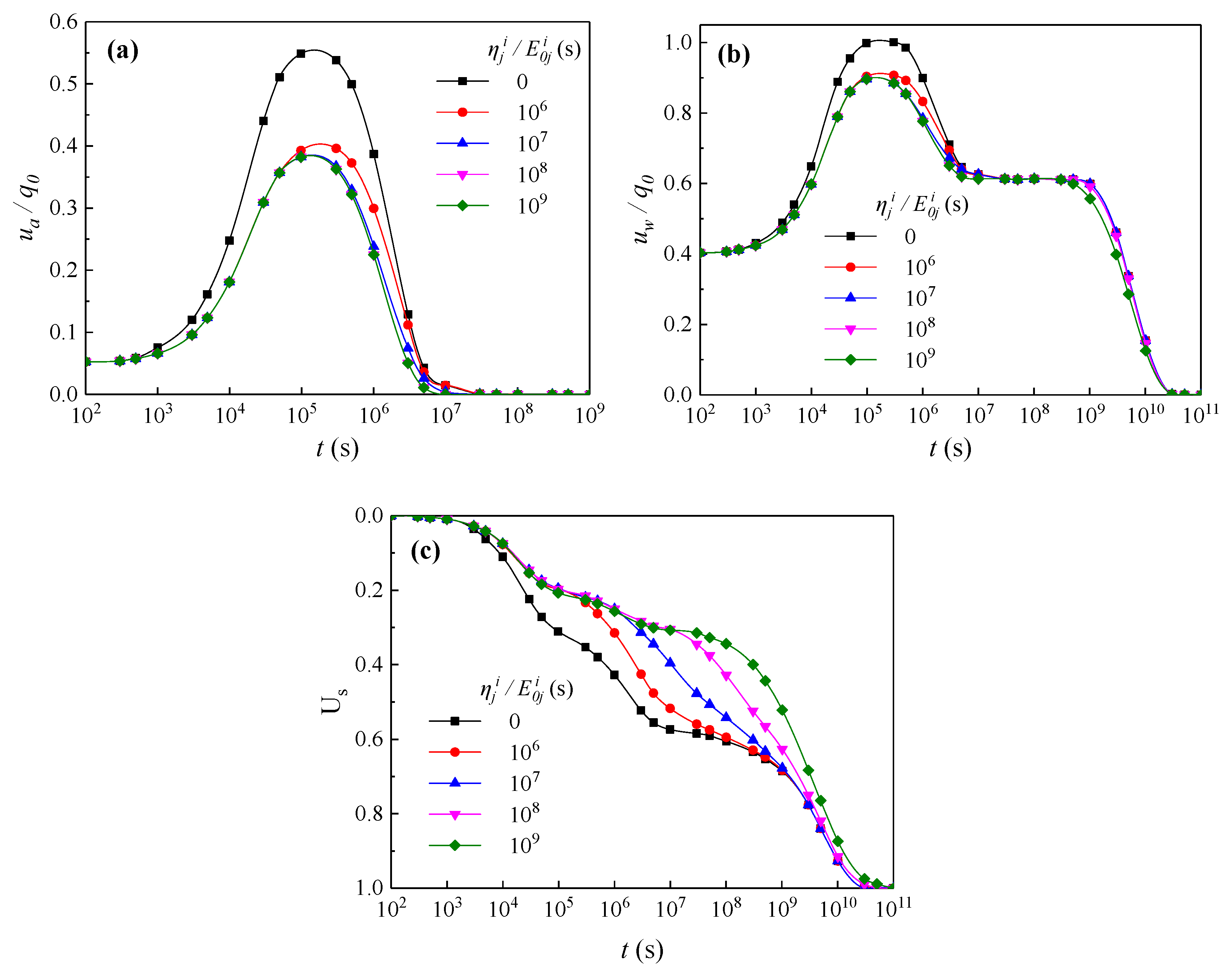
4.4. Influence of ${\eta }_j^i/E_{0j}^i$on Consolidation

Figure 8 depicts the changes in EPAP, EPWP, and ${\mathrm{U}}_{\mathrm{S}}$ with time at different values of ${\eta }_j^i/E_{0j}^i$. Figure 8a,b show that the value of the viscous coefficient has almost no effect on the dissipation of the EPAP and EPWP when $\eta \ne 0$. In addition, the peak of the dissipation curves for EPAP and EPWP at $\eta \ne 0$ is lower than those at $\eta =0$. Figure 8c shows that the larger the viscous coefficient η, the slower the consolidation rate. This phenomenon can be attributed to the fact that a higher coefficient of viscosity in the soil results in a slower rate of deformation of the soil skeleton, leading to an extended consolidation time.

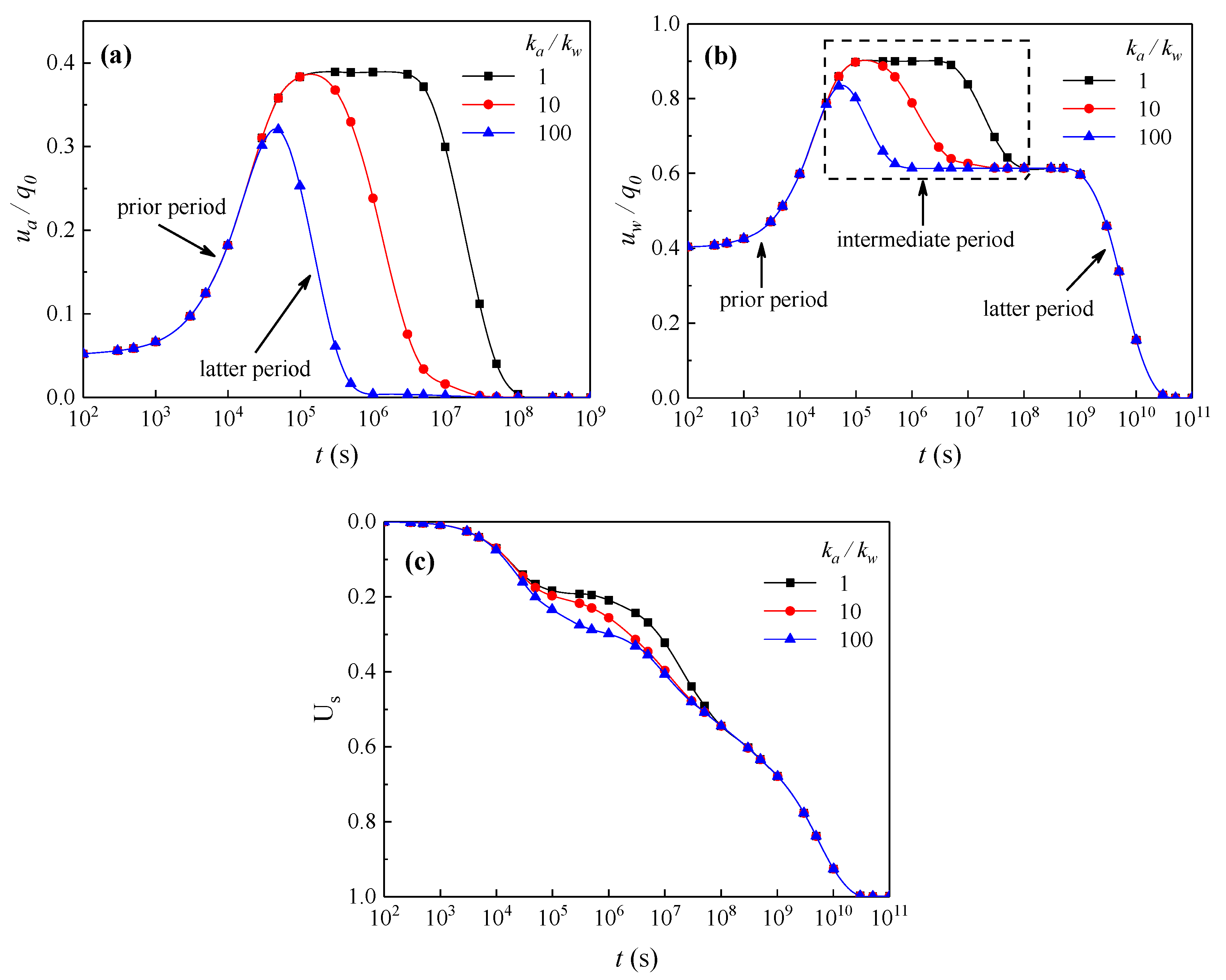
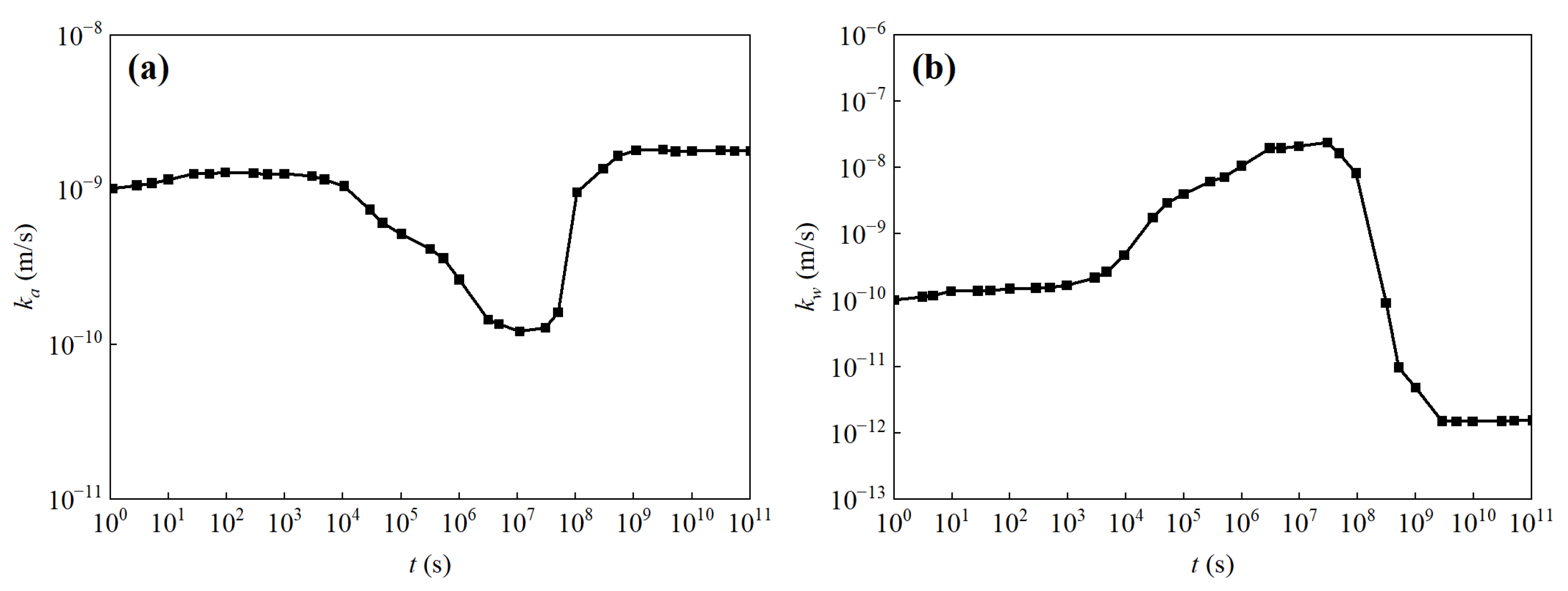
4.5. Analysis of the Permeability Coefficient Variation

Since increasing the permeability coefficient will significantly accelerate the dissipations of EPAP and EPWP, it is imperative to explore the variations of the permeability coefficients $k_{\mathrm{a}}$ and $k_{\mathrm{w}}$ during the consolidation process. Figure 9 shows the changes in the permeability coefficients of the air and water phases with time obtained through Figure 3. Figure 9a depicts the variation of the permeability coefficient of the air phase $k_{\mathrm{a}}$ under exponential loading in the time domain. It is shown that $k_{\mathrm{a}}$ increases slightly at first and that it reduces evidently until the end of the dissipation of the EPAP when the load approaches stability. Later, $k_{\mathrm{a}}$ increases quickly to the initial value after a period of stability. Figure 9b depicts the variation of the permeability coefficient of the water phase $k_{\mathrm{w}}$ under exponential loading in the time domain. It is shown that $k_{\mathrm{w}}$ displays the same phenomenon as $k_{\mathrm{a}}$ at first. However, $k_{\mathrm{w}}$ will increase quickly during the intermediate period, which is different from the changing regularity of $k_{\mathrm{a}}$. Finally, $k_{\mathrm{w}}$ reduces quickly to a smaller stable one compared to the initial value.

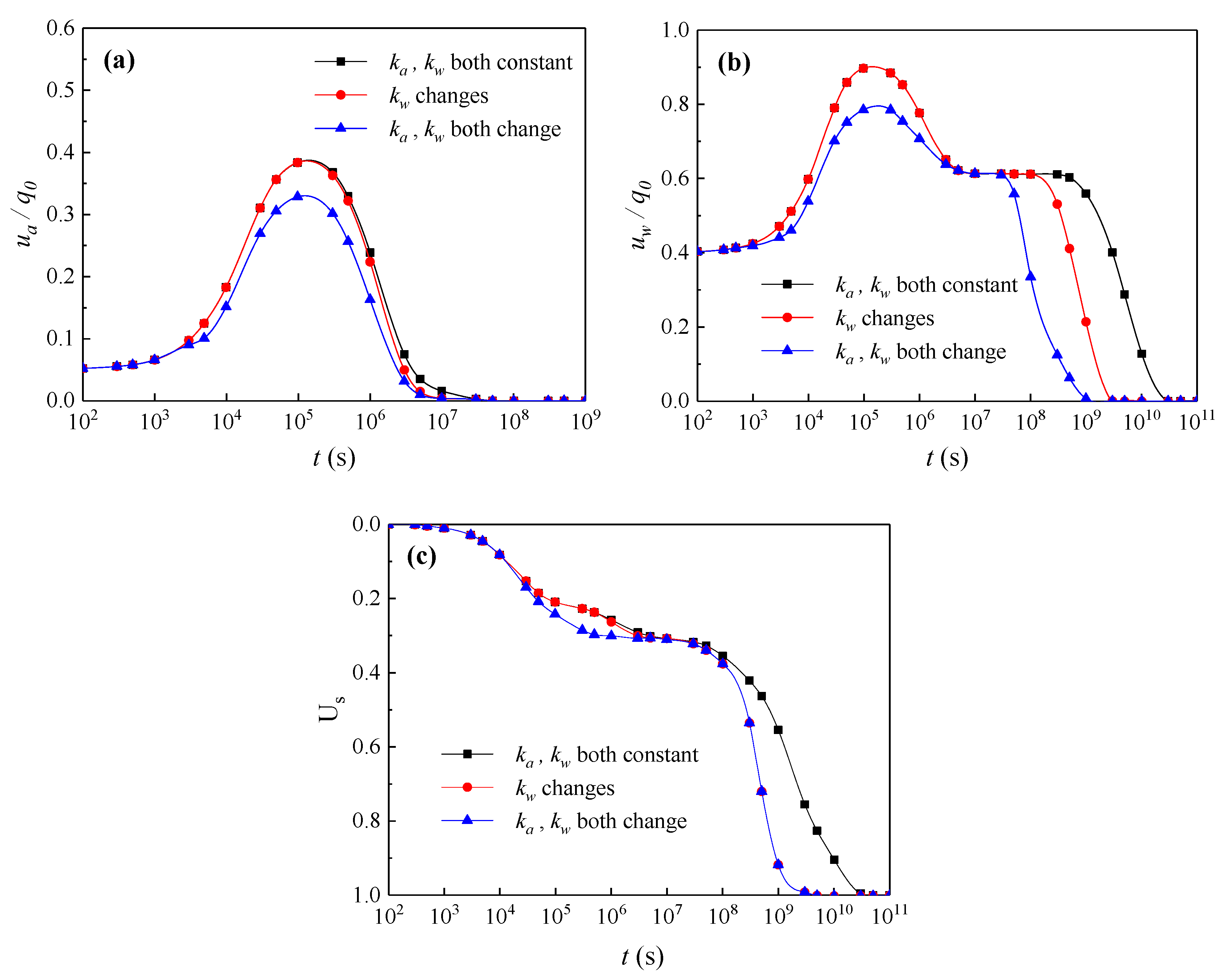
4.6. Influence of the Permeability Coefficient Variation on the Consolidation

In the following analysis, $k_{\mathrm{a}}/k_{\mathrm{w}}=10$, $k_{\mathrm{w}}={10}^{-10} \mathrm{m}/\mathrm{s}$, and other parameters are the same as given before. Figure 10 depicts the changes in EPAP, EPWP, and the degree of consolidation under three kinds of variation for the permeability coefficients. The alteration of $k_{\mathrm{a}}$ influences the dissipation of EPAP during the whole dissipation process and the EPWP in the prior and intermediate periods, but it has no influence on the dissipation of EPWP in the latter period. The change in $k_{\mathrm{w}}$ has no impact on the dissipation of EPAP during the whole dissipation process and the EPWP in the prior and intermediate periods. However, it has an impact on the dissipation of EPWP in the latter period.

5. Conclusions

(1)

The parameter $E_{1j}^i/E_{0j}^i$ has no impact on the dissipation of EPAP and EPWP during the early stage. As $E_{1j}^i/E_{0j}^i$ increases, the coefficient of consolidation becomes larger, and the dissipation of EPWP occurs earlier and more rapidly in the later stages.

(2)

The influence of the viscosity coefficient $\eta$ on EPAP and EPWP is very small. However, a larger viscosity coefficient $\eta$ slows the rate of soil deformation, leading to slower consolidation.

(3)

The permeability coefficients of the air and water phases both change during the consolidation process. The permeability coefficient of the air phase returns to the initial value after the completion of consolidation, while the permeability coefficient of the water phase is lower than the initial value.

(4)

Considering the variations of the permeability coefficient of the water phase and air phase, the dissipations of EPAP and EPWP will accelerate. Via comprehensive analysis, it can be found that $k_{\mathrm{a}}$ is the greater influencing factor in the early stage of the consolidation and $k_{\mathrm{w}}$ is more important in the later stage.