Research on Relative Position and Attitude Measurement of Space Maglev Vibration Isolation Control System
Abstract
1. Introduction
2. Relative Position and Attitude Measurement of Maglev Vibration Isolation System
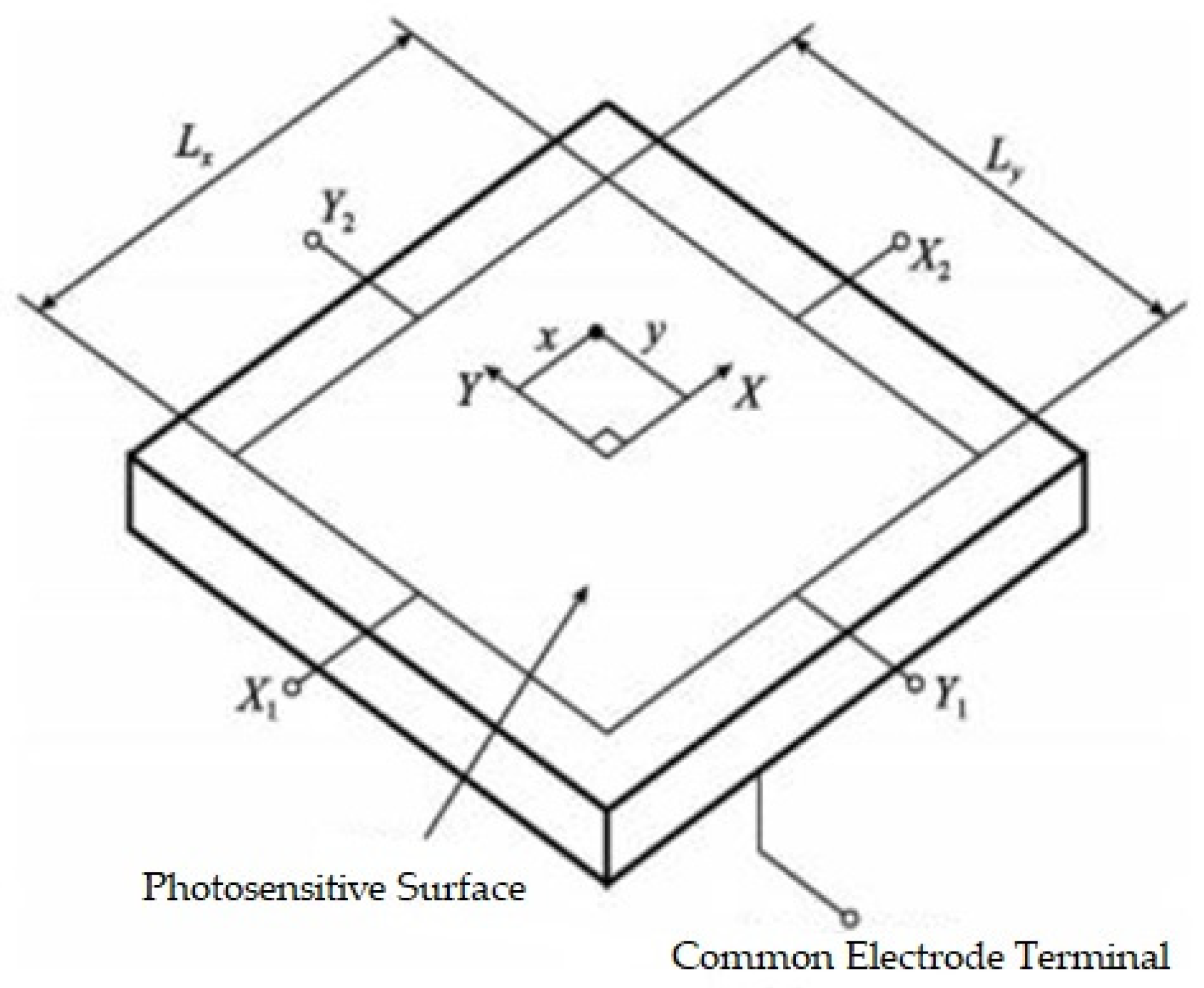
2.1. Measurement Scheme Based on Two-Dimensional PSD
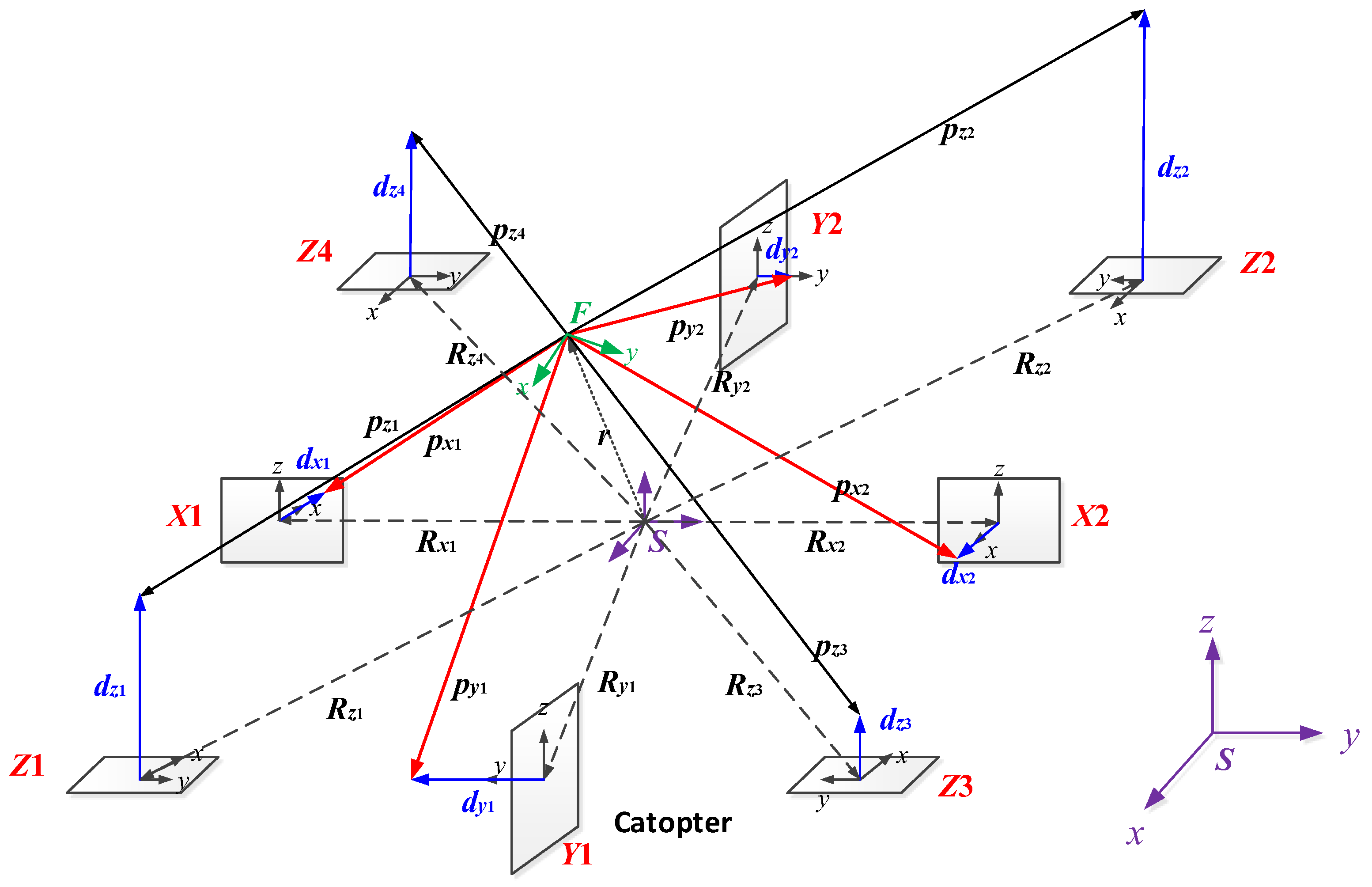
2.2. Relative Position and Attitude Measurement Model of Maglev Vibration Isolation System
2.3. Relative Position and Attitude Measurement Based on PSD
2.4. Relative Position and Attitude Measurement Based on Eddy Current
3. Failure Mode Analysis
3.1. Fully Redundant
3.2. Vertical Failure 1 Set
3.3. Horizontal Failure 1 Set
4. Displacement Sensing and Signal Acquisition
4.1. Selection of Displacement Sensor
- (1)
- Laser displacement sensor
- (2)
- Eddy current displacement sensor
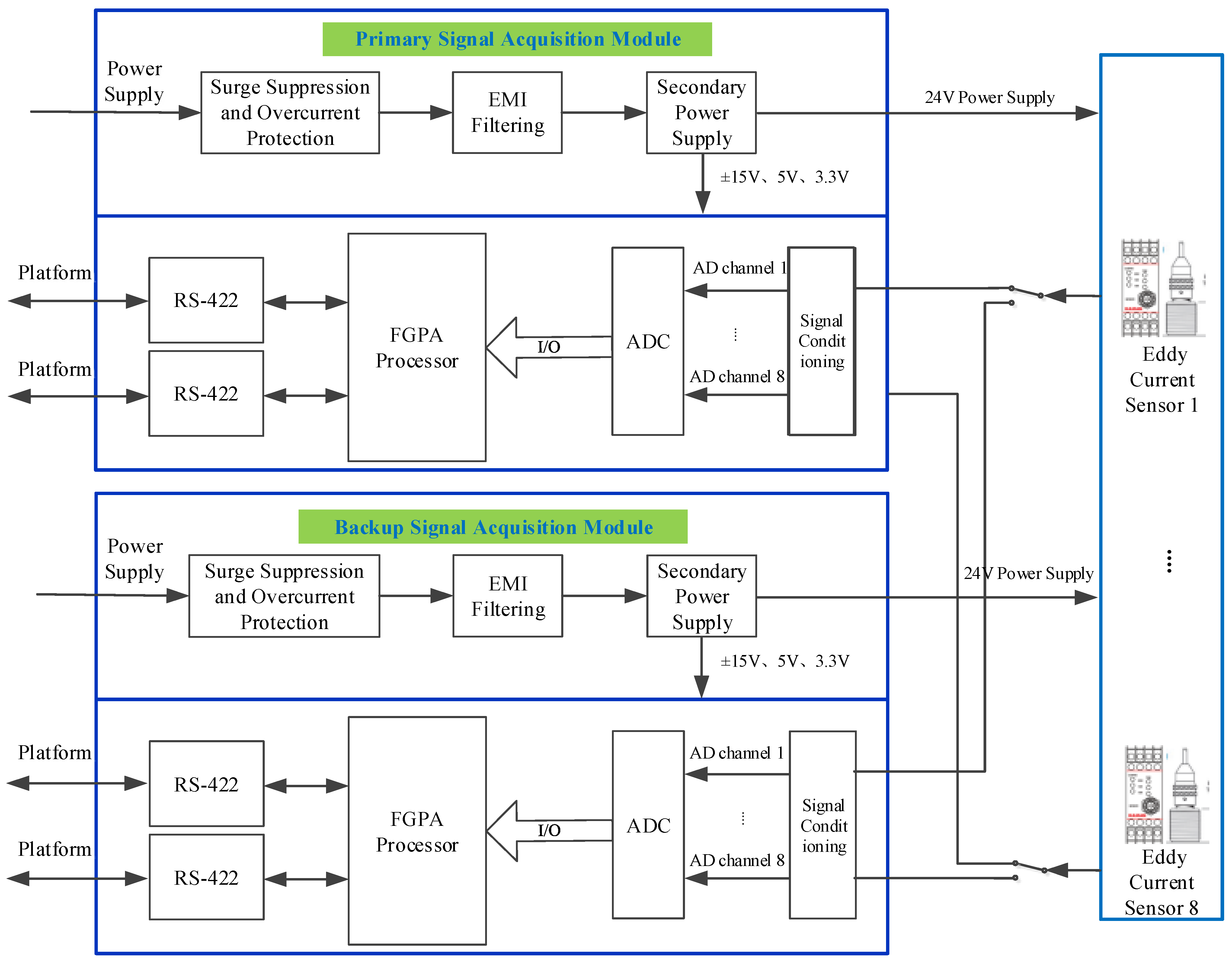
4.2. Sensor Circuit Box Design
- (1)
- The power supply includes several parts, including surge suppression and overcurrent protection, EMI filtering, and a secondary power supply. It provides various voltage levels of driving power supply for the functional circuit section and also provides input power supply for eight sensors.
- (2)
- The functional circuit includes a processor, ADC sampling circuit, sensing signal conditioning circuit, and 422 communication. Its main function is high-precision sampling of eddy current sensor signals, and it is also responsible for data exchange with the attitude and orbit control system.
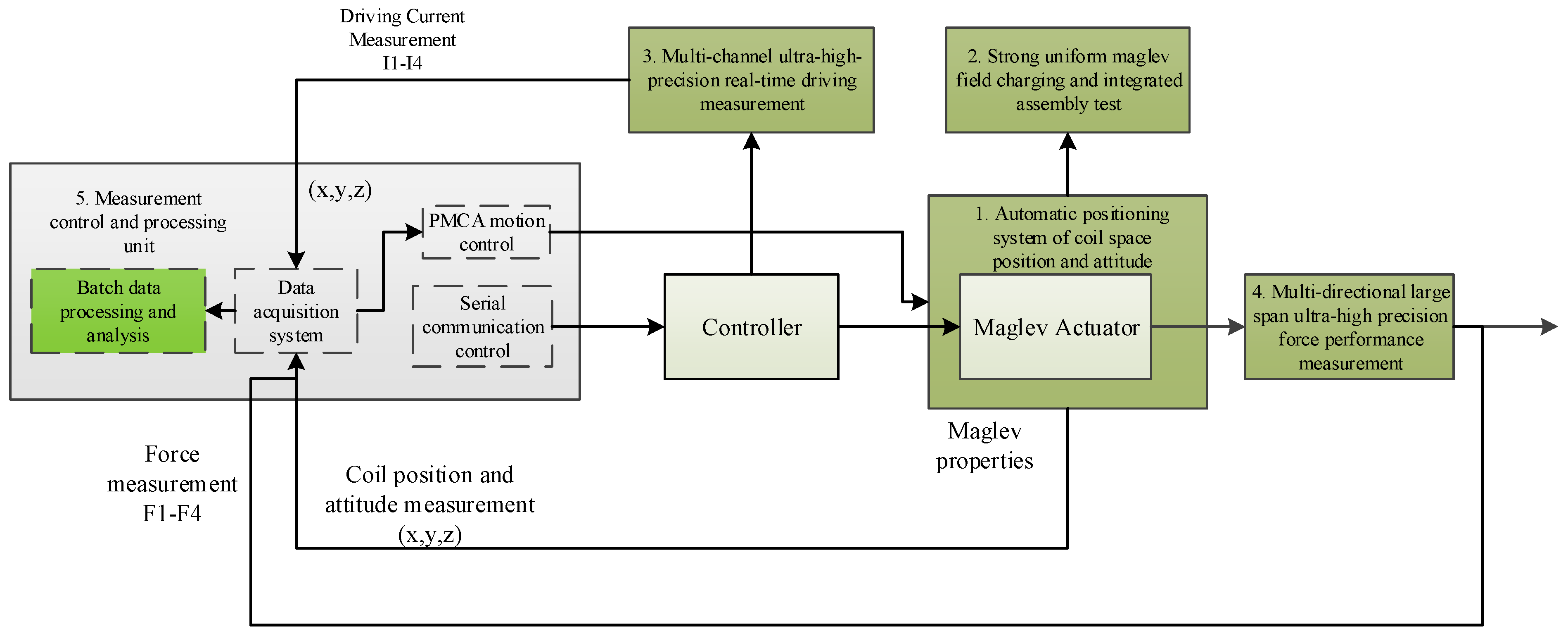
5. System Design and Testing
5.1. Maglev Vibration Isolation Control System Design
5.2. System Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, M.; Wang, J. Research on Space Maglev Vibration Isolation Control System Modeling and Simulation. Appl. Sci. 2025, 15, 1648. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, B.; Cui, N.; Zhao, S. Tracking Control of a Maglev Vibration Isolation System Based on a High-Precision Relative Position and Attitude Model. Sensors 2019, 19, 3375. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.; Johnson, L. Advanced Vibration Control Using Magnetic Levitation. J. Precis. Eng. 2020, 45, 234–249. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y. Relative Measurement Techniques in Maglev Systems. Int. J. Mech. Sci. 2019, 78, 112–125. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, R. Applications of Maglev Technology in High-Precision Industries. IEEE Trans. Ind. Electron. 2021, 68, 4567–4578. [Google Scholar]
- Lee, K.; Park, S. Design and Control of a Maglev-Based Vibration Isolation System with Relative Displacement Feedback. Mechatronics 2018, 52, 78–90. [Google Scholar] [CrossRef]
- Brown, T.; Davis, M. High-Precision Vibration Isolation Using Maglev and Optical Relative Measurement Sensors. Sens. Actuators A Phys. 2022, 335, 113–125. [Google Scholar]
- Jiang, D.; Shan, Y.; Wang, D.; Yang, J. Data analysis and processing for Maglev vibration test systems. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015. [Google Scholar] [CrossRef]
- Wu, Q.; Yue, H.; Liu, R.; Zhang, X.; Ding, L.; Liang, T.; Deng, Z. Measurement Model and Precision Analysis of Accelerometers for Maglev Vibration Isolation Platforms. Sensors 2015, 15, 20053–20068. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Xue, S.; He, N.; Long, Z. Electromagnetic field analysis and modeling of a relative position detection sensor for high speed maglev trains. Sensors 2012, 12, 6447–6462. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Gong, Z.; Ding, L.; Li, S.; Yue, H.; Gao, H.; Deng, Z. Payload-agnostic decoupling and hybrid vibration isolation control for a maglev platform with redundant actuation. Mech. Syst. Signal Process. 2021, 146, 106985. [Google Scholar] [CrossRef]
- Zhang, D.; Long, Z.; Xue, S.; Zhang, J. Optimal Design of the Absolute Positioning Sensor for a High-Speed Maglev Train and Research on Its Fault Diagnosis. Sensors 2012, 12, 10621–10638. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-S.; Cao, X.-K.; Guo, B.; Wang, Q.; Fu, Y.-H. An approach of Eddy Current Sensor Calibration in State Estimation for Maglev System. In Proceedings of the 2007 International Confernece on Electrical Machines and Systems, Seoul, Republic of Korea, 8–11 October 2007. [Google Scholar]
- Owen, R.B.; Maggiore, M. Implementation and model verification of a magnetic levitation system. In Proceedings of the 2005, American Control Conference, 2005, Portland, OR, USA, 8–10 June 2005; Volume 2, pp. 1142–1147. [Google Scholar] [CrossRef]
- Southwest Jiaotong University. Vibration Test Bench for Electrodynamic-Suspension Magnetic Levitation (Maglev) Trains and Testing Method Using Same. US17540622, 21 June 2022. [Google Scholar]
- Zhang, H.; Wang, L.; Yang, N.; Cao, X. Study of Sensor Calibration Method for the Maglev Control System. Trans. China Electrotech. Soc. 2006, 21, 71–76. [Google Scholar] [CrossRef]



| Design Value | Actual Measurement Value | Linear Fitting Current (mA) | Current Error (mA) | ||||
|---|---|---|---|---|---|---|---|
| Input Voltage (V) | Output Current (mA) | Up and Down Difference (mA) | Output Current (mA) | Up-and-Down Difference (mA) | Feedback Voltage (V) | ||
| −5 | 100 | 20 | −99.756 | −20.097 | −9.9615 | −99.7085 | −0.0475 |
| −4 | 80 | 20 | −79.659 | −19.994 | −7.9587 | −79.7228 | 0.0638 |
| −3 | 60 | 20 | −59.665 | −19.948 | −5.9615 | −59.7372 | 0.0722 |
| −2 | 40 | 20 | −39.717 | −19.914 | −3.9682 | −39.7515 | 0.0345 |
| −1 | 20 | 20 | −19.803 | −19.944 | −1.97738 | −19.7658 | −0.0372 |
| 0 | 0 | 20 | 0.141 | −19.99 | 18.422 mV | 0.2198 | −0.0788 |
| 1 | 20 | 20 | 20.131 | −20.005 | 2.0152 | 20.2055 | −0.0745 |
| 2 | 40 | 20 | 40.136 | −20.075 | 4.0178 | 40.1911 | −0.0551 |
| 3 | 60 | 20 | 60.211 | −20.045 | 6.0225 | 60.1768 | 0.0342 |
| 4 | 80 | 20 | 80.256 | −19.887 | 8.0258 | 80.1625 | 0.0935 |
| 5 | 100 | 20 | 100.143 | / | 10.0219 | 100.1481 | −0.0051 |
| Design Value | Actual Measurement Value | Linear Fitting Current (mA) | Current Error (mA) | ||||
|---|---|---|---|---|---|---|---|
| Input Voltage (V) | Output Current (A) | Up and Down Difference (mA) | Output Current (mA) | Up-and-Down Difference (mA) | Feedback Voltage (V) | ||
| −5 | 3.5 | / | −3310.4 | / | −9.441 | −3311.5314 | 1.1314 |
| −4 | 2.8 | −700 | −2647.8 | 662.6 | −7.5504 | −2648.4593 | 0.6593 |
| −3 | 2.1 | −700 | −1984.32 | 663.48 | −5.6606 | −1985.3872 | 1.0672 |
| −2 | 1.4 | −700 | −1322.9 | 661.42 | −3.7698 | −1322.3151 | −0.5849 |
| −1 | 0.7 | −700 | −660.58 | 662.32 | −1.8803 | −659.2430 | −1.3370 |
| 0 | 0 | −700 | 2.88 | 663.46 | 11.021 mV | 3.8291 | −0.9491 |
| 1 | 0.7 | −700 | 665.29 | 662.41 | 1.9066 | 666.9012 | −1.6112 |
| 2 | 1.4 | −700 | 1328.85 | 663.56 | 3.8027 | 1329.9733 | −1.1233 |
| 3 | 2.1 | −700 | 1993.1 | 664.25 | 5.6983 | 1993.0454 | 0.0546 |
| 4 | 2.8 | −700 | 2656.9 | 663.8 | 7.5943 | 2656.1175 | 0.7825 |
| 5 | 3.5 | −700 | 3321.1 | 664.2 | 9.4899 | 3319.1895 | 1.9105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Wang, J. Research on Relative Position and Attitude Measurement of Space Maglev Vibration Isolation Control System. Appl. Sci. 2025, 15, 4912. https://doi.org/10.3390/app15094912
Ye M, Wang J. Research on Relative Position and Attitude Measurement of Space Maglev Vibration Isolation Control System. Applied Sciences. 2025; 15(9):4912. https://doi.org/10.3390/app15094912
Chicago/Turabian StyleYe, Mao, and Jianyu Wang. 2025. "Research on Relative Position and Attitude Measurement of Space Maglev Vibration Isolation Control System" Applied Sciences 15, no. 9: 4912. https://doi.org/10.3390/app15094912
APA StyleYe, M., & Wang, J. (2025). Research on Relative Position and Attitude Measurement of Space Maglev Vibration Isolation Control System. Applied Sciences, 15(9), 4912. https://doi.org/10.3390/app15094912






