An Ultrathin Wideband Angularly Stable Frequency Selective Surface Bandpass Filter for S-C Band Coverage
Abstract
1. Introduction
2. Materials and Methods
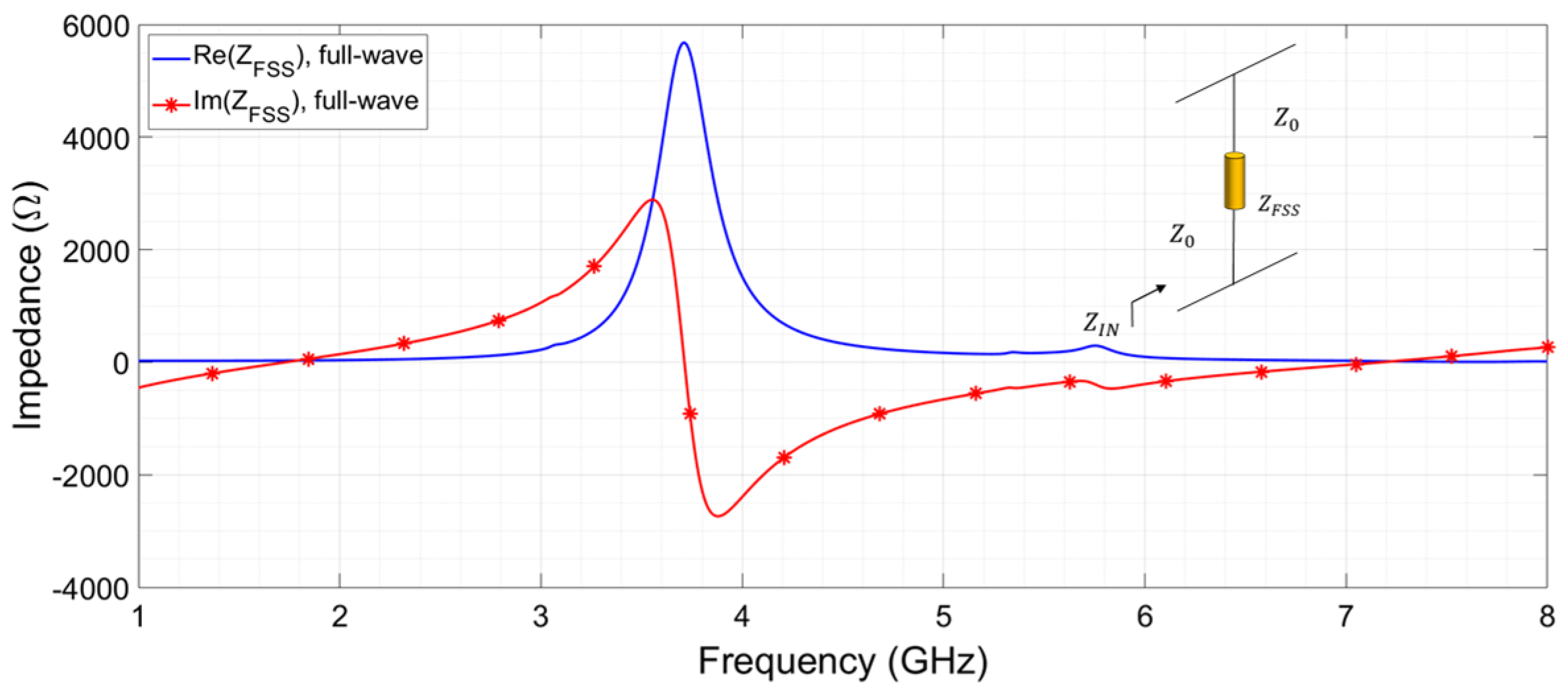
2.1. Design Procedure and Analysis of the FSS Element
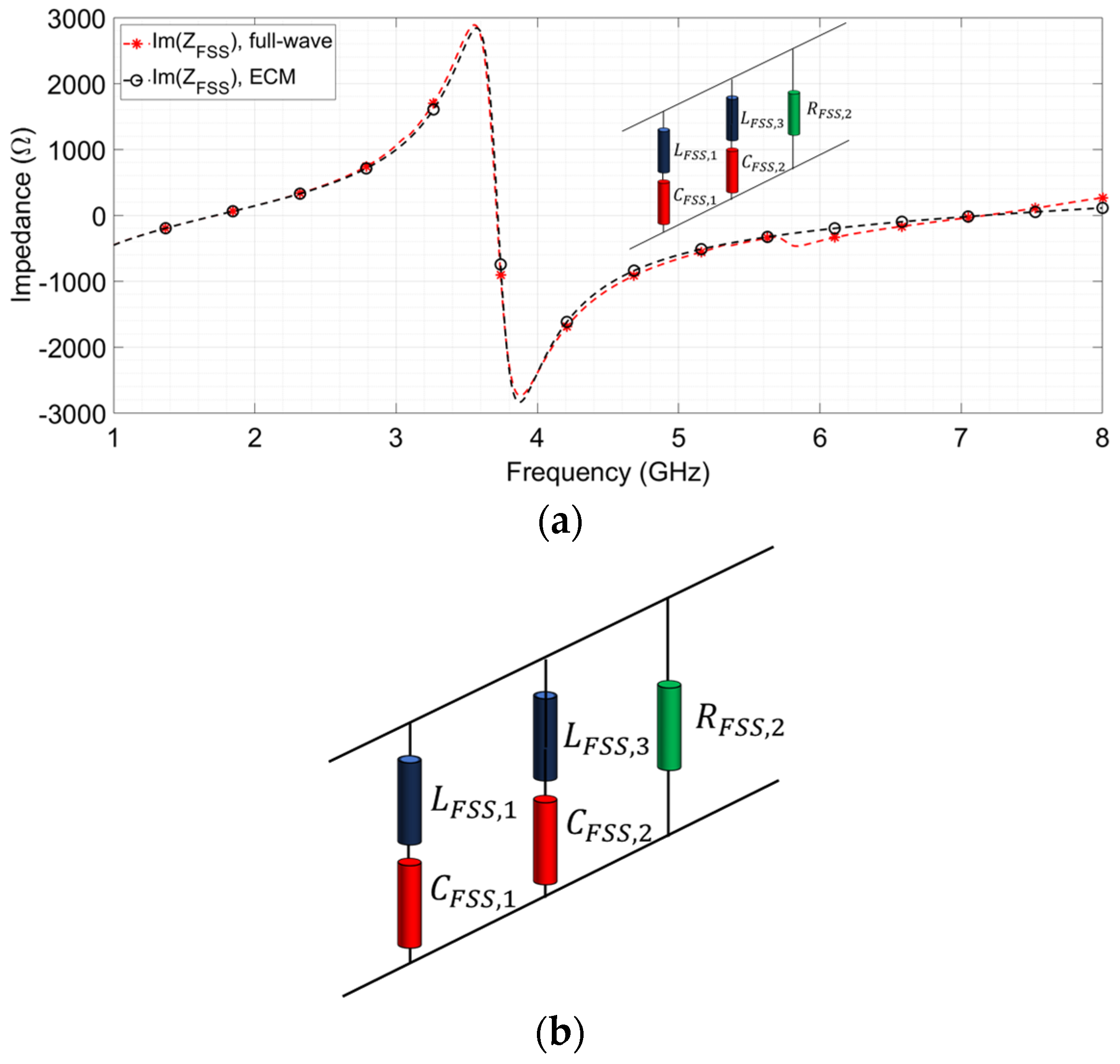
2.2. Equivalent Circuit Model Analysis
3. Results
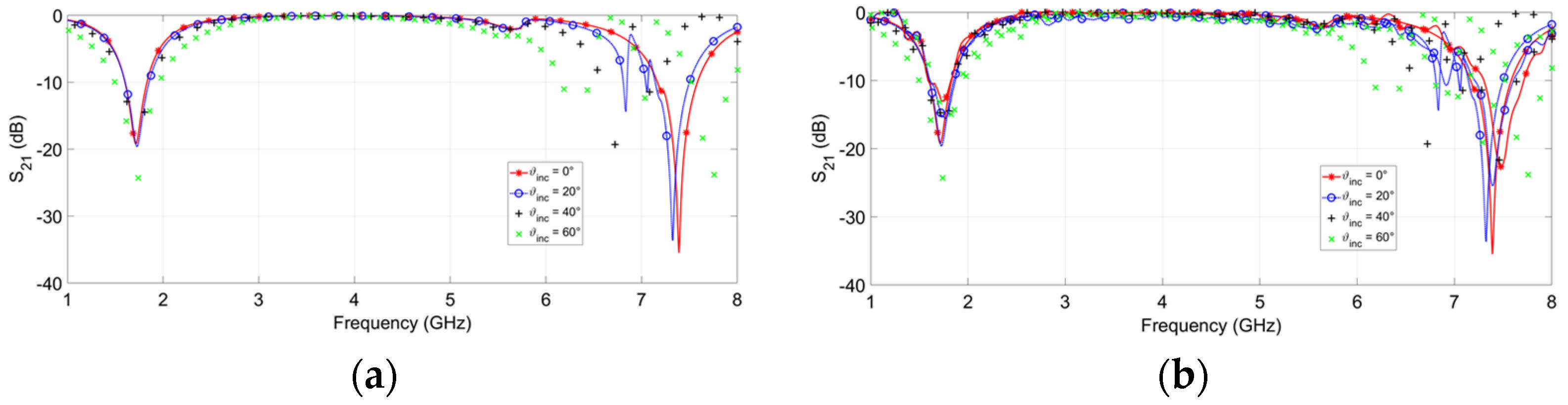
3.1. Numerical Results
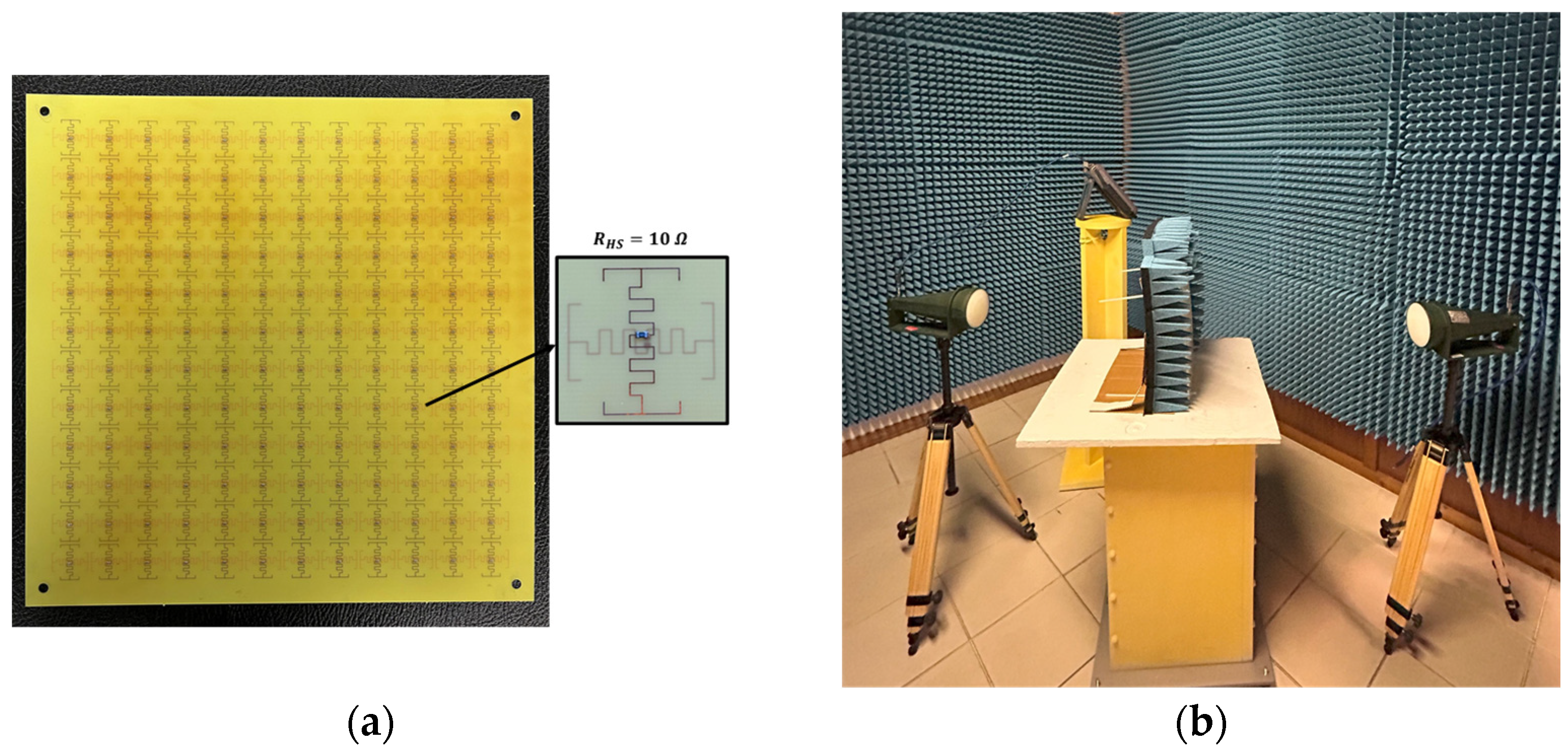
3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Tan, J.; Kang, L.; Tang, F.; Zhao, M.; Kato, N. Frequency Selective Surface towards 6G Communication Systems: A Contemporary Survey. IEEE Commun. Surv. Tutor. 2024, 26, 1635–1675. [Google Scholar] [CrossRef]
- Jha, K.R.; Singh, G.; Jyoti, R. A Simple Synthesis Technique of Single-Square-Loop Frequency Selective Surface. Prog. Electromagn. Res. B 2012, 45, 165–185. [Google Scholar] [CrossRef]
- Jie, H.; Zhao, Z.; Zeng, Y.; Chang, Y.; Fan, F.; Wang, C.; See, K.Y. A review of intentional electromagnetic interference in power electronics: Conducted and radiated susceptibility. IET Power Electron. 2024, 17, 1487–1506. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Hou, J.; Huang, J.; Hou, Z.; Song, M.; Denidni, T.A. Wideband and Wide-Angle Switchable Spatial Filter/Shielding With Polarization-Independent Response. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1421–1425. [Google Scholar] [CrossRef]
- Wang, D.; Zhuang, Y.; Shen, L.; Meng, X.; Wang, G.; Tang, S.; Cai, T. Stealth radome with an ultra-broad transparent window and a high selectivity transition band. Opt. Express 2022, 30, 16009–16019. [Google Scholar] [CrossRef] [PubMed]
- Varikuntla, K.K.; Singaravelu, R. Design of a hybrid A-sandwich radome using a strongly coupled frequency selective surface element. Int. J. Microw. Wirel. Technol. 2020, 12, 738–748. [Google Scholar] [CrossRef]
- De Sabata, A.; Matekovits, L.; Buta, A.; Dassano, G.; Silaghi, A. Frequency Selective Surface for Ultra-Wide Band Filtering and Shielding. Sensors 2022, 22, 1896. [Google Scholar] [CrossRef]
- Ghosh, J.; Dutta, R.; Sarkhel, A.; Abbasi, Q.H. Design of miniaturize flexible wideband frequency selective surface for electromagnetic shielding application. Waves Random Complex Media 2022, 32, 1–21. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Y.; Liu, P.; Tian, T.; Lin, M. An Ultra-Broadband Energy Selective Surface Design Method: From Filter Circuits to Metamaterials. IEEE Trans. Antennas Propag. 2023, 71, 5865–5873. [Google Scholar] [CrossRef]
- Duan, K.; Chen, K.; Jiang, T.; Zhao, J.; Feng, Y. Ultrawideband Frequency Selective Radome Utilizing 2.5-D Lossy Layers. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 2427–2431. [Google Scholar] [CrossRef]
- Yuan, H.; Brizi, D.; Mishra, V.; Fang, X.; Li, H.; Cao, Q.; Monorchio, A. A multifunctional frequency selective rasorber based on hybrid microfluidic-electronic control. J. Phys. D Appl. Phys. 2024, 57, 195002. [Google Scholar] [CrossRef]
- Li, H.; Feng, Y.; Zhao, M.; Wang, X.; Brizi, D.; Fang, X.; Hu, J.; Sima, B.; Zong, Z.; Wu, W.; et al. A Dual-Polarized and Wideband Switchable Absorption/Transmission Frequency Selective Surface With Multispectral Functionality. IEEE Open J. Antennas Propag. 2024, 5, 286–296. [Google Scholar] [CrossRef]
- Parameswaran, A.; Kundu, D.; Sonalikar, H.S. A dual polarized wideband frequency-selective rasorber with low inband insertion loss and high oblique incidence stability. IEEE Trans. Electromagn. Compat. 2021, 63, 1820–1828. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, S.; Monorchio, A.; Kong, X.; Brizi, D.; Wu, C.; Wen, Y. A Highly Selective Rasorber with Ultraminiaturized Unit Based on Interdigitated 2.5-D Parallel Resonator. IEEE Trans. Electromagn. Compat. 2022, 64, 1585–1592. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, S.; Monorchio, A.; Kong, X.; Brizi, D.; Zhang, X.; Wang, L. Miniaturized Wide-Angle Rasorber with a Wide Interabsorption High Transparent Bandpass Based on Multiple 2.5-D Resonators. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 416–420. [Google Scholar] [CrossRef]
- Jiang, X.; Rashid, A.K.; Xu, W.; Cheng, Q.; Shao, L.; Zhang, Q. An Ultrawideband Three-Dimensional Bandpass Frequency Selective Surface. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1238–1242. [Google Scholar] [CrossRef]
- Li, H.; Li, B.; Zhu, L. Wideband Bandpass Frequency-Selective Structures on Stacked Slotline Resonators: Proposal and Synthetic Design. IEEE Trans. Antennas Propag. 2020, 68, 7068–7078. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. All-Metal Wideband Frequency-Selective Surface Bandpass Filter for TE and TM Polarizations. IEEE Trans. Antennas Propag. 2022, 70, 2790–2800. [Google Scholar] [CrossRef]
- Yong, W.Y.; Glazunov, A.A. Miniaturization of a Fully Metallic Bandpass Frequency Selective Surface for Millimeter-Wave Band Applications. IEEE Trans. Electromagn. Compat. 2023, 65, 1072–1080. [Google Scholar] [CrossRef]
- Hong, T.; Wang, M.; Peng, K.; Zhao, Q.; Gong, S. Compact Ultra-Wide Band Frequency Selective Surface with High Selectivity. IEEE Trans. Antennas Propag. 2020, 68, 5724–5729. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Jin, M. High-Order Wideband Band-Pass Miniaturized Frequency-Selective Surface with Enhanced Equivalent Inductance. Electronics 2024, 13, 925. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Ahmed, M.; Fang, L.; Jin, N.; Li, B.; Huo, S.; Lei, X.; Sun, Z.; Yu, H.; et al. A Novel Miniaturized Ultra-Wideband Frequency Selective Surface with Rapid Band Edge. IEEE Access 2021, 9, 161854–161861. [Google Scholar] [CrossRef]
- Hu, D.; Zhai, H.; Liu, L.; Shi, J.; Nie, Z. A new miniaturized frequency selective surface designed for Ku-band absorption and low-frequency bandpass. Microw. Opt. Technol. Lett. 2020, 62, 315–321. [Google Scholar] [CrossRef]
- Li, J.; Hou, X.; Xu, Y. An Ultra-thin Flexible Double-Layer Dual-Band Frequency Selective Surface. J. Electron. Mater. 2023, 52, 514–522. [Google Scholar] [CrossRef]
- Kanchana, D.; Radha, S.; Sreeja, B.S.; Manikandan, E. A single layer UWB frequency selective surface for shielding application. J. Electron. Mater. 2020, 49, 4794–4800. [Google Scholar] [CrossRef]
- Can, S. Dual-band sub-6-GHz frequency filtering with optically transparent single-layer dual-polarized smart surface. Microw. Opt. Technol. Lett. 2023, 66, e33959. [Google Scholar] [CrossRef]
- Bharti, G.; Jha, K.R.; Singh, G.; Jyoti, R. Design of angular and polarization stable modified circular ring frequency selective surface for satellite communication system. Int. J. Microw. Wirel. Technol. 2016, 8, 899–907. [Google Scholar] [CrossRef]
- Shukoor, M.A.; Dey, S. Novel Dual-Mode Polarization Insensitive Wide Angular Stable Circular Ring Based Deca-Band Absorber for RCS and EMI Shielding Applications. IEEE Trans. Electromagn. Compat. 2022, 64, 1337–1345. [Google Scholar] [CrossRef]
- Karahan, M.; Aksoy, E. Design and analysis of angular stable antipodal F-type frequency selective surface with multi-band characteristics. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, e22466. [Google Scholar] [CrossRef]
- Li, T.; Li, D.; Qin, P.; Fan, Y.; Gu, Y.; Zuo, P.; Sha, W.E.I.; Li, E. A Novel Miniaturized Strong-Coupled FSS Structure With Excellent Angular Stability. IEEE Trans. Electromagn. Compat. 2021, 63, 38–45. [Google Scholar] [CrossRef]
- Bai, H.; Yan, M.; Li, W.; Wang, J.; Zheng, L.; Wang, H.; Qu, S. Tunable Frequency Selective Surface With Angular Stability. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1108–1112. [Google Scholar] [CrossRef]
- Hussein, M.; Zhou, J.; Huang, Y.; Al-Juboori, B. A Low-Profile Miniaturized Second-Order Bandpass Frequency Selective Surface. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2791–2794. [Google Scholar] [CrossRef]
- Afzal, W.; Ebrahimi, A.; Robel, M.R.; Rowe, W.S.T. Low-Profile Higher-Order Narrowband Bandpass Miniaturized-Element Frequency-Selective Surface. IEEE Trans. Antennas Propag. 2023, 71, 3736–3740. [Google Scholar] [CrossRef]
- Singh, C.; Jha, K.R.; Sharma, S.K.; Jibran, Z.A.P.; Singh, G. Design of a wideband square slot bandpass frequency-selective surface using phase range analysis. Eng. Rep. 2020, 2, e12085. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, X.; Wu, S.; Yuan, Y.; Yuan, N. A Hybrid 2-D–3-D Miniaturized Multiorder Wide Bandpass FSS. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 307–311. [Google Scholar] [CrossRef]
- Jian, D.; Ma, Y.; Li, Z.; Mo, J. A Miniaturized Quad-Stopband Frequency Selective Surface with Convoluted and Interdigitated Stripe Based on Equivalent Circuit Model Analysis. Micromachines 2021, 12, 1027. [Google Scholar] [CrossRef]
- Liu, J.; Liao, S.; Xue, Q.; Che, W. A Wide Bandpass Elliptical Filtering Response Frequency-Selective Slab Based on Slotline- Backed Split-Ring Resonators. IEEE Trans. Antennas Propag. 2024, 72, 5201–5211. [Google Scholar] [CrossRef]
- Chen, Y.; Wan, G.; Ma, X.; Fu, B.; Jiao, X. Frequency-Selective Rasorber for Wideband Transmission Based on Hybrid Resistive Sheet with Harmonic Suppression. IEEE Trans. Electromagn. Compat. 2024, 66, 1087–1093. [Google Scholar] [CrossRef]
- Costa, F.; Monorchio, A.; Manara, G. Efficient Analysis of Frequency-Selective Surfaces by a Simple Equivalent-Circuit Model. IEEE Antennas Propag. Mag. 2012, 54, 35–48. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Sayed, A.M.; Amr, A.M.; Sayed, M.O.; Hameed, M.F.O.; Obayya, S.S.A. Broadband polarization insensitive metamaterial absorber. Opt. Quantum Electron. 2023, 55, 652. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, Y.; Wang, Z.; He, J.; Quan, X.; Gao, D.; Cao, Z. On the Equivalent-Circuit-Based Design of Double-Lossy-Layer Wide Transmissive Rasorbers With Ultrawide Reflection Suppression Band. IEEE Trans. Antennas Propag. 2024, 72, 4999–5010. [Google Scholar] [CrossRef]


| Parameter | Value (mm) |
|---|---|
| D | 24 |
| t | 0.46 |
| w | 0.2 |
| 2 | |
| 11.6 | |
| 22 | |
| 3.8 | |
| 1.8 | |
| 2 |
| w (mm) | Q |
|---|---|
| 0.2 | 23.9 |
| 0.3 | 22.7 |
| 0.4 | 21.8 |
| 0.5 | 21.7 |
| 0.6 | 21.2 |
| Paper | Dimension | Thickness | Fractional BW (−3 dB) | Angular Stability |
|---|---|---|---|---|
| [31] | 0.08λL × 0.08λL | 0.3λL | 10% | 60° |
| [32] | 0.11λL × 0.11λL | 0.021λL | 5% | 60° |
| [33] | 0.15λL × 0.15λL | 0.025λL | 54% | - |
| [34] | 0.04λL × 5.7λL | 0.21λL | 130% | 40° |
| [35] | 0.09λL × 0.09λL | 0.02λL | - | 60° |
| [36] | 0.18λL × 0.18λL | 0.24λL | 40% | 45° |
| [this work] | 0.16λL × 0.16λL | 0.03λL | 108.6% | 40° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascarella, F.; Brizi, D.; Monorchio, A. An Ultrathin Wideband Angularly Stable Frequency Selective Surface Bandpass Filter for S-C Band Coverage. Appl. Sci. 2025, 15, 4887. https://doi.org/10.3390/app15094887
Pascarella F, Brizi D, Monorchio A. An Ultrathin Wideband Angularly Stable Frequency Selective Surface Bandpass Filter for S-C Band Coverage. Applied Sciences. 2025; 15(9):4887. https://doi.org/10.3390/app15094887
Chicago/Turabian StylePascarella, Francesca, Danilo Brizi, and Agostino Monorchio. 2025. "An Ultrathin Wideband Angularly Stable Frequency Selective Surface Bandpass Filter for S-C Band Coverage" Applied Sciences 15, no. 9: 4887. https://doi.org/10.3390/app15094887
APA StylePascarella, F., Brizi, D., & Monorchio, A. (2025). An Ultrathin Wideband Angularly Stable Frequency Selective Surface Bandpass Filter for S-C Band Coverage. Applied Sciences, 15(9), 4887. https://doi.org/10.3390/app15094887






