Cracking Behavior of Fiber-Reinforced Concrete Beams Made of Waste Sand
Abstract
1. Introduction
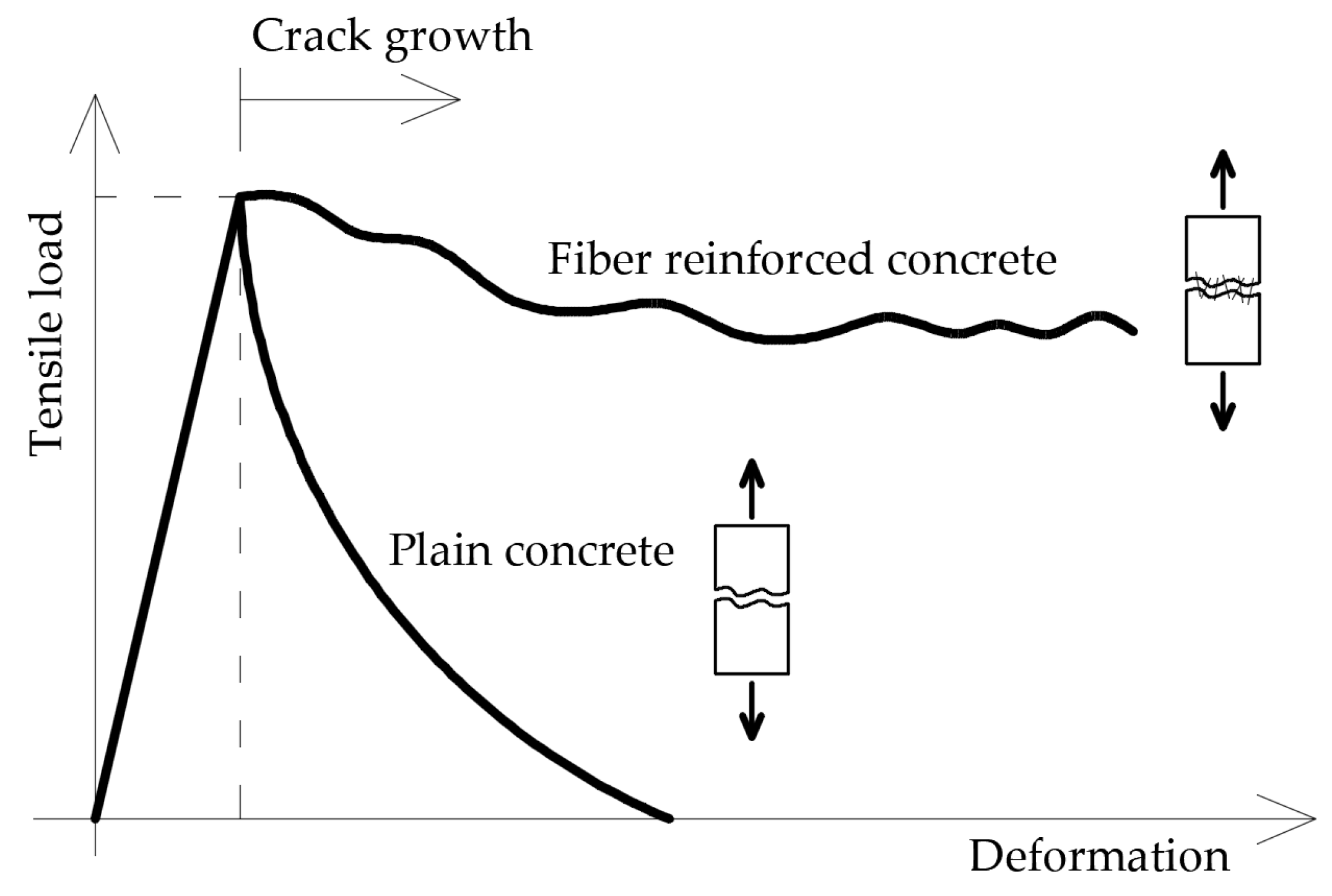
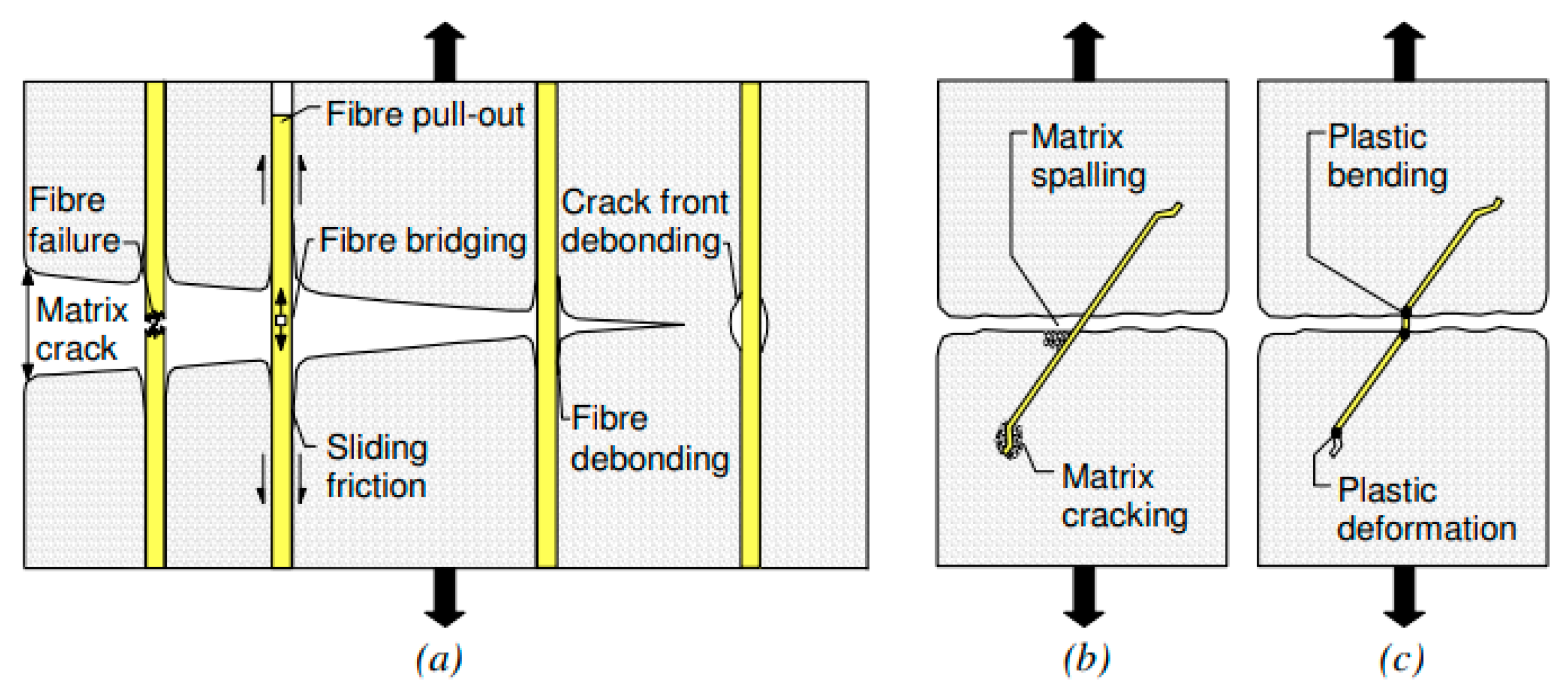
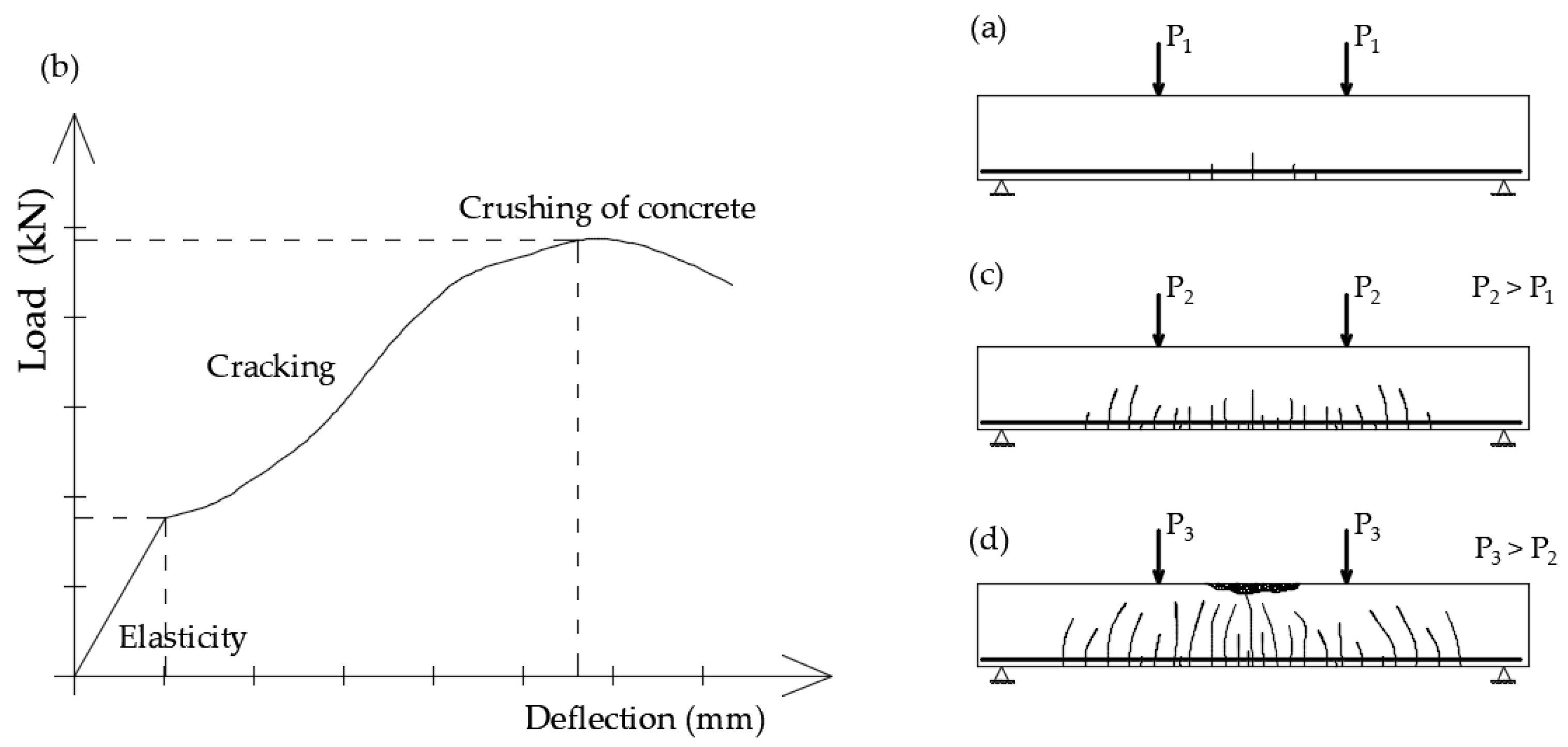
2. Mechanisms of Cracks
3. Materials and Methods
4. Methodology of Research
5. Test Results and Their Analysis
6. Conclusions
- The modification of the fine aggregate concrete mixture with steel fibers and superplasticizer significantly improves the tensile and compressive strengths of the matrix. For the initially designed sand concrete of class C12/15, the compressive strengths of the fiber-reinforced sand concrete corresponding to classes C25/30 and C30/37 were achieved, specifically for sand concrete with fibers measuring 30/0.55 mm and 50/0.8 mm, respectively.
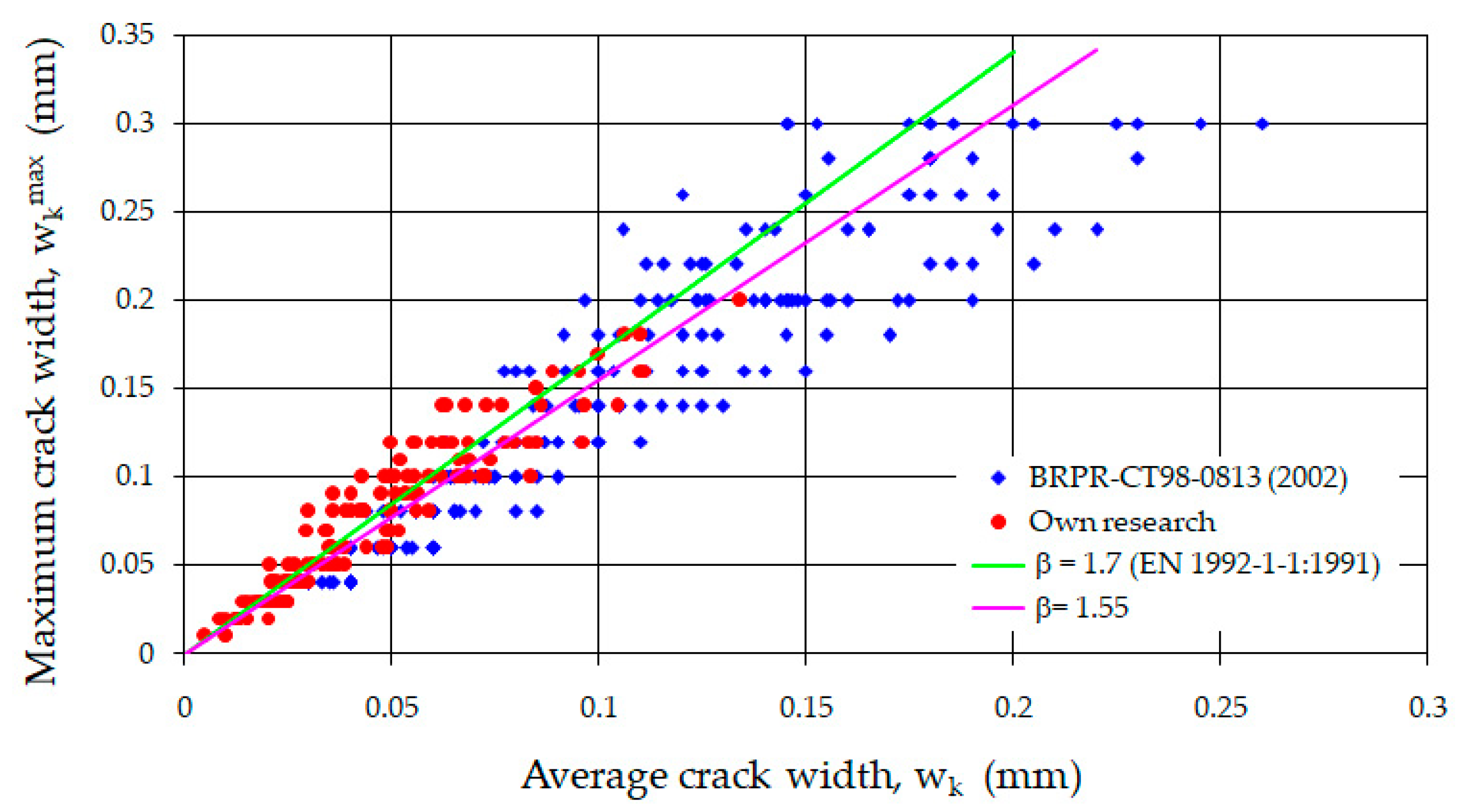
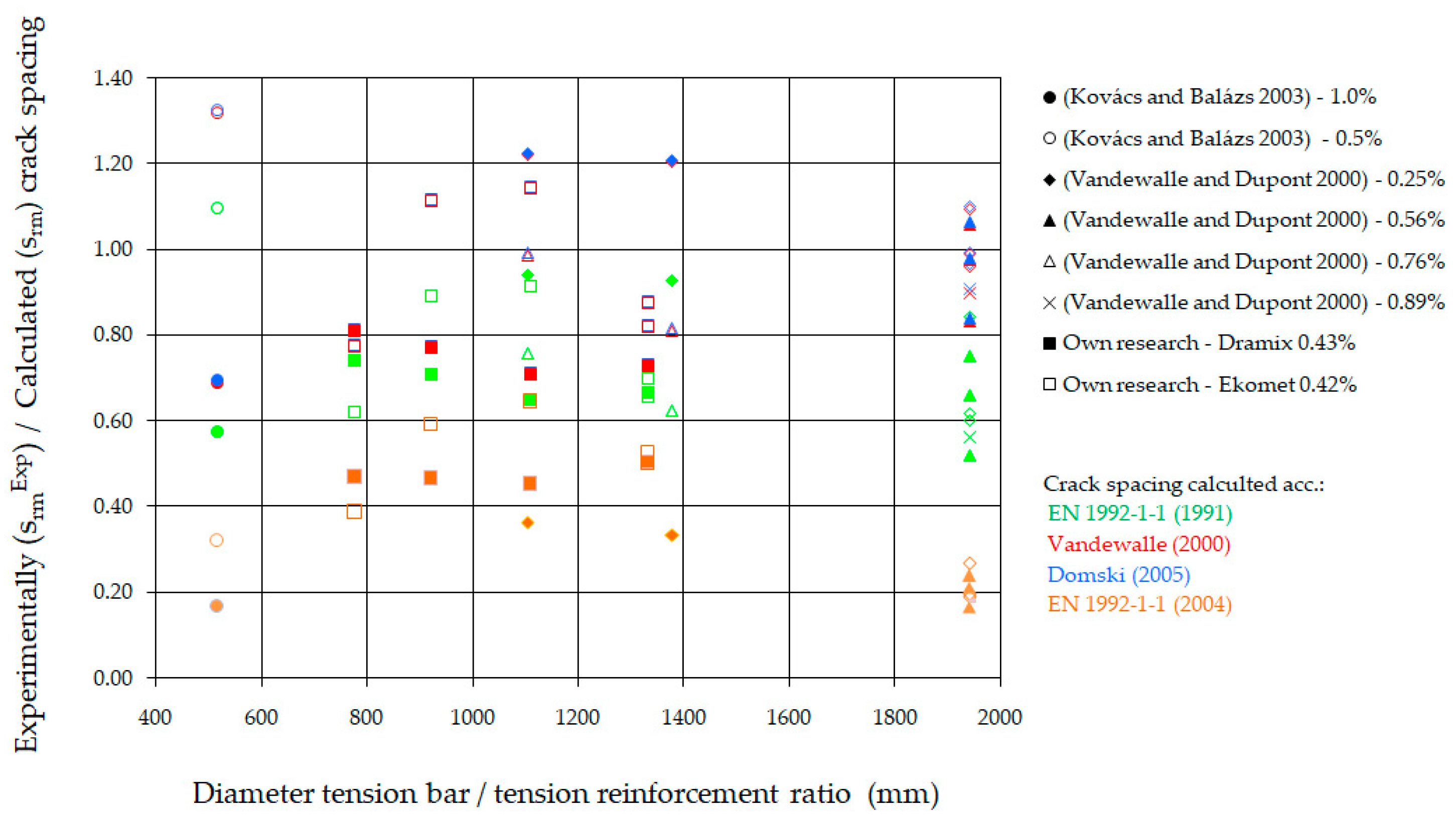
- Analyzing the crack spacing on the section of constant moment, it can be observed that the best agreement between measurements and calculations was achieved using Domski’s method [53]. This method produces a slight overestimation, averaging 19% above the measured values.
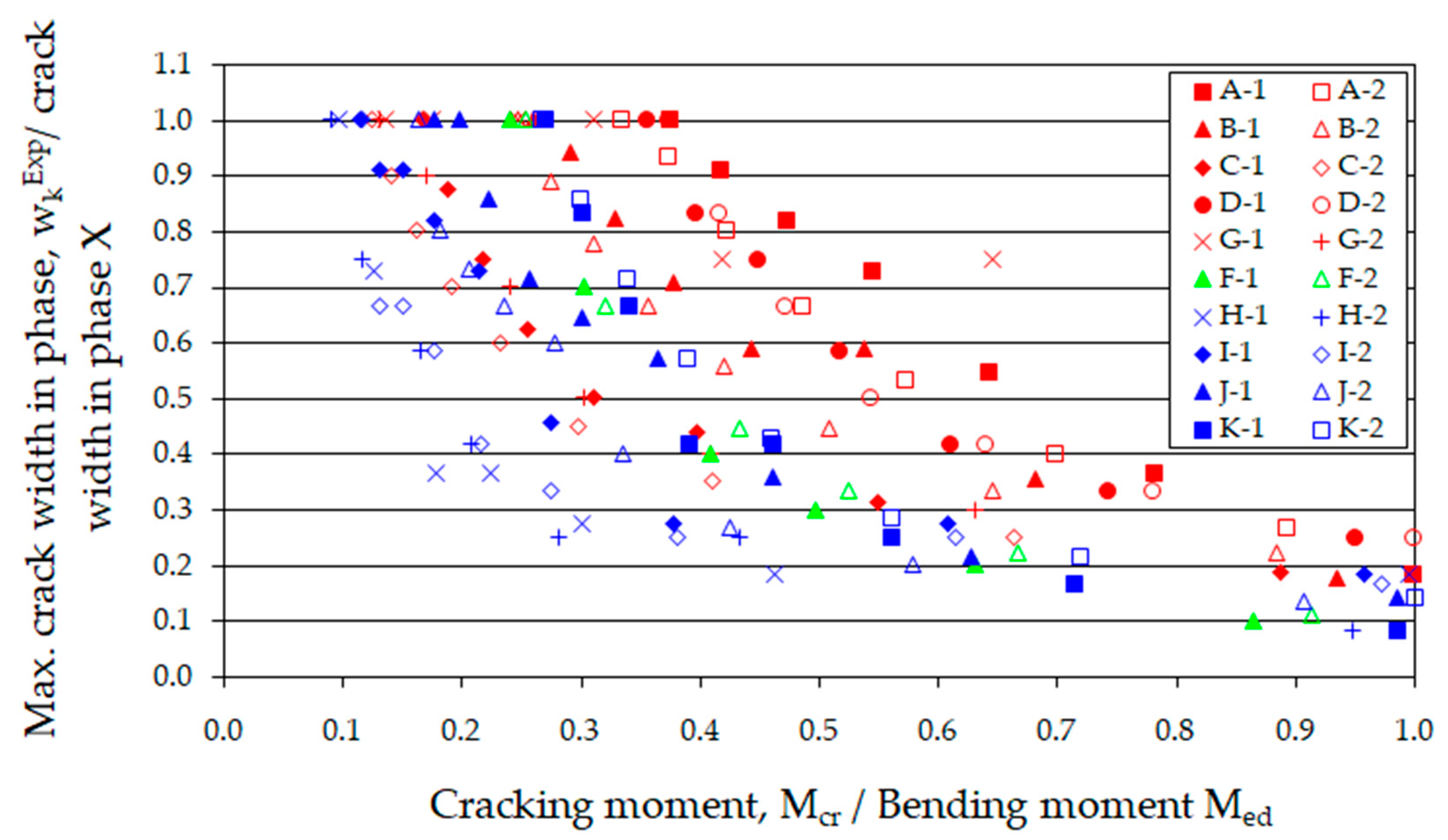
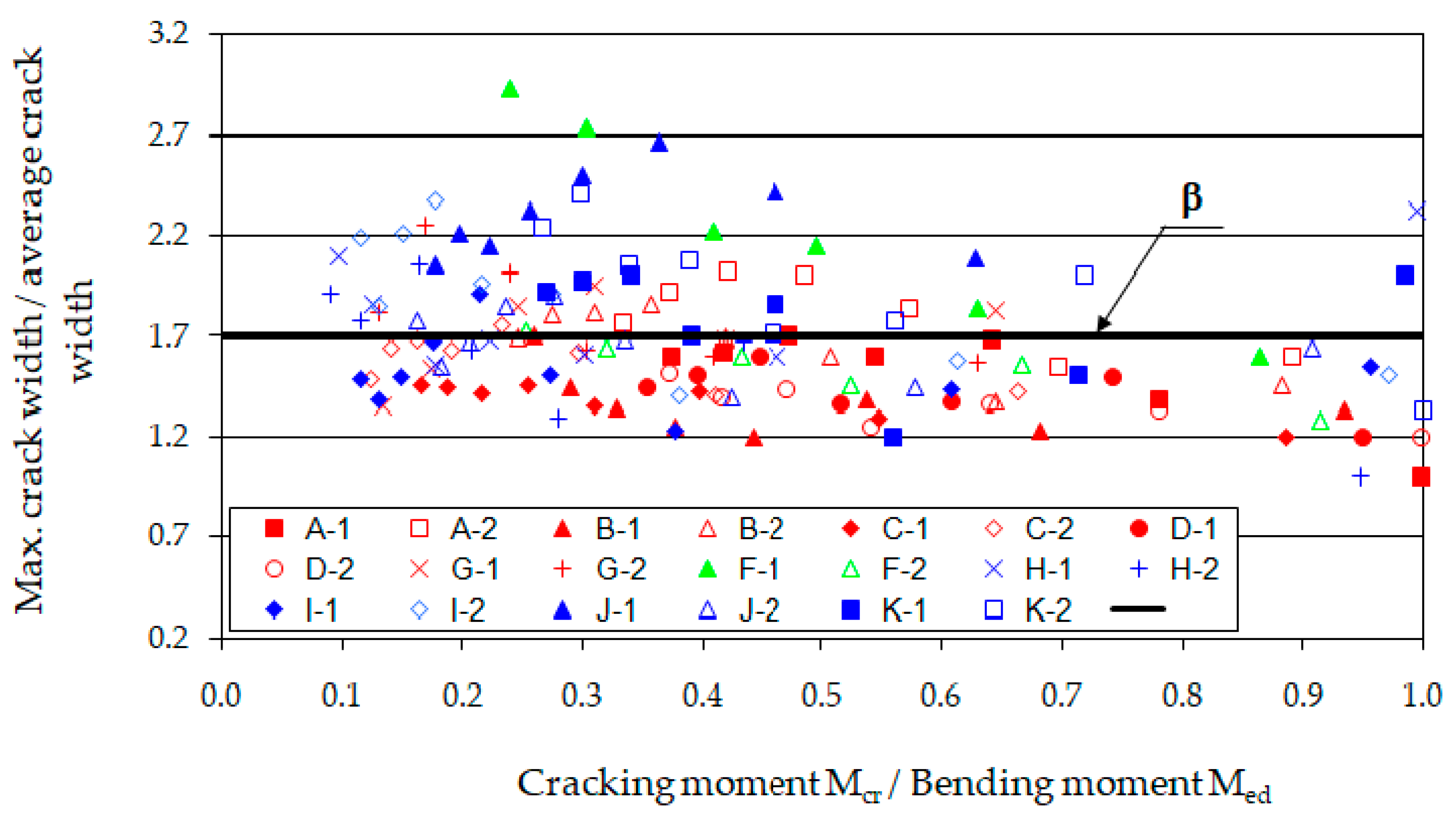
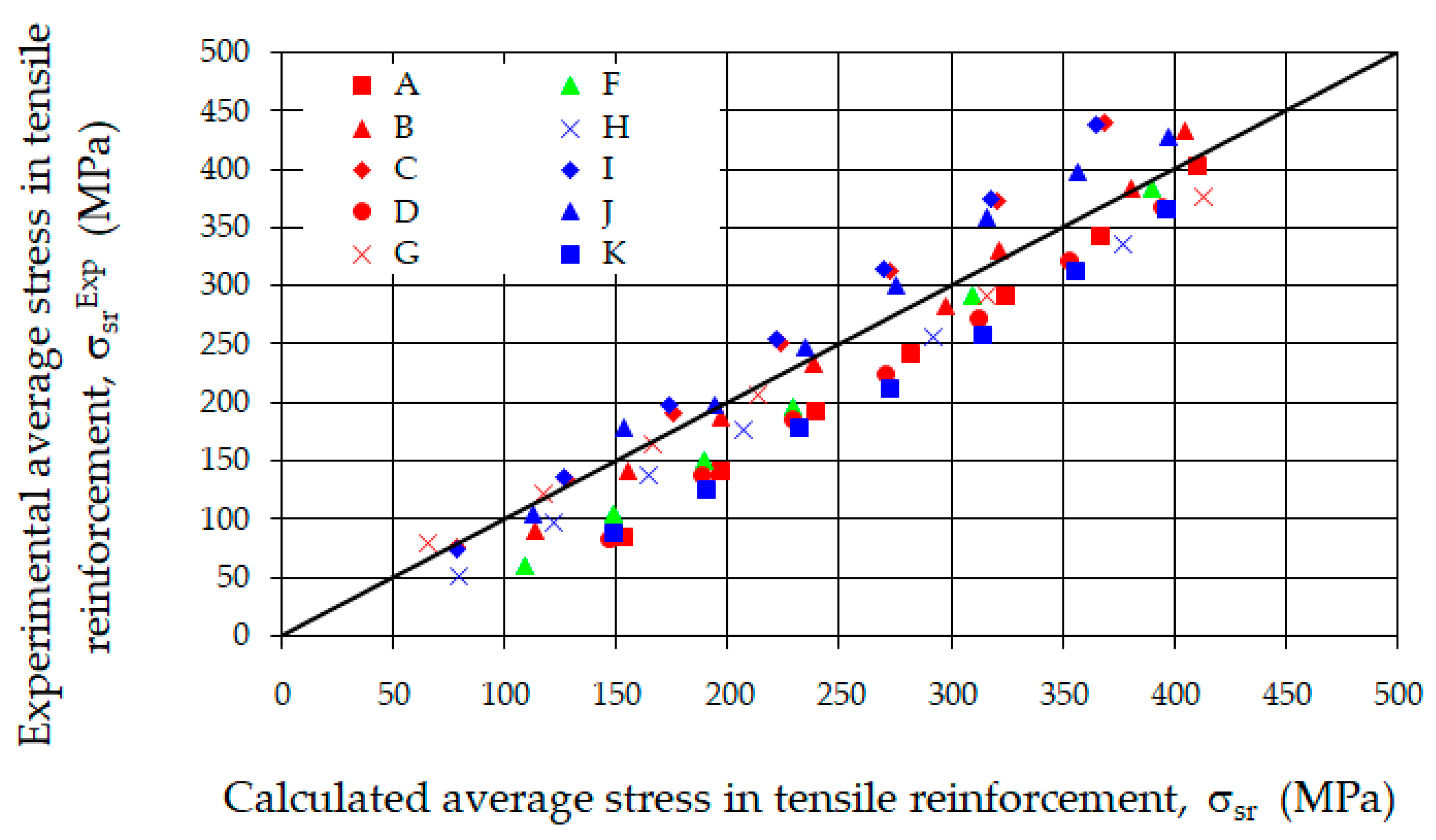
- The highest correspondence between the calculated crack widths and the test results were obtained for the proposal included in [53]. The average percentage error was 38.4%, with the lowest standard deviation being 45.1%. In contrast, the method outlined in EC2 [52] showed the lowest agreement with the experimental results, yielding an average error of 75.5% with a standard deviation of 58.5%. Therefore, in this case, it is advisable to use the method proposed in [53], which yields satisfactory results.
- The plain (commercial) concrete used in the tests, which had a declared compressive strength class of C35/45, exhibited higher strength properties compared to the two lower-class fiber-reinforced sand concretes (C25/30 and C30/37). Despite this, the widths of perpendicular cracks in the beams made of fine aggregate fiber-reinforced concrete and ordinary concrete were similar. Based on the tests conducted, it can be concluded that beams made of fine aggregate concrete (using waste sand) with steel fibers meet the requirements for ordinary concrete elements concerning the limit state of cracking.
- The waste sand used in the tests proved to be a fully valuable fine-grained aggregate. Its use in the production of structural fiberconcrete will help reduce the exploitation of natural resources and lower CO2 emissions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Mexp | Experimentally cracking moments |
| Mcr | Cracking moments |
| Med | Bending moment |
| Mmax | Bending moment corresponding to the ultimate load |
| MEks | Bending moment corresponding to the utility load |
| σsr | Average stress in tensile reinforcement |
| σsrExp | Experimental average stress in tensile reinforcement |
| srm | Average crack spacing |
| srmExp | Experimentally crack spacing |
| wk | Crack width |
| wkExp | Experimentally crack width |
| wkmax | Maximum crack width |
| fct,sp | Tensile splitting strength |
| fc,cube | Compressive cube strength |
| fc | Compressive cylinder strength |
| Ec | Static modulus of elasticity |
| ρL | Longitudinal reinforcement ratio |
References
- Nuge, T.; Fazeli, M.; Baniasadi, H. Elucidating the enduring transformations in cellulose-based carbon nanofibers through prolonged isothermal treatment. Int. J. Biol. Macromol. 2024, 275, 133480. [Google Scholar] [CrossRef] [PubMed]
- Mohajerani, A.; Hui, S.-Q.; Mirzababaei, M.; Arulrajah, A.; Horpibulsuk, S.; Kadir, A.A.; Rahman, M.T.; Maghool, F. Amazing types, properties, and applications of fibers in construction materials. Materials 2019, 12, 2513. [Google Scholar] [CrossRef]
- Navaratnam, S.; Selvaranjan, K.; Jayasooriya, D.; Rajeev, P.; Sanjayan, J. Applications of natural and synthetic fiber reinforced polymer in infrastructure: A suitability assessment. J. Build. Eng. 2023, 66, 105835. [Google Scholar] [CrossRef]
- Amran, M.; Huang, S.-S.; Onaizi, A.M.; Makul, N.; Abdelgader, H.S.; Ozbakkaloglu, T. Recent trends in ultra-high performance concrete (UHPC): Current status, challenges, and future prospects. Constr. Build. Mater. 2022, 352, 129029. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.A.; Alyousef, R.; Amran, Y.H.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Abidnejad, R.; Baniasadi, H.; Fazeli, M.; Lipponen, S.; Kontturi, E.; Rojas, O.J.; Mattos, B.D. High-fiber content composites produced from mixed textile waste: Balancing cotton and polyester fibers for improved composite performance. Int. J. Biol. Macromol. 2025, 292, 139227. [Google Scholar] [CrossRef]
- Flaga, K.; Piwowarczyk, K. Crack resistance of reinforced concrete beams additionally reinforced with steel fibers. In Proceedings of the XLI Conference N-T KILiW PAN i KN PZITB, Kraków-Krynica, Poland, 19–24 September 1995; pp. 37–44. (In Polish). [Google Scholar]
- Altun, F.; Haktanir, T.; Ari, K. Effects of steel fiber addition on mechanical properties of concrete and RC beams. Constr. Build. Mater. 2007, 21, 654–661. [Google Scholar] [CrossRef]
- Mangat, P. Tensile strength of steel fiber reinforced concrete. Cem. Concr. Res. 1976, 6, 245–252. [Google Scholar] [CrossRef]
- Song, P.S.; Hwang, S. Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. Build. Mater. 2004, 18, 669–673. [Google Scholar] [CrossRef]
- Yao, W.; Li, J.; Wu, K.R. Mechanical properties of hybrid fiber-reinforced concrete at low fiber volume fraction. Cem. Concr. Res. 2003, 33, 27–30. [Google Scholar] [CrossRef]
- Khan, M.; Cao, M.; Ali, M. Cracking behaviour and constitutive modelling of hybrid fibre reinforced concrete. J. Build. Eng. 2020, 30, 101272. [Google Scholar] [CrossRef]
- More, F.M.D.S.; Subramanian, S.S. Impact of Fibres on the Mechanical and Durable Behaviour of Fibre-Reinforced Concrete. Buildings 2022, 12, 1436. [Google Scholar] [CrossRef]
- Wang, D.; Ju, Y.; Shen, H.; Xu, L. Mechanical properties of high performance concrete reinforced with basalt fiber and polypropylene fiber. Constr. Build. Mater. 2019, 197, 464–473. [Google Scholar] [CrossRef]
- Marcalikova, Z.; Cajka, R.; Bilek, V.; Bujdos, D.; Sucharda, O. Determination of mechanical characteristics for fiber-reinforced concrete with straight and hooked fibers. Crystals 2020, 10, 545. [Google Scholar] [CrossRef]
- Almusallam, T.; Ibrahim, S.M.; Al-Salloum, Y.; Abadel, A.; Abbas, H. Analytical and experimental investigations on the fracture behaviour of hybrid fiber reinforced concrete. Cem. Concr. Compos. 2016, 74, 201–217. [Google Scholar] [CrossRef]
- Banthia, N.; Nandakumar, N. Crack growth resistance of hybrid fiber reinforced composite. Cem. Concr. Compos. 2003, 25, 3–9. [Google Scholar] [CrossRef]
- ACI PRC-544.2-17; Report on the Measurement of Fresh State Properties and Fiber Dispersion of Fiber-Reinforced Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2017.
- Jasiczak, J.; Mikołajczyk, P. Technology of Concrete Modified with Admixtures and Additives. Review of Domestic and Foreign Trends; Poznań University of Technology Publishing House: Poznań, Poland, 1997. (In Polish) [Google Scholar]
- Brandt, A.M.; Kasperkiewicz, J.; Glinicki, M. Basics of Using Fibre Concrete with Steel Fibres; PAN IPPT Mechanics Centre: Warsaw, Poland, 2001. (In Polish) [Google Scholar]
- ASTM C 1018-97; Standard Test Method for Flexural Toughness and First-Crack Strength of Fiber-Reinforced Concrete (Using Beam with Third-Point Loading). American Society for Testing and Materials: West Conshohocken, PA, USA, 1997.
- Kobayashi, K.; Cho, R. Test method for estimating first crack strength of steel fibre reinforced concrete. In Proceedings of the Rilem Symposium Testing and Test Methods of Fibre Cement Composites, Sheffield, UK, 5–7 April 1978; pp. 417–422. [Google Scholar]
- NBN B 15-238; Tests on Fibre Reinforced Concrete. Bending Test on Primatic Samples. Belgian Standard, IBN: Brussels, Blgium, 1992.
- JCI-SF4; Method of Test for Flexural Strength and Flexural Toughness of Fiber Reinforced Concrete. Japan Concrete Institute: Tokyo, Japan, 1984.
- Balaguru, P.; Narahari, R.; Patel, M. Flexural Toughness of Steel Fibre Reinforced Concrete. ACI Mater. J. 1992, 89, 541–546. [Google Scholar]
- Chen, L.; Mindess, S.; Morgan, D.R. Specimen geometry and toughness of steel-fibre-reinforced concrete. J. Mater. Civ. Eng. 1994, 6, 529–541. [Google Scholar] [CrossRef]
- Gopalaratnam, V.S.; Gettu, R. On the characteristic of flexural toughness in fiber reinforced concretes. Cem. Concr. Comp. 1995, 17, 239–254. [Google Scholar] [CrossRef]
- Johnson, C.D.; Skarendahl, A. Comparative flexural performance evaluation of steel fibre-reinforced concretes according to ASTM C1018 shows importance of fibre parameters. Mater. Struct. 1992, 25, 191–200. [Google Scholar] [CrossRef]
- Nataraja, M.C.; Dhang, N.; Gupta, A.P. Toughness characterization of steel fibre-reinforced concrete by JSCE approach. Cem. Concr. Res. 2000, 30, 593–597. [Google Scholar] [CrossRef]
- Zhu, D.Q.; Tang, A.P.; Wan, C.L.; Zeng, Y.S.; Wang, Z. Investigation on the flexural toughness evaluation method and surface cracks fractal characteristics of polypropylene fiber reinforced cement-based composites. J Build. Eng. 2021, 43, 103045. [Google Scholar] [CrossRef]
- Li, B.; Chi, Y.; Xu, L.; Shi, Y.; Li, C. Experimental investigation on the flexural behavior of steel-polypropylene hybrid fiber reinforced concrete. Constr. Build. Mater. 2018, 191, 80–84. [Google Scholar] [CrossRef]
- Giaccio, G.; Tobes, J.M.; Zerbino, R. Use of small beams to obtain design parameters of fibre reinforced concrete. Cem. Concr. Compos. 2008, 30, 297–306. [Google Scholar] [CrossRef]
- Piątek, Z.; Domski, J.; Staszak, I. Cracking of sand-fibre concrete beams. In Proceedings of the L Conference N-T KILiW PAN i KN PZITB, Krynica, Poland, 12–27 September 2004; Volume 3, pp. 75–84. (In Polish). [Google Scholar]
- Ibrahim, O.T.; Luxmore, A.R. Control of cracks width by inclusion of fibres in conventionally reinforced concrete. Int. J.Cem. Com. 1979, 1, 77–89. [Google Scholar]
- Ibrahim, O.T.; Luxmore, A.R. Control of cracks in reinforced concrete using steel fibres. In Proceedings of the Rilem Symposium FRC 86 Third International Symposium on Developments in Fibre Reinforced Cement and Concrete, Sheffield, UK, 13–17 July 1986. [Google Scholar]
- Al-Taan, S.A.; Al-Feel, J.R. Prediction of crack width in fibrous reinforced concrete members. In Fiber Reinforced Cements and Concretes. Recent Developments; Elsevier Science Publishers Ltd.: Essex, UK, 1989; pp. 209–218. [Google Scholar]
- Tan, K.H.; Paramasivam, P.; Tan, K.C. Cracking characteristics of reinforced steel fiber concrete beams under short- and long-term loadings. Adv. Cem. Based Mater. 1995, 2, 127–137. [Google Scholar] [CrossRef]
- Nemegeer, D.; Vandewalle, L.; Van Nieuwenburg, D.; Van Gysel, A.; Vyncke, J.; Deforche, E. Dramix guideline: Design of concrete structures—Steel wire fibre reinforced concrete structures with or without ordinary reinforcement. Infrastuct. Het Leefmilieu 1995, 4, 227–239. [Google Scholar]
- Nemegeer, D. Dramix: Design Guidelines for Dramix Steel Wire Fibre Reinforced Concrete; N.V. Bekaert S.A.: Harelbeke, Belgium, 1997. [Google Scholar]
- Rilem, T.C. 162-TDF. Test and design methods for steel fibre reinforced concrete: σ–ε Design method. Mater. Struct. 2003, 36, 560–567. [Google Scholar] [CrossRef]
- Vandewalle, L. Cracking behaviour of concrete beams reinforced with a combination of ordinary reinforcement and steel fibers. Mater. Struct. 2000, 33, 164–170. [Google Scholar] [CrossRef]
- Padmarajaiah, S.K.; Ramaswamy, A. Crack-width prediction for high-strength concrete fully and partially prestressed beam specimens containing steel fibers. ACI Struct. J. 2001, 98, 852–861. [Google Scholar]
- Brite Euram BRPR-CT98-0813; Test and Design Methods for Steel Fibre Reinforced Concrete. Subtask 7.2 Final Rep. Project funded by the European Community under the Industrial & Materials Technologies Programme (Brite-Euram II). K.U. Leuven Research and Development: Leuven, Belgium, 2002.
- Rilem, T.C. 162-TDF. Test and design methods for steel fibre reinforced concrete: Bending test. Mater. Struct. 2002, 35, 579–582. [Google Scholar] [CrossRef]
- Dupont, D. Modelling and Experimental Validation of the Constitutive Law (se) and Cracking Behaviour of Steel Fibre Reinforced Concrete. Ph.D. Thesis, Catholic University of Leuven, Leuven, Belgium, 2003. [Google Scholar]
- Dupont, D.; Vandewalle, L. The cracking behaviour of SFRC beams containing longitudinal reinforcement. In Proceedings of the 7th International Symposium on Brittle Matrix Composites, Warsaw, Poland, 13–15 October 2003; pp. 253–262. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, T.; Li, H.; Dong, T.; Li, Z.; Guo, X. Study of the flexural behavior of basalt fiber-reinforced concrete beams with basalt fiber-reinforced polymer bars and steel bars. Case Stud. Constr. Mater. 2025, 22, e04433. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Y.J.; Wu, T.; Liu, Y. Flexural cracks in steel fiber-reinforced lightweight aggregate concrete beams reinforced with FRP bars. Compos. Struct. 2020, 253, 12752. [Google Scholar] [CrossRef]
- Hamrata, M.; Boulekbache, B.; Chemrouk, M.; Amziane, S. Flexural cracking behavior of normal strength, high strength and high strength fiber concrete beams, using Digital Image Correlation technique. Constr. Buil. Mater. 2016, 106, 678–692. [Google Scholar] [CrossRef]
- Domski, J. Cracking of sand-fibre concrete beams under immediate loading. Engin. Constr. 2008, 64, 316–319. (In Polish) [Google Scholar]
- Domski, J. Cracking moment in steel fibre reinforced concrete beams based on waste sand. Ovidius Univ. Ann. Constantza Ser. Civ. Eng. 2011, 13, 29–34. [Google Scholar]
- ENV 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1 : General Rules and Rules for Buildings. European Union: Brussels, Belgium, 1991.
- Domski, J. Nośność Ugięcie i Zarysowanie Belek Piaskobetonowych z Włóknami Stalowymi pod Obciążeniem Doraźnym. Ph.D. Thesis, Koszalin University, Koszalin, Poland, 2005. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Union: Brussels, Belgium, 2004.
- Available online: http://geoportal.pgi.gov.pl/odpady/wytwarzanie (accessed on 20 February 2025).
- Głodkowska, W.; Laskowska-Bury, J. Proposition for Determining the Residual Strength of Fiber-Reinforced Cement Composite. Materials 2022, 15, 7546. [Google Scholar] [CrossRef]
- Domski, J.; Zakrzewski, M. Deflection of steel fiber reinforced concrete beams based on waste sand. Materials 2020, 13, 392. [Google Scholar] [CrossRef] [PubMed]
- Bentur, A.; Mindess, S. Fiber Reinforced Cementitious Composites, 2nd ed.; CRC Press: London UK, 2006. [Google Scholar]
- Holschemacher, K.; Mueller, T.; Ribakov, Y. Effect of steel fibers on mechanical properties of high strength concrete. Mater. Des. 2010, 31, 2604–2615. [Google Scholar] [CrossRef]
- Balendran, R.V.; Zhou, F.P.; Nadeem, A.; Leung, A.Y.T. Influence of steel fibres on strength and ductility of normal and lightweight high strength concrete. Build. Environ. 2002, 37, 1361–1367. [Google Scholar] [CrossRef]
- Michels, J. Bearing capacity of steel fiber reinforced concrete flat slabs. Ph.D. Thesis, Unilu—University of Luxembourg, Luxembourg, Luxembourg, 2009. [Google Scholar]
- Rilem, T.C. 162-TDF: Test and design methods for steel fibre reinforced concrete. Design of steel fibre reinforced concrete using the σ-w method: Principles and applications. Mater. Struct. 2002, 35, 262–278. [Google Scholar] [CrossRef]
- Alberti, M.G.; Enfedaque, A.; Gálvez, J.C. On the mechanical properties and fracture behaviour of polyolefin fiber-reinforced self-compacting concrete. Constr. Build. Mater. 2014, 55, 274–288. [Google Scholar] [CrossRef]
- Barros, J.A.O.; Cruz, J.S. Fracture energy of steel fiber-reinforced concrete. Mech. Adv. Mat. Struct. 2001, 8, 29–45. [Google Scholar] [CrossRef]
- Soutsos, M.N.; Le, T.T.; Lampropoulos, A.P. Flexural performance of fibre reinforced concrete made with steel and synthetic fibres. Constr. Build. Mater. 2012, 36, 704–710. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Yoon, Y.S.; Banthia, N. Flexural response of steel-fibre-reinforced concrete beams: Effects of strength, fiber content, and strain-rate. Cem. Concr. Compos. 2015, 64, 84–92. [Google Scholar] [CrossRef]
- Plagué, T.; Desmettre, C.; Charron, J.P. Influence of fiber type and fiber orientation on cracking and permeability of reinforced concrete under tensile loading. Cem Concr Res. 2017, 94, 59–70. [Google Scholar] [CrossRef]
- Löfgren, I. Fibre-Reinforced Concrete for Industrial Construction—A Fracture Mechanics Approach to Material Testing and Structural Analysis. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2005. [Google Scholar]
- Piątek, Z.; Bartnik, E.; Bierut, W.; Borjaniec, W.; Kamyno, R.; Kuncer, K.; Szyszko, A. Design Methods of Sand Concrete Developed Within the Framework of the B-219 Problem Entitled “Application of Sand Concrete for Conventionally Produced Prefabricated Building Elements”; Central Research and Development Centre of the Concrete Industry CEBET: Warsaw, Poland, 1981. (In Polish) [Google Scholar]
- ACI 544.3R-93 (Reapproved 1998); Guide for Specifying, Proportioning, Mixing, Placing and Finishing Steel Fiber Reinforced Concrete. Manual of Concrete Practice, American Concrete Institute: Farmington Hills, MI, USA, 2005.
- EN 12350-3:2019; Testing Fresh Concrete. Part 3: Vebe Test. European Union: Brussels, Belgium, 2021.
- EN 12390-3; Testing Hardened Concrete—Part 3 Compressive Strength of Test Specimens. European Union: Brussels, Belgium, 2019.
- EN 12390-6; Testing Hardened Concrete—Part 6: Tensile Splitting Strength of Test Specimens. European Union: Brussels, Belgium, 2023.
- EN 12390-13; Testing Hardened Concrete—Part 13: Determination of Secant Modulus of Elasticity in Compression. European Union: Brussels, Belgium, 2021.
- Benjamin, J.R.; Cornell, C.A. Probability, Mathematical Statistics and Decision Theory for Engineers; Wyd. N.-T.: Poland, Warsaw, 1977. [Google Scholar]
- Tan, K.H.; Paramsivam, P.; Tan, K.C. Instantaneous and long-term deflections of steel fibre reinforced concrete beams. ACI Struct. J. 1994, 91, 384–393. [Google Scholar]
- Lok, T.S.; Xiao, J.R. Flexural strength assessment of steel fibre reinforced concrete. ASCE J. Mat. Civ. Eng. 1999, 11, 188–196. [Google Scholar] [CrossRef]
- Brandt, A.M.; Babut, R.; Kasperkiewicz, J.; Marks, M. Selected Issues in Composite Mechanics; Białystok University of Technology: Białystok, Poland, 1982. (In Polish) [Google Scholar]
- Kubicki, J. The width of cracks perpendicular to the axis of reinforced concrete elements according to the project PrPN-B-03264. Engin. Constr. 1997, 12, 611–614. (In Polish) [Google Scholar]
- Mianowski, K.M. Cracking of Concrete Elements with Dispersed Reinforcement Under Tension; ITB PWN: Warsaw, Poland, 1976. (In Polish) [Google Scholar]
- Vandewalle, L.; Dupont, D. Prediction of crack widths in ordinary reinforced concrete elements containing steel fibres. In Proceedings of the 6th International Symposium on Brittle Matrix Composites, Warsaw, Poland, 9–11 October 2000; pp. 52–61. [Google Scholar]
- Kovács, I.; Balázs, G.L. Structural behaviour of steel fibre reinforced concrete. FIB Struct. Concr. 2003, 4, 57–63. [Google Scholar] [CrossRef]
- Piątek, Z.; Bierut, W.; Borjaniec, W. Concrete Structures. Part I. Dimensioning of Concrete and Reinforced Concrete Sections; WSInż: Koszalin, Poland, 1993. (In Polish) [Google Scholar]
- Brite Euram BRPR-CT98-0813. Test and Design Methods for Steel Fibre Reinforced Concrete. Final Report of Subtask 4.1: Trial Beams in Bending and Bending with Compression. Project funded by the European Community under the Industrial & Materials Technologies Programme (Brite-Euram II); K.U. Leuven Research and Development: Leuven, Belgium, 2002. [Google Scholar]

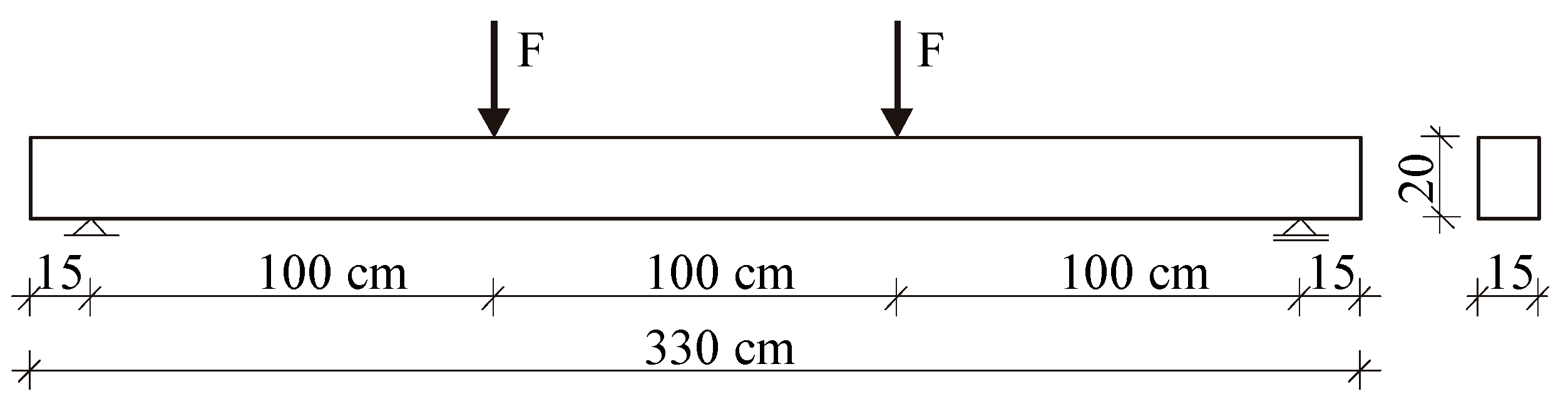


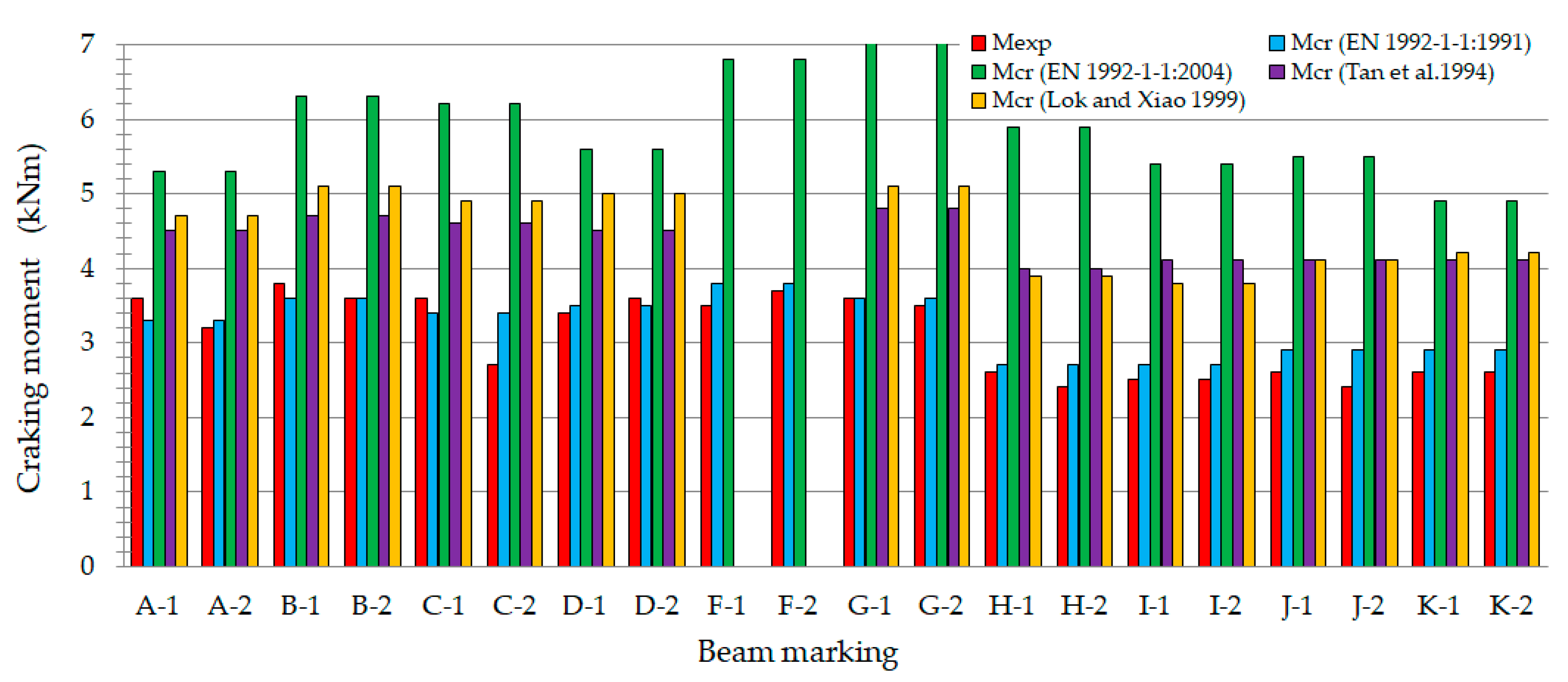
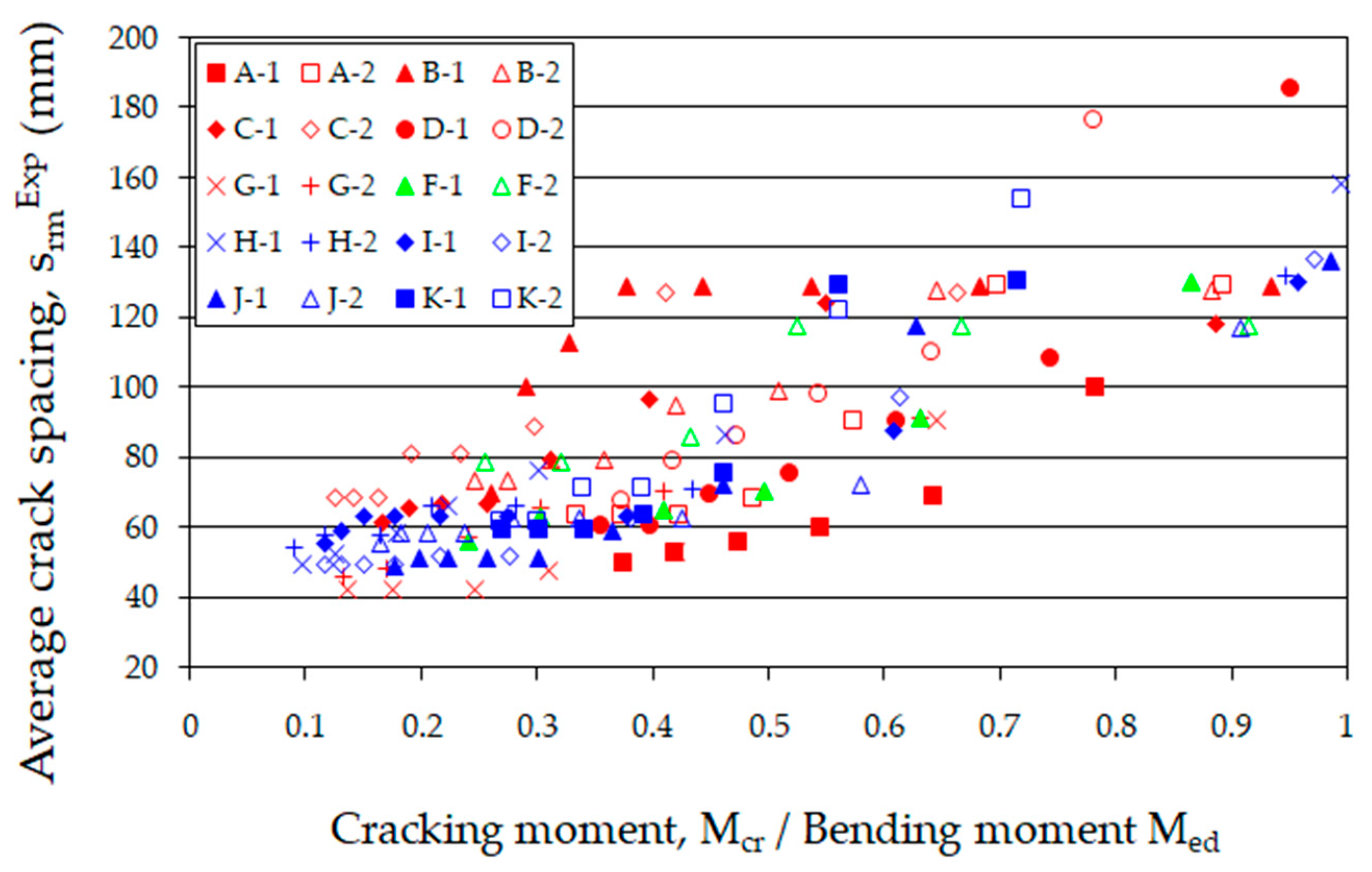
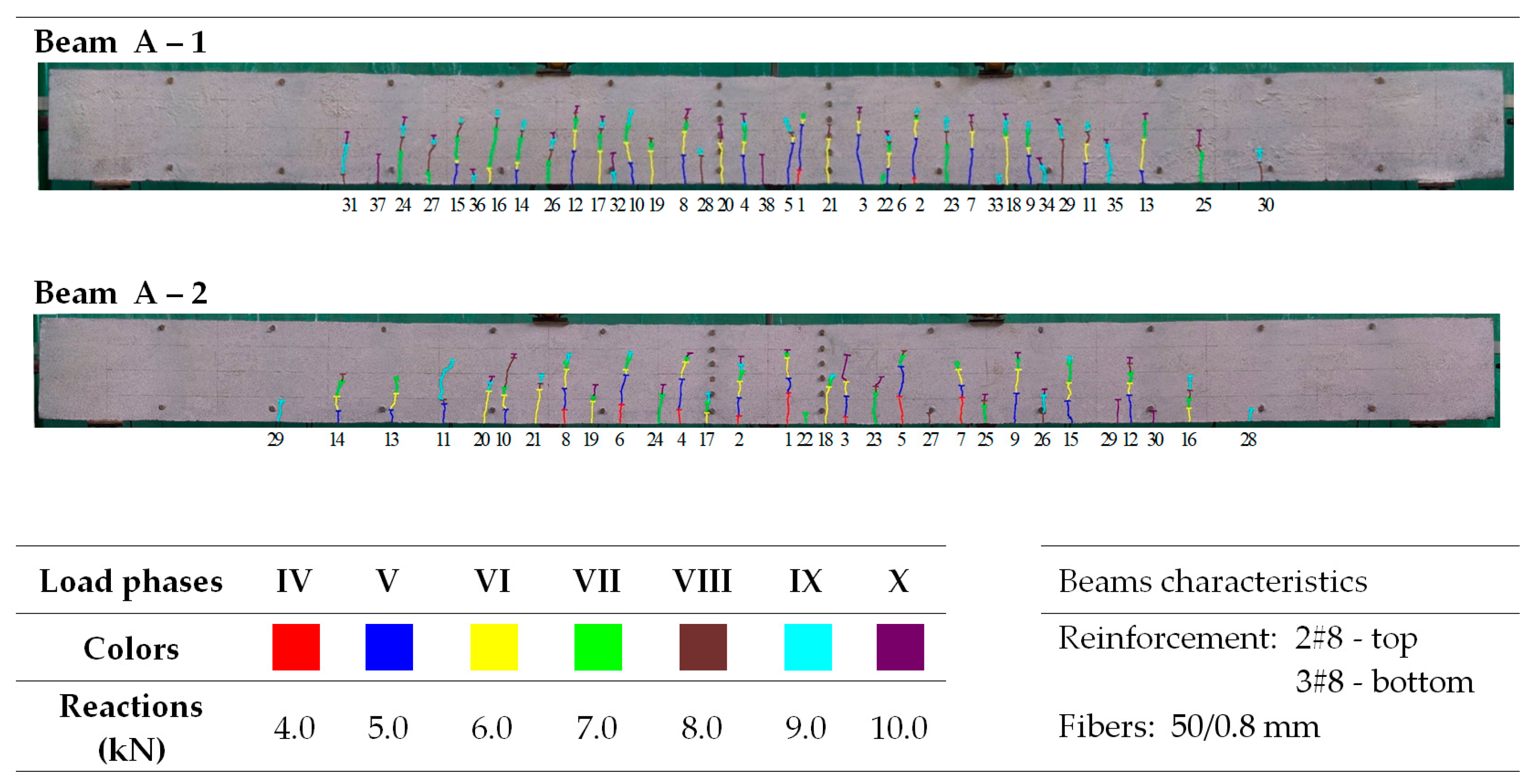
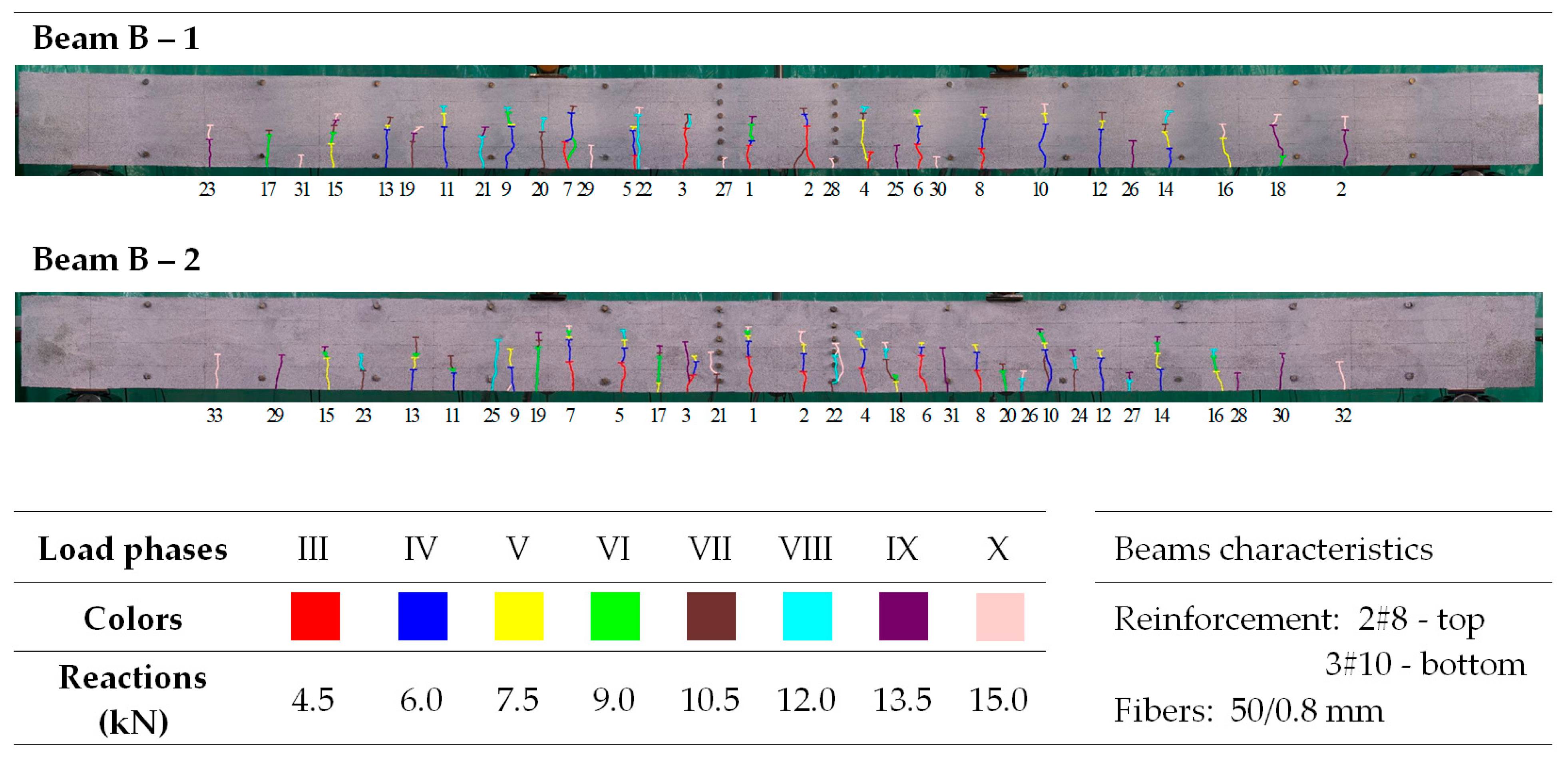
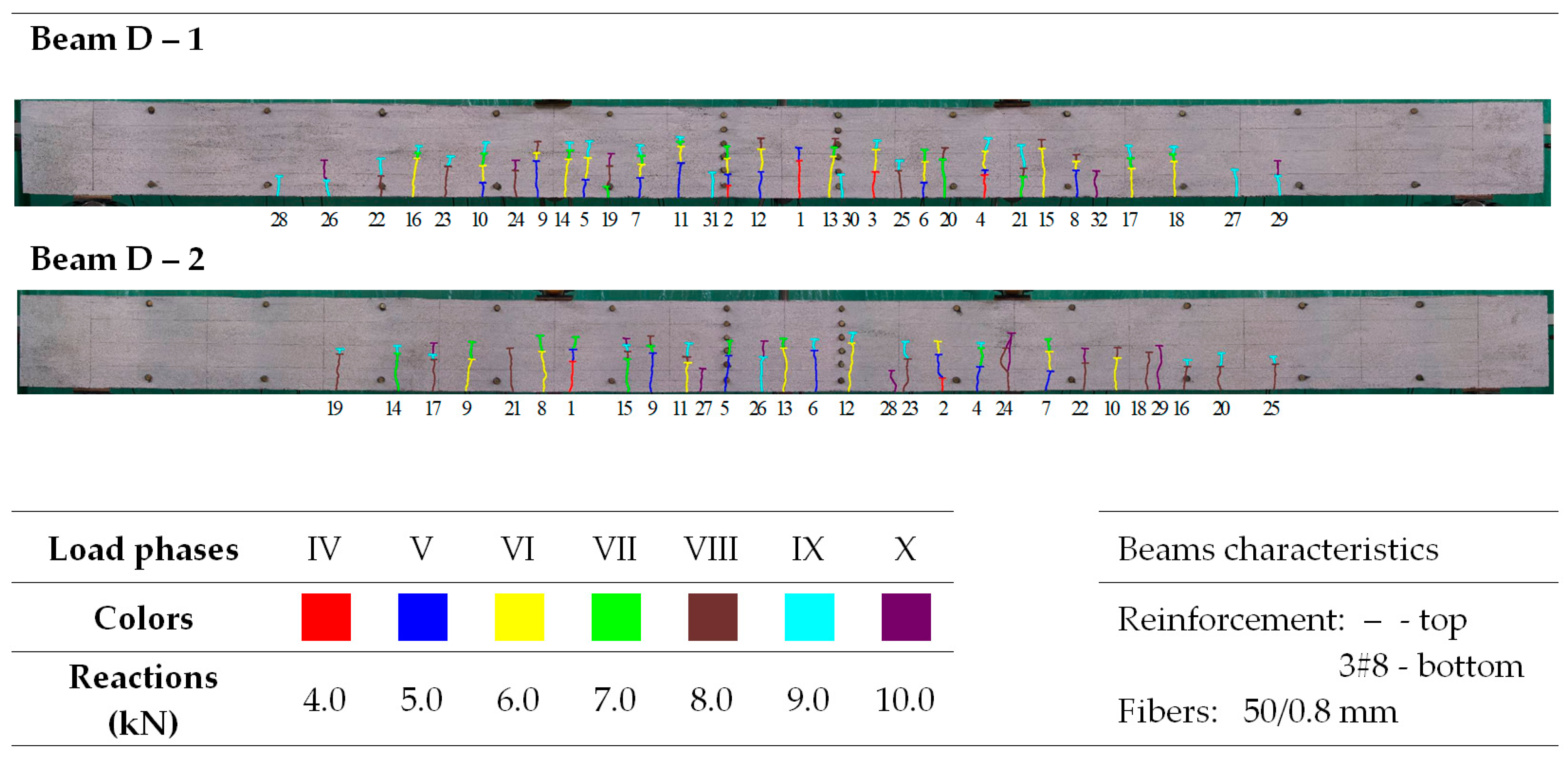
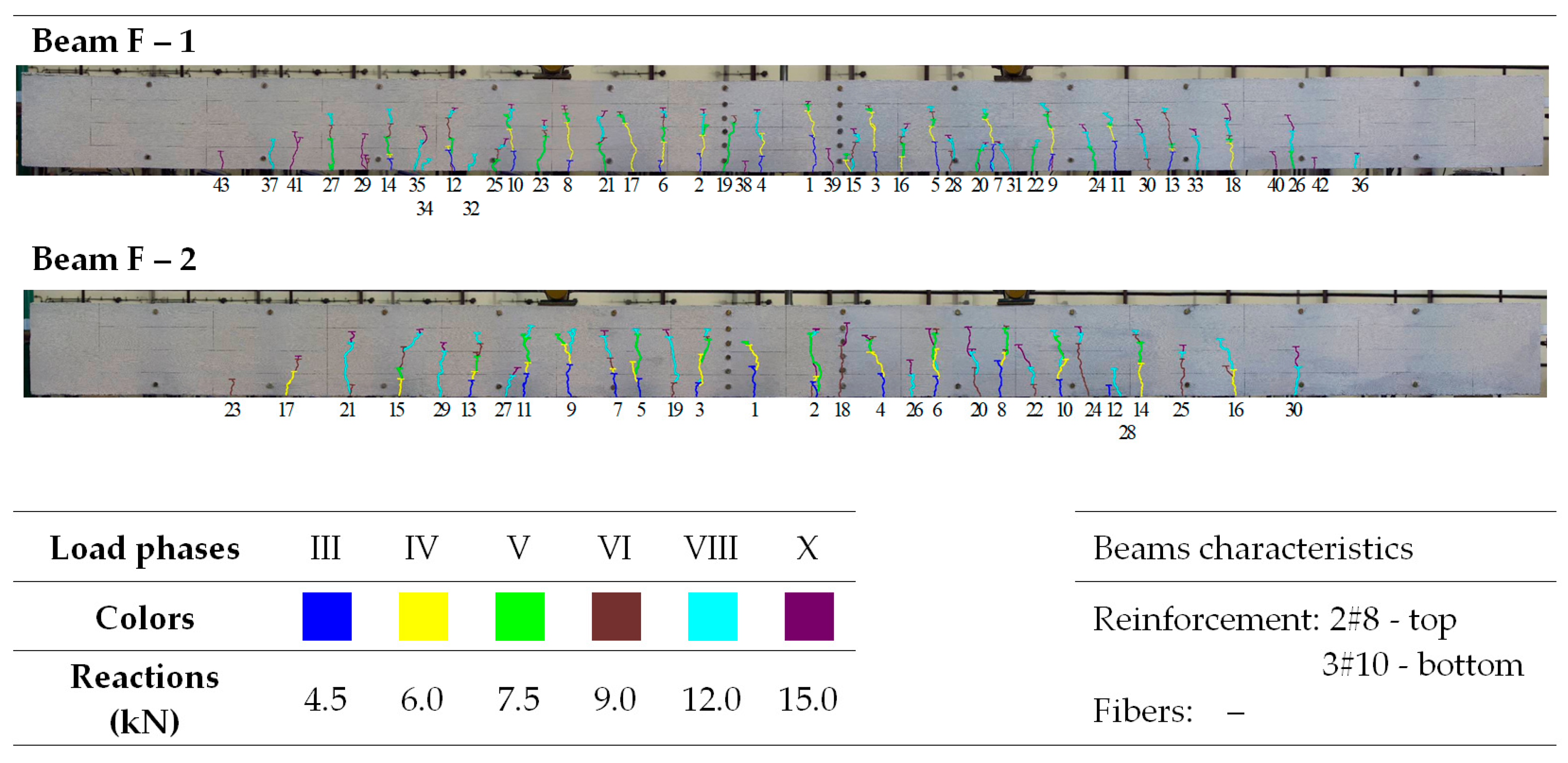
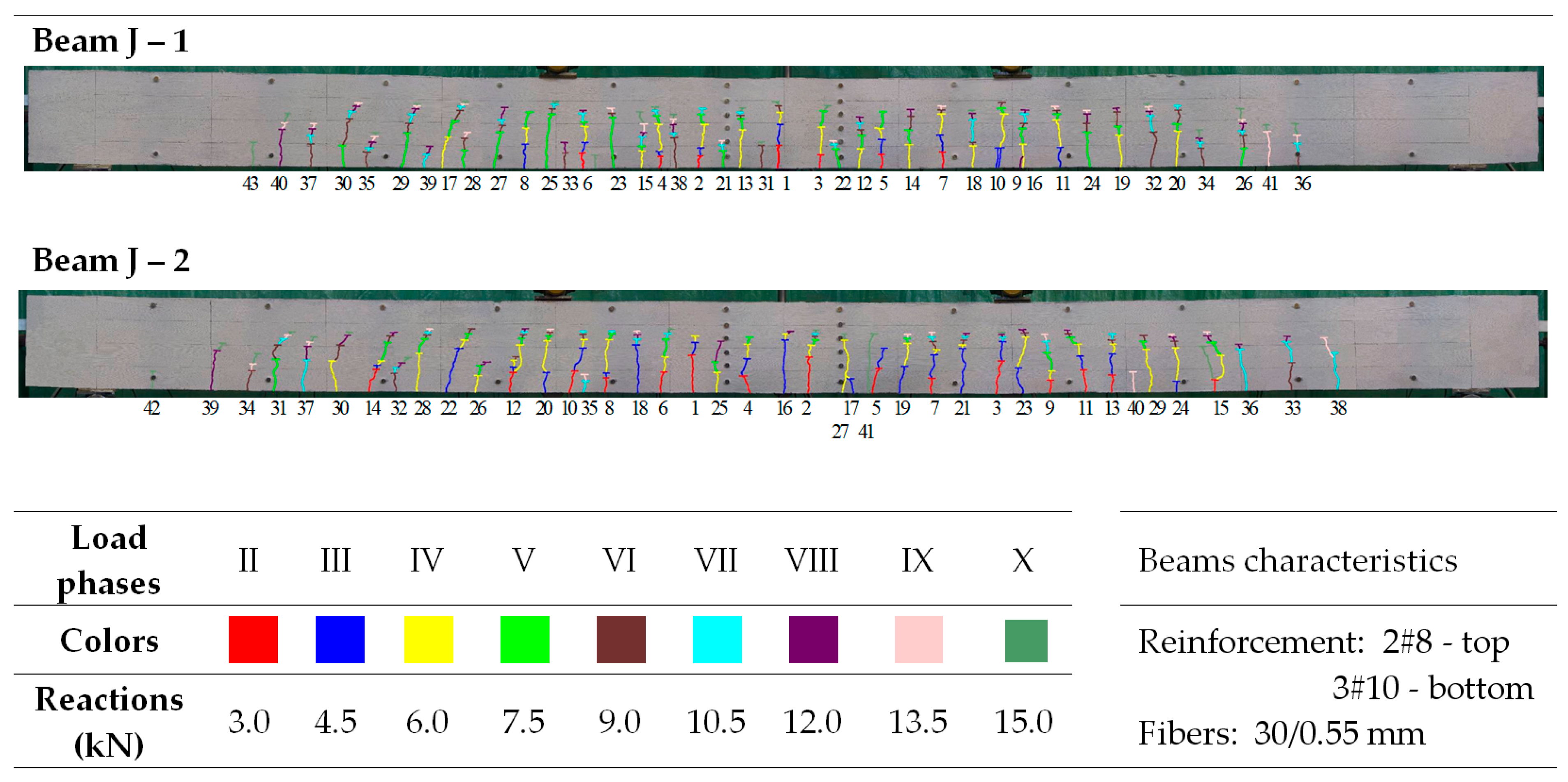
| Plain Commercial Concrete | Fiber-Reinforced Fine Aggregate Concrete | |||
|---|---|---|---|---|
| M1 | M2 | |||
| Components | (kg/m3) | Components | (kg/m3) | |
| Cement CEM I 32.5 R | 410 | Cement CEM II/B-V 32.5 R | 374 | 378 |
| Water | 188 | Water | 150 | 140 |
| Superplasticizer | 1.89 | Superplasticizer | 4.08 | 4.13 |
| Aggregate (0–2) | 646 | Waste sand (0–4) | 1835 | 1855 |
| Aggregate (2–8) | 576 | Steel fibers loose 50/0.8 mm | 33 | - |
| Aggregate (8–16) | 523 | Steel fibers glued 30/0.55 mm | - | 34 |
| w/c | 0.46 | Fiber-reinforcement ratio by volume (%) | 0.42 | 0.43 |
| w/c | 0.40 | 0.37 | ||
| Concrete | Series | Beams | Small-Sized Elements | ||||
|---|---|---|---|---|---|---|---|
| Beams Marking | Number of Elements (pcs.) | Dimensions | Reinforcement (Top, Bottom) | Number of Samples (pcs.) | Dimensions of Cubic and Cylinders Samples (mm) | ||
| with loose steel fibers 50/0.8 | A | A-1 A-2 | 2 | 150 × 200 × 3300 mm | 2 # 8 3 # 8 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 |
| B | B-1 B-2 | 2 | 2 # 8 3 # 10 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| C | C-1 C-2 | 2 | 2 # 8 3 # 12 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| D | D-1 D-2 | 2 | − 3 # 8 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| G | G-1 G-2 | 2 | 2 # 8 3 # 14 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| plain | F | F-1 F-2 | 2 | 2 # 8 3 # 10 | 12 * + 12 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | |
| with glued steel fibers 30/0.55 | H | H-1 H-2 | 2 | 2 # 8 3 # 14 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | |
| I | I-1 I-2 | 2 | 2 # 8 3 # 12 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| J | J-1 J-2 | 2 | 2 # 8 3 # 10 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| K | K-1 K-2 | 2 | 2 # 8 3 # 8 | 6 * + 6 ** 3 # + 3 ## | 150 × 150 × 150 150 × 450 | ||
| Total number: | 20 pieces | Total number: | 192 pieces | ||||
| Series | Longitudinal Reinforcement Ratio (ρL) | Load Phases/Reactions (kN) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| II | III | IV | V | VI | VII | VIII | IX | X | ||
| A | 0.6 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
| B | 0.9 | 3.0 | 4.5 | 6.0 | 7.5 | 9.0 | 10.5 | 12.0 | 13.5 | 15.0 |
| C | 1.3 | 3.0 | 4.5 | 7.0 | 9.5 | 12.0 | 14.5 | 17.0 | 19.5 | 22.0 |
| D | 0.6 | 2.0 | 3.0 | 4.0 | 5,0 | 6.0 | 7.0 | 8,0 | 9,0 | 10,0 |
| F | 0.9 | 3.0 | 4.5 | 6.0 | 7.5 | 9.0 | 10.5 | 12.0 | 13.5 | 15.0 |
| G | 1.8 | 3.0 | 6.0 | 9.0 | 12.0 | 15.0 | 18.0 | 21.0 | 24.0 | 27.0 |
| H | 1.8 | 3.0 | 6.0 | 9.0 | 12.0 | 15.0 | 18.0 | 21.0 | 24.0 | 27.0 |
| I | 1.3 | 3.0 | 4.5 | 7.0 | 9.5 | 12.0 | 14.5 | 17.0 | 19.5 | 22.0 |
| J | 0.9 | 3.0 | 4.5 | 6.0 | 7.5 | 9.0 | 10.5 | 12.0 | 13.5 | 15.0 |
| K | 0.6 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
| Concrete | Series | Mechanical Properties | |||
|---|---|---|---|---|---|
| fct,sp (MPa) | fc,cube (MPa) | fc (MPa) | Ec (GPa) | ||
| with loose steel fibers 50/0.8 | A | 3.29 | 36.5 | 45.5 | 33.6 |
| B | 3.57 | 48.3 | 50.2 | 34.2 | |
| C | 3.44 | 49.3 | 47.2 | 41.1 | |
| D | 3.51 | 44.8 | 45.6 | 33.2 | |
| G | 3.62 | 50.2 | 52.7 | 53.7 | |
| Plain | F | 3.82 | 59.7 | 51.9 | 35.9 |
| with glued steel fibers 30/0.55 | H | 2.74 | 36.2 | 34.8 | 32.1 |
| I | 2.69 | 35.9 | 38.1 | 28.3 | |
| J | 2.89 | 37.6 | 38.4 | 25.9 | |
| K | 2.94 | 38.4 | 37.5 | 30.4 | |
| Diameter (mm) | Cross Section (mm2) | The Yield Point (MPa) | Tensile Strength (MPa) | Modulus of Elasticity (GPa) |
|---|---|---|---|---|
| 8.2 | 53.0 | 424 | 695 | 223 |
| 10.2 | 81.1 | 454 | 714 | 220 |
| 12.2 | 116.7 | 430 | 678 | 205 |
| 14.3 | 160.6 | 451 | 688 | 214 |
| Marking of Crack | Crack Spacing (mm)—Beam B-2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Load Phases/Reactions (kN) | ||||||||
| III | IV | V | VI | VII | VIII | IX | X | |
| 4.5 | 6.0 | 7.5 | 9.0 | 10.5 | 12.0 | 13.5 | 15.0 | |
| 33 | ||||||||
| 130 | ||||||||
| 29 | ||||||||
| 113 | ||||||||
| 15 | ||||||||
| 182 | 77 | |||||||
| 23 | ||||||||
| 105 | ||||||||
| 13 | ||||||||
| 93 | ||||||||
| 11 | ||||||||
| 122 | 82 | |||||||
| 25 | ||||||||
| 40 | ||||||||
| 9 | ||||||||
| 134 | 55 | |||||||
| 19 | ||||||||
| 79 | ||||||||
| 7 | ||||||||
| 109 | ||||||||
| 5 | ||||||||
| 145 | 80 | |||||||
| 17 | ||||||||
| 65 | ||||||||
| 3 | ||||||||
| 133 | 65 | |||||||
| 21 | ||||||||
| 68 | ||||||||
| 1 | ||||||||
| 119 | ||||||||
| 2 | ||||||||
| 134 | 64 | |||||||
| 22 | ||||||||
| 70 | ||||||||
| 4 | ||||||||
| 133 | 71 | |||||||
| 18 | ||||||||
| 62 | ||||||||
| 6 | ||||||||
| 121 | 53 | |||||||
| 31 | ||||||||
| 68 | ||||||||
| 8 | ||||||||
| 150 | 57 | |||||||
| 20 | ||||||||
| 93 | 31 | |||||||
| 26 | ||||||||
| 62 | ||||||||
| 10 | ||||||||
| 118 | 53 | |||||||
| 24 | ||||||||
| 65 | ||||||||
| 12 | ||||||||
| 128 | 58 | |||||||
| 27 | ||||||||
| 70 | ||||||||
| 14 | ||||||||
| 130 | ||||||||
| 16 | ||||||||
| 41 | ||||||||
| 28 | ||||||||
| 93 | ||||||||
| 30 | ||||||||
| 140 | ||||||||
| 32 | ||||||||
| Marking of Crack | Crack Spacing (mm)—Beam I-1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Load Phases/Reactions (kN) | |||||||||
| II | III | IV | V | VI | VII | VIII | IX | X | |
| 3.0 | 4.5 | 7.0 | 9.5 | 12.0 | 14.5 | 17.0 | 19.5 | 22.0 | |
| 44 | 103 | ||||||||
| 36 | |||||||||
| 174 | 126 | 51 | |||||||
| 42 | |||||||||
| 75 | |||||||||
| 38 | |||||||||
| 48 | |||||||||
| 34 | |||||||||
| 77 | |||||||||
| 32 | |||||||||
| 89 | 48 | ||||||||
| 43 | |||||||||
| 41 | |||||||||
| 20 | |||||||||
| 96 | 42 | ||||||||
| 40 | |||||||||
| 54 | |||||||||
| 19 | |||||||||
| 98 | 47 | ||||||||
| 30 | |||||||||
| 51 | |||||||||
| 9 | |||||||||
| 203 | 116 | 77 | 28 | ||||||
| 41 | |||||||||
| 49 | |||||||||
| 35 | |||||||||
| 39 | |||||||||
| 17 | |||||||||
| 87 | 43 | ||||||||
| 28 | |||||||||
| 44 | |||||||||
| 7 | |||||||||
| 216 | 117 | 52 | |||||||
| 26 | |||||||||
| 65 | |||||||||
| 15 | |||||||||
| 99 | 64 | ||||||||
| 24 | |||||||||
| 35 | |||||||||
| 5 | |||||||||
| 133 | 64 | ||||||||
| 13 | |||||||||
| 69 | |||||||||
| 3 | |||||||||
| 136 | 76 | ||||||||
| 11 | |||||||||
| 60 | |||||||||
| 1 | |||||||||
| 134 | 47 | ||||||||
| 22 | |||||||||
| 87 | 22 | ||||||||
| 48 | |||||||||
| 65 | |||||||||
| 2 | |||||||||
| 121 | 59 | ||||||||
| 12 | |||||||||
| 62 | |||||||||
| 4 | |||||||||
| 142 | 56 | ||||||||
| 21 | |||||||||
| 86 | |||||||||
| 6 | |||||||||
| 115 | 58 | 19 | |||||||
| 45 | |||||||||
| 39 | |||||||||
| 23 | |||||||||
| 57 | |||||||||
| 8 | |||||||||
| 251 | 98 | 59 | |||||||
| 37 | |||||||||
| 39 | |||||||||
| 14 | |||||||||
| 153 | 67 | ||||||||
| 25 | |||||||||
| 86 | |||||||||
| 10 | |||||||||
| 191 | 61 | ||||||||
| 27 | |||||||||
| 74 | 19 | ||||||||
| 46 | |||||||||
| 55 | |||||||||
| 29 | |||||||||
| 56 | |||||||||
| 16 | |||||||||
| 18 | |||||||||
| 18 | |||||||||
| 136 | 54 | ||||||||
| 39 | |||||||||
| 82 | |||||||||
| 31 | |||||||||
| 132 | |||||||||
| 33 | |||||||||
| 131 | |||||||||
| 47 | |||||||||
| Beam Marking | Crack Spacing (mm) | (srmExp − srm)/srmExp (%) | (srmExp − srmV)/srmExp (%) | (srmExp − srmD)/srmExp (%) | (srmExp − srmEC)/srmExp (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Experimentally | Calculted From: | ||||||||
| [52] | [41] | [53] | [54] | ||||||
| srmExp | srm | srmV | srmD | srmEC | |||||
| A-1 | 50.1 | 87.0 | 69.6 | 69.3 | 113.9 | −73.7 | −38.9 | −38.3 | −127.3 |
| A-2 | 64.0 | −35.9 | −8.8 | −8.3 | −78.0 | ||||
| B-1 | 69.5 | 78.0 | 62.4 | 62.1 | 110.5 | −12.2 | 10.2 | 10.6 | −59.0 |
| B-2 | 73.1 | −6.7 | 14.6 | 15.0 | −51.2 | ||||
| C-1 | 61.4 | 73.0 | 58.4 | 58.2 | 109.7 | −18.9 | 4.9 | 5.3 | −78.6 |
| C-2 | 68.6 | −6.4 | 14.9 | 15.2 | −59.8 | ||||
| D-1 | 60.7 | 92.0 | 73.6 | 73.3 | 122.4 | −51.6 | −21.3 | −20.7 | −101.6 |
| D-2 | 68.1 | −35.1 | −8.1 | −7.6 | −79.7 | ||||
| G-1 | 42.3 | 71.0 | 56.8 | 56.6 | 113.5 | −67.8 | −34.3 | −33.7 | −168.3 |
| G-2 | 45.7 | −55.4 | −24.3 | −23.8 | −148.3 | ||||
| F-1 | 55.8 | 80.0 | — | — | 114.8 | −43.4 | — | — | −105.7 |
| F-2 | 78.5 | −1.9 | −46.2 | ||||||
| H-1 | 49.6 | 70.0 | 64.2 | 63.9 | 110.5 | −41.1 | −29.4 | −28.8 | −122.8 |
| H-2 | 54.3 | −28.9 | −18.2 | −17.7 | −103.5 | ||||
| I-1 | 55.6 | 74.0 | 67.8 | 67.5 | 112.2 | −33.1 | −21.9 | −21.4 | −101.8 |
| I-2 | 49.2 | −50.4 | −37.8 | −37.2 | −128.0 | ||||
| J-1 | 48.9 | 80.0 | 73.3 | 73.0 | 114.8 | −63.6 | −49.9 | −49.3 | −134.7 |
| J-2 | 55.2 | −44.9 | −32.8 | −32.2 | −107.9 | ||||
| K-1 | 59.5 | 91.0 | 83.4 | 83.1 | 120.7 | −52.9 | −40.2 | −39.7 | −102.9 |
| K-2 | 62.1 | −46.5 | −34.3 | −33.8 | −94.4 | ||||
| where k1, k2, ρr, φ coefficients. cross-sectional area ratio and bar diameter, respectively, acc. [52] Lf, df—fiber length and diameter Vf—volume of steel fiber in the mixture | |||||||||
| [54] | where k1, k2, k3, k4—coefficients acc. [54] c—cover to the reinforcement ρp,eff—effective cross-sectional area ratio φ—bar diameter | ||||||||
| Beams Marking | MExp/Mmax | Crack Width wk (mm) | (wkExp − wk)/wkExp (%) | (wkExp − wkV)/wkExp (%) | (wkExp − wkD)/wkExp (%) | (wkExp − wkEC)/wkExp (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Experimentally | Calculted From: | |||||||||
| [52] | [41] | [53] | [54] | |||||||
| wkExp | wk | wkV | wkD | wkEC | ||||||
| A-1 | 0.62 | 0.09 | 0.18 | 0.14 | 0.12 | 0.12 | −100.0 | −55.6 | −33.3 | −33.33 |
| A-2 | 0.56 | 0.12 | −50.0 | −16.7 | 0.0 | 0.00 | ||||
| B-1 | 0.63 | 0.14 | 0.17 | 0.14 | 0.13 | 0.14 | −21.4 | 0.0 | 7.1 | 0.00 |
| B-2 | 0.61 | 0.14 | −21.4 | 0.0 | 7.1 | 0.00 | ||||
| C-1 | 0.57 | 0.10 | 0.14 | 0.11 | 0.10 | 0.15 | −40.0 | −10.0 | 0.0 | −50.00 |
| C-2 | 0.58 | 0.14 | 0.0 | 21.4 | 28.6 | −7.14 | ||||
| D-1 | 0.61 | 0.10 | 0.21 | 0.17 | 0.15 | 0.14 | −110.0 | −70.0 | −50.0 | −40.00 |
| D-2 | 0.62 | 0.10 | −110.0 | −70.0 | −50.0 | −40.00 | ||||
| F-1 | 0.66 | 0.14 | 0.17 | — | — | 0.15 | −21.4 | — | — | −7.14 |
| F-2 | 0.66 | 0.12 | −41.7 | −25.00 | ||||||
| G-1 | 0.57 | 0.04 | 0.15 | 0.12 | 0.11 | 0.12 | −275.0 | −200.0 | −175.0 | −200.00 |
| G-2 | 0.60 | 0.09 | −66.7 | −33.3 | −22.2 | −33.33 | ||||
| H-1 | 0.57 | 0.08 | 0.15 | 0.14 | 0.13 | 0.12 | −87.5 | −75.0 | −62.5 | −50.00 |
| H-2 | 0.56 | 0.09 | −66.7 | −55.6 | −44.4 | −33.33 | ||||
| I-1 | 0.59 | 0.09 | 0.15 | 0.14 | 0.12 | 0.15 | −66.7 | −55.6 | −33.3 | −66.67 |
| I-2 | 0.59 | 0.07 | −114.3 | −100.0 | −71.4 | −114.29 | ||||
| J-1 | 0.63 | 0.12 | 0.18 | 0.17 | 0.15 | 0.16 | −50.0 | −41.7 | −25.0 | −33.33 |
| J-2 | 0.67 | 0.11 | −63.6 | −54.5 | −36.4 | −45.45 | ||||
| K-1 | 0.59 | 0.10 | 0.22 | 0.20 | 0.18 | 0.14 | −120.0 | −100.0 | −80.0 | −40.00 |
| K-2 | 0.61 | 0.12 | −83.3 | −66.7 | −50.0 | −16.67 | ||||
| Average error (%) | −75.5 | −54.6 | −38.4 | −41.78 | ||||||
| Standard deviation (%) | 58.5 | 49.8 | 45.1 | 54.8 | ||||||
| Confidence interval α = 0.05 (%) | −102.9 ÷ −48.1 | −79.4 ÷ −29.9 | −60.8 ÷ −15.9 | −64.3÷ −19.2 | ||||||
| Length of the Interval (%) | 54.8 | 49.5 | 44.9 | 45.1 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domski, J.; Laskowska-Bury, J.; Dudzińska, A. Cracking Behavior of Fiber-Reinforced Concrete Beams Made of Waste Sand. Appl. Sci. 2025, 15, 4790. https://doi.org/10.3390/app15094790
Domski J, Laskowska-Bury J, Dudzińska A. Cracking Behavior of Fiber-Reinforced Concrete Beams Made of Waste Sand. Applied Sciences. 2025; 15(9):4790. https://doi.org/10.3390/app15094790
Chicago/Turabian StyleDomski, Jacek, Joanna Laskowska-Bury, and Anna Dudzińska. 2025. "Cracking Behavior of Fiber-Reinforced Concrete Beams Made of Waste Sand" Applied Sciences 15, no. 9: 4790. https://doi.org/10.3390/app15094790
APA StyleDomski, J., Laskowska-Bury, J., & Dudzińska, A. (2025). Cracking Behavior of Fiber-Reinforced Concrete Beams Made of Waste Sand. Applied Sciences, 15(9), 4790. https://doi.org/10.3390/app15094790