Evaluation of Disassembling Process Inference Based on Positional Relations Matrix

Abstract

Disassembling is an important process in the maintenance, reparation, and disposal of mechanical as well as structural systems. More often than not, however, disassembling processes are not prepared in advance; we need to organize the disassembling process based on the obtained arrangement information of the constituent parts of the system. In this study, we deal with a disassembling process inference based on the positional relations matrix. On the basis of the positional relations matrix, the geometrical constraints among the parts can be expressed in a general form. The developed disassembling process inference based on the matrix is considered to be practical. We have evaluated the practicality of the proposed disassembling process inference based on a number of disassembling problems which were generated by means of a problem-generation system based on random number generator. The obtained evaluation demonstrated that the proposed approach does not always result in the optimal disassembling process but provides a fairly appropriate disassembling process in general, and the required computational cost is considerably small. We concluded that the proposed disassembling process inference is practical enough.

1. Introduction

Disassembling is an important process for the maintenance, reparation, and disposal of mechanical as well as structural systems. An improper disassembling operation may cause severe damage to the system, or may result in injuries to operators or customers, as described in [1]. Assembling and disassembling are reversal operations; however, disassembling a machine is more difficult than assembling in general [2]. In addition, more often than not, disassembling processes are not prepared in advance. We need to organize a disassembling process based on the obtained arrangement information of the parts that make up the system to be disassembled.

A number of studies dealing with disassembling process generation have been reported to date. Santochi et al. [3] studied the development of a computer-aided disassembly planning system. Zhu et al. [4] proposed an information model for disassembly and optimal disassembly sequence generation. The approach is based on a linear programming optimization model and has dynamic capabilities by means of state-dependent information. Go et al. [5] dealt with a method used to find an optimal disassembly sequence beforehand in the product design phase, to increase the reusability. Parsa and Saadat [6] introduced new optimization parameters that evaluate disassembly aptitude in order to take into account the difficulty and feasibility of the disassembly operation; the genetic algorithm was employed to optimize the process sequence.

In recent studies, various types of computer-aided vision and machine learning technologies have also been applied for supporting assembly/disassembly operations [7,8,9,10]. Frizziero et al. [11] offered an approach to the design for disassembly (DfD) to reduce the time and cost of disassembling a product and proposed a system that visualizes the generated disassembly sequence in augmented reality (AR) to support inexperienced operators in disassembly tasks; they used a gearbox as the target of their case study. De Fazio et al. [12] developed a method to visually map the disassembly of a product, showing different routes towards target components; the map was based on analyses of vacuum cleaners. Research on disassembly sequence generation for sustainability has attracted considerable attention as well [13,14]. To facilitate the long-term use and recyclability of vehicles, Toyota has worked to design parts to be more easily removed from their vehicles [15]; the easy-to-dismantle structures are practically applied to their modules. They have developed a matrix-based design method for circular economy.

In order to deal with the various disassembling problems in general form, we are studying an approach based on positional relation information among the parts [16]. On the basis of our approach [17] based on the positional relations matrix that contains positional relation information among the parts, it is considered to be possible to formulate and solve various disassembling problems. The approach is considered to be efficient and applicable to various cases in principle; however, the computational cost and the optimality of the generated disassembling processes have not yet been confirmed.

In the current study, we evaluate the applicability of the disassembling process inference based on the positional relations matrix. We have developed a disassembling-problem generation system that generates block pattern-based disassembling problems [18], which adopts a random walk process [19] for the placement of blocks. On the basis of the generated disassembling problems, we evaluate the applicability, the efficiency, and the optimality of the disassembling process inference approach based on the positional relations matrix.

2. Disassembling Process Inference Based on Positional Relations Matrix

For the disassembling process inference of a mechanical or structural system, we need to describe the relevant constraints among the parts. In the current study, we adopt the positional relations matrix that describes the geometrical constraints among the parts. In this section, we develop a generalized procedure of our previous disassembling process inference [17] based on the positional relations matrix. We also develop an optimal disassembling-process generation based on the positional relations matrix by means of the permutation.

2.1. Positional Relations Matrix

The positional relations matrix adopted in the current study describes the impeding conditions among the parts. The matrix is expressed as

$$\mathit{M}=\left[\begin{array}{ccc}{M}_{11}& \cdots & M_{1N}\\ ⋮& \ddots & ⋮\\ M_{N1}& \cdots & M_{NN}\end{array}\right]$$

for a system consisting of N parts. Matrix element $M_{ij}$ is expressed as a binary number and denotes the impeding conditions of part i for part j; the kth bit of $M_{ij}$ expresses that part i impedes (1) or does not impede (0) the motion of part j in its corresponding direction. For the diagonal elements of $\mathit{M}$, accordingly $M_{ii}=0$.

In the case that the motion of a part to be disassembled is confined to the translational directions of the spatial (3D) coordinates, $M_{ij}$ is expressed as a 6-bit binary number, where the bit 0 denotes the impeding condition in X-positive direction, the bit 1 corresponds to X-negative direction, the bit 2 corresponds to the Y-positive direction, and so on. For a system shown in Figure 1 that consists of 5 parts, the impeding conditions of part 1 for parts $2\sim 5$ are expressed as $M_{12}=101000$, $M_{13}=001000$, $M_{14}=110011$, $M_{15}=110011$, where the value of $M_{12}$ expresses that part 1 impedes the motion of part 2 in Y-negative and Z-negative directions that correspond to bit 3 and bit 5, and so on.

The positional relations matrix can be extended and generalized for any number of moving directions for disassembly. In addition, even curvilinear disassembling motions can be taken into account by adopting suitable curvilinear coordinates for such part motions, since the crucial point of the positional relations matrix is to describe the impeding conditions among the parts in an abstract sense. In the current study, we adopt two-dimensional disassembling problems for the computation example. In cases where the part motion is confined to the translational directions of the plane coordinates, each of the matrix element $M_{ij}$ is expressed as a 4-bit binary number.

2.2. Disassembling Process Inference

2.2.1. Preparation of Disassembly-Move Sets and Disassembly-Part Sets

We refer to a pair $(j,k)$ that consists of part j and disassembly direction k as a disassembly move. On the basis of the positional relations matrix, we can obtain the set of immediate disassembly moves; that is, the set of pairs of parts and disassembly direction that are immediately available, as follows:

$${\mathcal{A}}_1=\left\{(j,k)\right|M_{ijk}=0\mathrm{for}\mathrm{all}i\}$$

(1)

where $M_{ijk}$ denotes the kth bit value of $M_{ij}$. Equation (1) expresses that ${\mathcal{A}}_1$ consists of disassembly moves $(j,k)$, such that part j can be immediately disassembled in direction k, since there are no impeding parts i in the direction such that $M_{ijk}=1$. Set ${\mathcal{A}}_1$ gives the following set of immediate disassembly parts:

$${\mathcal{P}}_1=\left\{j\right|(j,k)\in {\mathcal{A}}_1\mathrm{for}\mathrm{some}k\}$$

(2)

The set of two-stage disassembly moves is then obtained as

$${\mathcal{A}}_2=\left\{(j,k)\right|(j,k)\notin {\mathcal{A}}_1 \mathrm{a}\mathrm{n}\mathrm{d} {\mathcal{P}}_1\ni i \mathrm{s}\mathrm{u}\mathrm{c}\mathrm{h} \mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t} M_{ijk}=1\}$$

(3)

Equation (3) denotes that a disassembly move $(j,k)$ in ${\mathcal{A}}_2$ is not immediately available but can be available after all of the parts in ${\mathcal{P}}_1$ are removed, since all the impeding parts i for the move $(j,k)$, such that $M_{ijk}=1$ are in the set of immediate disassembly parts ${\mathcal{P}}_1$. Set ${\mathcal{A}}_2$ accordingly gives the set of two-stage disassembly parts:

$${\mathcal{P}}_2=\left\{j\right|(j,k)\in {\mathcal{A}}_2 \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e} k\}$$

(4)

Accordingly, we obtain the set of n-stage disassembly moves in the same manner as

$${\mathcal{A}}_n=\left\{(j,k)\right|(j,k)\notin {\mathcal{A}}_{1\sim (n-1)} \mathrm{a}\mathrm{n}\mathrm{d} {\mathcal{P}}_{1\sim (n-1)}\ni i \mathrm{f}\mathrm{o}\mathrm{r} M_{ijk}=1\}$$

(5)

where ${\mathcal{A}}_{1\sim n}={\mathcal{A}}_1\cup \cdots \cup {\mathcal{A}}_n$ is the set of disassembly moves to be available by n stages and ${\mathcal{P}}_{1\sim n}={\mathcal{P}}_1\cup \cdots \cup {\mathcal{P}}_n$ is the set of parts to be disassembled by n stages. The set of n-stage disassembly parts is obtained as well.

$${\mathcal{P}}_n=\left\{j\right|(j,k)\in {\mathcal{A}}_n \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e} k\}$$

(6)

This preparation process continues until the Rth stage, where all the combinations of disassembly moves $(j,k)$ are included in the unified disassembly-move set ${\mathcal{A}}_{1\sim R}$. At the end of this preparation process, we obtain the disassembly-move sets ${\mathcal{A}}_1,\cdots ,{\mathcal{A}}_R$ as well as the corresponding disassembly-part sets ${\mathcal{P}}_1,\cdots ,{\mathcal{P}}_R$.

2.2.2. Generation of Disassembling Process for Specified Parts

On the basis of the disassembly-move sets, we can generate a disassembling process for specified part J by means of the following procedure:

• Procedure: Disassembling Process (J)

Generate a disassembling sequence for specified part J as follows:

(1)

Search for a disassembly move $(J,K)\in {\mathcal{A}}_N$ corresponding to the specified part J. The search of such ${\mathcal{A}}_N$ is conducted from ${\mathcal{A}}_1$ to ${\mathcal{A}}_R$, since a move that is available in earlier stage is expected to have fewer impeding parts. Adopt the first detected $(J,K)\in {\mathcal{A}}_N$.

(2)

Use Sub-Procedure A as Mark Move ($N,(J,K)$) to mark the disassembly moves required to be performed in order to make move $(J,K)\in {\mathcal{A}}_N$ feasible.

(3)

Use Sub-Procedure B as Generate Sequence (J) to generate the sequence of disassembly moves, finally achieving move $(J,K)\in {\mathcal{A}}_N$.

• Sub-Procedure A: Mark Move ($n,(j,k)$)

Mark the required disassembly moves in ${\mathcal{A}}_1,\cdots ,{\mathcal{A}}_n$ in order to achieve move $(j,k)\in {\mathcal{A}}_n$; that is, mark the moves corresponding to the impeding parts for move $(j,k)\in {\mathcal{A}}_n$ as well as the move itself.

(1)

Mark $(j,k)\in {\mathcal{A}}_n$.

(2)

If $n=1$, then the specified move $(j,k)\in {\mathcal{A}}_1$ is immediately feasible. Terminate this sub-procedure.

(3)

($n>1$) There are impeding parts for move $(j,k)\in {\mathcal{A}}_n$. For each part i, such that $M_{ijk}=1$, search for a disassembly move $(i,l)\in {\mathcal{A}}_m$ corresponding to part i from ${\mathcal{A}}_1$ to ${\mathcal{A}}_{n-1}$ and use this procedure in a recursive manner as Mark Move ($m,(i,l)$).

• Sub-Procedure B: Generate Sequence (J)

Generate a disassembling sequence for part J based on the disassembly moves that are marked by above Sub-Procedure A.

(0)

Set initial values as $m=1$ (stage number), $n=0$ (sequence length), $S_0=\left[\right]$ (sequence (empty)), $\mathcal{D}=⌀$ (already disassembled-part set (empty)).

(1)

For all the marked move $(j,k)\in {\mathcal{A}}_m$, if $j\notin \mathcal{D}$ then add the move $(j,k)$ at the end of sequence $S_n$ as $(j_{n+1},k_{n+1})$. Increment sequence length as $n\leftarrow n+1$ and update the disassembled-part set $\mathcal{D}\leftarrow \mathcal{D}\cup \left\{j\right\}$.

(2)

If $j_n=J$, that is, the disassembly of the target part is achieved, then the required sequence of moves is accomplished as $S_n=[(j_1,k_1),\cdots ,(j_n,k_n)]$ where $j_n=J$ is the target part; terminate this sub-procedure.

(3)

Increment stage number as $m\leftarrow m+1$ and repeat from step (1).

The procedure gives a feasible disassembling process as a sequence of disassembly moves; however, the optimality of the generated process is not guaranteed. There are plural possibilities of selection of candidate moves $(J,K)\in {\mathcal{A}}_N$ at step (1) and $(i,l)\in {\mathcal{A}}_m$ at step (3). In the current study, we adopt the corresponding move from the earliest stage; however, any such move can be available for the generation of a feasible disassembling process. In other words, there can be other selections of moves that result in a better disassembling process.

The recursive use of Sub-Procedure A: Mark Move in step (3) can be processed in a parallel manner. It should be noted that the information of marked disassembly moves has to be shared by all the processing units. This possibility of parallel processing is considered to be effective, especially in the case of the search for an optimal disassembling process.

2.3. Generating Optimal Disassembling Process

A disassembling sequence of n moves can be expressed as $S_n=[(j_1,k_1)$, $(j_2,k_2)$, ⋯, $(j_n,k_n)]$ where $j_{\alpha }\ne j_{\beta }$$(\alpha \ne \beta )$, which represents to remove part $j_1$ in direction $k_1$, then part $j_2$ in direction $k_2$, and so on. The mth move $(j_m,k_m)$ ($1\le m\le n$) is feasible in the case that for any i ($i=1,\cdots ,N$), $M_{i{j}_m{k}_m}=0$ or $i\in \{j_1,\cdots ,j_{m-1}\}$; that is, for any part i, it does not impede the move $(j_m,k_m)$ or it is already removed as a part of the preceding moves. Disassembling sequence $S_n=[(j_1,k_1)$, $(j_2,k_2)$, ⋯, $(j_n,k_n)]$ is a feasible disassembling process for part $j_n$, in the case that all the moves $(j_m,k_m)$ ($m=1,\cdots ,n$) are feasible.

A number sequence $j_1,\cdots ,j_n$ can create a feasible disassembling process for part $j_n$, in the case that there exist $k_1,\cdots ,k_n$ which make all the moves $(j_1,k_1)$, ⋯, $(j_n,k_n)$ feasible. Accordingly, for a disassembling problem of N parts, examining all the permutations of $1,\cdots ,N$ as $j_1,\cdots ,j_N$, checking the possibility of making its partial sequence $j_1,\cdots ,j_n$ $(1\le n\le N)$ feasible disassembling sequence where $j_n=J$, and evaluating the optimality of the sequence, we can obtain the optimal disassembling process for any specified part J. It should be noted that the computation cost required for this optimal disassembling process generation is $\mathcal{O}(N!)$.

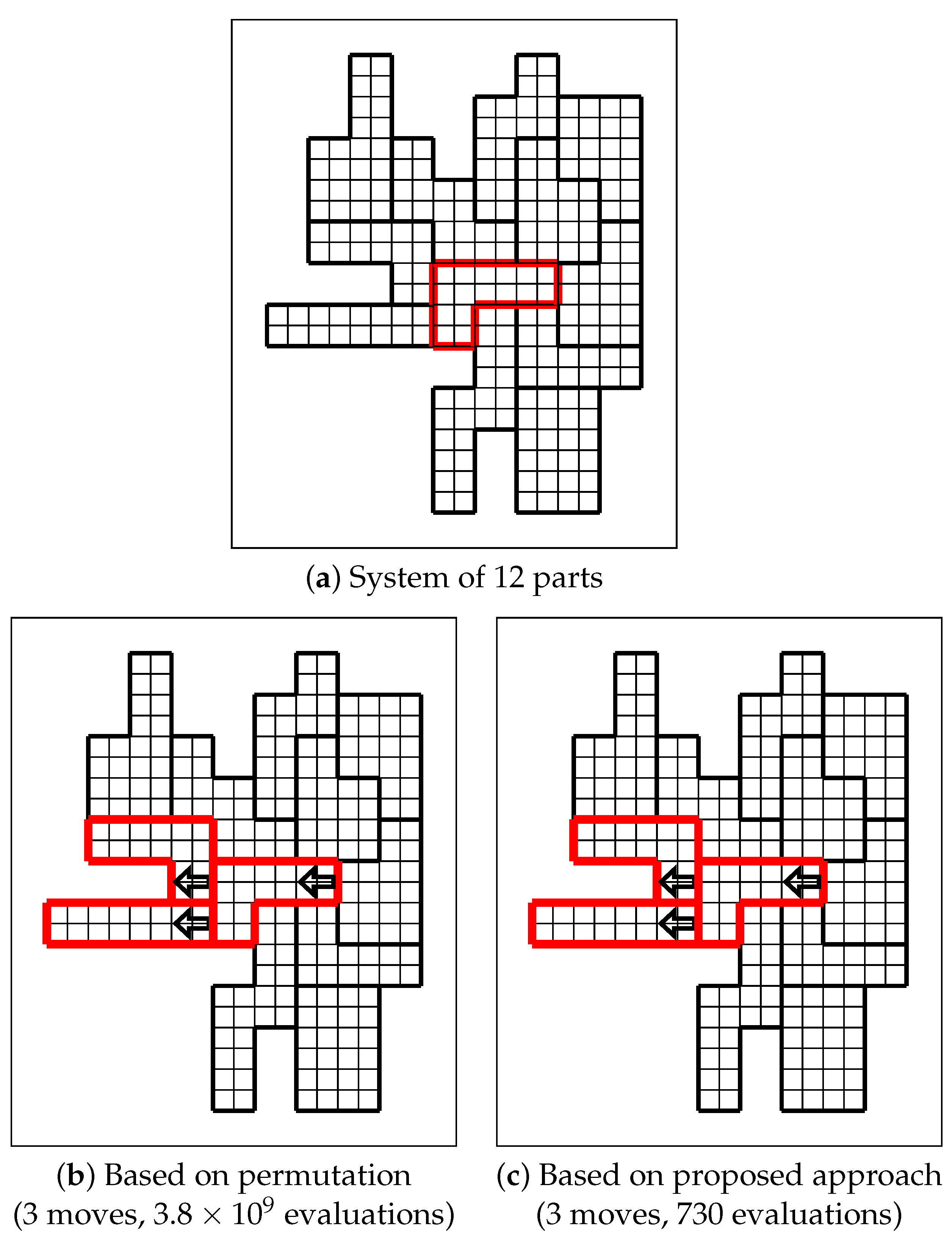
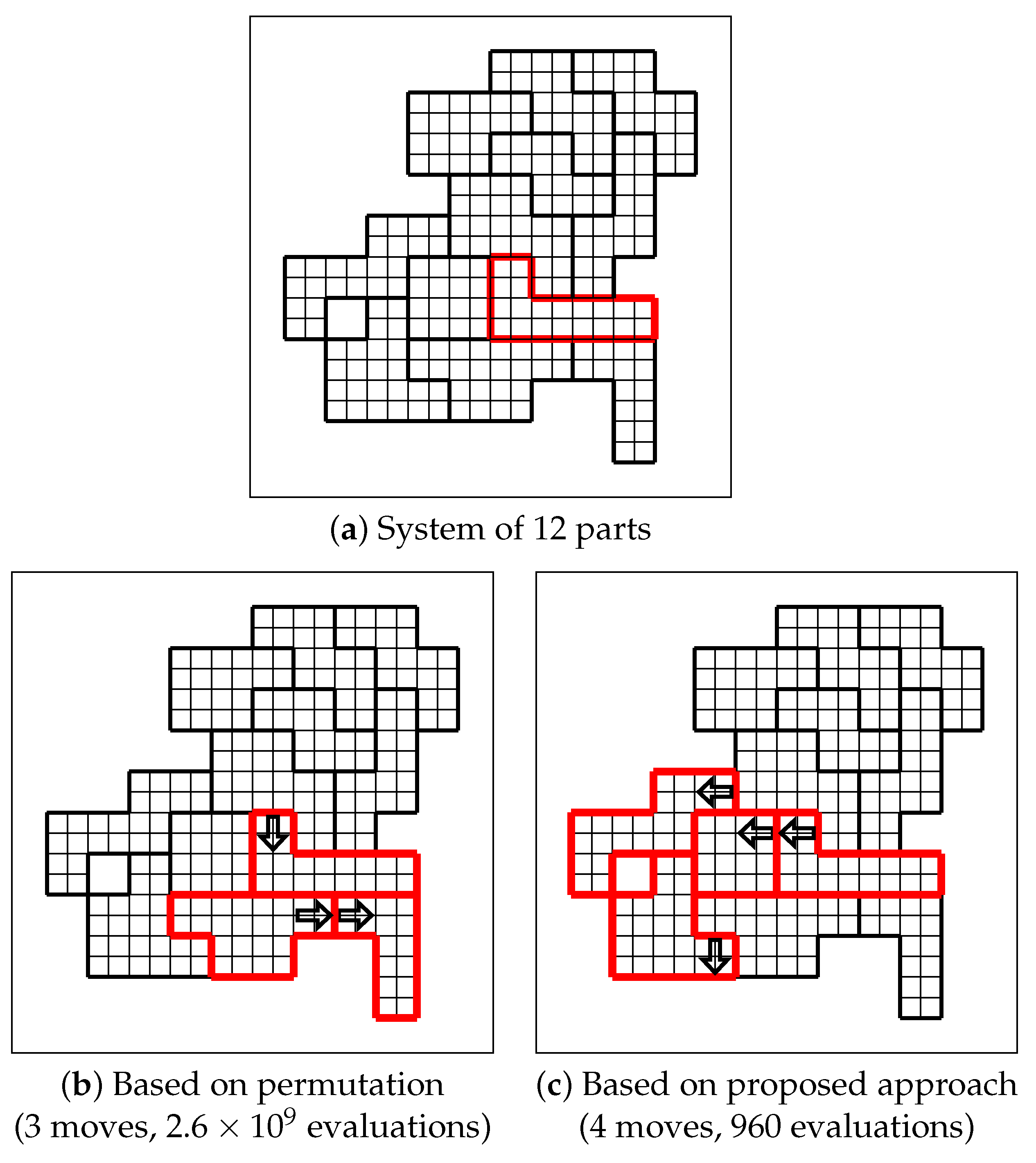
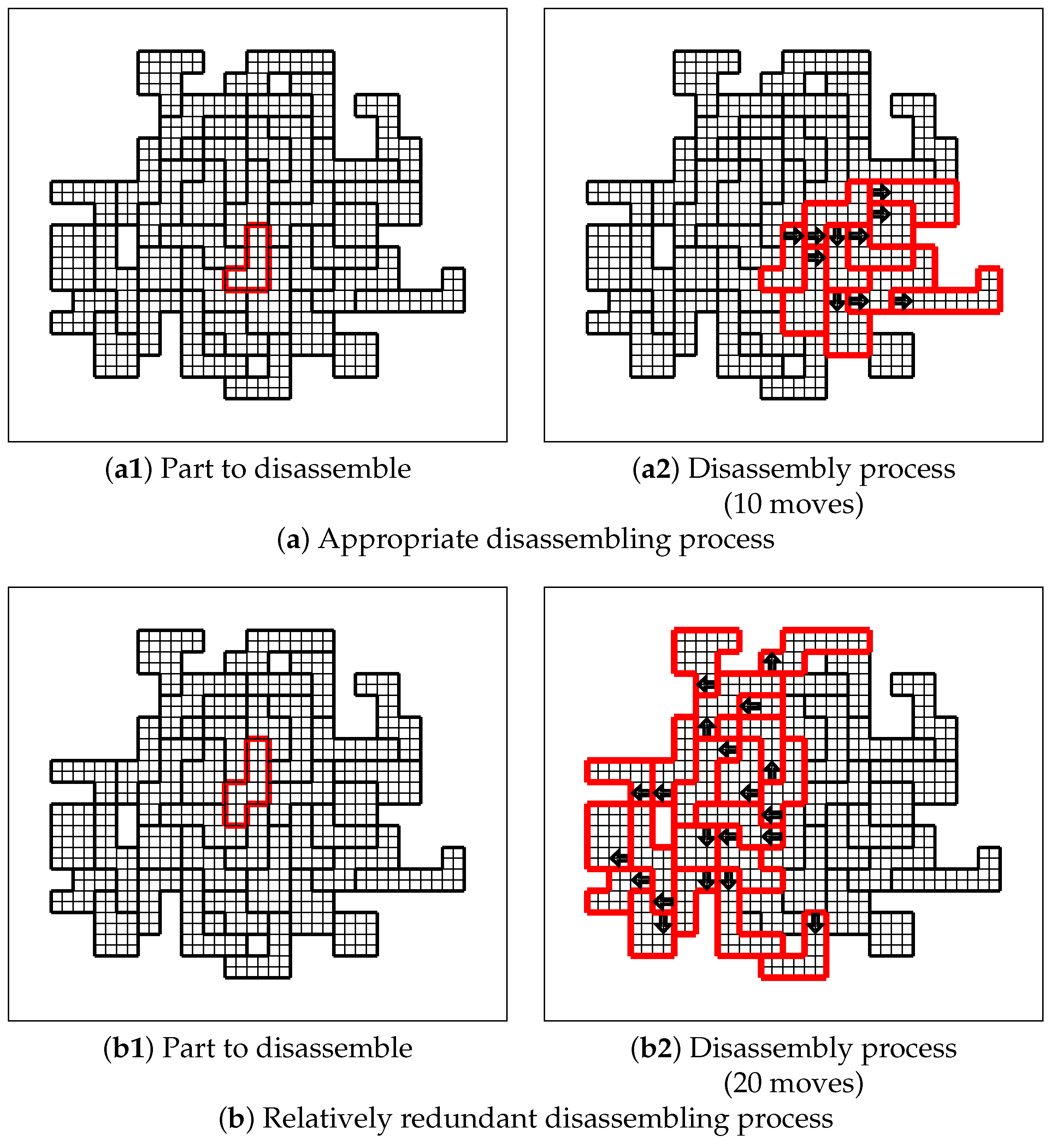
3. Evaluating Disassembling Process Inference

In order to evaluate the performance and efficiency of the disassembling process inference developed in Section 2.2, we employ a disassembling-problem generation system [18]. The system is able to generate two-dimensional block-pattern-based disassembling problems consisting of any number of parts. The approach is based on a weighted random walk; that is, it places parts consisting of four to six square blocks at empty cells in the course of the walk. The point is that the direction of the walk has a weak tendency towards the origin in order to keep the state of aggregation as an assembled system.

Figure 2 and Figure 3 show examples of randomly generated disassembling problems of 12 parts and their obtained disassembling processes. The red parts are the target part and the parts to be disassembled; the arrows in the parts indicate the disassembly moves. Figure 2b and Figure 3b are the optimal disassembling processes of minimum moves obtained by the permutation approach indicated in Section 2.3. Figure 2c and Figure 3c are the disassembling processes obtained by the proposed disassembling process inference.

The disassembling processes shown in Figure 2b,c are the same; however, the disassembling processes shown in Figure 3b,c are different. These results show that the proposed disassembling process inference is not guaranteed to generate the optimal disassembling process. We evaluate the computational cost for disassembling process inference in terms of the number of evaluations of elements of the positional relations matrix. Comparing the numbers of evaluations required to obtain the results shown in Figure 2b ($3.8\times {10}^9$) and Figure 2c (730) as well as Figure 3b ($2.6\times {10}^9$) and Figure 3c (960), it is demonstrated that the computational cost by means of the proposed approach is considerably less than the computational cost by means of the permutation approach.

On the basis of 20 randomly generated disassembling problems of 12 parts, the average numbers of disassembly moves are 2.70 by means of the permutation approach and 3.15 by means of the proposed inference approach. Fifteen of the twenty results (75%) are of the same numbers of moves for both permutation and the inference approaches in this case; however, there is one result that the inference approach gives seven moves while the optimal result has only three moves.

Table 1. Computational cost evaluations of proposed approach.

Number of parts	10	30	100	300	1000
Computational cost	$5.9\times {10}^2$	$4.2\times {10}^3$	$3.4\times {10}^4$	$2.5\times {10}^5$	$2.3\times {10}^6$

shows the averaged computational costs of the proposed disassembling process inference for the generated disassembling problems of various numbers of parts. The results indicate that the computational cost of the proposed inference approach is less than $\mathcal{O}\left(N^2\right)$ for the N-part problem. Compared with the computational cost $\mathcal{O}(N!)$ for N-part problem of the permutation approach, the proposed inference approach is considered to be practical enough from this point of view.

Figure 4 shows typical examples of a disassembling process for a 40-part system based on the proposed inference approach. Figure 4a shows an appropriate disassembling process; however, the result shown in Figure 4b seems fairly redundant. On the basis of the obtained disassembling process shown in Figure 4b2, we can see the possibility of a disassembling process of two fewer steps without the disassembly moves of the top and the bottom parts, by assuming the leftward move to all the parts to be disassembled. This result also demonstrates that the proposed inference approach does not always generate the optimal disassembling process. It should be noted, however, that the permutation approach cannot be applied to a disassembling problem of this number of parts because of the computational cost of $\mathcal{O}(N!)$.

4. Concluding Remarks

Geometrical constraints among the constituent parts are a fundamental factor for the disassembly of systems consisting of a number of parts. We adopt the positional relations matrix of binary elements to describe the geometrical constraints. On the basis of the matrix, a disassembling process inference approach was developed in a general form. The approach can be applied to any disassembling problem expressed in terms of the positional relations matrix.

In the current study, we have evaluated the proposed disassembling process inference approach based on two-dimensional disassembling problems, which were generated by a random number-based disassembling problem generation system. The disassembling problems adopted for the evaluation appear relatively simple because of their two-dimensionality; however, they exhibit a complicated nature comparable to practical problems in case of a sufficient number of constituent parts.

From the viewpoint of the optimality of the results, the obtained disassembling processes based on the proposed inference approach were fairly appropriate; however, it was confirmed that the proposed inference approach does not always result in the optimal disassembling process. In the proposed approach, there actually is some arbitrariness in the marking process of impeding parts, as mentioned in Section 2.2.2. We are studying this point to improve the disassembling process to be generated. From the viewpoint of the computational cost, it was demonstrated that the proposed inference approach is quite practical and the computational cost is $\mathcal{O}\left(N^2\right)$, compared with the computational cost of $\mathcal{O}(N!)$ of the permutation approach that always gives the optimal results. We conclude that the proposed disassembling process inference approach based on the positional relations matrix is practical enough.

The proposed disassembling process inference is expected to have a wide range of applicability because of the generality and extensibility of the positional relations matrix, as mentioned in Section 2.1. From the optimality viewpoint, it is considered to be possible to employ a criterion other than the number of disassembling moves for the target part, such as the required work time or the total mass of the disassembled parts, by customizing the selection from the possible candidate moves suggested in Section 2.2.2.

The positional relations matrix is assumed to be constant in the current study. Dynamic impeding conditions—that is, impeding conditions among parts depending on the order of disassembling parts or so-called compound moves—cannot be dealt with. Mechanical conditions of such as supported or supporting parts are currently not taken into account either. Expanding the positional relations matrix to include intermediate states of part condition and introducing logical operation among the matrix elements to determine a part’s propensity for disassembly are promising candidate topics to be undertaken. Such an extension of the disassembling process inference is also a topic that can be addressed in future work.