Crust and Upper Mantle Structure of Mars Determined from Surface Wave Analysis
Abstract
1. Introduction
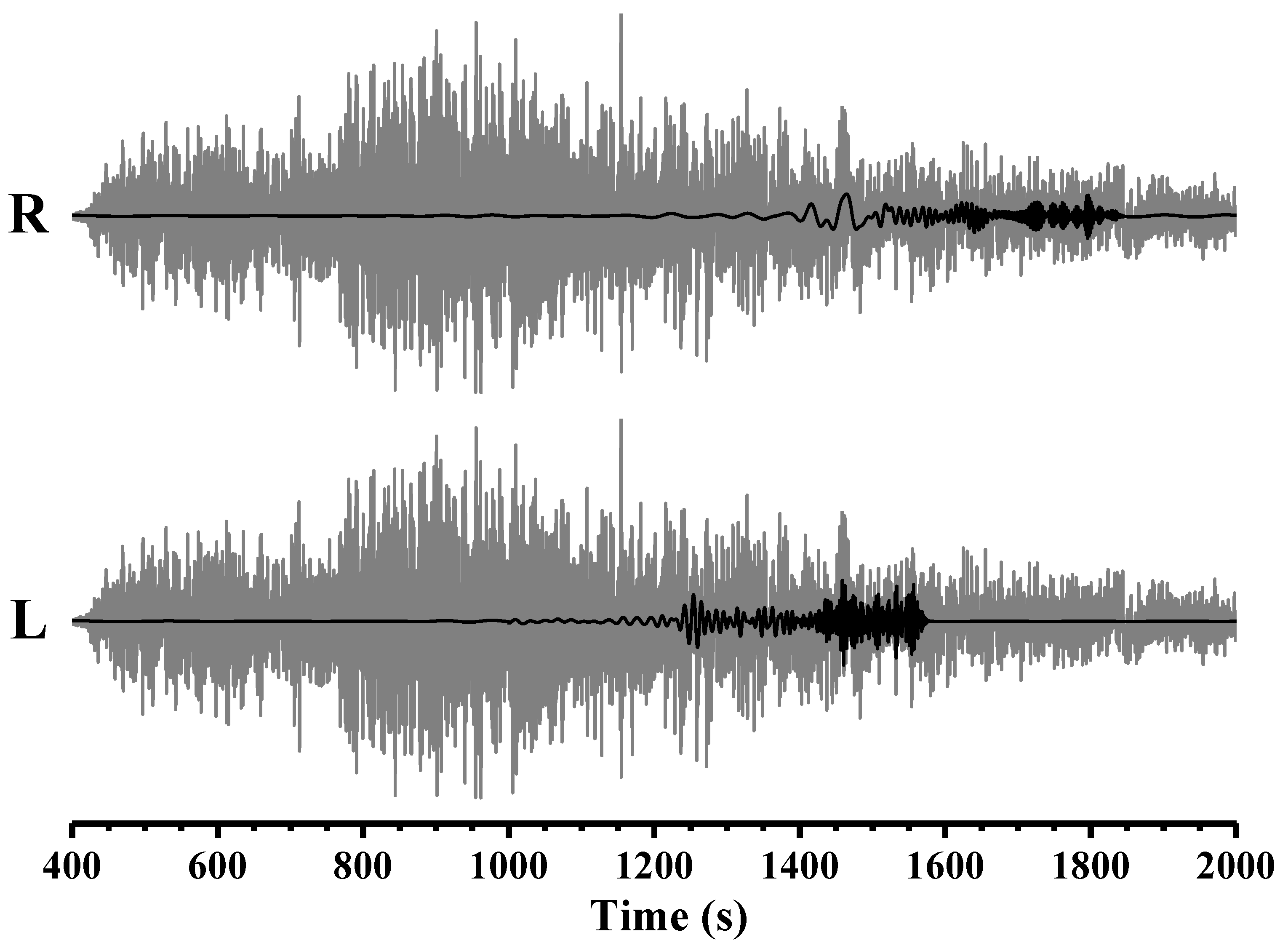
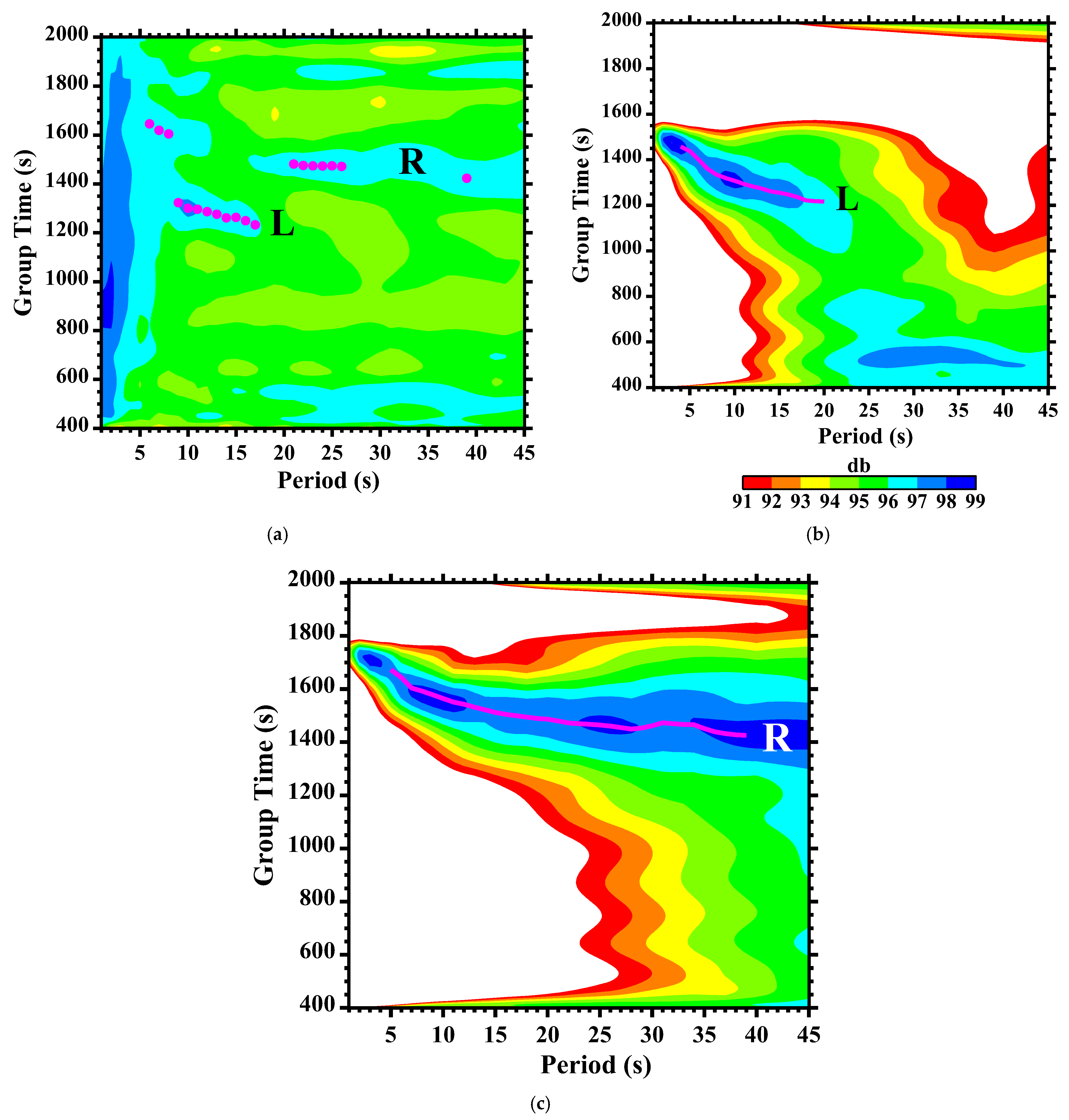
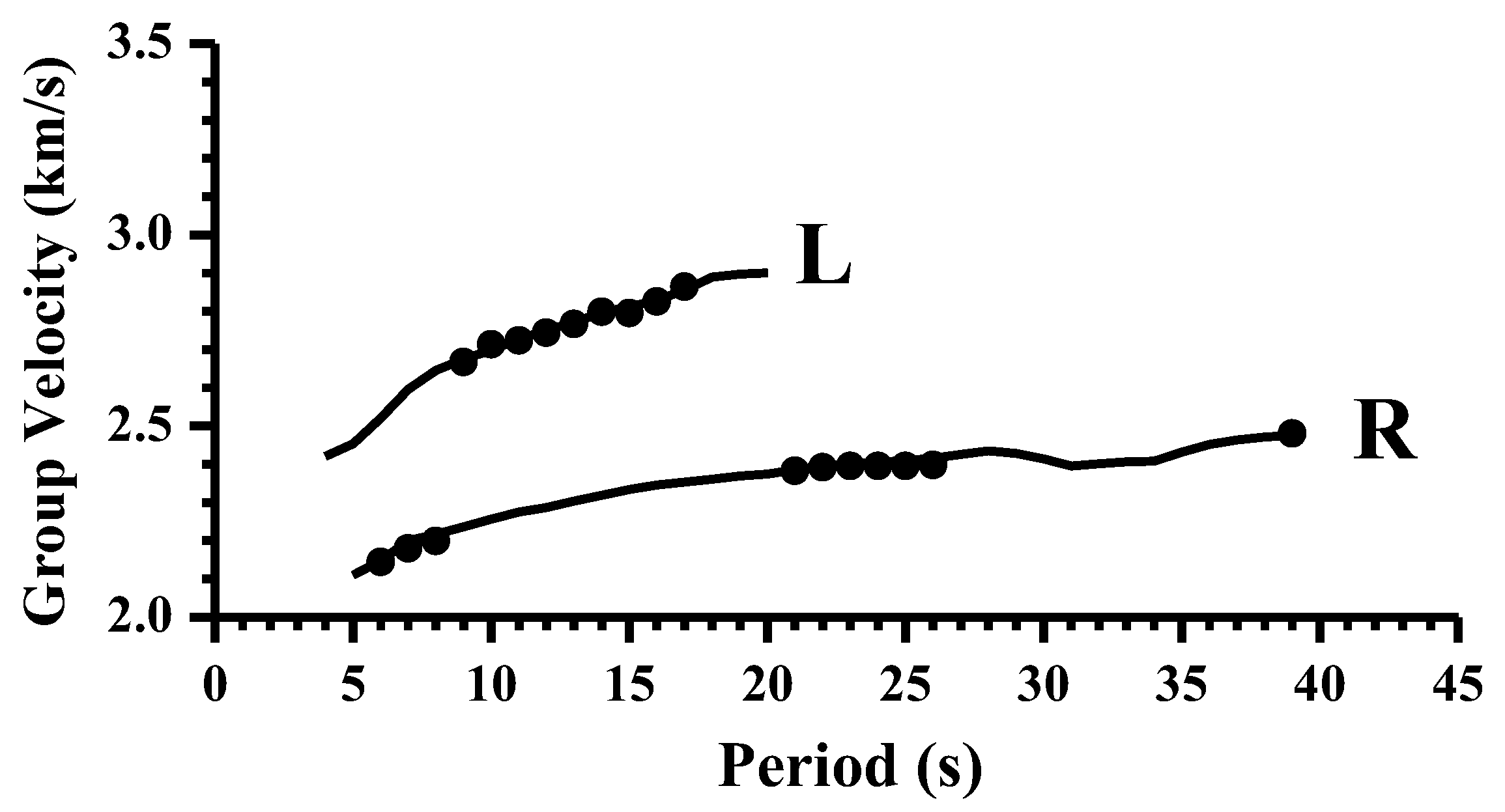
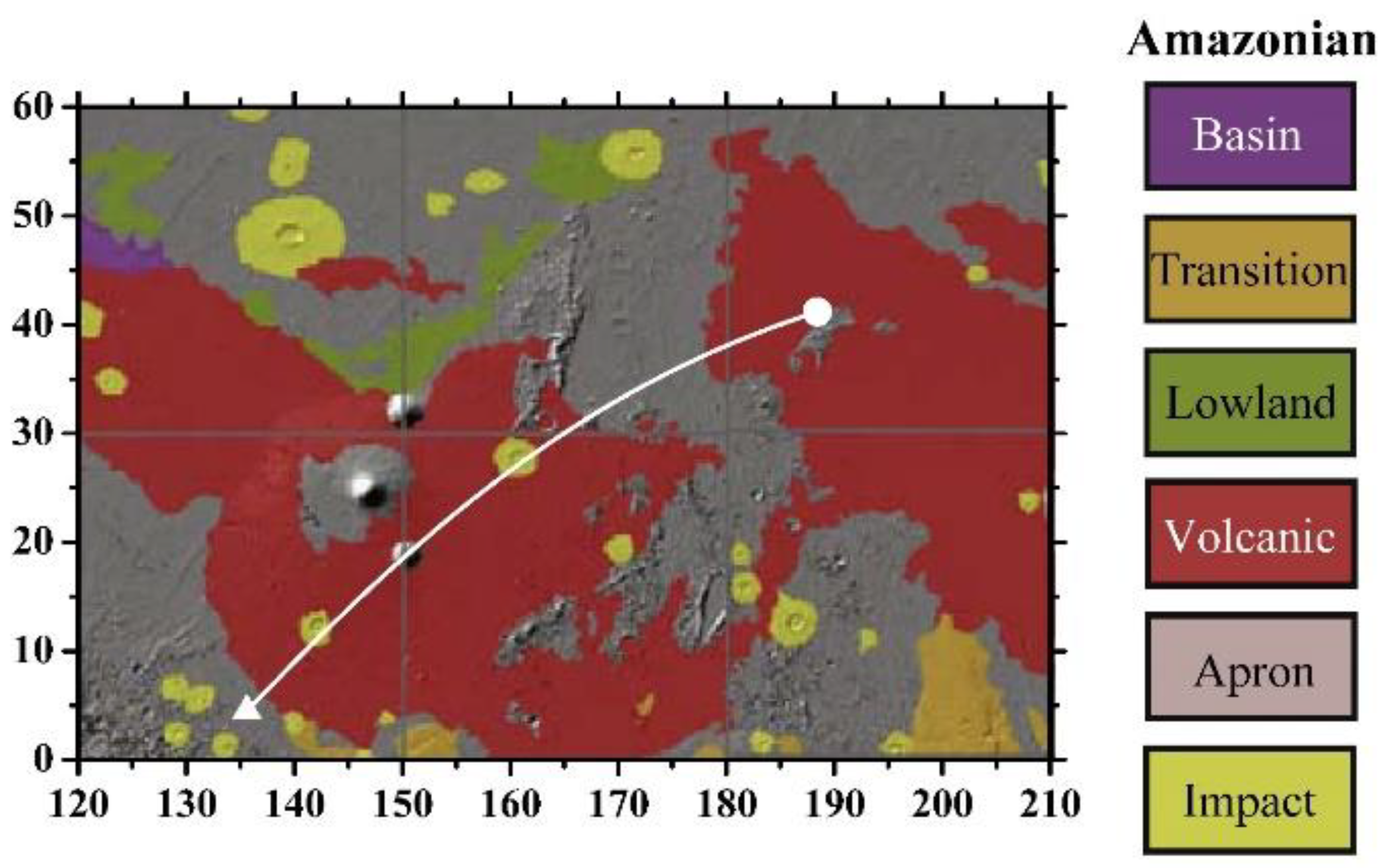
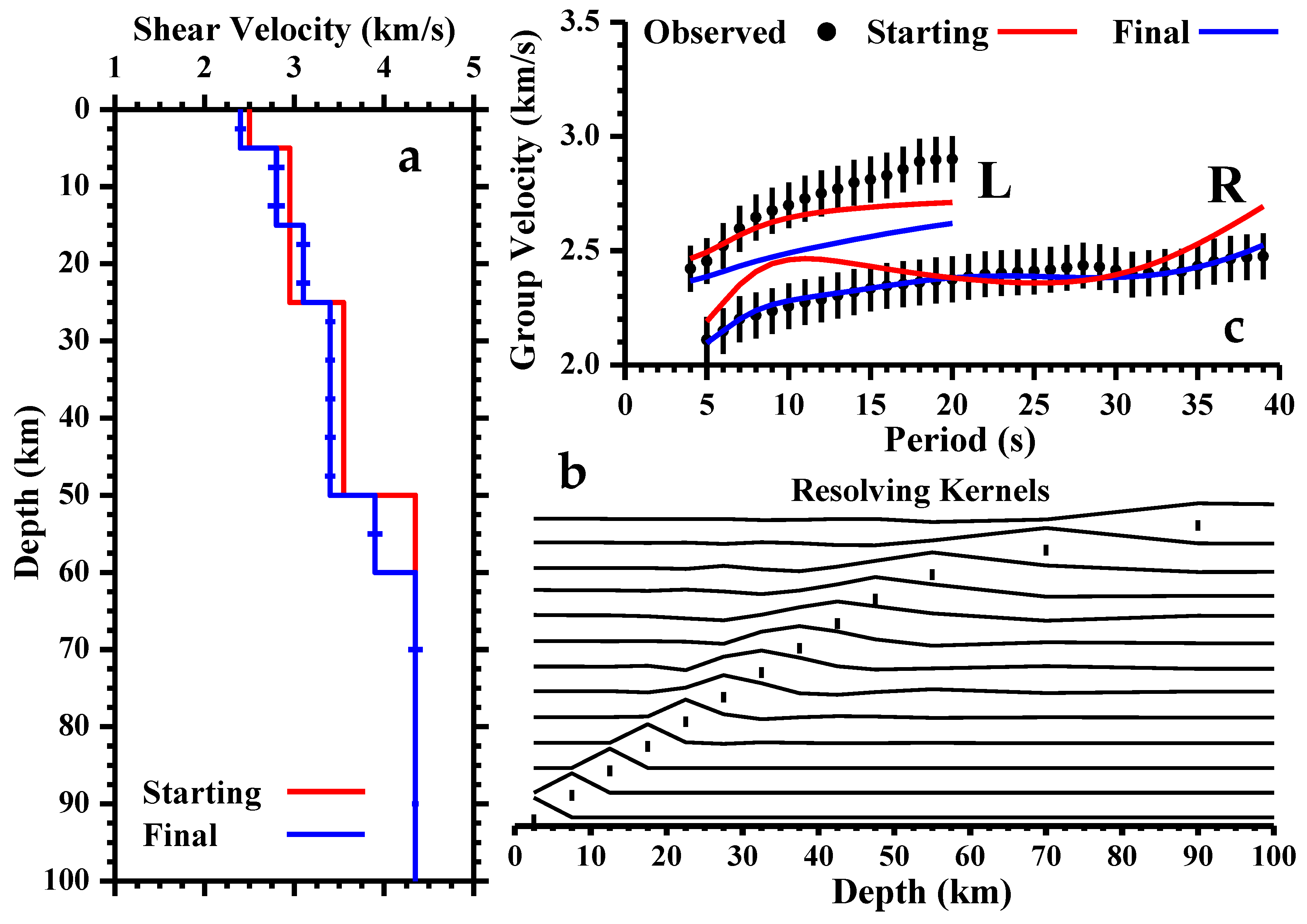
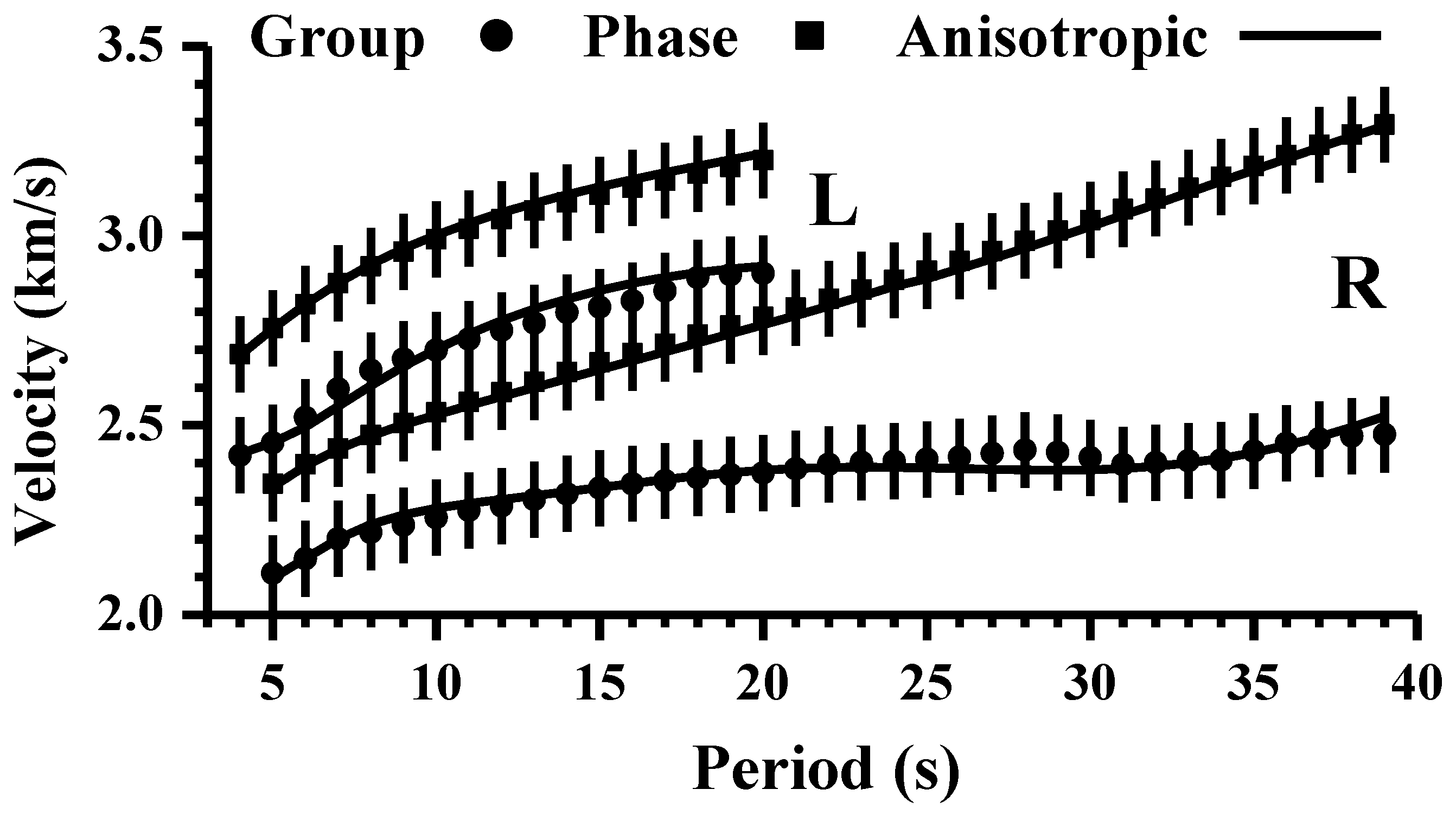
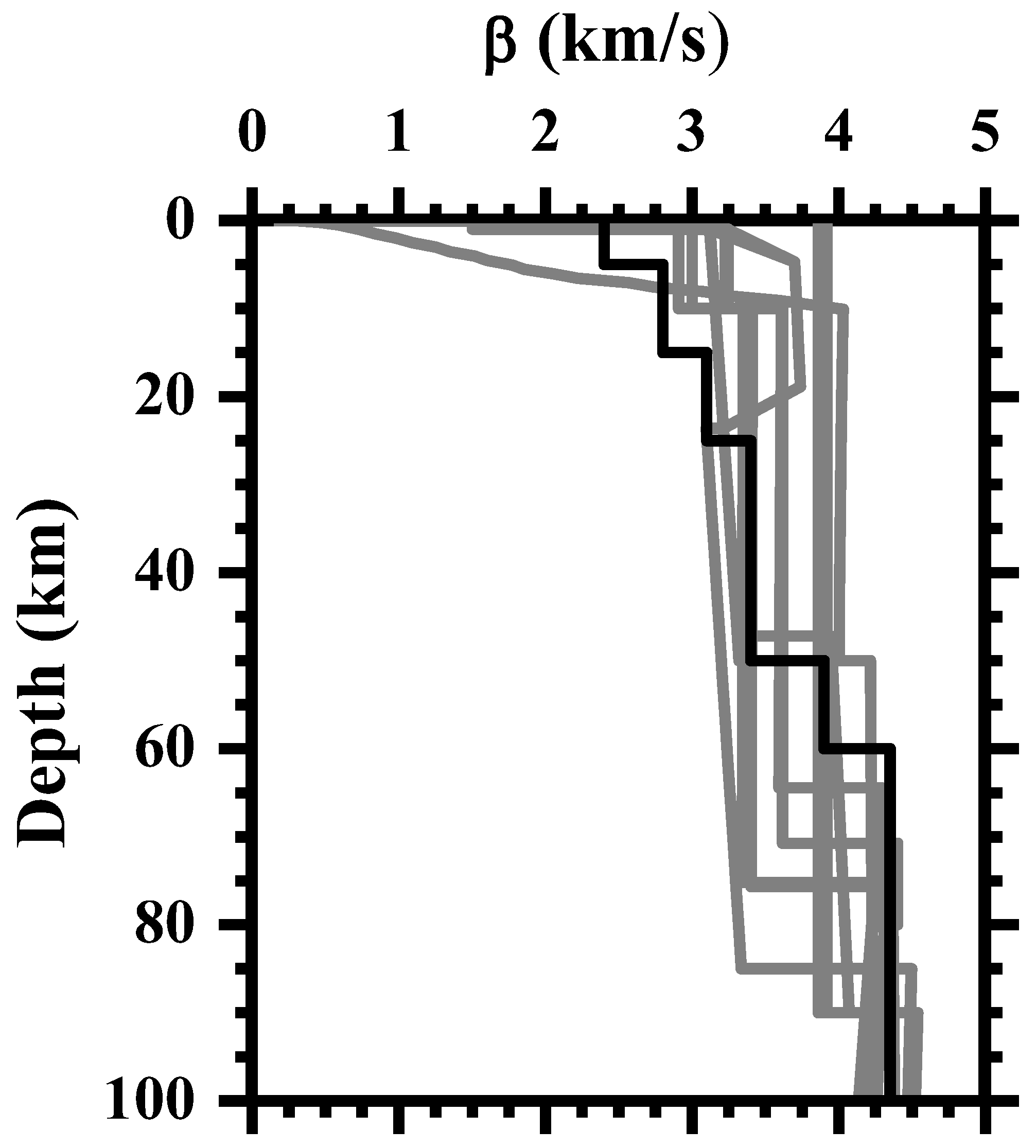
2. Data, Methodology, and Results
3. Interpretation and Discussion
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, A.; Ceylan, S.; van Driel, M.; Giardini, D.; Lognonné, P.; Samuel, H.; Schmerr, N.C.; Stähler, S.C.; Duran, A.C.; Huang, Q.; et al. Upper mantle structure of Mars from InSight seismic data. Science 2021, 373, 434–438. [Google Scholar] [CrossRef] [PubMed]
- Hobiger, M.; Halló, M.; Schmelzbach, C.; Stähler, S.C.; Fäh, D.; Giardini, D.; Golombek, G.; Clinton, J.; Dahmen, N.; Zenhäusern, G.; et al. The shallow structure of Mars at the InSight landing site from inversion of ambient vibration. Nat. Commun. 2021, 12, 6756. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Stähler, S.C.; Ceylan, S.; Lekic, V.; Maguire, R.; Zenhäusern, G.; Clinton, J.; Giardini, D.; Khan, A.; Panning, M.P.; et al. Structure along the martian dichotomy constrained by Rayleigh and love waves and their overtones. Geophys. Res. Lett. 2023, 50, e2022GL101666. [Google Scholar] [CrossRef]
- Beghein, C.; Li, J.; Weidner, E.; Maguire, R.; Wookey, J.; Lekić, V.; Lognonné, P.; Banerdt, W. Crustal anisotropy in the Martian lowlands from surface waves. Geophys. Res. Lett. 2022, 49, e2022GL101508. [Google Scholar] [CrossRef]
- Li, J.; Beghein, C.; Wookey, J.; Davis, P.; Lognonné, P.; Schimmel, M.; Stutzmann, E.; Golombek, M.; Montagner, J.-P.; Banerdt, W.B. Evidence for crustal seismic anisotropy at the InSight lander site. Earth Planet. Sci. Lett. 2022, 593, 117654. [Google Scholar] [CrossRef]
- Kim, D.; Banerdt, W.B.; Ceylan, S.; Giardini, D.; Lekić, V.; Lognonné, P.; Beghein, C.; Beucler, É.; Carrasco, S.; Charalambous, C.; et al. Surface waves and crustal structure on Mars. Science 2022, 378, 417–421. [Google Scholar] [CrossRef]
- Corchete, V.; Chourak, M.; Hussein, H.M. Shear wave velocity structure of the Sinai Peninsula from Rayleigh wave analysis. Surv. Geophys. 2007, 28, 299–324. [Google Scholar] [CrossRef]
- Corchete, V. Crustal and upper-mantle structure beneath the South China Sea and Indonesia. Geol. Soc. Am. Bull. 2022, 133, 177–184. [Google Scholar] [CrossRef]
- Dziewonski, A.; Bloch, S.; Landisman, M. A technique for the analysis of transient seismic signals. Bull. Seism. Soc. Am. 1969, 59, 427–444. [Google Scholar] [CrossRef]
- Cara, M. Filtering dispersed wavetrains. Geophys. J. R. Astron. Soc. 1973, 33, 65–80. [Google Scholar] [CrossRef]
- Lognonné, P.; Banerdt, W.B.; Giardini, D.; Pike, W.T.; Christensen, U.; Laudet, P.; de Raucourt, S.; Zweifel, P.; Calcutt, S.; Bierwirth, M.; et al. SEIS: Insight’s Seismic Experiment for Internal Structure of Mars. Space Sci. Rev. 2019, 215, 1–170. [Google Scholar] [CrossRef] [PubMed]
- Scholz, J.R.; Widmer-Schnidrig, R.; Davis, P.; Lognonné, P.; Pinot, B.; Garcia, R.F.; Hurst, K.; Pou, L.; Nimmo, F.; Barkaoui, S.; et al. Detection, analysis, and removal of glitches from InSight’s seismic data from Mars. Earth Space Sci. 2020, 7, e2020EA001317. [Google Scholar] [CrossRef]
- Tanaka, K.; Robbins, S.; Fortezzo, C.; Skinner, J.; Hare, T. The digital global geologic map of Mars: Chronostratigraphic ages, topographic and crater morphologic characteristics, and updated resurfacing history. Planet. Space Sci. 2014, 95, 11–24. [Google Scholar] [CrossRef]
- Smrekar, S.E.; Lognonné, P.; Spohn, T.; Banerdt, W.B.; Breuer, D.; Christensen, U.; Dehant, V.; Drilleau, M.; Folkner, W.; Fuji, N.; et al. Pre-mission InSights on the Interior of Mars. Space Sci. Rev. 2019, 215, 3. [Google Scholar] [CrossRef]
- Babuska, V.; Cara, M. Seismic Anisotropy in the Earth; Kluwer Academic: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Corchete, V. Review of the methodology for the inversion of surface-wave phase velocities in a slightly anisotropic medium. Comput. Geosci. 2012, 41, 56–63. [Google Scholar] [CrossRef]
- Abo-Zena, A. Dispersion function computations for unlimited frequency values. Geophys. J. R. Astron. Soc. 1979, 58, 91–105. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology. In Theory and Methods; Freeman: San Francisco, CA, USA, 1980. [Google Scholar]
- Smith, L.M.; Dahlen, F.A. The azimuthal dependence of Love and Rayleigh wave propagation in a slightly anisotropic medium. J. Geophys. Res. 1973, 78, 3321–3333. [Google Scholar] [CrossRef]
- Ben-Menahem, A.; Singh, S.J. Seismic Waves and Sources; Springer: New York, NY, USA, 1981. [Google Scholar]
- Jiang, C.; Schmandt, B.; Farrell, J.; Lin, F.-C.; Ward, K.M. Seismically anisotropic magma reservoirs underlying silicic calderas. Geology 2018, 46, 727–730. [Google Scholar] [CrossRef]
- Zuber, M.T. The crust and mantle of Mars. Nature 2001, 412, 220–227. [Google Scholar] [CrossRef]
- Neumann, G.A.; Zuber, M.T.; Wieczorek, M.A.; McGovern, P.J.; Lemoine, F.G.; Smith, D.E. Crustal structure of Mars from gravity and topography. J. Geophys. Res. 2004, 109, 08002. [Google Scholar] [CrossRef]
- Bouley, S.; Keane, J.T.; Baratoux, D.; Langlais, B.; Matsuyama, I.; Costard, F.; Hewins, R.; Payré, V.; Sautter, V.; Séjourné, A.; et al. A thick crustal block revealed by reconstructions of early Mars highlands. Nat. Geosci. 2020, 13, 105–109. [Google Scholar] [CrossRef]

| Layer (n) | αH (km/s) | βH (km/s) | αV (km/s) | βV (km/s) | ξ (βH/βV)2 | φ (αV/αH)2 | |
|---|---|---|---|---|---|---|---|
| 1 | 4.35 ± 0.12 | 2.51 ± 0.07 | 4.07 ± 0.14 | 2.35 ± 0.08 | 1.14 | 0.88 | 6.7 |
| 2 | 5.53 ± 0.16 | 3.19 ± 0.09 | 4.69 ± 0.14 | 2.71 ± 0.08 | 1.39 | 0.72 | 17.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corchete, V. Crust and Upper Mantle Structure of Mars Determined from Surface Wave Analysis. Appl. Sci. 2025, 15, 4732. https://doi.org/10.3390/app15094732
Corchete V. Crust and Upper Mantle Structure of Mars Determined from Surface Wave Analysis. Applied Sciences. 2025; 15(9):4732. https://doi.org/10.3390/app15094732
Chicago/Turabian StyleCorchete, Víctor. 2025. "Crust and Upper Mantle Structure of Mars Determined from Surface Wave Analysis" Applied Sciences 15, no. 9: 4732. https://doi.org/10.3390/app15094732
APA StyleCorchete, V. (2025). Crust and Upper Mantle Structure of Mars Determined from Surface Wave Analysis. Applied Sciences, 15(9), 4732. https://doi.org/10.3390/app15094732





