Thermally Induced Displacements and Rotations of Pillars for Precise Geodetic Measurements
Abstract
:Featured Application
Abstract
1. Introduction
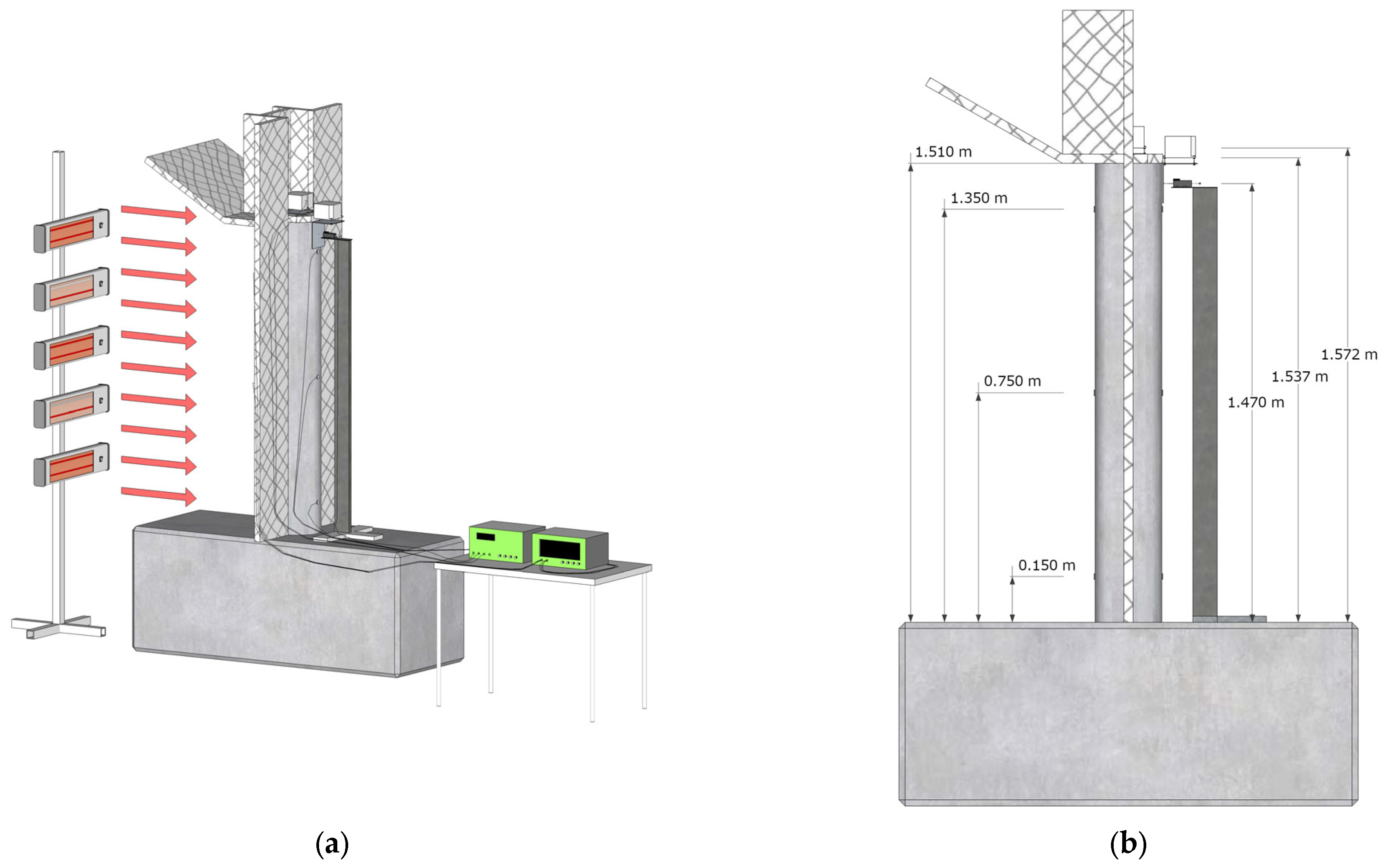
2. Experimental Setting and Computational Model
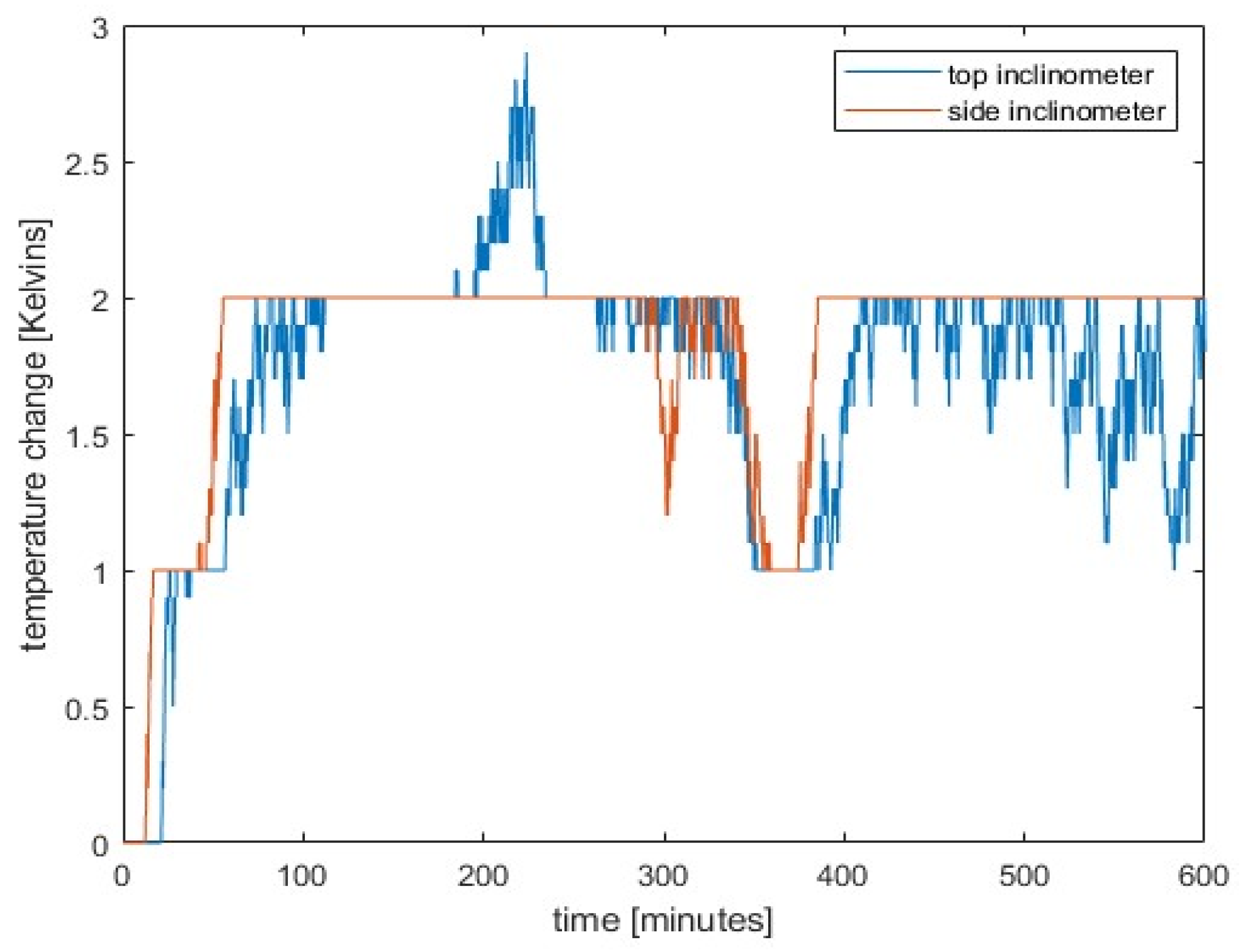
3. Experimental Results
4. Discussion
5. Conclusions
- (1)
- Measuring the displacement of a column caused by thermal stress in the field is almost impossible, as isolating the displacement sensor mount from external influences is a major challenge. However, it is much easier to isolate an inclinometer mounted on the column, which measures the inclination of the plate that holds the screw for forced centering. From the measured inclination, the thermally induced displacement can be calculated without much effort.
- (2)
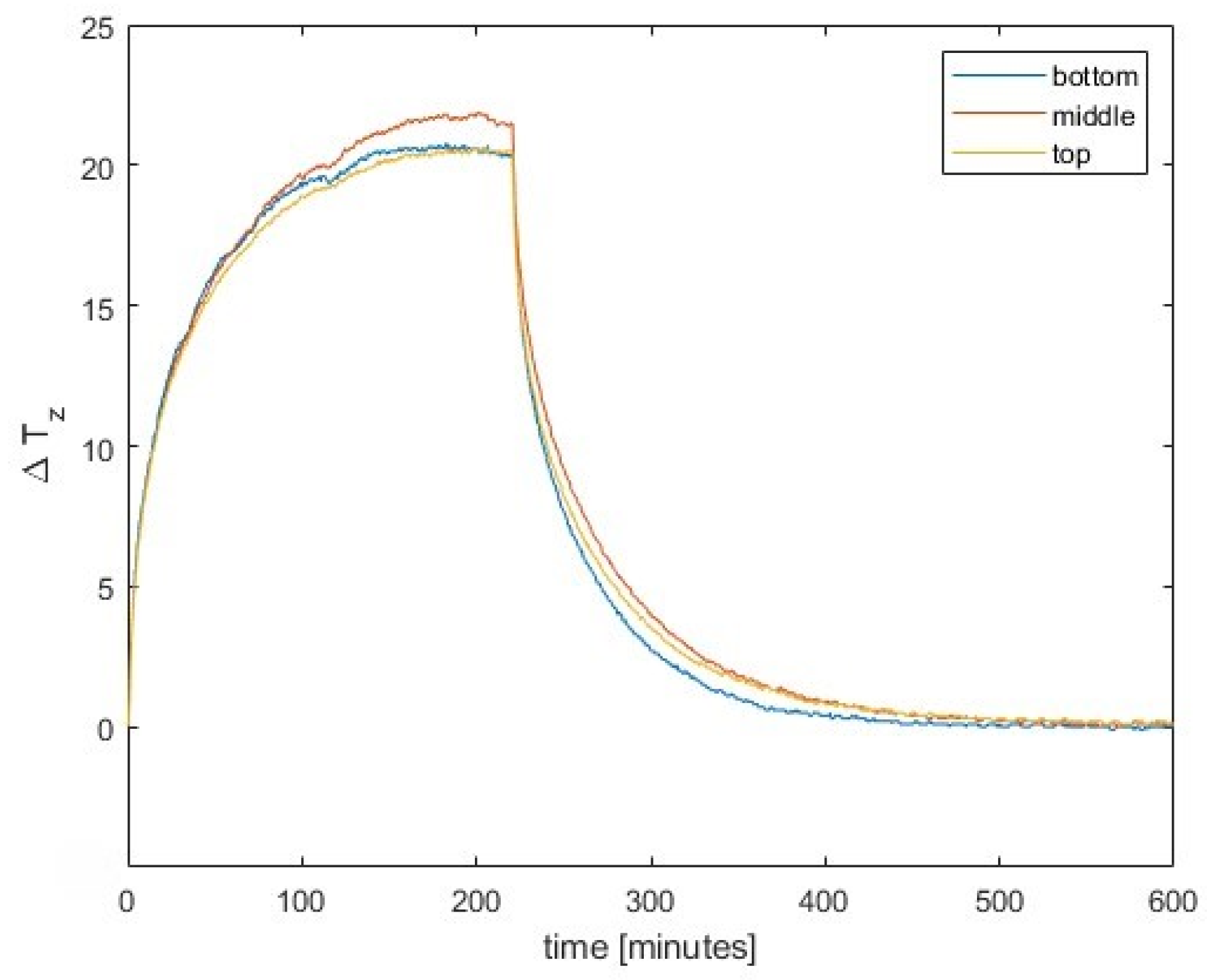
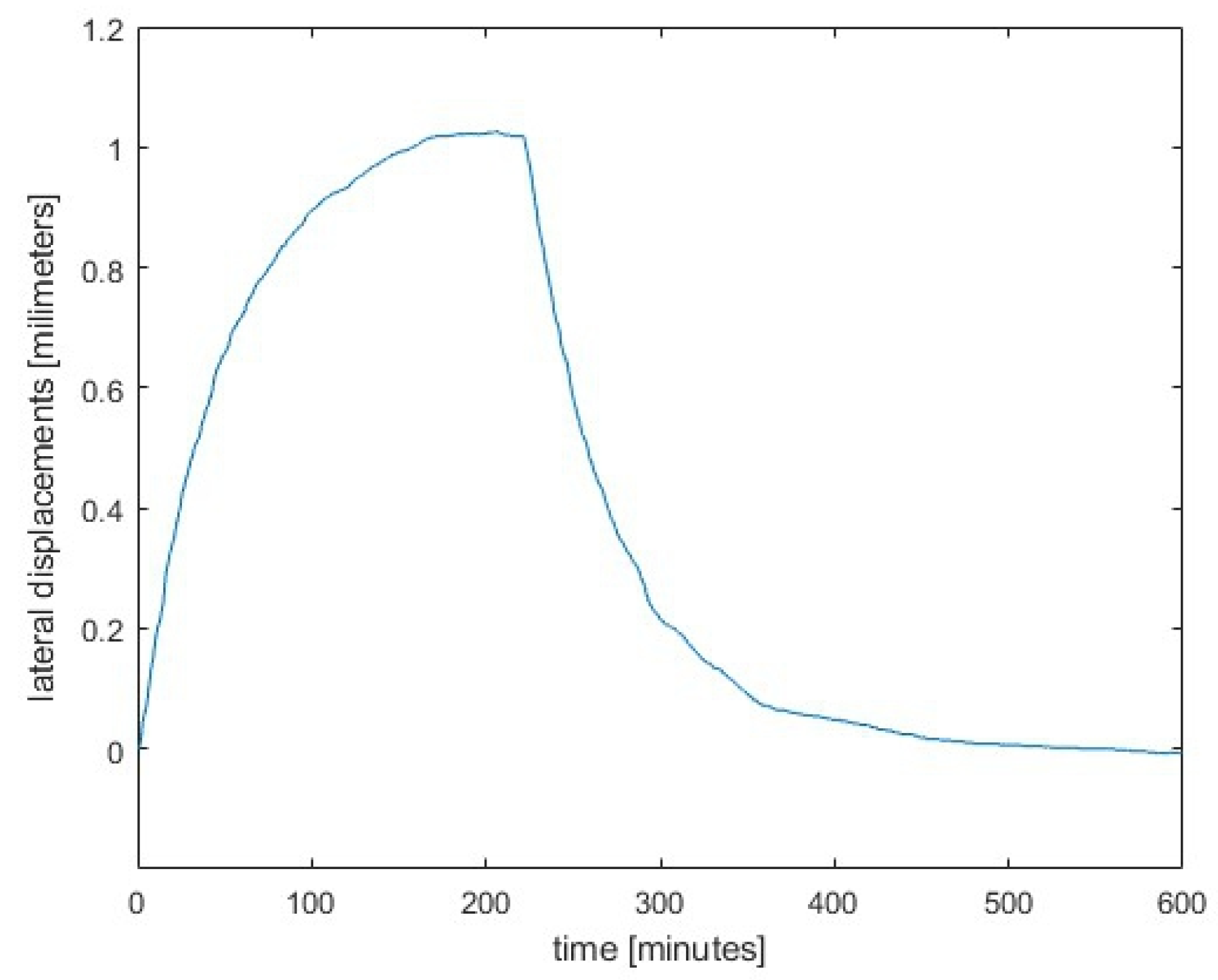
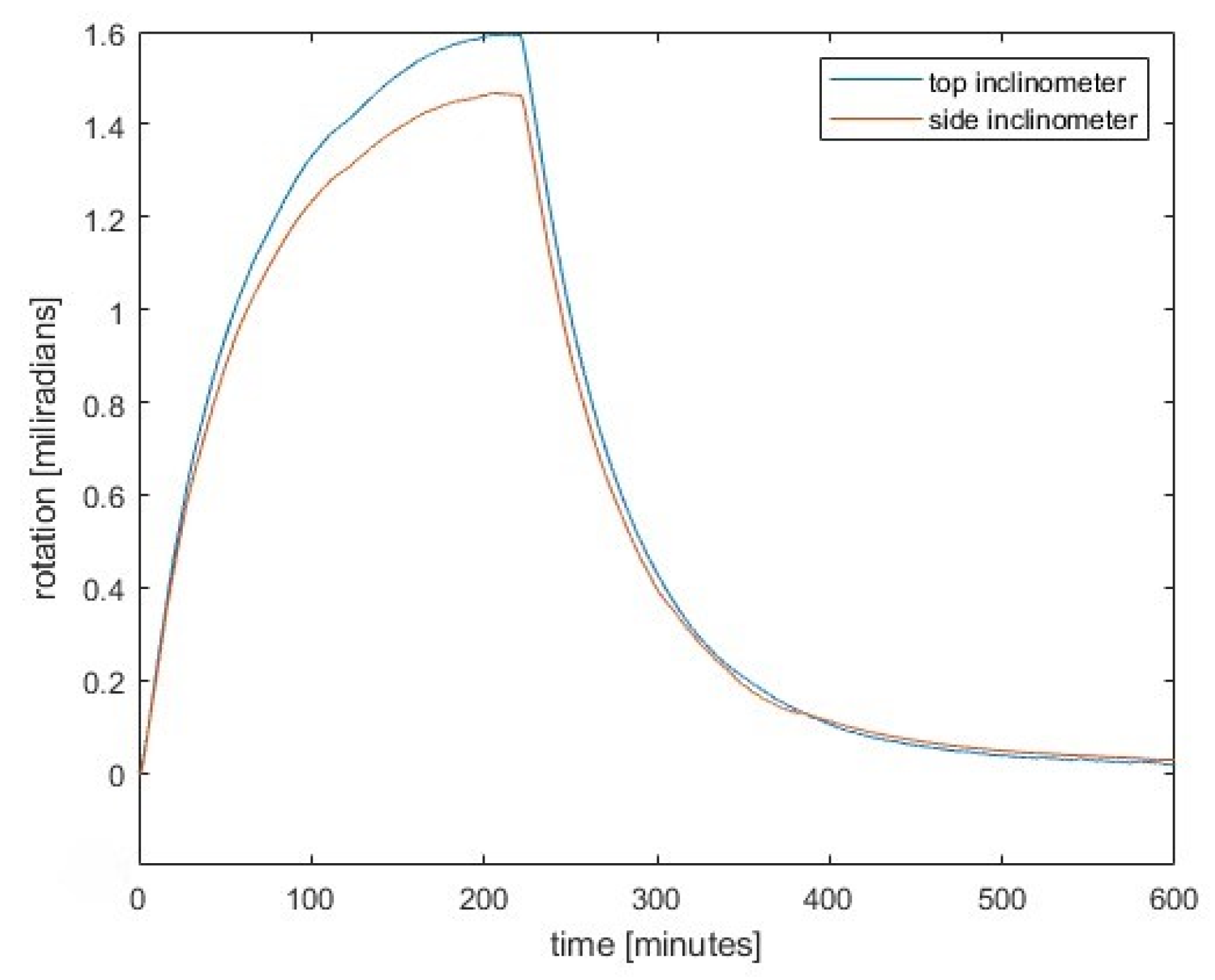
- In the laboratory, we heated a test column from one side and measured the temperatures on the hot and cold sides, the inclinations at the top of the column and on the side, as well as the displacements.
- (3)
- Using the equations presented, we calculated the displacements from the measured angles and adjusted them to the level of the displacement sensor so that the calculated displacements were directly comparable.
- (4)
- The displacement curves derived from the inclination measurements agree very well with the directly measured displacements over time.
- (5)
- During the heating phase, the temperature on the heated side of the pillar increased by 25.4 K, resulting in a lateral displacement of approximately 1 mm at the top of the pillar. The difference between measured displacements and the ones calculated from inclinations was less than 0.1 mm.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Močnik, R.; Koler, B.; Zupan, D.; Ambrožič, T. The Influence of Pillar Displacements on Geodetic Measurements. Appl. Sci. 2020, 10, 8319. [Google Scholar] [CrossRef]
- Močnik, R.; Koler, B.; Zupan, D.; Ambrožič, T. Investigation of the Precision in Geodetic Reference-Point Positioning Because of Temperature-Induced Pillar Deflections. Sensors 2019, 19, 3489. [Google Scholar] [CrossRef] [PubMed]
- Kopáčik, A.; Kyrinovič, P.; Lipták, I.; Erdély, J. Automated Monitoring of the Danube Bridge Apollo in Bratislava. In Proceedings of the FIG Working Week 2011, Marrakech, Morocco, 18–22 May 2011; pp. 1–11. Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2011/papers/ts01e/ts01e_kopacik_kyrinovic_et_al_4845.pdf (accessed on 29 December 2024).
- Lipták, I. Analysis of Bridge Structure Deformation Measured by Total Station. In Proceedings of the 5th International Conference on Engineering Surveying, Brijuni, Croatia, 22–24 September 2011; pp. 99–104. [Google Scholar]
- Gerhatova, L.; Hefty, J.; Papco, J.; Minarikova, M. Displacements of GNSS Antenna Position due to Thermal Bending of Pillar Monument. In Proceedings of the Report on the Symposium of the IAG Subcommission for Europe (EUREF), Leipzig, Germany, 3–5 June 2015; Available online: https://www.euref.eu/sites/default/files/symposia/2015Leipzig/p-03-02-Gerhatova.pdf (accessed on 29 December 2024).
- Gerhatova, L.; Hefty, J.; Spanik, P. Short-Term and Long-Term Variability of Antenna Position Due to Thermal Bending of Pillar Monument at Permanent GNSS Station. Rep. Geod. Geoinform. 2016, 100, 67–77. [Google Scholar] [CrossRef]
- Lehner, W.M. Evaluation of Environmental Stresses on GNSS-Monuments. Master’s Thesis, Chalmers University of Technology, Goteborg, Sweden, 2011. Available online: https://publications.lib.chalmers.se/records/fulltext/165054.pdf (accessed on 29 December 2024).
- Haas, R.; Bergstrand, S.; Lehner, W. Evaluation of GNSS Monument Stability. In Reference Frames for Applications in Geosciences, International Association of Geodesy Symposia; Altamimi, Z., Collilieux, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 138, pp. 45–50. [Google Scholar] [CrossRef]
- Lidberg, M.; Lilje, M. Evaluation of Monument Stability in the SWEPOS GNSS Network Using Terrestrial Geodetic Methods-up to 2003. In Reports in Geodesy and Geographical Information Systems, LMV-Rapport 2007: 10; Lantmäteriet: Gävle, Sweden, 2007. Available online: https://www.lantmateriet.se/contentassets/4a728c7e9f0145569edd5eb81fececa7/lmv-rapport_2007_10.pdf (accessed on 29 December 2024).
- Erol, B. Evaluation of High-Precision Sensors in Structural Monitoring. Sensors 2010, 10, 10803–10827. [Google Scholar] [CrossRef] [PubMed]
- Kümpel, H.J.; Fabian, M. Tilt monitoring to assess the stability of geodetic reference points in permafrost environment. Phys. Chem. Earth Parts A/B/C 2003, 28, 1249–1256. [Google Scholar] [CrossRef]
- Mentes, G.; Bányai, L. Observation of Landslide Movements by Geodetic and Borehole Tilt Measurements. In Proceedings of the INGEO 2014—6th International Conference on Engineering Surveying, Prague, Czech Republic, 3–4 April 2014; pp. 53–58. Available online: https://www.fig.net/resources/proceedings/2014/2014_ingeo/TS2-04_Mentes.pdf.pdf (accessed on 4 March 2025).
- Mentes, G. Investigation of Dynamic and Kinematic Landslide Processes by Borehole Tiltmeters and Extensometers. Procedia Earth Planet. Sci. 2015, 15, 421–427. [Google Scholar] [CrossRef]
- Glot, I.; Shardakov, I.; Shestakov, A.; Tsvetkov, R.; Gusev, G. Inclinometer-Based Long-Term Monitoring of the Headframe of Salt Mine Shaft. J. Phys. Conf. Ser. 2021, 1945, 012009. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1945/1/012009/pdf (accessed on 4 March 2025). [CrossRef]
- Hagedorn, R.; Martí-Vargas, J.R.; Dang, C.N.; Micah Hale, W.; Floyd, R.W. Temperature gradients in bridge concrete I-girders under heat wave. J. Bridge Eng. 2019, 24, 04019077. [Google Scholar] [CrossRef]
- Abid, S.R.; Tayşi, N.; Özakça, M. Temperature Records in Concrete Box-Girder Segment Subjected to Solar Radiation and Air Temperature Changes. In IOP Conference Series: Materials Science and Engineering, Proceedings of the International Conference on Engineering and Advanced Technology (ICEAT 2020); IOP; Bristol, UK, 2020; Volume 870, pp. 1–16. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/870/1/012074 (accessed on 11 March 2025).
- Wang, Z.W.; Zhang, W.M.; Tian, G.M.; Liu, Z. Joint values determination of wind and temperature actions on long-span bridges: Copula-based analysis using long-term meteorological data. Eng. Struct. 2020, 219, 110866. [Google Scholar] [CrossRef]
- Lu, Y.; Li, D.; Wang, K.; Jia, S. Study on solar radiation and the extreme thermal effect on concrete box girder bridges. Appl. Sci. 2021, 11, 6332. [Google Scholar] [CrossRef]
- Fan, J.S.; Liu, Y.F.; Liu, C. Experiment study and refined modeling of temperature field of steel-concrete composite beam bridges. Eng. Struct. 2021, 240, 112350. [Google Scholar] [CrossRef]
- Saad, S.; Nasir, A.; Bashir, R.; Pantazopoulou, S. Effect of Climate Change on Thermal Loads in Concrete Box Girders. J. Bridge Eng. 2025, 30, 04025004. [Google Scholar] [CrossRef]
- Newell, S.; Goggins, J. Investigation of Thermal Behaviour of a Hybrid Precasted Concrete Floor using Embedded Sensors. Int. J. Concr. Struct. Mater. 2018, 12, 66. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Cao, J.; Chai, J.; Yang, Y.; Li, M.; Qin, Y.; Xu, Z. Effect of temperature gradients on the microstructural characteristics and mechanical properties of concrete. Cem. Concr. Res. 2024, 184, 107608. [Google Scholar] [CrossRef]
- Larsson, O.; Thelandersson, S. Estimating extreme values of thermal gradients in concrete structures. Mater. Struct. 2011, 44, 1491–1500. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X.; Zhu, J. Research on temperature effect on reinforced concrete bridge pylon during strong cooling weather event. Eng. Struct. 2022, 273, 115061. [Google Scholar] [CrossRef]
- Zhang, K.; Lei, J.; Wang, Z.; Yuan, Q. A numerical algorithm for damage progression of reinforced concrete bridge piers during air temperature and solar radiation cycles. Eng. Struct. 2024, 319, 118876. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.; Ji, W.; Li, G.Q.; Wang, Y.; Qi, H. Development of High-Temperature Resistant Inclinometers for Structural Displacement Acquisition of the Buildings Subjected to Fire. Fire Technol. 2024, 1–30. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Strength of Materials, Part 1: Elementary Theory and Problems, 3rd ed.; Van Nostrand Company: New York, NY, USA; London, UK, 1955.



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Močnik, R.; Zupan, D.; Pal, A.; Ambrožič, T. Thermally Induced Displacements and Rotations of Pillars for Precise Geodetic Measurements. Appl. Sci. 2025, 15, 4678. https://doi.org/10.3390/app15094678
Močnik R, Zupan D, Pal A, Ambrožič T. Thermally Induced Displacements and Rotations of Pillars for Precise Geodetic Measurements. Applied Sciences. 2025; 15(9):4678. https://doi.org/10.3390/app15094678
Chicago/Turabian StyleMočnik, Robert, Dejan Zupan, Andrej Pal, and Tomaž Ambrožič. 2025. "Thermally Induced Displacements and Rotations of Pillars for Precise Geodetic Measurements" Applied Sciences 15, no. 9: 4678. https://doi.org/10.3390/app15094678
APA StyleMočnik, R., Zupan, D., Pal, A., & Ambrožič, T. (2025). Thermally Induced Displacements and Rotations of Pillars for Precise Geodetic Measurements. Applied Sciences, 15(9), 4678. https://doi.org/10.3390/app15094678





