Abstract
Predicting stock prices is a popular area of study within the realms of data mining and machine learning. Precise forecasting can assist investors in mitigating the risks associated with their investments. Given the unpredictable nature of the stock market, influenced by policy changes, stock data often display high levels of fluctuation and randomness, aligning closely with the prevailing market sentiment. Moreover, diverse datasets related to stocks are rich in historical data that can be leveraged to forecast future trends. However, traditional forecasting models struggle to harness this information effectively, which restricts their predictive capabilities and accuracy. To improve the existing issues, this research introduces a novel stock prediction model based on a deep-learning neural network, named after EL-MTSA, which leverages the multifaceted characteristics of stock data along with ensemble learning optimization. In addition, a new evaluation index via market-wide sentiment analysis is designed to enhance the forecasting performance of the stock prediction model by adeptly identifying the latent relationship between the target stock index and dynamic market sentiment factors. Subsequently, many demonstration experiments were conducted on three practical stock datasets, the CSI 300, SSE 50, and CSI A50 indices, respectively. Experiential results show that the proposed EL-MTSA model has achieved a superior predictive performance, surpassing various comparison models. In addition, the EL-MTSA can analyze the impact of market sentiment and media reports on the stock market, which is more consistent with the real trading situation in the stock market, and indicates good predictive robustness and credibility.
1. Introduction
The application of machine learning technology to predict stock trends is one of the most significant areas of research in the financial domain, attracting extensive attention from researchers [1]. Accurate stock prediction can provide substantial benefits to investors. However, unlike time series with clear regularity and periodicity, such as temperature, transportation, or electricity data, stock price fluctuations are influenced by numerous factors [2], making stock trend and price analysis particularly challenging.
The stock market is characterized by complexity and volatility, generating vast amounts of data. Among the most commonly used stock data are price-related metrics (e.g., opening price, closing price, high price, and low price) and trading-related metrics (e.g., trading volume and turnover). Price data directly reflect stock trends, while trading data indirectly indicate trends through market activity and capital dynamics. These datasets are considered fundamental, as they capture diverse information affecting stock price movements from various perspectives [3].
How to deeper mine these stock data and how to use them more effectively are the new challenges. At present, the methods of stock price prediction can be roughly divided into three categories. The first category uses time series models based on statistics and probability theory, the second category uses machine learning-based prediction models, and the third category uses deep learning models. However, most of the methods only use a single model or a series connection of multiple models to predict the future stock trend.
Whether using a single model or a cascaded model to enhance robustness, these methods are limited in their ability to extract comprehensive information from the data. The lack of an effective feature extraction directly constrains the model’s learning capacity, leading to a suboptimal prediction performance [4,5]. Ensemble learning (EL), a paradigm that combines multiple learning algorithms to form committees, has demonstrated superior performance compared to individual classifiers or regressors. EL techniques improve predictions through stacking and blending, reduce variance via bagging, and minimize bias through boosting [6,7]. EL has been successfully applied across various sectors, including healthcare [8], agriculture [9], energy [10], oil and gas [11], and finance [12]. In these applications, ensemble methods consistently achieve higher accuracy than standalone models, supporting their effectiveness.
However, the aforementioned methods primarily focus on stock data for mining and prediction. Recently, researchers have begun incorporating text mining techniques to extract sentiment indicators from various media sources, using these as additional features for stock price prediction. Studies have shown that integrating sentiment indices with models, such as the LSTM and SVM, can enhance prediction accuracy [13,14]. Nevertheless, the inclusion of more features demands stronger data mining capabilities, and effectively analyzing the potential relationships among multi-factor data has become a critical research focus.
In this context, we propose a novel multi-variable time series stock prediction framework. This approach leverages deep learning methods to uncover correlations and hidden patterns in multi-variable data across different time intervals. The novelty of our work lies not in the individual components but in their innovative integration to improve overall performance. Specifically, our framework incorporates a variational autoencoder (VAE) step, which enhances robustness to input data, and a neural network structure designed to capture both temporal patterns and relationships among predictive factors. The key contributions of this work are as follows.
- We propose a novel integrated approach to enhance the robustness of predictions. By applying discrete wavelet transform to data with different sampling frequencies, we effectively reduce noise and minimize correlations within the data. Additionally, the use of a variational autoencoder for sentiment data enables efficient and meaningful encoding, further improving the model’s performance.
- We incorporate news sentiment indicators into the dataset using a multimodal approach, promoting the interaction between external demand and cognitive inner demand to enhance data complementarity in predictions.
- We introduce a new method for processing high-frequency time series data, enabling the simultaneous representation of intra-cycle and intra-week variations.
- We employ Bayesian optimization to automate parameter selection and improve network efficiency.
2. Related Work
2.1. Traditional Stock Prediction Models
Traditional financial time series forecasting methods primarily include technical analysis and econometric models. Technical analysis [15] relies on technical indicators or their combinations to predict future stock trends. Econometric models, such as the autoregressive integrated moving average (ARIMA) [16] and the generalized autoregressive conditional heteroskedasticity (GARCH) [17], are grounded in time series analysis and statistical principles. However, these methods often fail to account for nonlinear relationships and complex structures within the data, limiting their ability to fully capture the dynamic characteristics of the stock market.
Compared with traditional models, machine learning methods have demonstrated stronger predictive capabilities in financial time series forecasting. These methods leverage computational algorithms and extensive historical data to identify patterns and trends, enabling more accurate predictions. Common machine learning techniques include linear regression [18], support vector machines (SVM) [19], decision trees [20], and random forests [21]. While machine learning has achieved notable success in stock prediction, the inherent noise and uncertainty in stock market data—driven by market sentiment fluctuations and policy changes—pose significant challenges. These factors can interfere with model training and prediction, ultimately reducing accuracy.
With the rapid advancement of the Internet and the widespread adoption of smart devices, deep learning models have emerged as powerful tools for financial analysis. Deep learning offers advantages such as automated feature extraction, effective handling of complex nonlinear relationships, and strong generalization capabilities. For financial data, deep learning methods, including long short-term memory (LSTM) [22], gated recurrent units (GRUs) [23], and convolutional neural networks (CNNs) [24], have shown significant promise. These approaches have achieved breakthroughs in stock prediction, particularly in addressing the limitations of traditional methods.
Multivariate time series forecasting, especially in stock prediction, remains one of the most challenging tasks in data analysis. Deep learning has demonstrated encouraging results in overcoming these challenges, offering improved accuracy and robustness.
In recent years, hybrid algorithms that integrate multiple machine learning models have become a focal point in financial stock forecasting research. Several combined networks have been successfully applied to financial time series prediction. For example, Nikhil et al. [25] proposed a novel GA-LSTM-CNN architecture to predict daily stock prices. Sulistio et al. [26] introduced a deep neural network algorithm combining CNNs, LSTM, and GRUs for stock market prediction. Similarly, Zheng et al. [27] developed an ARIMA–LightGBM hybrid model to forecast the stock trends of Gree Electric Appliances over a six-month period. These hybrid approaches highlight the potential of combining diverse methodologies to enhance predictive performance.
2.2. Sentiment Information and Stock Forecasting
Amid the rapid advancement and pervasive integration of network technologies, big data has emerged as a pivotal resource in the modern era. An increasing number of researchers [28,29,30] have focused on enhancing stock price prediction accuracy through sentiment analysis of news texts, incorporating sentiment indicators with traditional stock market data.
Bharti et al. [31] demonstrated that combining sentiment data extracted from news headlines with daily stock data significantly improves the prediction of stock trends and price movements. Similarly, Parashar et al. [32] utilized financial news headlines from the Financial Times website for stock prediction. Their approach highlights the ability of news headline analysis to capture market sentiment and underlying macroeconomic factors that are often difficult to discern from historical price data alone.
Cui et al. [33] introduced text mining techniques into stock price forecasting, showing that their proposed algorithm achieves superior performance in extracting sentiment values from news texts. Kiran et al. [34] employed historical stock market data and sentiment data from diverse textual sources, using the XGBoost model for stock price prediction. Their work explores the intersection of machine learning and finance, demonstrating the value of integrating sentiment analysis. Ho et al. [35] proposed a multi-channel collaborative network model that combines candlestick charts and social media data for stock trend prediction, achieving a prediction accuracy of 75.38% for Apple stock. These studies underscore the potential of analyzing sentiment in news and other textual sources to capture subtle shifts in market sentiment that may influence stock prices.
The aforementioned literature explores various methods for constructing sentiment indicators, such as investor sentiment and social media sentiment, and applies them to stock market forecasting. It has been established that sentiment indicators can significantly impact stock market volatility and returns. Incorporating sentiment indicators into time series models has been shown to enhance the accuracy of stock predictions. By integrating sentiment data with other market indicators, investors and researchers can gain deeper insights into market sentiment and achieve more accurate stock prediction results.
2.3. Applications of Ensemble Learning Models
Xue and Niu [36] proposed a multi-output hybrid ensemble learning model to predict student performance using data from the Superstar Learning Communication Platform (SLCP). Similarly, Santoni et al. [37] introduced a bagging (bootstrap aggregation) ensemble learning model applied to one-dimensional convolutional neural networks (1D CNN), one-dimensional residual networks (1D ResNet), and a hybrid ensemble deep learning model to predict engagement in online learning. Al-Andoli et al. [38] developed a novel parallel ensemble model based on hybrid machine learning and deep learning techniques for accurate fault detection and diagnosis tasks. These studies have demonstrated the effectiveness of ensemble learning methods in predictive tasks and fault detection tasks, highlighting their ability to improve accuracy and robustness in complex scenarios. In the domain of sentiment analysis, Thiengburanathum and Charoenkwan [39] proposed SETAR, a stacking ensemble learning-based polarity identification method for Thai sentiment classification, which outperformed baseline models across all classification metrics on both training and test datasets.
Recent studies have further expanded the applications of ensemble learning, emphasizing its potential to enhance prediction accuracy and decision-making speed. For instance, Chukwudi et al. [40] presented an innovative ensemble-based approach using prominent machine learning techniques to develop a vehicle engine prediction framework, achieving faster and higher decision accuracy. For short-term power load forecasting, Shen et al. [41] proposed a multi-scale ensemble method and a multi-scale ensemble neural network, with simulation results demonstrating superior comprehensive prediction performance.
Ensemble learning, as a robust machine learning paradigm, has transcended the boundaries of individual domains and found applications in diverse fields. By combining predictions from multiple learning algorithms, ensemble methods enhance prediction performance beyond the capabilities of single models. This collaborative approach has proven effective in tasks such as sentiment classification, student performance prediction, fault diagnosis, and power load forecasting. In the financial domain, ensemble learning has also been applied to stock prediction. For instance, one study [42] proposed a two-stage portfolio optimization method based on ensemble learning and the maximum Sharpe ratio portfolio theory, incorporating asset prediction information to improve portfolio performance and robustness. Another study [43] introduced an ensemble recurrent neural network (RNN) method, integrating long short-term memory (LSTM), gated recurrent units (GRUs), and SimpleRNN, to predict stock market trends. These examples underscore the versatility and effectiveness of ensemble learning in addressing complex prediction challenges across various domains.
3. Model Construction
As previously mentioned, we utilize two distinct datasets with varying sampling frequencies: (1) stock and sentiment data sampled at a daily frequency, and (2) single stock data sampled at 15-min or 30-min intervals. Due to the inherent misalignment in sampling frequencies, these datasets cannot be directly input into the same network. To address this, we leverage the strengths of different models: LSTM and GRU are employed to process the low-frequency sentiment and stock data, while Bi-LSTM and CNN–GRU are used to handle the high-frequency stock data. We adopt an ensemble learning-like approach to integrate the outputs of these models for the final prediction. The overall architecture is illustrated in Figure 1.
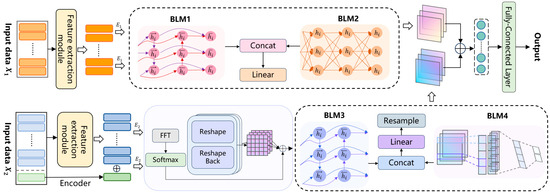
Figure 1.
Structure illustration of the proposed EL-MTSA model.
3.1. Feature Extraction Module
In this study, we propose a feature extraction module that employs a discrete wavelet transform (DWT) and a variational autoencoder (VAE) as independent components. During the data preprocessing stage, the DWT is applied to denoise the stock data, effectively removing noise while preserving critical information. This highlights the importance of the DWT in analyzing non-stationary signals. Additionally, the DWT serves as a powerful feature extraction tool, leveraging its multi-resolution analysis capability to capture localized features within the data. In parallel, during the training phase, the VAE is utilized to encode input sentiment data into latent representations, enabling the extraction of meaningful features for subsequent analysis.
The architecture of the proposed feature extraction module is depicted in Figure 2, where Figure 2a illustrates the model structure without sentiment indicators (six features), and Figure 2b presents the model structure incorporating sentiment indicators (seven features).
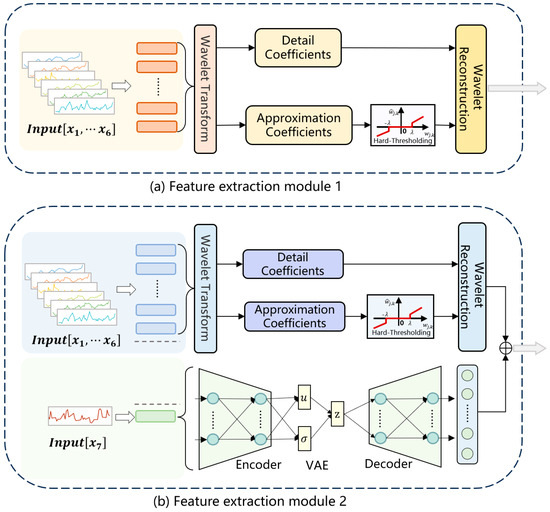
Figure 2.
Illustration of feature extraction module.
Let be the input data. The discrete wavelet transform (DWT) is defined as follows to perform the decomposition operation:
where is the scale factor, , and is the conjugate negative number of , and is the wavelet basis function, which is defined as follows:
For threshold processing, this paper chooses the hard threshold function as follows:
The determination principle of the threshold is to ensure that the size of the threshold is just greater than the amplitude level of the noise. Generally speaking, the threshold value is estimated by the statistical characteristics of the wavelet coefficients. In this paper, the global threshold proposed by Donoho and Johnstone is chosen as follows:
where denotes the standard deviation of the noise and is the signal length.
After threshold processing, an inverse discrete wavelet transform (iDWT) is used to realize the reconstruction of the denoised signal; that is, the denoised signal is obtained.
The variational autoencoder (VAE) consists of an encoder and a decoder. Unlike traditional autoencoders, the VAE introduces a probabilistic latent space with latent variables, capturing diverse patterns in the input data. Sampling from this space allows the generation of new, continuous data samples. The VAE employs a loss function linking the encoder and decoder, enabling the model to learn the data’s underlying probability distribution. By maximizing the likelihood of the observed data, the VAE effectively captures input data characteristics, learning meaningful latent representations and generating samples with strong generalization capabilities.
We treat each observed data point as a sample , and its corresponding representation in the high-dimensional space as . The VAE model architecture consists of two main components: an encoder and a decoder. The encoder maps the input data to the distribution of the latent variables , while the decoder maps the latent variables back to the distribution of the reconstructed data . During training, the VAE aims to minimize two key objectives: the reconstruction error, which ensures the fidelity of the generated data, and the KL divergence, which measures the difference between the latent variable distribution and a predefined prior distribution . The overall objective function of the VAE can be formally expressed as follows:
where represents the reconstruction error, which is the difference between the training data and the data generated by the decoder , calculated with the cross-entropy method, and denotes the KL divergence between the latent variable distribution and the prior distribution, which measures the distance between and .
Since is typically modeled as a Gaussian distribution, the encoder network maps the input data to a mean vector and a variance vector . The latent variable is then sampled from this distribution using the reparameterization trick, which can be expressed as follows:
where is the noise vector, and represents element-wise multiplication.
3.2. Deep-Learning-Based Sequential Prediction Network
As the basic sequential prediction network, we utilize the LSTM, GRU, Bi-LSTM, and CNN–GRU architecture introduced earlier. Each model generates a single prediction result for the given input data vectors. These models were selected based on extensive experimentation, and their effectiveness as part of the basic learning module has been demonstrated in subsequent experiments.
LSTM (long short-term memory) is a special type of recurrent neural network (RNN) designed to address the vanishing gradient problem encountered by traditional RNNs when processing long sequences. It controls the flow of information through the introduction of three gates: the forget gate, the input gate, and the output gate. The network structure diagram of LSTM is shown in Figure 3a.
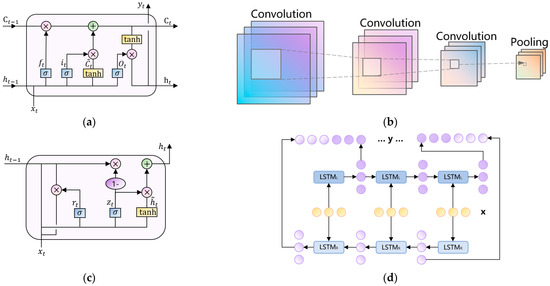
Figure 3.
Structure illustration of sequential prediction network. (a) LSTM unit (b) Convolution and pooling operation (c) GRU unit (d) Bi-LSTM architecture.
The forgetting gate formula is as follows:
The input gate formula is as follows:
The cell state is shown in the following equation:
The output gate formula is as follows:
Bi-LSTM (bidirectional long short-term memory) is an extension of LSTM that consists of two LSTM layers. One layer processes the sequence in the forward direction, while the other processes it in the backward direction. This allows it to capture both forward and backward dependencies in the sequence simultaneously. The specific structure is illustrated in Figure 3d.
GRU (gated recurrent unit) is a streamlined version of the recurrent neural network (RNN) designed to address the vanishing gradient problem inherent in traditional RNNs. It controls the flow of information through the introduction of two gates: the update gate and the reset gate, resulting in a more concise structure compared to LSTM. The network structure diagram of GRU is shown in Figure 3c.
The update gate formula is as follows:
The reset gate formula is as follows:
Candidate hidden state is as follows:
Hidden state at the current time step is as follows:
When processing time-series data, CNNs (convolutional neural networks) typically transform one-dimensional time-series data into a two-dimensional matrix format using a sliding window approach, which facilitates subsequent operations.
The formula for the convolution operation is as follows:
The formula for the max pooling operation is as follows:
The flatten operation can be expressed as follows:
The formulation of the fully connected layer is as follows:
Analyzing the frequency components of a time series using the fast Fourier transform (FFT) allows for the identification of its dominant periodic patterns. The FFT converts the time series from the time domain to the frequency domain, revealing the intensity of different frequency components. By selecting the top frequencies with the highest amplitudes, the most significant periodic patterns in the time series can be determined as follows:
Here represents the input time series, where is the length of the series and is the number of feature dimensions, denotes the fast Fourier transform applied to the time series, and calculates the amplitude at each frequency, while computes the average amplitude across all feature dimensions. The set consists of the frequencies with the highest amplitudes; is the period corresponding to the -th frequency; and represents the average amplitude.
In real-world scenarios, the time series frequently exhibits multi-periodicity, where overlapping and interacting periods complicate the modeling of temporal dynamics. To address this challenge, we propose a transformation of the one-dimensional time series, initially processed via the fast Fourier transform (FFT), into a set of two-dimensional tensors based on multiple periodic components. This transformation extends the analysis of temporal variations into a two-dimensional space, enabling the embedding of intra-period variations into the columns of the tensor and inter-period variations into its rows. By leveraging this structured representation, the two-dimensional patterns of temporal changes can be efficiently modeled using two-dimensional convolutional kernels, as illustrated in Figure 4. This approach allows the model to more effectively capture the intricate dynamics inherent in the time series, significantly improving its predictive accuracy and generalization capabilities. The transformation formulation is shown as follows:
where represents the transformed two-dimensional tensor. The function is used to zero-pad the time series to ensure it can be evenly divided by and . The function rearranges the time series into a two-dimensional tensor, where denotes the number of rows (period length) and represents the number of columns (number of points within a period).
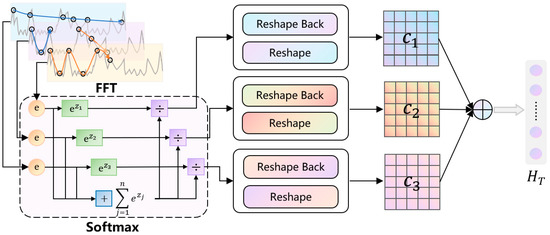
Figure 4.
Structure illustration of cycle layer.
Multi-scale features are extracted by applying two-dimensional convolution, as described in the following formula, to effectively capture both intra-period and inter-period variations.
where represents the feature map processed by two-dimensional convolution. The Inception module [44], denoted as , includes multiple convolutional kernels of different sizes, enabling the simultaneous capture of both local and global features.
The Softmax function is employed to transform the FFT output into a probability distribution. Specifically, it processes the weights corresponding to feature representations across different periods, normalizing them to facilitate more effective integration and fusion of these features.
Suppose the model identifies periods, with each period corresponding to a feature representation , and their respective weights being . After applying the Softmax function, the normalized weights are obtained as follows:
The weight of each period falls within the range of [0, 1], and the sum of these weights equals 1. This normalization process ensures that the feature representations of different periods are combined in a more balanced and rational manner.
3.3. Learning Optimization Module via Information Fusion Strategy
Ensemble methods are widely used in machine learning and statistics, offering techniques to combine multiple base classifiers into an ensemble that produces more accurate and robust predictions than individual models. By leveraging the strengths of each classifier while mitigating their weaknesses, ensemble learning enhances overall predictive performance.
The integrator module in our framework is designed to resample high-frequency data and aggregate predictions from multiple models to generate the final output. This module consists of two key components: a resampling mechanism and a CNN–linear layer model. The CNN and linear layer operate sequentially, with the linear layer featuring two branches. Branch 1 takes the prediction results of LSTM and GRU as input , , while branch 2 takes the prediction results of Bi-LSTM and CNN–GRU as input , . The linear layer captures temporal patterns and learns the reliability of each predictor under different conditions. The CNN then processes these inputs to identify relationships that can further enhance prediction accuracy. Finally, a fully connected layer integrates all information to produce the final output.
From the experimental findings, it can be inferred that the robust architecture of our ensemble model consistently delivers dependable predictions across a wide range of scenarios. Regarding the fine-tuning of hyperparameters, including the learning rate, we utilize Bayesian optimization to systematically enhance their configuration.
3.4. Hyperparameter Optimization Based on Bayesian Inference
As the complexity of the model increases, the selection of hyperparameters becomes a non-trivial challenge, and the appropriate configuration of hyperparameters is crucial to ensuring optimal model performance. In this study, we employ a Bayesian optimization algorithm (BOA) [45] for hyperparameter tuning. The BOA is a robust global optimization technique that iteratively refines results by leveraging an objective optimization function throughout the optimization process. The objective optimization function can be formulated as follows:
where represents the true value, represents the predicted value, and represents the length of the input time series. The objective function is minimized as follows:
where is the set of all parameters, denotes the best obtained parameter, and is the set of hyperparameter combinations.
During the parameter tuning process, the Gaussian function is adopted as the assumed distribution of the prior function. Subsequently, the next point for evaluation is determined in the posterior process based on the acquisition function. Gaussian processes represent an extension of multivariate Gaussian distributions and can be characterized by their mean and covariance functions as follows:
where is the mean of and is the covariance matrix of . Initially, it can be expressed in the following way:
During the optimization process, the covariance matrix is continuously updated with each iteration as new samples are incorporated into the dataset. The specific update rule for the covariance matrix is as follows:
The posterior probabilities can be obtained from the updated covariance matrix.
where D is the observed data, is the mean of at step , and of is the variance of at step .
Through the computation of the mean matrix and covariance matrix, we observe that the sampling function derived from the joint posterior distribution can significantly accelerate the determination of parameters and minimize the wastage of resources. For this purpose, we select the upper confidence bound (UCB) as the sampling function, which is formulated as follows:
where is the hyperparameter chosen in step , and are the mean and covariance of the joint posterior distribution of the objective function obtained in the Gaussian process, respectively.
4. Experimental Results and Discussion
4.1. Data Sources
The sentiment data utilized in this study is sourced from the Financial News Database of Chinese Listed Companies (CFND), available through the CNRDS China Research Data Service platform. This comprehensive database encompasses over 400 online media outlets and more than 600 newspaper publications, ensuring a robust representation of sentiment trends in the financial market. Specifically, the dataset includes news reports from twenty leading online financial media platforms, such as Hexun, Sina Finance, East Money, Tencent Finance, NetEase Finance, Phoenix Finance, China Economic Net, Sohu Finance, JRJ, Huaxun Finance, FT Chinese, Panorama, CNSTOCK, China Securities Journal, Stockstar, Caixin, The Paper, Yicai, 21CN Finance, and Caijing. These platforms are recognized for their authoritative coverage, high-quality reporting, and widespread influence among investors, making their content particularly valuable for sentiment analysis in financial markets. By leveraging this extensive and reliable dataset, our study aims to provide a more accurate and comprehensive reflection of market sentiment dynamics.
The financial sentiment for the daily stock index is derived using the BERT model, which quantifies sentiment by extracting the number of positive sentiment news headlines, the number of negative sentiment news headlines, and the total count of financial news headlines. The sentiment indicator is then computed based on the following formula:
In this formulation, denotes the number of news headlines with positive sentiment, represents the number of news headlines with negative sentiment, and corresponds to the total number of news headlines.
This study focuses on the CSI 300 Index, the SSE 500 Index, and the CSI A50 Index as the primary research subjects. Daily, 30-min, and 15-min trading data for these indices were collected via the Tushare API of stock block trading. The dataset include key features such as opening price, closing price, highest price, lowest price, trading volume, and transaction value. The selected data span from 15 January 2007 to 31 December 2020.
For comparative experiments, consistent datasets and model parameters were utilized, with an 8:2 ratio for the training and testing sets. The objective of this study is to predict the future closing prices of various stock indices. To ensure a rigorous evaluation of model performance, we employed a rolling-window time-series cross-validation approach. The input and output sequence lengths were set to 1, 3, 5, 7, 10, and 15, respectively. To enhance the robustness of our findings, each comparative experiment was independently repeated 10 times, and the average values were reported as the final results.
4.2. Training Parameter Setting
In this model, the mean squared error (MSE) is selected as the loss function, and its mathematical formulation is provided in Equation (40). The Adam optimizer is employed for training due to its efficiency and adaptability. The model is implemented in a Python 3.8 environment, utilizing the TensorFlow framework to construct the LSTM architecture for time series prediction tasks.
where represents the number of samples, represents the real value, and represents the predicted value.
The model’s training parameters are configured as follows: the number of epochs is set to 200, the learning rate is initialized to 0.0001, and the Adam optimizer is employed for training. The model involves several hyperparameters, among which the number of hidden layer units and the batch size are the most sensitive, significantly impacting the model’s performance. Other tunable hyperparameters include the batch size, the number of layers, and the number of hidden units. A comprehensive summary of the hyperparameter settings is provided in Table 1.

Table 1.
Specific parameter setting.
4.3. Evaluation Metrics
To more accurately evaluate the prediction performance, we employ three metrics: the root mean squared error (RMSE), the mean absolute error (MAE), and the symmetric mean absolute percentage error (SMAPE).
The root mean squared error (RMSE), also referred to as the residual standard deviation, is primarily used in regression analysis as a criterion for variable selection and model evaluation. It is calculated as follows:
The mean absolute error (MAE) quantifies the average absolute difference between predicted values and actual values. It measures the deviation of predictions from the ground truth, where lower values indicate higher prediction accuracy. It is calculated as follows:
The symmetric mean absolute percentage error (SMAPE) is an improved metric designed to address the limitations of the mean absolute percentage error (MAPE). It mitigates the issue of disproportionately large errors when the true values are small, providing a more balanced evaluation. It is calculated as follows:
In the above three equations, is the actual value, is the predicted value, and represents the total number of actual value and predicted value.
4.4. Experimental Results and Analyses
4.4.1. Reliability Analyses of Sentiment Indicators
To evaluate the reliability of sentiment indicators, we conducted a comparative study using benchmark models, including the LSTM, GRU, Bi-LSTM, and CNN–LSTM. Table 2 presents the comparative experimental results for sentiment indicators on the CSI 300, SSE 500, and CSI A50 datasets, where “s” denotes the inclusion of sentiment data as an additional feature. The visualization of these results is provided in Figure 5.

Table 2.
Experiment results of sentiment indicators.
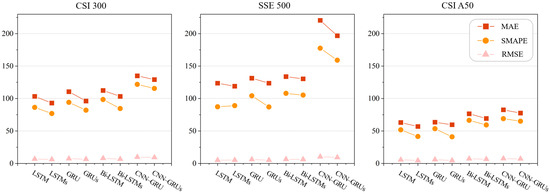
Figure 5.
Reliability study of sentiment indicators.
Through comparative experiments, it is observed that on the CSI 300, SSE 500, and CSI A50 datasets, the prediction performance of the four models significantly improves after incorporating sentiment features compared to using only the six original features (excluding sentiment data). Specifically, on the CSI 300 dataset, MAE decreases by 8.85%, SMAPE by 10.80%, and RMSE by 10.38%. On the SSE 500 dataset, MAE decreases by 5.75%, SMAPE by 6.80%, and RMSE by 6.57%. On the CSI A50 dataset, MAE decreases by 7.83%, SMAPE by 14.82%, and RMSE by 14.23%. These results demonstrate that integrating sentiment indicators into the model and dataset used in this study effectively enhances the model’s predictive performance.
4.4.2. Prediction Results for Different Window Steps
To investigate the impact of step size on the prediction accuracy of the model, we conducted experiments using the proposed EL-MTSA model with step sizes of 1, 3, 5, 7, 10, and 15, respectively. Table 3 presents the comparative experimental results for different synchronization lengths, while Figure 6 illustrates the prediction results for the CSI 300, SSE 500, and SCI A50 datasets.

Table 3.
Experiment results of different window step size.
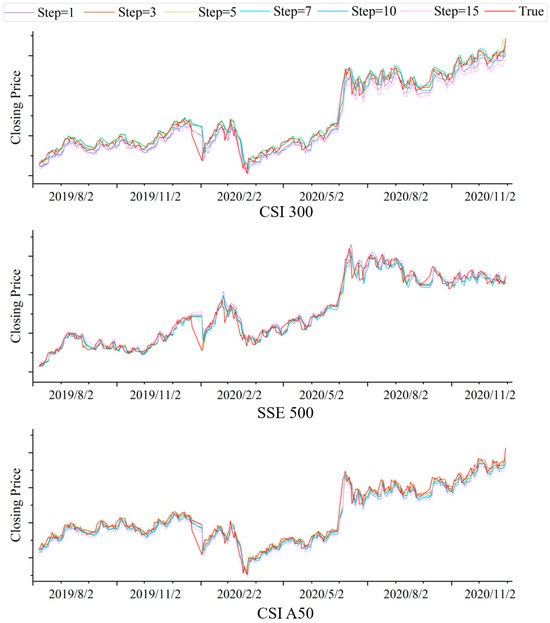
Figure 6.
Comparison of step size prediction results.
Through experimental comparison, it is observed that a step size of five yields the lowest errors and the highest prediction accuracy. Adjusting the step size allows the model to better align with the prediction time horizon, enabling more accurate capture of market fluctuations and trends. A step size of five is chosen primarily because there are exactly five trading days in a week, and sentiment indicators within this interval can effectively reflect specific market trends and emotional states. Additionally, a step size of five strikes a balance between prediction stability and sensitivity, mitigating the risks of overfitting or underfitting. These results demonstrate that selecting an appropriate step size can significantly enhance the accuracy and reliability of predictions when constructing sentiment indicator models.
4.4.3. Ablation Experiment Results and Analysis
To validate the effectiveness of incorporating the cycle layer, we conducted ablation experiments. Table 4 presents the comparative experimental results of the EL-MTSA model and the model without the cycle layer across different frequency data. The symbol “*” denotes the ablation model.

Table 4.
Ablation experiment results.
The resulting visualization is shown in Figure 7. Through comparative experiments, it is observed that the EL-MTSA model achieves a 7.54% reduction in MAE, a 10.55% reduction in SMAPE, and a 10.54% reduction in RMSE compared to the EL-MTSA* model. These results demonstrate that the inclusion of the cycle layer effectively captures temporal patterns in the data, significantly enhancing the model’s prediction accuracy.
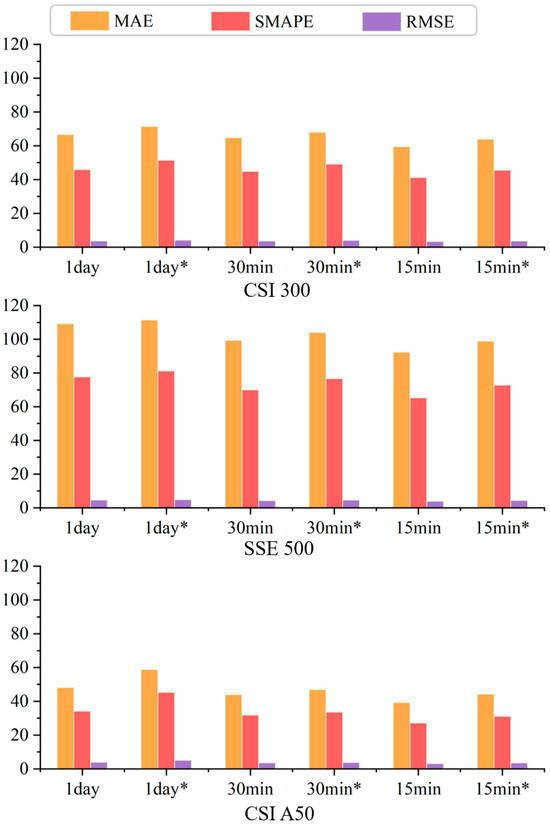
Figure 7.
Ablation experiment. The symbol “*” denotes the ablation model.
4.4.4. Comparative Analysis of Data Volume
Through comparative experiments, it is observed that the four baseline models evaluated in this study tend to achieve higher accuracy when the data frequency is high, as illustrated in Figure 8. This is because higher-frequency data typically contains more information, enabling the models to capture richer patterns, and thus improve prediction accuracy. However, the EL-MTSA model demonstrates exceptional capabilities in processing sentiment data and capturing long-term temporal patterns, particularly in the 1-day and 15-min data configurations. By leveraging a mechanism akin to ensemble learning, the EL-MTSA model effectively integrates the strengths of different sampling frequencies and sentiment data features, combining the advantages of the baseline models to significantly enhance predictive performance.
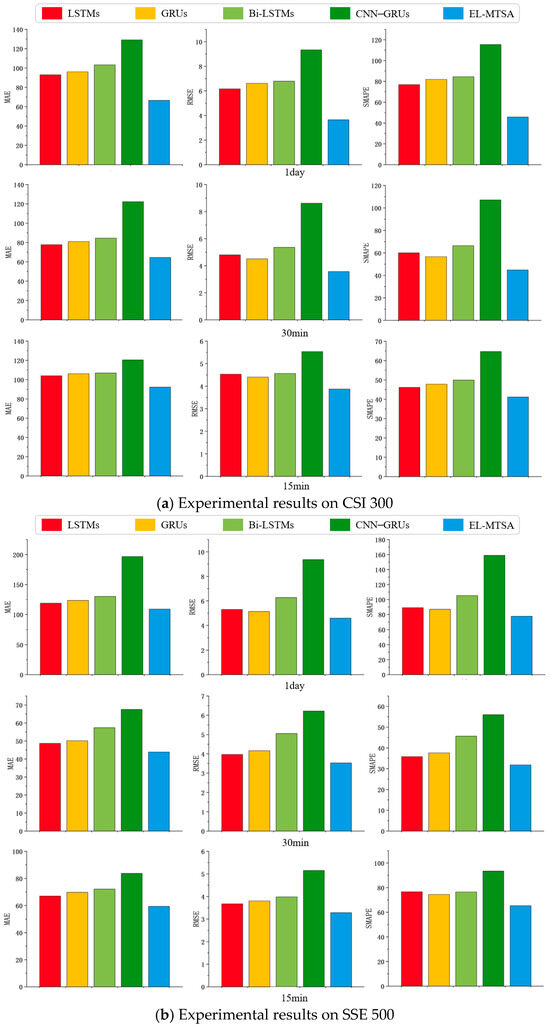
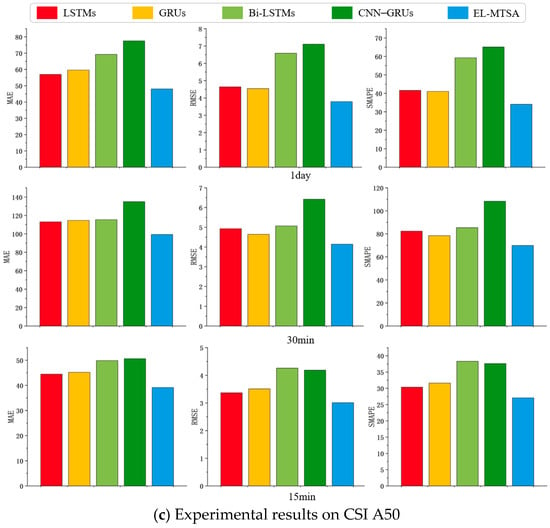
Figure 8.
Comparison experimental results of data volume on different stock datasets.
4.4.5. Comparative Analysis of Simulated Investments
In this section, we conducted simulated investments based on the predictive results of the EL-MTSA model and performed a comprehensive comparative analysis against the buy-and-hold strategy and the martingale model. Through this comparison, we aim to rigorously evaluate the effectiveness and advantages of the EL-MTSA model in forecasting stock prices, providing insights into its practical applicability in financial markets.
In this subsection, several key parameters were initialized to establish the trading environment. The initial capital was set at RMB 100,000, with the current capital also initialized to this amount. The number of shares held was initially set to 0, indicating no equity ownership at the outset. The value of the investment portfolio was recorded in a list, starting from the initial fund value of RMB 100,000. Slippage was set at 0.1%, representing the potential deviation between the expected and actual execution prices due to market volatility. Additionally, a fixed transaction fee of RMB 5 per trade was applied to account for brokerage charges.
We utilized the following performance metrics to evaluate the performance of the three strategies:
- (1)
- Final portfolio value (FPV) is the total value of the investment portfolio at the end of the simulation period, reflecting the cumulative growth of the initial capital.
- (2)
- Total profit (TP) is the absolute monetary gain achieved over the investment horizon, calculated as the difference between the final portfolio value and the initial capital.
- (3)
- Maximum drawdown (MDD) is the largest peak-to-trough decline in portfolio value during the simulation period, expressed as a percentage of the peak value. This metric quantifies the worst-case loss and serves as a critical measure of downside risk.
- (4)
- Sharpe ratio (SR) is a risk-adjusted performance measure that evaluates the excess return per unit of risk, with risk represented by the standard deviation of portfolio returns. This metric provides insights into the efficiency of returns relative to the level of risk undertaken.
These metrics collectively offer a comprehensive assessment of the strategies’ profitability, risk exposure, and risk-adjusted performance, ensuring a robust evaluation framework. Table 5 presents the evaluation metrics for the three distinct strategies, providing a comparative analysis of their performance.

Table 5.
Simulated investment experiment.
As shown in Table 5, the final portfolio value (FPV) of the EL-MTSA model’s predictive investment is RMB 151,876.98, which is 6.51% higher than that of the buy-and-hold strategy and 21.37% higher than that of the martingale model. This indicates that the EL-MTSA model possesses a certain advantage in predicting price movements.
The total profit (TP) of the EL-MTSA model is RMB 51,876.98, surpassing the buy-and-hold strategy by 21.78% and the martingale model by 106.43%. The annualized return of the EL-MTSA model is significantly higher than those of the other two strategies, demonstrating its potential in investment applications.
The Sharpe ratio (SR) of the EL-MTSA model is 3.76, compared to 1.42 for the buy-and-hold strategy and 1.16 for the martingale model. The higher Sharpe ratio of the EL-MTSA model suggests superior risk-adjusted returns, highlighting its efficiency in generating excess returns per unit of risk.
The maximum drawdown (MDD) of the EL-MTSA model is 3.59%, significantly lower than the 15.82% of the buy-and-hold strategy and the 10.18% of the martingale model. The relatively lower maximum drawdown of the EL-MTSA model indicates its robust performance in risk management and downside protection.
These results collectively underscore the EL-MTSA model’s effectiveness in achieving higher returns, managing risk, and delivering consistent performance compared to traditional strategies. Figure 9 illustrates the trajectory of portfolio value changes over time through a line chart, offering a visual representation of the investment outcomes. From top to bottom, the results correspond to the buy-and-hold strategy, the martingale model, and the EL-MTSA model, respectively.
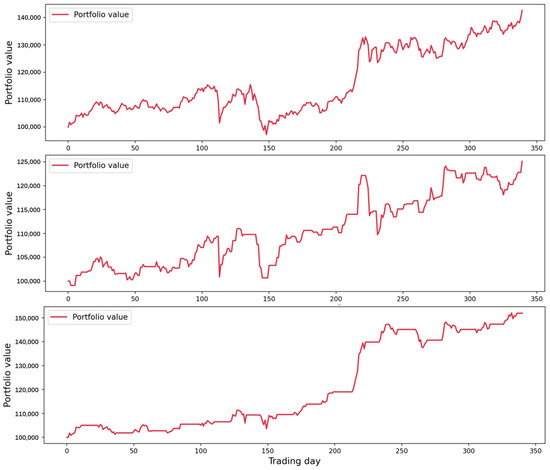
Figure 9.
Comparative analysis of simulated investments.
4.4.6. Cross-Market-Cycle Generalization Capability Assessment
To ensure the robustness of the model and the reliability of its predictions, rolling window cross-validation was employed for data validation. In this process, strict adherence to the temporal nature of the time-series data was maintained, ensuring that the chronological order of the data was preserved. The training and testing sets were allocated in an 8:2 ratio, allowing the model to leverage sufficient training data while maintaining strict isolation of the test data. Special attention was given to distinguishing between the training and testing sets in both temporal dimensions and operational steps, including independent normalization procedures, to prevent any form of data leakage or temporal inconsistency. This design ensured that the test data remained entirely unseen during the training process. The test set spanned 340 trading days and comprehensively covered diverse market conditions, including economic recession, growth, and stability phases not present in the training data. This section provides a detailed evaluation of the model’s cross-market-cycle generalization capability, with a focus on its performance across economic recession, growth, and stability phases. The methodology for rolling window cross-validation is also elaborated herein.
Rolling window cross-validation is a validation method specifically designed for time-series data. Its core idea is to dynamically adjust the window position to sequentially evaluate the model’s predictive capability across different time periods. First, the data is divided into a training set and a test set, and then the sliding window operation is carried out separately for each set. For a time series of length , starting at time point , the training data is and the testing data is . The window is then shifted forward by steps, resulting in a new training set and a new testing set . This process is repeated until the end position of the testing set exceeds the time series length T, until , where is the number of steps. As shown in Figure 10.
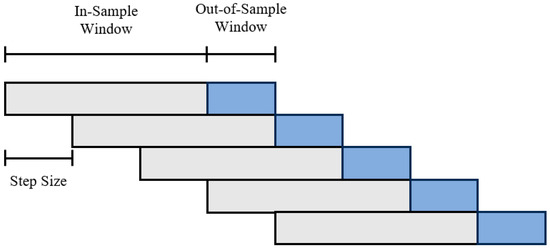
Figure 10.
Schematic diagram of rolling window cross-validation.
To evaluate the generalization capability of the EL-MTSA model across market cycles (recessionary, growth, and stable phases), we plotted the model’s predicted values against actual market values from 9 August 2019 to 31 December 2020. The chart highlights recessionary phases (green shaded regions), growth phases (red shaded regions), and stable phases (gray shaded regions), as shown in Figure 11.
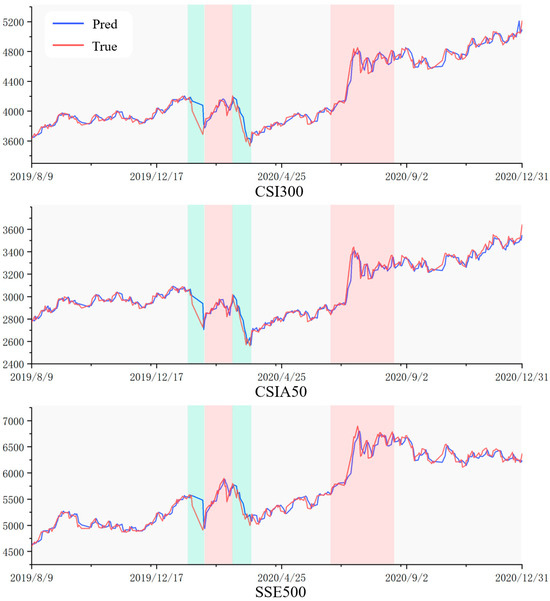
Figure 11.
Line Chart of Predicted vs. Actual Market Values.
The period under analysis encompasses significant market declines and rebounds, particularly during 17 January 2020 to 5 February 2020, and 6 March 2020 to 24 March 2020, driven by COVID-19 pandemic-induced panic selling, which created pronounced bearish market conditions. During this turmoil, certain sectors, such as pharmaceuticals, remote work, and online education, exhibited resilience or growth due to heightened demand. This led to capital reallocation from pandemic-impacted sectors to those benefiting from the crisis, driving sector-specific growth. As market sentiment stabilized, strategic buying at market lows contributed to subsequent rallies. Additionally, following effective domestic pandemic control measures and gradual economic reopening, heightened expectations of economic recovery prompted investor reallocation into equities, as evidenced by the upward market trajectory from 15 June 2020 to 19 August 2020.
Our analysis demonstrates that the EL-MTSA model exhibits robustness and effectiveness in capturing market dynamics across all phases—recessionary, growth, and stable—underscoring its reliability, even during periods of heightened market volatility.
4.5. Discussion
In this study, we proposed an ensemble learning-based multi-task sentiment analysis (EL-MTSA) model and applied it to stock price prediction. Through a comparative analysis with several traditional models, we found that the EL-MTSA model demonstrates significant advantages in predictive performance. However, we are also aware that these advantages are not accidental but are underpinned by deeper reasons.
Firstly, the ensemble learning mechanism of the EL-MTSA model is one of the key factors contributing to its enhanced performance. By aggregating the prediction results from multiple models, the model is able to leverage the diversity of different models to effectively reduce bias and variance. This mechanism is akin to the concept of “collective wisdom”, where different models analyze and predict data from various perspectives, ultimately yielding more accurate and reliable conclusions through integration. In the context of stock price prediction, the market is influenced by a multitude of factors. A single model may only capture the impact of certain factors, whereas an ensemble learning model can comprehensively consider multiple factors, thereby providing a more holistic reflection of market dynamics.
Secondly, the incorporation of sentiment indicators offers a new perspective to the model. Traditional stock data primarily reflect the historical price trends and trading information of the market. By contrast, sentiment indicators are capable of capturing the emotions and psychological states of market participants. Although these emotions and psychological states are not directly reflected in price data, they have a significant impact on market trends. For example, investor panic can lead to a substantial market downturn, while optimism can drive the market upward. By integrating sentiment indicators into the model, we can gain a better understanding of market expectations and investor behavior, thereby enhancing the model’s predictive capability.
However, we also recognize several limitations in our study. For example, the data sources are relatively limited, primarily relying on the sentiment analysis of news media. While the news media is an important channel for market information dissemination, other types of information sources, such as social media and investor forums, may also have an impact on the market. Future research could consider integrating more diverse data sources to provide a more comprehensive reflection of market information. In addition, the parameter selection and optimization process of the model is relatively complex and needs to be adjusted according to different market conditions. In practical applications, how to quickly and accurately determine the optimal parameters remains a problem that requires further investigation. In the future, parameter optimization strategy of the model structure, as well as advanced artificial intelligence technologies, can be adopted to further enhance the model’s performance [46,47,48].
To conclude, the EL-MTSA model provides investors with a new analytical tool that can help them better understand market dynamics and predict market trends from the perspective of financial markets. At the same time, this study offers some novel theoretical ideas and modeling methods for the intersection of sentiment analysis and stock price prediction, providing a reference for subsequent research.
5. Conclusions
Precise stock forecasting can assist investors in mitigating the risks associated with their investments, of which predictive capabilities and accuracy is restricted by traditional forecasting models. To improve the existing issues, this study proposed a novel stock prediction model, defined as EL-MTSA, based on a deep-learning neural network and ensemble technology optimization. Firstly, the EL-MTSA model aggregates the prediction results of multiple sub-models (LSTM, GRU, Bi-LSTM, and CNN–GRU) and leverages diversity to reduce bias and variance. This significantly enhances the model’s fitting performance and overall prediction accuracy while improving its robustness and generalization capability. Then, the novel evaluation index via market-wide sentiment analysis is proposed to enhance the forecasting performance of the stock prediction model. Those index indicators are derived from positive and negative counts as well as neutral news from media reports to capture the psychological states and behavioral patterns of market participants, which can reveal market expectations for future trends, and thereby facilitate a more comprehensive understanding of market dynamics and reduce prediction bias.
To verify the effectiveness of the EL-MTSA model in practical investment scenarios, we conducted many comparative experiments on three stock indices, the CSI 300, SSE 50, and CSI A50 indices. Abundant results demonstrated that the proposed EL-MTSA model achieved a superior predictive performance, surpassing various comparison models. On the CSI 300 dataset, EL-MTSA’s prediction results of three indicators, including MAE, SMAPE, RMSE, are specifically decreased by 8.85%, 10.80%, and 10.38%, respectively, as well as overperforming forecasting results on the SSE 500 and CSI A50 dataset. Additionally, we assessed the model’s generalization capability across market cycles through visualization. The results indicated that the EL-MTSA model exhibits stability and reliability in capturing market dynamics.
However, due to data size limitations and variant complexity, our proposed model still remains fraught with challenges rooted in autonomous data mining capabilities and the real-world unpredictability application to stock markets. Moreover, the proposed model also has insufficient performance in the aspects of multi-factor intrinsic law mining and single stock prediction. In future work, we will focus on hybrid modeling architecture, improve probabilistic frameworks, and adaptive normalization techniques to address these limitations. Furthermore, we plan to further evaluate the model’s generalization capability by simulating various market conditions, including financial crises, economic recessions, and public health crises. We will utilize simulated data to test the model’s performance under different market scenarios and intend to supplement the relevant analysis in the next version of our research.
Author Contributions
Conceptualization, X.J.; methodology, J.K. and X.Z.; software, X.Z. and X.J.; validation, W.H.; formal analysis, J.K. and X.Z.; investigation and data curation, W.H.; writing—original draft preparation, J.K. and X.Z.; writing—review and editing, J.K. and X.Y.; supervision, project administration, J.K. and X.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Project of ALL China Federation of Supply and Marketing Cooperatives (No. 202407), National Natural Science Foundation of China (Nos. 62433002, 62473008, 62476014 and 62173007), Beijing Nova Program (No. 20240484710), Beijing Scholars Program (No. 099), and Beijing Municipal University Teacher Team Construction Support Plan (No. BPHR20220104), Open Projects of the Institute of Systems Science, Beijing Wuzi University (No. BWUISS07), Science, Technology, and Innovation Program of National Regional Medical Center of Taiyuan Bureau of Science and Technology (No. 202243).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset presented in this study is available at the following website link: https://www.cnrds.com (accessed on 1 April 2024), and https://www.tushare.pro (accessed on 25 December 2023). The EL-MTSA model can be obtained from the following website link: https://pan.quark.cn/s/b8d9cdc665e8 (accessed on 1 March 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, X.; Guo, J.; Wang, H.; Zhang, F. Prediction of Stock Market Index Based on ISSA-BP Neural Network. Expert Syst. Appl. 2022, 204, 117604. [Google Scholar] [CrossRef]
- Debnath, P.; Srivastava, H.M. Optimizing Stock Market Returns During Global Pandemic Using Regression in the Context of Indian Stock Market. Risk Financ. Manag. 2021, 14, 386. [Google Scholar] [CrossRef]
- Fama, E.F. Efficient Capital Markets: A Review of Theory and Empirical Work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Lv, P.; Shu, Y.; Xu, J.; Wu, Q. Modal Decomposition-Based Hybrid Model for Stock Index Prediction. Expert Syst. Appl. 2022, 202, 117252. [Google Scholar] [CrossRef]
- Weng, B.; Ahmed, M.A.; Megahed, F.M. Stock Market One-Day Ahead Movement Prediction Using Disparate Data Sources. Expert Syst. Appl. 2017, 79, 153–163. [Google Scholar] [CrossRef]
- Ballings, M.; Van den Poel, D.; Hespeels, N.; Gryp, R. Evaluating Multiple Classifiers for Stock Price Direction Prediction. Expert Syst. Appl. 2015, 42, 7046–7056. [Google Scholar] [CrossRef]
- Akyüz, A.O.; Uysal, M.; Bulbul, B.A.; Uysal, M.O. Ensemble Approach for Time Series Analysis in Demand Forecasting: Ensemble Learning. In Proceedings of the 2017 IEEE International Conference on Innovations in Intelligent Systems and Applications, Gdynia, Poland, 3–5 July 2017; pp. 7–12. [Google Scholar]
- Bergquist, S.L.; Brooks, G.A.; Keating, N.L.; Landrum, M.B.; Rose, S. Classifying Lung Cancer Severity with Ensemble Machine Learning in Health Care Claims Data. In Proceedings of the 2nd Machine Learning for Healthcare Conference, Boston, MA, USA, 18–19 August 2017; pp. 25–38. [Google Scholar]
- Priya, P.; Muthaiah, U.; Balamurugan, M. Predicting Yield of the Crop Using Machine Learning Algorithm. Int. Eng. Sci. Res. Technol. 2018, 7, 1–7. [Google Scholar]
- Khairalla, M.A.; Ning, X.; Al-Jallad, N.T.; El-Faroug, M.O. Short-Term Forecasting for Energy Consumption through Stacking Heterogeneous Ensemble Learning Model. Energies 2018, 11, 1605. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, J.; Yu, L. A Deep Learning Ensemble Approach for Crude Oil Price Forecasting. Energy Econ. 2017, 66, 9–16. [Google Scholar] [CrossRef]
- Macchiarulo, A. Predicting and Beating the Stock Market with Machine Learning and Technical Analysis. Intern. Bank. Commer. 2018, 23, 1–22. [Google Scholar]
- Wu, S.; Liu, Y.; Zou, Z.; Weng, T.-H. S_I_LSTM: Stock Price Prediction Based on Multiple Data Sources and Sentiment Analysis. Connect. Sci. 2021, 34, 44–62. [Google Scholar] [CrossRef]
- Porshnev, A.; Redkin, I.; Shevchenko, A. Machine Learning in Prediction of Stock Market Indicators Based on Historical Data and Data from Twitter Sentiment Analysis. In Proceedings of the IEEE International Conference on Data Mining Workshops, Shenzhen, China, 14 December 2014. [Google Scholar]
- Matías, J.M.; Reboredo, J.C. Forecasting Performance of Nonlinear Models for Intraday Stock Returns. J. Forecast. 2012, 31, 172–188. [Google Scholar] [CrossRef]
- Challa, M.L.; Malepati, V.; Kolusu, S.N.R. S&P BSE Sensex and S&P BSE IT Return Forecasting Using ARIMA. Financ. Innov. 2020, 6, 47. [Google Scholar]
- Arnerić, J.; Poklepović, T. Nonlinear Extension of Asymmetric GARCH Model within Neural Network Framework. Comput. Sci. Inf. Technol. 2016, 6, 101–111. [Google Scholar]
- Sangeetha, J.M.; Alfia, K.J. Financial Stock Market Forecast Using Evaluated Linear Regression Based Machine Learning Technique. Meas. Sens. 2024, 31, 10095. [Google Scholar] [CrossRef]
- Santoso, M.; Sutjiadi, R.; Lim, R. Indonesian Stock Prediction Using Support Vector Machine (SVM). In Proceedings of the MATEC Web of Conferences, Bandung, Indonesia, 18 April 2018; p. 164. [Google Scholar]
- Loke, K.S. Impact of Financial Ratios and Technical Analysis on Stock Price Prediction Using Random Forests. In Proceedings of the IConDA, Kuching, Malaysia, 9–11 November 2017; pp. 38–42. [Google Scholar]
- Shih, C.M.; Yang, K.C.; Chao, W.P. Predicting Stock Price Using Random Forest Algorithm and Support Vector Machines Algorithm. In Proceedings of the IEEM, Singapore, 18–21 December 2023; pp. 133–137. [Google Scholar]
- Nelson, D.M.Q.; Pereira, A.C.M.; de Oliveira, R.A. Stock Market’s Price Movement Prediction with LSTM Neural Networks. In Proceedings of the IJCNN, Anchorage, AK, USA, 14–19 May 2017; pp. 1419–1426. [Google Scholar]
- Narayana, S.; Sri, S.N.D.; Kumar, S.R.; Ajay, T.; Vasiq, S.S. Predicting the Stock Market Index Using GRU for the Year 2020. In Proceedings of the ESIC, Bhubaneswar, India, 1 September 2024; pp. 399–404. [Google Scholar]
- Wu, J.M.-T.; Li, Z.; Srivastava, G.; Frnda, J.; Diaz, V.G.; Lin, J.C.-W. A CNN-Based Stock Price Trend Prediction with Futures and Historical Price. In Proceedings of the ICPAI, Taipei, Taiwan, 3–5 December 2020; pp. 134–139. [Google Scholar]
- Nikhil, S.; Sah, R.K.; Parki, S.K.; Tamang, T.B.; TR, M. Stock Market Prediction Using Genetic Algorithm Assisted LSTM-CNN Hybrid Model. In Proceedings of the ICCCNT, Delhi, India, 6–8 July 2023; pp. 1–6. [Google Scholar]
- Sulistio, B.; Warnars, H.L.H.S.; Gaol, F.L.; Soewito, B. Energy Sector Stock Price Prediction Using the CNN, GRU & LSTM Hybrid Algorithm. In Proceedings of the ICCoSITE 2023, Jakarta, Indonesia, 16–17 February 2023; pp. 178–182. [Google Scholar]
- Zheng, X.; Cai, J.; Zhang, G. Stock Trend Prediction Based on ARIMA-LightGBM Hybrid Model. In Proceedings of the ICTC, Nanjing, China, 6–8 May 2022; pp. 227–231. [Google Scholar]
- Chi, L.; Zhuang, X.; Song, D. Investor sentiment in the Chinese stock market: An empirical analysis. Appl. Econ. Lett. 2012, 19, 345–348. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Awad, M. Augmented Textual Features-Based Stock Market Prediction. IEEE Access 2020, 8, 40269–40282. [Google Scholar] [CrossRef]
- Shah, D.; Isah, H.; Zulkernine, F. Predicting the Effects of News Sentiments on the Stock Market. In Proceedings of the IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018. [Google Scholar]
- Bharti, S.K.; Tratiya, P.; Gupta, R.K. Stock Market Price Prediction Through News Sentiment Analysis & Ensemble Learning. In Proceedings of the iSSSC, Gunupur, India, 6–8 November 2022; pp. 1–5. [Google Scholar]
- Parashar, D.; D’Silva, M.; Kulshreshtha, S. A Machine Learning Framework for Stock Prediction Using Sentiment Analysis. In Proceedings of the GCAT, Bangalore, India, 6–8 December 2023; pp. 1–5. [Google Scholar]
- Cui, H.; Zhu, Y.; Gu, F.; Wang, L. Research on Stock Price Prediction Using TextRank-Based Text Summarization Technology and Sentiment Analysis. In Proceedings of the 2022 CIS, Chengdu, China, 16–18 December 2022; pp. 302–306. [Google Scholar]
- Kiran, S.; Dhana Lakshmi, P.; Sultana, N.; Naga Rama Devi, G.; Gothane, S.; Reddy Madhavi, K. Stock Market Price Prediction Using Sentiment Analysis. In Proceedings of the ICMEET, Singapore, 26–27 August 2023. [Google Scholar]
- Ho, T.-T.; Huang, Y. Stock Price Movement Prediction Using Sentiment Analysis and CandleStick Chart Representation. Sensors 2021, 21, 7957. [Google Scholar] [CrossRef] [PubMed]
- Xue, H.; Niu, Y. Multi-Output Based Hybrid Integrated Models for Student Performance Prediction. Appl. Sci. 2023, 13, 5384. [Google Scholar] [CrossRef]
- Santoni, M.M.; Basaruddin, T.; Junus, K.; Lawanto, O. Automatic Detection of Students’ Engagement During Online Learning: A Bagging Ensemble Deep Learning Approach. IEEE Access 2024, 12, 96063–96073. [Google Scholar] [CrossRef]
- Al-Andoli, M.N.; Tan, S.C.; Sim, K.S.; Seera, M.; Lim, C.P. A Parallel Ensemble Learning Model for Fault Detection and Diagnosis of Industrial Machinery. IEEE Access 2023, 11, 39866–39878. [Google Scholar] [CrossRef]
- Thiengburanathum, P.; Charoenkwan, P. SETAR: Stacking Ensemble Learning for Thai Sentiment Analysis Using RoBERTa and Hybrid Feature Representation. IEEE Access 2023, 11, 92822–92837. [Google Scholar] [CrossRef]
- Joseph Chukwudi, N.; Zaman, N.; Rahim, M.A.; Rahman, M.A.; Alenazi, M.J.F.; Pillai, P. An Ensemble Deep Learning Model for Vehicular Engine Health Prediction. IEEE Access 2024, 12, 63433–63451. [Google Scholar] [CrossRef]
- Shen, Q.; Mo, L.; Liu, G.; Zhou, J.; Zhang, Y.; Ren, P. Short-Term Load Forecasting Based on Multi-Scale Ensemble Deep Learning Neural Network. IEEE Access 2023, 11, 111963–111975. [Google Scholar] [CrossRef]
- Zhou, Z.; Song, Z.; Ren, T.; Yu, L. Two-Stage Portfolio Optimization Integrating Optimal Sharp Ratio Measure and Ensemble Learning. IEEE Access 2023, 11, 1654–1670. [Google Scholar] [CrossRef]
- Chiong, R.; Fan, Z.; Hu, Z.; Dhakal, S. A Novel Ensemble Learning Approach for Stock Market Prediction Based on Sentiment Analysis and the Sliding Window Method. IEEE Trans. Comput. Soc. Syst. 2023, 10, 2613–2623. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015. [Google Scholar]
- Frazier, P.I. A Tutorial on Bayesian Optimization. Tutor. Oper. Res. 2018, 255–278. [Google Scholar] [CrossRef]
- Ahmed, R.S.; Hasnain, M.; Mahmood, M.H.; Mehmood, M.A. Comparison of Deep Learning Algorithms for Retail Sales Forecasting. IECE Trans. Intell. Syst. 2024, 1, 112–126. [Google Scholar] [CrossRef]
- Lin, Y. Long-term Traffic Flow Prediction using Stochastic Configuration Networks for Smart Cities. IECE Trans. Intell. Syst. 2024, 1, 79–90. [Google Scholar] [CrossRef]
- An, Y.; Tan, Y.; Sun, X.; Ferrari, G. Recommender System: A Comprehensive Overview of Technical Challenges and Social Implications. IECE Trans. Sens. Commun. Control 2024, 1, 30–51. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).