1. Introduction
Traditional communication systems are primarily designed for reliable transmission of symbol (bit) streams, irrespective of specific requirements to support the task at the receiver. However, as communication technologies approach the Shannon capacity limit, traditional communication methods struggle to meet the growing demands for higher data volumes in 5G/6G networks and AI-driven applications [
1]. Unlike traditional communication, semantic communication focuses on extracting and transmitting meaningful, task-critical features of the source information [
2]. By preserving task-critical content while reducing redundancy, semantic communication shows higher efficiency and ensures better task performance at the receiver, making it a promising paradigm for next-generation intelligent communications [
3]. Recent studies have demonstrated the effectiveness of semantic communication across various data modalities, including images [
4,
5,
6,
7], texts [
8,
9,
10,
11], videos [
12,
13], and question-answering (QA) tasks [
14,
15].
For image-based semantic communication, several works leverage joint source-channel coding (JSCC) to enhance transmission efficiency while preserving task-critical information. An attention-based DeepJSCC model is introduced in [
4], which dynamically adapts to varying signal-to-noise ratio (SNR) levels during image transmission. Furthermore, the authors in [
5] extend this approach to a multi-task semantic communication framework, enabling image recovery and classification simultaneously.
For text-based semantic communication, deep learning-based methods have been widely adopted to enhance transmission reliability while reducing bandwidth usage. The authors in [
8] introduce DeepSC, a semantic communication system designed to maximize semantic accuracy in text transmission. To further optimize transmission efficiency, a lightweight distributed semantic communication model is proposed in [
9], which enables IoT devices to transmit textual information at the semantic level.
For video-based semantic communication, the authors in [
12] present an adaptive DeepJSCC framework tailored for wireless video delivery, ensuring high-quality transmission under varying network conditions. To reduce bandwidth requirement while maintaining perceptual quality, a novel video transmission framework, VISTA, is proposed in [
13] to transmit the most relevant video semantics.
In QA tasks, semantic communication systems are evolving toward human-like communication through contextual understanding. In [
14], DeepSC-VQA is introduced as a transformer-enabled multi-user semantic communication model for visual QA, which can effectively integrate text and image modalities at the transmitter and receiver. Similarly, the authors in [
15] propose a memory-aided semantic communication system that utilizes a memory queue to enhance context-awareness and semantic extraction at the receiver.
These studies highlight the diverse applications of semantic communication across different data types, each involving distinct tasks at the receiver. To effectively support these tasks, semantic coding plays a crucial role in extracting task-critical information while reducing redundancy. To this end, several recent studies have focused on semantic coding methods tailored to various application scenarios [
16,
17].
In [
18], the authors propose a deep learning-based joint transmission-recognition scheme for IoT devices to optimize task-specific recognition. This approach significantly enhances classification performance, particularly in low SNR conditions. Reference [
19] develops an adaptable, deep learning-based semantic compression approach, which can compress the semantics according to their importance relevant to the image classification task. In [
20], deep learning-based feature extraction with JSCC is leveraged to achieve efficient image retrieval in edge computing environments. A federated semantic learning (FedSem) framework is introduced in [
21], which collaboratively trains semantic-channel encoders of multiple devices to enable semantic knowledge graph construction with privacy preservation.
These studies on semantic coding leverage deep learning methods to extract task-critical features. However, most approaches operate as black-boxes, lacking explainability of the coding scheme [
22,
23]. To address this limitation, recent research has explored explainable semantic communication. For example, [
24] models control signals as semantic information and proposes a real-time control-oriented semantic communication framework that enables interpretable data transmission. However, this approach is not well-suited for transmitting image data. In [
25], a triplet-based representation for text semantics is introduced, incorporating syntactic dependency analysis to enhance interpretability in semantic extraction. However, this method is specifically tailored for text semantics and is not applicable to image-related tasks. The authors in [
26] present two information-theoretic metrics to characterize semantic information compression and select only task-critical features. However, these explainable semantic coding methods primarily focus on semantic extraction while overlooking effective data compression, which is crucial for ensuring reliable information transmission in communication systems.
In this paper, we propose a theoretically grounded and explainable deep semantic coding framework in a binary-classification-oriented communication (BCOC) scenario. Based on two fundamental information theoretic principles, rate-distortion theory and large-deviation theory, we formulate an optimization problem to effectively balance data compression efficiency and classification accuracy. Furthermore, we leverage deep learning techniques and variational methods to transform the theoretical optimization problem into a deep variational semantic coding (DVSC) model and develop a novel DVSC-Opt algorithm to efficiently obtain the deep semantic coding design. The contributions of this work are summarized as follows.
We formulate an optimization problem in the BCOC scenario from an information-theoretic perspective, addressing both source compression and task-critical information preservation under predefined distortion constraints. By explicitly optimizing a task-discriminative information measure, our framework effectively preserves the information that is critical to the binary classification task in an explainable manner.
We develop the DVSC model with respect to the formulated theoretical optimization problem. Without knowledge of probability distributions, we introduce discriminator networks to facilitate the estimation of information-theoretic terms. Additionally, we propose an efficient training algorithm for deep semantic coding design.
We conduct experimental validation on the CelebA dataset and the CIFAR-10 dataset, demonstrating that the proposed coding scheme effectively balances compression rate and classification accuracy while ensuring acceptable distortions.
Notably, the DVSC model is a combination of information-theoretic principles and deep learning techniques. Although hybrid frameworks such as InfoGAN [
27] and deep information bottleneck (Deep IB) [
28] have been widely adopted in representation learning and generative modeling, their problem formulations differ fundamentally from ours. InfoGAN is designed to learn disentangled representations by maximizing the mutual information between latent codes and generated samples in a generative adversarial framework, without explicitly addressing compression efficiency or task relevance. Deep IB, on the other hand, seeks to extract task-relevant features by optimizing an information bottleneck objective, but it is primarily used in supervised learning contexts and does not consider distortion constraints. In contrast, the DVSC model is explicitly designed for the BCOC scenario, jointly optimizing data compression and task performance subject to predefined distortion constraints, leveraging a theoretically principled and practically trainable architecture.
The rest of this paper is organized as follows:
Section 2 presents the semantic coding model of BCOC and formulates the theoretical optimization problem;
Section 3 develops the DVSC model and the DVSC-Opt algorithm;
Section 4 implements the proposed training algorithm on the CelebA dataset and the CIFAR-10 dataset, providing experimental results and performance analysis;
Section 5 concludes the paper.
2. System Model and Problem Formulation
In this section, we first introduce the semantic coding model in BCOC. Then we present related information theories and key concepts. Finally, an optimization problem is formulated to tradeoff the data compression efficiency, binary-classification task performance, and source reconstruction requirement.
2.1. System Model
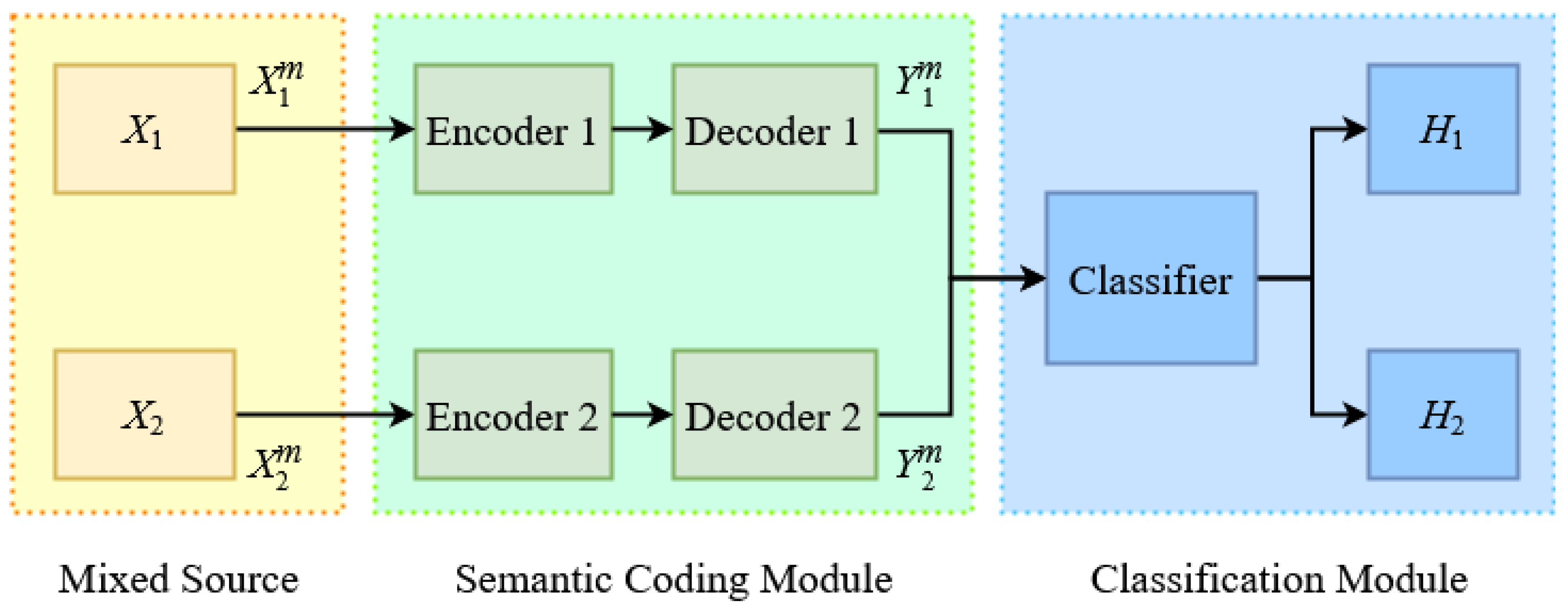
The system model consists of three components: the mixed source, the semantic coding module, and the binary classification module, as depicted in
Figure 1. The mixed source
X consists of two subsources,
and
, each of which corresponds to a distinct class attribute and is defined on the same support set
. In each time block, an independent and identically distributed (i.i.d.) source sequence of length
m,
or
, is generated either with respect to the marginal distribution
or
, with the prior probability
or
. For
, the source sequence
is first processed by the semantic coding module. By assuming a powerful channel coding scheme and error-free channel transmission, after encoding and decoding (hereinafter referred to as coding for brevity), the reconstructed sequence
is subsequently fed into the classification module. The objective of the binary classification task is to determine from which subsource each source sequence originates.
In the semantic coding module, we analyze the rate-distortion trade-off of a mixed source based on information theory and information spectrum methods. In the binary classification module, large deviation theory is utilized to evaluate the classification performance. Consequently, the overall performance of the BCOC is jointly determined by the source compression rate, reconstruction distortion, and classification accuracy. The next subsection provides an overview of the information-theoretical foundations.
2.2. Theoretical Foundations
2.2.1. Rate-Distortion Function of Mixed Source
Given the mixed source in
Figure 1, the probability of generating a source sequence
can be expressed as
where the prior probabilities satisfy
,
. Even though
and
are i.i.d. sequences, the mixed source sequence
is not an i.i.d. sequence. For mixed source coding, a rate-distortion pair
is said to be achievable if there exists a sequence of
source coding
that satisfies
where
denotes the distortion measure and mean squared error (MSE) is adopted in this paper.
Based on information spectrum methods [
29], given a distortion constraint
D, the infimum achievable rate of the mixed source coding is
where
for
is the rate-distortion function [
30] with respect to the i.i.d. source sequence
, given by
This result indicates that the rate-distortion relationship of the mixed source coding is determined by the rate-distortion functions of individual i.i.d. subsources. As a result, two separate sets of encoders and decoders are employed to compress the subsources respectively as illustrated in
Figure 1. Furthermore, the reconstructed sequence, either
or
, is an i.i.d. sequence generated with respect to the marginal probability distribution
or
. It can be straightforward to prove that the rate-distortion function of mixed source has an alternative expression as
2.2.2. Large Deviation Theory of Binary Hypothesis Testing
In the BCOC system model, the classification task at the receiver can be formulated as a binary hypothesis testing problem. Specifically, let denote the hypothesis that the source sequence originates from the subsource , i.e., the input of classifier is the i.i.d. sequence ; and let denote the hypothesis that the source sequence originates from the subsource , i.e., the input of classifier is the i.i.d. sequence . Under this setting, classification errors can be categorized into two types.
Since the source sequence is randomly generated from either
or
with prior probabilities
or
, the overall classification error probability
is given by
According to large deviation theory,
follows an exponential decay law when the sequence length
m is sufficiently large. More specifically,
is characterized by the Chernoff information [
30], given by
where the Chernoff information between probability distributions
and
is defined as
Chernoff information quantifies the statistical distinguishability between two probability distributions. A larger Chernoff information value indicates greater separability between the distributions, leading to a lower classification error probability in the asymptotic regime, as indicated by (
7). Consequently, enhancing classification accuracy can be formulated as improving the Chernoff information in (
8).
2.3. Problem Formulation
Different from the traditional source coding, the semantic coding needs to balance data compression efficiency, source reconstruction quality, and binary-classification task performance. To this end, we formulate an optimization problem based on the rate-distortion function of mixed source and large deviation theory of binary hypothesis testing as
where
is a predetermined weight coefficient to balance mixed source compression efficiency and binary-classification performance. Intuitively, the formulated problem (
9) can be seen as a weighted sum of the rate-distortion function (
5) and the Chernoff information (
8). Subject to a given distortion constraint, a larger
prioritizes classification accuracy at the expense of compression efficiency, and vice versa.
Based on the convex optimization principle, we introduce Lagrange multipliers
and
to incorporate the distortion constraints into the objective function and formulate the dual problem as
For the four optimization variables in the dual problem, we employ an iterative optimization process to reduce the complexity. Thus, we further decompose the dual problem into two sub-problems, given by
Although we consider semantic coding of source sequence and binary-classification task dependent on reconstructed sequence in the system model, it is worth noting that the assumption of mixed i.i.d. sources leads to single-letter rate-distortion function and Chernoff information. Thus, all subsequent formulations and analysis are expressed in terms of single-letter variables instead of sequences.
It is worth emphasizing that in this work, the notion of explainability stems from the principled objective-level design of the BCOC model. By explicitly incorporating Chernoff information, which quantifies class separability into the optimization objective, the model structurally preserves features that are critical for binary decision making. Instead of relying on attention mechanisms or saliency maps commonly used in deep neural networks, this formulation offers a task-oriented and theoretically grounded approach to preserving task-critical semantics throughout the coding process.
3. Deep Variational Semantic Coding
Directly solving the dual problem (
10) to obtain the optimal semantic coding represented by the conditional distributions
and
is generally difficult or even intractable. Recently, a popular approach is to parameterize the coding scheme using neural networks [
31]. However, estimating mutual information and Chernoff information through data sampling but without knowledge of probability distributions remains highly challenging. To address this, we employ variational methods and design discriminator networks for efficient estimation of these information-theoretic terms in the proposed DVSC model. In this section, we first construct the DVSC model and then propose a learning algorithm for efficient training and optimization.
3.1. Parameterized Mutual Information
Mutual information can be defined as a Kullback-Leibler (KL) divergence. To evaluate mutual information without knowledge of probability distributions, we can estimate the corresponding KL divergence through variational methods, as presented in the following.
3.1.1. Estimation of KL Divergence
KL divergence measures the difference between two probability distributions. Let
,
be two discrete probability distributions defined on the same finite or countable space. Assume that
is absolutely continuous with respect to
, i.e., for every event
x,
whenever
. The KL divergence between
and
is defined as
Evaluating KL divergence based on its definition requires knowledge of both probability distributions
and
, which is usually not available in the learning scenarios. A widely-used variational method leverages deep learning to optimize a discriminator network
to approximate KL divergence. The discriminator network
is trained with respect to the objective
where
Once the discriminator network is optimized, the KL divergence can be estimated as
This approach provides an efficient estimation of KL divergence and has been widely adopted in deep learning and information theory research [
32,
33].
3.1.2. Estimation of Mutual Information
Given two random variables
X and
Y, mutual information quantifies statistical dependency between them, defined as
Alternatively, mutual information can be expressed in terms of KL divergence, given by
This formulation allows for a similar deep variational approach for mutual information estimation. Specifically, we introduce a discriminator network
, and the training objective is given by
Once the neural network
is trained, the mutual information can be estimated as
We note that the mutual information term in Equation (
19) is estimated via a variational upper bound, which provides a tractable surrogate for optimization. While this introduces a relaxation compared to the exact mutual information, our experiments indicate that the training process converges stably, and the resulting approximation does not negatively affect the optimization of the overall objective in Equation (
11). This suggests that the bound is sufficiently tight for the purposes of our model.
3.2. Parameterized Chernoff Information
To achieve a deep variational approximation of Chernoff information, we leverage its mathematical relation with Rényi divergence, and utilize the latter as an intermediate quantity for estimation. Therefore, we begin by introducing the estimation of Rényi divergence.
3.2.1. Estimation of Rényi Divergence
Let
,
be two discrete probability distributions defined on the same finite or countable space. Assume that
is absolutely continuous with respect to
, i.e., for every event
x,
whenever
. For parameter
, the Rényi divergence of order
is defined as
According to Donsker-Varadhan Rényi variational formula [
34], Rényi divergence can be reformulated as
where
is a discriminator function parameterized by
, and is trained with respect to the objective
Once the optimal discriminator network
is obtained, the Rényi divergence can be approximated as
3.2.2. Estimation of Chernoff Information
By comparing Equations (
8) and (
20), we notice that when
, Chernoff information can be expressed in terms of Rényi divergence as
Based on the variational formulation of Rényi divergence in Equation (
21), the optimization of Chernoff information involves jointly training the discriminator network
and the Chernoff coefficient
. Specifically, after obtaining the optimized discriminator
,
is trained with respect the following objective:
With both
and
optimized, the Chernoff information can be estimated as:
In practice, the optimal coefficient in Chernoff information rarely attains an extreme value at or . Therefore, this numerical approximation over remains effective in most cases.
Overall, the estimation of Chernoff information in our framework involves two stages: a variational approximation of Rényi divergence and a numerical minimization over the coefficient
. The first stage is theoretically supported by the Donsker–Varadhan variational formulation [
34] using discriminator networks. The second stage is implemented via gradient-based optimization to update the parameter
. Our experimental results demonstrate stable convergence and effective estimation of Chernoff information throughout training.
3.3. The DVSC Model and Training Algorithm
We now revisit the BCOC optimization objective (
11). In this formulation, the expected distortion is directly computable using MSE, whereas the mutual information and Chernoff information terms are estimated via discriminator networks. With all components of the objective function now accessible, we propose the DVSC model, as illustrated in
Figure 2.
In
Figure 2, we employ two deep neural networks (DNNs) as encoder networks, denoted as
and
, respectively. Discriminator networks
and
are trained to estimate mutual information
and
, respectively. Similarly, discriminator network
along with the parameter
are optimized to estimate Chernoff information
. Therefore, for given distortion constraint
D and weight coefficient
, the encoders can be optimized according to the following objectives
and Lagrange multipliers can be optimized according to
In sum, the training process of DVSC model involves optimization of five neural networks, two Lagrange multipliers, and a Chernoff coefficient. The optimization process takes four key steps:
- 1.
Train discriminator networks and , and estimate mutual information;
- 2.
Train discriminator network and Chernoff coefficient , and estimate Chernoff information;
- 3.
Train encoders and ;
- 4.
Optimize Lagrange multipliers and .
These steps are performed iteratively until all network parameters and Lagrange multipliers converge. The detailed DVSC-Opt algorithm is given in Algorithm 1.
The overall training complexity of the DVSC-Opt algorithm per iteration is
, where
M is the mini-batch size and
n denotes the typical forward/backward cost of a neural network module. Across
T iterations, the total training cost becomes
. Although the training complexity introduces some modest overhead, each component in the framework is implemented with lightweight network architectures. As a result, the overall runtime remains practical and can support real-world deployment.
| Algorithm 1: The DVSC-Opt algorithm. |
- 1:
Distortion constraint D, weight coefficient ; Initialized hyper-parameters , and Chernoff coefficient ; Initialized network parameters .
- 2:
repeat - 3:
Step 1 Train Discriminator 1 () and Discriminator 2 () - 4:
Randomly sample mini-batches (batchsize is M) - 5:
- 6:
Compute loss functions and update using the Adam optimizer via backpropagation: - 7:
Step 2 Train Discriminator 3 () and Chernoff coefficient () - 8:
Compute loss functions and update and : - 9:
Step 3 Train Encoder 1 () and Encoder 2 () - 10:
Compute loss functions and update :
- 11:
Step 4 Train Lagrange multipliers () - 12:
Compute loss functions and update :
- 13:
until convergence - 14:
Output: Optimized parameters ; Lagrange multipliers , Chernoff coefficient .
|
The DVSC-Opt algorithm provides a semantic coding framework for BCOC systems, aiming to jointly optimize data compression while preserving task-critical information. Although several state-of-the-art semantic coding models, such as DeepSC [
8], VISTA [
13], and multi-task JSCC [
14] frameworks, have achieved notable progress in semantic communication, their problem formulations differ fundamentally from ours. These models typically consider noisy communication channels and focus on general semantic transmission across diverse tasks, whereas DVSC-Opt focuses solely on semantic source coding and is specifically tailored to the BCOC scenario.
Moreover, most of current semantic coding models primarily emphasize semantic extraction, often overlooking effective data compression and lacking theoretical interpretability. In contrast, the DVSC model is designed to preserve task-critical information while simultaneously enhancing data efficiency under explicit distortion constraints. By integrating information-theoretic principles with deep learning techniques, the DVSC-Opt algorithm achieves a favorable balance among theoretical grounding, structural explainability, and practical trainability. The effectiveness of the proposed framework will be demonstrated through experiments in the next section.
4. Experiments
To comprehensively evaluate the proposed DVSC-Opt algorithm, we conduct experiments on the CelebA dataset [
35] and a binary-class subset of the CIFAR-10 [
36] dataset. Experimental results from both datasets demonstrate the effectiveness of the DVSC-Opt algorithm. In the following, we present a detailed analysis based primarily on the CelebA dataset. Experiments are performed on an NVIDIA RTX 3090 GPU, using PyTorch 1.12.1 as the deep learning framework.
4.1. Dataset Description and Preprocessing
The CelebA dataset consists of 202,599 celebrity images, each annotated with 40 binary attributes stored in an attribute file. For our binary classification task, we use the “gender” attribute to categorize images into two classes: female and male.
Before training the DVSC model, several preprocessing steps are required. First, we partition the dataset into two subsets with respect to
(female) and
(male). Each image is then normalized to ensure numerical stability and consistency in training. Finally, the processed data from both subsets are fed into their respective encoders for learning and optimization. The hyperparameter settings for the DVSC-Opt algorithm are listed in
Table 1. The network architectures of the encoders and discriminators are listed in
Table 2,
Table 3 and
Table 4.
4.2. Evaluation Metrics
The optimization objective of the DVSC model involves a trade-off among compression rate, reconstruction distortion, and classification performance. When training is completed, these three design objectives can be evaluated as follows.
Reconstruction distortion: As the training of DVSC model converges, the final distortion satisfies its predefined constraint D. Therefore, a smaller value of D results in a lower reconstruction distortion.
Compression rate: The compression rate is assessed by estimating mutual information using the trained discriminator networks and . A smaller mutual information value indicates a higher degree of compression.
Classification performance: A lightweight two-layer neural network classifier is used to evaluate the task performance on reconstructed images. A higher classification accuracy indicates a better preservation of task-relevant semantic information during the encoding process.
Since the weight coefficient determines the relative importance of mutual information and Chernoff information in the objective, adjusting under a given distortion constraint D directly affects the trade-off between compression efficiency and classification performance. Furthermore, varying D also impacts both the compression rate and classification performance. Experiments are designed to investigate the influence of both and D on the overall system performance.
4.3. Experiment Results and Analysis
To validate the convergence of the DVSC-Opt algorithm, we show the training processes of two Lagrange multipliers,
and
, over training epochs under a specific setting of (
,
). As depicted in
Figure 3, both multipliers gradually stabilize after 600 epochs, indicating the convergence of training.
Additionally, other parameters involved in the training process, including , , , , , and , demonstrate similar convergence behavior. It is worth noting that all the subsequent experimental results and analysis are conducted under the premise that the training of DVSC model converges.
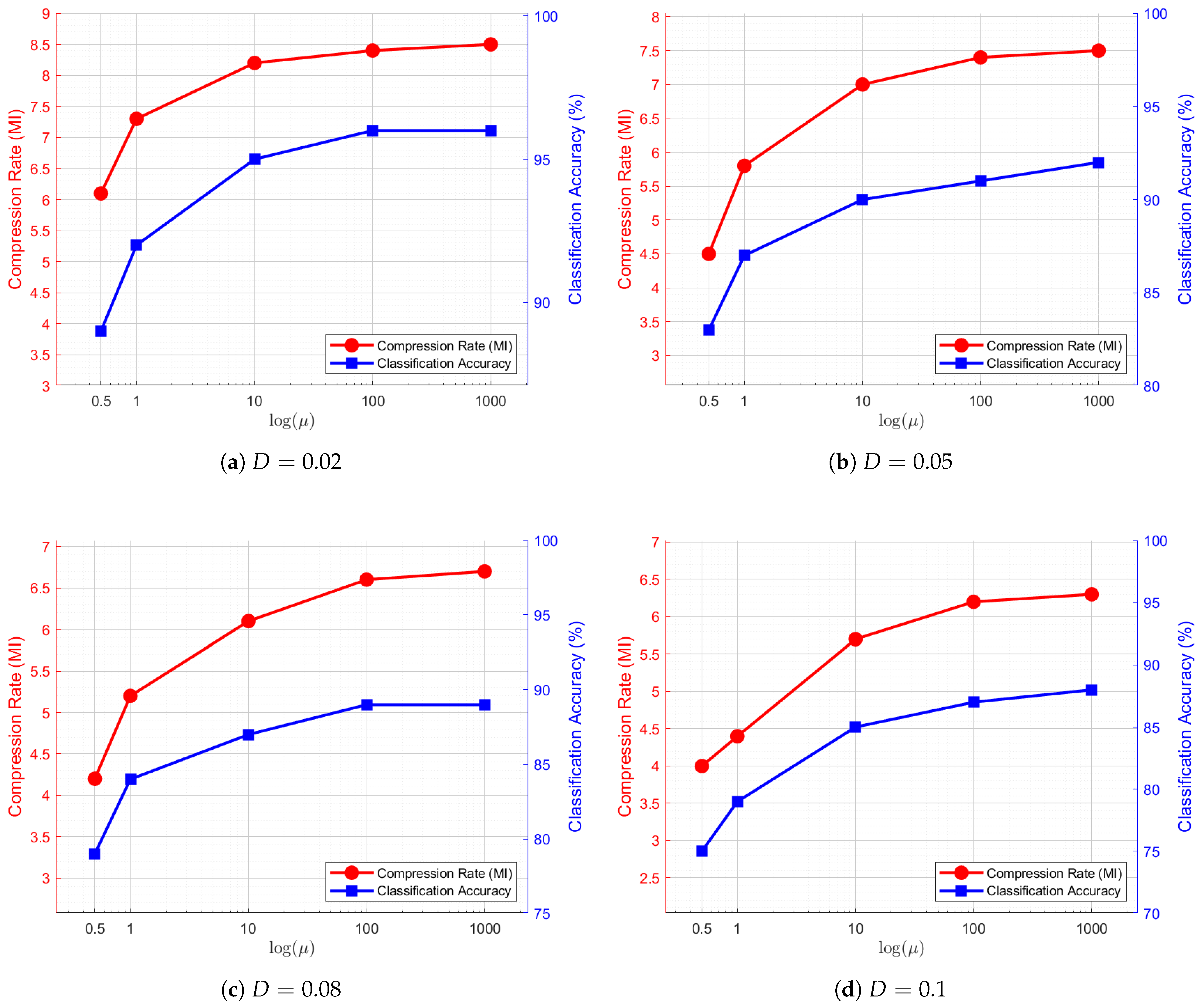
4.3.1. Trade-Off Analysis: Influence of with Fixed D
To investigate the trade-off influenced by
, we fix the distortion constraint
D and systematically adjust
to examine its effect on the compression rate and classification performance. Additionally, we conduct multiple experiments under varying values of
D. The corresponding results are illustrated in
Figure 4.
Across all subfigures in
Figure 4, a common trend shows that as
increases, both the compression rate and classification performance improve. This behavior suggests a shift in the optimization focus, where a larger
places greater emphasis on classification accuracy at the expense of compression efficiency. This trend aligns well with our theoretical analysis. Moreover, when
, the rate of improvement gradually diminishes. Beyond
, both the compression rate and classification accuracy reach a plateau, indicating that the preservation of task-critical information has an inherent upper bound.
Figure 5 presents the qualitative evaluation of the coding schemes for different values of
under a fixed distortion constraint of
. Notably, when
, the coding algorithm degrades to the conventional source coding scheme. We can observe that as
increases, gender-related features become more distinct, therefore leading to an improvement in classification accuracy.
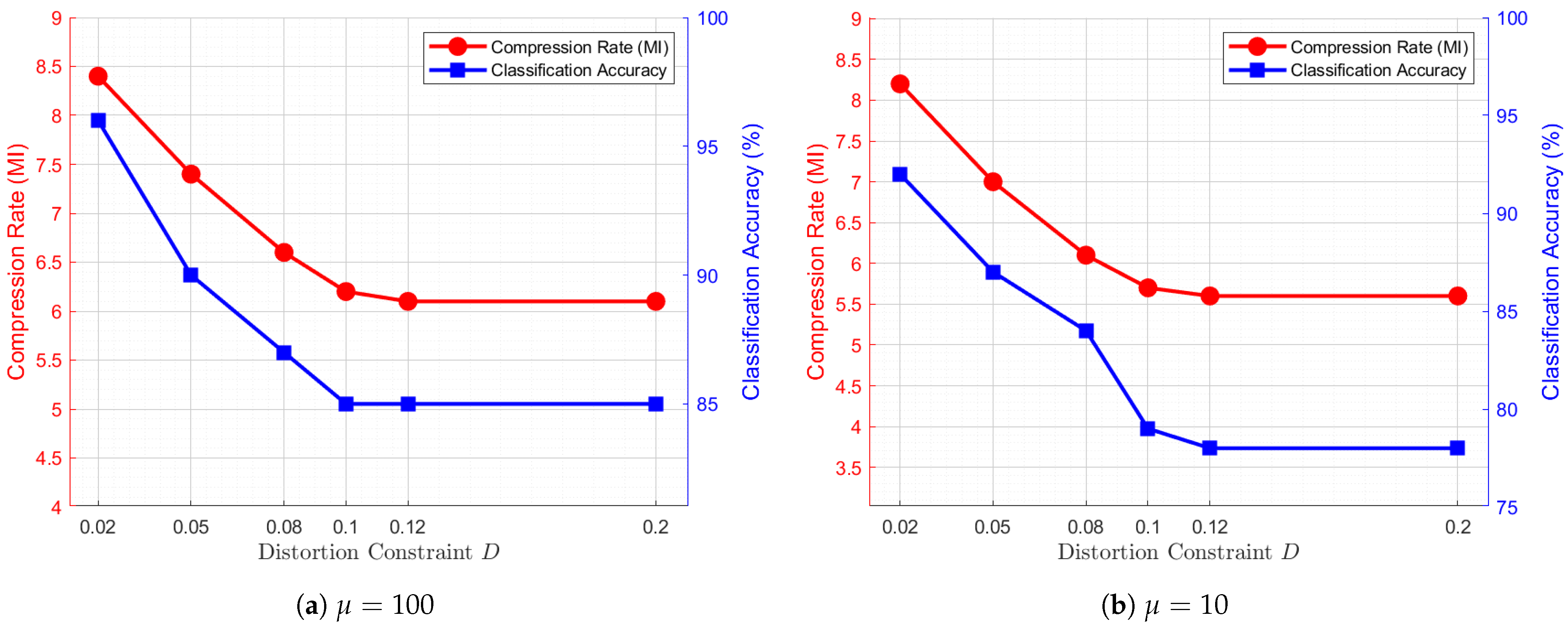
4.3.2. Trade-Off Analysis: Influence of D for Fixed
Similarly, we fix
and examine the relationships between compression rate and distortion constraint
D, as well as classification accuracy and
D. The corresponding curves are depicted in
Figure 6. A general trend observed across these subfigures is that when
, both the compression rate and classification accuracy exhibit a decreasing pattern as
D increases. This trend suggests that increasing
D allows for more efficient compression; however, it also leads to severer loss of task-critical information, ultimately degrading classification performance.
Figure 7 presents the qualitative evaluation of the coding schemes for different values of
D at
. As expected, when
D increases, the images become progressively blurred, leading to a noticeable loss of gender-related features and consequently a decline in classification accuracy.
4.3.3. Comparison with the Traditional Source Coding Scheme
As previously discussed, setting
corresponds to the conventional source coding scheme, as illustrated in
Figure 6d. Compared with
Figure 6a–c,
Figure 6d achieves the highest compression efficiency but at the cost of the lowest classification accuracy. For instance, at
,
in
Figure 6a, the coding scheme achieves a peak classification accuracy of
, outperforming the traditional scheme by
subject to the same distortion constraint, albeit with a
-bit loss in compression rate. From the perspective of the optimization objectives, since conventional coding scheme does not account for classification performance, the overall effectiveness is inherently lower than that of the semantic coding scheme, despite achieving superior data compression efficiency.
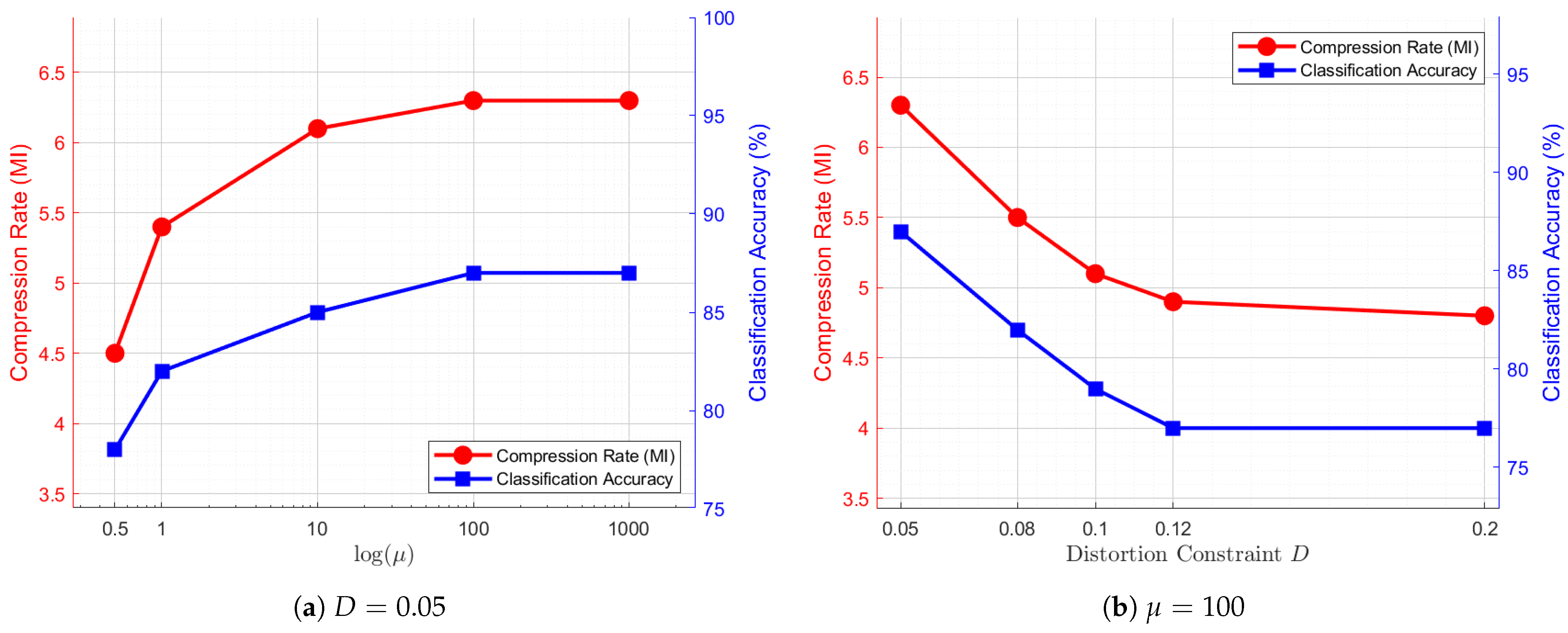
4.4. Extended Evaluation on the CIFAR-10 Dataset
To further evaluate the generalizability of the proposed DVSC-Opt algorithm, we conduct additional experiments on the CIFAR-10 dataset following the same experimental pipeline as described above. The CIFAR-10 dataset contains 60,000 color images evenly distributed across 10 object categories. For this evaluation, we select two semantically similar categories, deer and horse, to perform mixed-source semantic coding and binary classification with the DVSC model. The results of these experiments are reported in
Figure 8 and
Figure 9.
As shown in
Figure 8a, when the distortion constraint is fixed at
, increasing the weight coefficient
leads to improvements in both compression rate and classification accuracy, until the performance reaches a saturation point. This trend corresponds well with the visualization results in the first three rows of
Figure 9, where larger
values result in more prominent class-discriminative features. On the other hand, when the weight coefficient is fixed at
, as illustrated in
Figure 8b, increasing
D results in a gradual decline in both compression rate and classification accuracy, eventually stabilizing at a lower level. This effect is visually reflected in the last three rows of
Figure 9, where higher distortion levels lead to progressively blurred image reconstructions. These two trends are consistent with the experimental findings on the CelebA dataset, confirming that the DVSC-Opt model consistently handles the trade-off between compression rate and binary classification performance across different datasets.
4.5. Summary
Experiments on the CelebA dataset and the CIFAR-10 dataset demonstrate that the DVSC-Opt algorithm can effectively balance compression rate and classification performance, while ensuring the distortion under the predefined constraint. This result aligns well with our theoretical analysis. Moreover, for a given weight coefficient , increasing distortion constraint D also leads to a degradation in both compression efficiency and classification accuracy, indicating a trade-off among these three design objectives. From the perspective of optimization objectives, the DVSC-Opt algorithm encompasses traditional encoding scheme while offering a more comprehensive and flexible approach.
5. Conclusions
In this paper, we propose a theoretically-grounded and explainable deep semantic coding framework tailored for the BCOC scenario. From an information-theoretic perspective, we formulate a semantic coding problem that jointly optimizes compression rate and classification accuracy subject to predefined distortion constraints. Furthermore, we leverage deep learning techniques and variational methods to transform the theoretical optimization problem into a trainable DVSC model and propose the DVSC-Opt algorithm. Experiments on the CelebA dataset and the CIFAR-10 dataset demonstrate that the DVSC-Opt algorithm effectively balances compression efficiency and classification performance while ensuring acceptable reconstruction distortion.
An important future direction is extending our coding framework to multi-class classification tasks by studying mixed multi-source semantic coding schemes. Moreover, future work could explore adaptive optimization strategies that dynamically adjust the weight coefficient based on task complexity, dataset characteristics, or real-time feedback mechanisms.
In conclusion, this study introduces a deep semantic coding framework that is both explainable and mathematically principled, laying a solid foundation for future research in explainable semantic coding and efficient data compression strategies.