Study on the Charge Structure Optimization for Coal–Rock Mixed Blasting and Separate Mining in Open-Pit Mine with High Benches
Abstract
1. Introduction
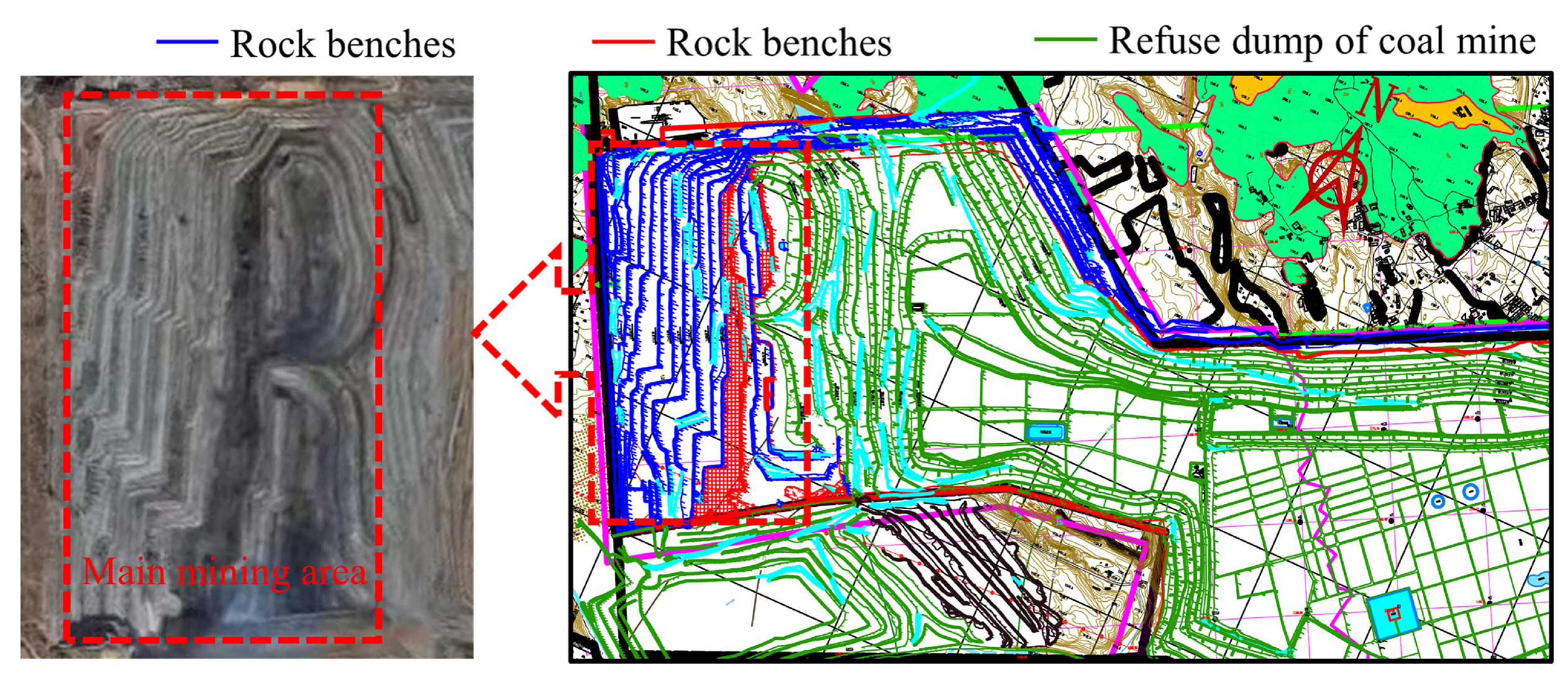
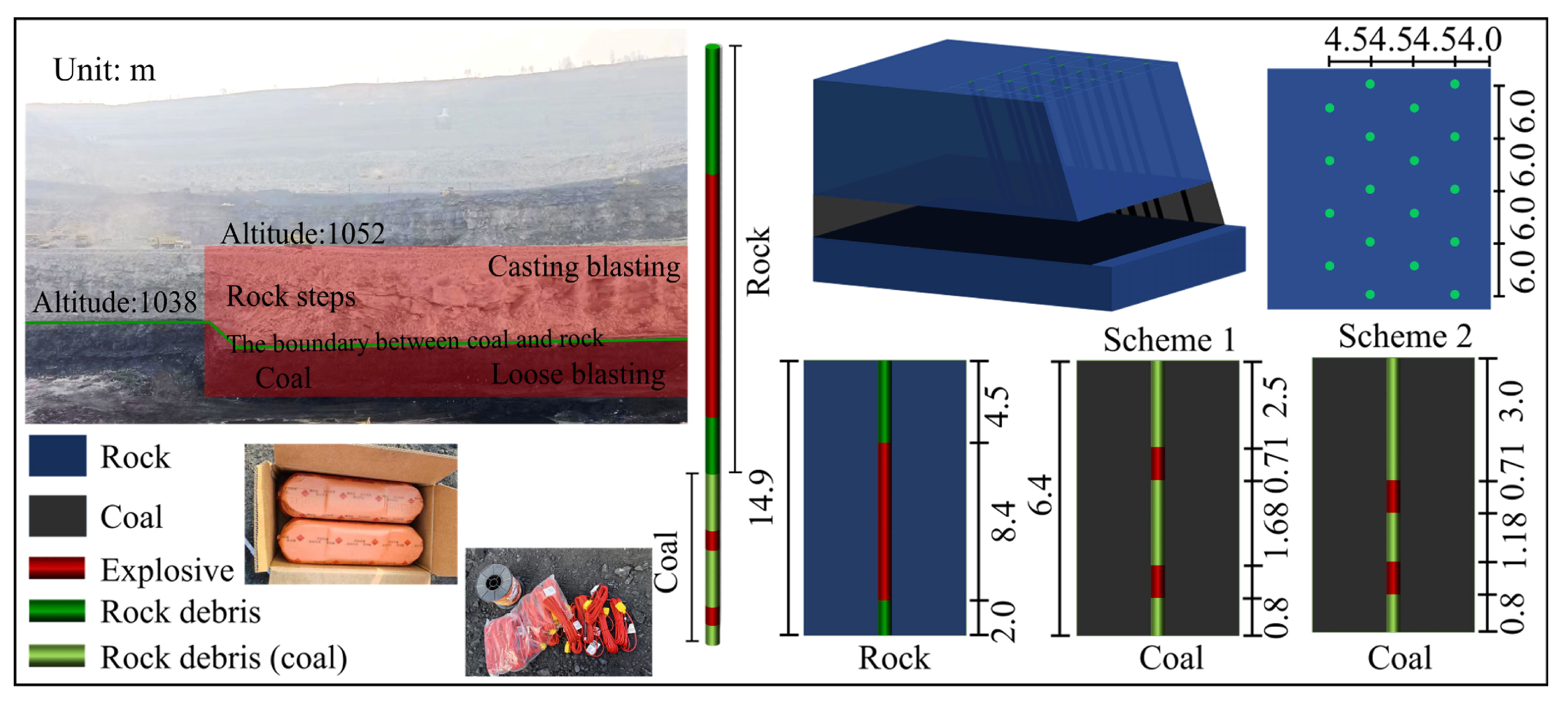
2. Site Overview
3. Single-Hole Column Charge Blasting Crater Test for Coal and Rock
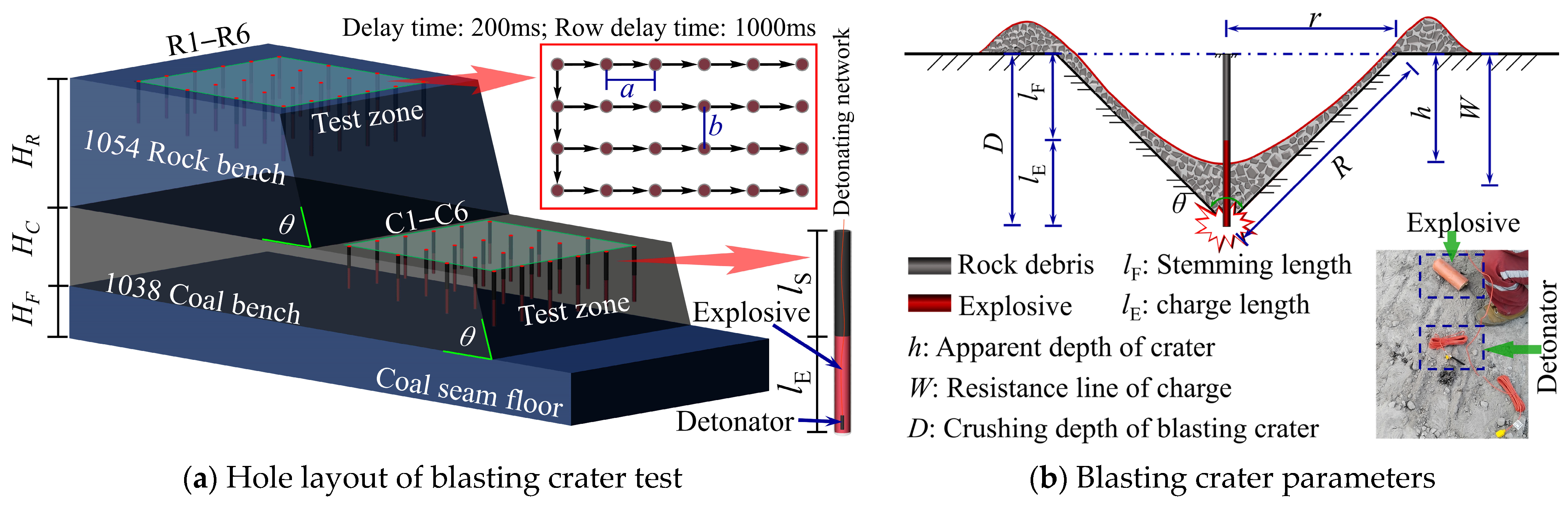
3.1. Blasting Crater Test Plan and Parameter Design
3.2. Analysis of Blast Crater Test Results
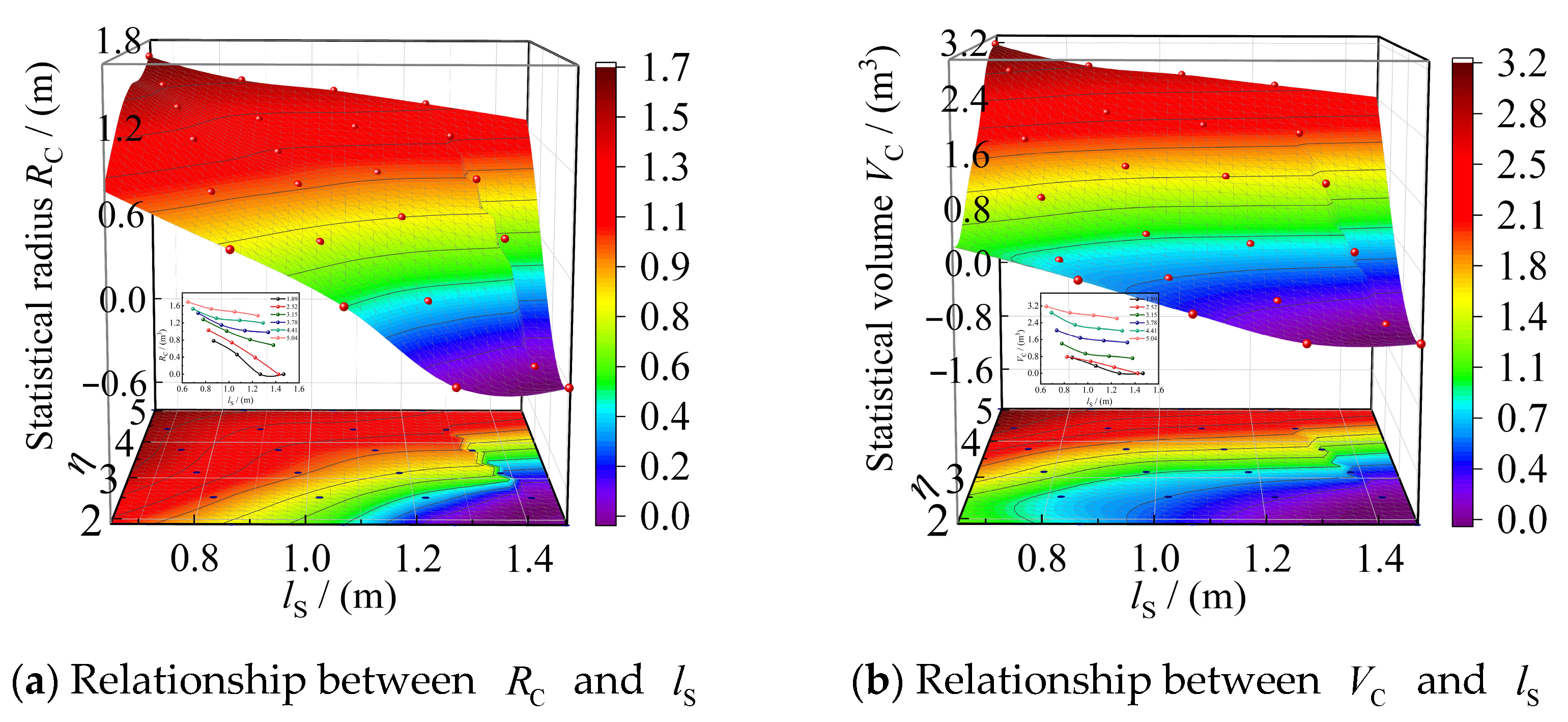
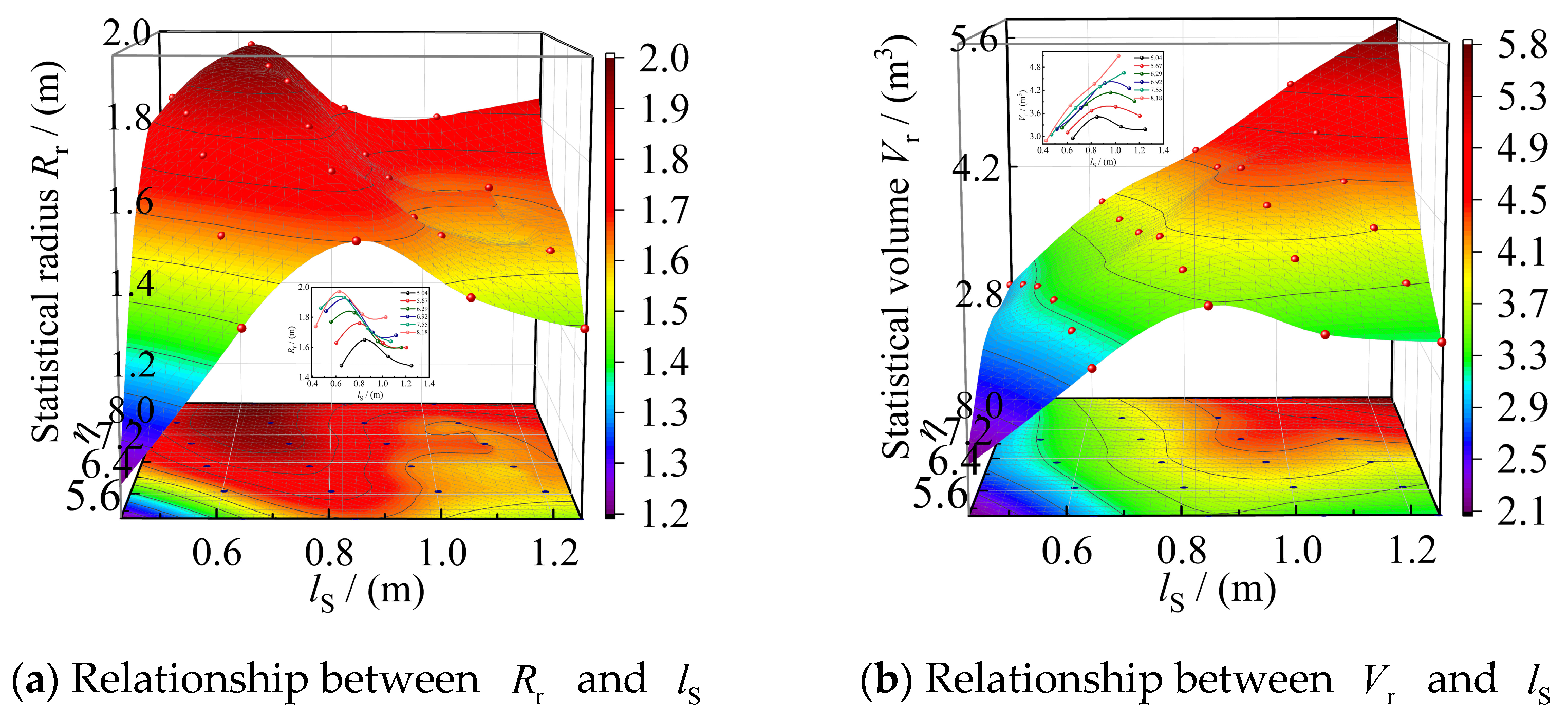
3.2.1. Measurement and Statistics of the Blast Crater Volume
3.2.2. Analysis of Blasting Crater Test Outcomes
- (1)
- Analysis of Blast Fragmentation Morphology
- (2)
- Analysis of Geometric Parameters of Blast Craters by Cartridges with Different Length-to-Diameter Ratios
3.2.3. Blasting Crater Throwing and Crushing Energy Distribution and Parameter Analysis
4. Numerical Simulation
4.1. Numerical Analysis of Charge Structure
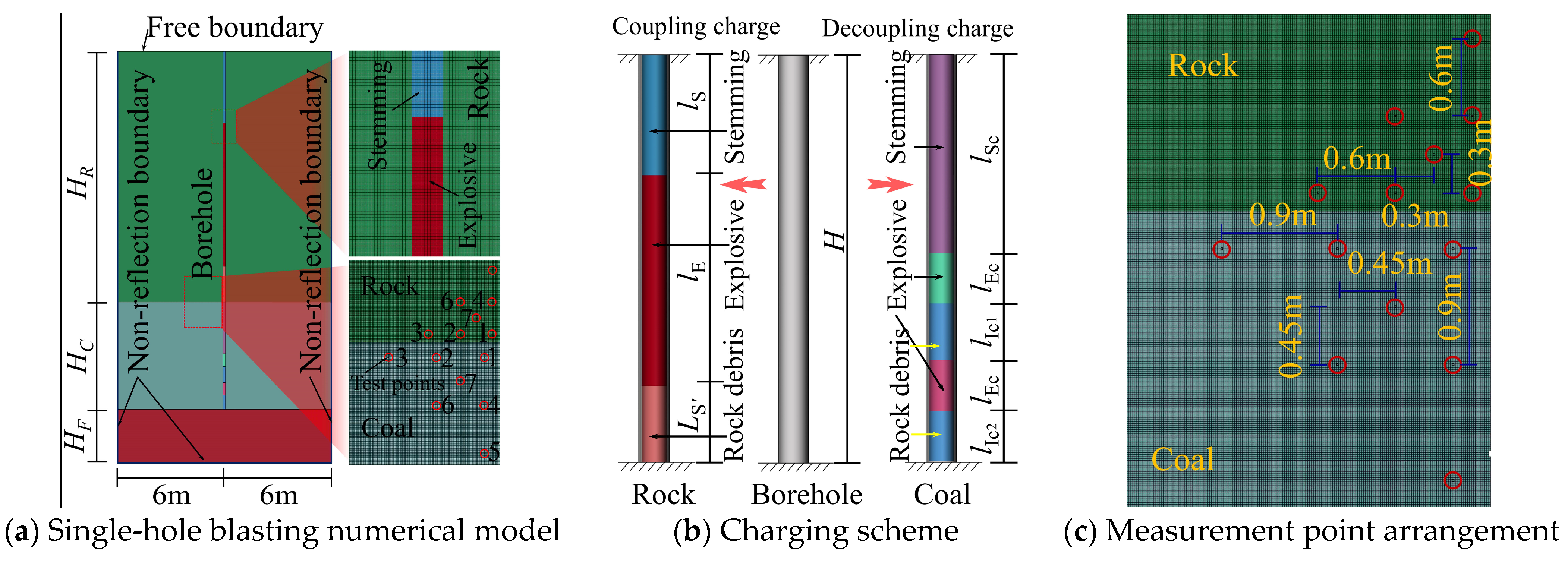
4.1.1. Numerical Model
4.1.2. Numerical Model Parameters
- (1)
- Constitutive Models and Parameters of Coal and Rock
- (2)
- Explosive Model and State Equation
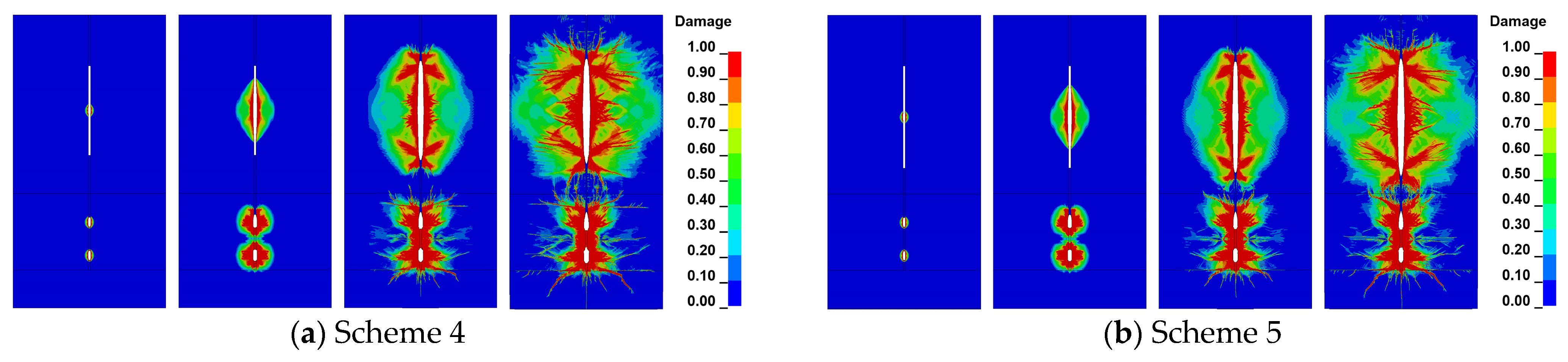
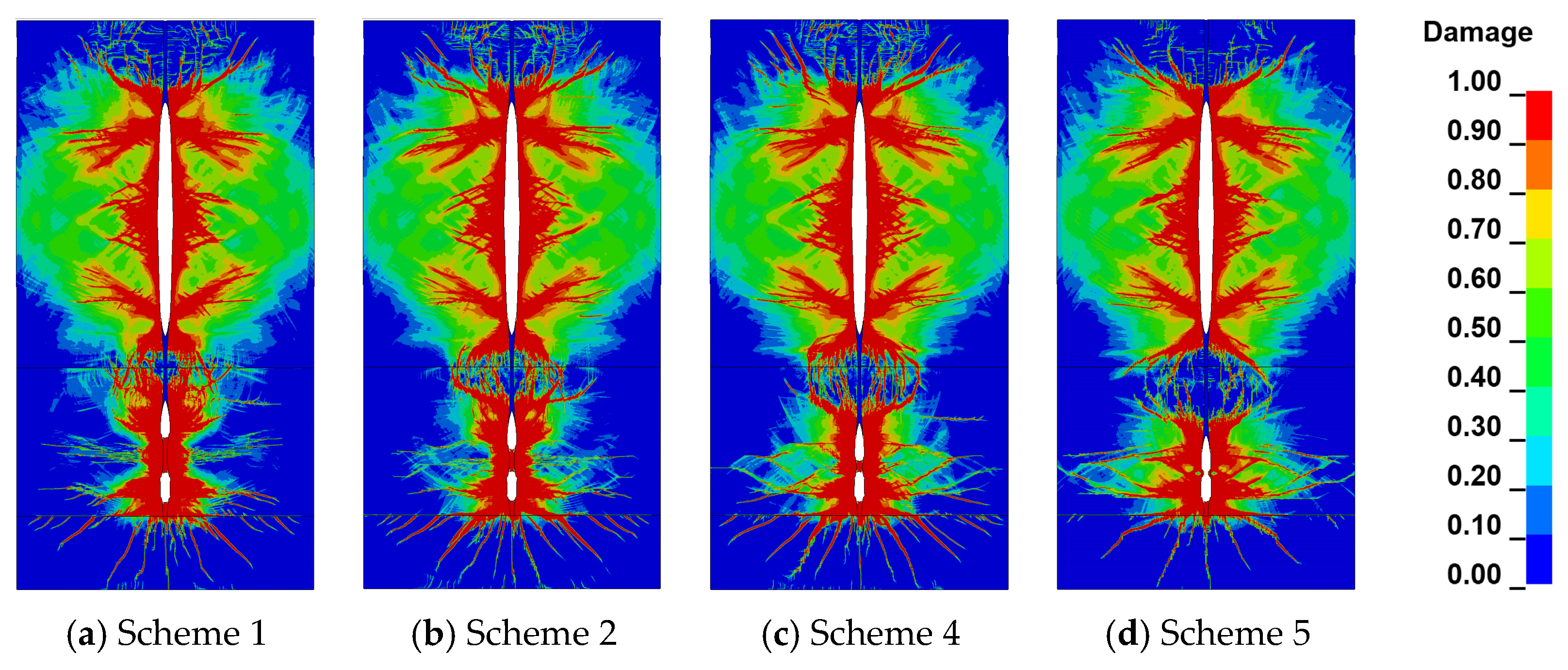
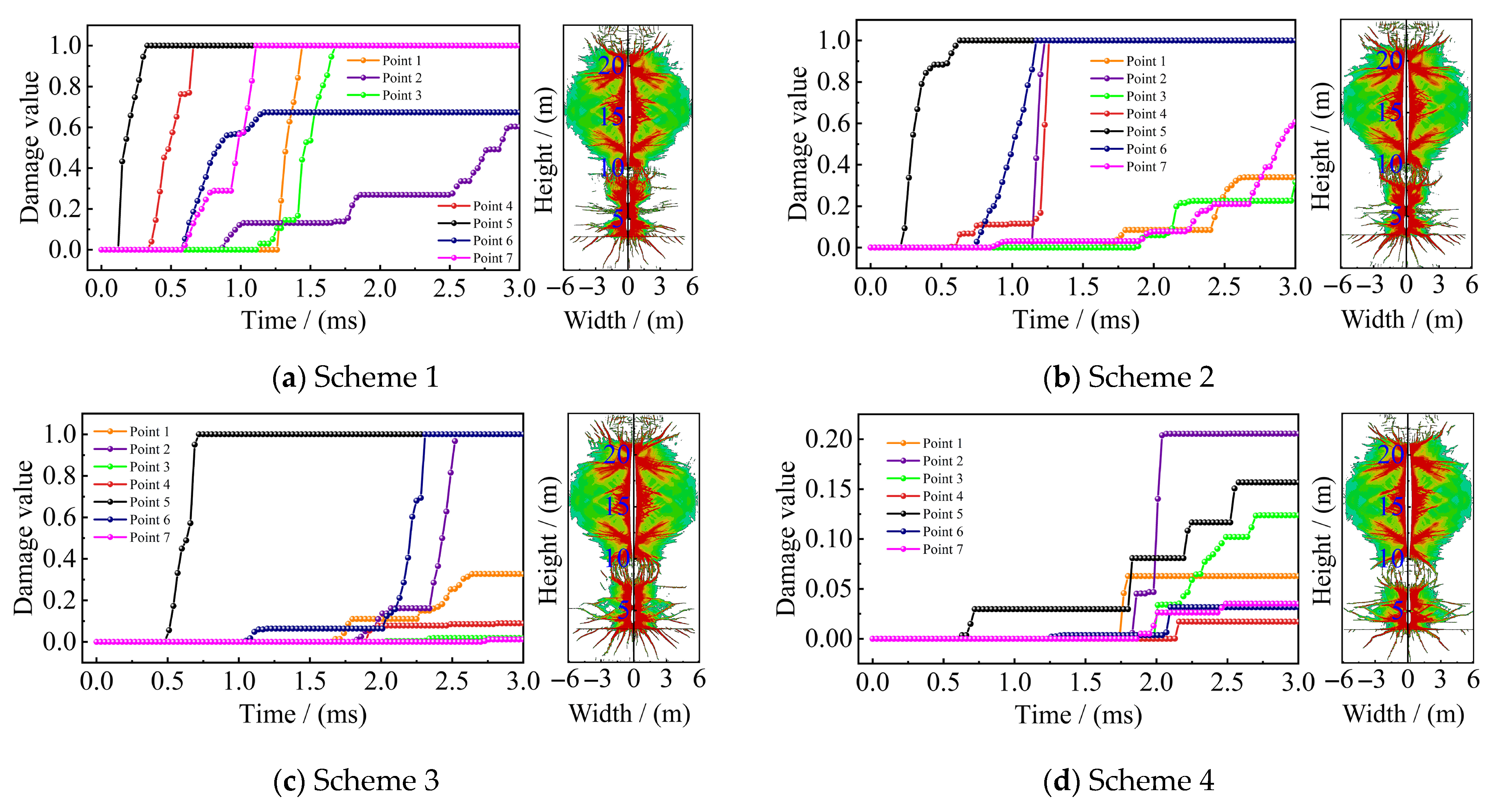
4.1.3. Numerical Results
- (1)
- Damage effect of rock blasting
- (2)
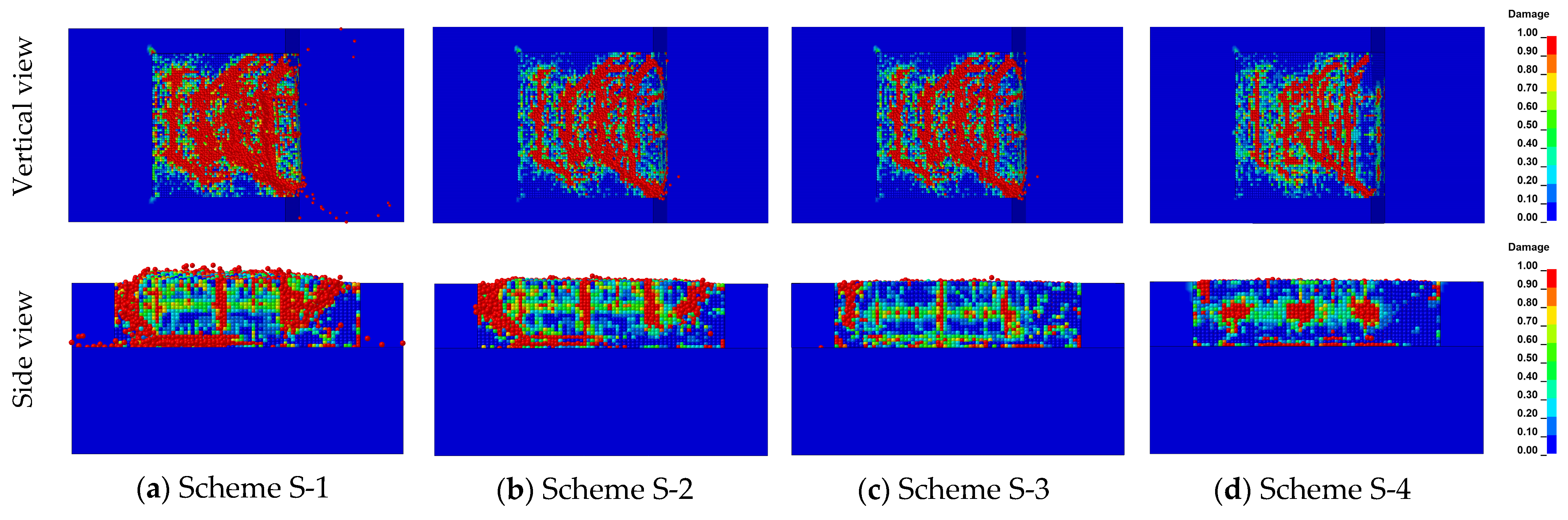
- Coal bench damage effect
4.2. Casting Blasting Simulation
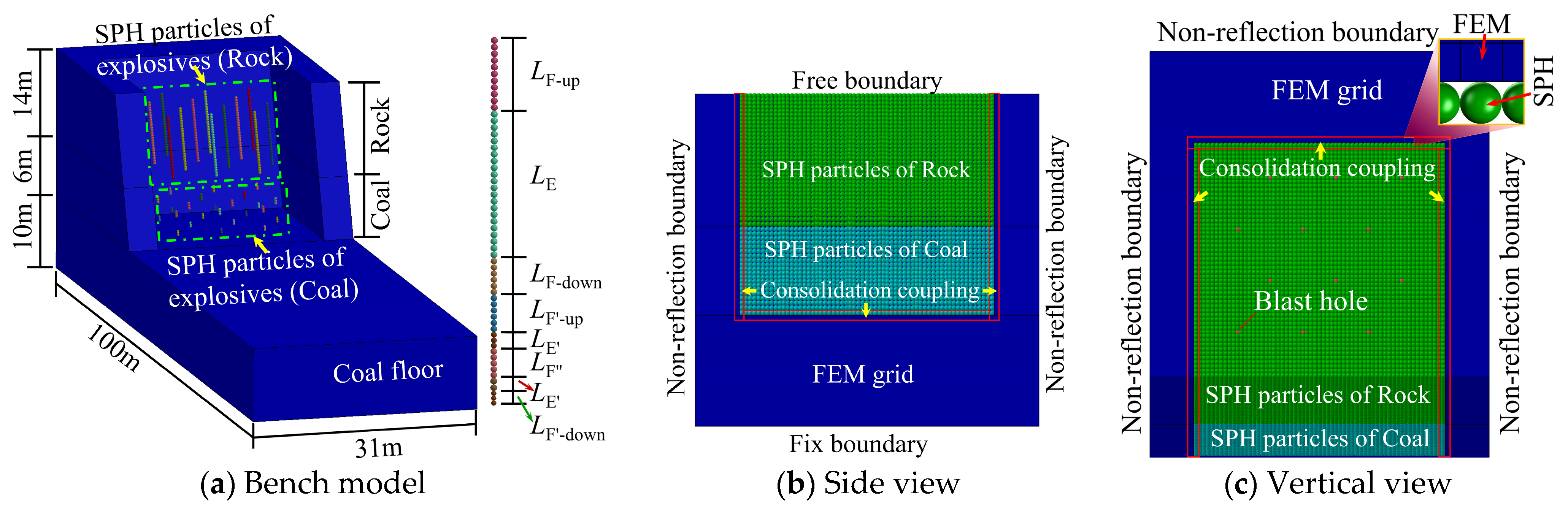
4.2.1. Establishment of the Casting Blasting Model
- (1)
- The SPH-FEM coupled analysis method was adopted, where explosives and the core blasting region (coal and rock mass) were modeled as SPH particles in the bench model, while the coal–rock boundary rock mass and coal bottom rock mass were modeled using FEM grid elements [48].
- (2)
- The *LOAD_BODY_Y command was employed to apply gravitational acceleration in the Y-direction, and fixed boundary conditions were applied at the bottom of the model.
- (3)
- Non-reflective boundary conditions were applied on all sides of the bench model, except for the free surface, to eliminate the influence of stress wave reflections on the accuracy of the simulation results.
- (4)
- The detonation time for each explosive SPH particle in the boreholes was set sequentially to achieve hole-by-hole detonation.
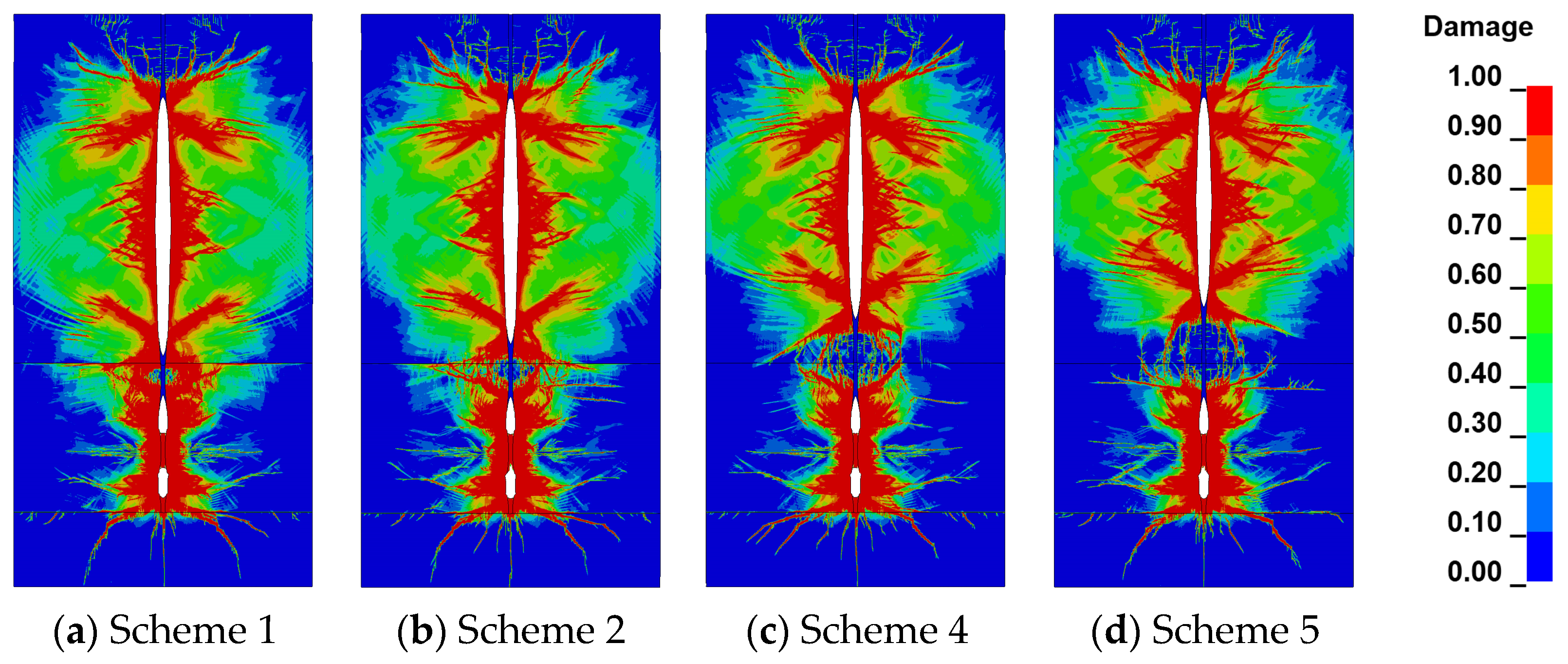
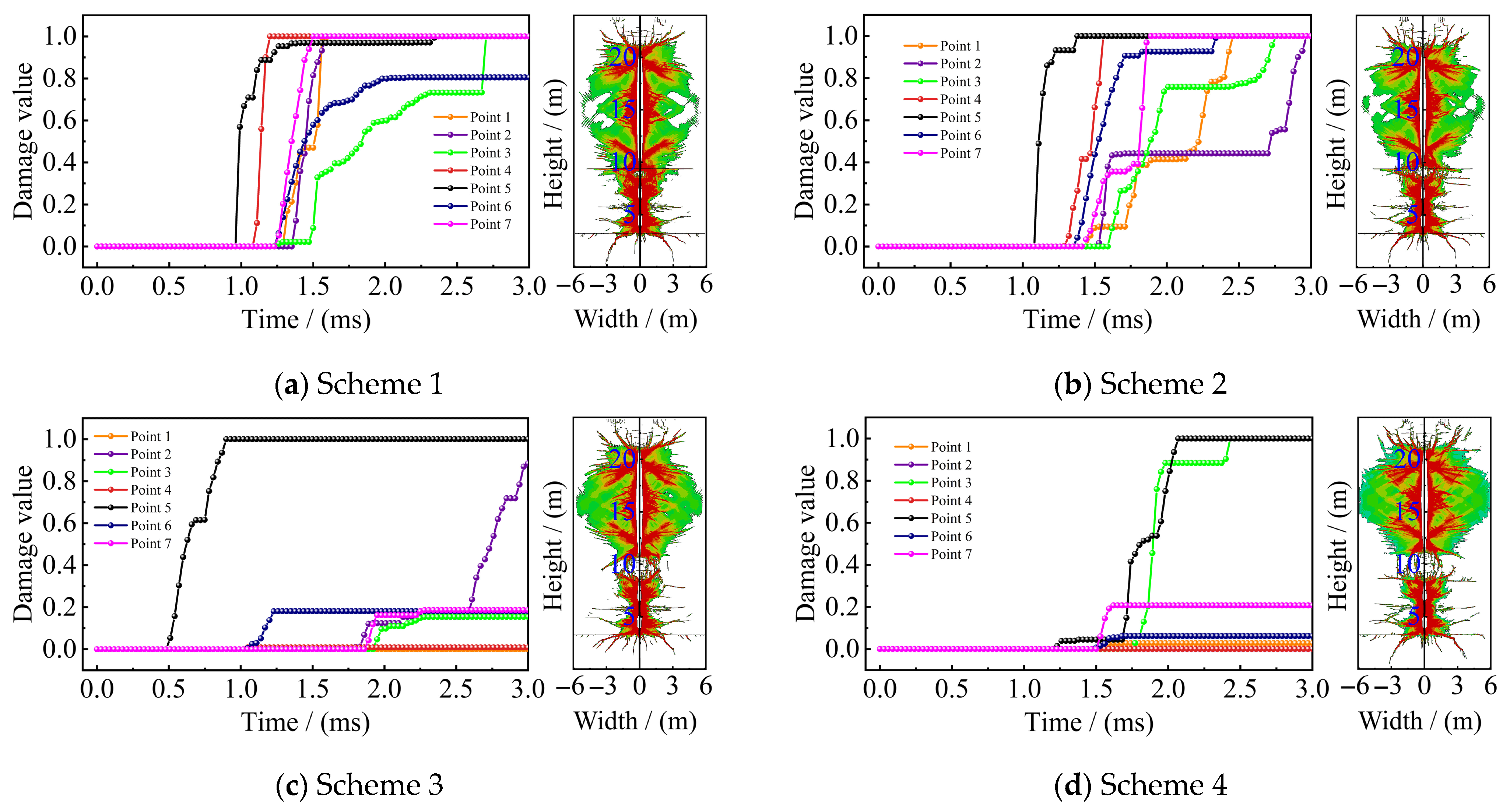
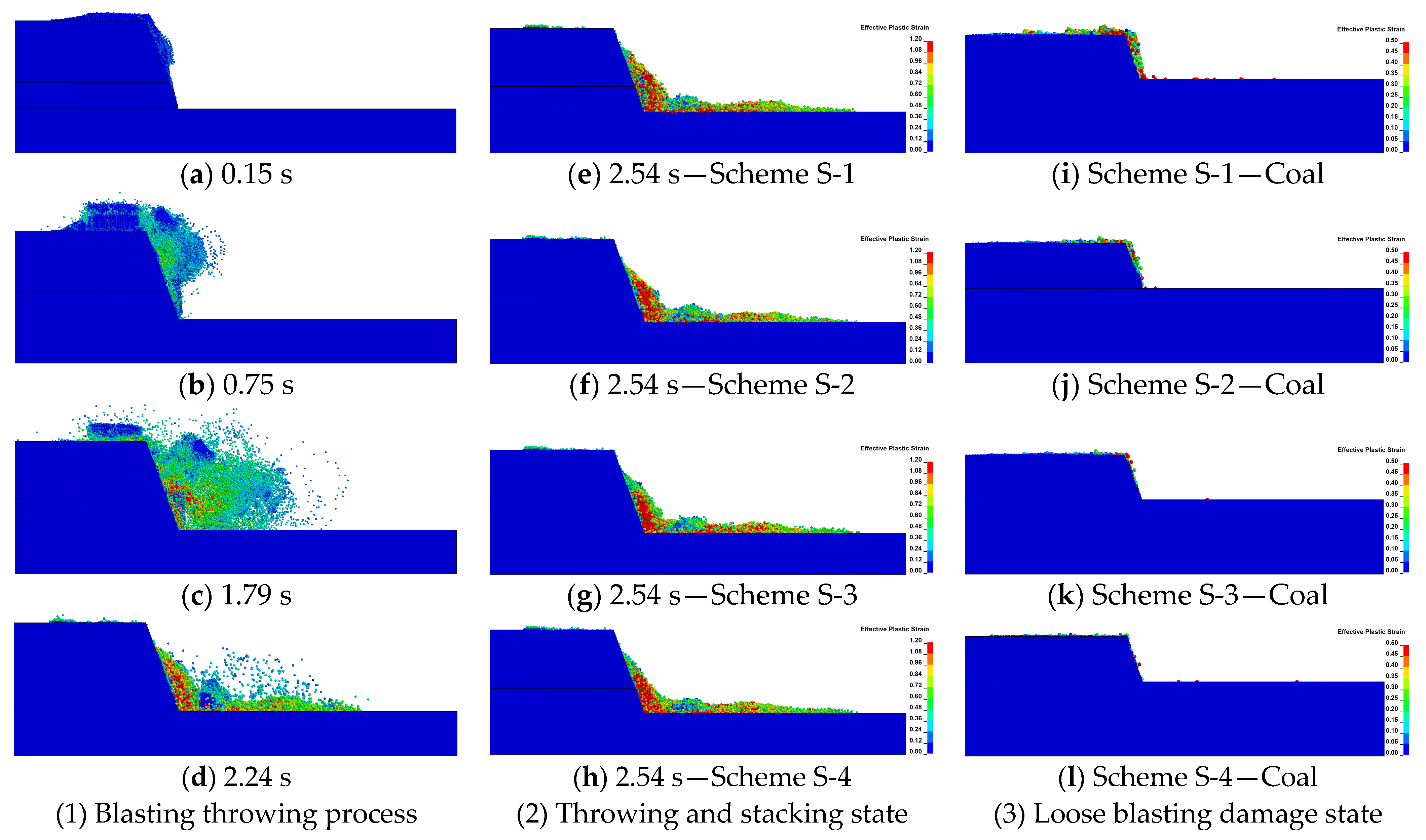
4.2.2. Blast Effect Analysis
- (1)
- Rock Throw Law and Coal–Rock Fragmentation Effect Analysis
- (2)
- Coal and Rock Blasting Damage Analysis
5. Field Experimental on Open-Pit Bench Coal–Rock Mixed Blasting
5.1. Mixed Blasting Experimental Plan
5.2. Mixed Blasting Test Results Analysis
6. Conclusions
- (1)
- A characteristic curve of the coal bench blasting crater is established based on the results of on-site blasting crater tests. When the ratio of charge length to stemming length in coal and rock bench blasting exceeds 0.91 and 0.74, respectively, the internal crushing effect of the rock mass is enhanced, and the utilization rate of explosive energy in coal and rock fragmentation gradually surpasses that in rock casting.
- (2)
- The numerical results of coal and rock mixed blasting indicate that when the bottom spacing length of the rock bench is 2 m, and the stemming length of the coal seam ranges from 2.5 to 3 m, the distribution of explosive energy within the rock mass near the stratified interface is optimized, enhancing the rational utilization of energy, facilitating the connectivity of rock damage cracks, and improving the tension cracks’ distribution at the coal seam’s top. In addition, no bulging or coal–rock interaction (explosive mixing) phenomenon occurs at the coal–rock interface, and the blasting effect satisfies the requirements of mixed separate mining.
- (3)
- The coal and rock mixed blasting test results indicate that a reasonable charge structure is one of the key factors in achieving coal and rock mixed blasting separate mining. After optimizing the charge structure, the cast blasting distance of the rock bench ranges from 21.65 to 32.59 m. The crushing effect of Scheme 1 at the stratified interface is superior to that of Scheme 2; however, both schemes meet the requirements of separation and crushing. These results demonstrate that the optimized charge structure effectively fulfills the purpose and requirements of coal and rock mixed blasting separate mining.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chironis, N.P. Efficient Stripping New Washer Build Markets. Coal Age 1962, 67, 64–67. [Google Scholar]
- Ray, S.K.; Zutshi, A.; Sarkar, M. Cast Blasting—State of the Art. Fragblast 1999, 3, 291–302. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, R.; Sun, J. Research on the Optimization of Open-Pit Mine Cast Blasting Parameters Based on the Optimal Economy of Dragline Stripping Technology. Appl. Sci. 2023, 13, 10888. [Google Scholar] [CrossRef]
- Sharma, P.D. Overburden Side Casting by Blasting—An Effective Way of Reducing Operating Cost in Large Opencast Coal Mines. J. Mines Met. Fuels 2006, 52, 284–288. [Google Scholar]
- Mishra, A.K.; Sinha, M.; Rout, M. Cast Blasting for Improved Mine Economics. In Proceedings of the Blasting in Mining-New Trends: 10th International Symposium on Rock Fragmentation by Blasting, FRAGBLAST; CRC Press: Boca Raton, FL, USA, 2013; Volume 10, pp. 73–80. [Google Scholar]
- XIAO, S.; DING, X.; Ma, L. Optimization on Bench Parameters of Casting Blast Based on Multi-Objective Programming. J. China Coal Soc. 2018, 43, 2422–2431. [Google Scholar]
- Ma, L.; Lai, X.; Zhang, J.; Xiao, S.; Zhang, L.; Tu, Y. Blast-Casting Mechanism and Parameter Optimization of a Benched Deep-Hole in an Opencast Coal Mine. Shock Vib. 2020, 2020, 1396483. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Z.; Zhang, Z.; Zhou, J.; Li, H.; Li, Y. Calculation Method of the Blasting Throwing Energy and Its Variation Affected by the Burden. Appl. Sci. 2022, 12, 6524. [Google Scholar] [CrossRef]
- Chironis, N.P. Angled Drilling Aids Casting. Coal Age 1984, 89, 64–67. [Google Scholar]
- Wang, P.; Zhou, W.; Yang, H.; Zhang, G. Analysis on Reasonable Layout and Row Spacing of Casting Blasting in Open Pit Coal Mine. Coal Eng. 2011, 11, 72–74. [Google Scholar]
- LI, X.; LUO, H.; HU, H.; ZHANG, S.; LI, K. High Bench Cast-Blasting Effects Influenced by Delay Time. Trans. Beijing Inst. Technol. 2018, 38, 579–584. [Google Scholar]
- Zuo, Y.F.; Zhang, J.Y.; Yang, L.D.; Wang, F.R.; Wang, Z.A. A Study on the Effect of Different Charge Structures on the Permeability Enhancement of Coal Seam Blasting. Processes 2024, 12, 1645. [Google Scholar] [CrossRef]
- Bhagade, N.V.; Murthy, V.M.S.R.; Ali, M.S. Enhancing Rock Fragmentation in Dragline Bench Blasts Using Near-Field Ground Vibration Dynamics and Advanced Blast Design. Powder Technol. 2021, 381, 421–439. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, J.; Lai, X. Optimization on Working Face Length of Blast Casting Stripping System in Comprehensive Technology. J. China Coal Soc. 2021, 46, 3186–3192. [Google Scholar] [CrossRef]
- Han, L.; Liu, D.-S.; Li, G.-J.; Wang, Y.-T. BP Neural Network Forecast of Blasting Muck Pile Form of High Bench Cast Blasting Based on Weibull Model. J. China Coal Soc. 2013, 38, 1947–1952. [Google Scholar]
- Huang, Y.-H.; Li, S.-L.; Fan, X.-W.; Wang, Y.-T.; Zhou, M.-G. Research and Application of Throwing Blast Effect Prediction Model of ELM Neural Network. J. China Coal Soc. 2012, 37, 65–69. [Google Scholar]
- Tingxin, W.; Xiaoyu, C.; Liangshan, S. Prediction on Parameters Optimized GA-ELM Model for Cast Blasting in Open-Pit Mine. J. China Coal Soc. 2017, 42, 630–638. [Google Scholar]
- Ma, N.; Ma, L.; Li, T.; Yang, S.; Wang, X.; Zhang, Q. HHO-LSSVM Prediction of Throwing Blasting Stockpile Morphology Based on Gaussian Distribution. J. China Coal Soc. 2024, 49, 4701–4712. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, R.; Sun, J.; Xu, X.; Tao, Y.; Lv, S.; Feng, D. Study on the Determination Method of Cast Blasting Stockpile Forms in an Open-Pit Mine. Appl. Sci. 2022, 12, 6428. [Google Scholar] [CrossRef]
- Huo, X.F.; Qiu, X.Y.; Shi, X.Z.; Chen, H.; Zong, C.X.; Xie, C. Attenuation Characteristics of Blasting Stress Under Decoupled Cylindrical Charge. Rock Mech. Rock Eng. 2023, 56, 4185–4209. [Google Scholar] [CrossRef]
- Ma, S.Z.; Liu, K.W.; Yang, J.C. Investigation of Blast-Induced Rock Fragmentation and Fracture Characteristics with Different Decoupled Charge Structures. Int. J. Impact Eng. 2024, 185, 104855. [Google Scholar] [CrossRef]
- Xia, X.; Yu, C.; Liu, B.; Liu, Y.; Li, H. Experimental Study on the Seismic Efficiency of Rock Blasting and Its Influencing Factors. Rock Mech. Rock Eng. 2018, 51, 2415–2425. [Google Scholar] [CrossRef]
- Yu, K.; Lin, P.; Chitombo, G.; Ma, L.; Peng, C. Study on the Optimization of Blasting Parameters and Blastholes Charging Structure for Broken Orebody. Tunn. Undergr. Space Technol. 2024, 152, 105948. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, W.; Su, X.; Li, J.; Li, Z.; Wen, L.; Chang, J. Numerical Study of the Impact Mechanism of Decoupling Charge on Blasting-Enhanced Permeability in Low-Permeability Sandstones. Int. J. Rock Mech. Min. Sci. 2018, 106, 300–310. [Google Scholar] [CrossRef]
- Hong, Z.X.; Tao, M.; Li, X.D.; Zhao, H.T.; Zhao, M.S. Experimental Study on the Influences of Charging Structure with Various Filling Mediums on Rock Blasting Performances. Powder Technol. 2023, 429, 118925. [Google Scholar] [CrossRef]
- Chen, M.; Ye, Z.; Lu, W.; Wei, D.; Yan, P. An Improved Method for Calculating the Peak Explosion Pressure on the Borehole Wall in Decoupling Charge Blasting. Int. J. Impact Eng. 2020, 146, 103695. [Google Scholar] [CrossRef]
- Li, X.; Liu, K.; Sha, Y.; Yang, J.; Song, R. Numerical Investigation on Rock Fragmentation under Decoupled Charge Blasting. Comput. Geotech. 2023, 157, 105312. [Google Scholar] [CrossRef]
- Chi, L.Y.; Wang, C.; Zhang, Z.X.; Xu, X.; Yang, J. Experimental Investigation of Decoupled Charge Effect on Rock Fragmentation by Blasting. Rock Mech. Rock Eng. 2022, 55, 3791–3806. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, W.; Su, X.; Wen, L.; Chang, J. Experimental and Numerical Study on the Effect of Water-Decoupling Charge Structure on the Attenuation of Blasting Stress. Int. J. Rock Mech. Min. Sci. 2019, 124, 104133. [Google Scholar] [CrossRef]
- Liu, J.; Gao, W.; Zhang, S.; Li, X. Distribution Law of Explosion Stress on Hole Wall of Water Interval Charge. Acta Armamentarii 2021, 42, 2646–2654. [Google Scholar] [CrossRef]
- Liu, S.; Sui, J.; Jia, H.; Fu, M.; Yu, T.; Yao, B. Optimization of Solid-Hydraulic Coupled Charge Structure and Borehole Arrangement in Deep Buried Bottom Draw Lane Gunnery. J. Min. Strat. Control Eng. 2023, 6, 5–16. [Google Scholar] [CrossRef]
- Lou, X.; Zhou, P.; Yu, J.; Sun, M. Analysis on the Impact Pressure on Blast Hole Wall with Radial Air-Decked Charge Based on Shock Tube Theory. Soil Dyn. Earthq. Eng. 2020, 128, 105905. [Google Scholar] [CrossRef]
- Lou, X.; Wang, Z.; Chen, B.; Wang, Z.; Yu, J. Initial Shock Pressure Analysis for Hole Wall with Air-Decked Charge. J. China Coal Soc. 2017, 11, 2875–2884. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Y.; Zhang, X.; Li, X.; Zhao, W.; Gao, W.; Li, H.; Li, Y.; Yan, T. Study on Explosion Impact Pressure and Damage Distribution Law of Rock Powder Segmented Charge. Eng. Fail. Anal. 2024, 163, 108517. [Google Scholar] [CrossRef]
- Jang, H.; Handel, D.; Ko, Y.; Yang, H.-S.; Miedecke, J. Effects of Water Deck on Rock Blasting Performance. Int. J. Rock Mech. Min. Sci. 2018, 112, 77–83. [Google Scholar] [CrossRef]
- Liu, J.; Gao, W.; Zhang, S.; Xu, H. Numerical Analysis and Application of Uncoupled Coefficient of Water Sealed Blasting on Blasting Effect. IOP Conf. Ser. Earth Environ. Sci. 2021, 719, 32035. [Google Scholar] [CrossRef]
- Wu, L.; Zhou, Y.; Guo, Z. The Rock Failure Mechanism of Air-Decked Blasting in Hole Bottom. Appl. Mech. Mater. 2012, 201–202, 375–378. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, X.; Wang, D.; Dang, Z.; Bi, J. Analysis and Application of Stress Distribution in 24-m High Bench Loosening Blasting with Axially Uncoupled Charge Structure in Barun Open-Pit Mine. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 22059. [Google Scholar] [CrossRef]
- Honglu, F. Blasting Theory and Applications; China Coal Industry Publishing House: Beijing, China, 2017; ISBN 750203305X. [Google Scholar]
- Borrvall, T.; Riedel, W. The RHT Concrete Model in LS-DYNA. In Proceedings of the 8th European LS-DYNA User Conference, Ulm, Germany, 23–24 May 2011; pp. 1–14. [Google Scholar]
- Wang, H.; Wang, Z.; Wang, J.; Wang, S.; Wang, H.; Yin, Y.; Li, F. Effect of Confining Pressure on Damage Accumulation of Rock under Repeated Blast Loading. Int. J. Impact Eng. 2021, 156, 103961. [Google Scholar] [CrossRef]
- LI, H.; LIU, D.; ZHAO, L.; LI, C.; ZHANG, Z. Study on Parameters Determination of Marble RHT Model. Trans. Beijing Inst. Technol. 2017, 37, 801–806. [Google Scholar]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of Damage Mechanisms and Optimization of Cut Blasting Design under High In-Situ Stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Qiu, X.; Liu, X.; Hu, A.; Li, H.; Wang, Y. Research on Numerical Simulation of Coal Dynamic RHT Constitutive Model. J. China Coal Soc. 2024, 49, 261–273. [Google Scholar]
- Himanshu, V.K.; Mishra, A.K.; Roy, M.P.; Vishwakarma, A.K.; Singh, P.K. Numerical Simulation Based Approach for Assessment of Blast Induced Deformation Pattern in Slot Raise Excavation. Int. J. Rock Mech. Min. Sci. 2021, 144, 104816. [Google Scholar] [CrossRef]
- Kan, J.; Dou, L.; Li, X.; Cao, J.; Bai, J.; Chai, Y. Study on Influencing Factors and Prediction of Peak Particle Velocity Induced by Roof Pre-Split Blasting in Underground. Undergr. Space 2022, 7, 1068–1085. [Google Scholar] [CrossRef]
- Zhang, H.; Li, T.; Du, Y.; Zhu, Q.; Zhang, X. Theoretical and Numerical Investigation of Deep-Hole Cut Blasting Based on Cavity Cutting and Fragment Throwing. Tunn. Undergr. Space Technol. 2021, 111, 103854. [Google Scholar] [CrossRef]
- Li, C.; Yang, R.; Wang, Y.; Kang, Y.; Zhang, Y.; Xie, P. Theoretical and Numerical Simulation Investigation of Deep Hole Dispersed Charge Cut Blasting. Int. J. Coal Sci. Technol. 2023, 10, 15. [Google Scholar] [CrossRef]




| Coal Seam ID | Coal Seam Thickness | Density | Elastic Modulus | Compressive Strength | Tensile Strength | Poisson’s Ratio | Rock Types of the Roof and Floor | |
|---|---|---|---|---|---|---|---|---|
| (Average) (m) | (kg∙m−3) | (GPa) | (MPa) | (MPa) | Roof | Floor | ||
| #1 | 1.1~2.92 (1.06) | 1248 | 6.42 | 18.37 | 1.97 | 0.27 | Sandy mudstone | Fine sandstone |
| #2 | 4.5~10.2 (8.8) | 1275 | 6.81 | 24.86 | 2.51 | 0.29 | Sandy mudstone | Fine sandstone |
| #3 | 4.4~6.8 (5.8) | 1310 | 5.94 | 21.07 | 1.99 | 0.27 | Fine sandstone | Coarse sandstone |
| Bench | Step Height | Borehole Diameter | Cartridge Diameter | Hole Pitch | Row Space | Hole Depth | Charge Quantity | Charge Length |
|---|---|---|---|---|---|---|---|---|
| (m) | (mm) | (mm) | (m) | (m) | (m) | (kg) | (m) | |
| Rock | 14.00 | 70.00 | 70.0 | 5.0 | 7.0 | 1, 1.2, 1.4, 1.6 | 1.6, 1.8, 2.0, 2.2, 2.4, 2.6 | 0.36, 0.40, 0.45, 0.50, 0.54, 0.58 |
| Coal | 6.00 | 70.00 | 70.0 | 5.0 | 7.0 | 1, 1.2, 1.4, 1.6 | 0.6, 0.8, 1.0, 1.2, 1.4, 1.6 | 0.13, 0.18, 0.22, 0.26, 0.31, 0.35 |
| Stratum | Type | Statistics of Experimental Results | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coal | Borehole depth (m) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.20 | 1.20 | 1.20 | 1.20 | 1.20 | 1.20 |
| Charge specifications | C1 | C2 | C3 | C4 | C5 | C6 | C1 | C2 | C3 | C4 | C5 | C6 | |
| Filling height (m) | 0.87 | 0.82 | 0.78 | 0.74 | 0.69 | 0.65 | 1.07 | 1.02 | 0.98 | 0.94 | 0.89 | 0.85 | |
| Statistical volume (m3) | 2.54 | 4.28 | 5.55 | 6.36 | 7.32 | 8.11 | 2.32 | 3.79 | 4.38 | 6.52 | 7.73 | 8.77 | |
| Specific charge (kg∙m−3) | 0.24 | 0.19 | 0.18 | 0.19 | 0.19 | 0.20 | 0.26 | 0.21 | 0.23 | 0.18 | 0.18 | 0.18 | |
| Borehole depth (m) | 1.40 | 1.40 | 1.40 | 1.40 | 1.40 | 1.40 | 1.60 | 1.60 | 1.60 | 1.60 | 1.60 | 1.60 | |
| Charge specifications | C1 | C2 | C3 | C4 | C5 | C6 | C1 | C2 | C3 | C4 | C5 | C6 | |
| Filling height (m) | 1.27 | 1.22 | 1.18 | 1.14 | 1.09 | 1.05 | 1.47 | 1.42 | 1.38 | 1.34 | 1.29 | 1.25 | |
| Statistical volume (m3) | -- | 2.80 | 4.09 | 5.27 | 7.08 | 8.30 | -- | -- | 3.34 | 4.73 | 6.54 | 7.47 | |
| Specific charge (kg∙m−3) | -- | 0.29 | 0.24 | 0.23 | 0.20 | 0.19 | -- | -- | 0.30 | 0.25 | 0.21 | 0.21 | |
| Rock | Borehole depth (m) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.20 | 1.20 | 1.20 | 1.20 | 1.20 | 1.20 |
| Charge specifications | R1 | R2 | R3 | R4 | R5 | R6 | R1 | R2 | R3 | R4 | R5 | R6 | |
| Filling height (m) | 0.65 | 0.60 | 0.56 | 0.52 | 0.47 | 0.43 | 0.85 | 0.80 | 0.76 | 0.72 | 0.67 | 0.63 | |
| Statistical volume (m3) | 3.65 | 4.74 | 5.93 | 6.77 | 7.06 | 6.28 | 4.93 | 5.74 | 6.45 | 7.19 | 7.76 | 8.35 | |
| Specific charge (kg∙m−3) | 0.44 | 0.38 | 0.34 | 0.33 | 0.34 | 0.41 | 0.32 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | |
| Borehole depth (m) | 1.40 | 1.40 | 1.40 | 1.40 | 1.40 | 1.40 | 1.60 | 1.60 | 1.60 | 1.60 | 1.60 | 1.60 | |
| Charge specifications | R1 | R2 | R3 | R4 | R5 | R6 | R1 | R2 | R3 | R4 | R5 | R6 | |
| Filling height (m) | 1.05 | 1.00 | 0.96 | 0.92 | 0.87 | 0.83 | 1.25 | 1.20 | 1.16 | 1.12 | 1.07 | 1.03 | |
| Statistical volume (m3) | 4.58 | 5.51 | 6.00 | 6.56 | 7.10 | 7.85 | 4.22 | 5.45 | 5.82 | 6.97 | 5.84 | 7.04 | |
| Specific charge (kg∙m−3) | 0.35 | 0.33 | 0.33 | 0.34 | 0.34 | 0.33 | 0.38 | 0.33 | 0.34 | 0.32 | 0.41 | 0.37 | |
| Type | (mm) | Rock | Coal | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scheme | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | |
| 1 | 170 | 14.9 | 4.5 | 9.0 | 1.0 | 6.4 | 2 | 0.715 | 0.8 | 2.17 |
| 2 | 170 | 14.9 | 4.5 | 8.5 | 1.5 | 6.4 | 2 | 0.715 | 0.8 | 2.17 |
| 3 | 170 | 14 | 4.5 | 8.0 | 2.0 | 6.4 | 2 | 0.715 | 0.8 | 2.17 |
| 4 | 170 | 14 | 4.5 | 7.5 | 2.5 | 6.4 | 2 | 0.715 | 0.8 | 2.17 |
| 5 | 170 | 14 | 4.5 | 7.0 | 3.0 | 6.4 | 2 | 0.715 | 0.8 | 2.17 |
| 6 | 170 | 14 | 4.5 | 8.0 | 2.0 | 6.4 | 2.5 | 0.715 | 0.8 | 1.67 |
| 7 | 170 | 14 | 4.5 | 8.0 | 2.0 | 6.4 | 3.0 | 0.715 | 0.8 | 1.17 |
| 8 | 170 | 14 | 4.5 | 8.0 | 2.0 | 6.4 | 3.5 | 0.715 | 0.8 | 0.67 |
| Parameter | Value | Parameter | Value | Parameter | Value | |||
|---|---|---|---|---|---|---|---|---|
| Rock | Coal | Rock | Coal | Rock | Coal | |||
| (kg⋅m−3) | 2300 | 1310 | 0.0368 | 0.0481 | 0.68 | 0.61 | ||
| (GPa) | 11.76 | 1.93 | 0.53 | 0.35 | 0.01 | 0.0105 | ||
| (MPa) | 34.4 | 21.07 | 0.7 | 0.45 | 2.1 | 1.6 | ||
| (GPa) | 34.20 | 8.90 | 0.0942 | 0.0944 | 0.637 | 0.61 | ||
| 1.22 | 1.68 | 0.21 | 0.18 | 0.6 | 0.45 | |||
| 1.22 | 1.68 | (GPa) | 34.19 | 8.90 | 1.61 | 1.25 | ||
| (MPa) | 22.93 | 14.05 | (GPa) | 41.72 | 14.96 | |||
| 0.0325 | 0.0487 | (GPa) | 8.77 | 9.14 | ||||
| PCJ | BETA | SIGY | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (kg/m3) | (m/s) | (GPa) | (Pa) | (GPa) | (GPa) | (J/m3) | |||||||
| 1100 | 4200 | 5.15 | 0 | 0 | 0 | 0 | 49.46 | 1.89 | 3.9077 | 1.118 | 0.33 | 2.668 × 109 | 1 |
| Scheme | Type | (m) | (mm) | (m) | (°) | (m) | (m) | (kg∙m−3) | (m) | (m) | (m) | (m) | Charge Form | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Up | Down | |||||||||||||
| Rock | 14 | 170 | 14.9 | 70 | 6.0 | 4.5 | 0.57 | 4.5 | 2 | 8.4 | 0 | 4.0 | coupled | |
| S-1 | Coal | 6 | 170 | 6.4 | 70 | 6.0 | 4.5 | 0.18 | 2.0 | 0.8 | 0.715 | 2.17 | 4.0 | interval |
| S-2 | Coal | 6 | 170 | 6.4 | 70 | 6.0 | 4.5 | 0.18 | 2.5 | 0.8 | 0.715 | 1.67 | 4.0 | interval |
| S-3 | Coal | 6 | 170 | 6.4 | 70 | 6.0 | 4.5 | 0.18 | 3.0 | 0.8 | 0.715 | 1.17 | 4.0 | interval |
| S-4 | Coal | 6 | 170 | 6.4 | 70 | 6.0 | 4.5 | 0.18 | 3.5 | 0.8 | 0.715 | 0.67 | 4.0 | interval |
| Scheme | Type | (m) | (mm) | (m) | (°) | (m) | (m) | (kg∙m−3) | (m) | (m) | (m) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Up | Down | ||||||||||||
| Rock | 14 | 170 | 14.9 | 70 | 6.0 | 4.5 | 0.57 | 4.5 | 2 | 8.4 | 0 | 4.0 | |
| T-1 | Coal | 6 | 170 | 6.4 | 70 | 6.0 | 4.5 | 0.18 | 2.5 | 0.8 | 0.715 | 1.67 | 4.0 |
| T-2 | Coal | 6 | 170 | 6.4 | 70 | 6.0 | 4.5 | 0.18 | 3.0 | 0.8 | 0.715 | 1.17 | 4.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, A.; Fei, H.; Yan, Y.; Liu, Y.; Bao, S.; Guo, J. Study on the Charge Structure Optimization for Coal–Rock Mixed Blasting and Separate Mining in Open-Pit Mine with High Benches. Appl. Sci. 2025, 15, 4521. https://doi.org/10.3390/app15084521
Jiang A, Fei H, Yan Y, Liu Y, Bao S, Guo J. Study on the Charge Structure Optimization for Coal–Rock Mixed Blasting and Separate Mining in Open-Pit Mine with High Benches. Applied Sciences. 2025; 15(8):4521. https://doi.org/10.3390/app15084521
Chicago/Turabian StyleJiang, Anjun, Honglu Fei, Yu Yan, Yanyu Liu, Shijie Bao, and Jian Guo. 2025. "Study on the Charge Structure Optimization for Coal–Rock Mixed Blasting and Separate Mining in Open-Pit Mine with High Benches" Applied Sciences 15, no. 8: 4521. https://doi.org/10.3390/app15084521
APA StyleJiang, A., Fei, H., Yan, Y., Liu, Y., Bao, S., & Guo, J. (2025). Study on the Charge Structure Optimization for Coal–Rock Mixed Blasting and Separate Mining in Open-Pit Mine with High Benches. Applied Sciences, 15(8), 4521. https://doi.org/10.3390/app15084521






