Spatio-Temporal Deformation Prediction of Large Landslides in the Three Gorges Reservoir Area Based on Time-Series Graph Convolutional Network Model

Abstract

The displacement–time curve of a landslide serves as a critical indicator of its movement state, with precise deformation prediction being essential for effective disaster early warning. While numerous studies have employed machine learning techniques to predict deformation at individual monitoring points, they often overlook the spatial correlations among monitoring points arranged along horizontal and vertical cross-sections. To address this limitation, this paper employs the Temporal Graph Convolutional Network (T-GCN) model, which integrates the strengths of Graph Convolutional Networks (GCNs) and Gated Recurrent Units (GRUs). The GCN captured spatial correlations among monitoring points, while the GRU modeled the temporal dynamics of displacement. The T-GCN model was applied to predict the spatio-temporal deformation of the Dawuchang landslide in the Three Gorges Reservoir area. Experimental results demonstrated that the T-GCN model effectively predicted the spatio-temporal displacement of landslides, offering a robust approach for landslide monitoring and early warning systems. The model also incorporated the temporal influence of external factors, such as rainfall and reservoir water levels, enhancing prediction accuracy and providing valuable insights for future research in landslide deformation forecasting.

1. Introduction

Landslide deformation prediction is crucial in landslide monitoring and early warning. An accurate and effective deformation prediction model provides a scientific basis for early warnings, enabling rapid and timely alerts before abrupt landslide failures, thereby minimizing disaster-induced losses [1,2]. Existing landslide forecasting models can be broadly categorized into empirical, statistical, and nonlinear theoretical [3]. Empirical models primarily rely on landslide formation mechanisms and long-term observational data for predictions and include the Saito [4] and Voight [5] models, which typically analyze the mathematical relationship between landslide velocity and the critical failure time. These models can effectively reflect the overall evolution trend in landslides; however, their predictive accuracy and applicability are constrained by their inability to account for the influence of external environmental factors such as rainfall. Statistical models use long-term observational data to predict landslide deformation, including the autoregressive integrated moving average [6,7,8] and the traditional GM (1, 1) [9,10,11] models. While these models effectively capture the historical evolutionary trends in landslide deformation, their predictive capability is limited by a lack of in-depth landslide physical mechanism modelling. Consequently, they struggle to accurately describe the dynamic influence of external environmental factors (e.g., rainfall and reservoir water levels) on the deformation process. With the rapid advancements in computer science and technology, nonlinear theoretical models have gained widespread applications in landslide prediction [12]. Machine learning models, owing to their strong data-driven capabilities and nonlinear mapping properties, can integrate multiple influencing factors such as rainfall and reservoir water levels. This overcomes the limitations of traditional empirical and statistical models in analyzing external factors, significantly enhancing the predictive performance of landslide deformation models [13,14,15,16,17,18,19,20,21]. Commonly used machine learning models include support vector machines [22,23], long short-term memory (LSTM) networks [24,25,26], and deep neural networks [27]. Moreover, researchers have proposed various improvements to machine learning models, such as optimizing hyperparameters using intelligent optimization algorithms or employing ensemble learning and hybrid modeling techniques to combine different machine learning models, thereby improving prediction accuracy and generalization performance [28,29,30]. Examples include the Genetic Algorithm (GA)-optimized Elman neural network [31], the least squares support vector machine (LSSVM) prediction method based on the particle swarm optimization (PSO) algorithm [32], and wavelet denoising (WD)-(GA)-LSSVM [33]. However, these studies primarily focus on the temporal characteristics of long-term landslide evolution without considering the inherent spatial correlations in the landslide sliding process.

Landslide deformation exhibits complex spatial correlations. Before experiencing overall instability and failure, a landslide typically undergoes a prolonged deformation evolution process [34]. Based on landslide dynamics and the initial failure location, landslides can be classified into four types: traction, thrust, translational, and composite landslides [35,36,37]. Thrust landslides are primarily driven by the development of tensile cracks in the upper slope, which induce the instability and initial sliding of the upper portion, subsequently pushing the lower section into motion. Translational landslides typically occur along relatively gentle sliding surfaces, where initial failure points are distributed across multiple locations on the sliding plane. These points slip simultaneously and gradually merge as deformation progresses. Traction landslides generally result from gradual instability caused by river erosion or artificial excavation at the slope’s base, triggering a bottom-up sliding process. Finally, composite landslides result from the combined effects of upper and lower initial failure zones [38,39,40]. Given these deformation characteristics, landslide sections exhibit a transmission effect, with adjacent areas exerting significant mutual influence. Therefore, spatial interactions between different sections should be considered in landslide deformation prediction.

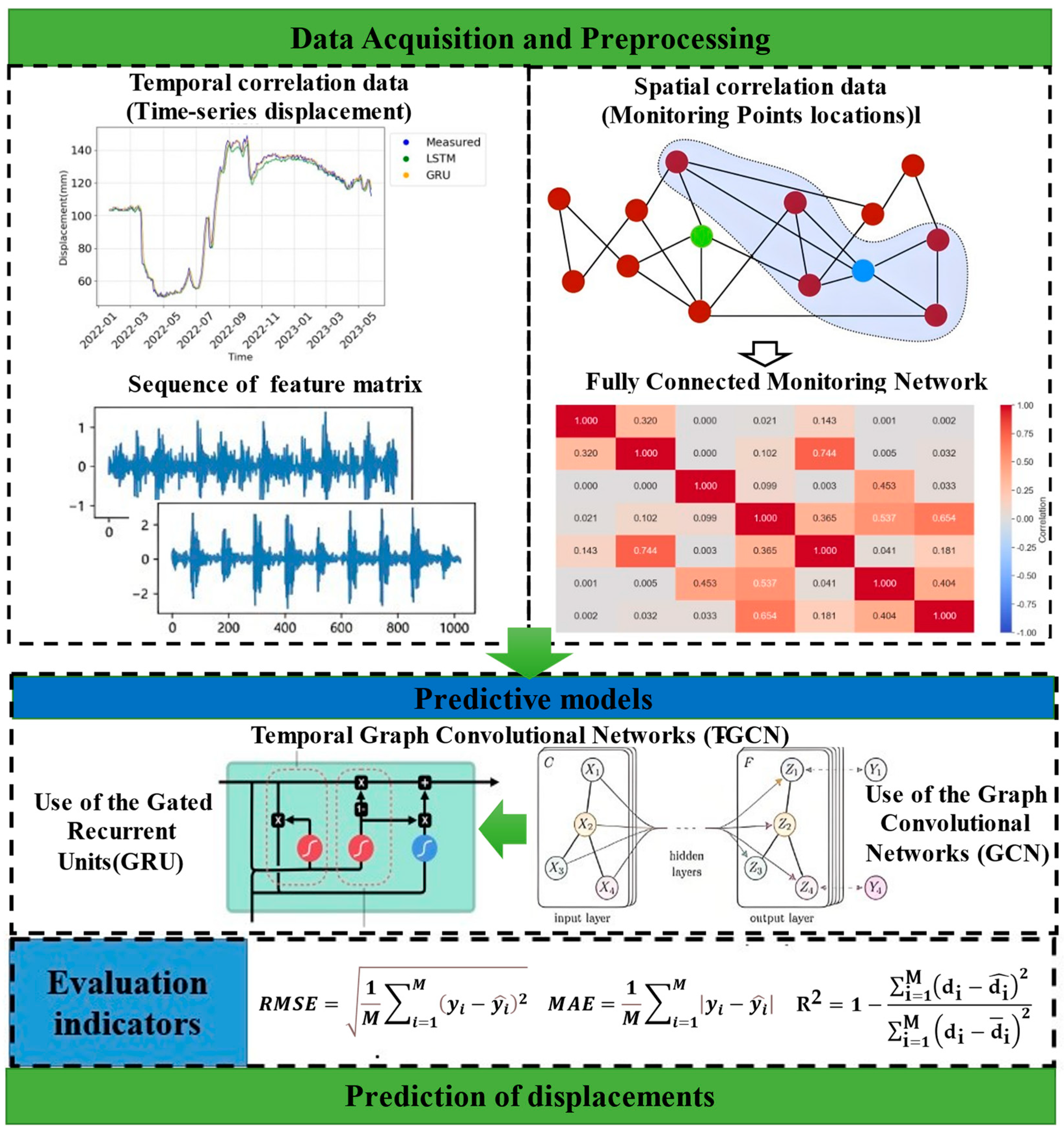
This study integrates GCN and GRU to model the spatio-temporal evolution of landslide deformation. The GRU architecture, characterized by its simplified structure, enables faster training compared to traditional LSTM models, while the GCN effectively captures the complex spatial dependencies among monitoring points—a critical aspect of landslide dynamics. Although transformer-based models were considered, their high computational cost and limited adaptability to graph-structured data rendered the T-GCN framework a more suitable and efficient choice. The temporal and spatial prediction method based on the T-GCN model of time-sequence Graph Convolutional Network used in this study can not only consider the spatial correlation of various parts of the landslide but also superimpose the temporal influence of external factors that induce landslide deformation to predict the displacement. The experimental results show that the deformation prediction model considering the spatio-temporal characteristics can be widely used in the time-series prediction of geological disasters with spatio-temporal attributes.

2. Case Study

2.1. Basic Characteristics of the Dawuchang Landslide

The Dawuchang landslide is located in Group 1 of Kaixia Village, Daxi Township, Wushan County, on the left bank of Cuokai Gorge, a tributary of the Yangtze River. It is a water-related landslide, with geographic coordinates of 109°41′23.19″ E and 30°58′59.19″ N, approximately 1.8 km from the river mouth. The left front boundary of the landslide is characterized by a microtopographic ridge, while the right boundary follows a natural erosion gully. The rear boundary is marked by a steep slope where bedrock transitions into fragmented stone soil, with an elevation ranging from 355 to 365 m. The front edge lies within the submerged zone of the Yangtze River water level. Based on cross-sectional measurements and previous data, the potential shear outlet is estimated to be at an elevation of approximately 130 m. A secondary shear outlet is located in the central part of the landslide at an elevation of 240–250 m. In plain view, the landslide exhibits a tongue-shaped morphology, extending approximately 860 m longitudinally and 330–370 m transversely. The rear scarp elevation ranges from 355 to 365 m, with a total area of approximately 30.1 × 10⁴ m². The average landslide thickness is 57 m, resulting in a total volume of approximately 1710 × 10⁴ m³. The primary sliding direction is 65°. This landslide is classified as an extremely large soil–rock mixed landslide, primarily induced by rainfall and reservoir water fluctuations. Currently, it is in a slow-creep deformation stage (Figure 1).

2.2. Deformation Monitoring Data of the Dawuchang Landslide

The primary monitoring parameters for the Dawuchang landslide include surface displacement, precipitation, reservoir water level, and macroscopic inspection data. Surface displacement is measured using an automated Global Navigation Satellite System (GNSS) monitoring method, with a total of six monitoring stations and one reference station arranged to form two longitudinal monitoring profiles. Precipitation is recorded using an automated rain gauge station, with one rain monitoring point installed in the middle to rear section of the landslide. Reservoir water level variations are documented through data collection. The basic information on the various monitoring points within the landslide is presented in

Table 1. Monitoring site data for the Dawuchang landslide.

Monitoring Content	Monitoring Method	Monitoring Point Number	Profile	Location	Elevation (m)
Landslide surface absolute displacement	Real-time GNSS	WS0101		On stable bedrock	204
		WS0102	I–I′	Upper middle of the profile	240
		WS0103	I–I′	Middle of profile	185
		WS0104	I–I′	Lower middle of profile	240
		WS0105	II–II′	Upper middle of profile	190
		WS0106	II–II′	Middle of profile	240
		WS0107	II–II′	Lower middle of profile	185
Rainfall	Real-time rain gauge	YLJWS01	II–II′	Upper middle section	192

, while the monitoring network layout is illustrated in Figure 1.

Since June 2016, the cumulative horizontal displacement duration curve of six automated GNSS surface displacement monitoring points (WS0102–WS0107) on the landslide body of Dawuchang is shown in Figure 1, and the cumulative horizontal displacement duration curve and the cumulative vertical displacement duration curve is shown in Figure 2 and Figure 3. It can be seen that the cumulative horizontal displacement of each monitoring point since 2016 is 9.4–121.9 mm, and the cumulative vertical displacement is −33.8–−10.4 mm. The average horizontal displacement rate was 0.1–1.5 mm/month, and the average vertical displacement rate was −0.4–−0.1 mm/month. From the perspective of space, there is obvious deformation in the right posterior edge of the landslide, and the deformation in other parts is small or there is no obvious deformation, which is a sliding landslide. In terms of time, the landslide of Dawuchang has obvious deformation from July to October every year, which is consistent with the rapid decline of reservoir water level or extreme rainfall events (heavy rainfall, continuous rainfall). It can be seen that the main influencing factor of landslide deformation in Dawuchang is rainfall, followed by reservoir water level. Especially in the case of rainfall, the groundwater permeability pressure rises sharply, and a large amount of surface water converges to the landslide area, which further reduces the shear strength of the soil in the slide zone and leads to the aggravation of landslide deformation.

Predicting the overall deformation trend in landslides in advance and judging their stable state is helpful to reduce the risks that landslides may bring to human life, property, and infrastructure. The monitoring data should first be pre-processed before making the forecast. In this paper, the method based on 3σ detection combined with Isolation Forest is used to eliminate the abnormal values existing in the daily monitoring data series. Subsequently, for the vacancy data, the KNN algorithm is used for interpolation. This method can make use of historical proximity observations to compensate for time-series breakpoints. In interpolation, only the displacement variable is used to measure the distance, and the data are standardized before interpolation to unify the dimension and improve the accuracy of interpolation in order to further improve the stability of the algorithm and provide a reliable time-series data basis for subsequent landslide warning and mechanism analysis.

3. Methodology

To simultaneously capture both spatial and temporal features from landslide monitoring data, we adopted the T-GCN model, which integrated a Graph Convolutional Network (GCN) and a Gated Recurrent Unit (GRU) [41,42] (Figure 4). The specific computational process is described in Equations (1)–(4), where $f\left(X_t,A\right)$ represents the spatial features input to the Recurrent Neural Network layer at time step t. The parameters W and b denote the weight and bias values during training, respectively; $\ast$ represents element-wise multiplication; and the function tanh is the hyperbolic tangent function, ensuring that the hidden state values remain within the range [−1, 1].

$$u_t=\sigma (W_u\left[f\left(X_t,A\right),h_{t-1}\right]+b_u),$$

(1)

$$r_t=\sigma (W_r\left[f\left(X_t,A\right),h_{t-1}\right]+b_r),$$

(2)

$$\tilde{h}=tanh(W\left[f\left(X_t,A\right),{(r_t\ast h}_{t-1})\right]+b),$$

(3)

$$h_t=u_t\ast h_{t-1}+\left(1-u_t\right)\ast \tilde{h}.$$

(4)

3.1. Spatial Correlation Analysis Method

The GCN model is highly effective in capturing spatial relationships in non-Euclidean structures and learning representative features for each node within a graph [43,44]. Therefore, we extracted spatial features by monitoring different sections of the landslide. This process was described using Equation (5):

$$F^{\left(of\right)}=h(A,F^{\left(if\right)}),$$

(5)

where $\mathrm{A}\in R^{N\times N}$ represents the adjacency matrix of a graph containing N nodes, and $F^{\left(if\right)}\in R^{N\times d_{if}}$ and $F^{\left(of\right)}\in R^{N\times d_{of}}$ represent the input feature matrix with dimension $d_{if}$ and the output feature matrix with dimension $d_{of}$, respectively.

3.2. Temporal Correlation Prediction Method

3.2.1. LSTM Model

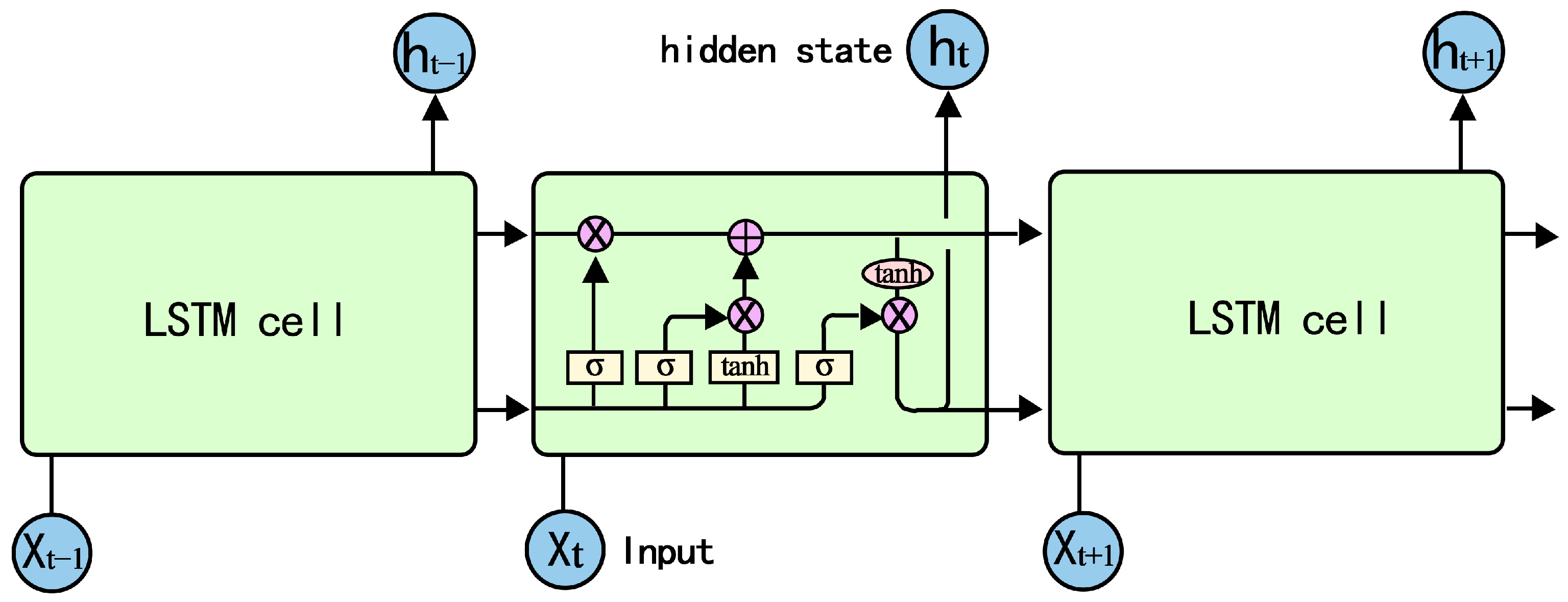
The LSTM network [45] is a deep learning method designed for sequential data. It can deeply mine crucial hidden information in time-series data and effectively capture long-term dependencies, making it highly sensitive to temporal changes. Therefore, we used the LSTM model to extract temporal features from landslide displacement monitoring data.

LSTM introduces a memory cell, which can store and access information, and controls the flow of information through a gating mechanism. The key components of LSTM include the input, forget, and output gates (Figure 5).

• Forget Gate

The first step in LSTM is to determine which information to forget from the cell state, which is determined by a sigmoid layer known as the “forget gate”. The forget gate takes the previous hidden state $h_{t-1}$ and the current input $x_t$ as inputs and outputs a value between 0 and 1. A value of 1 means “completely retain this value”, while a value of 0 means “completely forget this value”.

The computation of the forget gate was given by Equation (6):

$$f_t=\sigma \left(W_f·\left[h_{t-1},x_t\right]\right)+b_f.$$

(6)

2.

Input Gate

The second step determined which information to store in the cell state and consisted of two parts. First, a sigmoid layer, known as the “input gate”, decided which data must be updated. Then, a $\tan h$ layer created a vector ${\tilde{C}}_t$ of new candidate values that were added to the cell state. These two parts were then combined to update the cell state.

The computation of the input gate was given by Equations (7) and (8):

$$i_t=\sigma \left(W_i·\left[h_{t-1},x_t\right]\right)+b_i,$$

(7)

$${\tilde{C}}_t=\tan h\left(W_c·\left[h_{t-1},x_t\right]\right)+b_c,$$

(8)

The combination of the forget and input gates was given by Equation (9):

$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t.$$

(9)

3.

Output Gate

Finally, output information was determined, which was based on a filtered cell state.

• The computation of the output gate was given by Equations (10) and (11):

$$o_t=\sigma \left(W_o·\left[h_{t-1},x_t\right]\right)+b_o,$$

(10)

$$h_t=o_t\ast \mathit{tan}h\left(C_t\right),$$

(11)

where $h_{t-1}$ is the output from the previous layer; $x_t$ is the input vector; $\sigma$ is the sigmoid function; $W_f$ is the coefficient matrix for $f_t$ and $i_t$; $b_f$ is the bias for $f_t$; $b_i$ is the bias for $i_t$; $W_c$ is the coefficient matrix for ${\tilde{C}}_t$; $b_c$ is the bias for ${\tilde{C}}_t$; $C_{t-1}$ is the memory from the previous block; and $C_t$ is the memory from the current block.

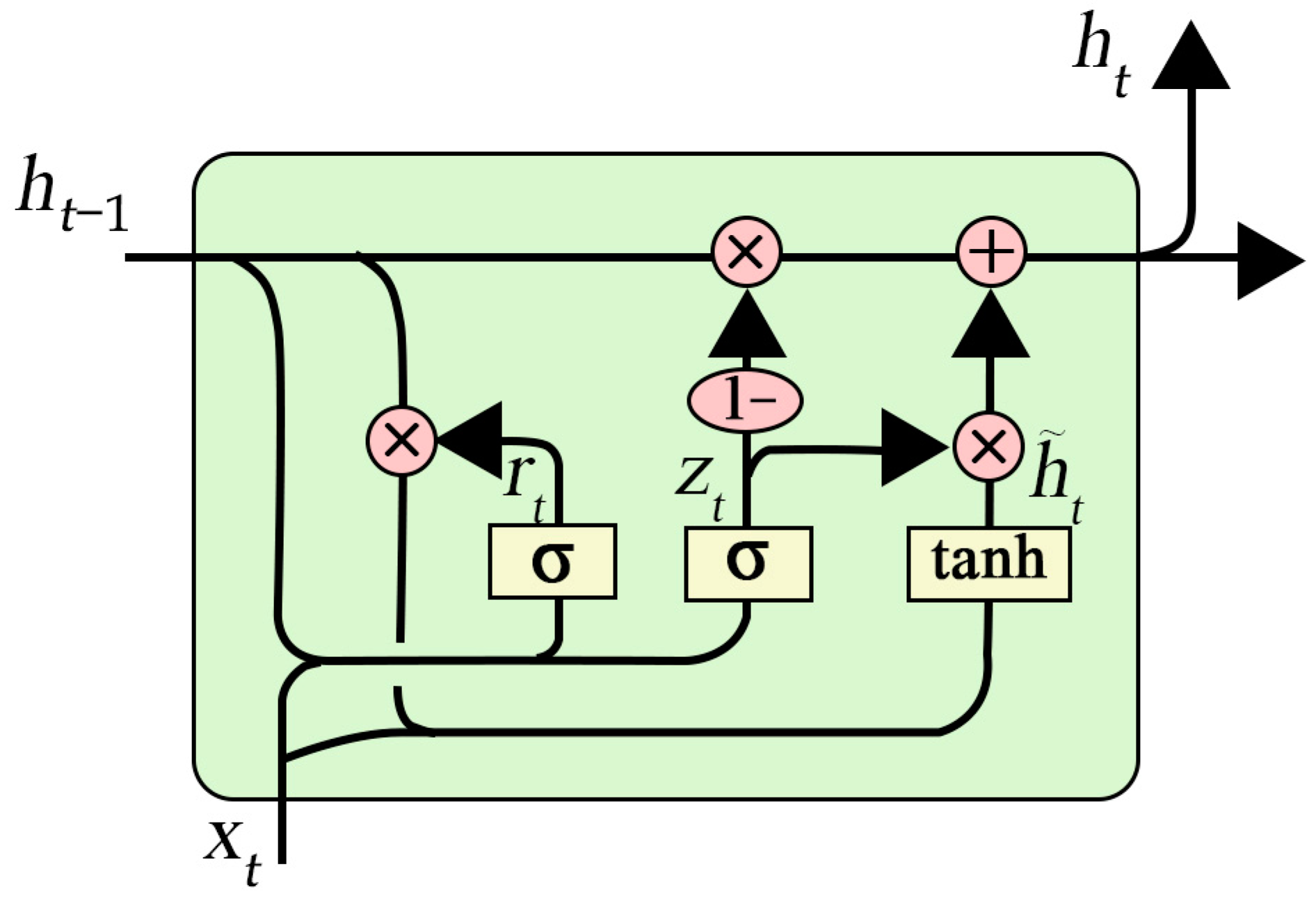
3.2.2. GRU Model

The GRU [46] is a type of Recurrent Neural Network (RNN). Like the LSTM, it was introduced to address issues such as long-term memory retention and the vanishing gradient problem in backpropagation. GRU simplifies the LSTM structure by reducing the number of gates from three (input, forget, and output gates) to two (reset and update gates) and merges the cell and hidden states. This design aimed to reduce complexity and computational resource requirements while preserving the ability to capture long-term dependencies. Compared to LSTM, which uses three gates, GRU uses two gates to regulate the flow and manage long-term memory retention, has fewer parameters, and trains faster (Figure 6).

For each time step t, the computation process of the GRU was as follows: the update gate ($z_t$) was computed as shown in Equation (12).

$$z_t=\sigma \left(W_Z·\left[h_{t-1},x_t\right]\right),$$

(12)

where $W_Z$ is the weight for the update gate; $\sigma$ is the sigmoid function; $h_{t-1}$ is the hidden state from the previous time step; and $x_t$ is the input at the current time step.

The reset gate ($r_t$) was computed as shown in Equation (13):

$$r_t=\sigma \left(W_r·\left[h_{t-1},x_t\right]\right),$$

(13)

where $W_r$ is the weight for the reset gate.

The candidate hidden state (${\tilde{h}}_t$) was computed as shown in Equation (14):

$${\tilde{h}}_t=\tan h\left(W·\left[r_t\ast h_{t-1},x_t\right]\right),$$

(14)

where W represents the weights of the hidden layer, and * denotes element-wise multiplication. This step applied the reset gate to the previous hidden state to determine how the new input $x_t$ will influence the candidate hidden state.

The hidden state at the current time step$x_t$ was calculated as shown in Equation (15):

$$h_t=\left(1-z_t\right)\ast h_{t-1}+z_t\ast {\tilde{h}}_t,$$

(15)

This step combines the previous hidden and current candidate hidden states to generate the current hidden state. The update gate $z_t$ determines how much of the previous hidden state $h_{t-1}$ to retain and how much of the new candidate hidden state ${\tilde{h}}_t$ to incorporate.

3.3. The Gaussian Similarity Function

The Gaussian similarity function is often used to measure the similarity between two vectors, and its expression is shown in Equation (16) [47]. where $\omega \left(i,j\right)$ represents the weight of the edge connecting nodes $v_i$ and $v_j$, indicating the spatial correlation between two monitoring points. The value $\omega \left(i,j\right)$ is larger, indicating stronger spatial correlation between the monitoring points.

$$\omega \left(i,j\right)=exp\left(-{‖v_i-v_j‖}^2/2{\sigma }^2\right),$$

(16)

3.4. Model Evaluation Metrics

To assess the predictive capability of the model for displacement monitoring data, four evaluation metrics—Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), R-squared (R²), and Efficiency Index—were used to measure the prediction performance of the T-GCN model [48,49]. Our evaluation uses standard metrics (RMSE, MAE, and R²) consistent with landslide prediction literature, enabling direct comparison with existing methods. The innovation lies in applying these metrics to assess spatio-temporal performance across interconnected monitoring points, extending their conventional single-point temporal usage.

(1)

Root Mean Squared Error (RMSE):

$$RMSE=\sqrt{{\displaystyle \frac{1}{M}}{\sum }_{i=1}^M{\left(y_i-\widehat{y_{\dot{i}}}\right)}^2},$$

(17)

(2)

Mean Absolute Error (MAE):

$$MAE={\displaystyle \frac{1}{M}}{\sum }_{i=1}^M\left|y_i-\widehat{y_{\dot{i}}}\right|,$$

(18)

where M represents the number of time samples, and $y_i$ and $\widehat{y_{\dot{i}}}$ denote the actual and predicted values, respectively.

(3)

R-squared (R²)

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{M}}{\left({\mathrm{d}}_{\mathrm{i}}-\widehat{{\mathrm{d}}_{\mathrm{i}}}\right)}^2}{{\sum }_{\mathrm{i}=1}^{\mathrm{M}}{\left({\mathrm{d}}_{\mathrm{i}}-{\overline{\mathrm{d}}}_{\mathrm{i}}\right)}^2}},$$

(19)

(4)

Efficiency Metrics

A standard metric for evaluating model efficiency is time complexity. In this study, the time taken for model training and prediction was measured to assess model efficiency. Specifically, RMSE, MAE, and R² were used to evaluate the prediction accuracy, with smaller values indicating better prediction performance. A shorter training and prediction time was considered more efficient.

4. Prediction Accuracy and Efficiency Comparison Experiment

Horizontal displacement was predicted, and two sets of comparative experiments were designed. The first group of experiments focused on the accuracy and efficiency of local slope displacement prediction, comparing the time-series prediction results of two models, LSTM and GRU. Based on the results from the first group, the model with better prediction accuracy was selected for the second group of experiments. This second group considered the overall spatial correlation of the landslide to construct the T-GCN deep learning prediction model. This model was then compared with the deep learning prediction method of T-GCN augmented by external influencing factors.

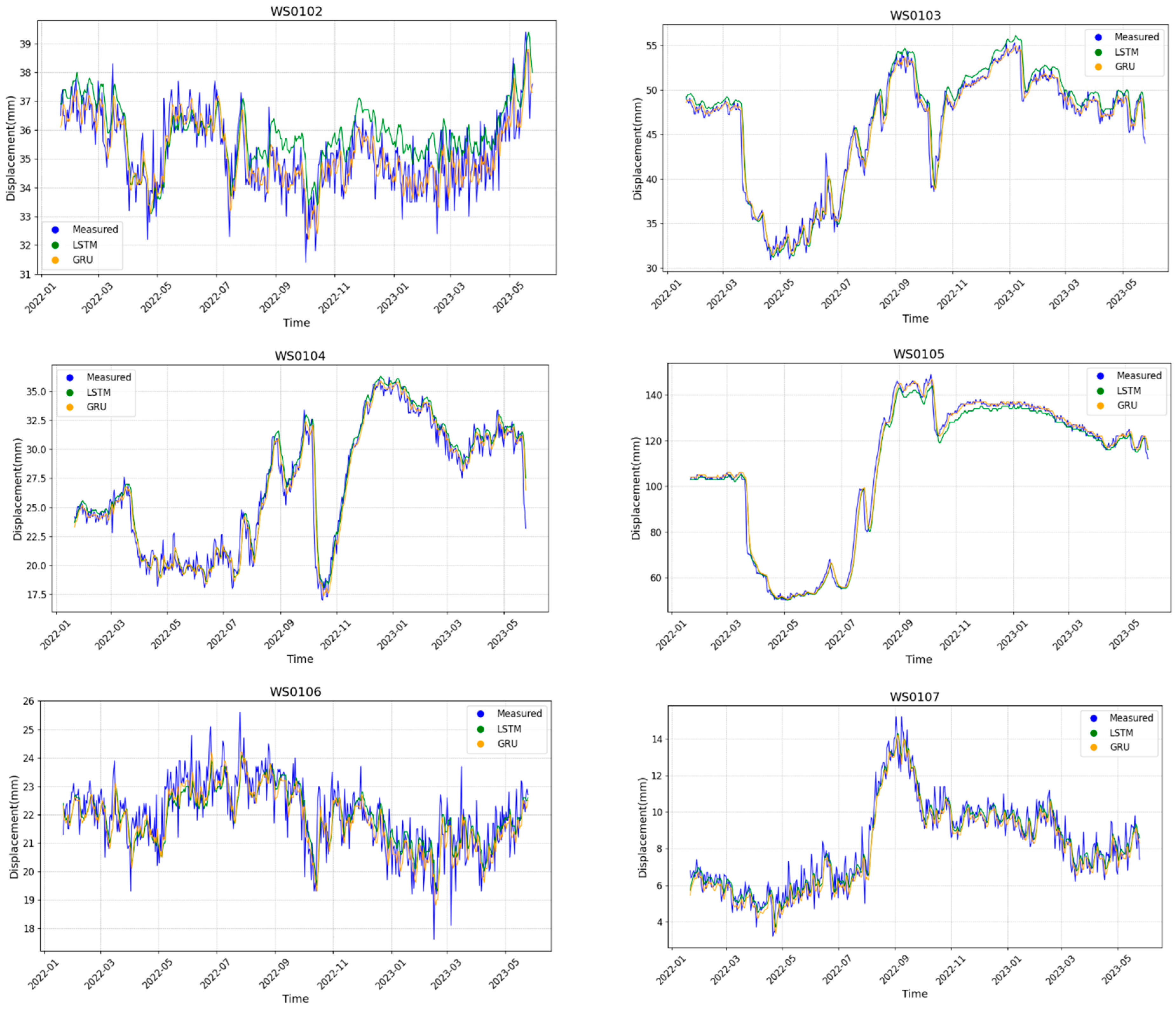
The first group of experiments used displacement deformation time-series data from six monitoring points on the Dawuchang landslide to build the prediction model. The dataset was divided into training and testing sets in an 8:2 ratio. The strategy involved using the displacement data from the previous 12 days to predict the displacement for the next 3 days. The specific prediction results from different sensors at the six monitoring points in the test set are shown in Figure 7 and

Table 2. Displacement prediction accuracy of the GRU model and the LSTM model.

Metric	Model	WS0102	WS0103	WS0104	WS0105	WS0106	WS0107
RMSE (mm)	LSTM	1.167	1.912	1.546	5.062	0.933	0.849
	GRU	0.909	1.561	1.441	4.343	0.915	0.880
MAE (mm)	LSTM	0.945	1.370	1.013	3.348	0.722	0.665
	GRU	0.716	1.025	0.975	2.443	0.709	0.685
R2	LSTM	0.175	0.915	0.916	0.974	0.402	0.871
	GRU	0.501	0.943	0.927	0.981	0.425	0.861

.

The two prediction models exhibited a good agreement with the actual deformation trends at the six monitoring points; however, both exhibited certain latency. The LSTM model at the WS0107 monitoring point was slightly more accurate in terms of RMSE, MAE, and R² indicators, while for other monitoring points, the GRU model predictions were closer to the actual values, as shown in the Table 2, bold data indicate the model with the best performance of the evaluation indicators. The modeling times for the LSTM and GRU models were 222.745 and 146.036 s, respectively. Regarding efficiency, the GRU model significantly reduced the modeling time at seven monitoring points, decreasing the time by 34% compared to the LSTM model. Therefore, in the second group of experiments, the GRU model was selected for training in time-series feature learning.

To further assess the effectiveness of the proposed approach, we systematically compared the T-GCN model with several classical methods, including Autoregressive Integrated Moving Average (ARIMA), Support Vector Regression (SVR), and physics-based models. The results showed that traditional statistical models like ARIMA struggled to capture the nonlinear responses of landslide deformation to external drivers, resulting in significantly higher prediction errors. While simpler machine learning models (e.g., SVR and Random Forest) outperformed ARIMA to some extent, they still exhibited considerable errors, particularly at complex deformation sites such as WS0105. Physics-based models performed well under steady-state creep conditions but were unable to characterize sudden or transient deformation events. In contrast, the T-GCN model consistently demonstrated superior predictive accuracy, effectively capturing rapid deformation episodes, spatially correlated displacements (e.g., WS0103–WS0104), and deformation responses driven by rainfall and reservoir fluctuations. Nonetheless, these advantages come with the trade-off of higher computational costs and greater data demands compared to conventional approaches.

In the second group of experiments, the spatial correlation between monitoring points was first analyzed. A complete graph of the Dawuchang landslide deformation monitoring network was established, and a Gaussian similarity matrix was created. Next, a feature matrix for the time-series deformation data was constructed to predict deep learning deformation using the T-GCN. Additionally, considering the lag effects of rainfall and reservoir water levels, external influencing factors were incorporated by selecting a time window t+m to replace the original attribute values corresponding to time t, and the deep learning prediction method of T-GCN with external influencing factors was employed.

First, the spatial correlation between monitoring points was calculated. Using the displacement monitoring data from the six GNSS monitoring points deployed on the Dawuchang landslide, a complete graph of deformation monitoring was constructed as G = (V, E, W), where V = {V₁, V₂, …, V_N} represented the nodes of the graph (GNSS monitoring points), and N was the number of monitoring points (Figure 8). A 7 × 7 Gaussian similarity matrix A based on spatial proximity was established to represent the spatial correlation between monitoring points. The values in this matrix were computed using the Gaussian similarity function. The computed spatial relationship matrix is represented as A_w. The results are shown in

Table 3. Side weightings of the Wushan County, Dawuchang landslide.

${\mathit{w}}_{\mathit{i}\mathit{j}}$	WS0102	WS0103	WS0104	WS0105	WS0106	WS0107
WS0102	1	0.243558	0.000771	0.588207	0.192366	0.000749
WS0103	0.243558	1	0.108942	0.125867	0.537414	0.078851
WS0104	0.000771	0.108942	1	0.000354	0.037876	0.525511
WS0105	0.588207	0.125867	0.000354	1	0.310246	0.001102
WS0106	0.192366	0.537414	0.037876	0.310246	1	0.096883
WS0107	0.000749	0.078851	0.525511	0.001102	0.096883	1

.

Next, the time-series deformation data characterization matrix X_t (7 × 2524) was constructed for all monitoring points. Each row represented a monitoring point, and the corresponding column was the amount of time-series deformation at that point. Using the sliding window method, the displacement data were divided by a window size of 15 to form training and test sets of size 15 × 7 × 2005 and 15 × 7 × 490.

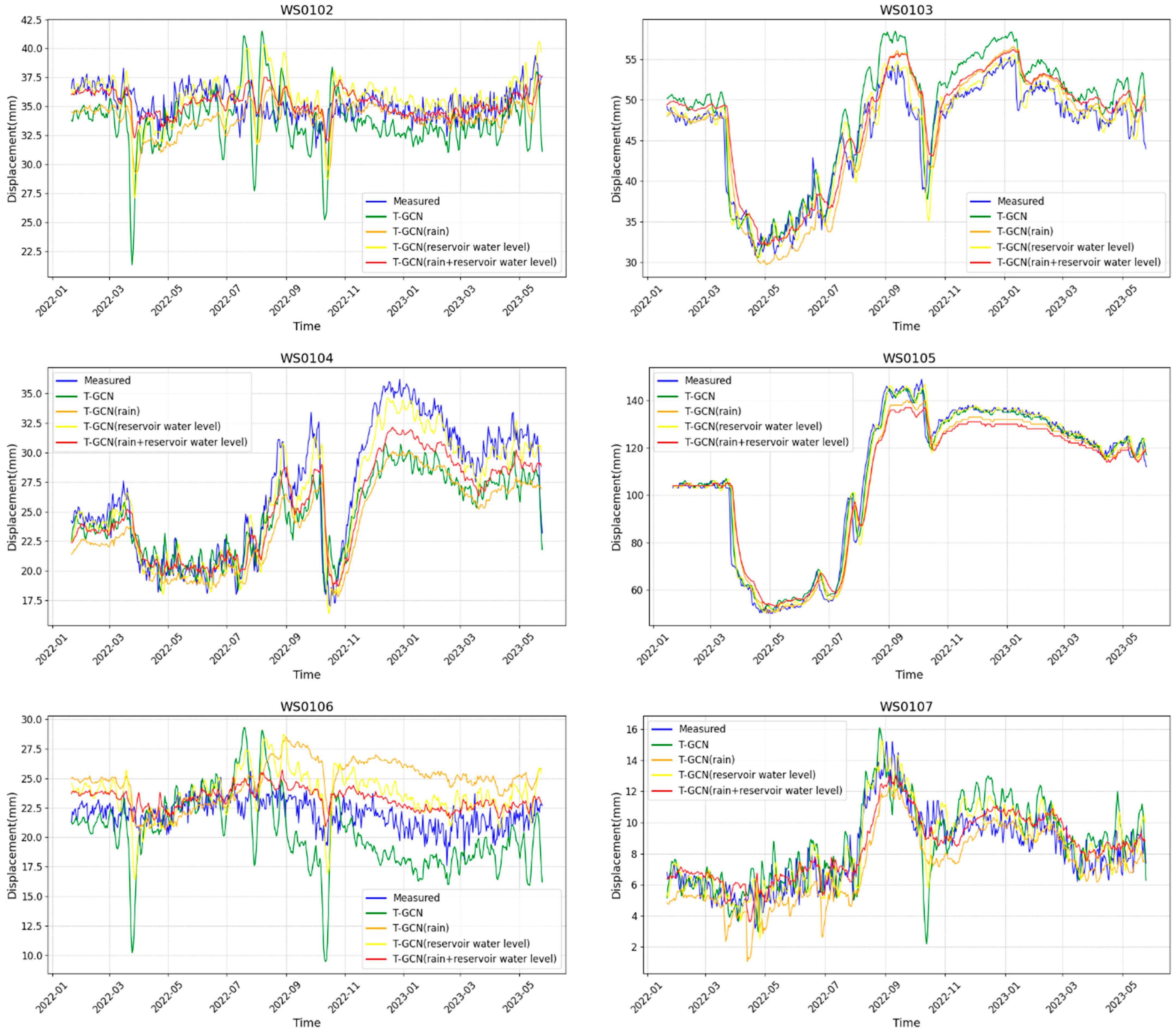
The third step was model training while comparing the deformation prediction results considering rainfall and reservoir level lags and without superimposing external influences. When considering external influences when constructing the feature matrix, the external influences were selected in the window t + m instead of the attribute value corresponding to the original moment t, and m was the empirical value. During the training process of the T-GCN model, the three hyperparameters of the learning rate, the number of training rounds (epoch), and the number of batch samples (batch size) were optimized using Bayesian optimization, and the final results were determined for the landslide prediction of Dawuchang. The overall T-GCN prediction model for the Dawuchang landslide was learning rate = 0.001, batch size = 128, and number of training rounds = 200. In addition, the number of hidden layer units was set to 64, and the ReLU activation function was used in the GCN module with the Adam optimizer and MSE least loss function. The specific prediction results on the set are shown in Figure 9 and

Table 4. Displacement prediction accuracy of T-GCN model with different external influencing factors.

Metric	Model	WS0102	WS0103	WS0104	WS0105	WS0106	WS0107
RMSE (mm)	T-GCN	2.917	3.558	3.256	4.542	2.984	1.725
	T-GCN (rain)	2.001	2.405	3.775	6.383	3.713	1.429
	T-GCN (reservoir water level)	1.922	1.754	1.591	4.132	2.371	1.184
	T-GCN (rain + reservoir water level)	1.407	2.299	2.795	6.621	1.801	1.170
MAE (mm)	T-GCN	2.223	2.995	2.679	2.763	2.285	1.330
	T-GCN (rain)	1.575	1.727	3.245	4.506	3.208	1.101
	T-GCN (reservoir water level)	1.356	1.202	1.235	2.294	1.988	0.937
	T-GCN (rain + reservoir water level)	1.093	1.630	2.328	4.945	1.544	0.914
R2	T-GCN	−4.138	0.704	0.979	−5.115	0.467	−4.138
	T-GCN (rain)	−1.450	0.865	0.501	0.959	−8.467	0.636
	T-GCN (reservoir water level)	−1.262	0.928	0.911	0.983	−2.861	0.750
	T-GCN (rain + reservoir water level)	−0.212	0.877	0.956	−1.228	0.756	−0.212
Modeling Time (s)	T-GCN	184.245	184.245	184.245	184.245	184.245	184.245
	T-GCN (rain)	247.297	247.297	247.297	247.297	247.297	247.297
	T-GCN (reservoir water level)	196.010	196.010	196.010	196.010	196.010	196.010
	T-GCN (rain + reservoir water level)	235.985	235.985	235.985	235.985	235.985	235.985

.

5. Discussion

Based on the prediction results from Table 3 and Table 4, the models exhibited high degrees of agreement with actual values. For the six monitoring points, the MAE and RMSE values were within 6.7 mm, with minimums of 0.665 and 0.709 mm. The performance of R² is not consistent at each monitoring point, except WS0102; the R² value of other monitoring points is higher than 0.4, generally between 0.7 and 1, respectively. The shortest modeling time was 146.036 s, and the longest was 247.297 s. When comparing the two models under the RNN category, the GRU model outperformed the LSTM model in terms of accuracy. The RMSE values decreased by 22.1%, 18.4%, 6.8%, 14.2%, and 1.9%, while the MAE values decreased by approximately 24.2%, 25.2%, 3.8%, 27%, and 1.8%. The value of R² increases by about 12.4%. Additionally, modeling time was reduced by 34.4%. This suggested that GRU effectively maintained long-term dependencies and learned from extended time-series features. By simplifying the LSTM structure from three gates to two, GRU reduced parameters, accelerated convergence, and shortened runtime. During practical training, it improved prediction accuracy while accelerating the prediction process.

Although the T-GCN model considered global spatial factors, the overall prediction accuracy did not significantly improve compared to the time-series network model, which only considered temporal dependencies. The introduction of adjacency matrices and feature matrices increased computational complexity and extended prediction time. This might be due to inaccuracies in calculating spatial distances or the simple Gaussian function used in the adjacency matrix, which may not adequately capture local deformations in landslides. During the construction of the complete graph for the monitoring points, the latitude and longitude of devices were converted to distances using the Vincenty algorithm, assuming the Earth is an ellipsoid, which could lead to discrepancies with actual distances. Furthermore, the method only estimated spatial correlation based on distance, which may not be precise, as landslides may experience local deformations that require additional constraints in the complete graph.

Considering the lag effects of external factors such as rainfall and reservoir water levels, the T-GCN model prediction accuracy notably improved. RMSE values for the six monitoring points decreased by 51.8%, 50.7%, 51.1%, 9%, 39.6%, and 32.2%, respectively, and MAE values decreased by 50.8%, 59.9%, 53.9%, 17.0%, 32.4%, and 17.0%, respectively. However, the response of different monitoring points to external factors varied. At WS0102, WS0106, and WS0107, the inclusion of both rainfall and reservoir water level improved prediction accuracy, while WS0103, WS0104, and WS0105 showed better results with only the reservoir water level as an external factor.

This discrepancy could be due to the selection of the time window being based on qualitative analysis of the Dawuchang landslide’s response to fluctuations in reservoir water levels and rainfall. However, the response to external factors, such as rapid reservoir water level drops or continuous heavy rainfall, is dynamic. Using a constant lag value may not accurately reflect these dynamic changes, and variations in the lag effects based on rainfall intensity and duration or changes in reservoir water levels are significant. Additionally, landslide deformation is a complex process influenced by both internal and external factors. Internal factors such as rock properties, slope geology, and internal structure were not considered in this study, which limited the comprehensiveness of the model. Future research should focus on accurately capturing the dynamic lag effects of external factors and their influence on landslide displacement, with the aim of improving predictive accuracy.

6. Conclusions

This study compared two landslide time-series network prediction models and four spatio-temporal prediction models that incorporated overall spatial correlations using data from six GNSS monitoring points on the Dawuchang landslide. The main conclusions were as follows:

• The GRU model outperformed the LSTM model in terms of prediction accuracy (RMSE and MAE) at five monitoring points, with a 34.4% decrease in modeling time. By simplifying the LSTM structure, GRU reduced the number of parameters, improving training efficiency and prediction accuracy.
• The T-GCN model, which considered spatial correlations, exhibited limited improvement in prediction accuracy. The added complexity in computation and prediction time was not justified by the marginal accuracy gains. This may be because of inaccuracies in spatial distance calculations or the insufficiency of the Gaussian function to capture local deformation effects in landslides.
• The inclusion of external factors (rainfall and reservoir water levels) significantly enhanced the T-GCN model prediction accuracy. The RMSE and MAE values decreased substantially at all monitoring points; however, the response to external factors varied among monitoring points. Future research should focus on refining the dynamic lag representation of external factors to improve the model’s predictive power.