Hybrid Improved PSO Algorithm for Soil Property Parameter Estimation
Abstract
1. Introduction
2. Off-Road Wheel–Soil Interaction Force Model
3. Improvement of the PSO Algorithm
3.1. Traditional PSO Algorithm
3.2. Improvement Strategies for the PSO Algorithm
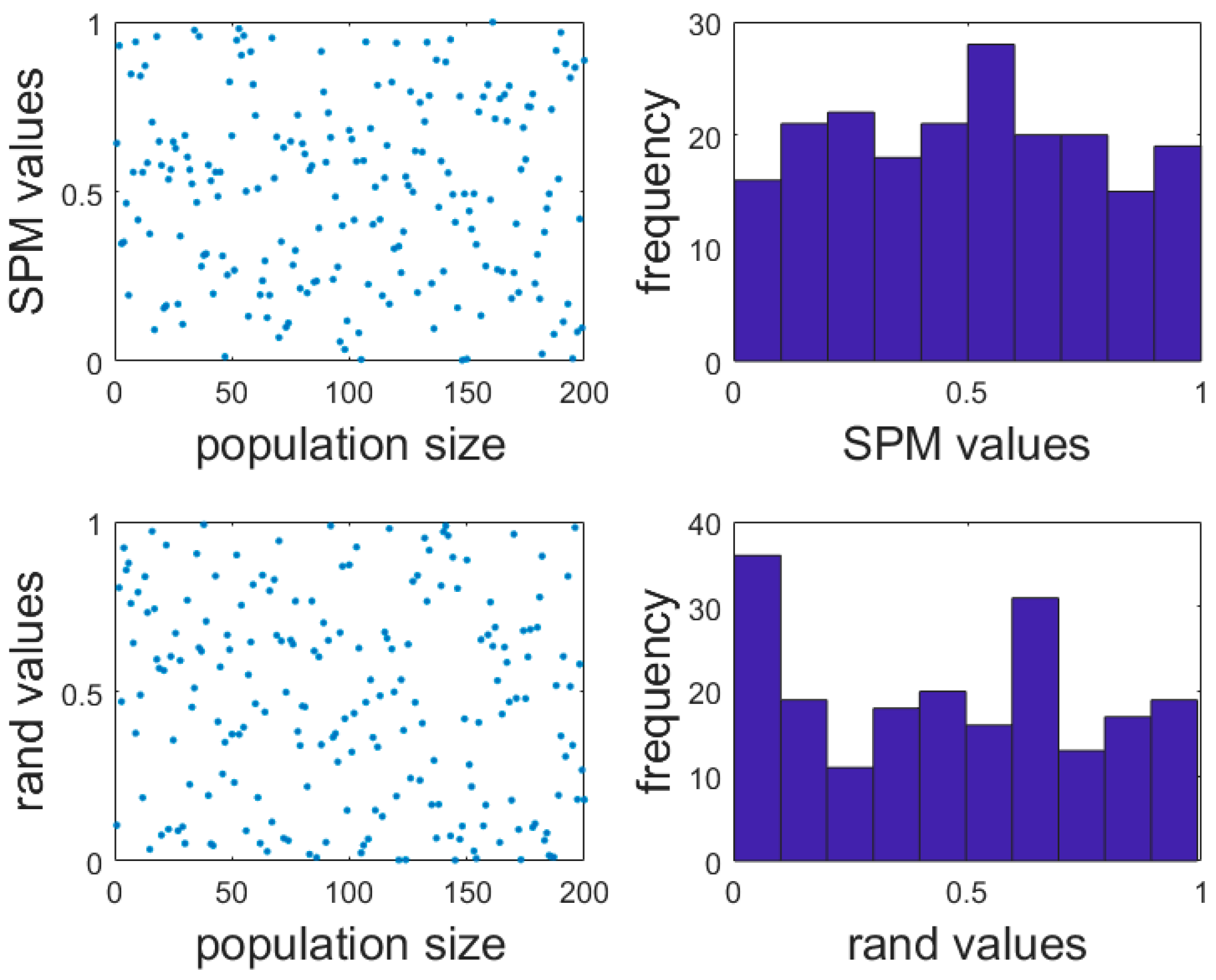
3.3. Improvement in Initialization of Positions
3.4. Inertia Weight of the PSO Algorithm
3.5. Improvement in Position Update
| Algorithm 1. Computational Process of the PSO-EDO Algorithm | |
| 01 | Set the maximum number of iterations K, the number of particles N, and the upper and lower bounds of the particle positions and the dimensions D of the fitness function. |
| 02 | Initialize the population based on SPM chaotic mapping. |
| 03 | Initialize the population X, compute the fitness of each individual, and sort them. |
| 04 | Initialize the memoryless matrix Y as Y = X. |
| 05 | for |
| 06 | Identify the top three optimal individuals and compute the guiding solution using Equation (24). |
| 07 | Calculate , , , and σ using Equations (22) and (23). |
| 08 | for |
| 09 | if |
| 10 | Update the position using Equation (21). |
| 11 | else |
| 12 | Update the position using Equation (25). |
| 13 | end if |
| 14 | |
| 15 | if |
| 16 | |
| 17 | end if |
| 18 | end for |
| 19 | Re-sort based on the fitness of the particle positions in matrix . |
| 20 | end for |
| 21 | Output the average optimal value, optimal value, standard deviation, and average computation time. |
3.6. Comparative Test Experiment
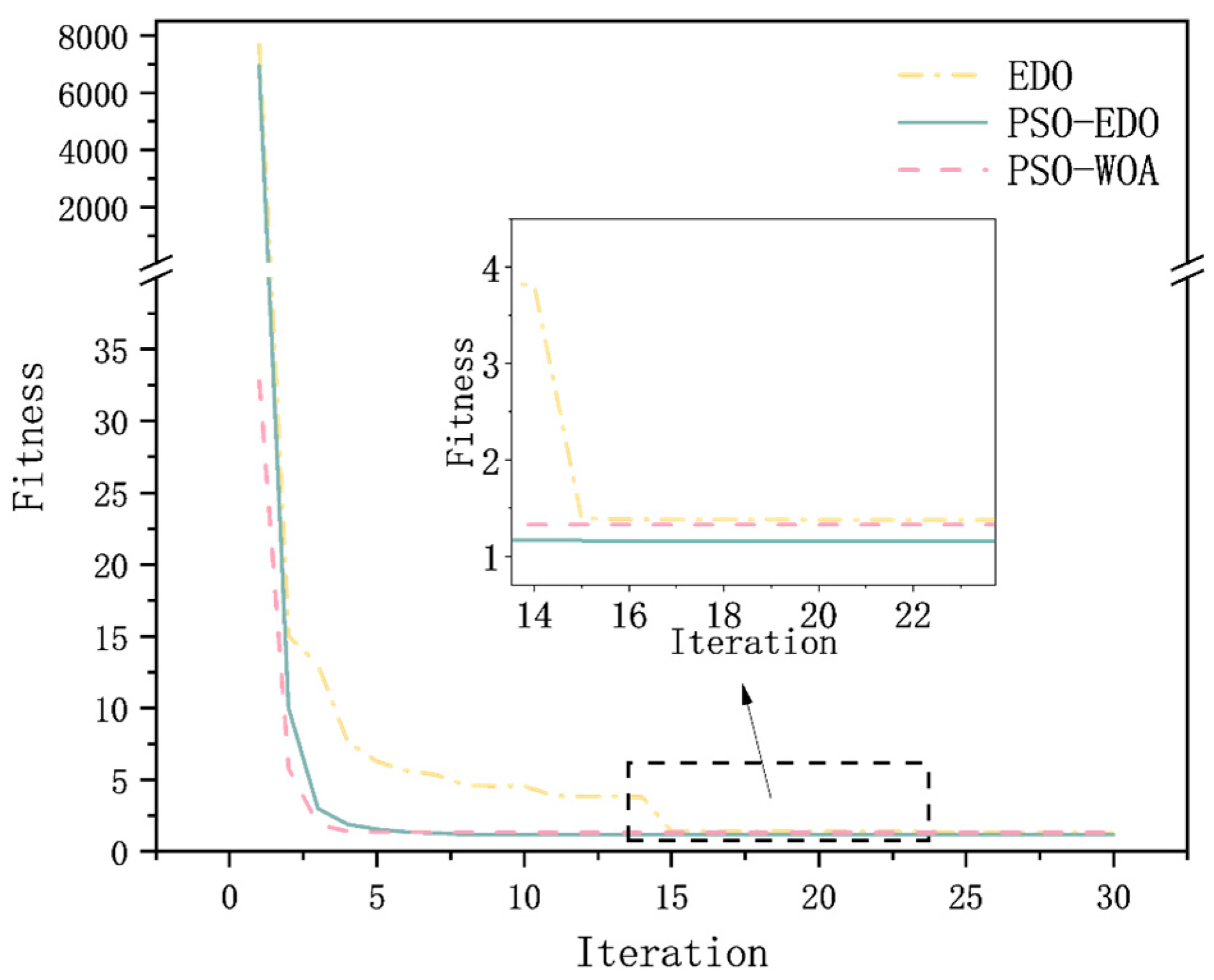
4. Simulation Results and Discussion
4.1. Simulation Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lyasko, M. Slip sinkage effect in soil–vehicle mechanics. J. Terramech. 2010, 47, 21–31. [Google Scholar] [CrossRef]
- Lopez-Arreguin, A.J.R.; Gundlach, B.; Stoll, E. Do lunar rover wheels sink equally on Earth and Moon? Results Phys. 2019, 15, 102617. [Google Scholar] [CrossRef]
- Bekker, M.G. Theory of Land Locomotion: The Mechanics of Vehicle Mobility; University of Michigan Press: Ann Arbor, MI, USA, 1956. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
- Reece, A.R. Principles of soil-vehicle mechanics. Proc. Inst. Mech. Eng. 1965, 180, 45–66. [Google Scholar] [CrossRef]
- Janosi, Z.; Hanamoto, B. The analytical determination of drawbar pull as a function of slip for tracked vehicle in deformable soils. In Mechanics of Soil-Vehicle Systems: Proceedings of the 1st International Conference on the Mechanics of Soil-Vehicle Systems; Edizioni Minerva Tecnica: Torino, Italy, 1961; Volume 41. [Google Scholar]
- Yin, Z.; Wang, F.; Tang, T.; Luo, Q.; Xiang, K. The forest fire prediction in JiangXi province based on PSO-GA-BP neural network. In Proceedings of the 2nd Workshop on Advanced Research and Technology in Industry Applications (WARTIA 2016), Dalian, China, 14–15 May 2016; Atlantis Press: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Song, Q.; Yu, L.; Li, S.; Hanajima, N.; Zhang, X.; Pu, R.; Rajamohan, V. A Review of Intelligent Ground Vehicle Technologies. Int. J. Intell. Syst. 2023, 2023, 1–20. [Google Scholar]
- Bansal, S.; Aggarwal, H. A multiobjective optimization of task workflow scheduling using hybridization of PSO and WOA algorithms in cloud-fog computing. Cluster Comput. 2024, 27, 10921–10952. [Google Scholar] [CrossRef]
- Zhu, H.; Ding, Y. Optimized Dynamic Collision Avoidance Algorithm for USV Path Planning. Sensors 2023, 23, 4567. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Lei, Z.; An, C. Research on battery thermal management system based on liquid cooling plate with honeycomb-like flow channel. Appl. Therm. Eng. 2023, 218, 119324. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Chen, Y.; Xie, L.; Wang, H.; Salem, O. SPSO-Pruner: A Network Pruning Method on YOLOv5 for Fewer Categories Scenarios. Neural Process. Lett. 2023, 55, 789–812. [Google Scholar] [CrossRef]
- Uzer, M.S.; Inan, O. Application of improved hybrid whale optimization algorithm to optimization problems. Neural Comput. Appl. 2023, 35, 12345–12360. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Ding, L.; Deng, Z.; Gao, H.; Tao, J.; Iagnemma, K.D.; Liu, G. Interaction mechanics model for rigid driving wheels of planetary rovers moving on sandy terrain with consideration of multiple physical effects. J. Field Robot. 2014, 32, 827–859. [Google Scholar] [CrossRef]
- Du, Y.; Gao, J.; Jiang, L.; Zhang, Y. Development and numerical validation of an improved prediction model for wheel-soil interaction under multiple operating conditions. J. Terramech. 2018, 79, 1–21. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the ICNN’95—IEEE International Conference on Neural Networks (ICNN), Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Altay, E.V.; Alatas, B. Bird swarm algorithms with chaotic mapping. Artif. Intell. Rev. 2019, 53, 1373–1414. [Google Scholar] [CrossRef]
- Ban, D.H.; Lü, X.; Wang, X.Y. Computer Science; Hohai University: Nanjing, China, 2019. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation (CEC 1999), Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report; National University of Defense Technology: Changsha, China, 2017. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Sun, D.-B.; Di, Y.-Q.; Cui, H.-H. A real-time vehicle-terramechanics model for visual simulation. In Proceedings of the International Conference on Materials Engineering and Information Technology Applications (MEITA 2015), Guilin, China, 30–31 August 2015. [Google Scholar]



| Symbol | Definition | Unit |
|---|---|---|
| The angle formed between the line connecting any point on the contact surface to the wheel center and the vertical direction, serving as the independent variable in theoretical integration calculations | rad | |
| The angle between the line connecting the front contact point of the tire–soil interface to the wheel center and the vertical direction | rad | |
| The angle formed between the line connecting the rear contact point of the tire–soil interface to the wheel center and the vertical direction | rad | |
| The angular position on the contact surface where the normal stress reaches its peak value | rad | |
| The vertical deformation of soil at the front contact point of the tire–soil interface | m | |
| The vertical deformation of soil at the rear contact point of the tire–soil interface | m | |
| Wheel radius | m | |
| Wheel torque | N·m | |
| Traction force | N | |
| kPa | ||
| kPa | ||
| kPa | ||
| kPa |
| Function | Range | Dimension | Optimal Value |
|---|---|---|---|
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 |
| Function | Performance Metrics | PSO | SPSO | PSO-GA | PSO-WOA | EDO | PSO-EDO |
|---|---|---|---|---|---|---|---|
| F1 | Mean | 46.6667 | 18.4343 | 1.9908 × 108 | 779.8416 | 0 | 0 |
| Best | 2.5343 × 10−7 | 0.0585 | 6.9623 × 107 | 0.0537 | 0 | 0 | |
| Std | 50.7416 | 38.0227 | 4.8996 × 107 | 869.0725 | 0 | 0 | |
| Time (s) | 0.1930 | 0.1904 | 0.2640 | 0.1445 | 0.3424 | 0.2043 | |
| F2 | Mean | 6.7014 × 1034 | 3.3667 × 1032 | 6.9615 × 1042 | 5.92 × 104 | 0 | 0 |
| Best | 1.0001 × 1014 | 1887.8 | 1.0061 × 1034 | 6.46 × 10−10 | 0 | 0 | |
| Std | 2.5362 × 1035 | 1.8252 × 1033 | 2.5332 × 1043 | 3.18 × 105 | 0 | 0 | |
| Time (s) | 0.3217 | 0.3005 | 0.3639 | 0.2461 | 0.4775 | 0.3178 | |
| F3 | Mean | 726.5842 | 105.8248 | 2.6968 × 105 | 1.0566 | 29 | 23.4577 |
| Best | 16.6368 | 17.8986 | 8.9816 × 104 | 2.03 × 10−4 | 29 | 0.1445 | |
| Std | 2.5265 × 103 | 195.028 | 1.2390 × 105 | 1.2549 | 0 | 5.8286 | |
| Time (s) | 1.5197 | 1.483 | 1.5197 | 1.3997 | 1.5758 | 1.4501 | |
| F4 | Mean | 2.1070 | 0.094 | 18.3392 | 0.0744 | 8.8818 × 10−16 | 8.8818 × 10−16 |
| Best | 3.2920 × 10−11 | 0.0013 | 16.0595 | 2.59 × 10−4 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| Std | 1.6360 | 0.3153 | 0.9442 | 0.058 | 0 | 0 | |
| Time (s) | 0.2049 | 0.2164 | 0.2867 | 0.1869 | 0.4092 | 0.2431 | |
| F5 | Mean | 106.7421 | 45.9901 | 300.5527 | 0.6695 | 0 | 0 |
| Best | 53.7277 | 21.8909 | 245.1119 | 7.44 × 10−5 | 0 | 0 | |
| Std | 33.7884 | 14.8105 | 27.1314 | 2.3247 | 0 | 0 | |
| Time (s) | 0.2174 | 0.2243 | 0.2872 | 0.1638 | 0.4060 | 0.2425 | |
| F6 | Mean | 0.1170 | 0.012 | 198.0842 | 0.3537 | 0 | 0 |
| Best | 0 | 6.83 × 10−5 | 136.4232 | 0.0105 | 0 | 0 | |
| Std | 0.1870 | 0.0121 | 44.3387 | 0.2968 | 0 | 0 | |
| Time (s) | 1.5253 | 1.413 | 1.5829 | 1.4101 | 1.6735 | 1.4597 |
| Iteration | F1 | F2 | F3 | F4 | F5 | F6 |
|---|---|---|---|---|---|---|
| 1 | 6.39 × 108 | 4.58 × 1051 | 2.93 × 106 | 20.67 | 443.87 | 610.03 |
| 2 | 1.18 × 108 | 1.74 × 1047 | 3.31 × 105 | 7.84 | 123.95 | 305.93 |
| 3 | 1.72 × 107 | 2.09 × 1045 | 9.03 × 104 | 4.24 | 26.41 | 128.03 |
| 4 | 8471.73 | 3.02 × 1039 | 1007.56 | 2.01 | 1.65 | 115.90 |
| 5 | 362.42 | 9.04 × 1030 | 32.21 | 1.32 | 0.02 | 75.45 |
| 6 | 13.47 | 3.49 × 1027 | 23.72 | 0.15 | 0.00 | 46.28 |
| 7 | 0.03 | 2.23 × 1020 | 24.16 | 0.00 | 0.00 | 40.38 |
| 8 | 0.00 | 7.92 × 108 | 23.86 | 0.00 | 0.00 | 45.85 |
| 9 | 0.00 | 0.00 | 24.01 | 0.00 | 0.00 | 38.42 |
| 10 | 0.00 | 0.00 | 24.00 | 0.00 | 0.00 | 0.23 |
| 11 | 0.00 | 0.00 | 23.73 | 0.00 | 0.00 | 0.00 |
| 12 | 0.00 | 0.00 | 23.76 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 23.57 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 23.71 | 0.00 | 0.00 | 0.18 |
| 15 | 0.00 | 0.00 | 23.87 | 0.00 | 0.00 | 0.08 |
| Comparison Groups | Test Statistic | p-Value | Significance Conclusion |
|---|---|---|---|
| PSO-EDO vs. PSO | 0.0 | Significant difference | |
| PSO-EDO vs. SPSO | 271.0 | Significant difference | |
| PSO-EDO vs. PSO-GA | 226,060.0 | Significant difference | |
| PSO-EDO vs. PSO-WOA | 15,510.0 | Significant difference |
| Category | Vehicle | Parameters for Terrain | |||||
|---|---|---|---|---|---|---|---|
| Symbol | r | b | K | KP | c | n | φ |
| Unit | m | m | m | kPam−n | kPa | - | |
| Value | 0.2 | 0.1 | 0.025 | 1532.4 | 1 | 1.1 | 30 |
| Source | Direct Measurement | Plate Penetration Test | Calculated as | Triaxial Test | Empirical Fitting | Direct Shear Test | |
| Function | Performance Metrics | K [m] | KP [kPa·m−n] | c [kPa] | n | φ [°] | Time [s] |
|---|---|---|---|---|---|---|---|
| EDO | Global Best | 0.0232 | 1620.54 | 1.0267 | 1.345 | 29.46 | 2.2803 |
| Mean Best | 0.0232 | 1620.54 | 1.0267 | 1.345 | 30.85 | ||
| Mean Error | 7.32% | 5.75% | 2.67% | 22.27% | 2.81% | ||
| PSO-EDO | Global Best | 0.0232 | 1620.54 | 1.0267 | 1.345 | 30.85 | 1.9487 |
| Mean Best | 0.0232 | 1620.54 | 1.0267 | 1.345 | 30.85 | ||
| Mean Error | 7.32% | 5.75% | 2.67% | 22.27% | 2.81% | ||
| PSO-WOA | Global Best | 0.0232 | 1620.54 | 1.0267 | 1.345 | 30.85 | 2.3773 |
| Mean Best | 0.0232 | 1620.54 | 1.0267 | 1.345 | 30.85 | ||
| Mean Error | 7.32% | 5.75% | 2.67% | 22.27% | 2.81% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Shi, A.; Shi, Y.; Zhang, T.; Qu, C.; Ye, L. Hybrid Improved PSO Algorithm for Soil Property Parameter Estimation. Appl. Sci. 2025, 15, 4451. https://doi.org/10.3390/app15084451
Li M, Shi A, Shi Y, Zhang T, Qu C, Ye L. Hybrid Improved PSO Algorithm for Soil Property Parameter Estimation. Applied Sciences. 2025; 15(8):4451. https://doi.org/10.3390/app15084451
Chicago/Turabian StyleLi, Mude, Aiping Shi, Yefan Shi, Tao Zhang, Cu Qu, and Lihua Ye. 2025. "Hybrid Improved PSO Algorithm for Soil Property Parameter Estimation" Applied Sciences 15, no. 8: 4451. https://doi.org/10.3390/app15084451
APA StyleLi, M., Shi, A., Shi, Y., Zhang, T., Qu, C., & Ye, L. (2025). Hybrid Improved PSO Algorithm for Soil Property Parameter Estimation. Applied Sciences, 15(8), 4451. https://doi.org/10.3390/app15084451





