Numerical Study of the Mechanical Properties and Failure Mechanisms of Shale Under Different Loading Conditions
Abstract
1. Introduction
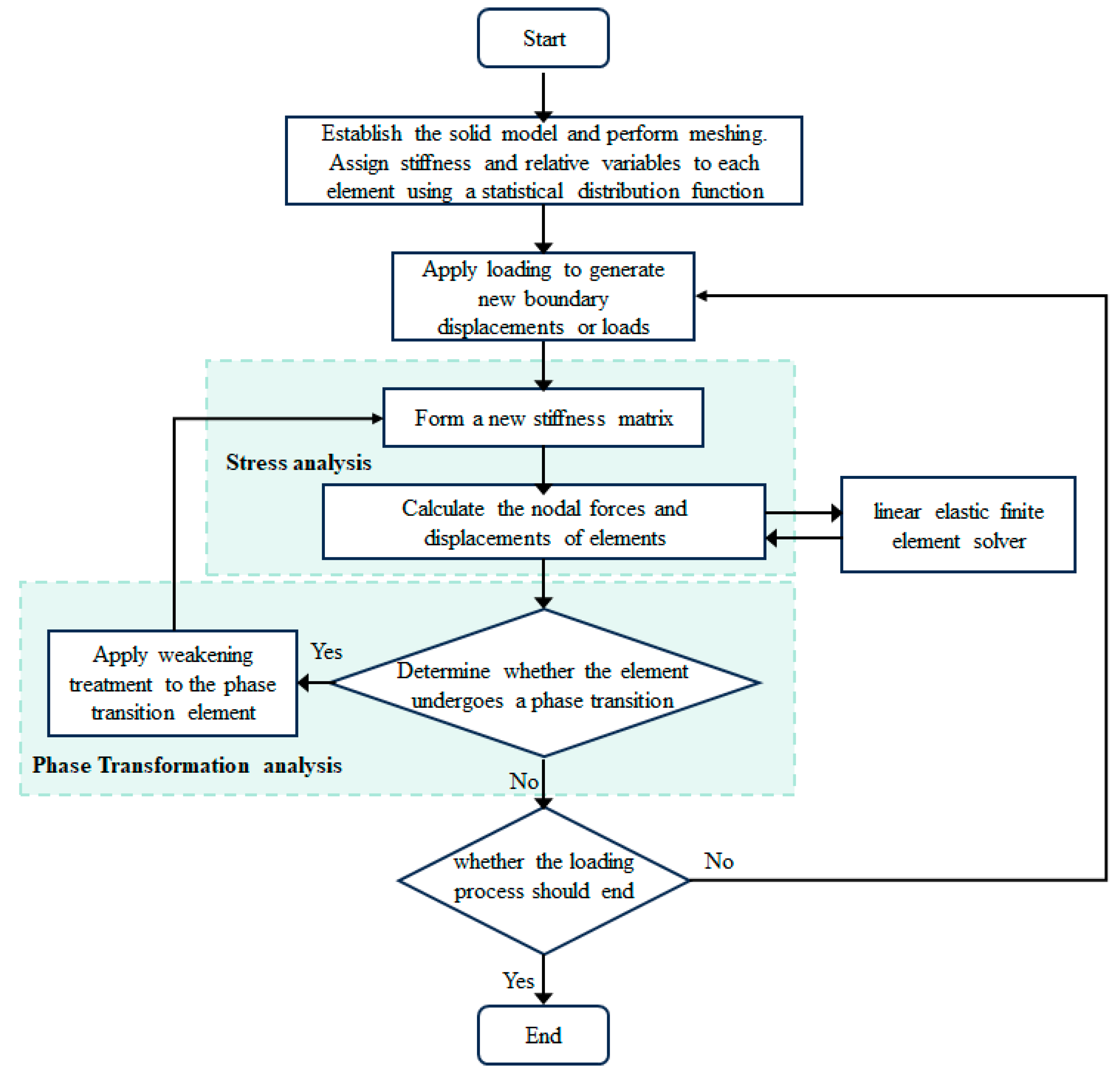
2. Numerical Simulation Method
2.1. RFPA
2.2. Numerical Model
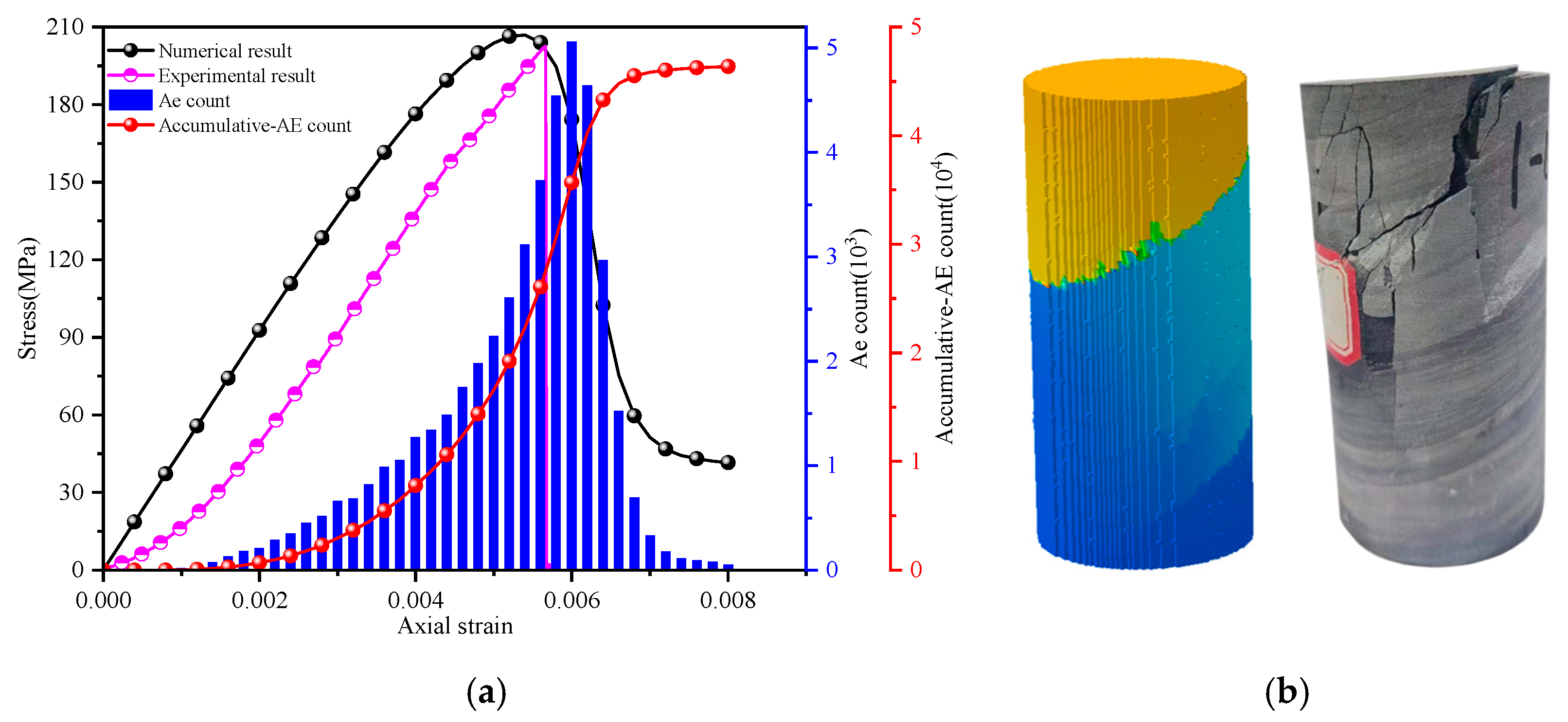
2.3. Model Validation
3. Simulation Results and Analysis
3.1. Uniaxial Loading Conditions
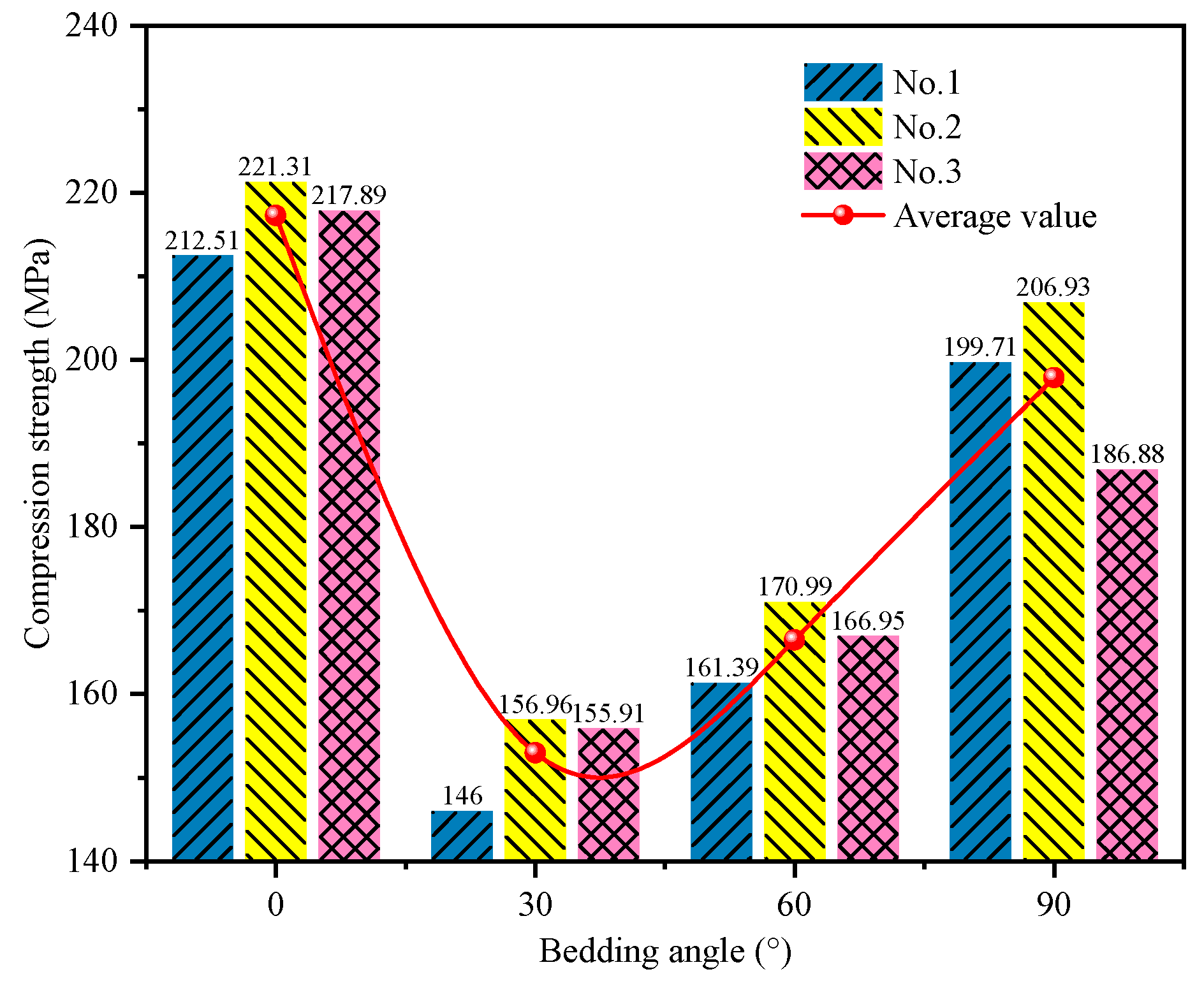
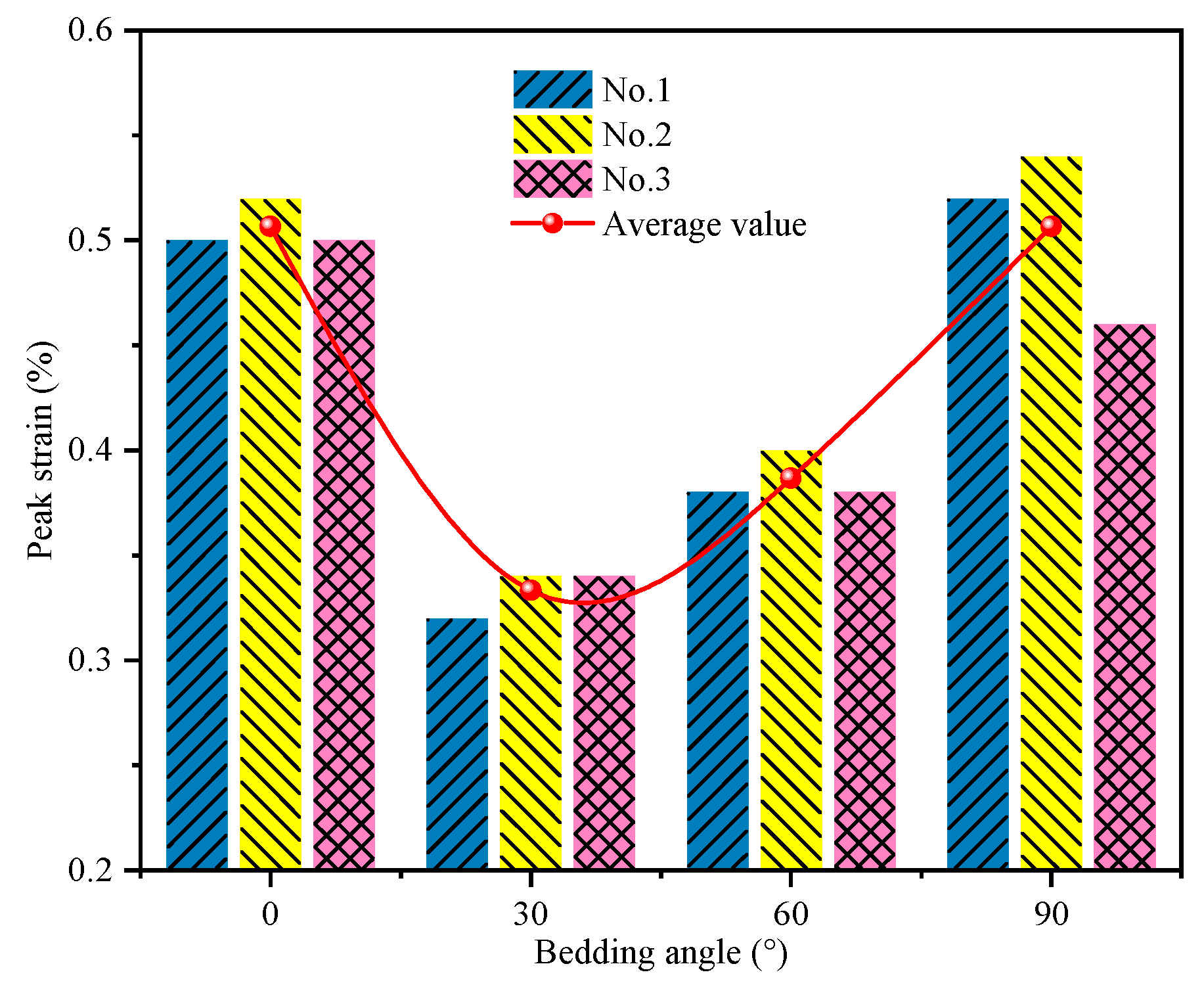
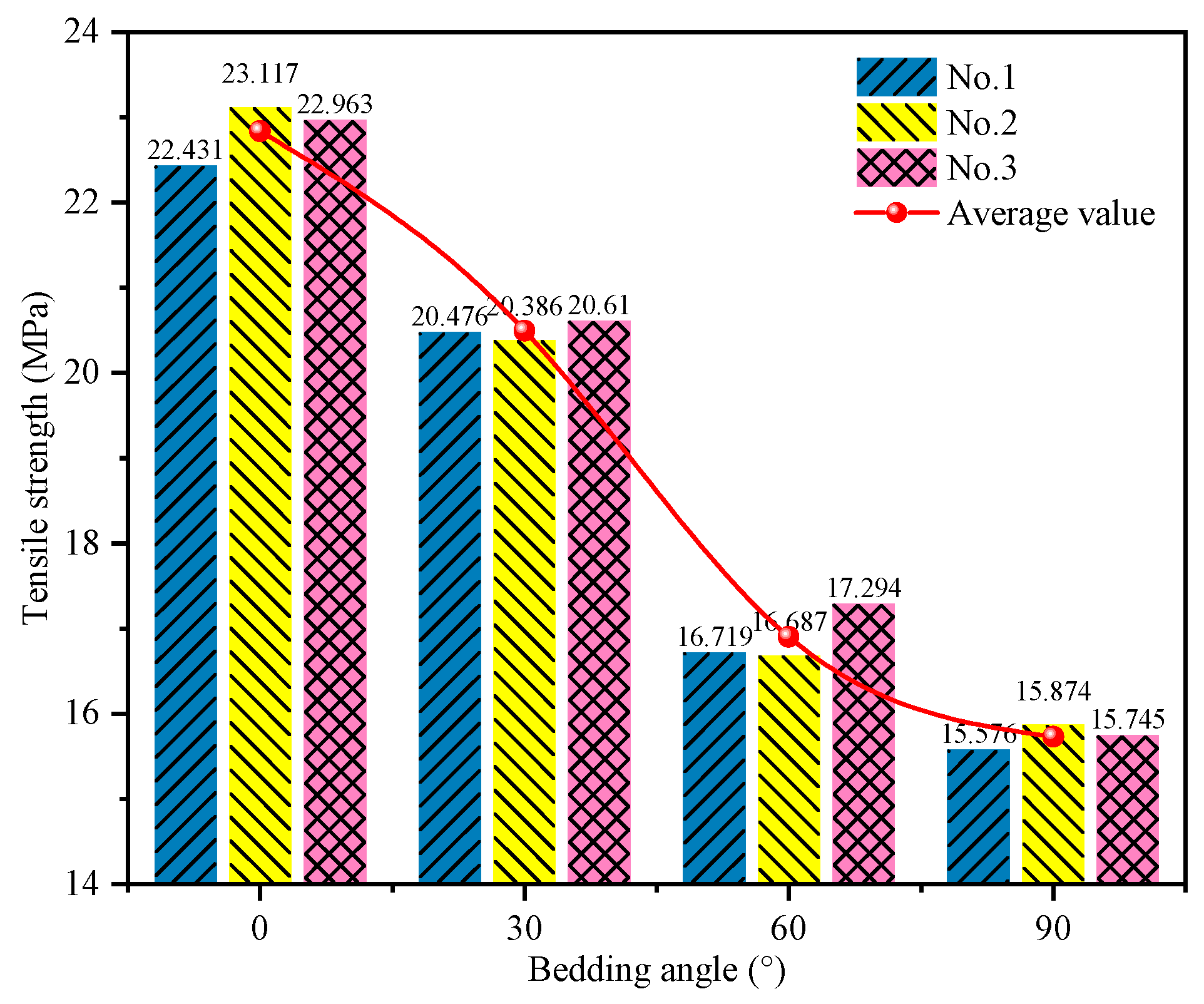
3.1.1. Mechanical Properties
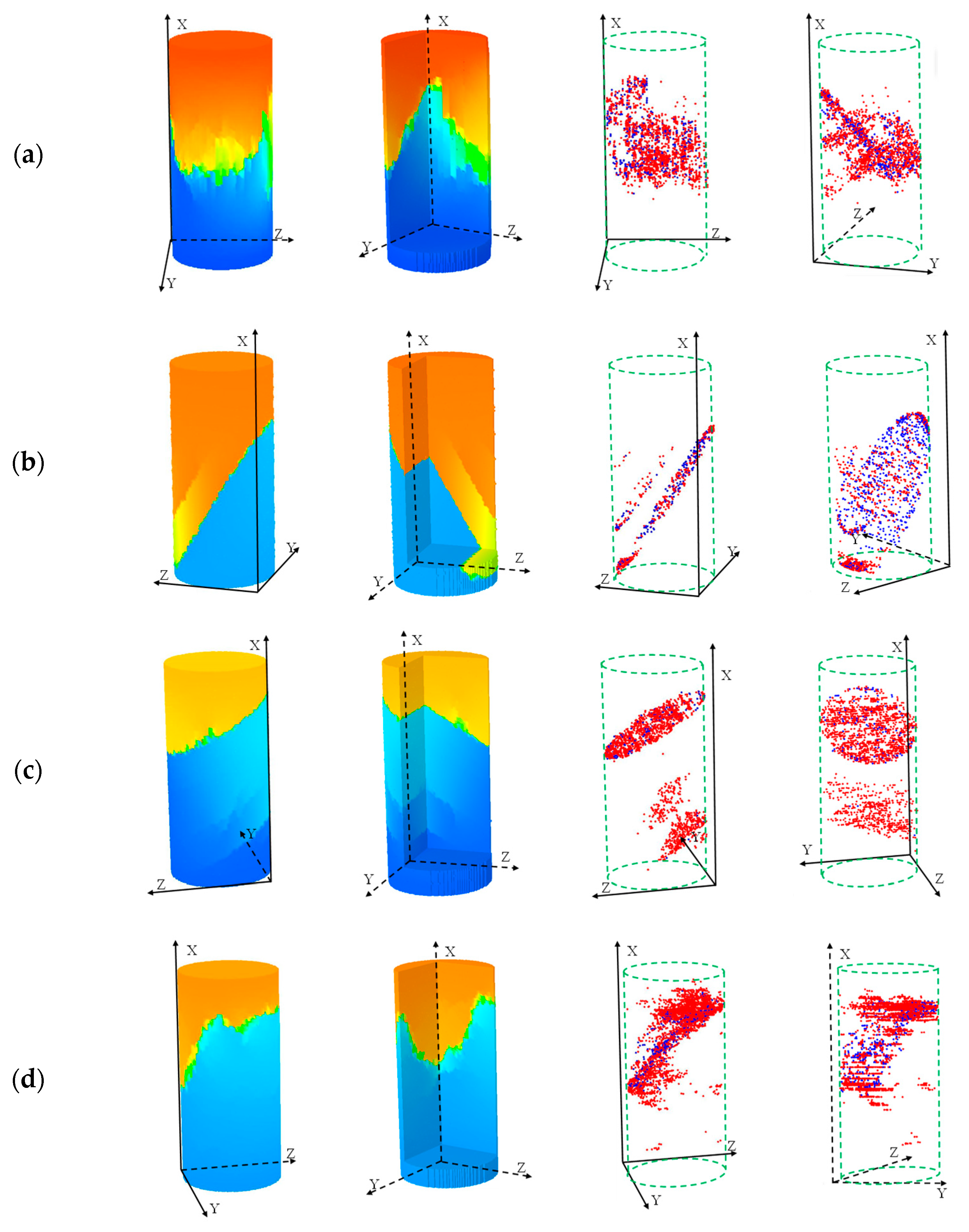
3.1.2. Anisotropic Characteristics of Failure Modes
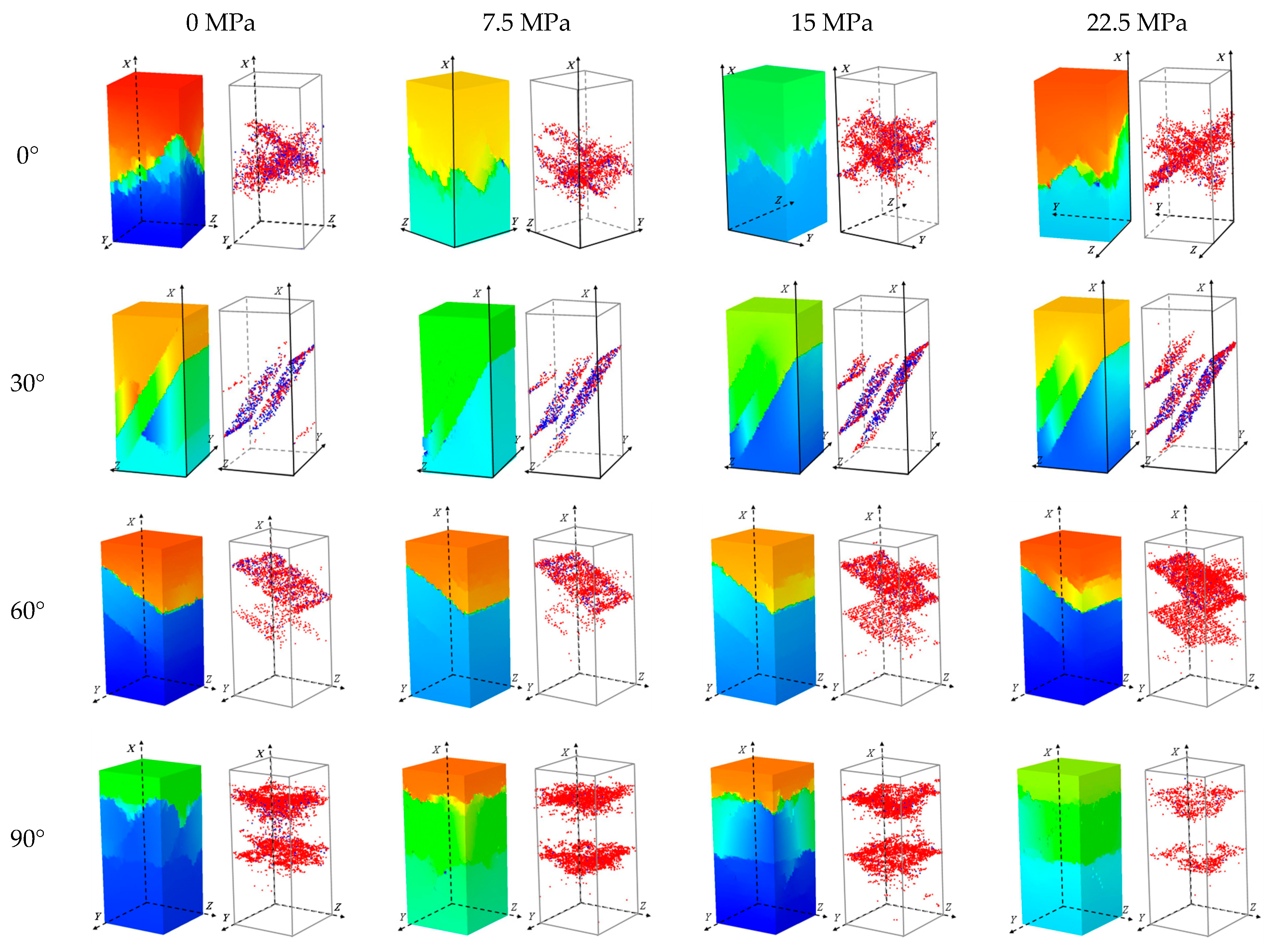
3.2. Triaxial Loading Conditions
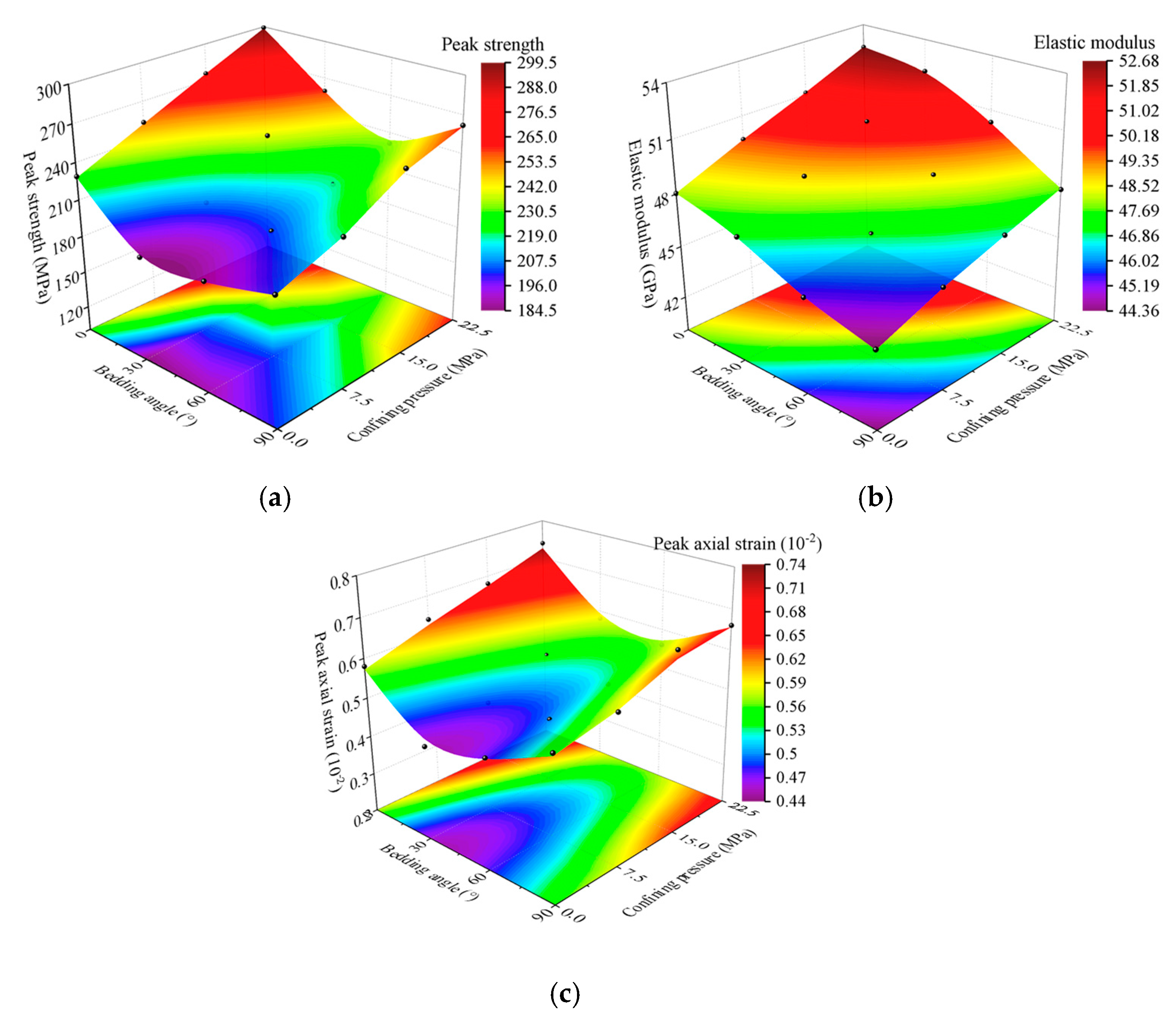
3.2.1. Mechanical Properties
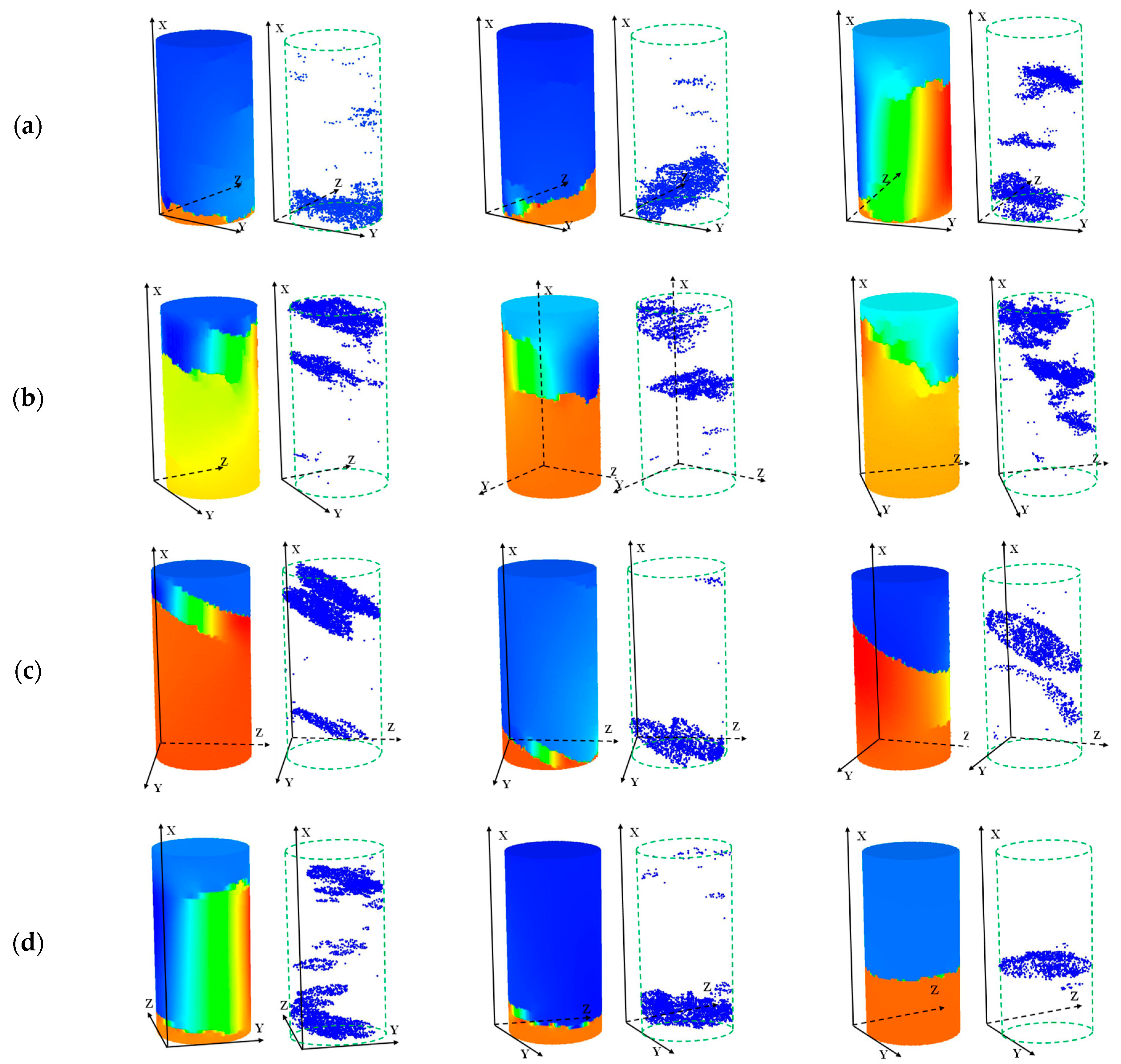
3.2.2. Failure Modes
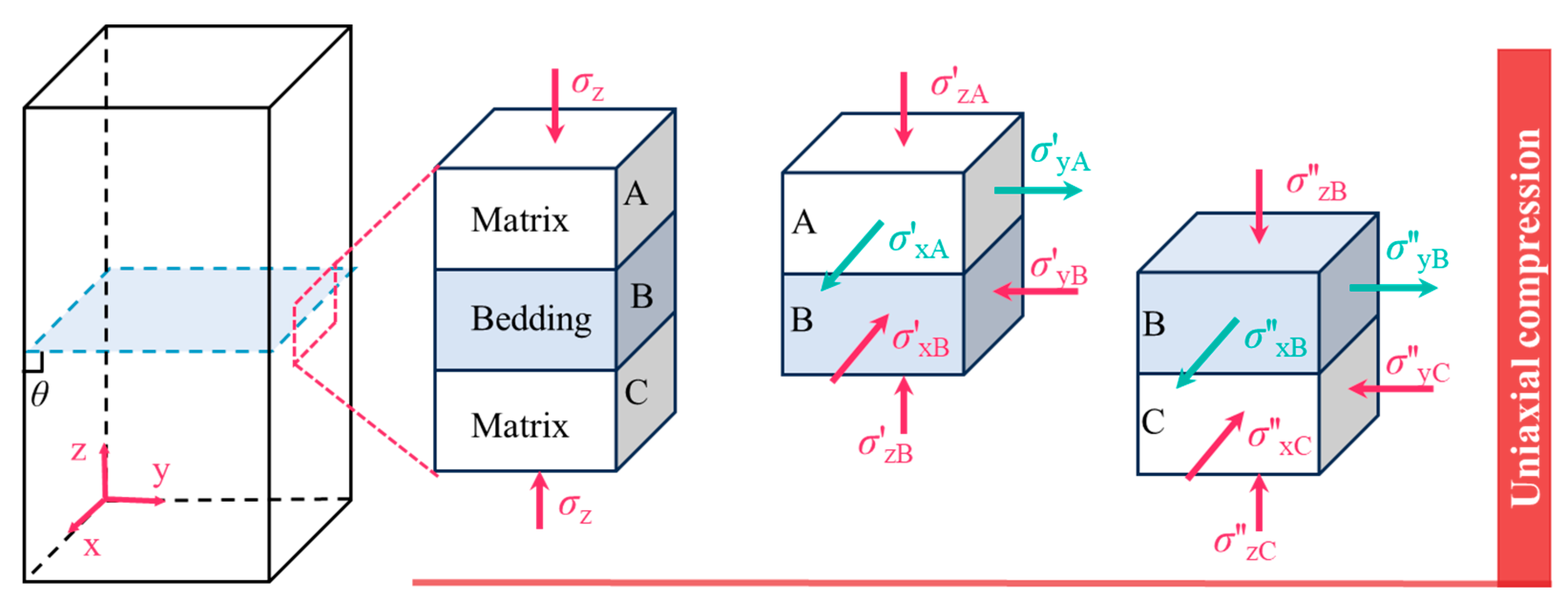
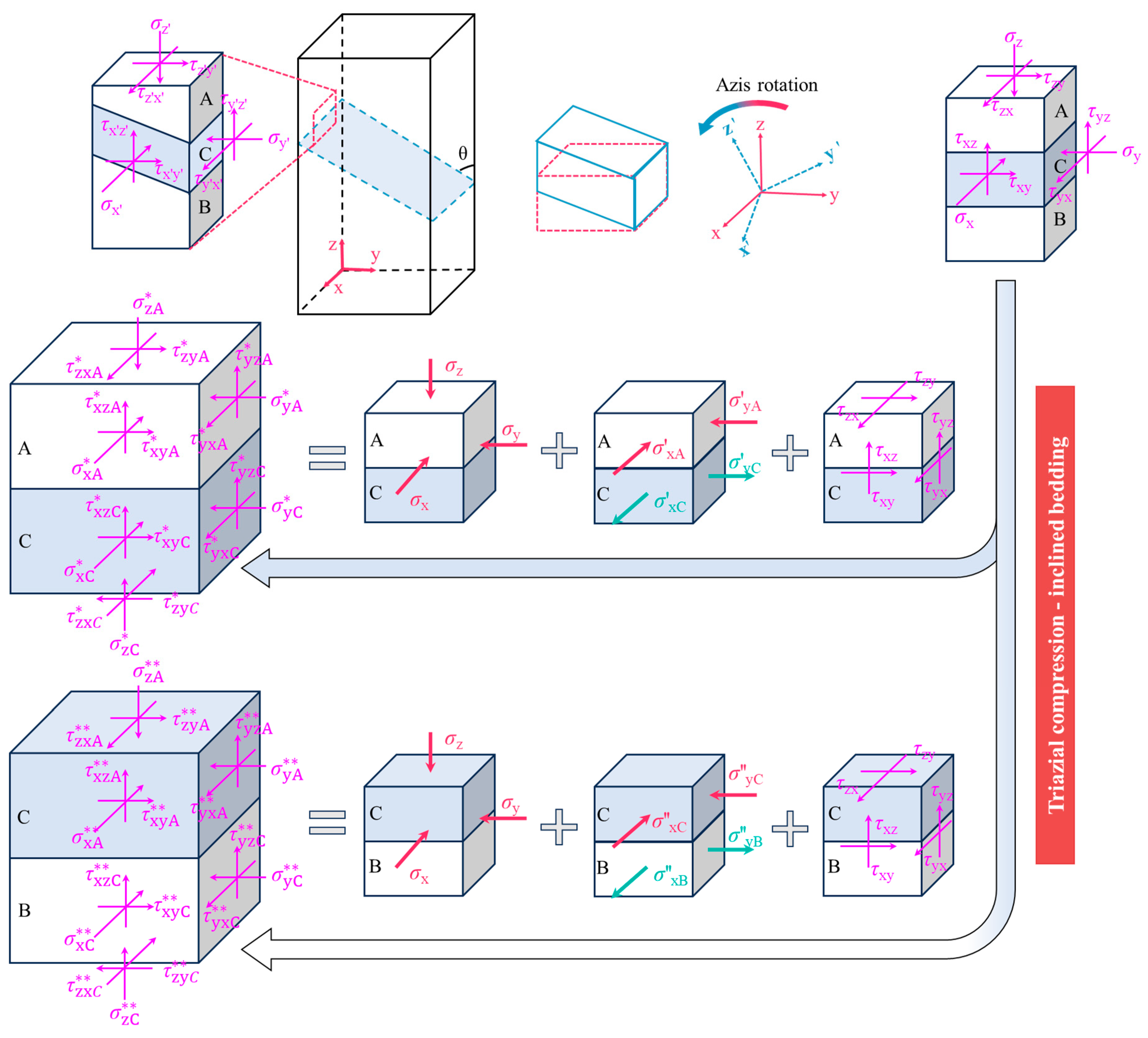
3.3. Mechanical Analysis Under Compression Conditions
4. Shape Effects of Shale
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shang, X.; Long, S.; Duan, T. Fracture system in shale gas reservoir: Prospect of characterization and modeling techniques. J. Nat. Gas Geosci. 2021, 6, 157–172. [Google Scholar] [CrossRef]
- Memon, A.; Li, A.; Jacqueline, N.; Kashif, M.; Ma, M. Study of gas sorption, stress effects and analysis of effective porosity and permeability for shale gas reservoirs. J. Pet. Sci. Eng. 2020, 193, 107370. [Google Scholar] [CrossRef]
- Tao, J. Analysis of co2 effects on porosity and permeability of shale reservoirs under different water content conditions. Geoenergy Sci. Eng. 2023, 226, 211744. [Google Scholar] [CrossRef]
- Wu, M.; Chang, X.; Guo, Y.; Liu, J.; Yang, C.; Suo, Y. Advances, challenges, and opportunities for hydraulicfracturing of deep shale gas reservoirs. Adv. Geo-Energy Res. 2025, 15, 1–4. [Google Scholar] [CrossRef]
- Xie, W.; Wang, M.; Chen, S.; Vandeginste, V.; Yu, Z.; Wang, H. Effects of gas components, reservoir property and pore structure of shale gas reservoir on the competitive adsorption behavior of co2 and ch4. Energy 2022, 254, 124242. [Google Scholar] [CrossRef]
- Xie, W.; Chen, S.; Vandeginste, V.; Yu, Z.; Wang, H.; Wang, M. Review of the effect of diagenetic evolution of shale reservoir on the pore structure and adsorption capacity of clay minerals. Energy Fuels 2022, 36, 4728–4745. [Google Scholar] [CrossRef]
- Hu, L. A review of mechanical mechanism and prediction of natural fracture in shale. Arab. J. Geosci. 2022, 15, 474. [Google Scholar] [CrossRef]
- Wopara, O.F. Geochemical properties of shale gas reservoirs and their impacts on gas development: A review. Int. J. Multidiscip. Curr. Educ. Res. 2021, 3, 154–165. [Google Scholar]
- Wang, H.; Hu, J.; Xia, Z.; Liu, C.; Yang, B.; Chen, B.; Zhang, L.; Wang, X. Mechanical properties and damage evolution characteristics of composite rock mass with prefabricated fractures. Comput. Part. Mech. 2024, 11, 1937–1957. [Google Scholar] [CrossRef]
- Lin, Q. Strength and failure characteristics of jointed rock mass with double circular holes under uniaxial compression: Insights from discrete element method modelling. Theor. Appl. Fract. Mech. 2020, 109, 102692. [Google Scholar] [CrossRef]
- El-Aal, A.K.A.; Radwan, A.E.; Hussain, J.; Ali, M.A.M. Experimental study on the impact of perpendicular and parallel bedding planes on the physical and geomechanical characteristics of carbonate rocks. J. Pet. Explor. Prod. Technol. 2025, 15, 28. [Google Scholar] [CrossRef]
- Cao, H.; Gao, Q.; Ye, G.; Zhu, H.; Sun, P. Experimental investigation on anisotropic characteristics of marine shale in northwestern Hunan, China. J. Nat. Gas Sci. Eng. 2020, 81, 103421. [Google Scholar] [CrossRef]
- Lyu, Q.; Wang, K.; Hu, C.; Dick, J.M.; Shi, J.; Tan, J. Experimental study on the mechanical properties of shale after long-term of immersion in fracturing fluids with different ph. Rock Mech. Rock Eng. 2022, 55, 5047–5061. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Yin, P.-F.; Ranjith, P.G. Experimental study on mechanical behavior and brittleness characteristics of longmaxi formation shale in Changning, Sichuan basin, China. Rock Mech. Rock Eng. 2020, 53, 2461–2483. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, J.; Xu, D.; Zhang, L.; Lyu, C.; Ren, Y. Investigation on mechanical properties, ae characteristics, and failure modes of longmaxi formation shale in Changning, Sichuan basin, China. Rock Mech. Rock Eng. 2023, 56, 1239–1272. [Google Scholar] [CrossRef]
- Kramarov, V.; Parrikar, P.N.; Mokhtari, M. Evaluation of fracture toughness of sandstone and shale using digital image correlation. Rock Mech. Rock Eng. 2020, 53, 4231–4250. [Google Scholar] [CrossRef]
- Li, C.; Zou, B.; Zhou, H.; Wang, J. Experimental investigation on failure behaviors and mechanism of an anisotropic shale in direct tension. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 98. [Google Scholar] [CrossRef]
- Guo, W.; Guo, Y.; Yang, H.; Wang, L.; Liu, B.; Yang, C. Tensile mechanical properties and ae characteristics of shale in triaxial Brazilian splitting tests. J. Pet. Sci. Eng. 2022, 219, 111080. [Google Scholar] [CrossRef]
- Heng, S.; Li, X.; Liu, X.; Chen, Y. Experimental study on the mechanical properties of bedding planes in shale. J. Nat. Gas Sci. Eng. 2020, 76, 103161. [Google Scholar] [CrossRef]
- Xie, Y.; Hou, M.Z.; Liu, H.; Li, C. Anisotropic time-dependent behaviors of shale under direct shearing and associated empirical creep models. J. Rock Mech. Geotech. Eng. 2023, 16, 1262–1279. [Google Scholar] [CrossRef]
- He, J.; Afolagboye, L.O.; Zheng, B.; Mao, T.; Wu, Y.; Li, G.; Li, S.; Li, X. Effect of strain rate on anisotropic mechanical behavior of the shale under uniaxial compression conditions. Rock Mech. Rock Eng. 2022, 55, 5297–5305. [Google Scholar] [CrossRef]
- Yang, S.-Q. Strength, deformability and x-ray micro-ct observations of transversely isotropic composite rock under different confining pressures. Eng. Fract. Mech. 2019, 214, 1–20. [Google Scholar] [CrossRef]
- Shao, Y.; Yang, J.; Kim, J.; Song, J.-J.; Moon, J.; Han, J. A comprehensive experimental study on mechanical anisotropy and failure mode of 3d printed gypsum rocks: From composition and microstructure to macroscopic mechanical properties response. Rock Mech. Rock Eng. 2023, 56, 6503–6528. [Google Scholar] [CrossRef]
- He, F.; Liu, Q.; Deng, P. Investigation of the anisotropic characteristics of layered rocks under uniaxial compression based on the 3d printing technology and the combined finite-discrete element method. Adv. Mater. Sci. Eng. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Zhu, J.B.; Tang, C.A. Numerical investigation of rock tensile strength determined by direct tension, Brazilian and three-point bending tests. Int. J. Rock Mech. Min. Sci. 2019, 115, 21–32. [Google Scholar] [CrossRef]
- Fan, Z.; Zhou, Q.; Nie, X.; Yao, Z.; Li, C.; Wang, J.; He, L.; Wang, M.; Ren, L. 3D anisotropic microcracking mechanisms of shale subjected to direct shear loading: A numerical insight. Eng. Fract. Mech. 2024, 298, 109950. [Google Scholar] [CrossRef]
- Song, Y.; Yang, S.-Q.; Li, K.-S.; Yin, P.-F.; Pan, P.-Z. Mechanical behavior and fracture evolution mechanism of composite rock under triaxial compression: Insights from three-dimensional dem modeling. Rock Mech. Rock Eng. 2023, 56, 7673–7699. [Google Scholar] [CrossRef]
- Zhai, M.; Li, L.; Chen, B.; Zhang, Q.; Zhang, Z.; Zhang, L. Investigation on the anisotropy of mechanical properties and brittleness characteristics of deep laminated sandstones. Eng. Fract. Mech. 2023, 289, 109386. [Google Scholar] [CrossRef]
- Feng, X.H.; Gong, B.; Liang, Z.Z.; Wang, S.Y.; Tang, C.A.; Li, H.; Ma, T.H. Study of the dynamic failure characteristics of anisotropic shales under impact Brazilian splitting. Rock Mech. Rock Eng. 2024, 57, 2213–2230. [Google Scholar] [CrossRef]
- Gong, B.; Zhao, T.; Thusyanthan, I.; Tang, C.A.; Zhou, G.G.D. Integrating RFPA and DEM in adaptive RDFA modeling of rock fracturing process. Rock Mech. Rock Eng. 2025, 58, 2569–2587. [Google Scholar] [CrossRef]
- Gong, B.; Zhao, T.; Thusyanthan, I.; Tang, C.A.; Zhou, G.G.D. The random RFPA method for modelling rock failure. Rock Mech. Rock Eng. 2025. [Google Scholar] [CrossRef]
- Chen, B.; Gong, B.; Wang, S.; Tang, C. Research on zonal disintegration characteristics and failure mechanisms of deep tunnel in jointed rock mass with strength reduction method. Mathematics 2022, 10, 922. [Google Scholar] [CrossRef]
- Gong, B.; Zhao, T.; Thusyanthan, I.; Tang, C.A. Modelling rock fracturing by a novel implicit continuous to discontinuous method. Comput. Geotech. 2024, 166, 106035. [Google Scholar] [CrossRef]
- Gong, B.; Wang, Y.; Chen, X.; Song, W.; Wang, K.; Yu, J. Analysis of sensitivity factors on CJB mechanical behavior from specimen scale to engineering scale. Eng. Fract. Mech. 2025, 314, 110673. [Google Scholar] [CrossRef]
- Liang, Z.Z. Three-Dimensional Failure Process Analysis of Rock and Associated Numerical Tests. Ph.D. Thesis, Northeastern University, Shenyang, China, 2005. [Google Scholar]
- Al-Bukhaiti, K.; Yanhui, L.; Shichun, Z.; Daguang, H.; Abas, H. Effect of cross-section shape on RC specimen’s behavior under asymmetrical impact loading. In Proceedings of the 9th International Conference on Civil Engineering; Feng, G., Ed.; Springer Nature: Singapore, 2023; Volume 327, pp. 497–511. [Google Scholar]
- Štambuk Cvitanović, N.; Nikolić, M.; Ibrahimbegović, A. Influence of specimen shape deviations on uniaxial compressive strength of limestone and similar rocks. Int. J. Rock Mech. Min. Sci. 2015, 80, 357–372. [Google Scholar] [CrossRef]
- Du, K.; Su, R.; Tao, M.; Yang, C.; Momeni, A.; Wang, S. Specimen shape and cross-section effects on the mechanical properties of rocks under uniaxial compressive stress. Bull. Eng. Geol. Environ. 2019, 78, 6061–6074. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, H.; Qiu, C.; Jiang, T.; Zhang, J. The effect of cross-section shape on deformation, damage and failure of rock-like materials under uniaxial compression from both a macro and micro viewpoint. Int. J. Damage Mech. 2020, 29, 1076–1099. [Google Scholar] [CrossRef]
- Zhao, X.G.; Cai, M.; Wang, J.; Li, P.F. Strength comparison between cylindrical and prism specimens of Beishan granite under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2015, 76, 10–17. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, M. Numerical study on the influence of cross-sectional shape on strength and deformation behaviors of rocks under uniaxial compression. Comput. Geotech. 2017, 84, 129–137. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Sun, S.R.; Shi, W.; Liu, G. Influence of sample shape on mechanical properties of composite rock mass with inclined weak interlayer. Geotech. Investig. Surv. 2024, 52, 1–8. (In Chinese) [Google Scholar]




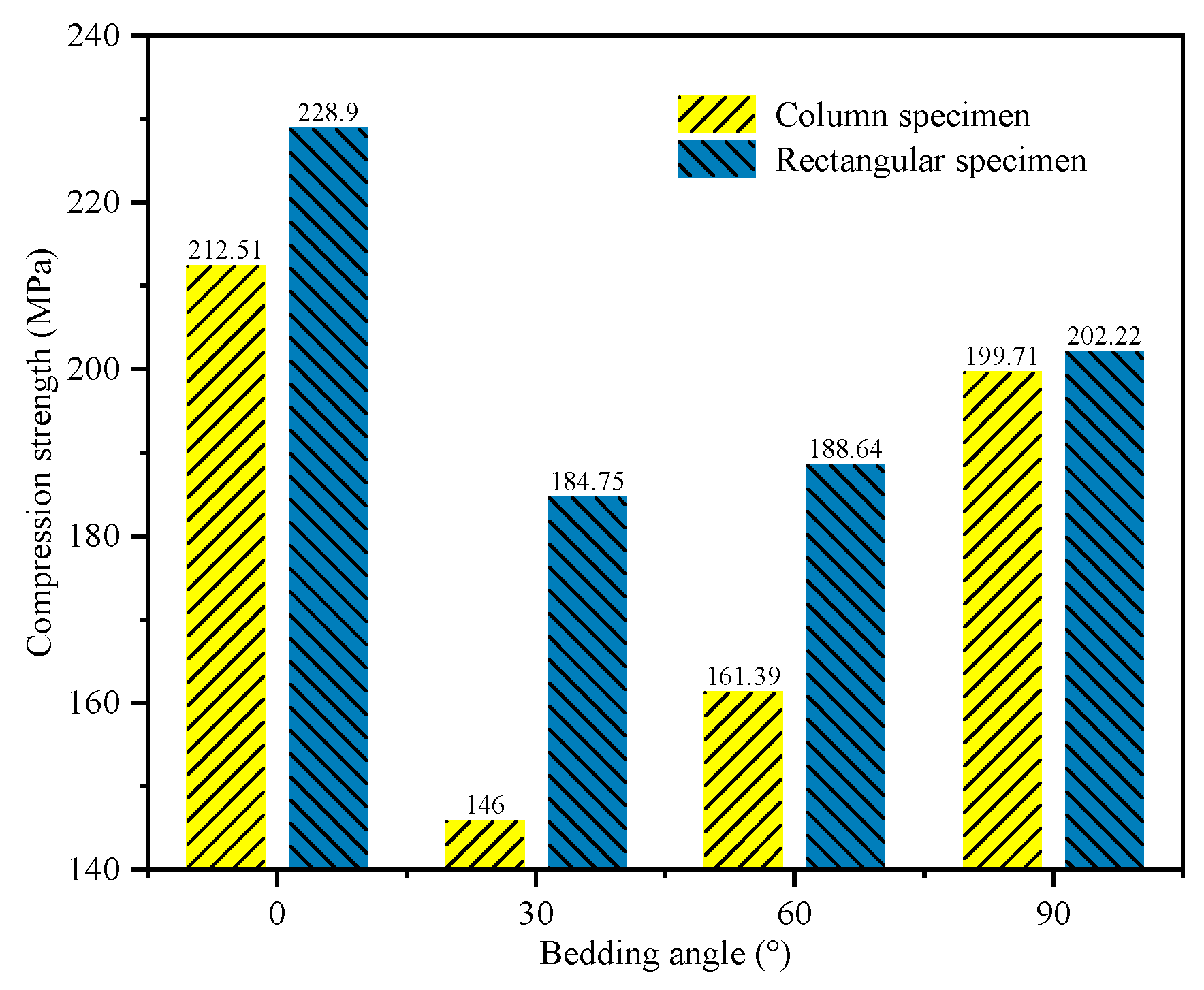
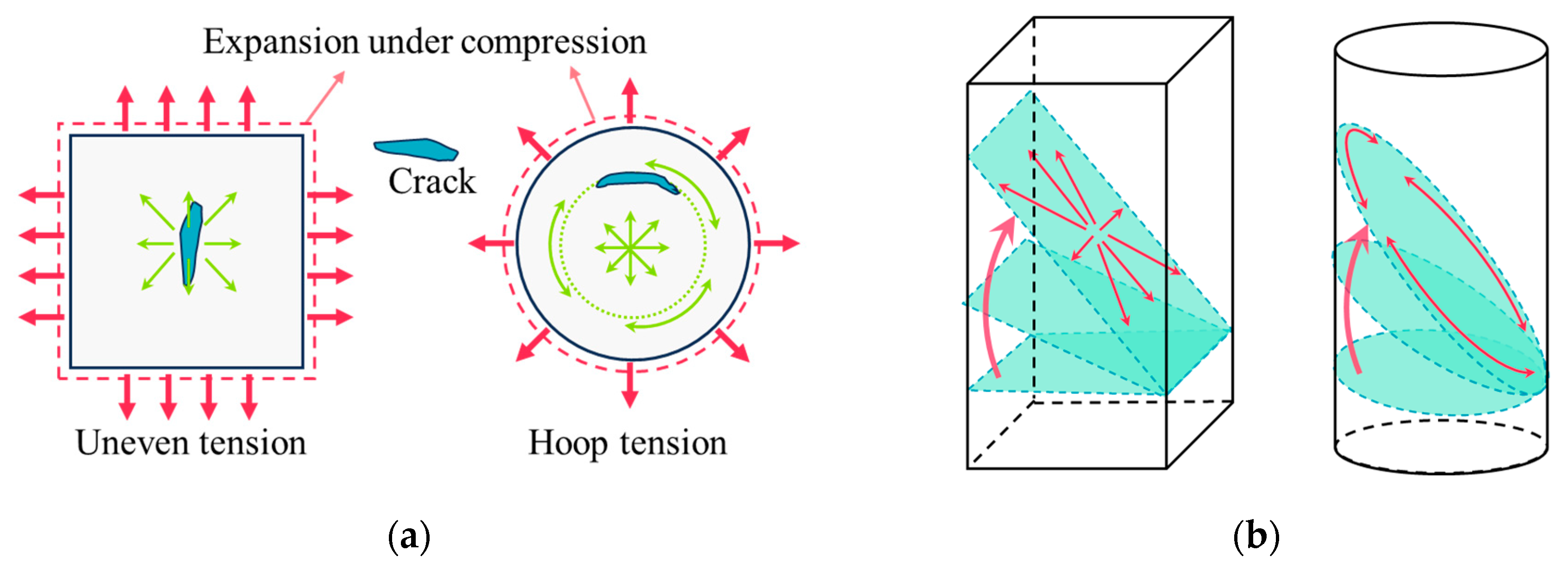

| Material | Homogeneity | Elastic Modulus/GPa | Compressive Strength/MPa | Poisson’s Ratio | Friction Angle/° |
|---|---|---|---|---|---|
| Matrix | 3 | 68.756 | 710.56 | 0.25 | 36 |
| bedding | 4 | 34.378 | 340.28 | 0.2 | 24 |
| Anisotropy Index | Compressive Strength | Elastic Modulus | Peak Strain |
|---|---|---|---|
| Column specimen | 1.420 | 1.094 | 1.523 |
| Rectangular | 1.239 | 1.083 | 1.318 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, T.; Dong, Z.; Gong, B. Numerical Study of the Mechanical Properties and Failure Mechanisms of Shale Under Different Loading Conditions. Appl. Sci. 2025, 15, 4405. https://doi.org/10.3390/app15084405
Lin T, Dong Z, Gong B. Numerical Study of the Mechanical Properties and Failure Mechanisms of Shale Under Different Loading Conditions. Applied Sciences. 2025; 15(8):4405. https://doi.org/10.3390/app15084405
Chicago/Turabian StyleLin, Tianran, Zhuo Dong, and Bin Gong. 2025. "Numerical Study of the Mechanical Properties and Failure Mechanisms of Shale Under Different Loading Conditions" Applied Sciences 15, no. 8: 4405. https://doi.org/10.3390/app15084405
APA StyleLin, T., Dong, Z., & Gong, B. (2025). Numerical Study of the Mechanical Properties and Failure Mechanisms of Shale Under Different Loading Conditions. Applied Sciences, 15(8), 4405. https://doi.org/10.3390/app15084405







