Research on Path and Sequence Planning for Multi-Cabin Onboard Transportation of Large Cruise Ships
Abstract
1. Introduction
2. Mathematical Model of Multi-Cabin Transportation Path Planning
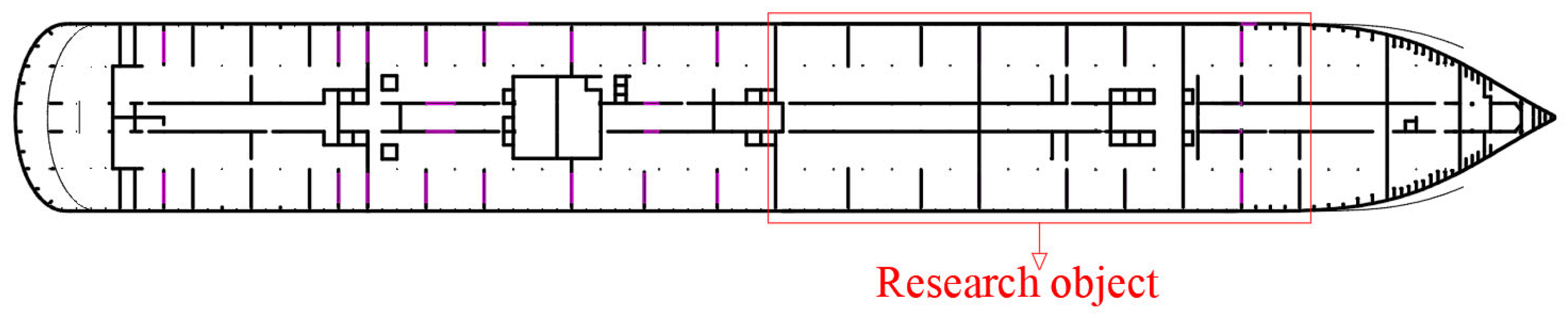
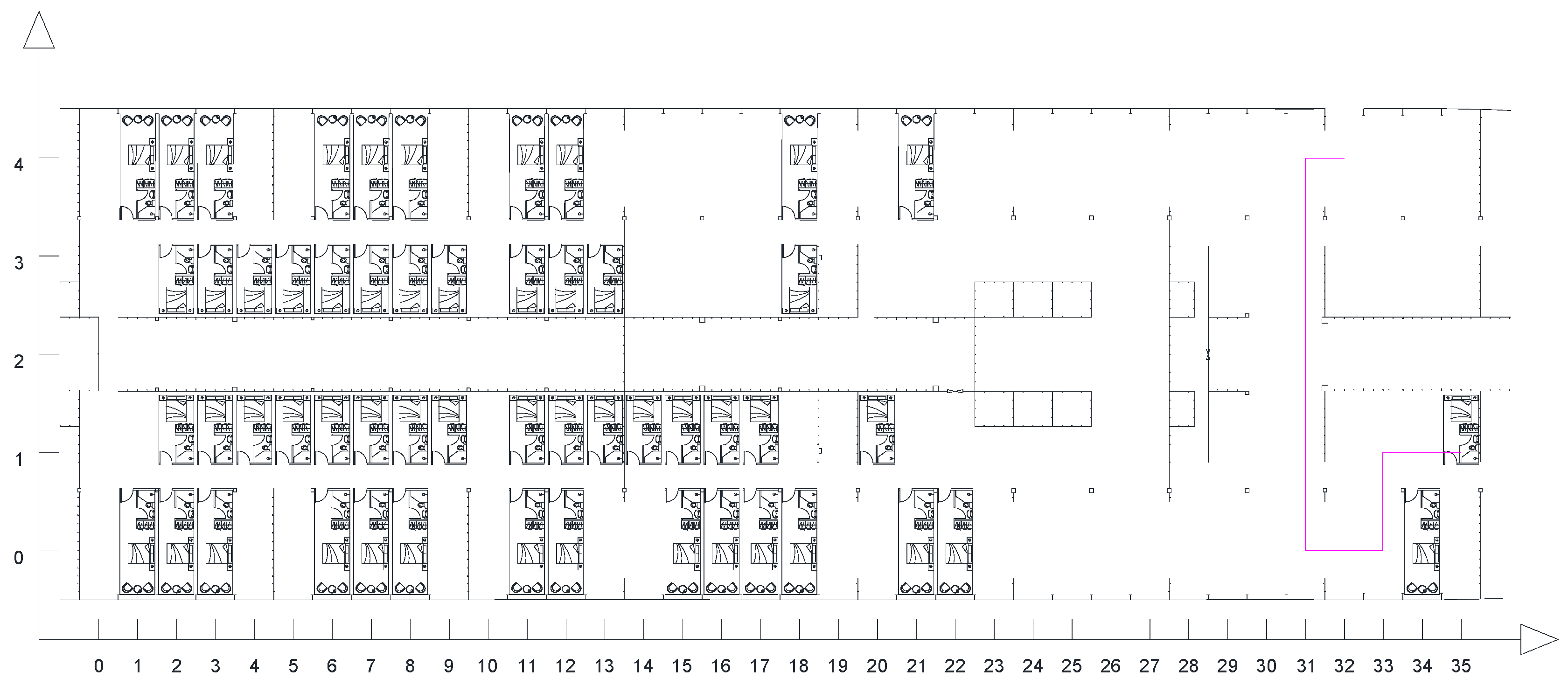
2.1. Problem Description
2.2. Design of Model Variables and Constraints
2.3. Objective Function
3. Improved A-Star Algorithm Designing
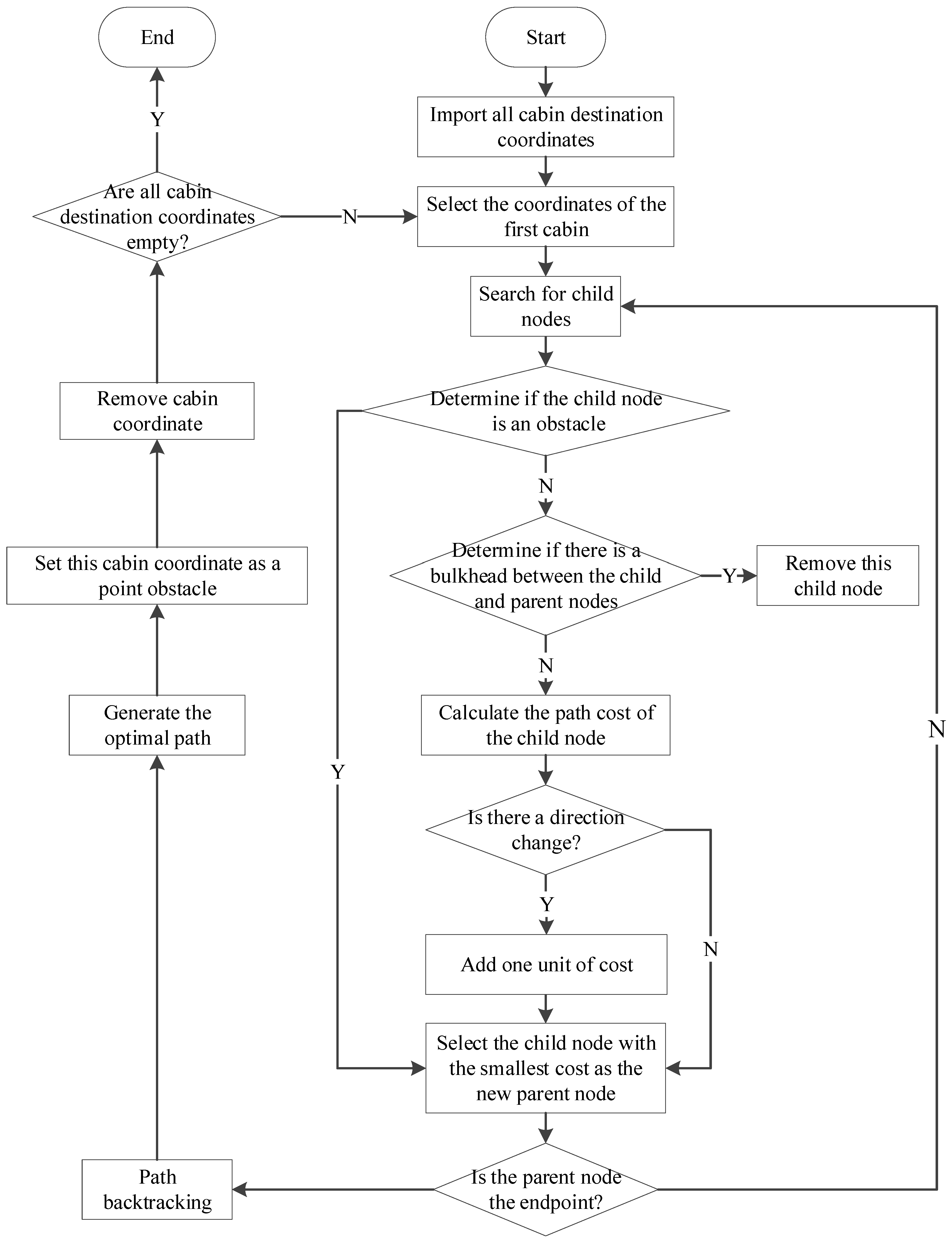
3.1. A-Star Algorithm Principle
- Build the grid map, input the coordinates of the start and end points, and initialize the open list and the closed list.
- Expand from the start point and search for neighboring nodes, while updating the open and closed lists.
- If a neighboring node is an obstacle, remove it; otherwise, calculate the cost of the neighboring node.
- Select the node with the smallest cost as the next node to expand for further search.
- If the target node is found, backtrack through the recorded nodes and output the optimal path; otherwise, repeat steps (2)–(4).
3.2. Improved A-Star Algorithm
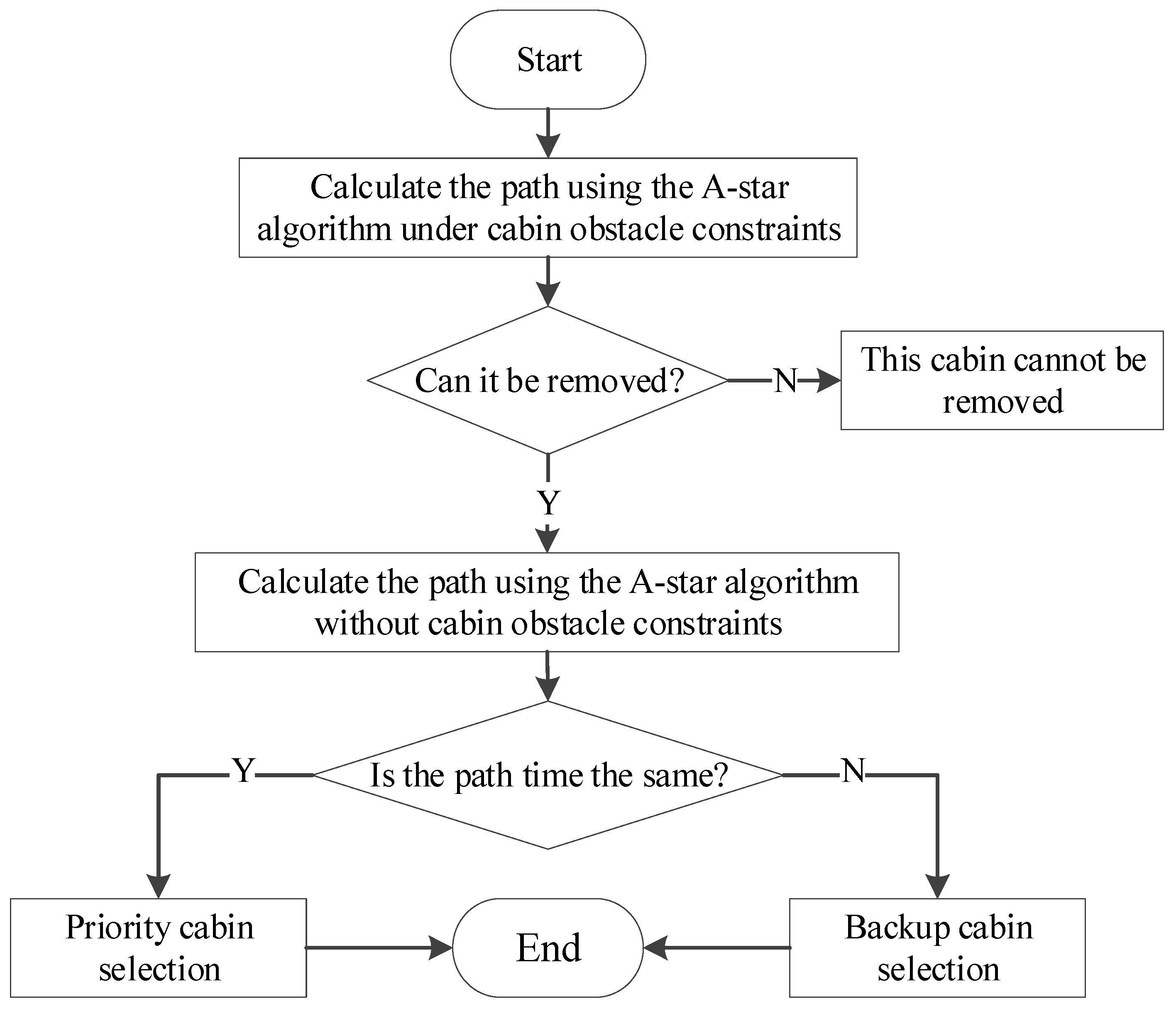
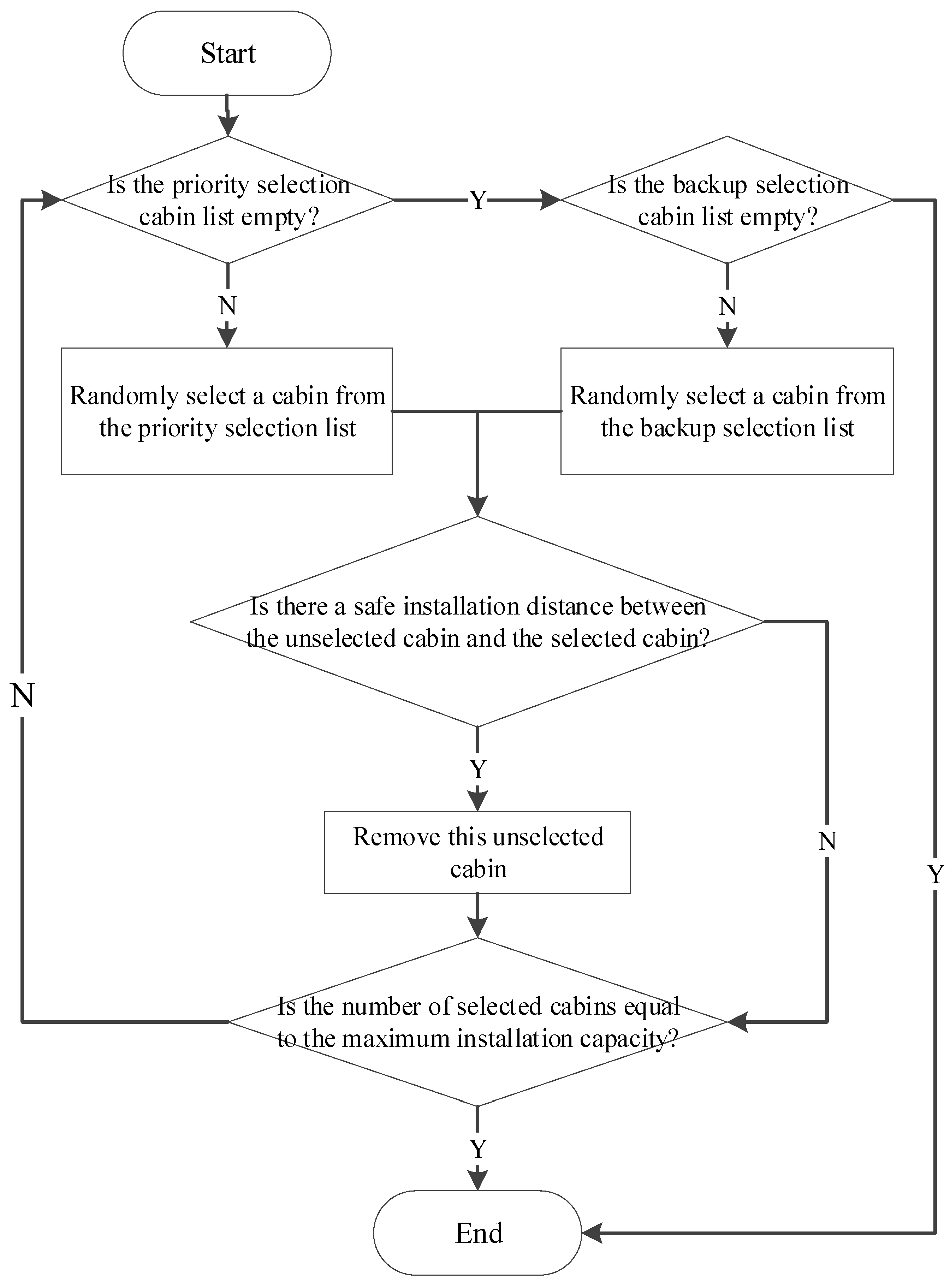
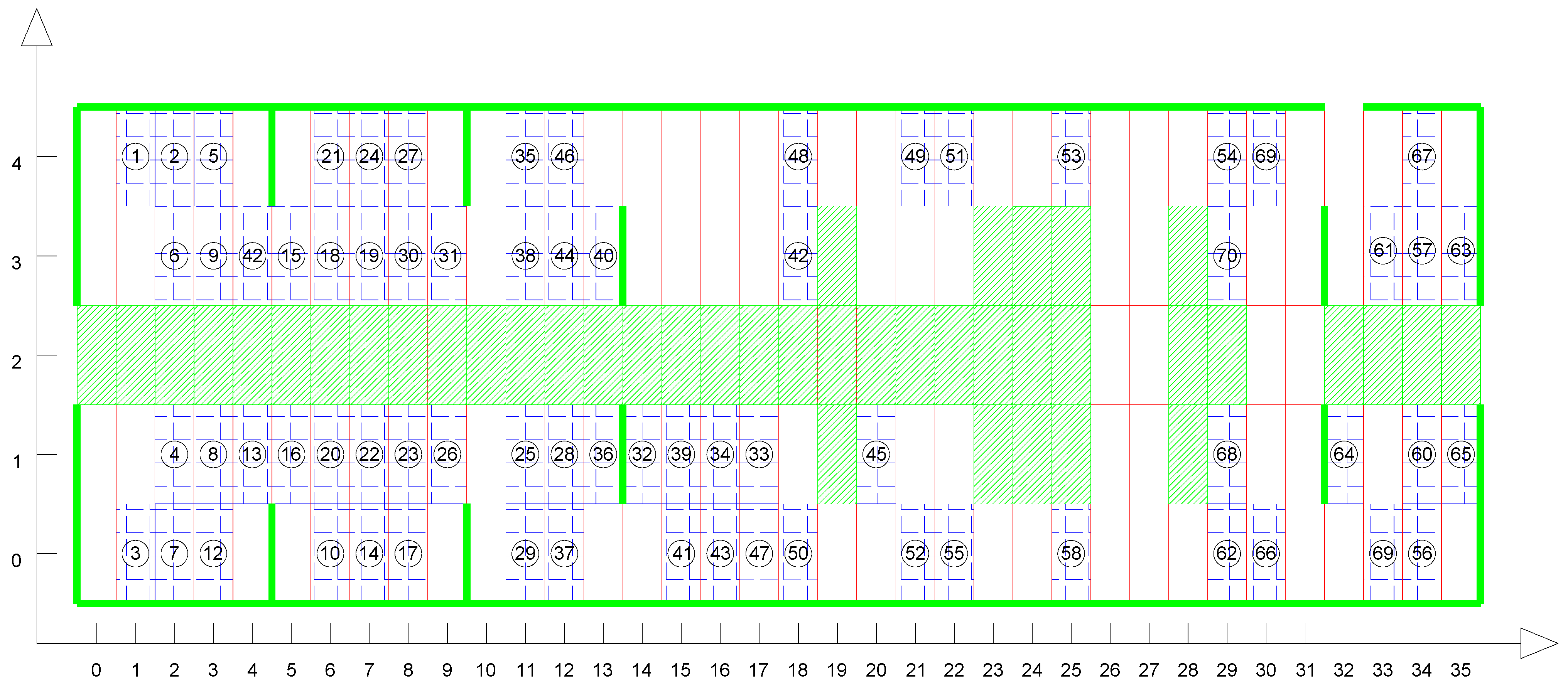
3.3. Reverse Planning Strategy for Cabin Transport Sequence Optimization
- (1)
- Selection Principle for Removable Cabins
- (2)
- Selection Principle for Installation
- (3)
- Selection Principle for Transportation
4. Multi-Transportation Path Planning Based on the Improved A-Star Algorithm
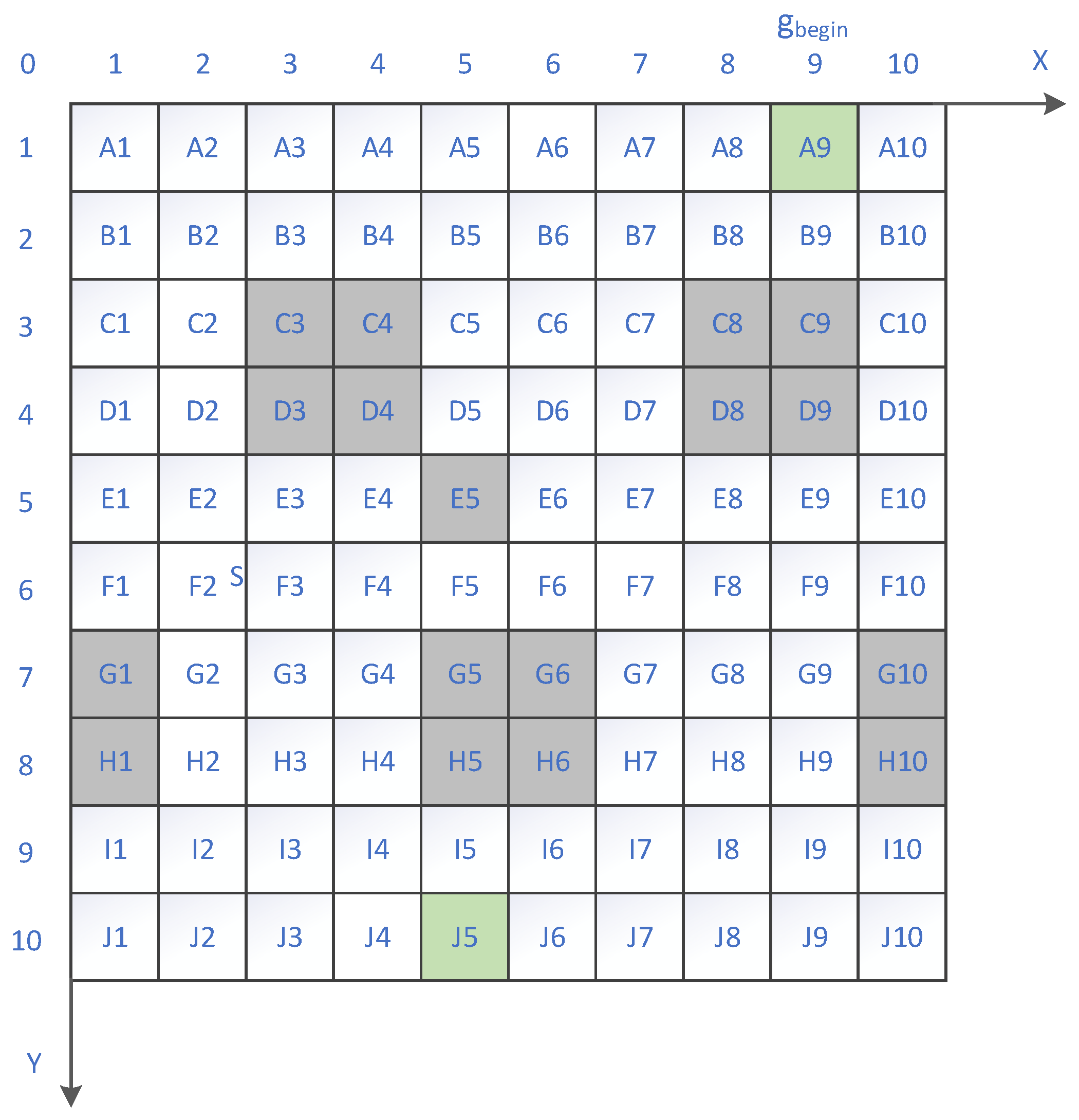
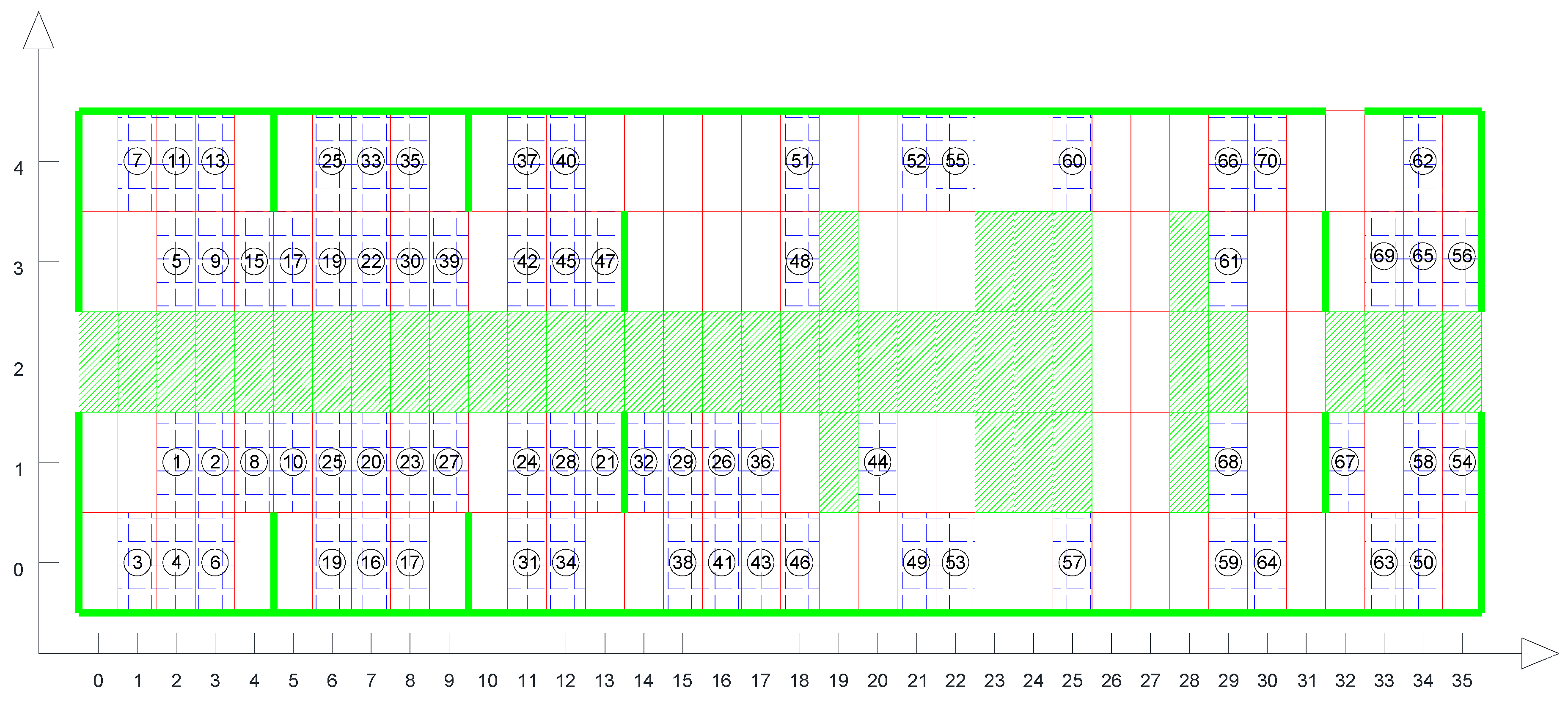
4.1. Definition of the Grid Map
- (1)
- The grid size should be uniform to facilitate accurate calculation of push-in path distances and time.
- (2)
- The grid should evenly cover each deck of the ship’s structure to ensure comprehensive path search.
- (3)
- Multiple modules should not occupy the same grid cell, to avoid interference and conflicts between the cabins.
- (4)
- Existing cabins and other obstacles should be represented by one or more grids to accurately reflect their position and shape.
- (5)
- A grid cell should not simultaneously contain both obstacles and modular cabins, to avoid interference and misjudgment during the path search.
- (6)
- Bulkheads and outer plates, as boundary constraints, must lie on the grid lines to limit the scope of the path search.
- (7)
- The grid should be as simple as possible to facilitate computation and reduce calculation time.
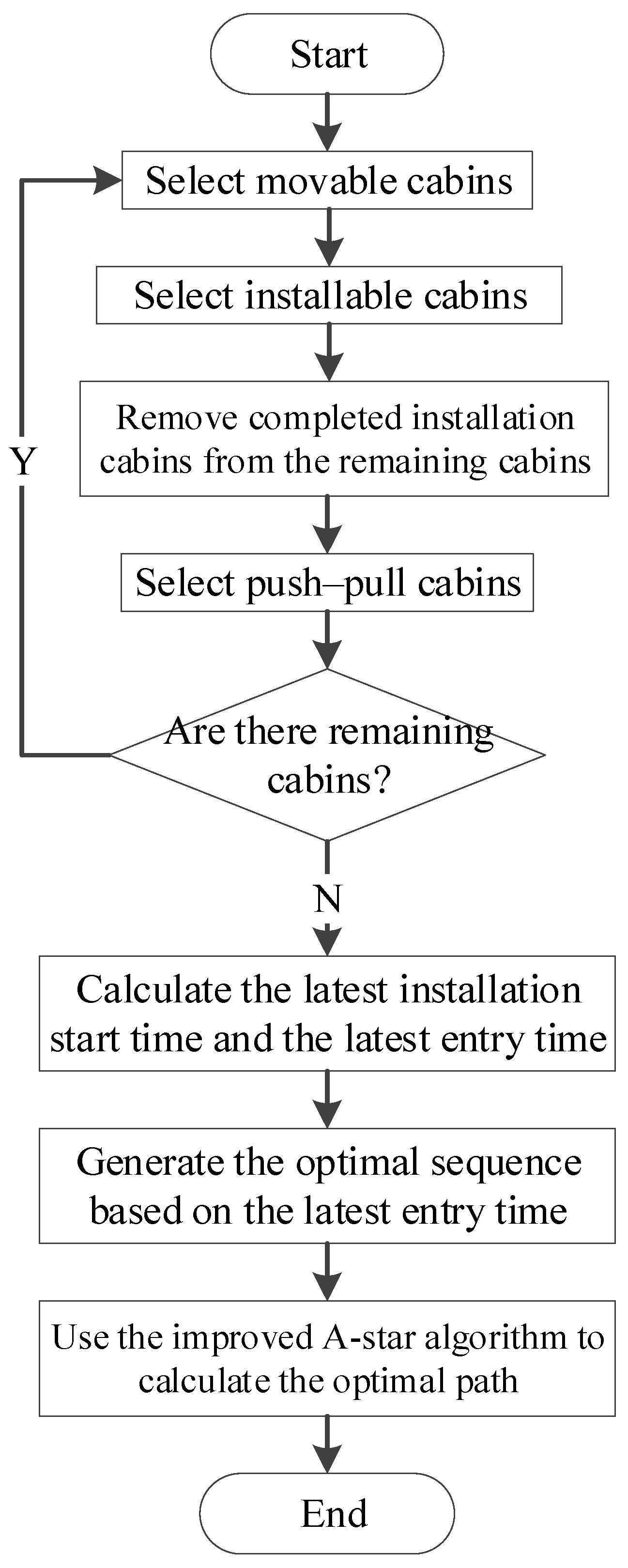
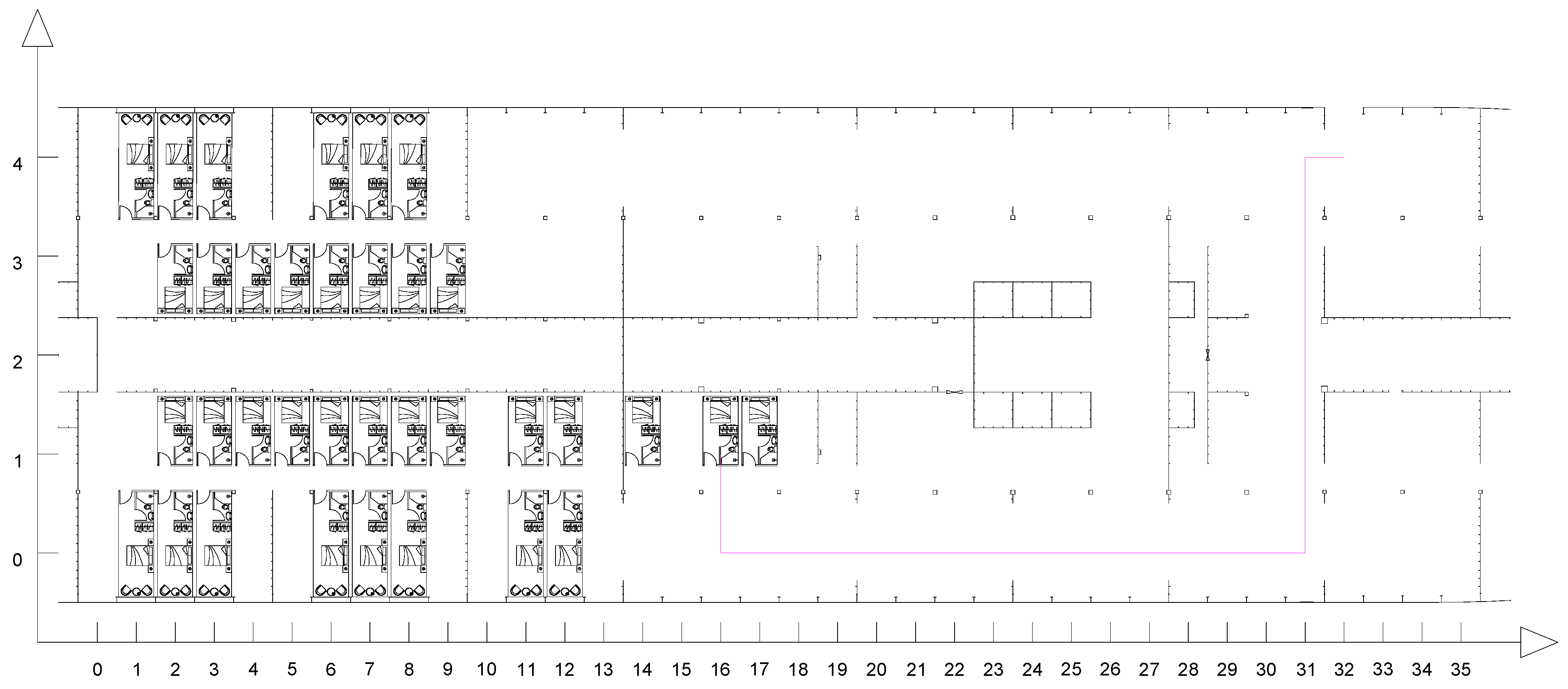
4.2. Transport Path Planning
- (1)
- Establish the Grid Map: Input the coordinates of the start and end points, and place all cabins inside the ship.
- (2)
- Select Movable Cabins: Identify all currently movable cabins, and use the A-Star algorithm to compute the shortest transport time for these cabins.
- (3)
- Select Installable Cabins: Based on the installation capacity requirements, select the cabins that can be installed. Once all installations are complete, sequentially select cabins from these to perform the transportation.
- (4)
- Check for Completion of All Cabin Transportation: Determine whether all cabins have been transported. If any cabins remain, repeat steps (2)–(3). If all cabins have been transported, proceed to the next step.
- (5)
- Calculate Entry Times: Compute the entry time for each cabin, and determine the actual sequence of entries.
- (6)
- Output the Optimal Path: Using the improved A-Star algorithm, output the optimal path for each cabin based on the actual entry sequence.
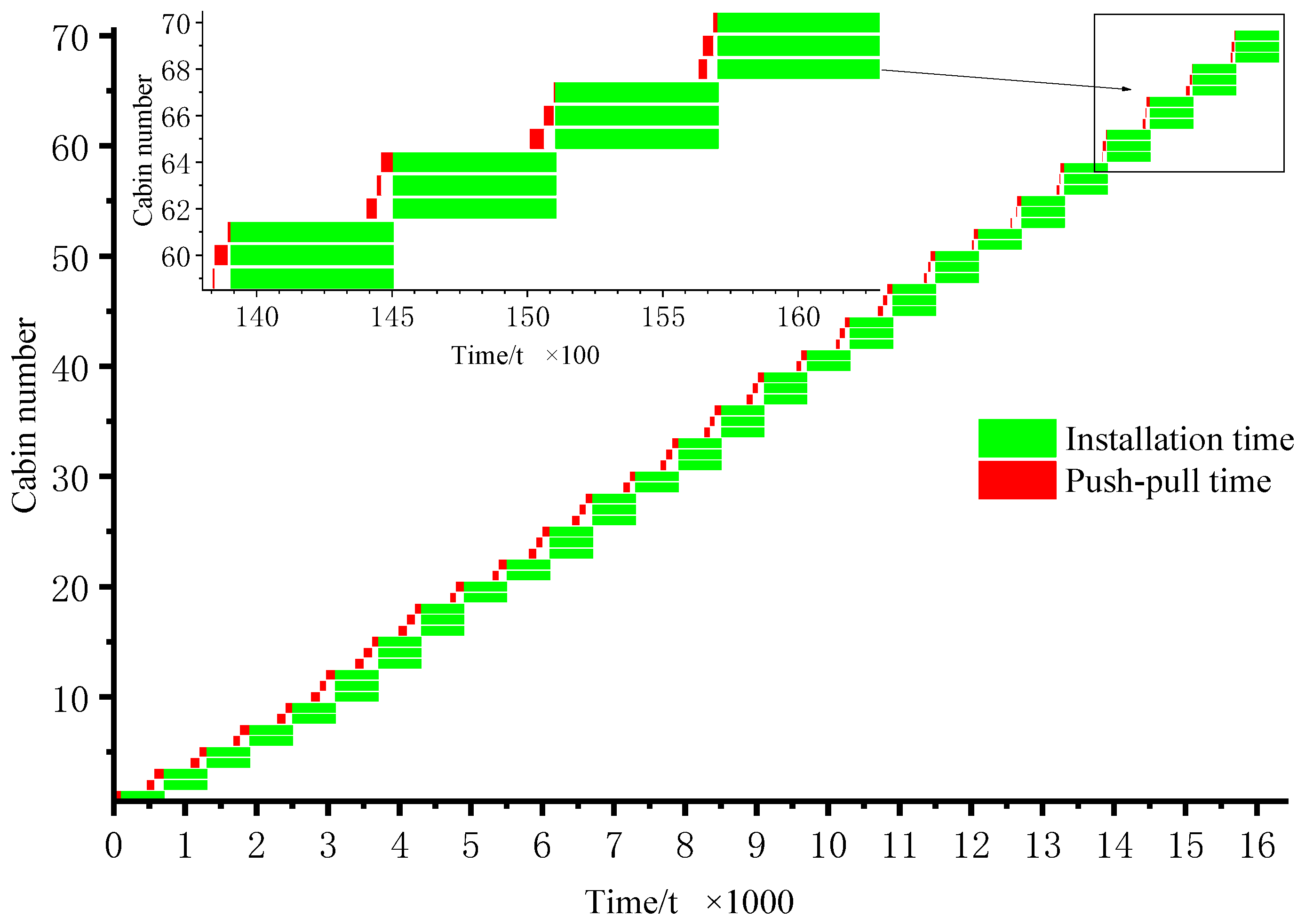
5. Comparative Analysis of Optimization Results Under Different Conditions
- (1)
- No Limitation on Number of personnel
- (2)
- Limited Number of Push–Pull and Installation Personnel
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arrichiello, V.; Gualeni, P. Systems engineering and digital twin: A vision for the future of cruise ships design, production and operations. Int. J. Interact. Des. Manuf. (IJIDeM) 2020, 14, 115–122. [Google Scholar] [CrossRef]
- Romano, P.; Formentini, M.; Bandera, C.; Tomasella, M. Value analysis as a decision support tool in cruise ship design. Int. J. Prod. Res. 2010, 48, 6939–6958. [Google Scholar] [CrossRef]
- Kawser, Z.A. A Modular Design Methodology for OSV Accommodation Areas. Master’s Thesis, Institutt for Marin Teknikk, Trondheim, Norway, 2012. [Google Scholar]
- Bednarek, M.; Parkes, A. Legacy of fordism and product life cycle management in the modern economy. Manag. Prod. Eng. Rev. 2021, 12, 61–71. [Google Scholar]
- Jiang, H.; Zeng, J.; Huang, C.; Yang, M. Design of the Hoisting Device for the Module in the Living of Medium-Sized Cruise Ship. Int. Core J. Eng. 2021, 7, 167–174. [Google Scholar]
- Vaz-Serra, P.; Wasim, M.; Egglestone, S. Design for manufacture and assembly: A case study for a prefabricated bathroom wet wall panel. J. Build. Eng. 2021, 44, 102849. [Google Scholar] [CrossRef]
- Xu, J.H.; Pan, C.X.; Jiang, J.; Huang, L. Research on modular building system for accommodation s of large luxury cruise. In Maritime Technology and Engineering 5; CRC Press: Boca Raton, FL, USA, 2017; Volume 1, pp. 793–799. [Google Scholar]
- Krause, D.; Gebhardt, N.; Greve, E.; Oltmann, J.; Schwenke, J.; Spallek, J. New trends in the design methodology of modularization. In Proceedings of the 11th IDE Workshop, Valencia, Spain, 5–7 April 2017; Volume 5. [Google Scholar]
- Yi, Z.; Mi, S.; Tong, T.; Li, H.; Lin, Y.; Wang, W.; Li, J. Intelligent initial model and case design analysis of smart factory for shipyard in China. Eng. Appl. Artif. Intell. 2023, 123, 106426. [Google Scholar] [CrossRef]
- Kunkera, Z.; Željković, I.; Mimica, R.; Ljubenkov, B.; Opetuk, T. Development of augmented reality technology implementation in a shipbuilding project realization process. J. Mar. Sci. Eng. 2024, 12, 550. [Google Scholar] [CrossRef]
- Ujkani, A.; Hohnrath, P.; Grundmann, R.; Burmeister, H.C. Enhancing Maritime Navigation with Mixed Reality: Assessing Remote Pilotage Concepts and Technologies by In Situ Testing. J. Mar. Sci. Eng. 2024, 12, 1084. [Google Scholar] [CrossRef]
- Wiśnicki, B.; Wagner, N.; Wołejsza, P. Critical areas for successful adoption of technological innovations in sea shipping–the autonomous ship case study. Innov. Eur. J. Soc. Sci. Res. 2024, 37, 582–608. [Google Scholar] [CrossRef]
- Ma, C.; He, R.; Zhang, W. Path optimization of taxi carpooling. PLoS ONE 2018, 13, e0203221. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, Q.X. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Seet, B.C.; Liu, G.; Lee, B.S.; Foh, C.H.; Wong, K.J.; Lee, K.K. A-STAR: A mobile ad hoc routing strategy for metropolis vehicular communications. In Networking 2004: Networking Technologies, Services, and Protocols; Performance of Computer and Communication Networks; Mobile and Wireless Communications Third International IFIP-TC6 Networking Conference Athens, Greece, 9–14 May 2004; Proceedings 3; Springer: Berlin/Heidelberg, Germany, 2004; pp. 989–999. [Google Scholar]
- Yang, J. Application of Floyd algorithm in the design of a coastal tourism route optimization system. J. Coast. Res. 2020, 106, 668–671. [Google Scholar] [CrossRef]
- Al Salami, N.M. Ant colony optimization algorithm. UbiCC J. 2009, 4, 823–826. [Google Scholar]
- Mirjalili, S.; Mirjalili, S. Evolutionary algorithms and neural networks: Theory and applications. In Genetic Algorithm; Springer: Berlin/Heidelberg, Germany, 2018; pp. 43–55. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO)-A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.; Aarts, E.H.; van Laarhoven, P.J.; Aarts, E.H. Simulated Annealing; Springer: Dordrecht, The Netherlands, 1987; pp. 7–15. [Google Scholar]
- Arai, H.; Maung, C.; Schweitzer, H. Optimal column subset selection by A-Star search. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Yang, G.; Li, M.; Gao, Q. Multi-Automated Guided Vehicles Conflict-Free Path Planning for Packaging Workshop Based on Grid Time Windows. Appl. Sci. 2024, 14, 3341. [Google Scholar] [CrossRef]





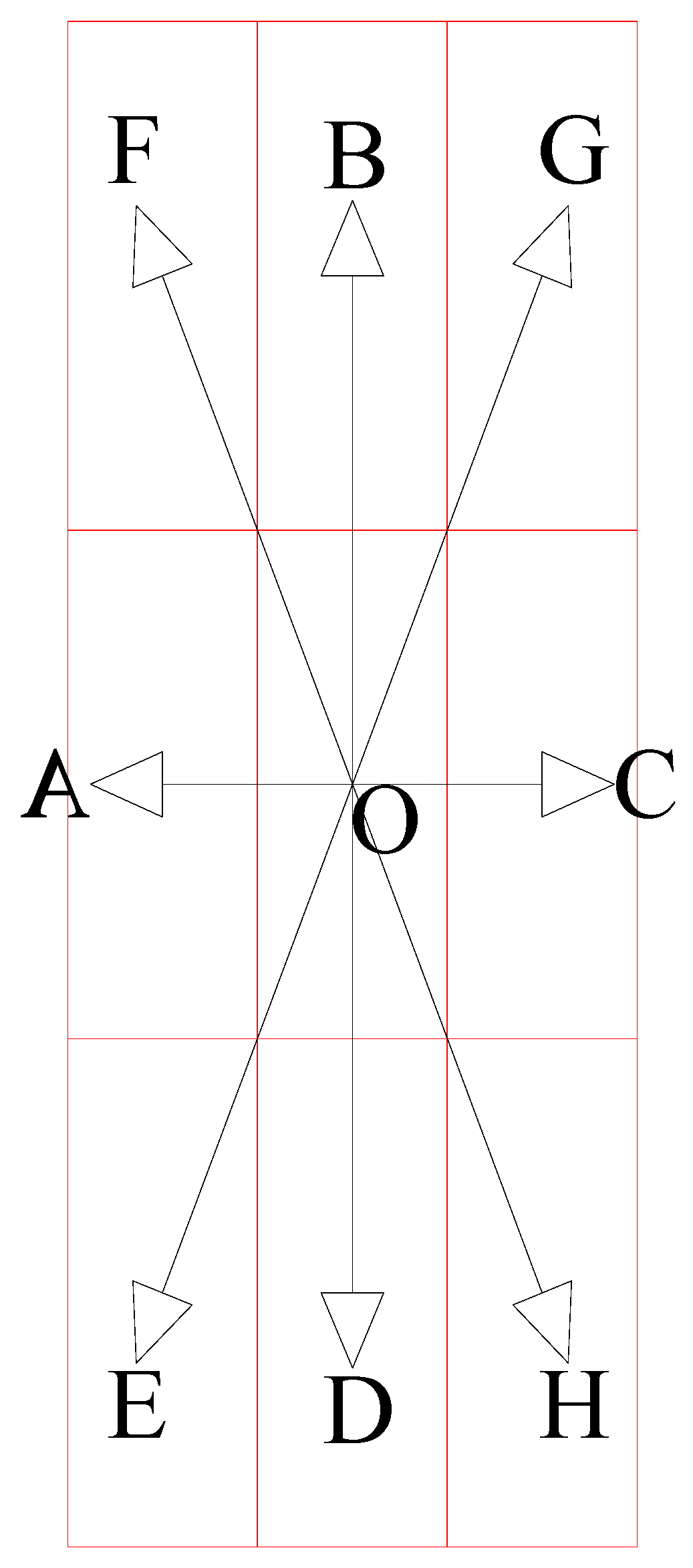

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, L.; Wu, X.; Zhao, Y.; Liu, J.; Liu, K. Research on Path and Sequence Planning for Multi-Cabin Onboard Transportation of Large Cruise Ships. Appl. Sci. 2025, 15, 4406. https://doi.org/10.3390/app15084406
Ju L, Wu X, Zhao Y, Liu J, Liu K. Research on Path and Sequence Planning for Multi-Cabin Onboard Transportation of Large Cruise Ships. Applied Sciences. 2025; 15(8):4406. https://doi.org/10.3390/app15084406
Chicago/Turabian StyleJu, Liyang, Xiaoyuan Wu, Yixi Zhao, Jianfeng Liu, and Kun Liu. 2025. "Research on Path and Sequence Planning for Multi-Cabin Onboard Transportation of Large Cruise Ships" Applied Sciences 15, no. 8: 4406. https://doi.org/10.3390/app15084406
APA StyleJu, L., Wu, X., Zhao, Y., Liu, J., & Liu, K. (2025). Research on Path and Sequence Planning for Multi-Cabin Onboard Transportation of Large Cruise Ships. Applied Sciences, 15(8), 4406. https://doi.org/10.3390/app15084406





