Abstract
In the application of digital twin technology for the heading workface in coal mining, real-time state data will be transmitted to the remote control platform through a gateway device. This cross-system and cross-software data transmission method inevitably introduces transmission delays, resulting in a certain spatiotemporal discrepancy in the virtual model control for the remote control of the physical equipment. In this paper, by analyzing the operational process of the cantilever roadheader, a state evolution dynamics model construction method for the cantilever roadheader is proposed, which includes three stages, the discretization of the operating state based on the cutting path, event-driven graph construction of the cutting state evolution, and real-time data-driven dynamics evolution, so to continuously monitor, analyze, and adjust the operational dynamics of the cantilever roadheader based on real-time state data, thus improving the efficiency, performance, and adaptability. The construction of the model provides a theoretical basis and technical support for the construction and alignment of the digital twin multidimensional model of the cantilever roadheader.
1. Introduction
With the rapid development of technologies such as the industrial Internet [1], 5G communication [2], and sensor network [3], the intelligent heading workface has significantly enhanced its perception capabilities for all elements, including the equipment operation status, personnel spatiotemporal information, geological information, and the roadway environment [4]. At the same time, the volume and dimensions of real-time state data have also increased substantially. In fact, due to the limitations of data computing capabilities, the increase in a large amount of high-dimensional data during the operation process of the intelligent cantilever roadheader cannot be directly applied to the equipment control decision, resulting in a significant waste of real-time state data [5].
Digital twin technology represents a groundbreaking paradigm that creates dynamic, bidirectional linkages between physical entities and their virtual models [6]. The key advantage of digital twin technology is its interactivity and collaborative capability, where the virtual model is able to monitor the physical entity in real time using sensor data, realize dynamic mapping, and validate the control strategy in the virtual environment, and then control the physical entity [7]. This process involves communication and cooperation between physical devices, information exchange between virtual models, and synchronization and dynamic adjustment between virtual and physical models [8].
In the domain of digital twins and virtual–physical interaction modeling, Tao Fei proposed a comprehensive theoretical framework for digital twin connectivity and interaction encompassing the following five core components: perception, communication, physical–virtual mapping, data–model coupling, and fusion. They established the “accurate, real-time, consistent, safe, and reliable” criteria for connectivity and interaction, which not only provides an in-depth analysis of each element along the temporal dimension but also constructs theoretical relationships between cross-dimensional elements. This work fundamentally strengthens the scientific rigor and practical applicability of digital twin connectivity and interaction [9,10].
In intelligent mining systems, digital twin technology drives digital transformation and intelligent advancement across mine construction, extraction operations, monitoring systems, and maintenance processes. By establishing multidimensional equipment models that enable virtual–physical mapping and real-time interaction, this technology enhances mining safety, operational efficiency, and intelligent performance [11]. For remote intelligent excavation applications, digital twin solutions effectively address excavation challenges while boosting productivity and fostering intelligent development. Through state evolution dynamic modeling, the technology achieves real-time equipment monitoring and operational optimization, facilitating the critical transition from automated to fully intelligent excavation operations [12,13].
The fundamental prerequisite for achieving effective virtual–physical interaction lies in maintaining temporal synchronization between the control decision states of physical entities and their digital counterparts. However, the inherent latency across system layers in tunneling systems, arising from sensor data acquisition, network transmission, and computational processing, creates fundamental synchronization challenges between virtual–physical spaces. This cumulative latency disrupts the alignment of decision-making states across virtual and physical systems, significantly diminishing the operational relevance of digital twin-derived decisions, particularly in the intelligent tunneling scenarios demanding rapid response coordination. In addition, the characteristic of physical control decision making is based on simple logical judgment and behavior execution through the collection of physical sensor data. The characteristic of virtual control decision making is based on the in-depth calculation of collected sensor data, thereby extracting the deep information of sensor data and making more precise control decisions in response to changes in the external environment. The key to virtual–physical interaction control is the alignment and unification of the starting points of the states of physical control decision making and virtual control decision making.
Discretization of the running state is an effective method which can establish a state alignment baseline for virtual and physical control decisions. Amanda et al. proposed a state space discretization method incorporating pseudo-random networks for episodic unsupervised learning in Q-learning. This method is particularly suitable for the closed-loop control of deformed or highly reconfigurable systems, and can be used as an effective learning agent [14]. To address the computational challenges of continuous state spaces in epidemic control Markov decision processes, Zhang and Suen developed a state discretization algorithm that outperformed uniform discretization in both synthetic tests and COVID-19 case studies [15]. Leland proposed a discretization filter method for the efficient estimation of nonlinear non-Gaussian state space models, which provides strongly consistent and asymptotically efficient maximum likelihood estimation while being orders of magnitude faster than existing nonlinear methods in low-dimensional settings [16]. Dadashi proposed a reinforcement learning framework that learns state-dependent action space discretization from human demonstrations to enable effective continuous control. The method automatically extracts demonstrator priors and multimodal behavior by identifying plausible action sets for each state [17]. Shi et al. proposed a discrete-time recurrent neural network model that pioneers direct discretization for time-variant problems, departing from conventional continuous system discretization approaches. The model employs second-order Taylor expansion to handle discrete time-variant nonlinear systems originating from robot manipulator modeling, with the theoretical analysis demonstrating its convergence and precision [18].
The event-driven control strategy is a periodic dynamic approach that uses carefully designed trigger states to optimize the control process. Only when these conditions are satisfied does the system update the control instructions. The event-driven control strategy significantly reduces the communication frequency and eases the burden on the bus bandwidth, thus improving the efficiency and responsiveness of the whole system [19]. Santos et al. demonstrated how Discrete Event Simulation serves as an effective digital twin for non-automated processes in Industry 4.0, offering automated data collection, real-time analysis, and continuous decision support. Their systematic approach covers the full DES lifecycle from model construction to real-time integration, showing superior advantages over traditional simulation through case studies that highlight enhanced process adaptability, user-friendly interfaces, and multi-level autonomy capabilities [20]. Karakra et al. presented an approach that builds a digital twin platform using a Discrete Event Simulation system connected to Internet of Things devices. The purpose of this platform is to construct pathways for hospital patients, enabling near-real-time monitoring and predictive simulation [21]. Cubukcuoglu et al. introduced a Discrete Event Simulation tool to aid decision making in hospital space planning and demonstrate the application capabilities of this tool through a specific real-world example [22]. Wang et al. developed a data-driven event-triggered control framework for unknown discrete-time networked systems, proposing a novel distributed event-triggering strategy based on periodic sampling with model-based stability guarantees using discrete-time looped functionals, with numerical validation showing effective transmission reduction in networked control systems [23]. Ge et al. presented a comprehensive review of dynamic event-triggered mechanisms for networked control systems, establishing a unified framework that systematically addresses event-triggered mechanism design and implementation challenges [24].
While continuous state discretization and event-driven mechanisms provide valuable theoretical foundations for virtual–physical synchronization, current research remains insufficient in addressing dynamic state alignment during virtual–physical space interactions, particularly in leveraging virtual control decisions to enhance the system performance. Aimed at the problem of the unification of virtual–physical interaction states caused by frequent changes in control benchmarks under complex working conditions, a discrete state evolution dynamic analysis method for the cantilever roadheader is proposed by introducing the discretization of the operating status and the event-driven mechanism. The logic of the discretization of tunneling operation states is analyzed, the static and dynamic state evolution graph of the cantilever roadheader is constructed, and the state evolution mechanism of the cantilever roadheader driven by real-time data is studied. An application example of the dynamic analysis for the operating state evolution of the intelligent roadheader is designed in the simulation environment.
2. Dynamics Model of the State Evolution of Cantilever Roadheader
Figure 1 shows the architecture of the state evolution dynamics model construction method for the cantilever roadheader, which mainly consists of the following three parts: the discretization of the operating state based on the planned cutting path, the event-driven graph construction of the cutting state evolution, and the real-time data-driven dynamics evolution of the cutting operation state of the cantilever roadheader.
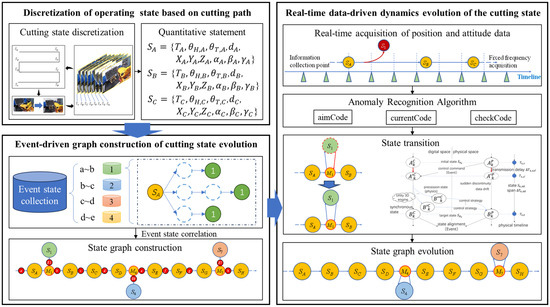
Figure 1.
Logic framework of the state evolution dynamics model for the cantilever roadheader.
Based on the planned cutting trajectory, the deterministic state nodes are discretized uniformly, and each deterministic state node is quantitatively described by the fuselage positional state parameters and timestamp. The relationships between the deterministic state nodes are established based on the temporal sequence of node activations. Descriptions of the deterministic state are used as node attributes to construct a state evolution graph using Neo4j.
During the cutting operation of the heading section, the key position parameters of the roadheader are collected in real time to monitor the operating state of the equipment, and the positional state parameters are screened by the disturbance recognition algorithm. The stochastic state nodes caused by the events are updated in the constructed state evolution graph. To ensure the real-time feedback of the digital twin model to the physical machine, a state transition mechanism is employed to synchronize the benchmark between the virtual control state and the physical control state.
2.1. Discretization of Operating State Based on Cutting Path Planning
Discrete state processing transforms complex physical tunneling behavior into digitally replicable and controllable units through state space discretization, enabling the precise tracking of the state evolution path.
Based on cutting operation requirements, an S-shaped cutting path is planned for the implementation in the heading section, as shown in Figure 2. The cutting head moves from coordinate point SA to point SH within the heading section to complete the cutting work. During this process, the cutting head’s motion alternates between the vertical and horizontal directions, and each transition point between operation modes is defined as a key state node. According to this path, the cutting state is discretized into eight key state nodes (SA to SH). Each state node is quantitatively described by the 10 operating state parameters listed in Table 1, which are categorized into the following four groups:
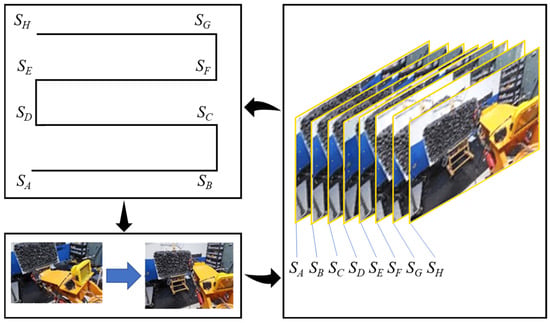
Figure 2.
Schematic of the operating state discretization.

Table 1.
State parameters of the cantilever roadheader.
(1) Fuselage position coordinates: comprising X, Y, and Z coordinate values. X represents the position along the roadway’s forward direction; Y represents the lateral position perpendicular to the roadway; Z represents the vertical height. These parameters define the 3D spatial location of the roadheader.
(2) Fuselage attitude angles: comprising , , , and three angle parameters. (Yaw) represents the steering angle around the Z-axis; (Pitch) represents the tilting angle around the Y-axis; (Roll) represents the tilting angle around the X-axis.
(3) Cutting arm attitude parameters: comprising three kinematic parameters, , , and . represents the rotary platform’s rotating angle; represents the cutting arm’s lifting angle; represents the cutting arm’s extension length. These parameters are used for the precise motion control and pose characterization of the cutting arm of the roadheader.
(4) Timestamp: a UTC-synchronized timestamp marking the data acquisition moment, providing temporal indexing for the virtual–physical state synchronization. The pose vector defines the fuselage state of the roadheader, while the kinematic vector parameterizes the cutting arm motion.
2.2. Event-Driven Graph Construction of Operating State Evolution
2.2.1. Operating State Evolution Relationship and Graph Construction
(1) Static Graph Construction
Based on the cutting state discretization results shown in Figure 3, the equipment position will sequentially transition from state to under ideal working conditions. The inter-node relationships in the graph can be characterized by the following variations in the specific attitude parameters: when transitioning from to , the cutter arm’s rotating angle changes unidirectionally by ; when transitioning from to , the lifting angle changes by . Correspondingly, the transition between nodes and can be expressed as , and between and as .

Figure 3.
Static operating state evolution graph.
(2) Dynamic State Evolutionary Logic
In the cutting process of the heading section, due to the complexity of the underground operating environment, the cutting process will inevitably encounter various disturbance events, which will have a certain impact on the cutting state, resulting in cutting abnormalities. For example, Figure 4a shows the schematic diagram of the normal fuselage posture, and Figure 4b shows the schematic diagram of the fuselage posture after sliding. In the cutting process from to , the reaction force of the cutting head may cause the fuselage to slide sideways, and the changed fuselage position and attitude state of the cantilever roadheader cannot ensure optimal cutting quality according to the planned cutting trajectory.
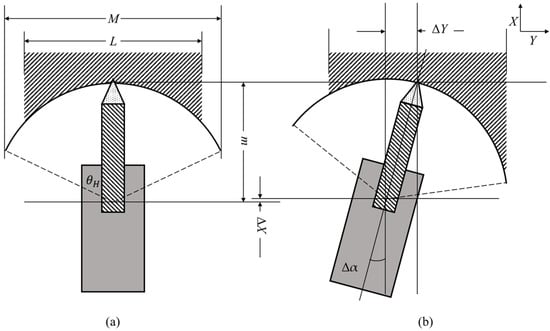
Figure 4.
Fuselage slippage of the cantilever roadheader.
If the current fuselage slip event is regarded as an abnormal perturbation event, then the original fuselage attitude state evolution graph must be dynamically changed to ensure the feedback reliability of the graph. The abnormal perturbation occurs during the transition from state to , so the relationship between and will be changed, and a new abnormal state node will be added between and due to the perturbation event. As shown in Figure 5, the planned state node at the moment before the anomalous state is generated will be recorded as the intermediate state node, and, at the same time, will be used as the target node for the correction of this anomalous state in order to ensure that the evolution of the state node returns to normal.
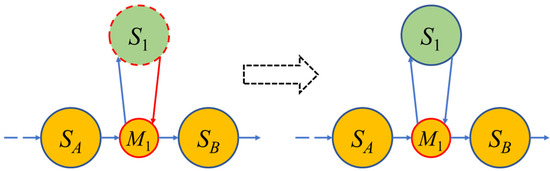
Figure 5.
State branches in the state evolution graph.
During the intelligent cutting operations, abnormal disturbance events can cause the original cutting path to be disrupted at any time. In order to ensure the cutting quality of the heading section, adjustments must be made to restore the roadheader state to the intended route when the operation state is disturbed. In this context, the state evolution network of the heading workface needs to realize closed-loop control when abnormal state branches appear, i.e., it automatically corrects the abnormal changes in the tunneling state caused by disturbances and returns to the planned operation path.
As shown in Figure 6, and are both intermediate state nodes of the same type as within the established state evolution path. In addition, the downtime mechanism at the time of perturbation enhances the executability of the state regression, and the anomalous state nodes return to the planned state evolution graph with the intermediate state nodes as the evolution target.
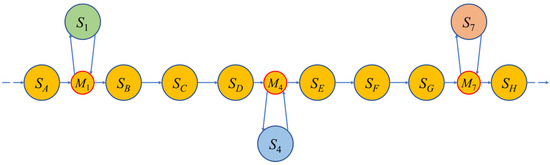
Figure 6.
Closed-loop state evolution graph.
2.2.2. Event State Model
The automated mapping change relies on event triggering, which requires a predefined anomaly judgment scheme. Monitoring the acceleration variation in key cutting actions is essential to detect operational event changes. During normal operation, key cutting actions maintain uniform speed, and acceleration fluctuations indicate state abnormalities. For example, the platform’s rotary speed and acceleration are calculated by the following formula based on current time and the specific rotation angle :
where , , denote the respective parameters at time step .
By monitoring these parameters, the operating state normality can be determined, enabling timely measures to ensure safety and operational continuity. Abnormal acceleration fluctuations may signal operational anomalies, necessitating corrective actions for inspection.
The operational state of the equipment is characterized by the following four key parameters: the timestamp, rotation angle, lifting angle, and extension length. Variations in the acceleration of critical movements stem from the following two distinct sources: controlled adjustments following operational commands and kinematic deformations caused by external disturbances. During command-driven movements, the system maintains stable states before and after adjustments with near-zero acceleration, where the magnitude and duration of acceleration changes strictly correspond to control instructions, enabling precise action range determination. In contrast, the disturbance generates irregular acceleration patterns, whose abnormality can be identified through non-zero acceleration residuals combined with deviations from the expected command execution timelines, providing a robust mechanism for operational anomaly detection.
When acceleration deviations diverge from control commands or maintain non-zero values beyond the prescribed operation period, this indicates potential disturbance impacts on the operational behavior. Immediate corrective measures are then required to ensure the operational quality and safety. This approach enables the effective monitoring of intelligent cutting processes, allowing for timely responses to various disturbance events. The definition and characterization of events directly determine the effectiveness of the detection algorithms. Event definitions must encompass both command-triggered behaviors specified in the planned cutting trajectory and unplanned disturbances caused by complex geological conditions.
The core of event analysis lies in state monitoring and control. Therefore, event description methods should be derived from the state definition model. The cutting state is defined through temporal nodes and spatial coordinates, with discretization based on operational plans. Each state transition reflects significant changes in equipment parameters, representing the triggering of planned events. Based on state discretization and key state node definitions, events can be characterized through variations in the key kinematic parameters of the cutting arm of the roadheader.
As shown in Figure 7, each state node is preceded by a corresponding event node. Events A to H are triggered by the planned operation instructions, which cause the state of the cutting operation to change in an orderly manner according to the planned cutting trajectory. Events , , and are caused by parameter shifts due to unexpected situations, and the occurrence of such disturbing events leads to the shift of the operation state beyond the planned threshold, thus failing to guarantee the heading section quality. Based on the correspondence between events and states, events can be defined vectorially, . This definition method helps to clarify the relationship between events and state changes, and provides a basis for event detection and processing. Through this method, the events in the cutting process can be accurately captured and described, and then effective state control can be realized.
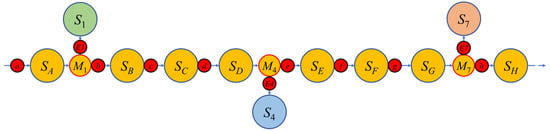
Figure 7.
Key event state schematic.
2.2.3. Event and State Storage Model
Building a state evolution graph requires storing and retrieving historical states, and event state models require a database to record historical events. Anomalous states from prior excavation cycles are integrated into the state set to initialize new cycles. With the accumulation of data from multiple intercepts, the state evolution graph will be more comprehensive in covering the perturbation event states, thus improving the accuracy of the state evolution graph-based roadheader position recognition and control.
The stored deterministic event states are based on the key features of previous states, including threshold descriptions. To reduce the computational burden in the evolution process, the established event states and perturbed event states should be stored in a unified mode. However, the perturbation event states do not require threshold delineation, so the threshold descriptions of the key feature values are not included when storing such states. Therefore, a unified storage model should be designed for these two different categories of events. The event states are categorized and stored hierarchically according to the division of the state thresholds and the different stages of the truncation operation, using the threshold division results as the criteria for determining the state intervals, and the state descriptions are based on the current spatial and temporal attitude parameters, and the state points within different state intervals are defined as different types.
In the same cutting trajectory, different perturbation states are categorized as the same type. For example, in Figure 8, the three potential perturbation event states derived during the transition from state to are all considered to be of type 1. Despite the fact that these events belong to the same type, there are significant differences between them. These differences arise because multiple error accumulations are experienced as the state deviates from the normal path, and the type and degree of error is influenced by the specific scenario, resulting in anomalies of the same type that may end up being very different. Therefore, the hierarchical classification storage scheme adopted is actually an organization of the irregular state evolution process. As shown in Figure 8, the upward protruding state node and the opposite direction are of the same type of abnormal event because they both occurred during the same truncation stage. As for , it represents a normal truncation state that does not exceed the constraint threshold.
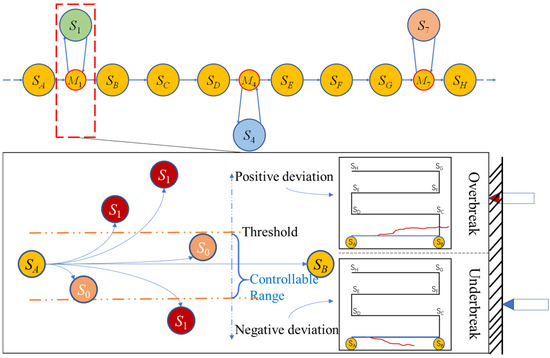
Figure 8.
Schematic diagram of the classification of event types.
2.3. Real-Time Data-Driven Dynamics Evolution of the Cutting State
2.3.1. Disturbance Recognition Algorithm
The basis of the model operation lies in the ability to identify anomalous states. The method of identifying event state types is critical to the endogenous evolution of the model’s dynamics. As shown in Figure 9, the disturbance recognition algorithm consists of the following three state identifiers: aimCode, currentCode, and checkCode, which are consistently judged through a different-or-other (XOR) relationship. The 0 or 1 in these identifiers represents a change in the acceleration of a parameter at the current timestamp, with a change being 1 and no change being 0.
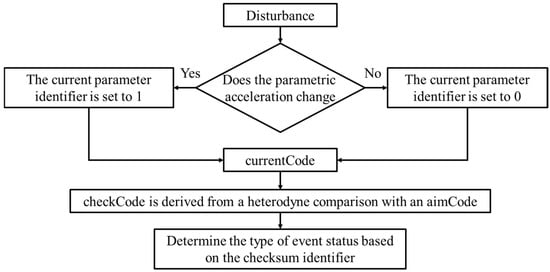
Figure 9.
Flowchart of disturbance recognition algorithm.
The aimCode represents a control command event at the current timestamp. For example, during the cutting process from state to , the system needs to adjust the motion mode, stop rotating, and start lifting the cutting arm, and the overall fuselage position remains unchanged. Taking the case of not considering the cutting arm extension as an example, the system command event identifier at should be T110000000, where T stands for the timestamp of the system command, and the numbers from the left to the right represent the platform rotating acceleration, the cutting arm lifting angle acceleration, the cutting arm extension, the spatial coordinates of X, Y, and Z, the fuselage yaw angle α acceleration, the fuselage pitch angle β acceleration, and the fuselage roll angle acceleration. The other parameters are 0 if they are unchanged, the rotating angle acceleration of rotation platform becomes negative when the rotating stops, and the cutter arm lifting angle acceleration increases suddenly when the lifting starts.
As shown in Figure 8, abnormal perturbations usually occur in non-system command bits. Under these conditions, when branch state node is generated, the cutting state should maintain the original operation state, i.e., the aimCode should be 000000000. If the current state is the lifting angle abnormality, the corresponding acceleration of the lifting angle will change, i.e., the current state identification code currentCode is 010000000. Comparing aimCode and currentCode, we can obtain the specific variable of the unplanned change, i.e., checkCode is 010000000. According to checkCode, we can determine the type of current event.
Before constructing the event-triggering mechanism, it is crucial to clarify its role and the significance of its construction. The core objective of the mechanism is to ensure the synchronization of the virtual and physical in the intelligent cutting process. In the current synchronization scheme, the virtual control platform and the physical cutting process synchronize their operations according to the instructions of the planned operation. If the cutting process encounters disturbances that lead to unplanned changes in the operation, the virtual–real synchronization that was originally maintained by synchronizing the operation instructions will be destroyed. The virtual cutting scene needs to be adjusted according to the real data feedback from the physical cutting, but this process generates a time delay. If the virtual cutting state is adjusted in real time according to sensor data, the virtual cutting state will always lag behind the physical cutting state, which cannot accurately reflect the current cutting state, affecting the corrective decision making of the intelligent tunneling system on cutting anomalies. The event-triggering mechanism identifies the disturbance event when it occurs and adjusts the virtual synchronization strategy.
When a change in the cutting state is detected by an acceleration comparison, the value of the specific parameter change is calculated and compared with the last two control instruction change nodes. If the established operation control instructions do not contain the current change, it means that the state change is caused by a disturbance event.
Determining the class of disturbance events is crucial to change the virtual–physical alignment strategy. The state evolution graph contains various event trees, as shown in Figure 10. Based on the event tree structure after the current state change, according to the categorized hierarchical storage model, starting from the type of stage at which the event occurs, one by one, a downward comparison with the event trees already existing in the network is filtered. If the same event tree exists in the formed state evolution graph, the strategy to correct the current perturbation is determined based on the historical processing scheme of the corresponding event. If the search and comparison results show that it does not exist, a new strategy needs to be formulated based on the current specific situation, and the new event tree is bound to the current processing strategy and stored into the existing state evolution graph.
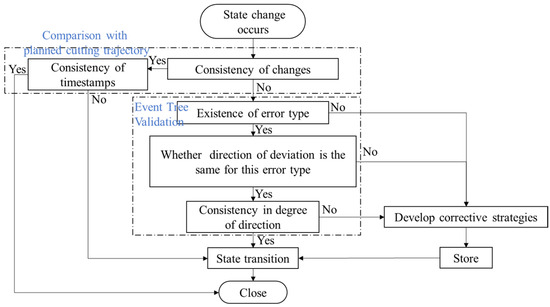
Figure 10.
Disturbance event recognition flowchart.
2.3.2. Real-Time Data-Driven
First, data are collected at a fixed frequency to monitor changes in the equipment position parameters. The key parameters of the roadheader, such as the position, attitude, and velocity, can be accurately tracked mainly by periodically collecting them. A schematic diagram of real-time data acquisition is shown in Figure 11. The data acquisition system operates at a preset fixed frequency, e.g., once per second or multiple times per second, depending on the operating characteristics of the equipment and the required monitoring accuracy. Each time data are collected, they are instantly processed and analyzed to determine if the equipment is in a normal operating condition. If an abnormal change in a monitored parameter is detected, the system immediately triggers a subsequent processing program. This process is automated, ensuring a rapid response to abnormal conditions.

Figure 11.
Real-time data acquisition.
Abnormality detection relies on parameter threshold monitoring. As soon as a parameter falls outside of these preset ranges, the system recognizes the abnormality and initiates the appropriate processing. This involves not only automatically adjusting the equipment settings or performing operations such as emergency shutdown, but also issuing alarms to notify the operators to prevent potential equipment damage or production accidents.
In addition, the mechanism can record the exact time the disturbance occurred and the stage of operation the equipment was in. This is critical for subsequent troubleshooting and system optimization, as it provides a detailed timeline and contextual information to help engineers analyze why the anomaly occurred and take targeted measures for improvement.
Real-time data will be used as a guarantee of the timeliness of the event triggering of the model, and the specific flow logic of the event triggering is shown in Figure 12, which sequentially connects the modules in series according to the flow direction of the perturbation event information, and the fuselage slipping event is used as an example to illustrate the operation mechanism of the state evolution dynamics model.
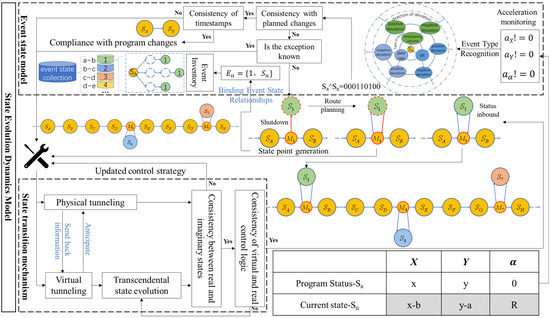
Figure 12.
Disturbance event information flowchart.
When fuselage slip occurs, the coordinate positions (X, Y) as well as the orientation (α) of the fuselage undergo different degrees of change. At time point , by monitoring the acceleration changes in X, Y, and α, the event state model can recognize the cutting state transition. By performing the XOR operation on the actual state parameters and the planned state parameters, a result of 000110100 is obtained. Based on this result, the type of perturbation of the current event can be identified and compared with the historical event database to determine if the event type has been recorded. If the event matching result indicates that the type is known, the corresponding historical processing scheme is immediately activated. Conversely, if the matching result indicates that the current event type is unprecedented, a new state node is created in the state evolution dynamics model and the state is associated with the event type, the event state vector is constructed, and the event is recorded according to the storage rules of the event library.
Emerging state nodes, triggered by unknown events, generate branches in the original state evolution graph. Depending on the details of the state offsets and the criteria of the job plan, a trajectory needs to be planned to guide the current abnormal state back to the normal state before the next scheduled job change node. Based on the results of the path planning, a control strategy for the state change can be developed and implemented.
Regardless of whether the event is known or not, the quality of the synchronization of the virtual cutting scene with the physical cutting scene needs to be ensured by the state transition mechanism during the execution of the state correction policy. The virtual and physical cutting operation will execute the control strategy simultaneously, and the physical cutting scene will continuously feedback the changed state to the virtual control platform. The virtual cutting model performs over-the-top state evolution based on the feedback information and control strategy to reduce the lag of the virtual–physical information transfer.
When the physical state evolves according to the control command to the moment corresponding to the predicted state, the virtual-reality consistency evaluation will be performed. The evaluation first checks the state similarity; if it does not meet the alignment criteria, the control strategy is adjusted according to the state deviation. If the similarity meets the criteria, the consistency of the control strategy is checked. If both the state and the control strategy are consistent at this moment, it indicates that the information transmission delay problem has been solved and the virtual–physical synchronization has been achieved, and no further loop feedback and strategy adjustment is required. Virtual and physical tunneling will synchronize to adjust the cutting state to within the planned range according to the latest control strategy, and the state evolution graph records this change path to form a closed loop. After the disturbance event is processed, the new state evolution path will be used as a reference for future processing. As the process is triggered multiple times, the disturbance event types will be more comprehensive, the state evolution graph will be more complete, and the efficiency and reliability of the state evolution dynamics model will be improved.
2.3.3. State Transition Mechanism
After the abnormal state is recognized, a state transition mechanism is employed to ensure that the transition to the normal operating state is both rapid and smooth. To ensure the accuracy of the information feedback from the remote control system, the state transition involves the synchronization of the physical and virtual control environment. This synchronized processing improves the accuracy and reliability of the transition process, enabling an efficient transition from abnormal to normal conditions. By keeping the data of the two environments synchronized in real time, the time delay of information transmission is minimized, which enhances the ability to instantly control the operation status.
The leap process involves synchronization work in both spatial and temporal dimensions, including threshold synchronization and periodic synchronization. As shown in Figure 13, at timestamp T1, the physical spatial model executes a control instruction that is scheduled to perform a state change at the same time as the digital twin. However, the moment when the digital spatial model executes this instruction is not synchronized with the physical model due to the inherent time delay. The digital model completes the state change to A1 at timestamp T2, corresponding to the state B1 of the physical model at timestamp T1. At this point, the digital space side is already behind compared to the time when the instruction was executed in the physical space, and the state of the physical model has transitioned to an intermediate state B1′.
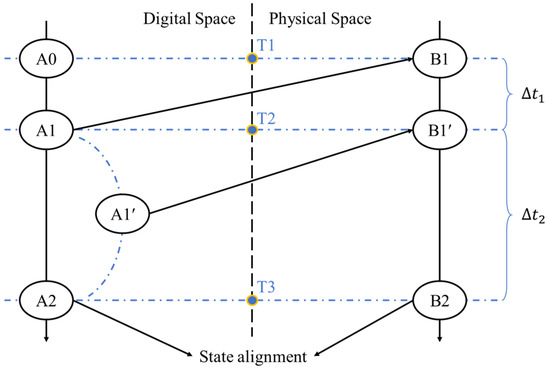
Figure 13.
State transition schematic.
In order to optimize the digital twin hysteresis problem caused by the inherent time delay, the digital model will predict the future state evolution of the physical model when the state change is performed at timestamp T2. The predicted state of the physical model will be changed to B2 at timestamp T3, and the digital model will take the predicted B2 as the goal of the state change, and take timestamp T3 as the endpoint of the change to carry out the state leap of the digital twin model. At this time, the digital model will no longer follow the state evolution route of the physical model via the intermediate state B1′, and the state of the object on one side of the digital space will be changed directly from A1 to A2 via .
After completing the leap, the bilateral spatial model state will reach a real sense of spatiotemporal synchronization at timestamp T3. By predicting and adjusting the state change target and time of the digital model, the effect of the inherent time delay on the digital twin lag can be effectively reduced, and more accurate spatiotemporal synchronization can be achieved.
Threshold synchronization, based on the state transition principle, identifies the critical state B1′ achieved at timestamp T2 when lateral slippage occurs during physical tunneling. Upon exceeding preset thresholds, cutting arm adjustments alone become insufficient to meet the operational requirements, triggering classification as a new disturbance event. This event state mapping relationship is archived in the database and integrated into the state evolution graph. The physical operation must adjust the body parameters to return to the normal operation state. The state evolution path of the digital twin may deviate from the physical tunneling because the operation state experiencing the sudden perturbation is not in the planned trajectory. To ensure the synchronization between the virtual and physical state after a disturbance event, the corrective control commands of the physical tunneling operation need to be combined with the auxiliary guidance of the digital twin. Based on the current physical operation state, the digital twin predicts the future operation state of the physical machine based on the corrective control instructions to carry out the super-evolutionary state evolution, adjusts the corrective control instructions appropriately according to the degree of compliance of the evolution results, and carries out the super-evolutionary state evolution again. Through multiple cyclic leaps, the physical cutting operation is finally brought back on track, realizing the temporal and spatial alignment of the bilateral space operation at timestamp T3.
Periodic synchronization, on the other hand, refers to conducting a virtual–physical consistency evaluation when initiating each intercept, whenever an operation instruction is issued, thereby enhancing the synchronization reliability. By performing this evaluation at the cycle start, potential deviations are detectable and correctable, ensuring virtual–physical consistency. This method improves the cutting operation accuracy and stability while mitigating disturbance-induced deviation risks.
3. Experimental Verification
3.1. Static State Evolution Graph Construction of a Cantilever Roadheader
According to the operation plan, the initial state evolution graph structure is constructed using Neo4j, and deterministic state nodes are embedded into the state evolution graph. As shown in Figure 14, the relevant parameter nodes of each state node are determined according to the planned cutting trajectory. During stable cutting operation, the state evolution path will pass through each node from to in sequence.
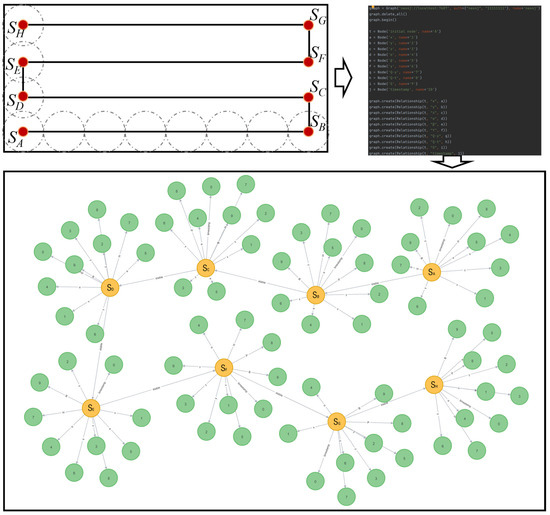
Figure 14.
Static state evolution graph construction.
3.2. Simulation and Analysis of Abnormal Events
Firstly, according to the anomalies of the fuselage position, they are categorized into the following four basic anomaly modes: fuselage slip, fuselage head-up, fuselage forward tilt, and fuselage roll; at the same time, they contain a variety of composite situations, and the anomalies that may occur in this phase are shown in Table 2. It should be noted that the fuselage side tilt and slip cases have the possibility of anomalies occurring in two different directions, and the specific direction of the attitude change will be derived from the data analysis.

Table 2.
Abnormal event type.
The first step of the experiment will start with the simulation of disturbance events. As shown in Figure 15, the inertial guidance module can monitor the displacement and deflection of the fuselage in three axial directions, and the occurrence of the above abnormal events is simulated by the directional interference of the inertial guidance module. Then, a single abnormal event is used as the basis for the analysis, and the composite event is split into several single events to be analyzed separately.
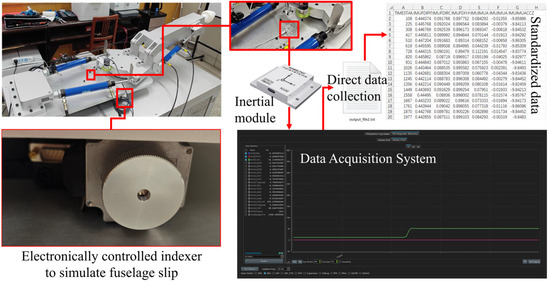
Figure 15.
Data acquisition.
Figure 16 sequentially presents the fuselage parameter variation trends under the four single-event conditions. While the previous section has explained the changes caused by the pure slip event in this figure, the underlying principles for the other single-event scenarios follow the same analytical methodology.
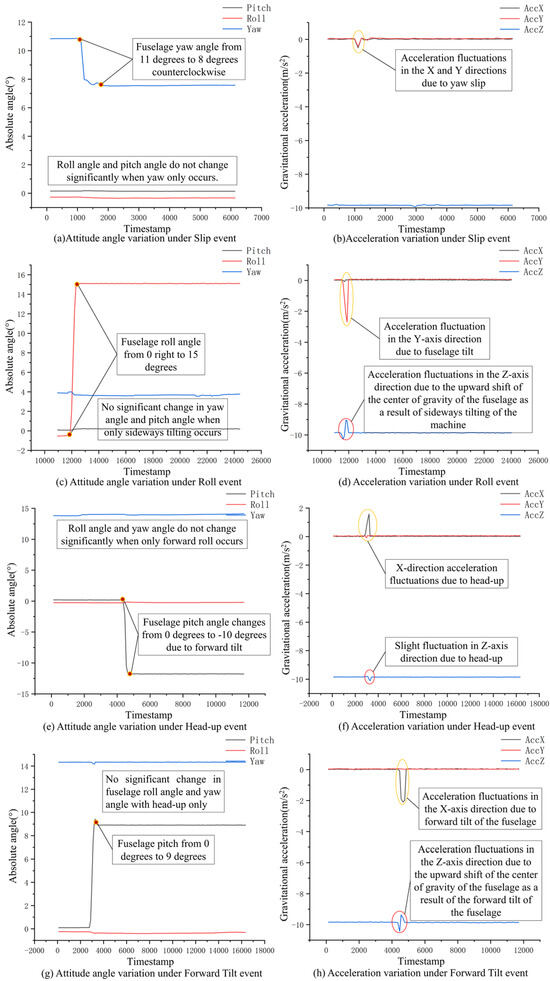
Figure 16.
Change trend in the fuselage parameters under a single event.
Figure 16a illustrates the variation trends in key attitude angles during a pure fuselage slip event. The yaw angle decreases from 11° to 8°, indicating a leftward deviation in heading, while the roll and pitch angles remain stable—confirming that the attitude change is exclusively yaw-axis-oriented. This conclusion is further validated by Figure 16b, which displays the corresponding gravity acceleration trends along each axis during the event. The synchronized fluctuations observed in both X-axis and Y-axis accelerations are attributed to the displacement of the center of gravity during slipping, with differential magnitudes reflecting asymmetric center of gravity shifts. Notably, the absence of Z-axis acceleration variations confirms no significant vertical motion, ruling out concurrent pitch or roll events. Figure 16c and Figure 16d show the changes in fuselage attitude parameters and acceleration fluctuations under a single roll event. Figure 16e and Figure 16f show the changes in fuselage attitude parameters and acceleration fluctuations under a single head-up event. Figure 16g and Figure 16h show the changes in fuselage attitude parameters and acceleration fluctuations under a single forward tilt event. The acceleration fluctuations in these situations are caused by the displacement of the center of gravity due to changes in its attitude angle.
Due to space limitations, this paper presents only representative analysis results of fuselage parameter variations under composite event conditions.
Figure 17a quantifies the following associated attitude changes: the yaw angle increasing from 7° to 9°, the roll angle developing from 0° to 6°, and the pitch angle rising from 0° to 8°. Figure 17b presents the variation trends in axial accelerations during concurrent fuselage pitch, roll, and yaw motions. The observed Z-axis gravitational acceleration fluctuations result from the elevated center of gravity due to combined pitch and roll effects, while the X-axis variations reflect the backward center of gravity displacement during pitch, and the Y-axis oscillations correspond to the lateral center of gravity shifts induced by roll. These analytical principles equally apply to simultaneous forward pitch, roll, and lateral tilt scenarios.
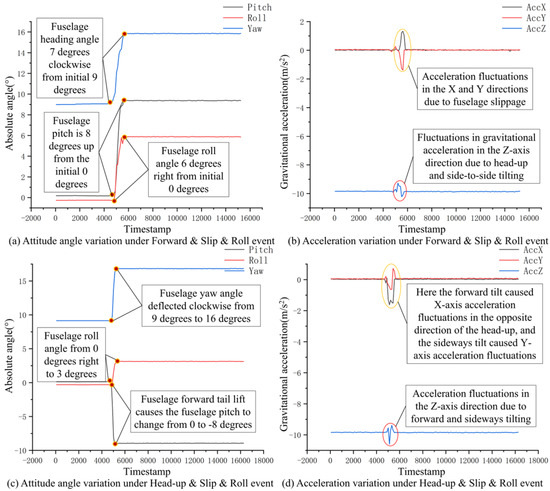
Figure 17.
Change trend in the fuselage parameters under multiple composite events.
Figure 17c shows that the fuselage pitch angle changes from 0 degrees to -8 degrees, and the change in the absolute angle value of the pitch angle to a negative value shows that the fuselage is tilted forward; if the value of the absolute angle value changes in the opposite direction, it means that the fuselage lifts its head. The yaw angle of the fuselage changes from about 9 degrees to 16 degrees, and, according to the direction of the change in the value of the absolute angle, it can be obtained that the fuselage slips clockwise; if the value of the absolute angle changes in the opposite direction, it means that the fuselage slips in the opposite direction. The roll angle of the fuselage changes from 0 degrees to 3 degrees, and, according to the direction of its absolute angle changes, it can be concluded that the fuselage has a right tilt phenomenon; if the absolute angle changes in the opposite direction, it means that the fuselage has a left tilt. Figure 17d shows the acceleration monitoring results of the three axes of the fuselage position. The Z-axis acceleration fluctuation indicates that the center of gravity of the fuselage is upward, and the X-axis and Y-axis acceleration fluctuations indicate that the fuselage is displaced in the X-axis and Y-axis directions.
3.3. Abnormal Event Recognition Algorithm
The analysis of the data was carried out by the event recognition algorithm, and the basic content of the event recognition algorithm is the identification of abnormal changes in the fuselage position state data and the judgment of the abnormal threshold value.
(1) Abnormal Status Recognition
As shown in Figure 18, aimCode denotes the fuselage control command checksum at current timestamp, currentCode (e.g., 001110) captures real-time event signatures, while checkCode flags anomaly detection results. Detected abnormalities induce fuselage displacement on dual axes with heading deviation, triggering dynamic graph updates. The node embodies emergent anomaly states, whereas preserves planned reference states for attitude recovery. Once a disturbance event is detected on the fuselage, the cutting operations will be suspended, and can be seen as instantaneously generated, while is the target state node for fuselage attitude correction.
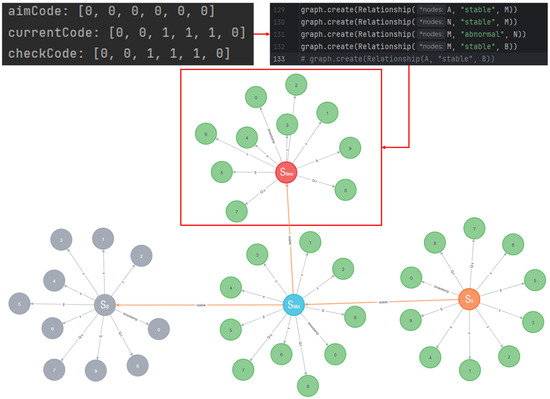
Figure 18.
The process of generating abnormal states triggered by state identification codes.
(2) Abnormal Degree Judgment
When analyzing a standalone fuselage slip event, the yaw angle deviation post-slip necessitates compensatory adjustments to maintain the cutting quality. As illustrated in Figure 19, the algorithmic logic integrates the following three core parameters: fuselage positional correction, cutting arm rotating compensation, and yaw angle recalibration. This multi-parameter coordination ensures operational continuity while addressing slip-induced deviations.
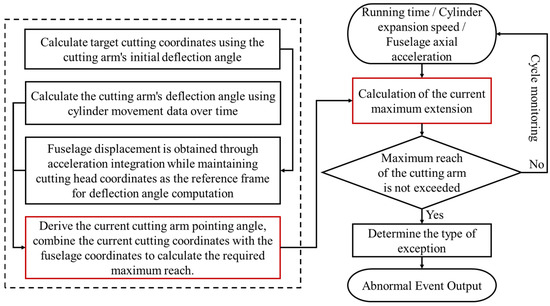
Figure 19.
Disturbance event detection algorithm based on the maximum extension of the cutting arm.
As shown in Figure 20, first determine the relationship between the cylinder expansion and angle change, where τ is the angle formed by the fixed points of the two oil cylinders on the rotating platform and the center of rotation; φ is the angle between the radius of rotation where the cylinder on this side is located at the fixed point of the rotary platform, the straight line where the center of rotation is located, and where the rear end of the cylinder on that side is located.
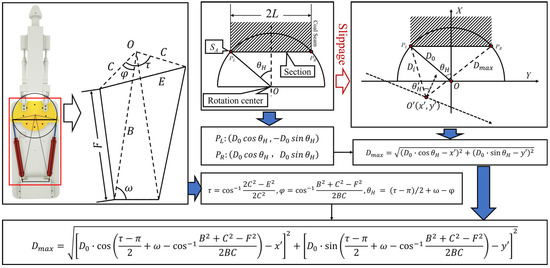
Figure 20.
Maximum cutting arm elongation algorithm required after sliding.
The formal descriptions of τ and φ are given by the following formulas:
Then, determine the relationship between the change in the pointing angle of the cutting arm, where is the angle between the cutting arm and the heading direction, and set the initial operation, i.e., the cutting head is in the state when the angle is , the target cutting width of the roadway is 2L, and the initial length of the cutting arm is , so that the following relationship can be obtained:
Take the slewing center of the rotary platform as the origin, and obtain the coordinates of the horizontal left endpoint and the right endpoint of the roadway interface in the Z-direction projection, as follows:
The cutting arm length required to meet the effective cutting in the current situation is calculated by setting the slewing center of the rotary platform to slip from to after the fuselage slip; is the maximum length of the cutting arm required; at the moment when the slip occurs, the default slewing angle of the rotary platform is zero (the slewing angle can also be calculated based on the timestamp acquisition to derive the result of the slip); x, y are the relative displacements of the fuselage in the X, Y coordinate direction at the present time of the slip. The calculation formula for the maximum cutting arm extension length is shown in Figure 20.
If the maximum length of the cutting arm has exceeded the fixed length of the cutting arm that satisfies the safe cutting, it means that an abnormality has occurred in the current fuselage position, and the slip event experienced by the current fuselage can be regarded as a disturbance event.
3.4. Dynamic Graph Update
When an anomaly occurs during state evolution, the anomaly state type code is matched against known disturbance states in the database. If a match is found, it is processed according to the historical scheme; if the same type of event is not found, a new state node is created in the state evolution network and a new event state is established to record the disturbance event into the database. Figure 14 demonstrates that the initial state evolution graph generates new state nodes after experiencing a fuselage offset event, and the updated state evolution network structure is shown in Figure 21. In the transition from state to state , different anomalous events cause different disturbance state branches. The blue nodes connected by the red STABLE relationship are the initial state evolution graph, i.e., the planned state evolution path, and the orange state node is the last state node on the planned path before downtime, from which the abnormal state evolution crosses over to the unplanned evolution path. Red state nodes, such as , , and , are newly generated anomalous event state nodes, and successful node generation implies that the event state has been deposited into the historical event repository of the event state model.
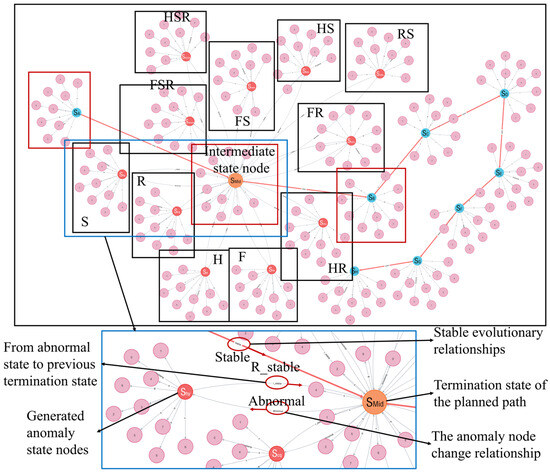
Figure 21.
State evolution graph dynamic update.
While dynamically updating the anomalous event state node in the state evolution graph, the event state model will formulate and execute the fuselage attitude correction strategy based on the current fuselage position parameters, with as the target state node, to ensure the quality of the subsequent cutting operation. The evolutionary relationship STABLE from to is consistent with that of the conventional state evolution path, demonstrating the effectiveness of the state regression scheme after the correction of the abnormal state.
Figure 22 shows the constructed event state monitoring upper platform, which can monitor the changes in various parameters of the roadheader, the dynamics of the state evolution graph, and the log records of the execution of control commands in real time, and, in this case, it can provide visual feedback on the processing and processing results of the state evolution dynamics model after a disturbance event.
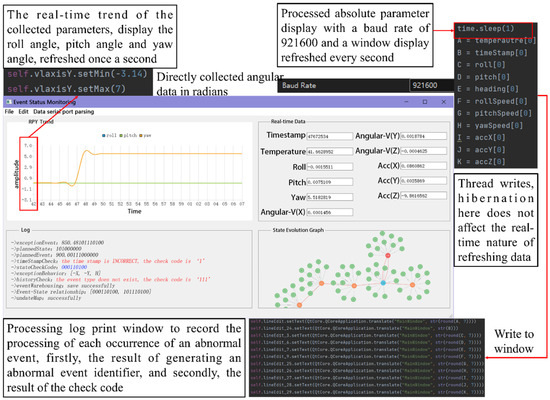
Figure 22.
Event status monitoring platform.
4. Results Analysis
In this study, the monitoring, receiving, and processing of the fuselage position parameters, the operation of the abnormal event recognition algorithm and the abnormal event type recognition algorithm, and the dynamic update of the tunneling state evolution network are accomplished from the simulation of abnormal fuselage disturbance events and the recognition and processing of abnormal events. The results of this case validate the feasibility of the state evolution dynamics model proposed in this paper, but there are also many limitations.
The shortcoming is that the model’s current scope of application is mainly limited to the digging operation within a single section, and the adaptability and long-term stability of the model for the long-cycle operation of multiple sections still need to be further researched and verified. Future research will be devoted to expanding the applicability of the model, especially in complex and variable long-cycle tunneling operations, by improving the adaptive conditions of the model and optimizing the operation modes, so as to enhance the stability and robustness of the model. This will bring more innovation and value to the field of remote intelligent tunneling and promote the development of tunneling technology to a higher level.
4.1. Reflection on Limitations
(1) Strong single-intercept scenario dependence: the model performs well in single-intercept operations, but the state evolution graph complexity grows exponentially in long-period multiple-intercept scenarios, leading to an increase in computational resource consumption and a decrease in real-time performance.
(2) Insufficient algorithm robustness: the classification accuracy of the anomaly identification algorithm for composite perturbations is low and needs to be combined with machine learning to optimize the feature extraction logic.
(3) Simplified experimental scenarios: the current experiments only simulate a single model and a fixed roadway heading section, and do not cover the full cross-section roadheader or complex geological conditions.
4.2. Improvement Direction
(1) Introducing a lightweight model: adopting federated learning or edge computing technology to distribute the state evolution network to multiple computing nodes to reduce the computational load of the multi-section scenario.
(2) Fusion of multi-source data: combine geo-radar and inertial navigation data to enhance the prediction ability of disturbance events and reduce the proportion of passive response.
(3) Extended application validation: cooperate with coal mining enterprises to deploy the model in real digging faces to verify its applicability in extreme working conditions, such as gas protrusion and surrounding rock fragmentation.
5. Conclusions
This study innovatively addresses the virtual–physical synchronization challenges in the digital twin-enabled remote intelligent control of the cantilever roadheader. By introducing an event-driven mechanism and state discretization methodology, an operating state evolution dynamic model is developed to achieve real-time equipment monitoring and active anomaly response capabilities. The proposed model integrates several of the following key innovations: real-time equipment state monitoring, event extraction and classification, operating state discretization, and dynamic evolution modeling of state transitions. The model’s architecture supports the construction of static and dynamic state evolution graphs, providing a theoretical foundation for multidimensional digital twin correlation mapping and virtual–physical synchronization in intelligent tunneling operations. Validation in single-cycle excavation scenarios demonstrates robust virtual–real state convergence stability and composite disturbance identification performance. While current limitations persist in the multi-cycle operational adaptability and heterogeneous equipment platform compatibility, future work will focus on breakthrough innovations in model self-optimization for prolonged operations through distributed intelligent computing architectures and multi-source data fusion technology. The findings provide theoretical foundations for constructing intelligent excavation ecosystems with autonomous perception–decision–execution capabilities. The proposed methodological framework offers universally applicable guidance for digital transformation in complex underground operations, including tunnel engineering and subsea drilling.
Author Contributions
Conceptualization, Y.W., X.Z. and Y.Z.; methodology, Y.W. and Z.Y.; software, Y.W. and Z.Y.; validation, Z.Y. and H.K. and Y.G.; formal analysis, Z.Y.; investigation, Z.Y. and H.K.; resources, Y.W. and Y.Z.; data curation, Z.Y.; writing—original draft preparation, Z.Y.; writing—review and editing, Y.W. and Z.Y.; visualization, Y.W., Z.Y. and H.K.; supervision, Y.W.; project administration, Y.W.; funding acquisition, Y.W.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52204176), the China Postdoctoral Science Foundation (No. 2023MD734221), and the Natural Science Foundation of Shaanxi Province (No. 2019JQ-101).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Authors Y.W. and Y.Z. were employed by the company Xi’an Coal Mining Machinery Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, G.; Chen, C.-H.; Cao, X.; Zhong, R.Y.; Duan, X.; Li, P. Industrial Internet of Things-enabled monitoring and maintenance mechanism for fully mechanized mining equipment. Adv. Eng. Inform. 2022, 54, 101782. [Google Scholar] [CrossRef]
- Zhan, P. Application of 5G Communication Technology Based on Intelligent Sensor Network in Coal Mining. J. Sens. 2023, 2023, 2114387. [Google Scholar] [CrossRef]
- Thirumal, G.; Kumar, C. Multilevel sensor deployment approach in IIoT-based environmental monitoring system in underground coal mines. Comput. Commun. 2022, 195, 1–13. [Google Scholar] [CrossRef]
- Wang, P.; Shen, Y.; Li, R.; Zong, K.; Fu, S.; Wu, M. Multisensor information-based adaptive control method for cutting head speed of roadheader. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1941–1955. [Google Scholar] [CrossRef]
- Wang, G.; Ren, H.; Zhao, G.; Zhang, D.; Wen, Z.; Meng, L.; Gong, S. Research and practice of intelligent coal mine technology systems in China. Int. J. Coal Sci. Technol. 2022, 9, 24. [Google Scholar] [CrossRef]
- Semeraro, C.; Lezoche, M.; Panetto, H.; Dassisti, M. Digital twin paradigm: A systematic literature review. Comput. Ind. 2021, 130, 103469. [Google Scholar] [CrossRef]
- Zhou, Y.; Fu, Z.; Zhang, J.; Li, W.; Gao, C. A Digital Twin-Based Operation Status Monitoring System for Port Cranes. Sensors 2022, 22, 3216. [Google Scholar] [CrossRef]
- Wang, Y.; Kou, H.N.; Zhang, X.H.; Wei, S.R.; Yang, Z.W.; Zhao, Y.J. Virtual-physical interaction control method for intelligent cantilever roadheader driven by digital twin. J. China Univ. Min. Technol. 2025, 54, 1–13. [Google Scholar]
- Tao, F.; Liu, W.; Zhang, M.; Hu, T.L.; Qi, Q.; Zhang, H.; Sui, F.; Wang, T.; Xu, H.; Huang, Z.; et al. Five-dimension digital twin model and its ten applications. Comput. Integr. Manuf. Syst. 2019, 25, 1–18. [Google Scholar]
- Fei, T.A.; Xin, M.A.; Qinglin, Q.I.; Weiran, L.I.; He, Z.H.; Chenyuan, Z.H. Theory and key technologies of digital twin connection and interaction. Comput. Integr. Manuf. Syst. 2023, 29, 1–10. [Google Scholar]
- Ge, S.R.; Zhang, F.; Wang, S.B.; Wang, Z.B. Digital twin for smart coal mining workface: Technological frame and construction. J. China Coal Soc. 2020, 45, 1925–1936. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, W.; Xue, X.; Zhang, C.; Wan, J.; Mao, Q.; Lei, M.; Du, Y.; Ma, H.; Zhao, Y.; et al. Challenges and developing of the intelligent remote control on road-headers in coal mine. J. China Coal Soc. 2022, 47, 579–597. [Google Scholar]
- Wang, Y.; Zhang, X.; Cao, X.; Zhao, Y.; Yang, W.; Du, Y.; Shi, S. Construction of digital twin and parallel intelligent control method for excavation face. J. China Coal Soc. 2022, 47, 384–394. [Google Scholar]
- Lampton, A.; Valasek, J.; Kumar, M. Multiresolution state-space discretization for Q-Learning with pseudorandomized discretization. J. Control Theory Appl. 2011, 9, 431–439. [Google Scholar] [CrossRef]
- Zhang, S.; Suen, S.C. State discretization for continuous-state MDPs in infectious disease control. IISE Trans. Healthc. Syst. Eng. 2024, 15, 96–115. [Google Scholar] [CrossRef]
- Farmer, L.E. The discretization filter: A simple way to estimate nonlinear state space models. Quant. Econ. 2021, 12, 41–76. [Google Scholar] [CrossRef]
- Dadashi, R.; Hussenot, L.; Vincent, D.; Girgin, S.; Raichuk, A.; Geist, M.; Pietquin, O. Continuous control with action quantization from demonstrations. arXiv 2021, arXiv:2110.10149. [Google Scholar]
- Shi, Y.; Zhao, W.; Li, S.; Li, B.; Sun, X. Novel discrete-time recurrent neural network for robot manipulator: A direct discretization technical route. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2781–2790. [Google Scholar] [CrossRef]
- Lin, Z.; Lu, G.; Lv, W.; Wu, B. Adaptive Event-Triggered Control for Spacecraft Attitude Tracking. Aerosp. Control 2021, 39, 32–39. [Google Scholar]
- Santos, C.H.; De Queiroz, J.A.; Leal, F.; Montevechi, J.A. Use of simulation in the industry 4.0 context: Creation of a Digital Twin to optimise decision making on non-automated process. J. Simul. 2022, 16, 284–297. [Google Scholar] [CrossRef]
- Karakra, A.; Fontanili, F.; Lamine, E.; Lamothe, J. A discrete event simulation-based methodology for building a digital twin of patient pathways in the hospital for near real-time monitoring and predictive simulation. Digit. Twin 2022, 2, 1. [Google Scholar] [CrossRef]
- Cubukcuoglu, C.; Nourian, P.; Sariyildiz, I.S.; Tasgetiren, M.F. A discrete event simulation procedure for validating pro-grams of requirements: The case of hospital space planning. SoftwareX 2020, 12, 100539. [Google Scholar] [CrossRef]
- Wang, X.; Sun, J.; Wang, G.; Allgöwer, F.; Chen, J. Data-driven control of distributed event-triggered network systems. IEEE/CAA J. Autom. Sin. 2023, 10, 351–364. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Zhang, X.M.; Ding, D. Dynamic event-triggered control and estimation: A survey. Int. J. Autom. Comput. 2021, 18, 857–886. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).