Theoretical Approach for Micro-Settlement Control in Super-Large Cross-Section Tunnels Under Sensitive Environments
Abstract
1. Introduction
2. Calculation Method for Surface Settlement
2.1. Overview
2.2. Surface Settlement from Tunnel Excavation (u1)
- (1)
- Calculation of transverse settlement in tunnel
- (2)
- Calculation of longitudinal settlement in tunnel
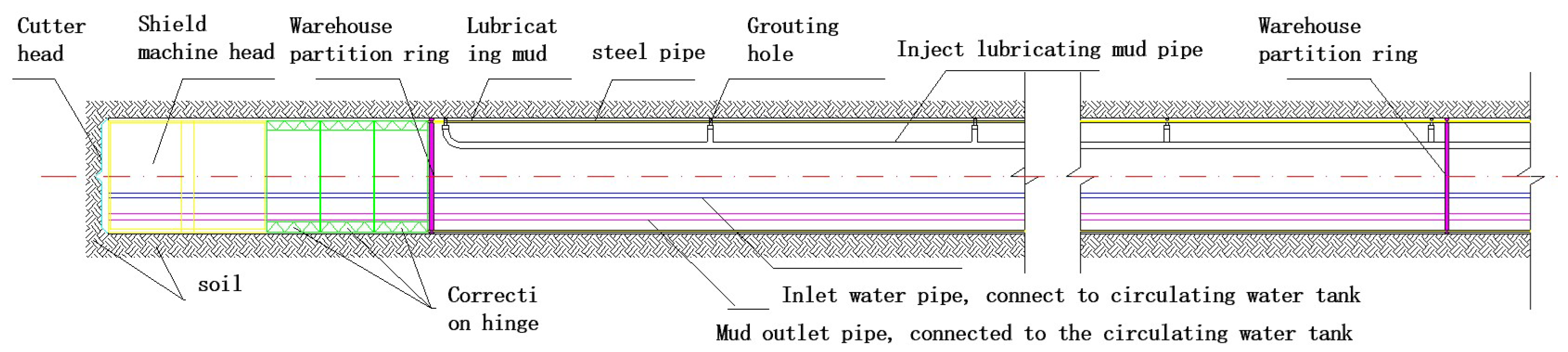
2.3. Surface Settlement Induced by Pipe Roof Construction (u2)
- (1)
- Surface settlement induced by single-pipe construction
- (2)
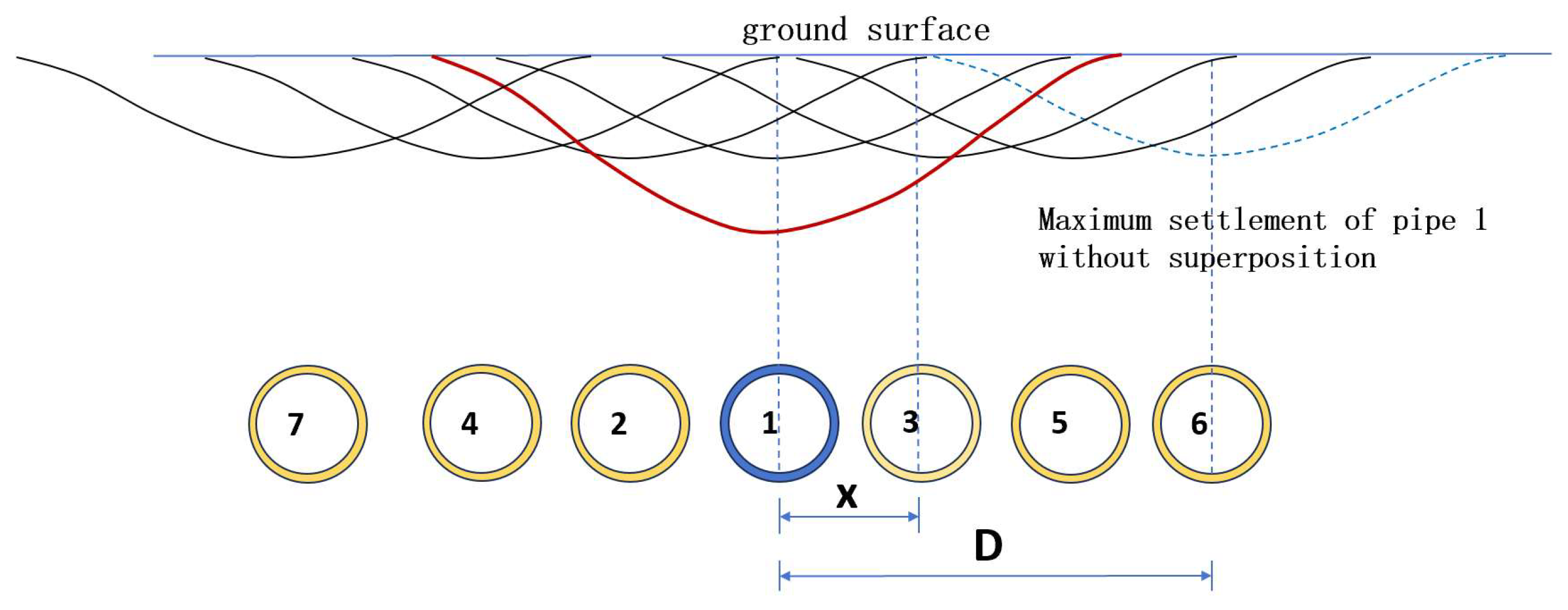
- Surface settlement caused by the construction of multiple pipes
2.4. Surface Settlement Induced by Groundwater Level Drawdown (u3)
2.5. Total Surface Settlement
3. Micro-Settlement Control Techniques
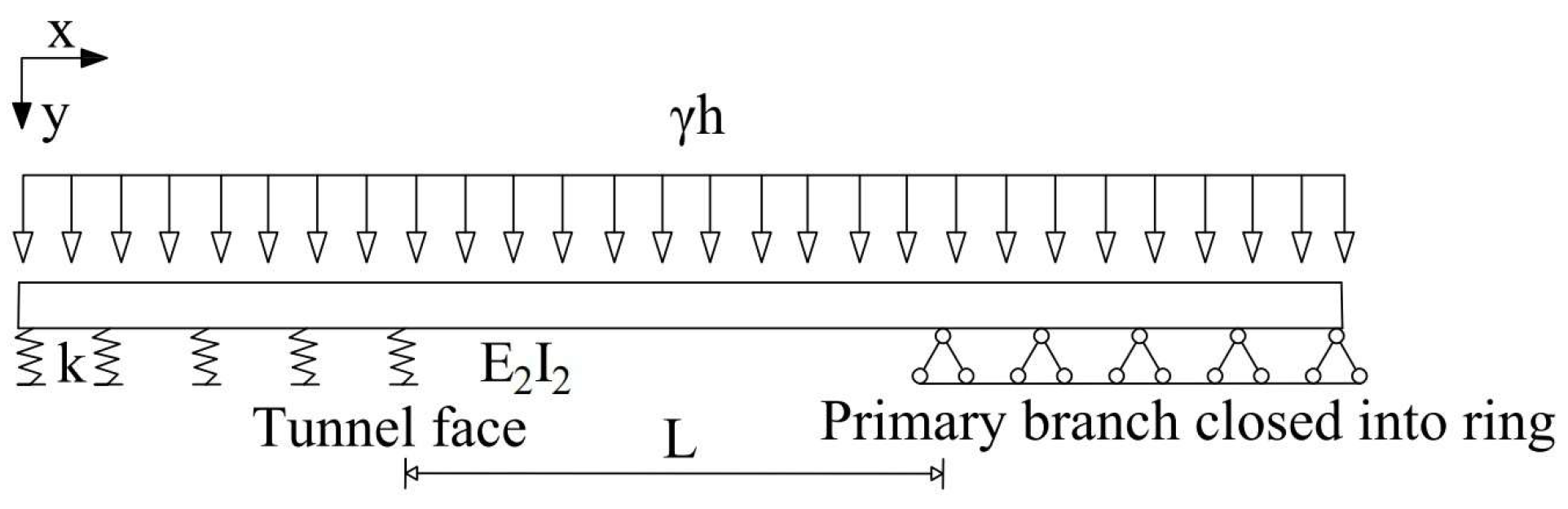
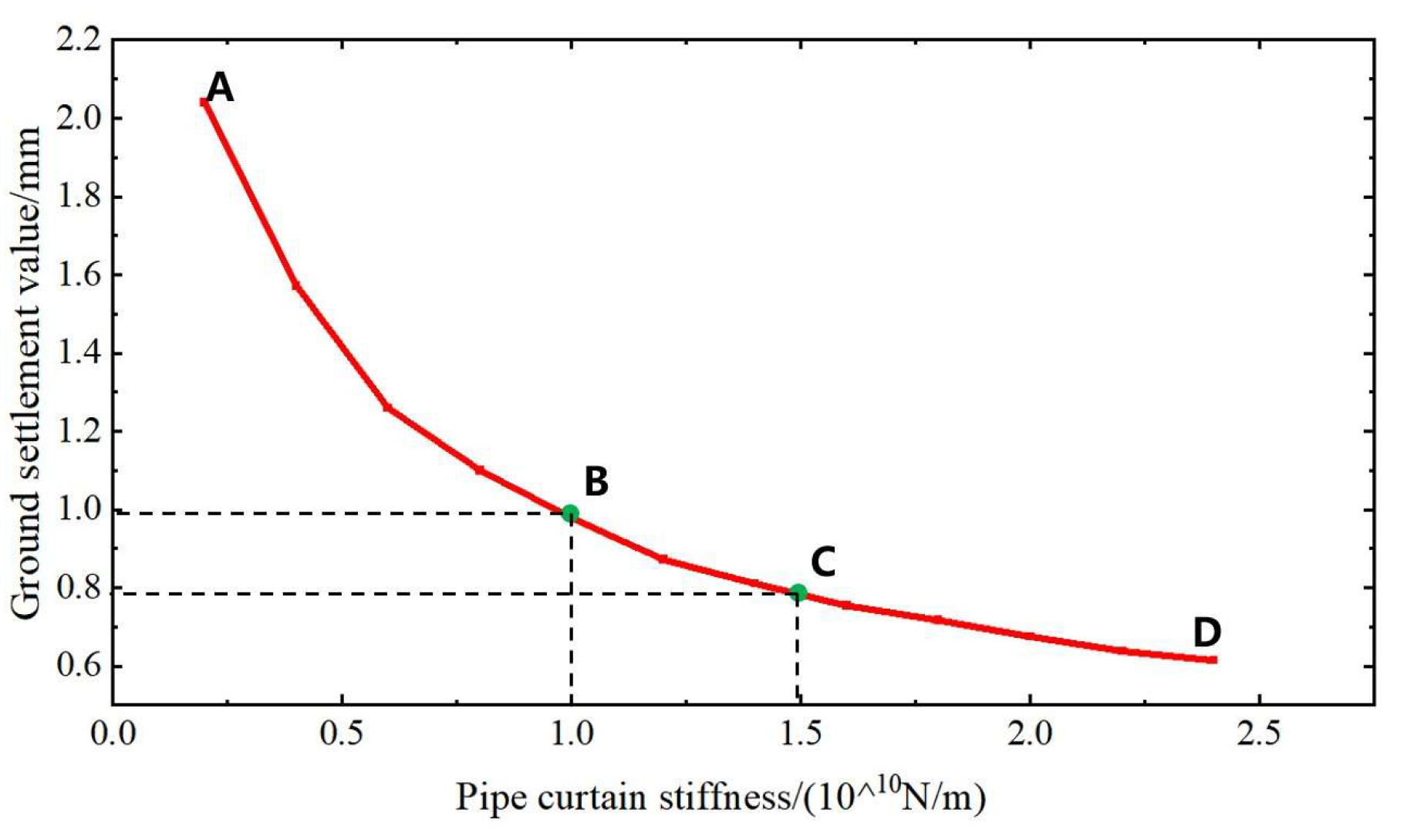
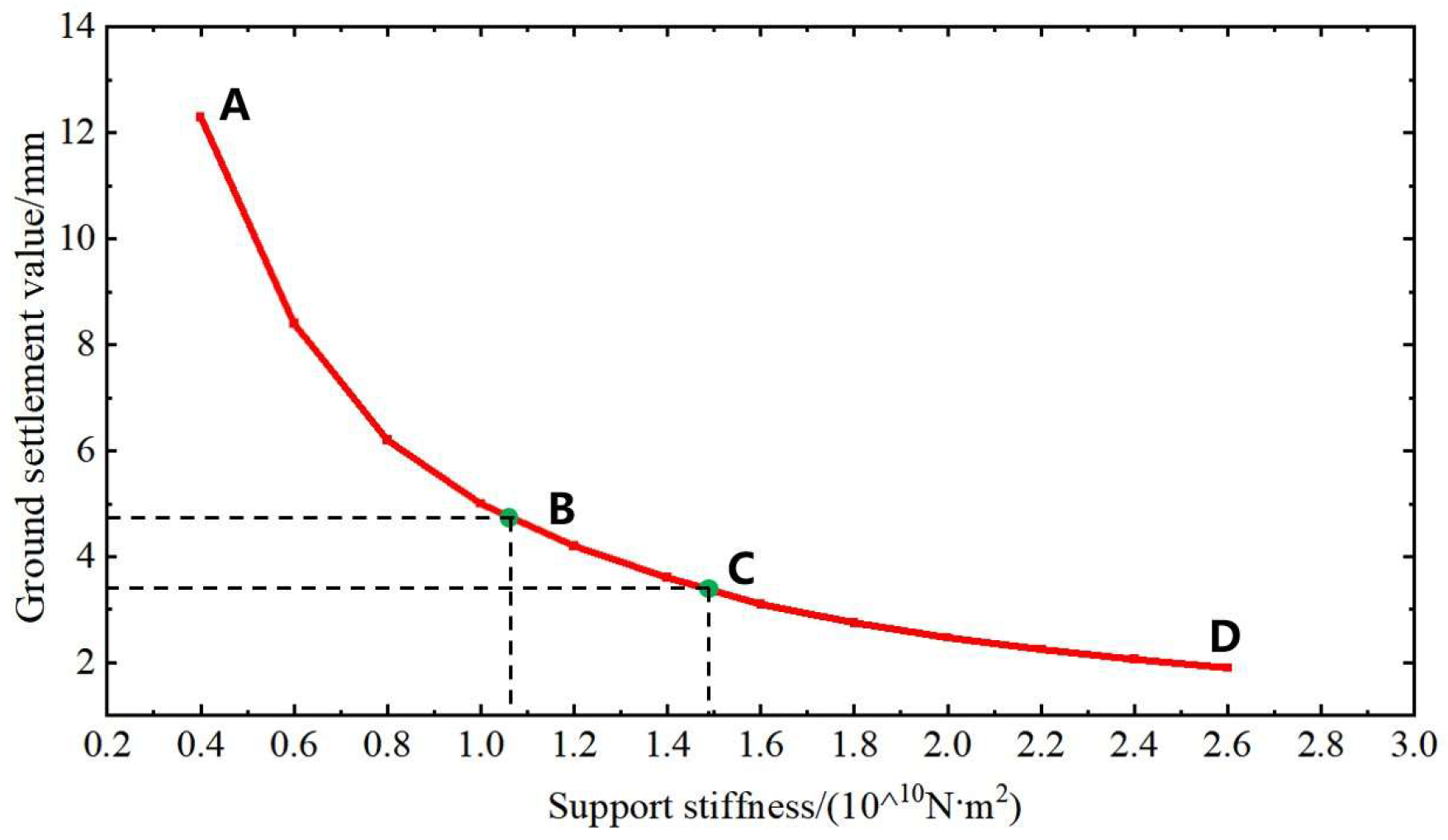
3.1. Method for Determining the Appropriate Pipe Roof Stiffness
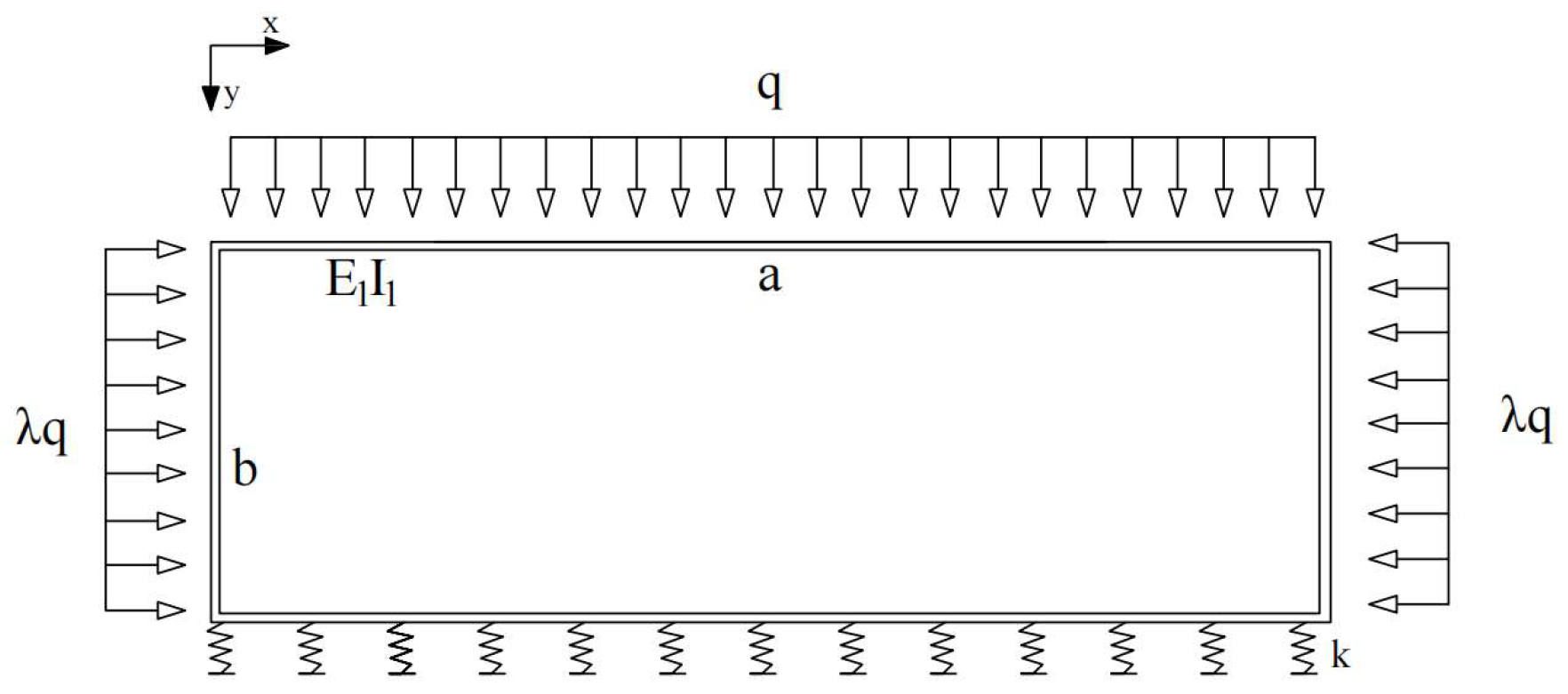
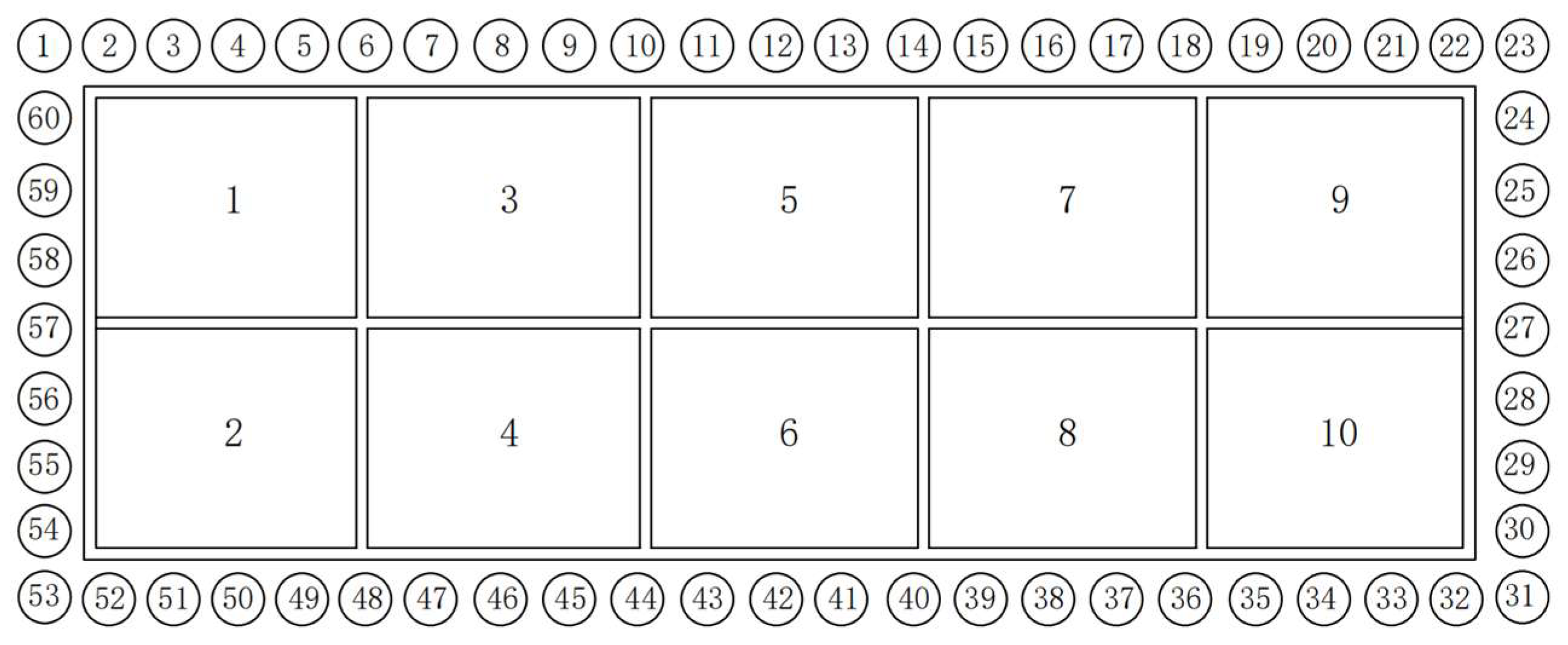
3.2. Method for Determining the Appropriate Support System
- (1)
- Main forms of support systems
- (2)
- Determining the appropriate stiffness of the support system
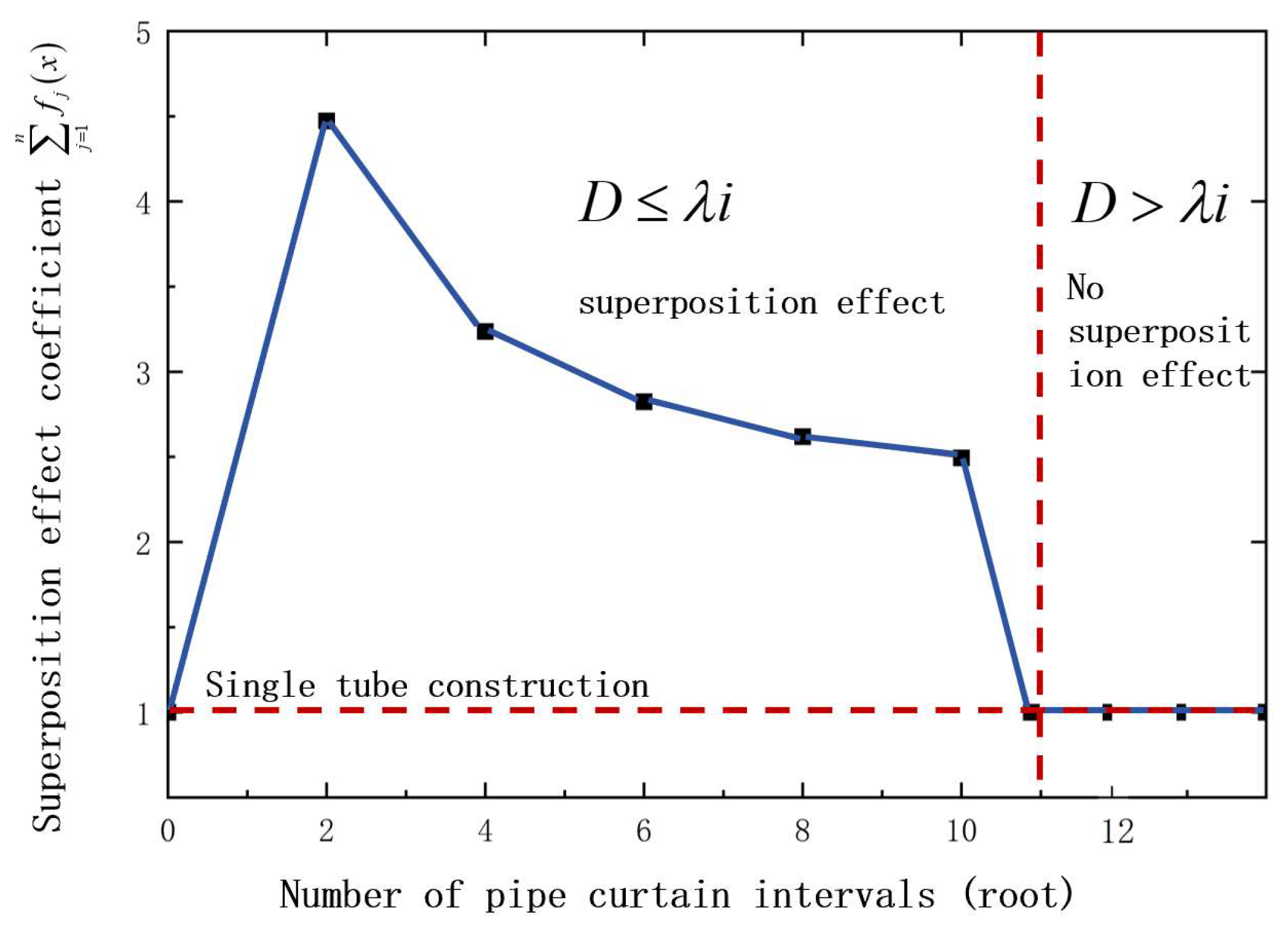
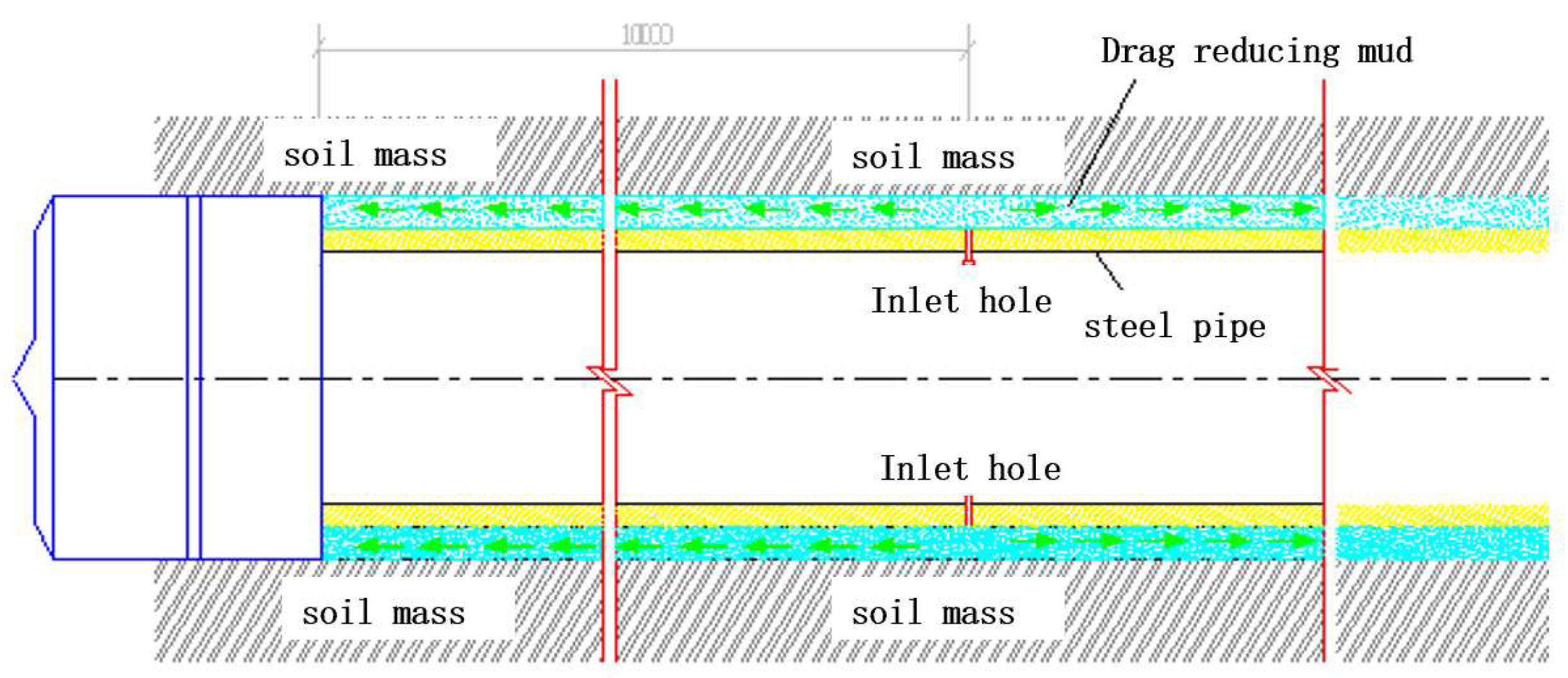
3.3. Techniques for Reducing the Settlement Superimposition Effect Induced by Group Pipe Construction
3.4. Grouting Pressure Maintenance Technique Around the Pipe During the Pipe-Roof Jacking Process
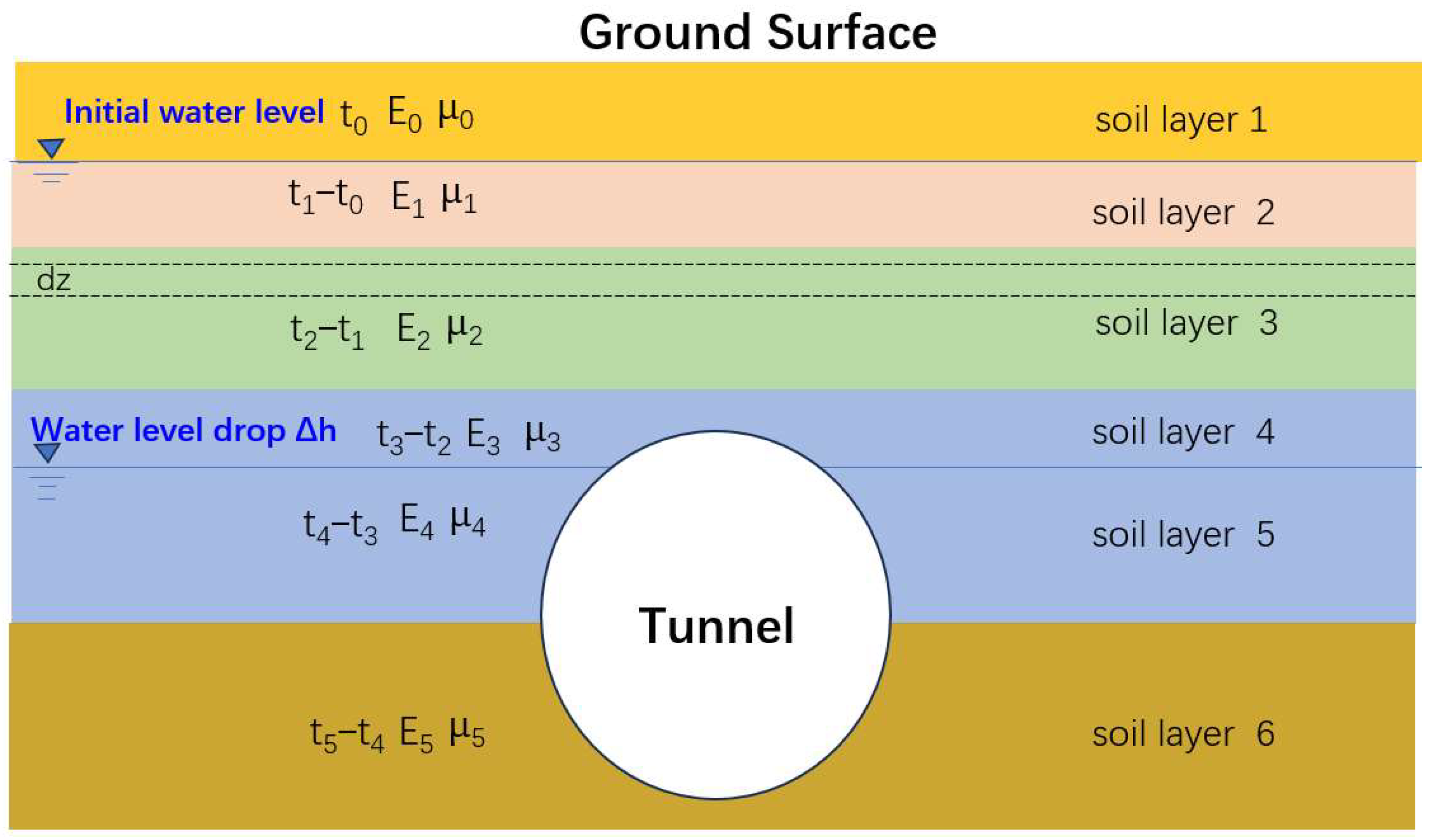
3.5. Groundwater Level Control Techniques
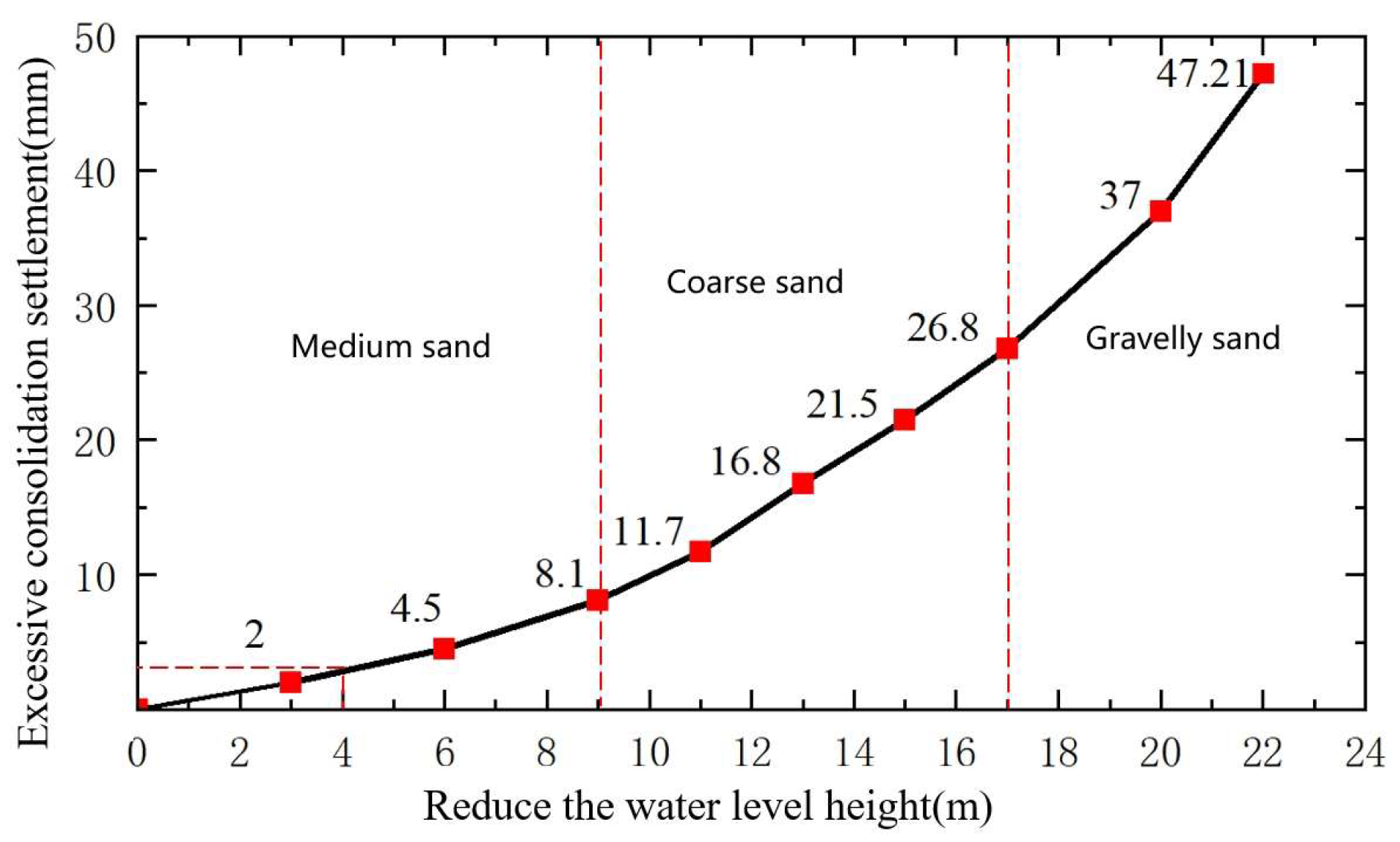
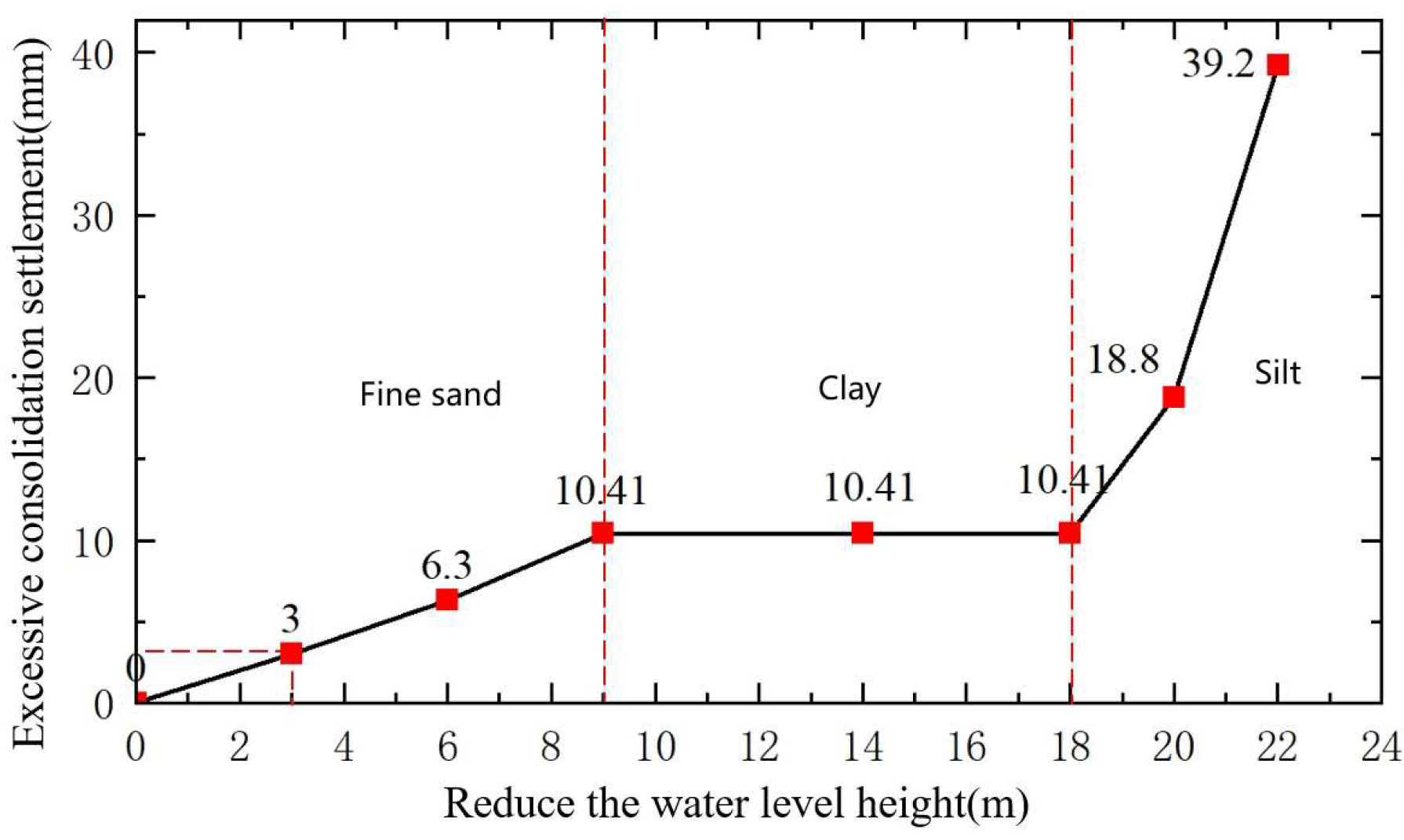
- (1)
- Over-consolidation settlement calculations for soil layers
- (2)
- Groundwater control measures
4. Case Studies
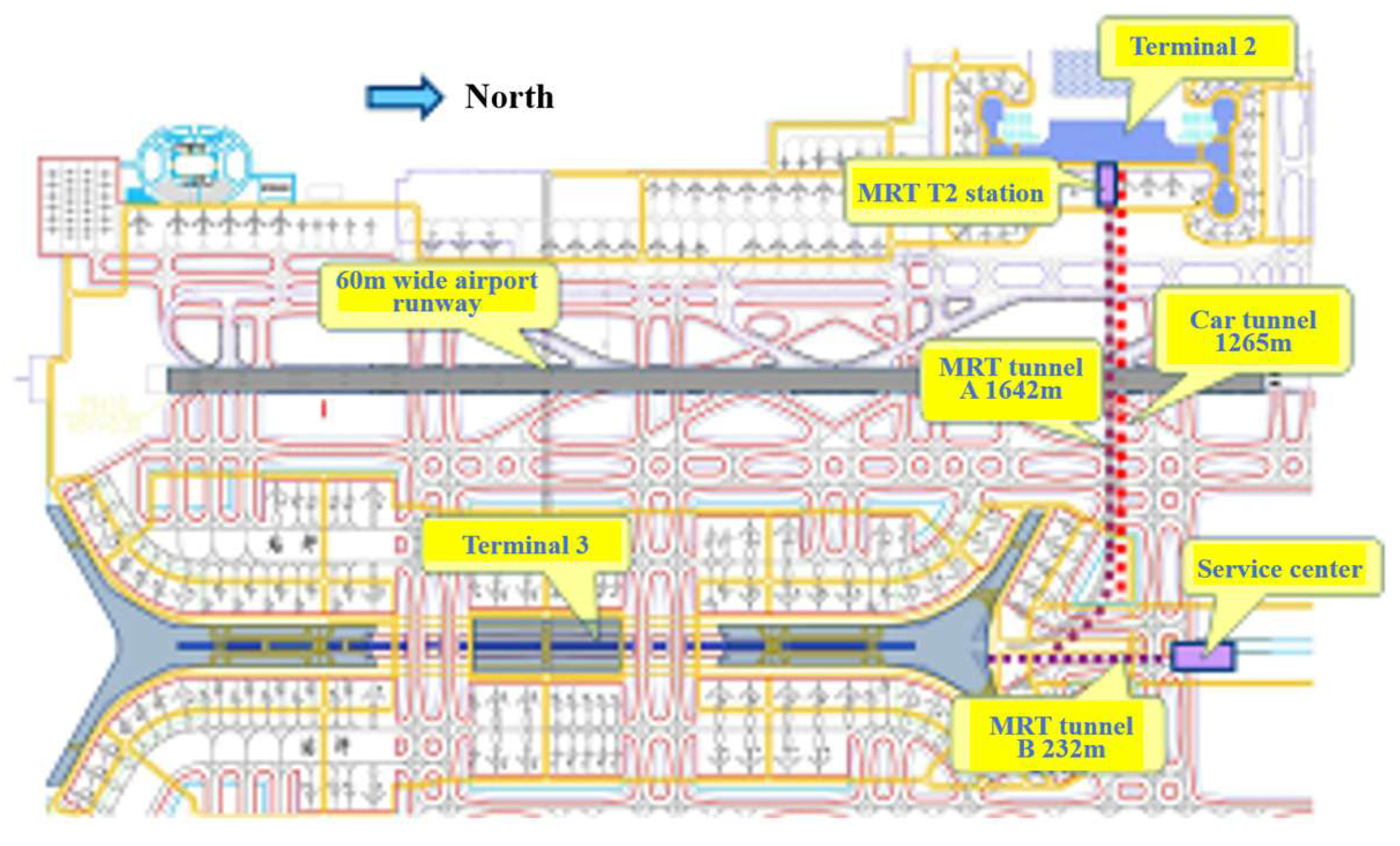
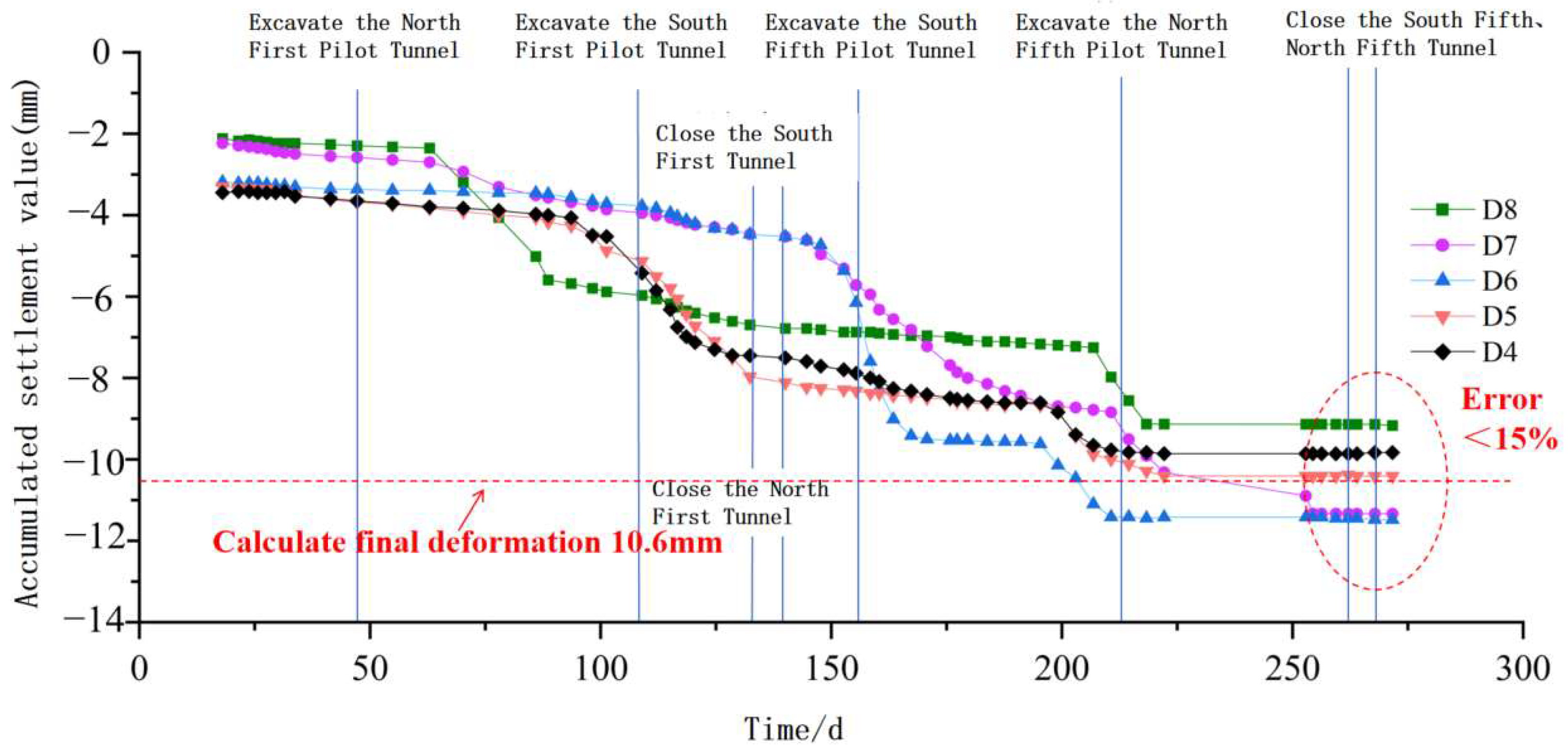
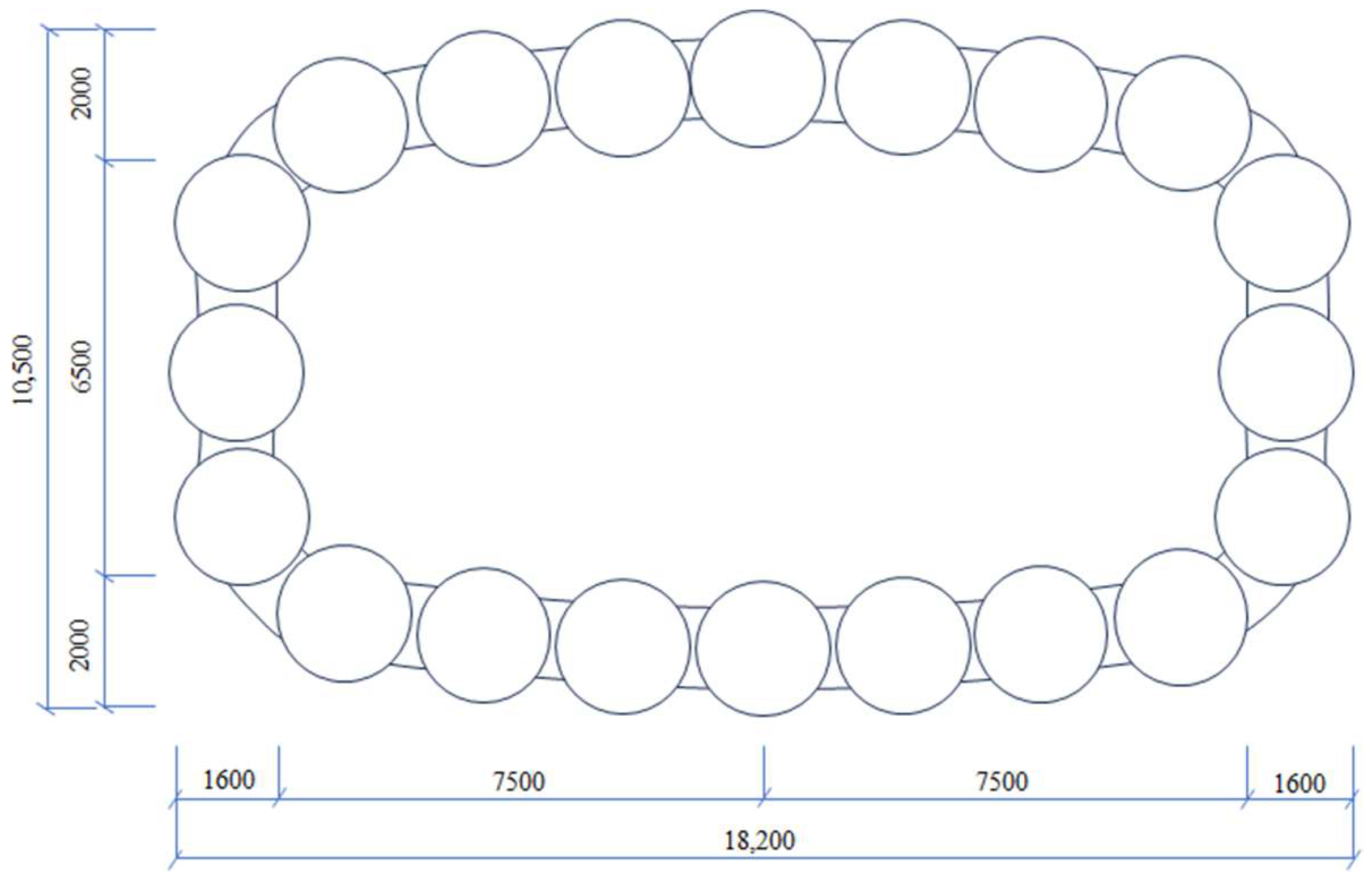
4.1. Tunnel Beneath the Capital Airport Runway
4.2. Tunnel Beneath the Taiyuan Railway Station
5. Conclusions
- (1)
- A theoretical method for surface micro-settlement control in large-section tunnels is proposed. A calculation formula is derived to reveal the relationships between surface settlement and factors such as pipe roof stiffness, support system stiffness, pipe roof construction procedures, and groundwater level changes. Surface micro-settlement control techniques, including increasing the pipe roof stiffness, reinforcing the support system, reducing the group pipe effects, maintaining pressure and reducing resistance around the pipe, and controlling the groundwater level, are proposed.
- (2)
- The stiffness of the pipe roof and the overall stiffness of the support system are critical factors in controlling surface micro-settlement in large-section tunnels. This study proposes a method for determining the appropriate stiffness for the pipe roof and support system. The stiffness should be selected from the transition segment between the steep decline and the gentle slope on the stiffness-settlement curves of the pipe roof and the support system. If the stiffness of the pipe roof combined with the primary and temporary supports fails to meet the requirements for micro-settlement control, an integrated support system with higher stiffness can be adopted.
- (3)
- The primary causes of surface settlement during pipe roof construction are voids between the pipes and the surrounding soil, as well as the settlement superimposition effect of group pipe construction. This study proposes a pressure-maintaining and resistance-reducing technique around the pipe by appropriately regulating grouting pressure to minimize surface settlement during single-pipe jacking. It is recommended that the spacing between simultaneously installed jacked pipes be greater than half the width of the settlement trough (λi) to mitigate the settlement superimposition effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J. Effects of reinforcement on behaviors of shallow tunnel and settlement of ground surface. J. Guizhou Univ. (Nat. Sci.) 2015, 32, 126–130. [Google Scholar]
- Dai, Y.; Ai, G.; Huang, D.; Chen, G.; Zhou, C. Research on the optimization of support structure and construction method of metro station in muddy siltstone. Mod. Tunn. Technol. 2020, 57, 996–1001. [Google Scholar]
- Guo, J.; Yu, S.; Ding, H. Optimized analysis of support parameters of 3-lane highway tunnels. Technol. Highw. Transp. 2013, 6, 76–80+84. [Google Scholar]
- Zhan, H. Research on ground deformation caused by pipe jacking construction. Chin. J. Undergr. Space Eng. 2008, 4, 583–585. [Google Scholar]
- Peck, R.B. Deep excavations and tunneling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969; pp. 225–290. [Google Scholar]
- Gong, S.; Yang, Y.; Chen, S. Analyses on ground surface settlement due to extra-shallow-underground-pipe jacking with curve by stochastic medium theory. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2005, 24, 95–98+103. [Google Scholar]
- Sun, M.; Xu, W. 3D numerical simulation of pipe-curtain method in soft soils. Chin. J. Geotech. Eng. 2006, 28, 1497–1500. [Google Scholar]
- Ji, X.; Long, B.; Yang, X. 3D simulation analysis of closely jacking pipe in pipe curtaining pre-reinforcement. Chin. J. Undergr. Space Eng. 2016, 28, 267–274. [Google Scholar]
- Yang, X.; Zhang, K.; Li, Z.; Deng, M.; Xiao, Z. Influence of steel pipe jacking on earth surface settlement in pipe roof pre-construction method. J. Shenyang Univ. Technol. 2012, 34, 469–473. [Google Scholar]
- Yang, Q.; Zhao, B. Experimental and theoretical study on the surface subsidence by dewatering of foundation pit in phreatic aquifer. Chin. J. Rock Mech. Eng. 2018, 37, 1506–1519. [Google Scholar]
- Wu, Y. Research on the deformation due to dewatering and excavation of deep foundation pit of subway station in phreatic aquifer. Lanzhou Univ. Technol. 2016. [Google Scholar]
- Wen, S. Estimation method for ground settlements of the karst tunnel in soil surrounding rock. Mod. Tunn. Technol. 2018, 55, 73–79. [Google Scholar]
- Gu, S.; Li, Z.; Li, Y. Analyses on ground settlement induced by pre-precipitation in deep foundation pit project. Sci. Technol. Eng. 2018, 18, 233–237. [Google Scholar]
- Tan, Z.; Ma, D.; Sun, X.; Chen, Y.; Wang, W. Construction technology of large span tunnel under the non-stop flight runway. China Civ. Eng. J. 2015, 48, 378–382. [Google Scholar]
- Liu, Y.; Shi, P.; Pan, J.; Yu, C. Analysis of transverse ground settlement and pipe interaction of super-large pipe roofing in Gongbei Tunnel. Tunn. Constr. 2018, 38, 1680–1687. [Google Scholar]
- Wang, X. Study on Key Techniques for Settlement Control in the Construction of Yingze Street Beneath Taiyuan Station. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2021. [Google Scholar]
- Tan, Z.; Sun, X.; Ma, D.; Ma, Y. Experimental research of pipe-roof pre-supporting technology for the shallow large-span tunnel. China Civ. Eng. J. 2015, 48, 429–434. [Google Scholar]
- Aghajari, M.; Dehghan, A.N.; Lajevardi, S.H. Optimizing Se-quential Excavation Method for Ground Settlement Control in Tehran Subway Tunnel Line 6. Geotech. Geol. Eng. 2024, 42, 3595–3614. [Google Scholar] [CrossRef]
- Morovatdar, A.; Palassi, M.; Ashtiani, R.S. Effect of pipe characteristics in umbrella arch method on controlling tunneling-induced settlements in soft grounds. J. Rock Mech. Geotech. Eng. 2020, 12, 984–1000. [Google Scholar] [CrossRef]
- Chakeri, H.; Ozcelik, Y.; Unver, B. Effects of important factors on surface settlement prediction for metro tunnel excavated by EPB. Tunn. Undergr. Space Technol. 2013, 36, 14–23. [Google Scholar] [CrossRef]
- Mousapour, H.; Chakeri, H.; Darbor, M.; Hekmatnejad, A. Evaluating the wear of cutting tools using a tunnel boring machine laboratory simu-lator. Min. Miner. Depos. 2023, 17, 28–34. [Google Scholar] [CrossRef]
- Chakeri, H.; Darbor, M.; Shakeri, H.; Mousapour, H.; Mohajeri, V. Experimental and numerical investigation of the TBM disc cutter wear using a new tunnel boring machine laboratory simulator. Heliyon 2024, 10, e37148. [Google Scholar] [CrossRef] [PubMed]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Ding, Z.; Zhou, Z.; Li, Z. Theoretical Approach for Micro-Settlement Control in Super-Large Cross-Section Tunnels Under Sensitive Environments. Appl. Sci. 2025, 15, 4375. https://doi.org/10.3390/app15084375
Tan Z, Ding Z, Zhou Z, Li Z. Theoretical Approach for Micro-Settlement Control in Super-Large Cross-Section Tunnels Under Sensitive Environments. Applied Sciences. 2025; 15(8):4375. https://doi.org/10.3390/app15084375
Chicago/Turabian StyleTan, Zhongsheng, Zhengquan Ding, Zhenliang Zhou, and Zhanxian Li. 2025. "Theoretical Approach for Micro-Settlement Control in Super-Large Cross-Section Tunnels Under Sensitive Environments" Applied Sciences 15, no. 8: 4375. https://doi.org/10.3390/app15084375
APA StyleTan, Z., Ding, Z., Zhou, Z., & Li, Z. (2025). Theoretical Approach for Micro-Settlement Control in Super-Large Cross-Section Tunnels Under Sensitive Environments. Applied Sciences, 15(8), 4375. https://doi.org/10.3390/app15084375





