Pedestrian Trajectory Prediction Based on Dual Social Graph Attention Network
Abstract
1. Introduction
- A novel dual social graph attention network is proposed for pedestrian trajectory prediction, capable of comprehensively quantifying individual and group pedestrian features, fully harnessing dynamic interaction patterns, and substantially improving the model performance.
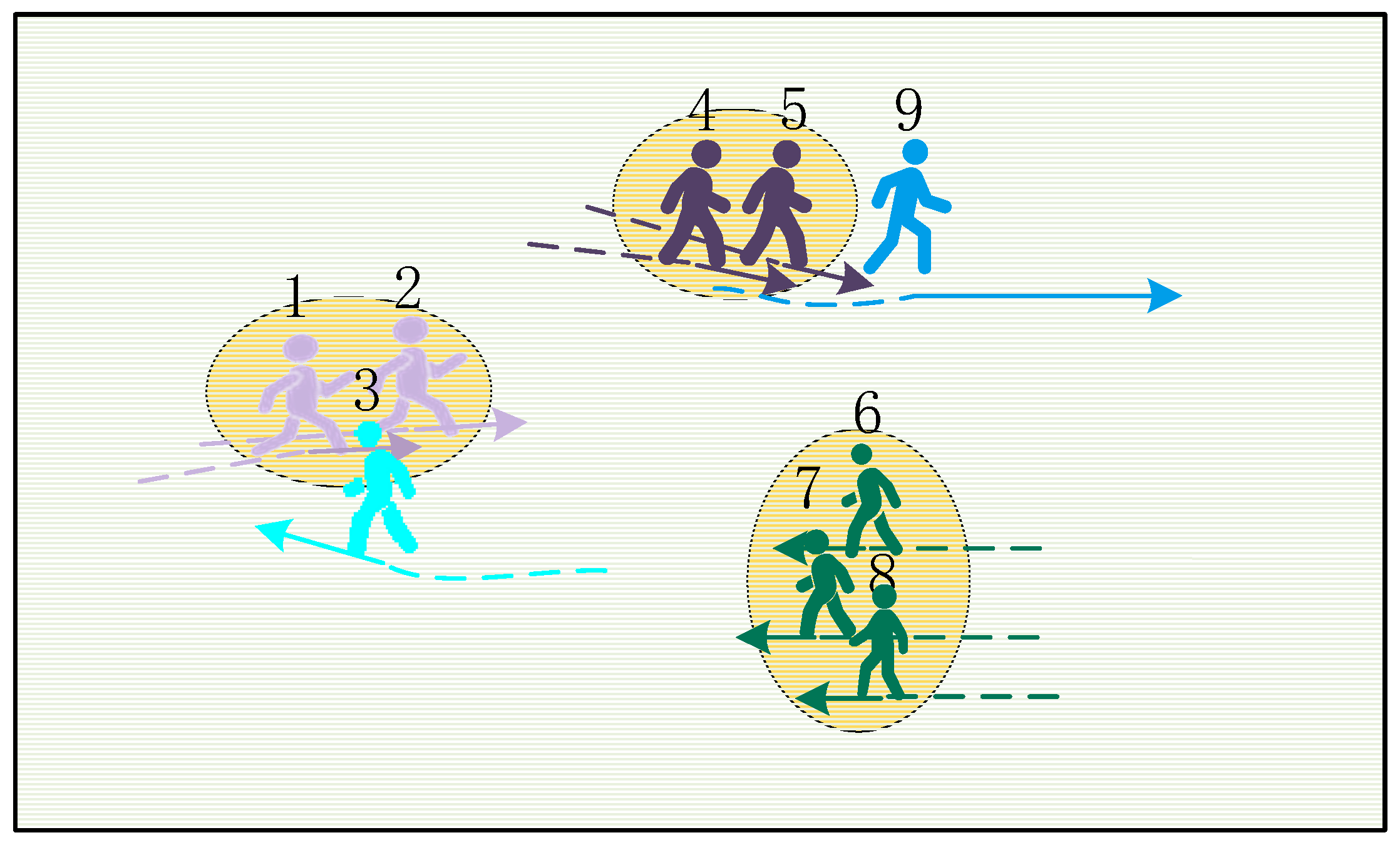
- A directed social attention function was developed, introducing the concept of directed interaction relationships, explicitly incorporating factors such as vision, position, and distance to quantify directed pedestrian interactions. Furthermore, a spatiotemporal weighted graph attention network was proposed to process these graphs.
- A group attention function was designed, the group division rules were improved, groups were effectively divided from the crowd, and the interaction intensity of groups was quantified.
- Experimental evaluations conducted on the ETH/UCY pedestrian trajectory prediction dataset demonstrate that the proposed dual social graph attention network outperforms the existing methods in terms of both Average Displacement Error (ADE) and Final Displacement Error (FDE).
2. Related Work
2.1. Research on Spatiotemporal Interactions
2.2. Social Awareness in Pedestrian Trajectory Prediction
2.3. Graph Neural Networks in Pedestrian Trajectory Prediction
3. Methods
3.1. Definition of the Pedestrian Trajectory Prediction Problem
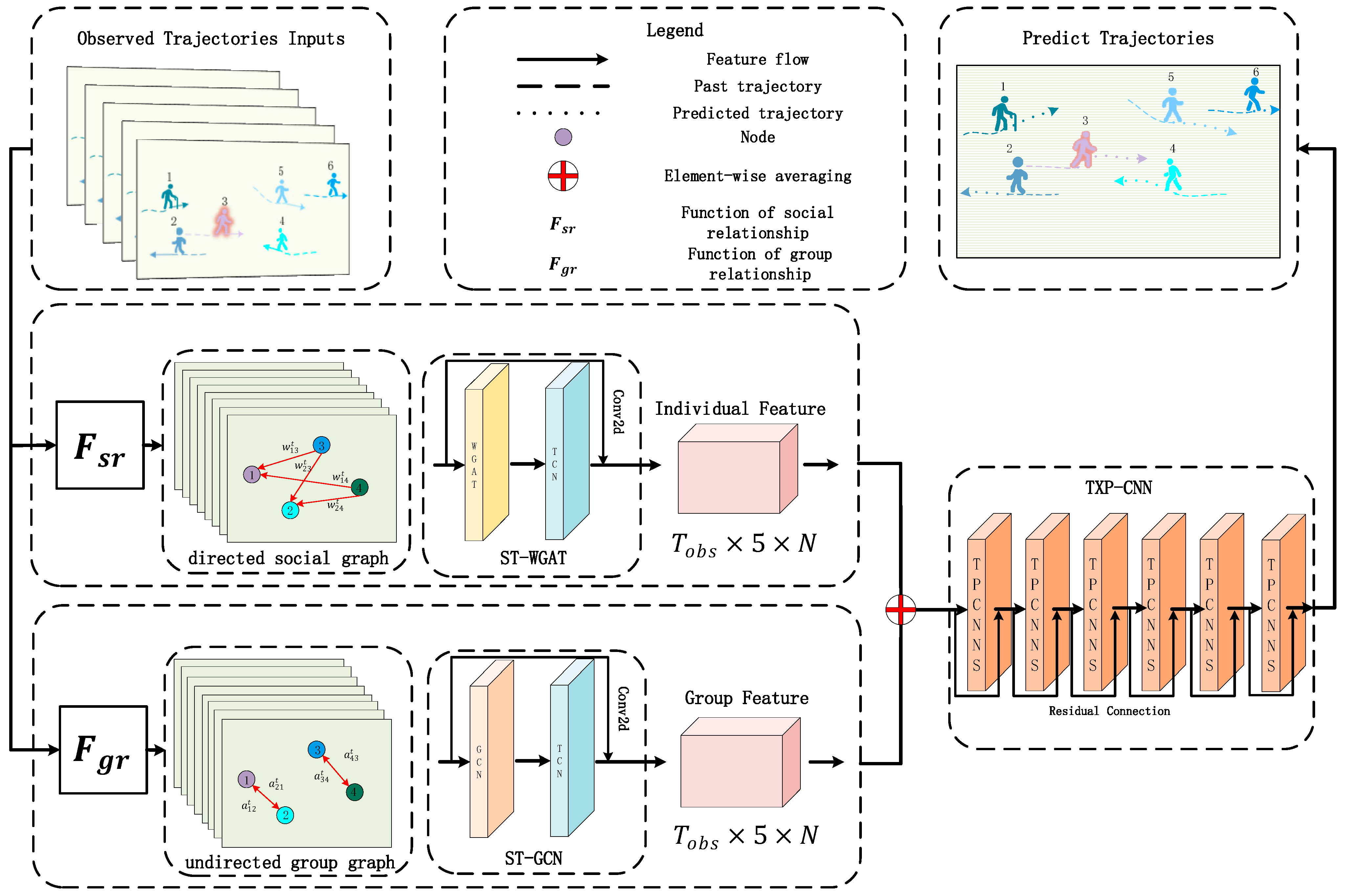
3.2. Network Architecture
3.3. Dual Social Graph Attention Network
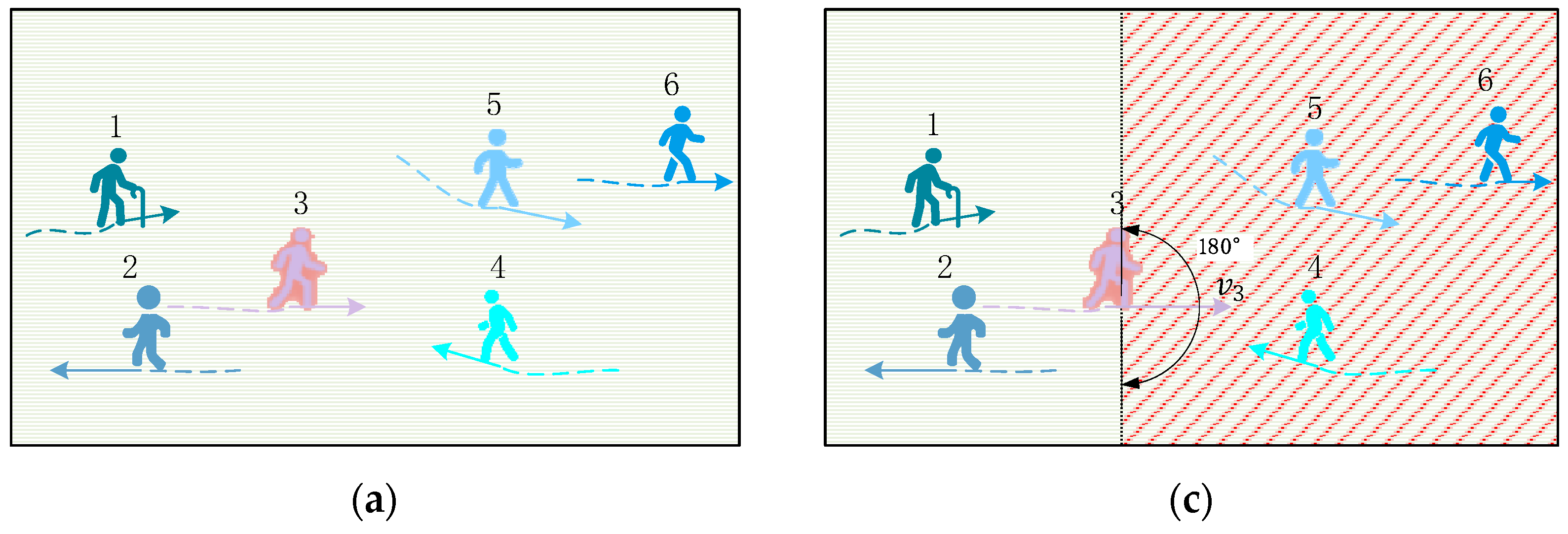
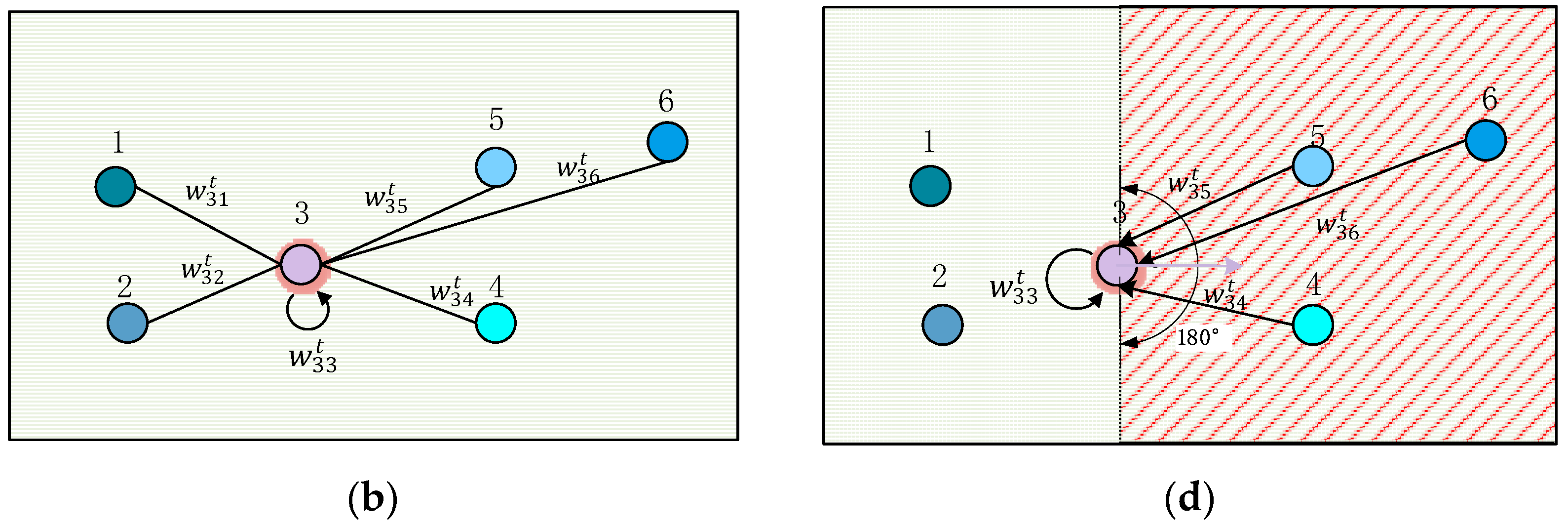
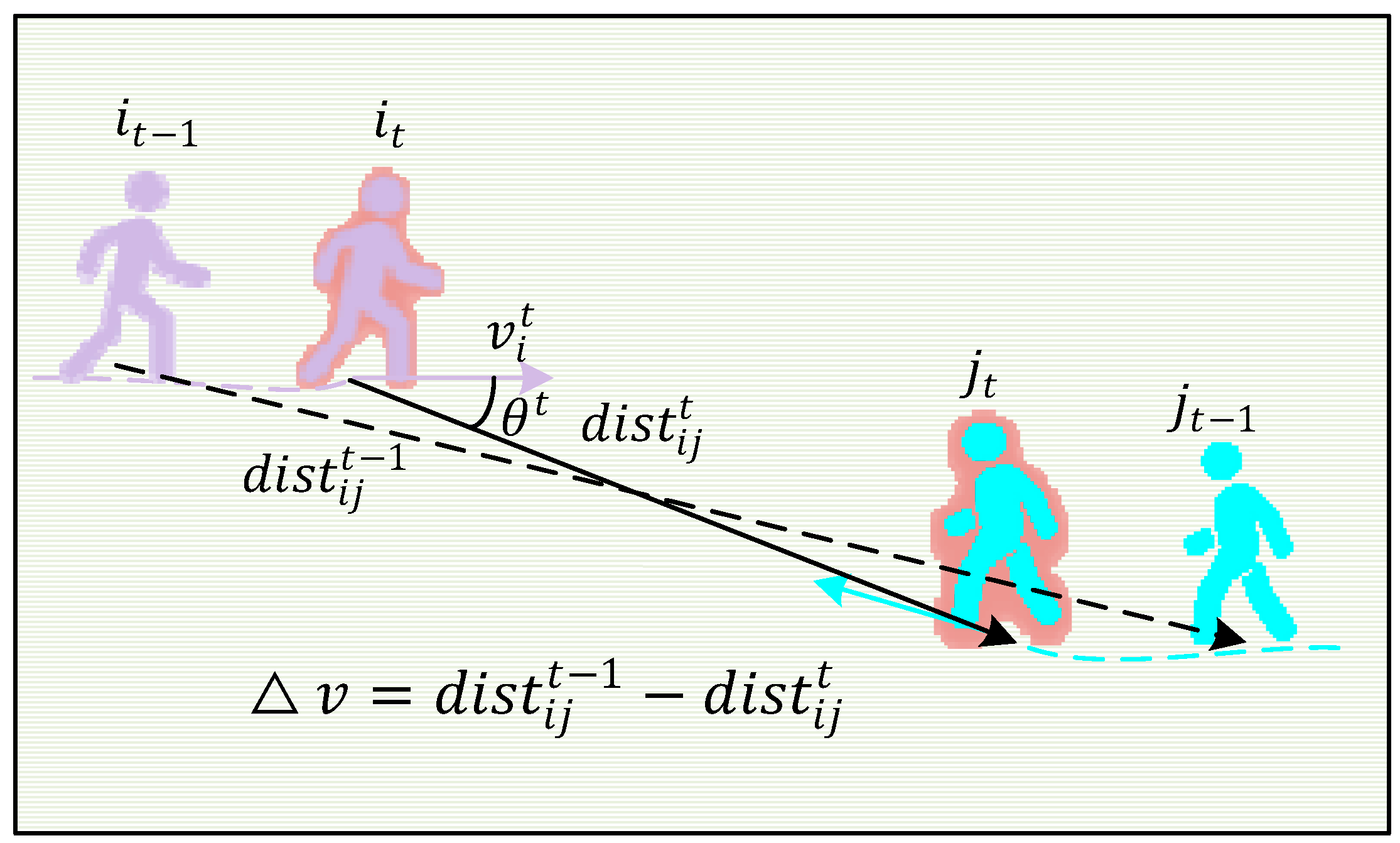
3.3.1. Directed Social Attention Function
3.3.2. Spatiotemporal Weighted Attention Network
3.3.3. Group Attention Function
3.4. Loss Function
4. Experiment and Results
4.1. Datasets
4.2. Evaluation Metrics
4.3. Implementation Details
4.4. Quantitative Analysis
4.5. Ablation Experiments
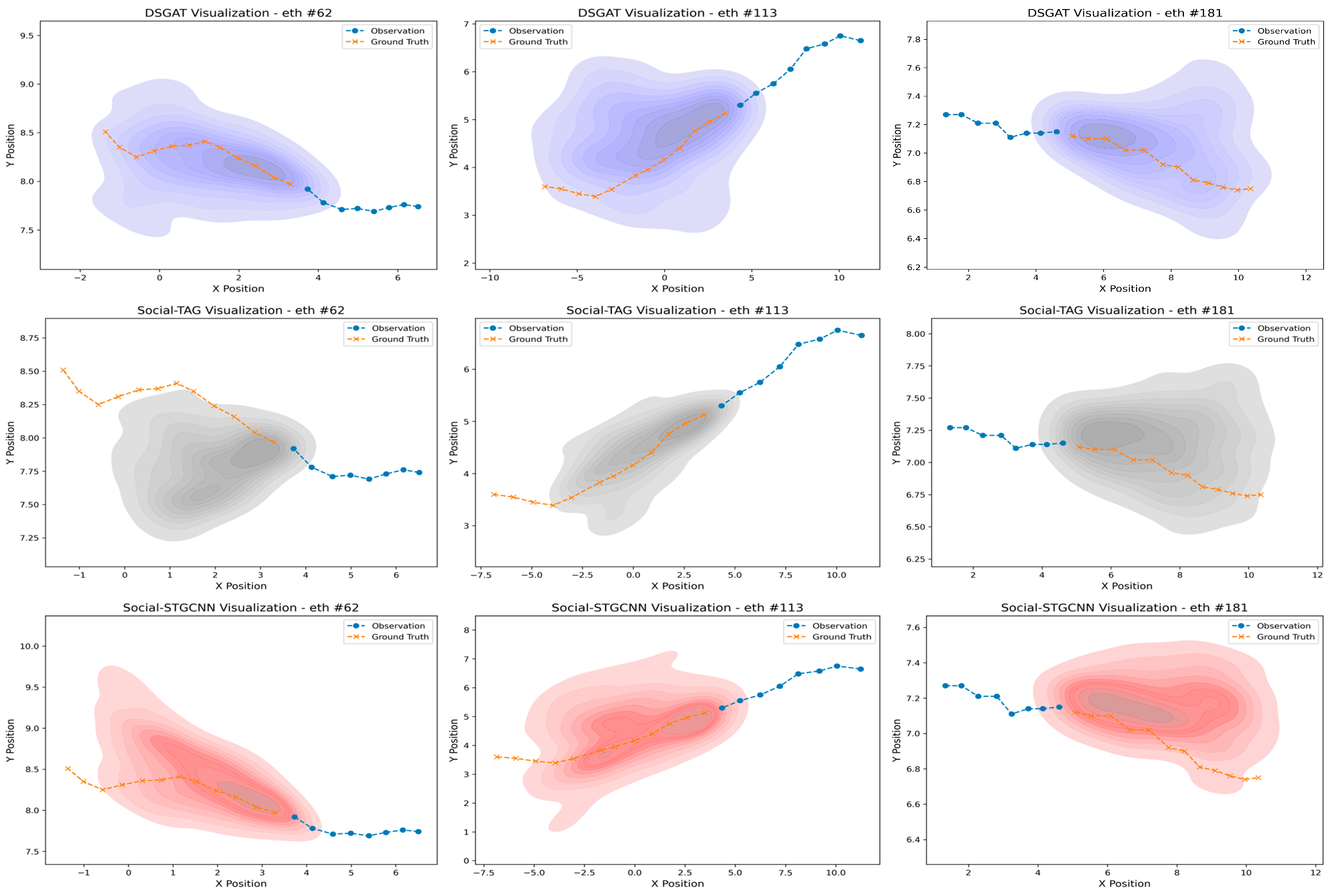
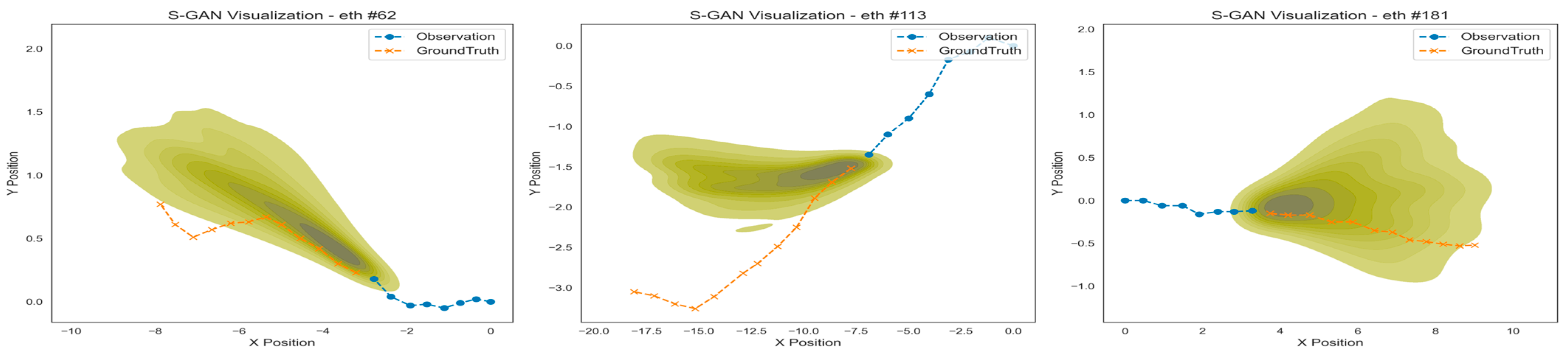
4.6. Qualitative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Berger, C. Pedestrian Behavior Prediction Using Deep Learning Methods for Urban Scenarios: A Review. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10279–10301. [Google Scholar] [CrossRef]
- Golchoubian, M.; Ghafurian, M.; Dautenhahn, K.; Azad, N.L. Pedestrian Trajectory Prediction in Pedestrian-Vehicle Mixed Environments: A Systematic Review. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11544–11567. [Google Scholar] [CrossRef]
- Helbing, D.; Molnár, P. Social Force Model for Pedestrian Dynamics. Phys. Rev. E 1995, 51, 4282–4286. [Google Scholar] [CrossRef]
- Kim, S.; Guy, S.J.; Liu, W.; Wilkie, D.; Lau, R.W.H.; Lin, M.C.; Manocha, D. BRVO: Predicting Pedestrian Trajectories Using Velocity-Space Reasoning. Int. J. Robot. Res. 2015, 34, 201–217. [Google Scholar] [CrossRef]
- Jiang, J.; Yan, K.; Xia, X.; Yang, B. A Survey of Deep Learning-Based Pedestrian Trajectory Prediction: Challenges and Solutions. Sensors 2025, 25, 957. [Google Scholar] [CrossRef]
- Sighencea, B.I.; Stanciu, R.I.; Căleanu, C.D. A Review of Deep Learning-Based Methods for Pedestrian Trajectory Prediction. Sensors 2021, 21, 7543. [Google Scholar] [CrossRef] [PubMed]
- Fernando, T.; Denman, S.; Sridharan, S.; Fookes, C. Soft + Hardwired attention: An LSTM framework for human trajectory prediction and abnormal event detection. Neural Netw. 2018, 108, 466–478. [Google Scholar] [CrossRef]
- Leon, F.; Gavrilescu, M. A Review of Tracking and Trajectory Prediction Methods for Autonomous Driving. Mathematics 2021, 9, 660. [Google Scholar] [CrossRef]
- Shao, L.; Ling, M.; Yan, Y.; Xiao, G.; Luo, S.; Luo, Q. Research on Vehicle-Driving-Trajectory Prediction Methods by Considering Driving Intention and Driving Style. Sustainability 2024, 16, 8417. [Google Scholar] [CrossRef]
- Shi, L.; Wang, L.; Long, C.; Zhou, S.; Zhou, M.; Niu, Z.; Hua, G. SGCN: Sparse Graph Convolution Network for Pedestrian Trajectory Prediction. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8990–8999. [Google Scholar]
- Huang, Y.; Bi, H.; Li, Z.; Mao, T.; Wang, Z. STGAT: Modeling Spatial-Temporal Interactions for Human Trajectory Prediction. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6271–6280. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social LSTM: Human trajectory prediction in crowded spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Xue, H.; Huynh, D.Q.; Reynolds, M. SS-LSTM: A Hierarchical LSTM Model for Pedestrian Trajectory Prediction. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1186–1194. [Google Scholar]
- Hasan, I.; Setti, F.; Tsesmelis, T.; Bue, A.D.; Cristani, M.; Galasso, F. “Seeing is believing”: Pedestrian trajectory forecasting using visual frustum of attention. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1178–1185. [Google Scholar]
- Yang, B.; Yan, G.; Wang, P.; Chan, C.-Y.; Song, X.; Chen, Y. A Novel Graph-Based Trajectory Predictor with Pseudo-Oracle. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7064–7078. [Google Scholar] [CrossRef]
- Sun, J.; Jiang, Q.; Lu, C. Recursive Social Behavior Graph for Trajectory Prediction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 657–666. [Google Scholar]
- Zhang, X.; Angeloudis, P.; Demiris, Y. Dual-Branch Spatio-Temporal Graph Neural Networks for Pedestrian Trajectory Prediction. Pattern Recognit. 2023, 142, 109633. [Google Scholar] [CrossRef]
- Ellis, D.; Sommerlade, E.; Reid, I. Modelling pedestrian trajectory patterns with Gaussian processes. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 1229–1234. [Google Scholar]
- Yin, D.; Jiang, R.; Deng, J.; Li, Y.; Xie, Y.; Wang, Z.; Zhou, Y.; Song, X.; Shang, J.S. MTMGNN: Multi-time multi-graph neural network for metro passenger flow prediction. GeoInformatica 2023, 27, 77–105. [Google Scholar] [CrossRef]
- Bicocchi, N.; Mamei, M. Investigating ride sharing opportunities through mobility data analysis. Pervasive Mob. Comput. 2014, 14, 83–94. [Google Scholar] [CrossRef]
- Cavallaro, C.; Verga, G.; Tramontana, E.; Muscato, O. Multi-Agent Architecture for Point of Interest Detection and Recommendation. In Proceedings of the CEUR Workshop Proceedings, Parma, Italy, 26–28 June 2019; Volume 2404, pp. 98–104. [Google Scholar]
- Guo, Y.; Zhang, Y.; Boulaksil, Y.; Tian, N. Multi-dimensional spatiotemporal demand forecasting and service vehicle dispatching for online car-hailing platforms. Int. J. Prod. Res. 2022, 60, 1832–1853. [Google Scholar] [CrossRef]
- Zou, G.; Lai, Z.; Ma, C.; Tu, M.; Fan, J.; Li, Y. When Will We Arrive? A Novel Multi-Task Spatio-Temporal Attention Network Based on Individual Preference for Estimating Travel Time. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11438–11452. [Google Scholar] [CrossRef]
- Zong, M.; Chang, Y.; Dang, Y.; Wang, K. Pedestrian Trajectory Prediction in Crowded Environments Using Social Attention Graph Neural Networks. Appl. Sci. 2024, 14, 9349. [Google Scholar] [CrossRef]
- Liu, S.; Liu, H.; Bi, H.; Mao, T. CoL-GAN: Plausible and Collision-Less Trajectory Prediction by Attention-Based GAN. IEEE Access 2020, 8, 101662–101671. [Google Scholar] [CrossRef]
- Pang, S.M.; Cao, J.X.; Jian, M.Y.; Lai, J.; Yan, Z.Y. BR-GAN: A Pedestrian Trajectory Prediction Model Combined with Behavior Recognition. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24609–24620. [Google Scholar] [CrossRef]
- Dou, W.; Lu, L. SISGAN: A Generative Adversarial Network Pedestrian Trajectory Prediction Model Combining Interaction Information and Scene Information. Appl. Sci. 2024, 14, 9537. [Google Scholar] [CrossRef]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social GAN: Socially Acceptable Trajectories with Generative Adversarial Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2255–2264. [Google Scholar]
- Zhou, X.; Zhang, Y.; Wang, Y.; Liu, Z. CSR: Cascade Conditional Variational Auto Encoder with Socially-aware Regression for Pedestrian Trajectory Prediction. Pattern Recognit. 2023, 133, 109030. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, X.; Ren, D.; Huang, H.; Fan, M. CSIR: Cascaded Sliding CVAEs with Iterative Socially-Aware Rethinking for Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14957–14969. [Google Scholar] [CrossRef]
- Mohamed, A.; Qian, K.; Elhoseiny, M.; Claudel, C. Social-STGCNN: A Social Spatio-Temporal Graph Convolutional Neural Network for Human Trajectory Prediction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 14412–14420. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Petar, V.; Cucurull, G.; Casanova, A.; Romero, A.; Pietro, L.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Youssef, T.; Zemmouri, E.; Bouzid, A. STM-GCN: A Spatiotemporal Multi-Graph Convolutional Network for Pedestrian Trajectory Prediction. J. Supercomput. 2023, 79, 20923–20937. [Google Scholar] [CrossRef]
- Sighencea, B.I.; Stanciu, I.R.; Căleanu, C.D. D-STGCN: Dynamic Pedestrian Trajectory Prediction Using Spatio-Temporal Graph Convolutional Networks. Electronics 2023, 12, 611. [Google Scholar] [CrossRef]
- Kosaraju, V.; Sadeghian, A.; Martín-Martín, R.; Reid, I.; Rezatofighi, H.; Savarese, S. Social-bigat: Multimodal trajectory forecasting using bicycle-gan and graph attention networks. Adv. Neural Inf. Process. Syst. 2019, 32, 137–146. [Google Scholar]
- Grassia, M.; Mangioni, G. wsGAT: Weighted and Signed Graph Attention Networks for Link Prediction. In Complex Networks & Their Applications X: Volume 1, Proceedings of the Tenth International Conference on Complex Networks and Their Applications; Springer: Cham, Switareland, 2022; pp. 369–375. [Google Scholar]
- Pellegrini, S.; Ess, A.; Van Gool, L. Improving Data Association by Joint Modeling of Pedestrian Trajectories and Groupings. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. 452–465. [Google Scholar]
- Lerner, A.; Chrysanthou, Y.; Lischinski, D. Crowds by example. Comput. Graph. Forum 2007, 26, 655–664. [Google Scholar] [CrossRef]
- Amir, S.; Vineet, K.; Ali, S.; Noriaki, H.; Hamid, R.; Silvio, S. Sophie: An attentive gan for predicting paths compliant to social and physical constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1349–1358. [Google Scholar]
- Sekhon, J.; Fleming, C. SCAN: A Spatial Context Attentive Network for Joint Multi-Agent Intent Prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 6119–6127. [Google Scholar]

| Dataset | Scene Description | Frames | Pedestrians | Time |
|---|---|---|---|---|
| ETH | Campus | 12,380 | 367 | 518 s |
| HOTEL | Hotel Surrounding | 18,060 | 420 | 774 s |
| UNIV | University Campus | 9830 | 849 | 393 s |
| ZARA1 | Mall Environment | 9010 | 148 | 361 s |
| ZARA2 | Mall Environment | 10,520 | 204 | 420 s |
| Method | ETH | HOTEL | UNIV | ZARA1 | ZARA2 | AVG |
|---|---|---|---|---|---|---|
| Social-GAN | 0.81/1.52 | 0.72/1.61 | 0.60/1.26 | 0.34/0.69 | 0.42/0.84 | 0.58/1.18 |
| Social-BiGAT | 0.69/1.29 | 0.49/1.01 | 0.55/1.32 | 0.30/0.62 | 0.36/0.75 | 0.48/1.00 |
| Sophie | 0.70/1.43 | 0.76/1.67 | 0.54/1.24 | 0.30/0.63 | 0.38/0.78 | 0.54/1.15 |
| SCAN | 0.84/1.58 | 0.44/0.90 | 0.63/1.33 | 0.31/0.85 | 0.37/0.76 | 0.51/1.08 |
| Social-TAG | 0.61/1.00 | 0.37/0.56 | 0.51/0.87 | 0.33/0.50 | 0.30/0.49 | 0.42/0.68 |
| Social-STGCNN | 0.64/1.11 | 0.49/0.85 | 0.44/0.79 | 0.34/0.53 | 0.30/0.48 | 0.44/0.75 |
| D-STGCN | 0.63/1.03 | 0.37/0.58 | 0.46/0.78 | 0.35/0.56 | 0.29/0.48 | 0.42/0.68 |
| SISGAN | 0.63/0.95 | 0.58/1.62 | 0.50/1.10 | 0.31/0.68 | 0.30/0.73 | 0.46/1.01 |
| STGAT | 0.65/1.12 | 0.35/0.66 | 0.52/1.10 | 0.34/0.69 | 0.29/0.60 | 0.43/0.83 |
| DSGAT(our) | 0.60/0.97 | 0.34/0.54 | 0.42/0.76 | 0.31/0.49 | 0.29/0.47 | 0.39/0.64 |
| Basel | Social | Group | ETH | HOTEL | UNIV | ZARA1 | ZARA2 | AVG |
|---|---|---|---|---|---|---|---|---|
| √ | 0.66/1.21 | 0.45/0.77 | 0.49/0.91 | 0.37/0.60 | 0.35/0.56 | 0.46/0.81 | ||
| √ | √ | 0.68/1.27 | 0.43/0.71 | 0.54/0.97 | 0.36/0.55 | 0.33/0.53 | 0.47/0.80 | |
| √ | √ | 0.61/1.05 | 0.38/0.60 | 0.44/0.74 | 0.34/0.53 | 0.31/0.50 | 0.42/0.68 | |
| √ | √ | √ | 0.60/0.97 | 0.34/0.54 | 0.42/0.76 | 0.31/0.49 | 0.29/0.47 | 0.39/0.64 |
| Method | AVERAGE ADE | AVERAGE FDE |
|---|---|---|
| M1(DGCN) | 0.41 | 0.68 |
| M2(Weighting Factor) | 0.44 | 0.73 |
| M3(Addition) | 0.47 | 0.78 |
| M4(WSGAT) | 0.39 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liang, Y.; Yang, Z.; Li, J. Pedestrian Trajectory Prediction Based on Dual Social Graph Attention Network. Appl. Sci. 2025, 15, 4285. https://doi.org/10.3390/app15084285
Li X, Liang Y, Yang Z, Li J. Pedestrian Trajectory Prediction Based on Dual Social Graph Attention Network. Applied Sciences. 2025; 15(8):4285. https://doi.org/10.3390/app15084285
Chicago/Turabian StyleLi, Xinhai, Yong Liang, Zhenhao Yang, and Jie Li. 2025. "Pedestrian Trajectory Prediction Based on Dual Social Graph Attention Network" Applied Sciences 15, no. 8: 4285. https://doi.org/10.3390/app15084285
APA StyleLi, X., Liang, Y., Yang, Z., & Li, J. (2025). Pedestrian Trajectory Prediction Based on Dual Social Graph Attention Network. Applied Sciences, 15(8), 4285. https://doi.org/10.3390/app15084285





