Dynamic Scheduling and Preventive Maintenance in Small-Batch Production: A Flexible Control Approach for Maximising Machine Reliability and Minimising Delays

Abstract

Single- and small-batch production requires flexible production control to maximise machine reliability and minimise delivery delays. Existing planning approaches often do not take into account the dynamic production conditions of these environments, where machine breakdowns, variable order volumes and short-term changes lead to inefficiencies. This paper presents an enhanced job-shop scheduling model that integrates preventive maintenance strategies directly into production control. Using a mixed-integer programming approach, machine allocation and maintenance measures are optimised simultaneously in order to reduce unplanned downtimes and make efficient use of free time slots. The model is implemented in Python with Pyomo (Python 3.13.0 and Pyomo Version: 6.8.0) and validated using a scenario. The results show that an adaptive maintenance strategy contributes significantly to reducing machine downtimes without compromising production output. Visualisations support users in their decision-making by clearly presenting machine availability, maintenance slots and production orders. The approach is specifically designed for production and maintenance planners who need efficient and adaptable scheduling in volatile production environments. Compared to traditional maintenance models, this approach improves schedule adherence and optimises resource utilisation by dynamically linking production control and maintenance planning.

1. Introduction

In view of the challenges of Industry 4.0, the manufacturing industry faces a multitude of changes [1,2]. Particularly affected is order-based single zu- and small-batch production, which features a high variety of variants, small batch sizes and a heterogeneous machine park [3]. In single- and small-batch production, the high variety of variants leads not only to complex production processes but also to uneven machine utilisation [4]. Different material properties, specialised processing steps and varying process chains result in certain machines being used more while others remain underutilised.

The increasing demand for customer-specific products, combined with complex production processes and the requirement for reliability, necessitates new approaches in production control to flexibly and efficiently respond to dynamic conditions [3,5]. Unforeseen events such as machine failures, sudden demand fluctuations, changes in delivery dates, or material shortages often cause unexpected adjustments in the production schedule [6]. As a result, unused time slots emerge that are not efficiently utilised, leading to a waste of valuable resources such as time and personnel [5]. In response to these challenges, the focus of recent research has been on the integration of production control and maintenance strategies, particularly in single-part and low-volume production environments. A previous systematic literature review [3] identified relevant research gaps and pointed out the need for dynamic and flexible optimisation approaches. It highlighted the limitations of current models in dealing with contingencies and the potential for a combination of preventive and reactive maintenance in operational planning.

Scientific databases such as Dimensions.ai and Scopus formed the foundation for this literature review. The findings indicate that while existing studies propose models for integrating maintenance strategies into production planning, they often fail to address the dynamic requirements of single- and small-batch production [7]. In particular, the integration of preventive and reactive maintenance within an operational planning horizon remains under-researched. The literature further shows that while existing approaches consider various aspects such as preventive or reactive maintenance strategies, they are often designed for stable production environments like mass production [7,8]. As a result, short-term dynamic adjustments remain insufficiently supported. Existing models and algorithms, which base their calculations on fixed maintenance intervals, lack the flexibility to effectively handle unplanned events [9].

Previous research has developed various methods to integrate production control and maintenance strategies, including genetic algorithms for minimising lead time [10], multi-objective optimisation problems [11], and dynamic control algorithms [6]. However, these approaches often do not fully address short-term dynamic adjustments.

The approach presented in this work builds on an extended job-shop scheduling model, which closely integrates preventive maintenance strategies with production control. In particular, it considers complex machine chains and dynamic events such as sudden machine failures or short-term order arrivals, which are highly relevant in single- and small-batch production. The model combines both time-based and condition-based maintenance measures, enabling flexible adjustments to machine allocation in response to unforeseen events. A key difference from existing approaches lies in the dynamic integration of maintenance measures into the production schedule. As a result, unused time slots serve either for preventive maintenance or for optimising the sequence of production orders, minimising downtime and improving resource utilisation.

In contrast to traditional models that assume fixed maintenance intervals [12,13], the proposed approach allows for the dynamic scheduling of maintenance activities based on machine conditions and operational requirements. This integration proves particularly important in the case of the single- and small-batch production of complex products, where production conditions change frequently and require rapid adaptability.

Some existing approaches, such as the model described in [14], develop a dynamic scheduling strategy for machine failures but exhibit significant limitations. The imperial competitive algorithm (ICA) used in this approach primarily targets continuous optimisation problems, which restricts its applicability to discrete scheduling problems. Additionally, the approach relies on the accurate prediction of repair duration, which often proves unrealistic in highly dynamic production environments and can lead to inefficient rescheduling. These limitations reduce adaptability to short-term changes and increase computational effort, especially in the case of unexpected disruptions [6].

The developed production control system not only considers preventive measures but also enables dynamic adaptation to short-term changes in the production process. Unforeseen events, such as machine failures or demand fluctuations, can be mitigated through the efficient use of unused time slots. As a result, production planning remains flexible and undergoes continuous optimisation.

The following sections present the developed model, the underlying methods and the results and their practical implications. The central focus addresses the key question of whether the proposed concept enables flexible and efficient planning in dynamic production environments and how it contributes to addressing the challenges of single- and small-batch production.

2. Materials and Methods

In this section, the methodology for the integration of preventive maintenance into production planning is presented. First, the mathematical optimisation model extends the classic job-shop scheduling approach by incorporating maintenance tasks. The model formulation, including decision variables and constraints, is described in detail. Next, the model’s implementation in Python using Pyomo and the CBC solver is discussed. Finally, the data processing and visualisation techniques are presented, followed by an outline of the pseudocode describing the optimisation process.

2.1. Mathematical Optimisation Model

The model developed extends the classic job-shop scheduling approach by integrating preventive maintenance measures in addition to production tasks. A mixed-integer programming (MIP) model is used to enable the integration of both tasks. This allows dynamic machine allocation, taking into account maintenance intervals, resource availability and delivery dates [15,16]. This model is particularly suitable for the short-term planning horizon in production environments with a high number of variants, in which production steps need to be organised efficiently. The model recognises and uses unused time slots that arise due to changes in the production plan. This replanning allows machine downtimes to be minimised and maintenance measures to be integrated efficiently without unnecessarily disrupting the production flow. By using MIP, both integer and continuous variables can be modelled in order to optimise machine allocations, maintenance intervals and production processes [15]. These variables enable flexible and precise mapping of time-based and organisational decision-making processes in the model. The objective function aims to minimise production time and maximise machine availability through strategic maintenance measures while at the same time complying with all constraints.

Although the model is initially based on predefined order sequences and time slots to ensure practical applicability in small-batch production environments, it already contains mechanisms for flexible adaptation. These include prioritisation constraints between jobs and dynamic machine assignments that allow production sequences to be restructured within the feasible planning horizon. In addition, task priorities influence scheduling through time window constraints and are reflected in the objective function through weighted penalties. While real-time sequencing is not yet implemented, future research will focus on integrating the current machine status and workload into the sequencing logic. Maintenance tasks are directly integrated as decision variables in the MIP model. The optimisation logic identifies and utilises idle times not as a downstream processing step, but as an integral part of the central planning strategy. Maintenance affects both the objective function and machine availability. In addition, the model iteratively reschedules when wear limits are reached, ensuring that maintenance is prioritised without disrupting critical order sequences.

The production plan is calculated again in an iterative optimisation process that is carried out at regular intervals or in the event of unplanned events (e.g., machine failure). Real-time data from production are used to create an updated, customised production and maintenance plan. At the same time, the model identifies unused time slots that arise due to changes in the production plan. When rescheduling, new time dependencies and the availability of resources are taken into account in the operational planning horizon. The model also shows when maintenance tasks can be inserted into existing time slots without affecting the production flow [17]. The model ensures that realistic constraints such as machine availability and precedence conditions are taken into account.

The objective function and the constraints are described in mathematical detail in Section 2.4. In the model presented, MIP enables precise mapping of machine allocation, maintenance planning and sequencing of production orders by integrating both discrete and continuous decision variables. This results in dynamic and flexible control that can react flexibly to short-term changes in the production process [18].

2.2. Implementation and Data Processing

The model is implemented in Python, as this programming language offers powerful support for optimisation tasks and data processing. This is particularly due to the large number of available libraries that enable efficient mathematical modelling, numerical calculations, and data analysis. Pyomo, a flexible library for the mathematical formulation of complex optimisation problems [19], is used to model and solve MIP. Pyomo enables the use of various solvers, and the CBC (Coin-or Branch and Cut) solver is applied in this model [20]. CBC is an open-source solver based on branch-and-bound methods and is particularly efficient for medium-sized optimisation problems. However, the calculation time can increase significantly with increasing problem size, especially with a high number of binary variables and decision options. The planning horizon considered in the model is restricted to short-term decisions within a limited period of time. The computation time for the considered problem instance, which consists of 4 machines, 8 production orders (each with 3–4 subtasks) and 2 planned maintenance tasks, is measured to evaluate the computational efficiency of the model. The recorded computation times are 0.21 s for CPU processing time and 0.22 s for total elapsed time, indicating that the approach is efficient for small to medium-sized problems. However, as the number of machines, jobs or constraints increases significantly, the computational effort grows exponentially. The initial tests show that computational complexity increases exponentially with the number of binary variables, which is particularly relevant for larger production environments. Future improvements should explore decomposition techniques or heuristic approaches to maintain computational feasibility. This issue can be mitigated by using more advanced solvers such as CPLEX or Gurobi or by implementing heuristic approaches to improve computational efficiency. NumPy (Version: 2.0.2) is used for data processing in order to efficiently analyse and process large volumes of data. Matplotlib and Gantt (Version: 3.9.2) charts are applied to visualise the results, which show the machine allocation, production planning and maintenance intervals clearly. The input parameters of the model are derived from typical data for single- and small-batch production. These include machine capacities, wear limits, production order details, maintenance tasks and set-up times. These parameters enable a realistic representation of the production environment and practical optimisation of machine and maintenance planning. These aspects are described further in Section 2.5.

2.3. The Positioning of the Proposed Model in the Existing Literature

In order to clearly differentiate the proposed model from existing research approaches,

Table 1. A comparison of the selected literature approaches with the model proposed in this paper regarding maintenance integration, the handling of unplanned events, and applicability to small-batch production.

Source	Method	Maintenance Integration	Unplanned Events	Small-Batch Focus
Proposed model (this paper)	MIP-based model with integrated dynamic planning and maintenance scheduling	Yes	Yes	Yes
Fnaiech et al. (2015) [10]	Heuristic (genetic algorithm) for joint job-shop scheduling and maintenance	Yes	No	No
Wang et al. (2021) [11]	NSGA-II multi-objective optimisation for flexible job shops	No	No	No
Wang and Yu (2010) [9]	Heuristic with fixed maintenance intervals	Yes	No	No
Pan et al. (2012) [21]	Joint model for production scheduling and predictive maintenance	Yes	No	No answer
Wang et al. (2022) [14]	Simulation and online rescheduling using Imperialist Competitive Algorithm (ICA)	Yes * (not preventive)	Yes	Yes

*: Although the authors of Wang et al. [14] formally address all three aspects, their model focuses solely on reactive maintenance and does not include preventive or condition-based strategies. Further differences can be observed in how production priorities and available time slots are handled.

presents a structured comparison of relevant works from the literature. It summarises key features such as objectives, applied methods and the capabilities of the selected optimisation approaches referenced throughout this article. This comparison highlights the novelty of the proposed model, particularly in terms of its dynamic responsiveness, the integration of production planning and maintenance, and its specific orientation towards the requirements of single- and small-batch production. Unlike existing approaches, the model enables condition-based maintenance planning within a unified MIP-based optimisation framework. It incorporates critical factors such as machine wear, maintenance tasks and order assignments—an integration not yet addressed in the literature, especially for small-series production.

In addition to the structured comparison above, several related approaches from the literature are discussed in more detail in the following. While Pan et al. [21] propose a predictive maintenance scheduling model that accounts for machine conditions, the proposed model extends this by integrating both preventive and reactive strategies within a unified optimisation framework. Similarly, the optimisation approach of Wang et al. [11] addresses dynamic conditions in flexible job-shop environments, but does not fully combine job scheduling and maintenance in a condition-based manner. The heuristic method of Fnaiech et al. [10] supports adaptive maintenance planning but lacks the mathematical integration of machine wear, task prioritisation, and scheduling flexibility.

While Wang et al. [14] present a dynamic rescheduling approach for flexible manufacturing in the event of machine failures, their model is limited to purely reactive measures and only aims to minimise lead time with the help of simulation and improved ICA. The model presented here, on the other hand, integrates both preventive and reactive maintenance strategies into a uniform MIP optimisation framework. It takes machine conditions, load factors and wear patterns directly into account in the planning logic. In this way, it not only reacts to faults at short notice, but also prevents them from occurring in the first place by proactively maximising machine availability. The asterisk in Table 1 indicates that, although the authors of Wang et al. [14] formally address all three aspects, their model focuses solely on reactive maintenance and does not include preventive or condition-based strategies. Further differences can be observed in how production priorities and available time slots are handled. For instance, Lee et al. [6] presents a capacity control model for a single machine aimed at minimising idle times, but it does not dynamically integrate maintenance into these time slots. In contrast, the proposed model makes targeted use of such free capacities to schedule maintenance in a way that improves both machine availability and production efficiency. Finally, models such as that in Penchev et al. [4] rely on static rules or threshold-based triggers for maintenance scheduling. The presented approach differs by enabling adaptive planning based on actual machine load and production priorities. This ensures that high-priority jobs are not delayed by rigid maintenance schedules, and that maintenance is strategically timed according to real-time conditions.

2.4. Mathematical Model Formulation

The mathematical formulation of the model aims to minimise production time while maximising machine reliability through preventive maintenance measures. A particular strength of the model lies in the integration of preventive and reactive maintenance measures within a single optimisation environment. In the following, the architecture of the model is described in detail, including the model structure, the methods used and the implementation. Subsequently, the mathematical definitions for the parameters, decision variables, objective function and constraints used are presented precisely. These formulations form the theoretical basis for the subsequent implementation of the optimisation model.

2.5. Input Parameters

The input parameters define the framework of the model and determine the production and maintenance tasks. They include key variables for planning machine capacity, maintenance intervals and production orders. The data used are fictitious due to confidentiality constraints and the complexity of obtaining comprehensive real-world datasets. However, to ensure a realistic representation of production conditions, the input parameters were carefully derived using best practices and expert judgment. To validate the accuracy and relevance of the data, a joint session was conducted with a production manager from a single- and small-batch production environment. The selection of influencing indicators for maintenance planning in the proposed model was based on a structured literature review. The aim was to derive selected indicators that are both theoretically sound and practically relevant. Three main categories of influence indicators were identified from the literature and form the basis for the following discussion.

Machine-specific characteristics are integrated into the model, such as the age of the machines, which is modelled using operating hours, as well as their failure history, which was included as part of an expert interview using experience-based knowledge. Other theoretically relevant variables such as the mean time between failures or the criticality of individual machines are emphasised as important in the literature [22,23], but are deliberately abstracted in the model in order to ensure feasibility in a dynamic production environment. Production-related aspects, including machine utilisation, order deadlines and planning flexibility, are directly taken into account in the model, as they represent key influencing variables for the interaction between production and maintenance [24,25]. Organisational and strategic elements, such as the chosen maintenance strategy, are integrated into the model. However, aspects such as “availability of personnel and spare parts” and “quality of the data basis” will be discussed in the context of future extensions, as they are highly company-specific and are currently not systematically recorded in the application environment under consideration [26,27,28].

This reduced set of indicators was deliberately chosen to balance completeness and simplicity. It was confirmed in the expert session to be practically sufficient for operational maintenance decision-making. During this session, both the input parameters and the overall model structure were reviewed and confirmed to align with practical manufacturing scenarios. The expert assessment ensured that the selected values accurately reflected typical operating constraints, machine wear rates, and maintenance scheduling practices. Furthermore, the expert confirmed that no data elements critical for the model to effectively represent real-world production dynamics were missing. This validation ensures that the optimisation approach accounts for real-world constraints and operational requirements, making both the dataset and the model suitable for practical production planning. Maintenance tasks are defined with explicit durations, which serve as input parameters for the optimisation model. These durations are considered in the scheduling logic to ensure that maintenance activities can only be assigned to time windows of sufficient length.

• Machine capacities determine the number of available machines and their specific properties.
• Task priorities determine the urgency and importance of production orders. These priorities influence the scheduling by narrowing time windows and indirectly shaping the objective function. As a result, high-priority jobs are preferentially completed within their due dates, while delays are more acceptable for low-priority tasks. Order priorities are currently modelled by penalties and weighting in the objective function, which indirectly influence the schedule. However, dynamic reprioritisation based on real-time system states or evolving constraints is not yet implemented. This extension allows the model to adjust priorities during execution.
• Wear thresholds determine when preventive maintenance is required based on the condition of the machines.
• Processing times and due dates define the time requirements for production orders.

These parameters are mathematically described by the following sets and variables.

J—

Set of production and maintenance tasks

M—

Set of machines.

T—

Set of possible task-to-machine assignments $(j,m)\in J\times M$.

r_jm—

Processing time of task j on machine m, defined individually for each task–machine pair to reflect both machine-specific and task-specific characteristics in execution time.

l_jm—

Earliest possible start time of task j on machine m.

q_jm—

Latest completion time of task j on machine m.

O—

Set of precedence constraints $(j,m,k,n)$ ensuring that task $(j,m)$ starts only after $(k,n)$.

D—

Set of disjunctive constraints $(j,k,m)$ guaranteeing that no two tasks are executed simultaneously on machine m.

BIG—

A sufficiently large constant for constraints with binary variables.

2.6. Decision Variables

The decision variables describe the main assignments and time sequences within the model. They include both integer and continuous variables. Integer variables model machine allocation, while continuous variables capture temporal aspects such as start and end times. The sequence and scheduling of tasks are accurately modelled using these variables.

s_jm —

Start time of task j on machine m.

y_jm ∈ {0,1}—

Binary variable indicating whether task j is assigned to machine m. This allows the model to flexibly allocate tasks to different machines based on processing times, availability and scheduling constraints.

w_jkm ≥ 0—

Waiting time between tasks j and k on machine m.

Z—

Total completion time of the production schedule.

2.7. Objective Function

The objective function of the model aims to optimise several goals. It takes into account both temporal and structural aspects to optimise the control of production processes. This includes reducing production time and minimising idle periods by dynamically determining the optimal sequencing of jobs on machines. Unlike fixed-job-order approaches, the model flexibly adjusts the job sequence based on delivery deadlines, precedence relations, and resource availability, resulting in improved machine utilisation and scheduling efficiency. In addition, preventive maintenance is integrated to limit machine wear, extend machine life and reduce unplanned downtime. Moreover, dynamic adaptation to unforeseen events enables greater planning accuracy. This minimises delays and ensures the stability of the production process. The formal representation of the objective function is achieved by minimising the total completion time Z, taking into account the start times and waiting times:

$$minZ·\mathrm{BIG}+\sum _{(j,k,m)\in D}{w}_{jkm}+\sum _{(j,m)\in T}{s}_{jm}$$

(1)

There are three main terms in the objective function:

$$Z·\mathrm{BIG}$$

The term Z represents the total completion time of the production schedule. It is multiplied by a sufficiently large constant $\mathrm{BIG}$ to ensure correct scaling when solving the optimisation problem.

$$\sum _{(j,k,m)\in D}{w}_{jkm}$$

This summation accounts for waiting times $w_{jkm}$ between consecutive tasks j and k on the same machine m. The model aims to minimise these waiting times, reducing idle time and improving resource utilisation.

$$\sum _{(j,m)\in T}{s}_{jm}$$

This term represents the start times $s_{jm}$ of all tasks j assigned to machines m. By minimising start times, the model prioritises the early completion of tasks, which reduces overall production time.

2.8. Constraints

The constraints ensure that the real restrictions of the production process are adhered to and that a smooth process is guaranteed. Each machine can only process one task at a time, which limits machine availability. The sequence of tasks must be adhered to by precedence conditions so that the production process is not interrupted. Furthermore, no two tasks may be performed simultaneously on the same machine, which is ensured by disjunctivity conditions. In addition, set-up times are taken into account, which record the time required to switch between different task types. The mathematical formulation of the constraints ensures that all tasks are correctly assigned and executed within the planning period.

Each task must be completed within the total time Z:

$$s_{jm}+r_{jm}·y_{jm}\le Z,\forall (j,m)\in T$$

(2)

The earliest possible start time of a task must not be violated:

$$l_{jm}-(1-y_{jm})·BIG\le s_{jm},\forall (j,m)\in T$$

(3)

Each task must be completed before its due time:

$$s_{jm}+r_{jm}\le q_{jm},\forall (j,m)\in T$$

(4)

Precedence constraints ensure that a subsequent task starts only after its predecessor is completed:

$$s_{kn}+r_{kn}·y_{kn}\le s_{jm}+(1-y_{jm})·BIG,\forall (j,m,k,n)\in O$$

(5)

A task may only be executed on one machine at a given time:

$$\sum _{m\in M}{y}_{jm}=1,\forall j\in J$$

(6)

Disjunctive constraints prevent two tasks from being executed simultaneously on the same machine:

$$s_{jm}+r_{jm}·y_{jm}+w_{jkm}=s_{km},\forall (j,k,m)\in D$$

(7)

The total completion time Z is a non-negative real number:

$$Z\ge 0$$

(8)

The formulations developed form the basis for the subsequent explanation of the optimisation model. The pseudocode, which describes the structured implementation of the model in practice, is presented below.

2.9. Pseudocode

The following pseudocode (see Algorithm 1) illustrates the structure and functionality of the developed optimisation model. The model is formulated as an MIP problem and solved using the CBC solver. Unlike heuristic approaches, this method ensures rigorous mathematical optimisation of job-shop scheduling while incorporating preventive maintenance measures. The solver determines an optimal schedule, strictly adhering to machine capacities, priority constraints, wear thresholds and processing times. The optimisation process consists of several key steps: First, the model is formulated, defining decision variables and constraints. Next, the solver iteratively assigns jobs to machines, optimising task sequencing, machine utilisation, and maintenance scheduling. Throughout this process, machine wear levels are continuously monitored, allowing proactive scheduling of additional maintenance in idle time slots before critical thresholds are reached. This ensures that maintenance is not only planned at fixed intervals but also adaptively integrated based on real-time machine availability and condition. Finally, the optimisation results are validated to ensure that all constraints are met and that the generated production schedule is both feasible and efficient. The updated pseudocode explicitly reflects these steps, providing a clearer representation of the optimisation logic, including the iterative nature of the solver-driven process and the dynamic allocation of maintenance tasks in unused time slots.

Algorithm 1 Mixed-Integer Programming Model for Production and Maintenance Optimization

1: Inputs:  2: Set of jobs $J=\{j_1,j_2,...,j_n\}$  3: Set of machines $M=\{m_1,m_2,...,m_k\}$  4: Processing times $r_{jm}$ for job j on machine m  5: Earliest start time $l_{jm}$, latest completion time $q_{jm}$  6: Wear thresholds and initial wear levels per machine  7: Precedence constraints for job dependencies  8: Setup times for task transitions  9: Maintenance requirements and intervals   10: Model Formulation: 11: Define decision variables: $s_{jm}$: Start time of job j on machine m $y_{jm}\in \{0,1\}$: Binary assignment of job j to machine m $w_{jkm}\ge 0$: Waiting time between tasks j and k on machine m Z: Total completion time    12: Objective Function: 13: Minimise total completion time while balancing machine usage: $$minZ·BIG+\sum _{(j,k,m)\in D}{w}_{jkm}+\sum _{(j,m)\in T}{s}_{jm}$$ (9)   14: Constraint Definition: 15: Ensure job precedence constraints are met 16: Ensure that no two jobs run simultaneously on the same machine 17: Include setup times for transitions between tasks 18: Prevent exceeding machine wear thresholds 19: Schedule preventive maintenance when needed   20: Optimisation Process: 21: Solve the MIP model using the CBC solver: 22: while solution is not optimal and solver time limit not exceeded do 23:   Sort jobs $j\in J$ by priority level (e.g., high → low) 24:   Preferentially assign high-priority jobs within feasible time windows 25:   Assign jobs to machines based on availability and priority 26:   Adjust start times and incorporate maintenance slots 27:   Update machine wear levels based on assigned tasks 28:   Calculate objective function: 29:   Compute Z as the total completion time 30:   Compute total waiting times $\sum w_{jkm}$ 31:   Compute total start times $\sum s_{jm}$ 32:   if maintenance is required then 33:     Schedule maintenance before the next critical wear threshold 34:   end if 35:   if a machine has an idle period and has not exceeded its wear threshold then 36:     Schedule additional preventive maintenance in the available time slot 37:   end if 38:   Recalculate job scheduling based on updated conditions 39: end while   40: Validation: 41: Ensure that all constraints are met: Jobs must be completed within deadlines Maintenance must be scheduled within limits No machine overloading allowed   42: Outputs: 43: Optimised job and maintenance schedule 44: Machine utilisation report 45: Maintenance forecasts and Gantt chart visualisation

3. Results and Visualisation

Based on the developed optimisation model, this section presents key findings that illustrate its impact on production planning and maintenance management. The following visualisations, generated directly from the model calculations, show the dynamic allocation of production and maintenance tasks within a given time frame, the evolution of machine conditions over time and relevant recommendations for maintenance personnel. The advantages of this model include the integration of fixed maintenance intervals based on time and wear, together with the flexibility to incorporate individual maintenance actions into the production schedule. The visualisations generated serve as a decision-making tool for production planners and maintenance teams, improving coordination and efficiency within the operational planning horizon, especially when dealing with short-term adjustments.

3.1. Production and Maintenance Tasks in the Machine Allocation Schedule

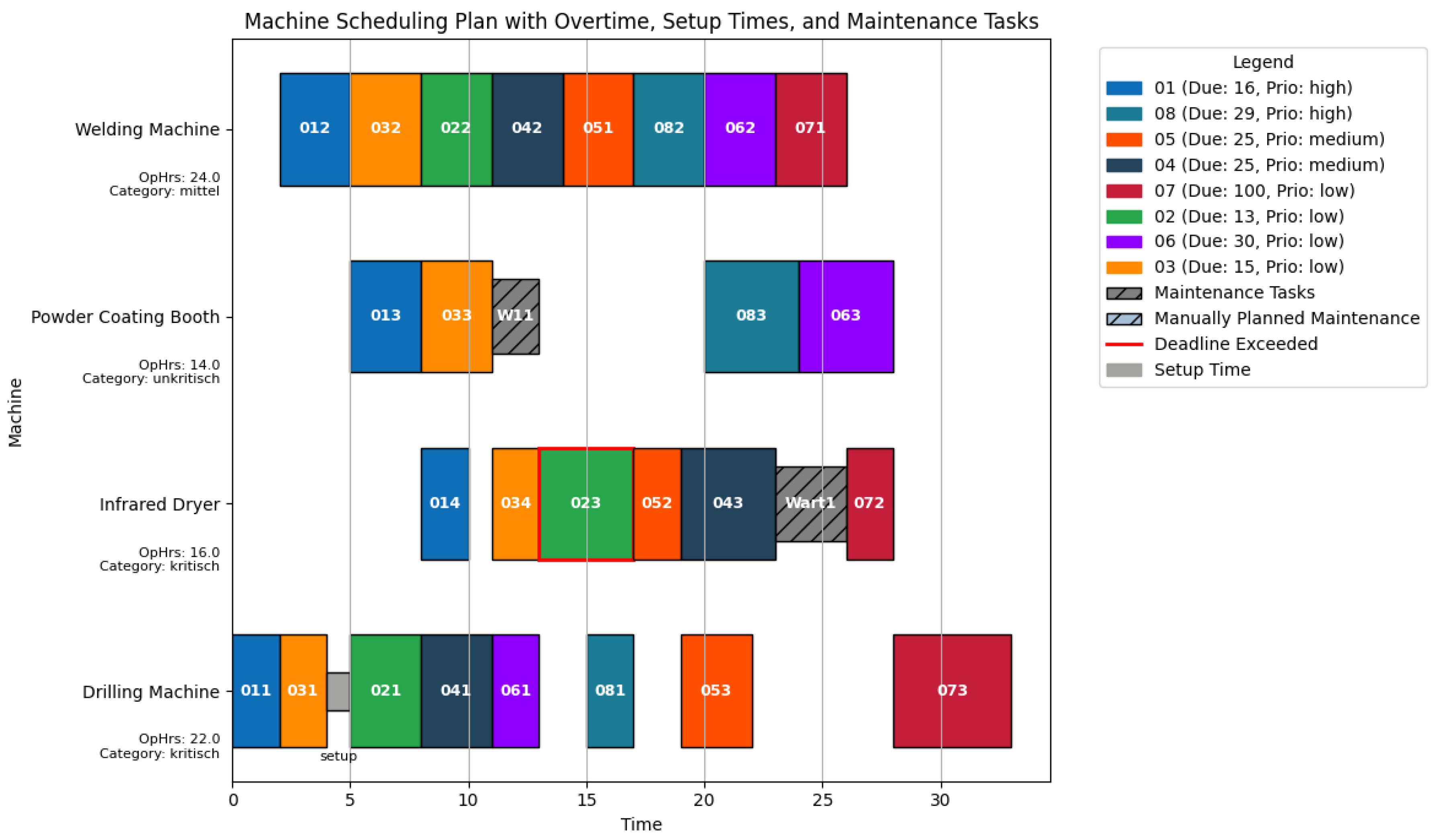
The machine schedules (see Figure 1) visualise the timing of production orders and maintenance tasks on the individual machines. The colour coding indicates production orders that belong together and consist of several production steps with defined predecessor and successor relationships and priorities. Maintenance slots are marked separately to visualise their influence on machine availability. Other relevant factors, such as set-up times or unused time slots, can also be mapped in the model. The latter become particularly clear in the visualisation and can be used for more efficient planning. A red border around a production step indicates that the completion date has been exceeded. The model is designed in such a way that delays occur preferentially for low-priority orders, while high-priority orders are completed on time wherever possible.

3.2. Machine Status and Wear Progression

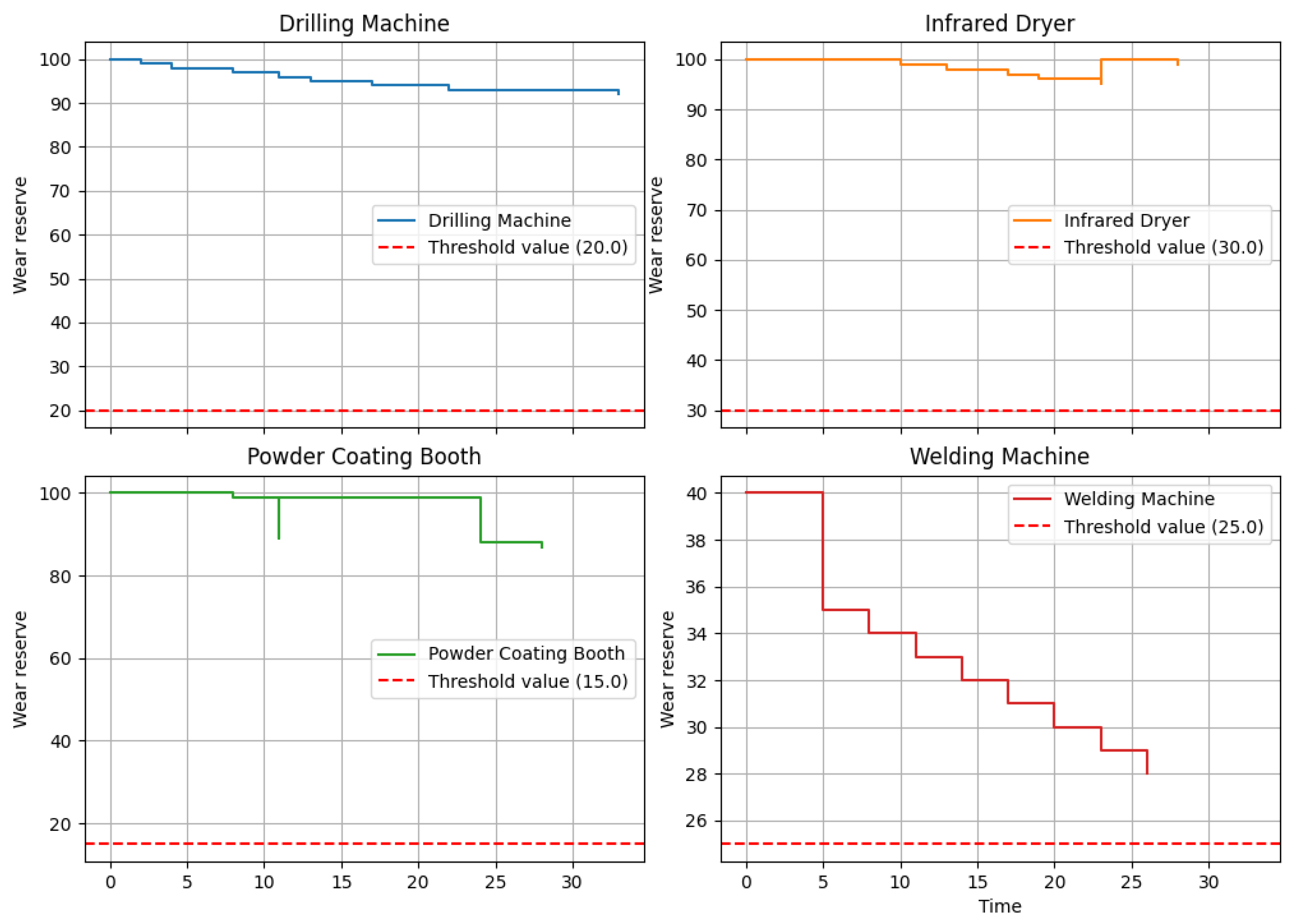
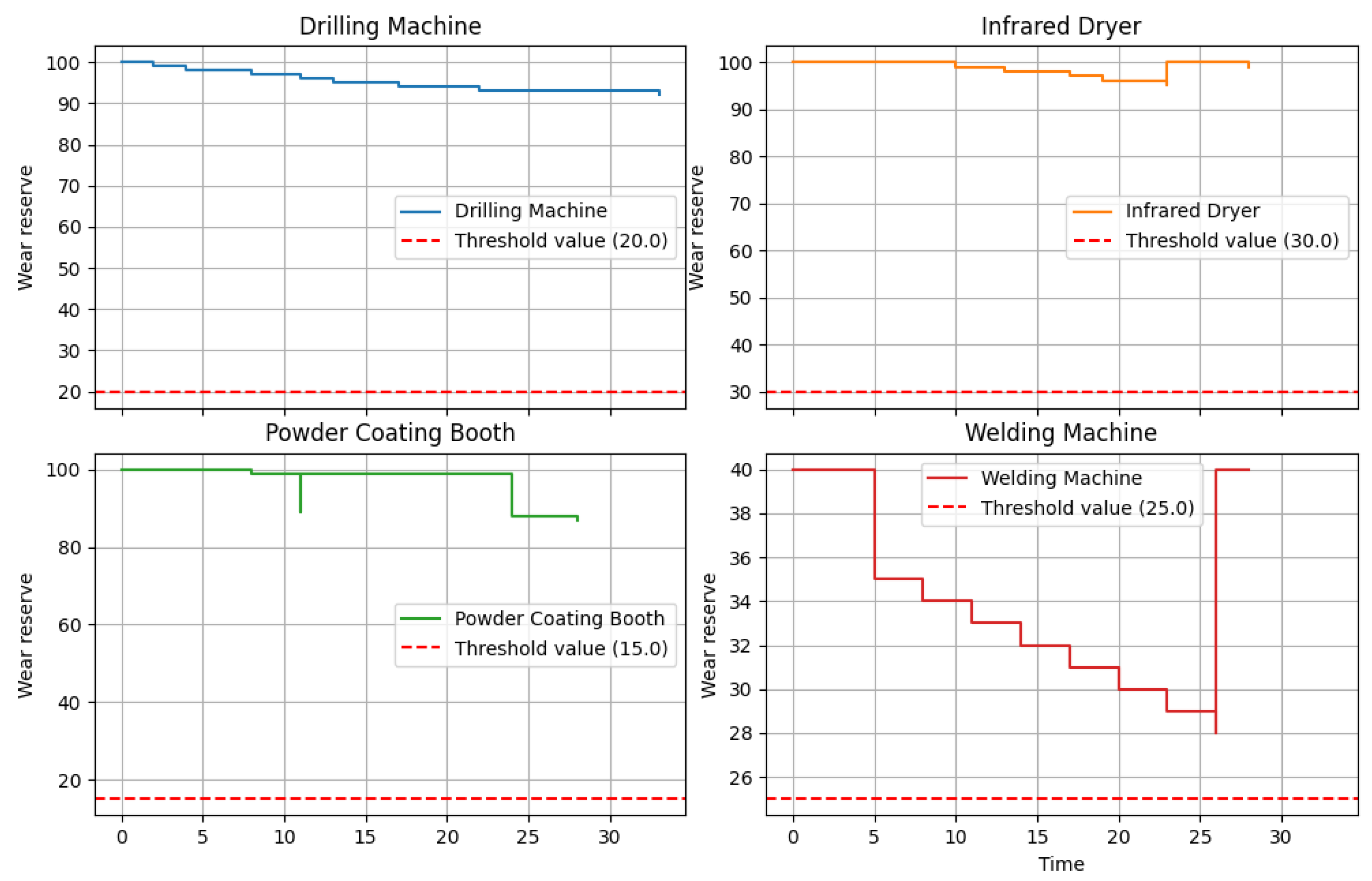
The wear curves (see Figure 2 and Figure 3) illustrate the condition of the machines over the planning period. Each machine has a wear reserve that describes its remaining planned operational capability [29]. This reserve decreases with each use, with the rate of wear depending on the type of production order and the specific utilisation of the machine. Each order is assigned an individual wear level for the machine. In addition, the planner can assign a stress level to each order, which accounts for other influencing factors. Together, these two parameters determine how much a job contributes to the wear of a machine.

To further enhance the accuracy of wear assessment, the model accounts for varying stress levels associated with different production tasks. Each job type has a distinct impact on machine wear, depending on factors such as processing intensity, material properties and operating conditions. By assigning specific wear coefficients to different task categories, the model provides a more refined evaluation of machine degradation over time. Future extensions incorporate advanced predictive analytics to further improve wear estimation and optimise maintenance planning. The model thus supports three types of maintenance strategies to meet different operational needs and levels of flexibility:

• As shown in

  Table 2. Maintenance measures and their effects on machine condition. Regular inspections maintain performance, while more extensive measures restore the wear reserve partially or completely.

  Interval	Maintenance Measure	Effect on Machine Condition
  Weekly	Lubrication of the drill spindle	No change
  Monthly	Inspection of the drill spindle and screws	No change
  Annually or every 3000 h	Replacement of ball bearings (partial overhaul)	Reset to 70%
  Every 5 years or 20,000 h	Replacement of spindle components (partial overhaul)	Reset to 80%
  After 10 years or 50,000 h	Full spindle overhaul	Reset to 100%

  , this variant follows fixed schedules, such as weekly, monthly or after a specific number of operating hours. Since these are planned independently of actual machine utilisation, they offer limited flexibility but enable regular maintenance that can be scheduled automatically.
• This approach monitors machine wear continuously instead of merely tracking operating hours. Maintenance planners assess task impact in advance by evaluating workload and stress levels. When critical thresholds are reached, the model automatically suggests maintenance windows during idle periods in the production schedule. Compared to the first variant, this method dynamically integrates maintenance activities into available time slots based on real-time machine conditions.
• The model also allows planners to schedule maintenance manually at any time, regardless of predefined intervals or wear levels. This offers full decision-making freedom and allows maintenance to be performed on demand.

This multi-tiered approach ensures that maintenance planning remains adaptable to real-world conditions—balancing predictability and optimisation-driven efficiency, as well as manual control for exceptional cases.

The input parameters of all maintenance tasks include defined durations, which are considered within the optimisation model. These durations are explicitly used in the scheduling logic to ensure that maintenance is only assigned when a time window of sufficient length is available. For dynamically scheduled maintenance, users can specify the expected duration manually or select predefined types. This guarantees that both static and reactive maintenance activities are realistically integrated into the production plan.

To ensure this flexibility, the model combines different approaches. Maintenance measures can be adjusted to reduce machine wear while simultaneously increasing overall availability. The model continuously monitors machine wear levels and dynamically schedules maintenance when predefined usage thresholds are exceeded. Instead of relying on static time-based maintenance, the system integrates both fixed intervals and condition-based triggers. As soon as a machine reaches its predefined limit (e.g., 3000 operating hours for ball bearing replacement), the model automatically suggests the next available maintenance slot within the production schedule to minimise disruptions. Depending on the type of maintenance, different effects on machine condition can be observed. While regular inspections and lubrication stabilise the machine condition, more extensive overhauls lead to a significant restoration of the wear reserve. The maintenance intervals shown in Table 2 serve as input parameters for the scheduling model. The system tracks machine hours, checks them against defined thresholds, and automatically integrates maintenance activities into the production plan when necessary.

Figure 2 clearly shows that the drilling machine has almost reached its wear threshold, making scheduled maintenance necessary to prevent failure. The model not only recognises machines that have already reached the threshold value, but also reports at an early stage when a machine is approaching this value. This allows preventative measures to be taken before critical conditions occur. After planning, the model identifies machines with critical wear and tear and shows available time slots for maintenance. The planner chooses a suitable time slot and defines the type of maintenance and the expected reduction in the wear value. The maintenance is then integrated into the production plan, and the condition of the machine is updated. Figure 3 shows the complete reset of wear after maintenance on the drilling machine.

The visualisation of the machine conditions is based on the current production orders in order to identify overloads at an early stage and counteract them in a focused manner [8]. This allows resources to be used efficiently, maintenance measures to be planned proactively and reactive measures to be minimised. At the same time, the analysis helps to ensure balanced machine utilisation and avoid long-term differences in wear between machines.

3.3. Key Performance Indicators for Optimisation

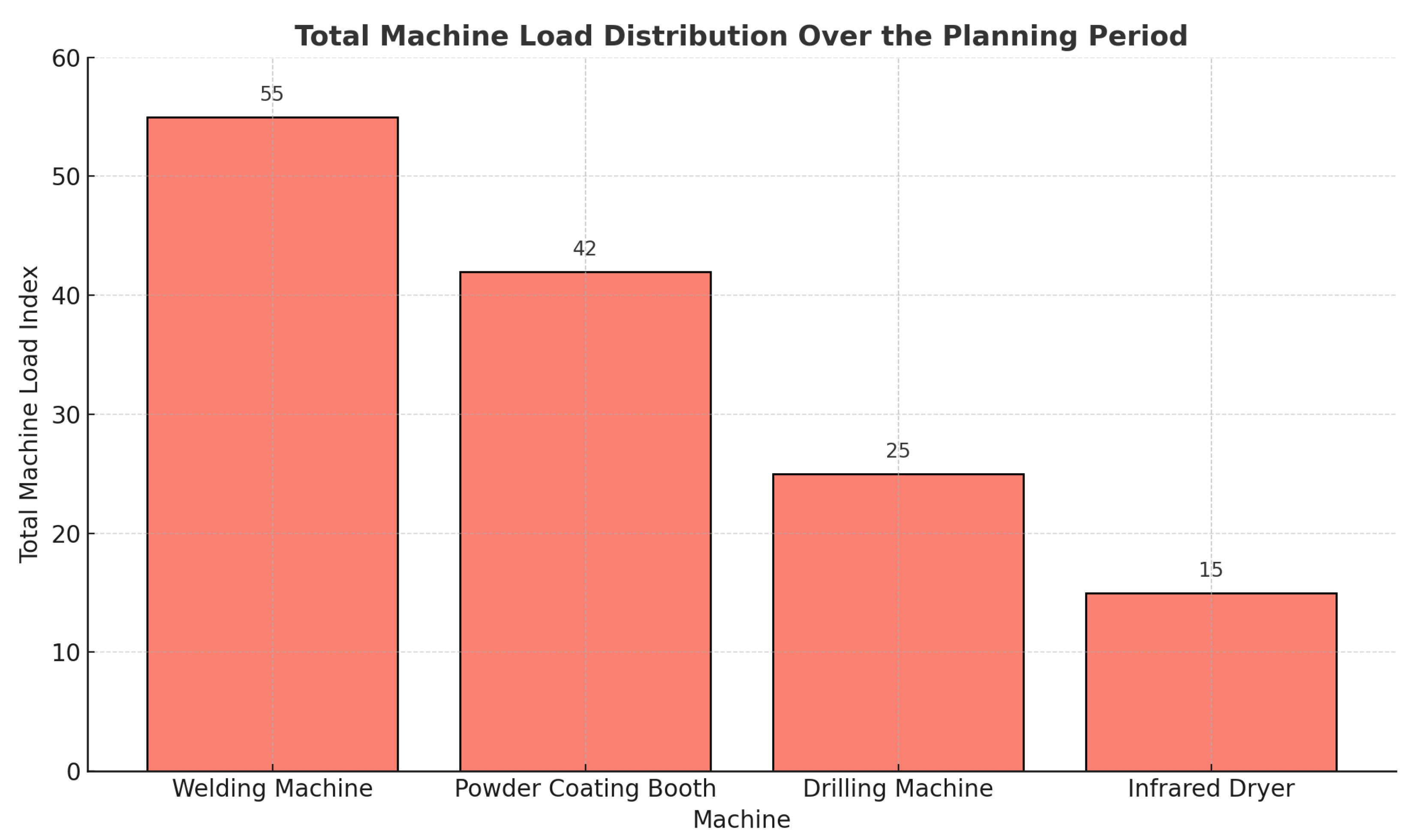
The bar chart shown in Figure 4 presents the total machine load over the planning period. This total load is calculated as a combination of three factors:

• Operational Load—The amount of time a machine spends actively processing production orders.
• Mechanical Stress—The workload intensity based on production parameters, such as cutting forces or thermal influences.
• Additional Stress Factor—Production-specific influences, such as material properties or special manufacturing requirements.

The selection of these three indicators is based on their practical relevance for maintenance planning. Together, they reflect both time utilisation and physical stress on the machines, providing a comprehensive picture of machine load. Combining them into a composite indicator supports intuitive visualisation and enables a direct comparison between machines. The number of indicators is deliberately limited to three to ensure clear interpretation without redundancy. The selected indicators are validated in collaboration with maintenance experts. In particular, the additional stress factor incorporates empirical experience from practitioners and accounts for machine-specific influences that are not captured by operating time or mechanical load alone.

The welding machine has the highest overall load. This is due to intensive use and high mechanical stress levels. This may indicate a higher proportion of complex processing steps or longer processing times per job. The visualisation provides valuable insights for future maintenance planning, as an uneven distribution of machine loads can lead to accelerated wear. The results highlight the importance of a dynamic maintenance model that proactively detects heavily loaded machines and schedules preventive maintenance in order to reduce unplanned downtime.

If multiple identical machines are available, this analysis enables a direct comparison of their workloads. For example, it is possible to determine whether one machine is handling a disproportionately high number of demanding tasks while another remains underutilised. This information allows better load balancing, reducing bottlenecks and extending machine service life by distributing wear more evenly.

4. Discussion

In this study, a model was developed that integrates production and maintenance planning to increase efficiency in dynamic manufacturing environments such as single- and small-batch production. Its results show that the flexible use of free time slots for preventive maintenance can significantly reduce unplanned downtime. On the whole, this is in line with previous research that has emphasised the importance of adaptive maintenance strategies. Several studies have demonstrated that integrating predictive and preventive maintenance strategies into production planning can significantly enhance machine availability and reduce unexpected downtime [10,11,21]. Pan et al. [21] highlight the benefits of predictive maintenance integration, while Wang et al. [11] emphasise multi-objective optimisation approaches for scheduling. Fnaiech et al. [10] propose a heuristic method to improve scheduling efficiency by dynamically integrating maintenance activities. These findings support the notion that adaptive strategies, such as those implemented in our model, are crucial for the improvement of overall production efficiency. Thus, the claim regarding the significance of adaptive maintenance strategies is well supported by a range of studies addressing various aspects of predictive and preventive maintenance integration in production planning.

4.1. Advantages of the Model

The analysis of the developed model shows both its strengths and potential areas for improvement. Its ability to dynamically link production and maintenance planning and to react flexibly to changes is particularly impressive. One advantage of the model is its ability to increase machine availability by allowing targeted preventive maintenance and reducing unplanned downtimes. This helps to increase the overall productivity of production. The model also enables a high degree of flexibility in the event of short-term changes by reacting in real time to unexpected order fluctuations, for example. As a result, the production process remains stable and flexible.

This transparency helps with resource-efficient planning and ensures that available machines are utilised to their full potential. Another positive aspect is that the model ensures better adherence to delivery deadlines by prioritising critical production orders and completing them on time. The model also provides a detailed overview of machine capacities, wear and tear statuses and free time slots.

4.2. Limitations of the Model

At the same time, there are aspects that require further development for even broader application. Simultaneously optimising production and maintenance tasks is very computationally intensive, especially when there are many machines and jobs. The CBC solver is suitable for medium-sized problems but reaches its limits as complexity increases. Strong solvers such as CPLEX or Gurobi, heuristic methods, or learning methods can reduce the computational effort [11]. Solvers can also be made more efficient by dynamically adapting to previous optimisation runs, thus reducing computation time. Alternatively, heuristic or metaheuristic methods can reduce computational time by providing an approximate solution of acceptable quality in a shorter period. This is particularly relevant in highly variable production scenarios, where fast decision-making is essential. A further challenge lies in the modelling assumptions. The quality of the results depends heavily on the reliability of the input data, especially when predicting machine wear and failure probabilities [30]. Inaccurate or incomplete data can lead to maintenance measures being scheduled too early or too late, which impairs the efficiency of the model. Therefore, accurate data collection and regular updates are essential for reliable planning.

The current model calculates machine wear based on task-specific load factors and task-specific utilisation patterns. Although no real-time sensor data are used, this approach is a condition-based strategy. The maintenance timing is dynamically adjusted as soon as certain thresholds are exceeded. Future research could investigate the integration of real-time monitoring to further improve maintenance decisions. The model does not contain any formal stochastic elements or interruption scenarios, so it supports limited responsiveness through iterative replanning. Rescheduling can be triggered by updated machine conditions, e.g., progressive wear or the occurrence of free capacity. This allows the model to respond to changing production conditions within short-term planning horizons, which it is designed to do.

To further evaluate the robustness of the model, a sensitivity analysis can be conducted by systematically varying key input parameters such as machine availability, maintenance thresholds or production order priorities. This provides insights into how stable the optimisation results remain under changing conditions and whether specific parameter ranges significantly impact scheduling efficiency. Analysing how variations in job sequencing affect machine utilisation and maintenance scheduling is particularly relevant, as fluctuations in incoming orders are common in real-world production environments. Future research should integrate such an analysis to strengthen the empirical validation of the approach and assess its adaptability to dynamic production scenarios.

In addition, the model requires interlinking between production and maintenance planners, as they are responsible for data maintenance, the validation of data, and the integration of empirical values. Acceptance and utilisation of the model by planners is crucial to fully exploit its potential.

4.3. Implications for Practice

Parallel to the model analysis, an expert interview was conducted to assess the practical applicability and possible challenges in implementation. The expert interviewed comes from a one-off production company with a batch size of 1 and has in-depth knowledge of production planning and dealing with unplanned maintenance measures. His assessments are based on many years of experience in a diverse production environment with a large number of critical machines and a machine park with varying production requirements. The results show that although machine runtimes and maintenance data are available in many companies, they are not systematically used for optimised maintenance planning, and that there is often a lack of structured data evaluation and the ability to dynamically adapt maintenance decisions to current machine conditions.

The model offers the option of utilising unused production time windows to carry out preventative maintenance measures. One expert confirmed that maintenance intervals have so far often been based on empirical values and that flexible, data-driven adjustments hardly ever take place. Intelligent planning could help to schedule maintenance more in line with demand, reduce unplanned downtime and lower external maintenance costs. A more precise maintenance strategy would be of great benefit, especially for companies with critical machines whose failure would affect the entire production process.

However, the introduction of such a model requires better integration into existing IT systems as well as a consistent and reliable database. Many companies lack a centralised overview of machine conditions and maintenance measures, which means that information on necessary maintenance is not consistently recorded or used. A digital dashboard could help here to enable maintenance teams to plan more clearly.

4.4. Potential Further Developments and Optimisation Approaches

A combination of improved data integration, adaptive algorithms and AI-supported forecasting models can be used to further optimise the challenges of the area under consideration. A central further development could be the automated collection and evaluation of sensor data and the integration of machine conditions. This would expand the database and enable more precise planning. Machine learning could also be used to recognise patterns in machine loads and failures and improve maintenance decisions based on historical data and real-time information. This can further reduce unplanned downtime and enable more targeted deployment of maintenance measures.

The current model works with a short-term tactical planning horizon and supports iterative replanning based on updated machine conditions. However, it does not include adaptive learning from historical performance data. Future extensions could explore the integration of reinforcement learning or rolling horizon strategies to enable continuous improvement and self-adaptive behaviour in dynamic production environments. Expert interviews show that maintenance decisions are often based on empirical values and do not always reflect the actual machine load. It would therefore make sense to integrate manual maintenance decisions directly into the model—for example, through user-defined entries or automatic reminders based on specific utilisation values. In addition, the integration of real-time information from production and the consideration of input from planners could further improve the quality of decisions.

Heuristic or metaheuristic procedures could also reduce the calculation time for complex optimisation problems. In the long term, the model could conceivably be developed into a self-learning system that continuously optimises existing maintenance intervals and avoids inefficient cycles. Such data-driven optimisation would enable a more targeted and needs-based maintenance strategy.

Another possible extension would be to consider machine-specific operating costs or energy consumption in the objective function or the constraints. This would enable more differentiated machine allocation, as the optimisation could then reconcile machine availability with cost efficiency or sustainability targets. Such extensions would enable the model to take into account not only technical feasibility but also economic and ecological criteria in future planning scenarios.

5. Conclusions

The presented model offers an optimised approach to integrating production planning and maintenance scheduling, outperforming conventional methods. By proactively incorporating preventive maintenance, it reduces machine downtime and enhances operational efficiency. The results of this study confirm that this planning approach improves both machine availability and adherence to delivery deadlines, as demonstrated in

Table 3. A comparison between traditional static planning and the proposed dynamic planning model. The model optimises machine availability and delivery reliability through proactive maintenance planning and adaptive job-shop optimisation.

Criterion	Traditional Method (Static Planning)	Proposed Model (Dynamic Planning)
Machine Availability	Fixed maintenance intervals without considering the actual machine condition. Unexpected failures lead to unplanned downtime.	Maintenance is scheduled into available time slots. Dynamic adjustments based on wear reserves reduce unplanned downtime.
Delivery Reliability	Production planning is independent of maintenance planning, which can cause delays due to unexpected machine failures.	Integrated planning avoids conflicts between maintenance and production. Maintenance is flexibly scheduled to minimise delays.
Utilisation of Free Machine Capacity	Maintenance slots are not optimised, leading to unused production capacity.	Available machine capacity is actively used for maintenance, optimising production utilisation.
Reaction to Unplanned Events	Static planning makes short-term adjustments difficult when dealing with machine failures or changes in orders.	Dynamic optimisation enables flexible responses to machine conditions and production requirements.
Maintenance Strategy	Preventive maintenance based on fixed time intervals, independent of actual machine usage.	Combined strategy withtime-based intervals, condition-based schedulingand reactive measures.
Wear Assessment	No direct influence of job types on machine wear, as fixed maintenance intervals are used.	Wear is individually assessed based on job workload and process parameters, allowing for a more accurate prediction.

. By scheduling maintenance tasks based on machine wear and available idle times, the model effectively minimises unplanned machine failures. Additionally, the job-shop optimisation ensures on-time order fulfilment by dynamically adapting to fluctuating production conditions.

Compared to existing approaches, the model stands out due to its adaptability to varying machine loads and production priorities. This flexible scheduling approach enables strategic maintenance planning, reducing production disruptions and enhancing overall efficiency. The priority-based allocation of production orders and maintenance activities ensures a high degree of flexibility, particularly in volatile production environments. However, scalability remains a challenge, especially for large problem instances. For larger problem instances, computational efficiency could be improved using more advanced solvers or heuristic methods, as discussed in the Limitations of the Model section. The computational effort could be reduced by leveraging advanced optimisation techniques, such as heuristics or AI-driven predictive scheduling. The integration of high-performance solvers, machine learning algorithms or heuristic optimisation methods could further improve scalability and computational efficiency. Additionally, sensitivity analyses could help assess the model’s robustness against variations in input parameters, such as fluctuating machine wear rates. Furthermore, the accuracy of results heavily depends on precise input data, necessitating continuous monitoring and updating of machine conditions.

Future research could focus on expanding the model with AI-based predictive processes, adaptive maintenance strategies and deeper integration with real-time production control systems. Further validation through industrial case studies could provide valuable insights into its practical applicability and operational impact. Real-world implementation would help determine the necessary adjustments to maximise its effectiveness in a production setting.