Incorporating Epistemic Uncertainties in Ship Operability Study

Abstract

Ship operability diagrams are commonly defined based on the seakeeping analysis, showing which course and speed can safely be taken at the sea state to satisfy pre-defined seakeeping limiting values. Although ship operability diagrams are inherently probabilistic, because of the random nature of the environmental loads, their outcome is deterministic, showing if the seakeeping criteria are satisfied or not for a certain combination of environmental and operational parameters. In the present study, uncertainties in seakeeping predictions and limiting values, which are usually neglected, are integrated into the ship operability analysis. This results in probabilistic operability diagrams, where the seakeeping criteria are exceeded with certain probabilities. The approach is demonstrated in the example of the passenger ship on a route in the Adriatic Sea. Semi-analytical closed-form expressions are used for seakeeping analysis, while limiting values for vertical bow acceleration, pitch, slamming, roll, and propeller emergence are analyzed. The second-order reliability method is used to calculate probabilities of the exceedance of the seakeeping criteria, and the results are presented as probabilistic operability diagrams. The method enables the determination of a new probabilistic operability index applicable to the ship design and represents a prerequisite for risk-based decision making in ship operation. It is also presented how the method can be validated for the existing shipping route using numerical wave databases.

1. Introduction

The prediction of the seakeeping behavior of ships for a variety of probable environmental and operational conditions has wide application in the shipping industry, providing important information about the design and efficient/safe operation of modern ships. For a ship sailing in waves, the basic controllable parameters are the forward speed and the heading to the waves, so the ship operability study aims to determine in which sea states, described by a significant wave height (H_S) and peak spectral periods (Tp), the ship can maintain a given course and speed.

In ship design, ship operability studies could be utilized to determine the operability index (OI), which represents basically the proportion of time a ship is accessible for perfect operation [1]. The OI considers simultaneously the wave characteristics of the sailing area, the dynamic ship response to the waves, and the ship mission. The ship OI may be used as a decision-making tool when acquiring a new ship for a specific service, to compare the comfort level of different ships [2], and for ship form optimization [3]. There are variations of the OI, such as the operability robustness index (ORI), a performance criterion used to assess the robustness of a vessel in different sea states [4]. The Habitability Index (HI) refers to the assessment of onboard comfort and livability, particularly for passenger vessels [5]. The Comfort Index (CI) is used to assess passenger comfort aboard vessels, especially on longer journeys. This index considers factors like motion sickness, noise levels, and vibrations, using probabilistic methods to predict comfort levels under various sea conditions. It allows operators to anticipate discomfort and optimize routes to minimize passenger distress [6].

In ship operations, operability studies are used for real-time decisions in Decision Support Systems (DSS), where the time frame may be hours (tactical decisions) or days (strategic decisions relating to route planning) [7]. Tactical decisions are made at the navigation bridge, related to the choice of ship speed and course having an impact on the ship motions and loads due to the wave action. In that respect, the following commands could be given: no change is required, speed reduction, course change, or speed and course change [8]. The strategic decision is to determine, before the mission, which route the ship may take, duly accounting for structural safety, the total travel time, fuel consumption, etc. A strategic decision about ship routing is, therefore, a multi-attribute decision-making process [9]. Examples of operational decision-making include predicting first-order vessel responses as a key component of decision support systems, examining the effects of uncertainties in sea state descriptions on operational limits, and presenting a new model for adaptive weather routing based on seakeeping analysis and optimization, aimed at reducing operational risks [10,11,12]. Operability analysis as a part of weather routing is presented in [13].

In the common ship operability studies, the seakeeping calculations and assessments are based on specific ship-inherent and environmental data and assumptions. Thus, seakeeping tools are employed assuming their results as ground truth, while seakeeping limiting values are also considered as fixed, prescribed values. However, different seakeeping theories may result in rather different outcomes of the operability studies [14]. The uncertainties associated with the sea state descriptions used in the numerical analysis influence the operational limits (in terms of H_S and Tp) [11]. The effect of the seakeeping criteria on the seakeeping performance assessment for passenger vessels shows that the OI is strongly affected by the chosen limiting values [15].

It becomes evident from this review that operability studies are dependent not only on inherent (or aleatory) uncertainties of random sea surface elevation and wave environmental variations in ship operating zones, but also on the knowledge-based (or epistemic) uncertainties, encompassing modeling uncertainties of seakeeping theories and tools and uncertainties of seakeeping limiting values [16]. Obviously, both uncertainty types need to be included in the consistent probabilistic ship operability analysis [17].

The concept of the risk-based Navigation Decision Assistant (NDA) was proposed initially in [7]. The concept described the evaluation of probabilities and consequences, accounting for the uncertainties of the input variables. Another concept of the risk-based DSS was introduced, incorporating aleatory and epistemic uncertainties related to the parameters of the problem of ship motions in waves [18]. It is concluded that the system can be applied to both the ship’s operational assessment and the design procedure, but there is a need to improve the efficiency of the probabilistic assessment for practical onboard applications [19]. A procedure to incorporate random variables and associated uncertainties in the calculations of the outcrossing rates that are the basis for risk-based DSS is suggested in [20].

The present study aims to continue this development of the risk-based DSS by formulating and solving the probabilistic problem of ship operability analysis for different seakeeping limiting criteria. Epistemic uncertainties are included in this operability study, resulting in probabilistic operability polar plots being more informative compared to the “deterministic” polar plots. While previous studies (e.g., [18,19]) included seakeeping uncertainties in operability analysis, the present work extends these studies by incorporating uncertainties in operability limiting values. The limit state equations are formulated and solved using Comrel 2021 software for structural reliability analysis. This study also proposes extending the conventional OI for ship design to the Probabilistic Operability Index (POI) as a more rational measure of ship operability. The potential application of probabilistic operability diagrams for tactical DSS is also shown.

An examination of probabilistic operability is provided for a passenger ship traveling on the actual sailing route across the Adriatic Sea. Fuel consumption and corresponding CO₂ emissions along common ferry routes in the Adriatic have recently been studied in [21]. To demonstrate the concept of probabilistic operability analysis, a simplified seakeeping approach is used, where transfer functions of heave, pitch, and roll are calculated by closed-form expressions (CFE), formulated in [22]. 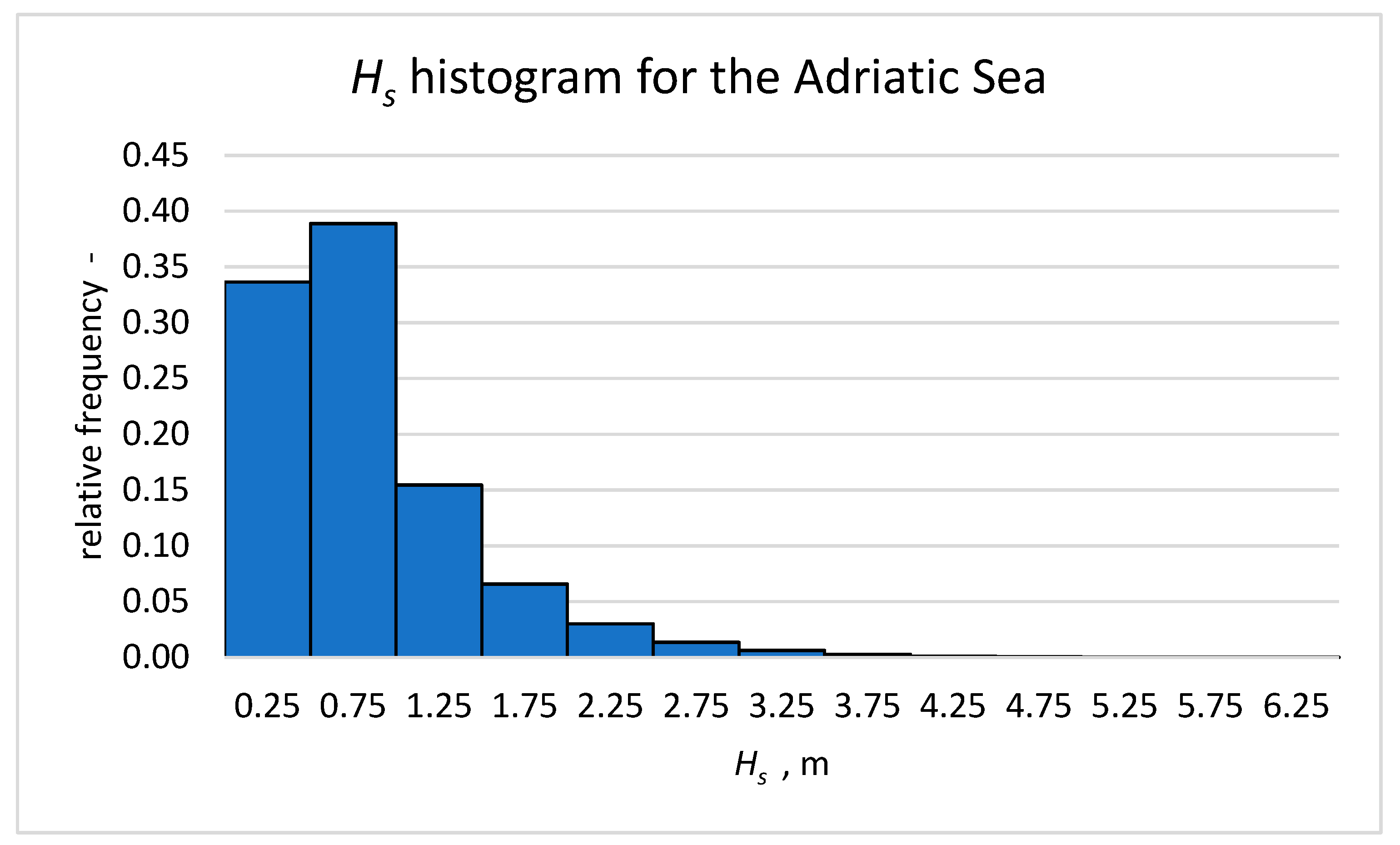The model uncertainty of CFE for heave and pitch is defined by comparison to the model-scale experiments for a relatively large number of ships [23]. In previous studies, model uncertainties in seakeeping methods were assumed. In contrast, this study consistently employs a seakeeping method while explicitly defining the corresponding modeling uncertainty. For the sake of simplicity, a single-parameter wave spectrum, which is representative for the Adriatic Sea, defined only by a significant wave height, is used for the description of short-term sea conditions. 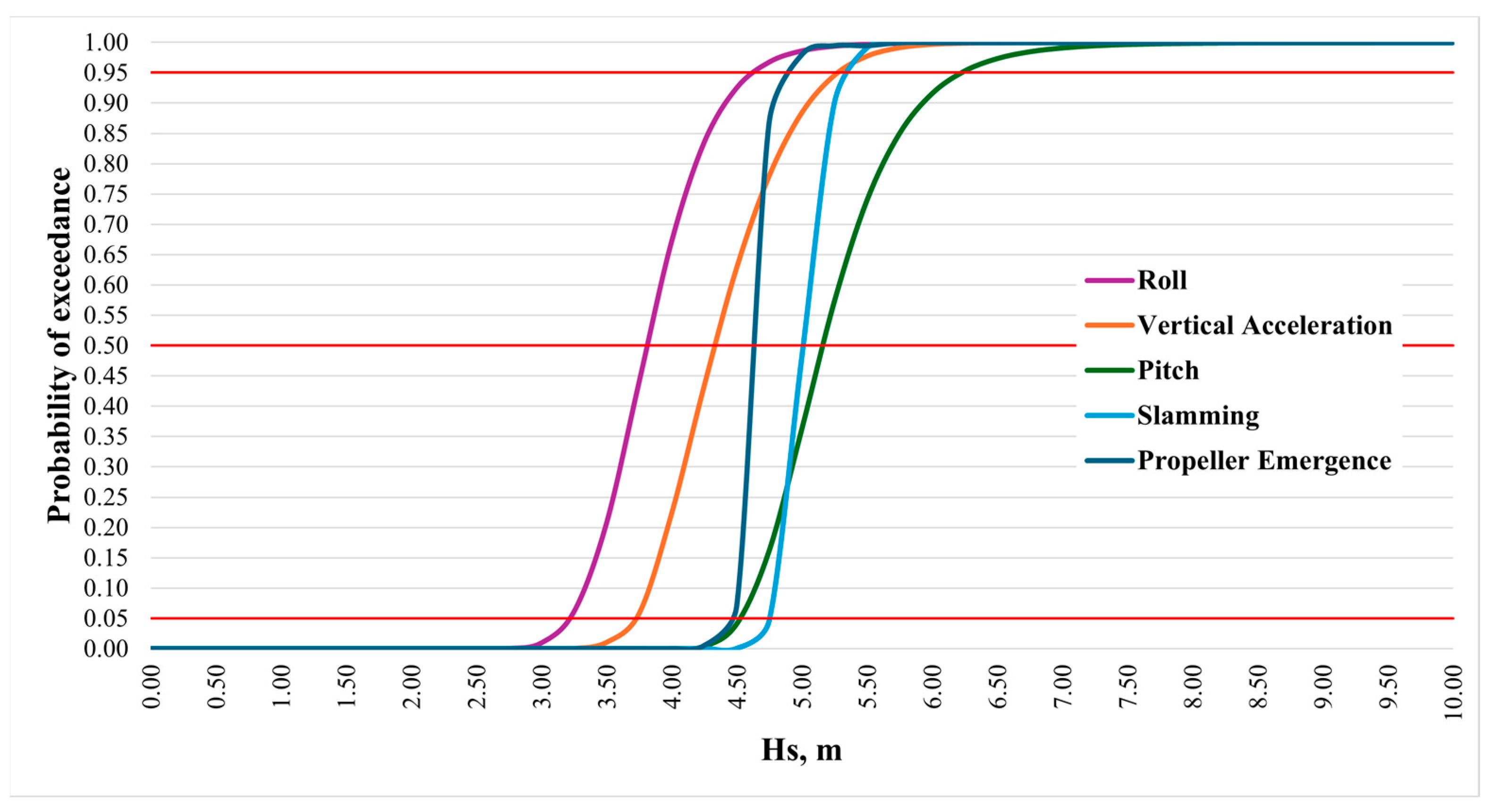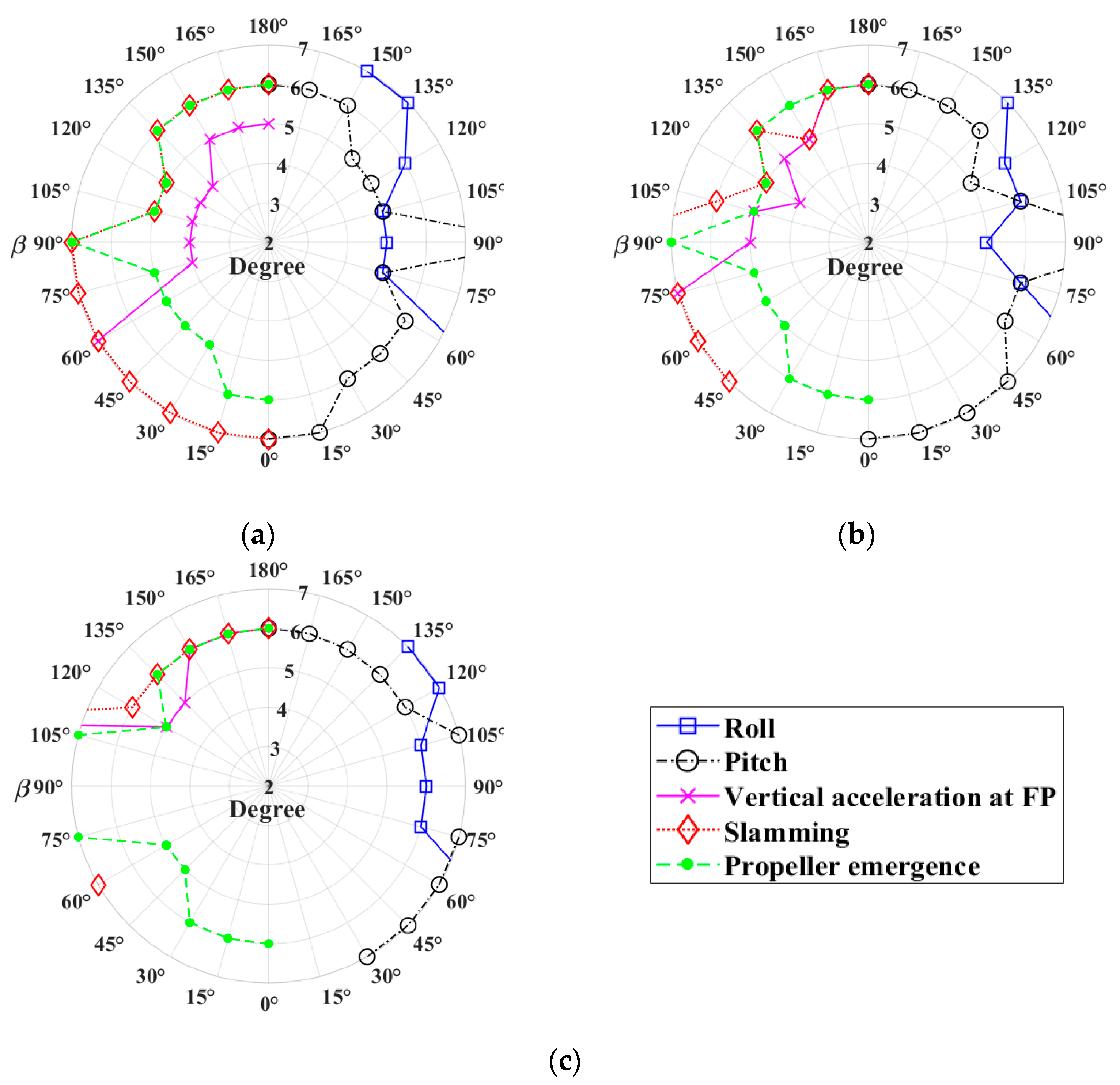A histogram of sea states along the sailing route is obtained from the wave hindcast database, described in [24]. The seakeeping limiting criteria of roll, pitch, vertical acceleration on forward perpendicular, slamming, and propeller emergence are considered as random variables to illustrate the procedure. The second-order reliability method (SORM) is used to calculate probabilities of exceedance of the seakeeping criteria, and the results are presented in probabilistic polar plots.

This paper is organized as follows. The seakeeping method, wave spectrum model, uncertainty model of CFE based on a frequency-independent model error, reliability analysis, and risk-based decision making are described in Section 2. The results of the operability analysis for the case ship are given in Section 3. The discussion section includes the application of the POI in ship design, potential usage of probabilistic operability plots in ship operation, correlation of the results with past experience on the sailing route concerned, and limitations of the developed model. Conclusions and recommendations for future development are given in the last section of this paper.

2. Methods

2.1. Seakeeping Analysis

Linear seakeeping analysis is used in the present study. The analysis consists of the computation of transfer functions in the frequency domain and the definition of the wave energy spectrum. Then, the response spectrum is calculated by multiplying the square of transfer functions by the wave spectrum. Spectral moments are then obtained by integrating the response spectrum.

2.1.1. Transfer Functions

Transfer functions for heave and pitch are calculated using semi-analytical closed-form expressions (CFE) [22]. These simple formulas are determined for the motion of a prismatic barge in the vertical plane using standard linear strip theory assumptions, assuming a constant sectional added mass equal to the displaced water volume and ignoring the coupling components between pitch and heave. The main ship attributes—length L, breadth B, draft T, block coefficient Cb, and speed V—are the only necessary input data for the procedure.

In this section, the procedure is briefly outlined, while details may be found in the original reference [22].

The frequency response functions for heave (${\mathit{\Phi }}_w)$ and pitch (${\mathit{\Phi }}_{\theta })$ are given as:

$${\mathit{\Phi }}_w=\eta F,$$

(1)

$${\mathit{\Phi }}_{\theta }=\eta G,$$

(2)

where F and G are heave and pitch forcing function, and:

$$\eta ={\left(\sqrt{{\left(1-2kT{\alpha }^2\right)}^2+{\left({\displaystyle \frac{A^2}{kB{\alpha }^2}}\right)}^2}\right)}^{-1},$$

(3)

where k is the wave number, T is draft, A is approximation of the sectional hydrodynamic damping, B is breadth of ship, and $\alpha$ is parameter:

$$\mathsf{\alpha }=1-F_n\sqrt{kL}\mathrm{c}\mathrm{o}\mathrm{s}\beta ,$$

(4)

where F_n is Froude number, L is the ship length, and $\beta$ is heading of the ship.

The transfer functions of vertical motion ${\mathit{\Phi }}_u$ and vertical acceleration ${\mathit{\Phi }}_v$ at the forward perpendicular are given as:

$${\mathit{\Phi }}_u=\sqrt{{\mathit{\Phi }}_w^2+{\mathrm{x}}_{\mathrm{F}\mathrm{P}}^2{\mathit{\Phi }}_{\theta }^2},$$

(5)

$${\mathit{\Phi }}_v={\overline{\omega }}^2{\mathit{\Phi }}_u,$$

(6)

where x_FP is the longitudinal distance of the forward perpendicular from the center of gravity, and $\overline{\omega }$ is the encounter frequency.

The transfer function for roll motion is obtained by solving the equation of the motion for roll in regular waves, and it can be written as:

$${\mathit{\Phi }}_{\mathsf{\phi }}={\displaystyle \frac{\left|M\right|}{{\left({\left[{-\overline{\omega }}^2{\left({\mathrm{T}}_{\mathrm{N}}/2\mathsf{\pi }\right)}^2+1\right]}^2{C}_{44}^2+{\overline{\omega }}^2{B}_{44}^2\right)}^{1/2}}},$$

(7)

where $\left|M\right|$ is the amplitude of the excitation moment; T_N is the natural roll period; C₄₄ is the restoring moment coefficient; and B₄₄ is the hydrodynamic roll damping for the ship which is considered 20% in this study.

The CFEs are semi-analytical formulae, so they can be easily calculated using a usual spreadsheet application. CFEs have been used for seakeeping predictions in conceptual design, enabling an efficient sensitivity analysis regarding operational profiles and different wave environments [25]. CFEs have also been used in hydro-elastic studies [26], for the computation of extreme wave loads using the hindcast wave database, and for tuning the transfer function for the prediction of ship responses [27].

In the present paper, CFEs are considered for the development of the risk-based ship DSS for heavy weather maneuvering. The numerical efficiency of DSS could be crucial if DSS is used for decision making onboard the ship on heavy seas [19]. CFEs have already been considered for DSS application in [28].

2.1.2. Wave Spectrum

Short-term stationary irregular sea states are for engineering purposes traditionally described by wave energy spectrum. The formulation of the wave energy spectrum depends on the geographical area under consideration with local bathymetry and the severity of the sea state. The Pierson–Moskowitz spectrum and JONSWAP spectrum are frequently applied for wind seas. The former was originally proposed for a fully developed sea in the open ocean, while the latter is appropriate for fetch limited seas, describing developing sea states.

The shipping route in the Adriatic Sea is considered in the present study. For such an enclosed sea, modification of the JONSWAP type of wave spectrum is used. Tabain’s single-parameter wave spectrum, developed specifically for the Adriatic, has been used for naval architecture and marine engineering applications [29]. Recently, Tabain’s spectrum was optimized using a wave database obtained by combining satellite measurements and numerical re-analysis [30]. Thus, the following one-parameter spectral formulation relevant to the Adriatic Sea is used:

$$S\left(\omega \right)=0.8626{\displaystyle \frac{5}{16}}{\displaystyle \frac{H_s^2{\omega }_m^4}{{\omega }^5}}exp\left[-{\displaystyle \frac{5}{4}} {\left({\displaystyle \frac{{\omega }_m}{\omega }}\right)}^4\right] {1.78}^{ exp\left[-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\omega -{\omega }_m}{\sigma {\omega }_m}}\right)}^2\right]},$$

(8)

$${\omega }_m=0.52+{\displaystyle \frac{1.4}{H_s+0.7}},$$

(9)

$$\sigma \left\{{\displaystyle \frac{{\sigma }_a=0.06 za \omega \le {\omega }_m }{{\sigma }_b=0.08 za \omega >{\omega }_m}}.\right.$$

(10)

where ω_m = 2π/Tp is the peak of the wave energy spectrum.

Obviously, that one-parameter formulation cannot cover all combinations of significant wave heights and zero-crossing periods occurring in the Adriatic [24].

2.1.3. Ship Response in Short-Term Irregular Waves

The ship’s response spectrum’s general equation is expressed as:

$$S_R\left(\overline{\omega }\right)={\left|\mathit{\Phi }\left(\overline{\omega }\right)\right|}^2{S}_J\left(\overline{\omega }\right) ,$$

(11)

where $\overline{\omega }$ is the encounter frequency and $S_J\left(\overline{\omega }\right)$ is the encounter wave spectrum.

The variance of the ship response represents the area under the response spectrum:

$$m_{0R}={\int }_0^{\mathrm{\infty }}{S}_R\left(\overline{\omega }\right)·d\overline{\omega } .$$

(12)

The root mean square (RMS) represents the standard deviation, and it is obtained as the square root of the response variance.

2.1.4. Model Uncertainty of Transfer Functions

The Frequency Independent Model Error (FIME) is developed and utilized to formulate the model uncertainty of transfer functions [31]. The fundamental concept of FIME involves multiplying transfer functions by a constant fit factor φ, which is expressed as follows:

$$\phi ={\displaystyle \frac{{\sum }_i{\widehat{H}}_i{H}_i}{{\sum }_i{H}_i^2}},$$

(13)

where ${\widehat{H}}_i$ and $H_i$ are measured and calculated transfer functions at the frequency ${\omega }_i,$ respectively. This allows the transfer function to be adjusted to match, on average, with the experimental results at all frequencies.

According to its geometrical meaning, φ is the slope of the regression line that must pass through the origin when comparing experimental and calculated transfer functions. The theory overestimates the experimental results when φ is less than 1, whereas it underestimates readings when φ is more than 1 [17].

By comparing transfer functions computed by CFEs with model-scale experiments for 13 ships of various types, speeds, and relative heading angles, the parameter φ was found for heave and pitch in [23]. Using linear multivariate regression analysis, the dependence of φ on the main parameters was expressed as:

$$\phi =\mathrm{A}+\mathrm{B}\beta +\mathrm{C}{C}_b+\mathrm{D}{F}_n,$$

(14)

where $F_n$, $C_b$, and $\beta$ are Froude number, block coefficient, and heading angle, respectively.

Table 1. Intercept and regression coefficients for the regression Equation (14).

	A	B	C	D
Heave	0.623	−0.000447	0.076	0.990
Pitch	0.540	−0.000527	0.135	0.950

provides the regression coefficients and intercept [23].

Values in Table 1 represent a mean value for each speed and heading angle and a standard deviation of 0.19 and 0.27 is determined for pitch and heave, respectively, in [23]. Due to the lack of relevant comparisons with experiments, mean value and standard deviation for the model uncertainty of the roll angle are assumed in the present study as 2.5 and 0.2, respectively. The normal distribution is used to represent the model uncertainty of the seakeeping calculations.

2.2. Seakeeping Criteria

Most seakeeping criteria are concerned with operability, i.e., crew ability and willingness to operate a vessel and all its installed equipment in a specified seaway. Operability criteria are typically expressed in terms of roll and pitch angles, roll motion, vertical and lateral acceleration, deck wetness, propeller emergence, and slamming. In addition, there is a group of criteria expressing the interaction between ship motion and human reactions, such as motion sickness incidence and motion-induced interruptions. Limiting values of these criteria are not standardized and do not cover all vessel types, but there are well-established criteria sets referring to the overall vessel system’s operability or habitability of the vessel. There are different reasons for discrepancies in criteria between different sources, even if they refer to the similar ship types, such as complexities and inaccuracies of motion prediction methods and discrepancies in the definition of seakeeping amongst naval architects and how vessel owners viewed seakeeping. A critical review of currently used standards and criteria is provided in [32].

An example of discrepancies of limiting values among different operability standards is given for the case of vertical acceleration at forward perpendicular in [8]. The limiting values read from 0.2 g RMS according to NATO and US Coast Guard Standards, to 0.275 g RMS according to NORDFORSK for Merchant ships less than 100 m in length. There are also other options to express the limiting value of vertical acceleration at the forward perpendicular, such as the probability of exceeding individual acceleration amplitudes and Subjective Magnitude (SM) values [33]. Limiting values for some criteria are less scattered, e.g., limiting value for RMS of the pitch angle of 1.5° is often found [8].

The brief review in the preceding paragraph indicates that limiting values are uncertain and that captains could have a different attitude against limiting values for operability criteria. In other words, it is reasonable to consider limiting operability values as random variables. The definition of parameters of probability distributions of such random variables is a challenging task. Performing a questionnaire among experienced seafarers, such as the one presented in [34], could be the right way to define these parameters. The main problem found was the lack of onboard measurements, thus preventing clear quantification of the seakeeping limiting criteria. A large spread among answers to some of the questions, e.g., estimation of pitch angle, was found. That finding about the uncertainty of operability limiting values supports the necessity of their probabilistic description, as proposed in the present study.

For illustration of the procedure, the mean values of the operability limiting value are taken from those given in

Table 2. Mean values of operability criteria limits [8].

Criteria	Statistical Property	Mean Value
Pitch	RMS	1.5°
Vertical acceleration at FP	RMS	0.05 g
Roll	RMS	2.5°
Slamming	Probability	0.03
Propeller emergence	Probability	0.25

, while their coefficient of variation (CoV) is assumed as 0.05 in all cases. Gaussian distribution is used to model this uncertainty.

2.3. Reliability Problem Formulation

As explained in the preceding section, the accuracy of the seakeeping calculations is uncertain, as well as limiting values of seakeeping criteria. Therefore, the seakeeping criteria are exceeded with a certain probability, which is calculated based on the limit state functions. In general, the limit state function g(X) is given as:

$$g\left(x_1,x_2,\dots x_n\right)<0,$$

(15)

where $x_1,x_2,\dots x_n$ is a vector of random variables and g takes negative value when the limiting criterion is exceeded. In the present study, the random variables are epistemic uncertainties of the seakeeping results and criteria.

To describe the procedure, let us consider the simplest limit state function, which is for pitch angle. The limit state function, in this case, reads:

$$x_{\theta }-\sqrt{\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left|{\phi }_{\theta }{\mathit{\Phi }}_{\theta }\left(\overline{\omega }\right)\right|}^2{S}_J\left(\overline{\omega }\right)·d\overline{\omega }}<0$$

(16)

$x_{\theta }$ in Equation (16) is a normally distributed random variable representing pitch criterion, with a mean value equal to 1.5°, according to Table 2, and CoV of 0.05. ${\phi }_{\theta }$ is also normally distributed with the mean value calculated by Equation (14), depending on the heading angle and ship speed, and a standard deviation of 0.19. ${\mathit{\Phi }}_{\theta }\left(\overline{\omega }\right)$ is a transfer function of pitch, given by Equation (2), while the wave energy spectrum $S_J\left(\overline{\omega }\right)$ is defined by Equations (8)–(10). The limit state function for the roll is defined in similar way, only that the random variable representing criterion uncertainty $x_{roll}$ with a mean value of $2.5°$ is used. The transfer function of roll motion is ${\mathit{\Phi }}_{\phi }\left(\overline{\omega }\right)$, defined by Equation (7).

The limit state function for vertical acceleration at FP is a bit more complicated, as the transfer function for vertical acceleration at FP (Equation (6)) depends on heave and pitch transfer functions (Equation (5)). Each of these transfer functions is multiplied by the corresponding epistemic uncertainty, calculated by Equation (14), using parameters from Table 1. The limit state function is then readily defined using an expression like Equation (16).

The limit state function for propeller emergence requires the calculation of the probability of the propeller emergence:

$$p_{pe}=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\left({\displaystyle \frac{D_p^2}{2m_{0\_r}}}\right)\right]$$

(17)

where D_p is the propeller blade tips’ depth, while $m_{0\_r}$ is the variance of the relative motion at the location of the propeller. The transfer function of the relative motion is given by an expression analogous to Equation (5). Transfer functions of heave and pitch are multiplied by corresponding modeling uncertainties. The limit state function for propeller emergence is then given as:

$$x_{pe}-p_{pe}<0$$

(18)

where $x_{pe}$ is normal distribution with a mean value of 0.25, according to Table 2, and with assumed CoV of 0.05.

The slamming probability, p_s, employed in the slamming limit state function, is given as:

$$p_s=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\left({\displaystyle \frac{T_{\mathrm{e}}^2}{2m_{0\_r}}}+{\displaystyle \frac{v_{kr}^2}{2m_{0\_v}}}\right)\right],$$

(19)

where T_e is the effective draft; m_{0_r} is the variance of the relative vertical motion at ship FP; v_kr is the critical vertical velocity; and m_{0_v} is the variance of the relative velocity at FP. Critical velocity is calculated from Ochi’s equation:

$$v_{kr}=0.093\sqrt{\mathrm{g}{L}_P},$$

(20)

where LP is a ship length between perpendiculars.

The limit state function for bow slamming is then given as:

$$x_s-p_s<0,$$

(21)

where $x_s$ is a normal distribution with a mean value of 0.03, according to Table 2, and with assumed CoV of 0.05. Model uncertainties in heave and pitch are used in the definition of the variances of the ship relative motion and velocity.

2.4. Reliability Analysis

The software program Comrel is used for reliability analysis, and the basic steps to perform the analysis are [35]:

• Formulating the limit state functions in standard mathematical notation;
• Preparation of the stochastic model for the variables;
• Selecting computation options;
• Performing the reliability analysis with embedded Symbolic Processor;
• Analysis of the results and graphical post-processing.

Second-Order Reliability Method (SORM) is chosen as the computational option for reliability analysis. First-Order Reliability Method (FORM), which is often used in ship structural reliability analysis, is not performing well in all cases, as some of the limit state functions are complex, including integration, and are formulated in several lines.

The Multiple Runs option was used for calculation over different periods, and in one pass, the calculation was made for all significant wave heights H_S, and each pass calculated for different angles β.

Except for Comrel, other commercial and in-house software tools have been used for risk-based DSS concepts. Specifically, the commercial probability analysis program PROBAN was used in [18], while the in-house structural system reliability analysis program RELSYS was used in [36].

2.5. Risk-Based Perspective

A review and analysis of general risk definitions, perspectives, and scientific approaches to risk analysis in the maritime transportation application area are provided in [37]. The results indicate that risk is strongly associated with probability, though alternative views exist. Additionally, various scientific approaches to risk analysis have been identified. More recently, a multi-attribute-based assessment model has been proposed in [38] to support decision making on risk control options. A discussion on risk assessment and key risk factors affecting ferry navigation safety is presented in [39].

The prevailing approach to risk analysis in maritime defines the risk (R) as the product of the probability of an event (P) and its associated consequence (C), e.g., [7]. The total risk for a combination of N uncorrelated serial events is given as:

$$R=\sum _{i=1}^N{R}_i=\sum _{i=1}^N{P}_i{C}_i$$

(22)

while the expression for the case of correlated events may be found in [7]. In addition, each individual risk R_i may be multiplied by the company-specific aversion factor A_i.

While the probabilities of an adverse event $P_i$ are obtained through reliability analysis, the associated consequences are determined via consequence analysis, categorized as follows:

• Safety of people (loss of life, injuries, and health);
• Risk to the maritime environment;
• Economic risk (damage to ship structure, equipment and cargo, including total loss, and loss of reputation).

Quantifying the first two categories in monetary terms is controversial and typically beyond the scope of risk-based DSS. Events related to these risk categories generally have a low probability of occurrence (less than 10⁻³). Such extremely hazardous situations are classified as “intolerable” risks that must be mitigated regardless of cost. These risks may be considered at the ship design stage and addressed through proper masters’ training or qualitative guidance [18].

Additionally, due to the well-known “tail sensitivity” issue in structural reliability analysis, the probabilities of such rare events are highly dependent on the uncertainty model used and cannot be applied universally [7]. In risk terminology, DSS is used in the “As Low as Reasonably Practicable” (ALARP) region, which lies between “intolerable” and “negligible” (broadly acceptable) risk levels [40].

The economic losses necessary for risk estimation can be expressed as:

$$C_{tot}=C_c+C_{eq}+C_s+C_d+C_{rp}$$

(23)

where

• $C_c$ represents damage to cargo;
• $C_{eq}$ accounts for damage to equipment;
• $C_s$ represents damage to ship;
• $C_d$ is costs related to delays;
• $C_{rp}$ represents costs associated with loss of reputation.

The latter component, $C_{rp}$, includes factors such as passenger seasickness, reduced crew performance, and the consequences of delays, all of which directly impact the economic viability and reputation of maritime services [18]. Estimates of economic losses should ideally be provided by the owner or operator, preferably supported by data from insurance companies [7].

An example of a consequence analysis for an oil tanker, including specific costs associated with potential hull failure or the exceedance of specific limit states, is presented in [36]. In that study, total consequences are divided into:

• Direct consequences, i.e., losses due to damage or failure itself;
• Indirect consequences, i.e., losses related to system failures or malfunctions that result in external monetary impacts.

The primary risk control parameters for a ship sailing in waves are forward speed and heading relative to waves. For each combination of these parameters, the probability of exceeding seakeeping criteria is determined through reliability analysis, while the total risk is calculated using Equation (22).

Some alternative combinations of ship speed and heading angles will likely result in lower total risk compared to the current settings, suggesting that risk reduction can be achieved. However, at the same time, altering speed and/or course will certainly increase anticipated voyage costs, such as higher fuel consumption due to a longer route.

The risk criterion is expressed as the ratio of the potential cost $∆R$ and the related certain cost $∆c$, i.e.,

$${\displaystyle \frac{∆R}{∆c}}={\displaystyle \frac{R_{current}-R_{alter}}{∆c}}>M$$

(24)

where

• $R_{current}$ and $R_{alter}$ represent the risk of the current and alternative combination of speed and heading, respectively;
• $∆c$ is the increased costs because of choosing alternative sailing parameters;
• M is the risk control ratio, typically greater than 1, which serves as the decision criterion for the ship master when making maneuvering choices in heavy weather.

More elaborated discussion on the risk control options using Equation (24) is provided in [18].

3. Results

3.1. Example Ship Description

This study is presented for a model of a liner ship operating in the Adriatic Sea (Figure 1). The main particulars of the ship are given in

Table 3. Main particulars of the ship.

Feature	Value	Measuring Unit	Description
LOA	114	m	Length overall
LPP	103.2	m	Length between perpendiculars
B	18.7	m	Breadth
T	5	m	Draft
V	17	kn	Nominal ship speed

. The main particulars of the ship model correspond to the features of the vessels within the “larger ferry category”.

The shipping route between Ancona (Italy) and Split (Croatia) is assumed (Figure 2).

The histogram of sea states along this shipping route is presented in Figure 3. Data in Figure 3 are obtained from the extensive analysis of sea states in the Adriatic Sea, using a reanalysis database [24].

Based on the prior study of the shipping route, it is expected that the ship would only face waves from 45° and 135° directions, which correspond to the routes from Split to Ancona and vice versa.

3.2. Probabilistic Operability Diagrams

Cumulative probability distributions for each criterion are obtained by the procedure presented in Section 2.2 in a way that, for the nominal ship speed, for each sea state, given by a significant wave height Hs and wave spectrum presented in Section 2.1.3, and for each heading angle β, probabilities of not satisfying limit state functions given in Section 2.3 are calculated. Probability distribution functions for pitch, vertical acceleration at FP, slamming, propeller emergence for a heading angle of 180°, and a roll angle for beam seas (β = 90°) are presented in Figure 4. Horizontal lines denote exceedance probabilities of 5%, 50%, and 95%, where it may be noticed that they correspond to different Hs, depending on the seakeeping criterion.

The results are then presented in the form of probabilistic operability diagrams. Probability plots for each of the five criteria evaluated are presented in Figure 5 for three exceedance probabilities: 5%, 50%, and 95%. Radial coordinates indicate the sea state according to the Douglas scale, while the angular coordinate is a heading angle between the ship and waves, where 180° denotes head seas. For the clarity of presentation, sea states are presented in the Douglas scale, given in

Table 4. Douglas scale of sea states.

Degree	Wave Height (m)	Description
0	0	Calm (glassy)
1	0–0.1	Calm (rippled)
2	0.1–0.5	Smooth (wavelets)
3	0.5–1.25	Slight
4	1.25–2.5	Moderate
5	2.5–4	Rough
6	4–6	Very rough
7	6–9	High
8	9–14	Very high
9	>14	Phenomenal

.

Obviously, the severity of the sea state for which each criterion is exceeded is increasing with an increased probability level. Thus, for sea states in the first diagram, there is only a 5% chance of exceeding each criterion. If the ship owner or ship master is averse to taking the risk, he will consider that diagram. On the other hand, if he is willing to take the risk, then a third diagram can be used, as the operability values would almost certainly be exceeded on the sea states indicated on the diagram.

4. Discussion

4.1. Application in Ship Design

The probabilistic approach to the operability diagrams may be used in ship design as the decision-making tool when acquiring a new ship for a specific service. For that purpose, the Operability Index (OI) is proposed, representing the ratio, expressed as a percentage, between the number of sea states (for all available peak periods) with significant wave heights that do not exceed the limiting significant wave height (n_ss, β) over the total number of sea states (N) in a certain wave scatter diagram. The OI reads [1]:

$$\mathrm{O}\mathrm{I} (\%)={\displaystyle \frac{{\sum }_{H_{1/3},T_P}{n}_{ss,\beta }\left(H_s<H_s^{lim}\right)}{N}}·100,$$

(25)

In the present study, the Probabilistic Operability Index (POI $\left(\mathrm{\%}\right)$) is proposed as:

$$\mathrm{P}\mathrm{O}\mathrm{I}(\%)={\sum }_{H_{1/3},T_P}{f}_{H_{1/3},T_p}P\left(H_s<H_s^{lim}\right)·100,$$

(26)

where $f_{H_{\mathrm{s}},T_P}$ is the relative frequency of the occurrence of the sea state, described by H_s and Tp, given as

$$f_{H_s,T_P}={\displaystyle \frac{n_{H_s,T_p}}{N}},$$

(27)

where $n_{H_{\mathrm{s}},T_P}$ is the number of sea states with H_S and Tp. $P \left(H_s<H_s^{lim}\right)$ is the probability that the seakeeping limiting value is not exceeded at sea states defined by H_S and Tp, calculated by the approach outlined in Section 2. Expressions (25)–(27) require a wave scatter diagram relevant to the ship’s operational area to determine the number of sea states defined by H_S and Tp. Additionally, it should be clarified that the application of these expressions assumes a constant ship speed. Consequently, different operability indices are calculated for varying ship speeds.

The process is illustrated by calculating the POI (%) and OI (%) for the histogram of significant wave heights (Figure 3) for the shipping route in the Adriatic Sea (Figure 2). Thus, POI = 98.7% and OI = 98.9% for a speed of 17 kn are obtained.

The POI, as defined by Equation (26), is well-suited for application in risk-based decision making. To incorporate this into decision making, the cost of the non-fulfillment of ship operations should be included by estimating the total risk associated with a given sailing route. However, estimating the cost of non-fulfillment is challenging, as it is company-specific and lacks publicly available references.

A rough estimate can be made by considering the primary cost categories associated with delays, namely:

• The operational costs of delay, including increased fuel consumption due to rerouting, which can be approximately USD 3000–USD 5000 per additional hour of voyage time. A similar cost may apply for crew overtime;
• Port and logistics costs related to late arrivals, rescheduling, and supply chain disruptions, estimated at USD 5000–USD 25,000;
• Passenger compensation, including partial refunds, food, and accommodation expenses, which can exceed USD 25,000.

According to a response generated by ChatGPT (GPT-4-turbo, OpenAI, April 2024; retrieved 31 March 2025), for a 3 to 6 h delay—a realistic scenario previously observed on the Ancona–Split route—the estimated cost could be anywhere from USD 10,000 to USD 100,000+, depending on fuel adjustments, port penalties, and passenger compensation. Longer delays (overnight cancellations) could push costs beyond USD 250,000. For a lifetime risk assessment, this value should be scaled based on the total number of voyages.

4.2. Application in DSS for Ship Operation

The probabilistic approach can be used in ship operation for tactical DSS. When a ship encounters heavy weather, a probabilistic operability plot could be a useful tool to help the ship master evaluating the consequences of potential maneuvers, i.e., changing the course and/or reducing the ship speed. This is illustrated in Figure 6, where the effect of maneuvering in heavy weather is presented. On the right-hand side of the polar plot, results are presented for a nominal ship speed of 17 kn, while results on the left-hand side refer to the reduced ship speed of 5 knots. Although differences in this example are not very large, the shipmaster could evaluate what would be the consequences of the potential speed or course changes.

If the costs related to the delay specified in Section 4.1 are considered, then it may be stated that for the 5% exceeding probability, the risk involved, obtained by multiplying the costs of delay with 0.05, is rather small and hardly altering the sailing route would be justified. This is not the case for the 95% exceeding probability, where risk reduction by modifying the sailing parameters would be cost-efficient and a different combination can be considered.

4.3. Correlation with the Experience on the Shipping Route

The ship analyzed in the present study is similar to the actual ship sailing on the route from Ancona to Split and vice versa. Although the ship is not the same, it is of interest to analyze publicly available heavy weather examples that occurred on the route concerned. There are rare examples of the inconveniences that big waves generated by ‘jugo’ wind caused to the passenger ships, like the one analyzed herein. ‘Jugo’ is a southeast wind causing the highest waves in the Adriatic Sea [41].

The marine accident that happened on 1 November 2012, just after midnight, was described in [42]. Seventy vehicles were damaged in a ferry on the voyage from Ancona to Split because of the large roll amplitudes. During a severe storm, vehicles began to slide and collide with other vehicles and sides of the ferry. The maximum significant wave height along the route on the night of the accident was 5.31 m, as may be seen from the Mediterranean Sea Wave Reanalysis database [43]. This significant wave height corresponds to Sea State 6 according to the Douglas scale (Table 4). The significant wave height at the time of the accident is shown in Figure 7.

Another accidental event was recorded recently, on 23 December, when a delay of 6 h occurred because of the heavy weather. The reconstruction of sea states in the time of the delay can be carried out using Mediterranean Sea Waves Analysis and Forecast [45]. The sea states along the route are shown in Figure 8. The maximum significant wave height along the route was only about 3.13 m. The significant wave height corresponds to Sea State 5 according to the Douglas scale.

It is interesting to mention that the maximum recorded significant wave height along the route in the Mediterranean Sea Wave Reanalysis database, since January 1985, was 6.12 m, which occurred on 1 February 1986. The severity of sea states along the route from 1 January 1985 to 31 May 2013 is presented in Figure 9. One may notice that rough Sea State 5 (2.5 m < H_S < 4 m), according to the Douglas scale, is not rare along the shipping route. Very rough seas, corresponding to 6 on the Douglas scale, with a significant wave height above 4 m occur on average once per year.

The examples presented from the sailing route concerned may be compared to the operability diagrams in Figure 5, where special attention should be paid to the heading angles of 45° and 135°. One may see that diagrams with a 5% exceeding probability are rather pessimistic, as even Sea State 4 is considered critical regarding the criterion of vertical acceleration at FP. However, for the 50% and 95% exceeding probabilities, the operability diagrams look credible, as the ship operability in Sea States 5 and 6 is questionable. For Sea State 5, the most critical criteria are the vertical acceleration at FP and propeller emergence, while for Sea State 6, most of the criteria are unsatisfactory.

4.4. Limitations of the Model

This study focuses on a single ship model, specifically a passenger ferry operating on a key and frequent route in the Adriatic Sea. This route is significant due to its high frequency of use and delays attract public attention, as discussed in Section 4.3. Another reason for selecting this route is that the environmental conditions along the route are well-defined [24]. For shipping routes in general, considerable uncertainty in environmental descriptions should be included in the limit state equations discussed in Section 2.3.

One simplification applied in this study is the use of a single-parameter JONSWAP-type wave spectrum for the Adriatic Sea [30]. Although this formulation provides a reasonable approximation for many fully developed wind-generated sea states in the Adriatic, the variation of peak wave periods (Tp) with significant wave heights (H_S) should be considered. Particularly, if other wave environments, such as the North Sea or open oceans, are considered, the operability plots should be extended for different combinations of H_S and Tp, as well as for other wave spectral models.

Although this study can be extended to other ship types, the careful consideration of ship-specific uncertainties in the ship response, heavy weather maneuvering, seakeeping criteria, and limiting values should be conducted. These additional considerations limit the generalizability of this study’s conclusions to other vessel types.

This study does not consider wind effects, although strong winds, including crosswinds or headwinds, can influence ship maneuverability. It is important to note that maritime disasters have occurred due to wind effects in addition to the wave action. In the Adriatic, however, the strongest winds and highest waves do not occur simultaneously [24]. Extreme wind speeds are recorded during the northeastern ‘bura’ wind, which blows across the shorter axis of the Adriatic basin and generally lasts for a short duration. Despite being the strongest wind, the ‘bura’ does not generate the highest waves because of the limited fetch. In contrast, the southeastern ‘jugo’ winds blow with a lower intensity but are more persistent and have a longer fetch, generating the highest waves in the Adriatic [24].

As a result, the ‘bura’ wind creates maneuverability challenges and can lead to dangerous situations for ships in ports and confined waters, while shipping safety in open seas is more affected by high waves generated by the ‘jugo’. An example of the ‘bura’ wind’s impact on maneuvering a cruise ship in the protected Bay of Kotor in the Adriatic can be found in [47]. In contrast, ferry accidents in the open Adriatic Sea, as discussed in Section 4.3, are generally attributed to waves, as reported by witnesses.

It is important to clarify that only delay-related costs are considered in the present study (Section 4.1 and Section 4.2), while other potential costs caused by heavy weather, such as damage to cargo, equipment, or ship structures, are omitted. This approach is justified for the Adriatic Sea, which is the mildest sea basin in the Mediterranean [24]. As a result, ship structural damage is rare due to the extremely low probability of severe environmental conditions in the Adriatic. Ship structures are generally designed to withstand more extreme conditions.

However, the inclusion of other costs in the risk assessment is straightforward, as described in Section 2.5. Using risk as a performance indicator to account for structural consequences induced by different limit states to evaluate optimal ship routing is presented in [36].

5. Conclusions

This study contributes by formulating and solving limit state functions for various ship operability criteria, incorporating epistemic uncertainties in seakeeping responses and uncertainties in operability limiting values. The reliability analysis was conducted using Comrel software, employing the second-order reliability method.

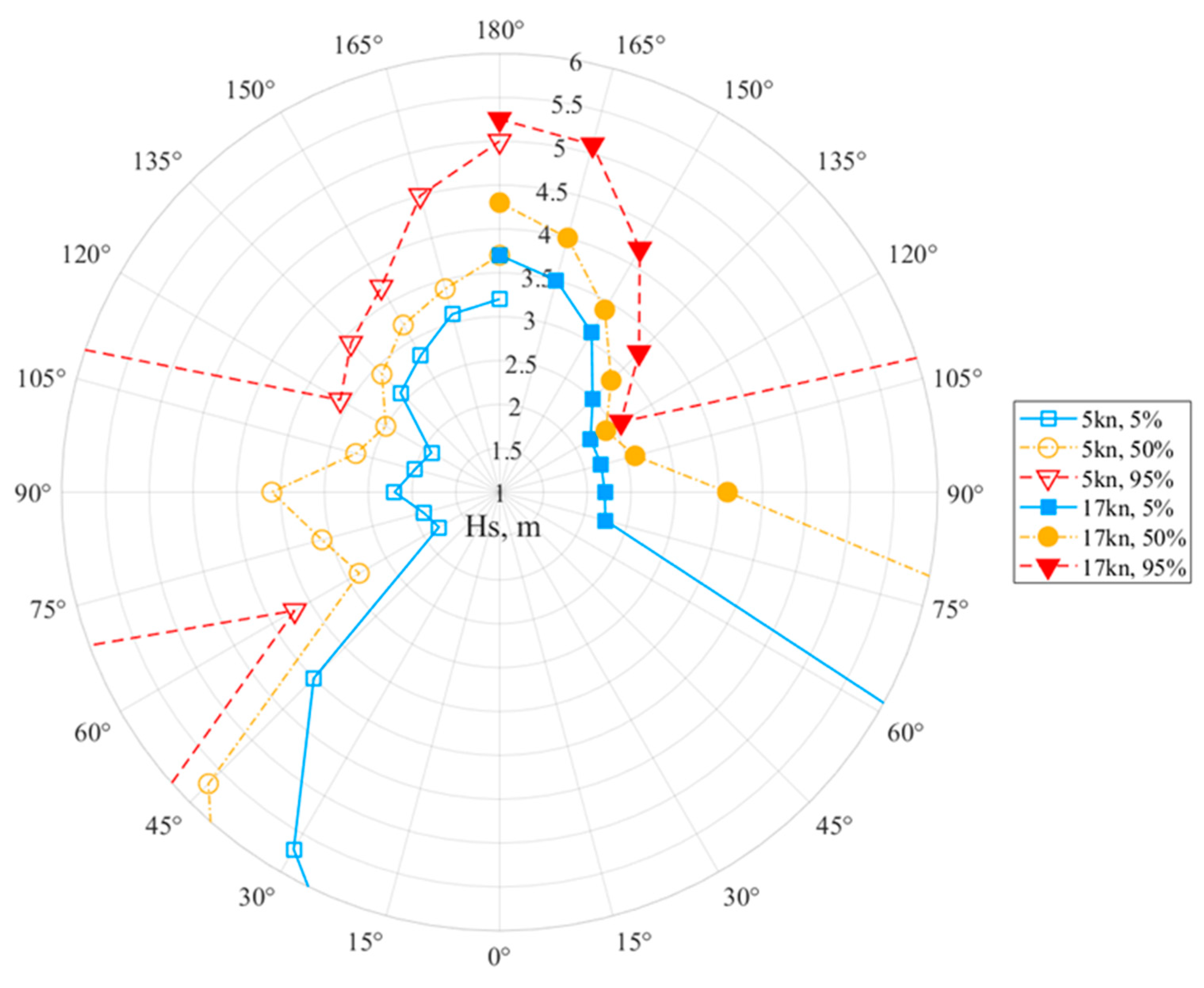
The results of this study are presented in probabilistic operability diagrams, i.e., polar plots providing significant wave heights and heading angles for which seakeeping criteria will be exceeded with certain probabilities. Probabilistic operability diagrams are more informative than “deterministic” diagrams, and this approach could be further extended for use in risk-based decision making, providing that consequences of exceeding seakeeping criteria are defined.

The probabilistic approach can be used in ship design as the decision-making tool when acquiring a new ship for a specific service. For that purpose, a novel probabilistic operability index is defined, representing an extension of the commonly used operability index. Furthermore, the approach can be used as a part of an advanced, risk-based tactical decision support system, assisting ship masters in making real-time decisions on heavy weather maneuvering.

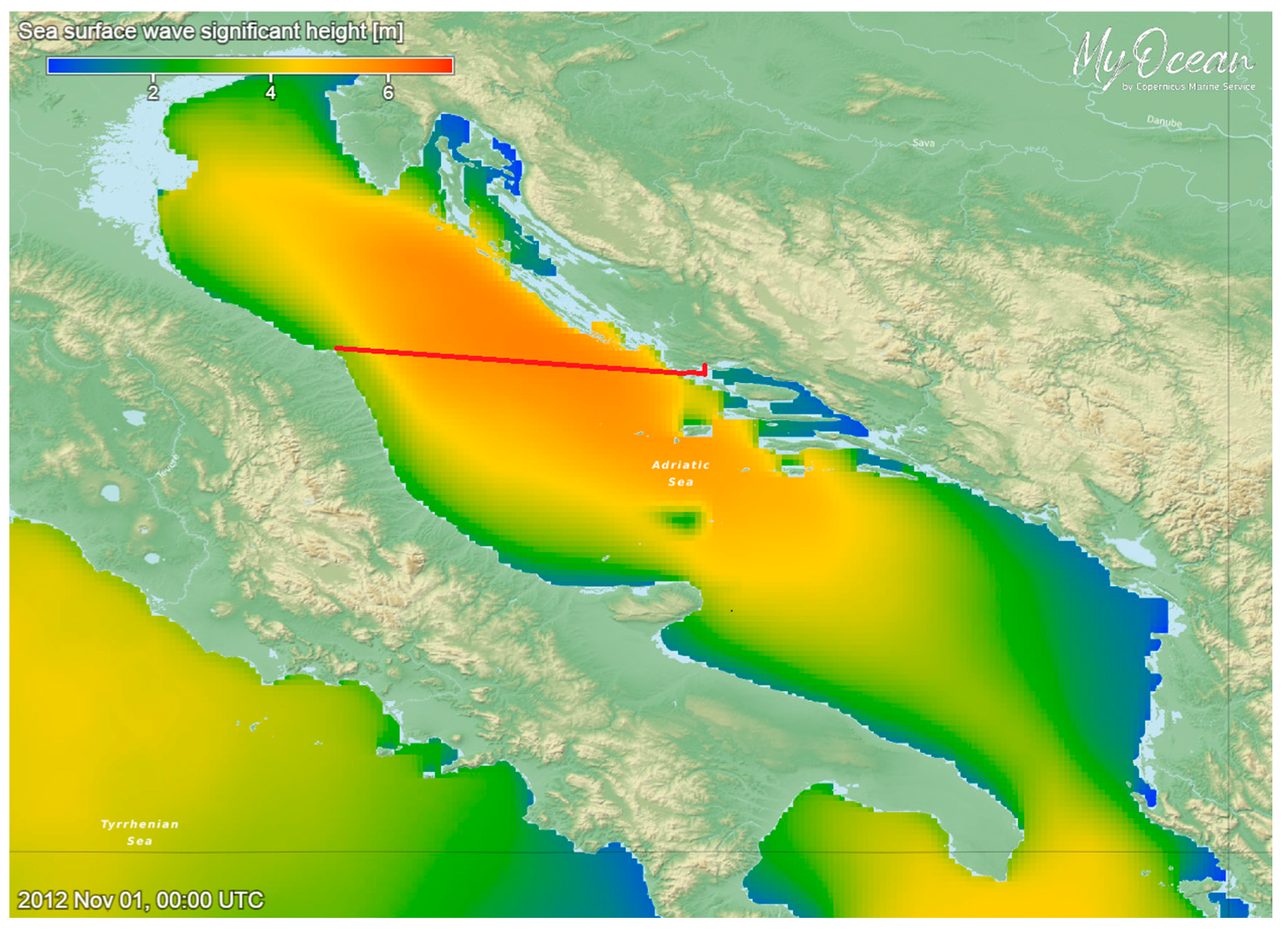
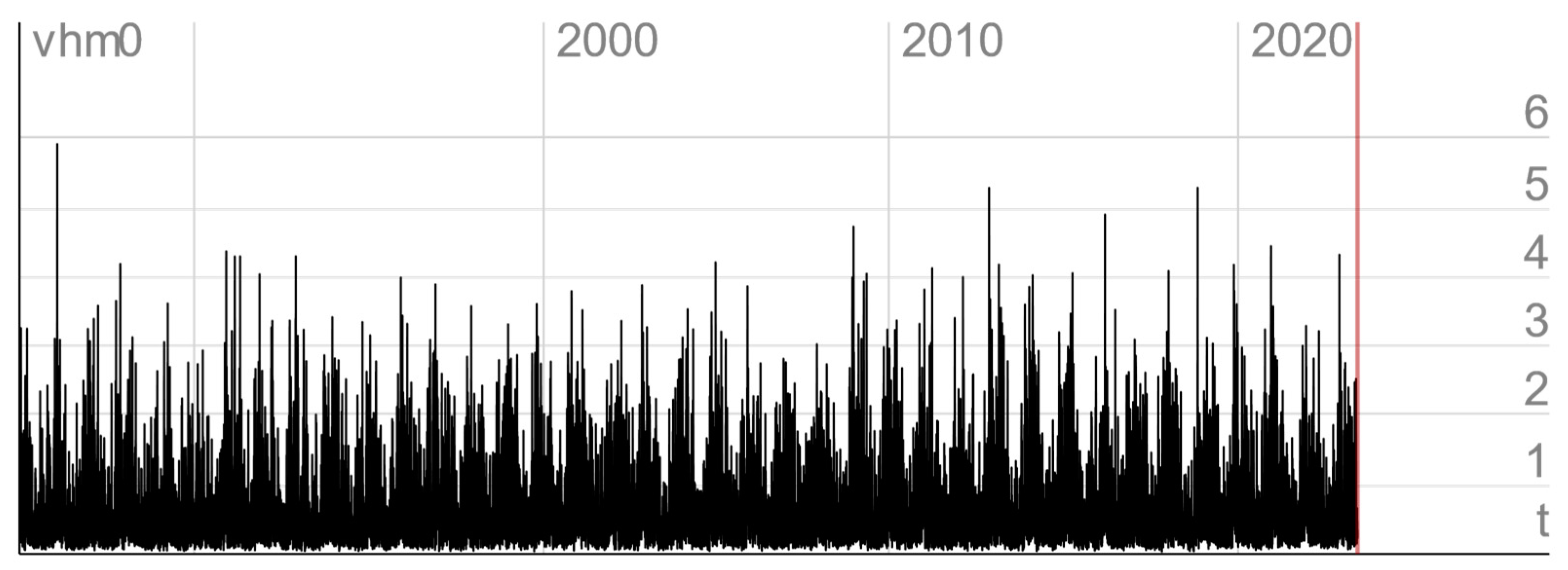
It was also shown how the proposed system can be validated using numerical wave databases, in this case, Mediterranean Sea Wave Reanalysis and Mediterranean Sea Waves Analysis and Forecast, both part of the Copernicus Marine Service.

Recommendations for Future Development

This study is limited to a passenger ferry operating on a route in the Adriatic Sea. However, the analysis can be extended to other ship types, such as container ships and tankers, which operate in significantly more severe oceanic conditions. The influence of strong winds, including crosswinds and headwinds, on the ship maneuverability should also be considered. Additionally, incorporating a wave–structure interaction could be crucial for certain vessel types, such as large container ships.

To ensure the reliability of the model, validation using ships operating in extreme conditions is necessary. Furthermore, integrating artificial intelligence methods could enhance the model’s predictive accuracy.