Research on Advance Rate Effects and Their Regulation of Strata Pressure Behavior in Deeply Buried Weakly Cemented Longwall Panels Under High-Intensity Mining Conditions
Abstract
1. Introduction
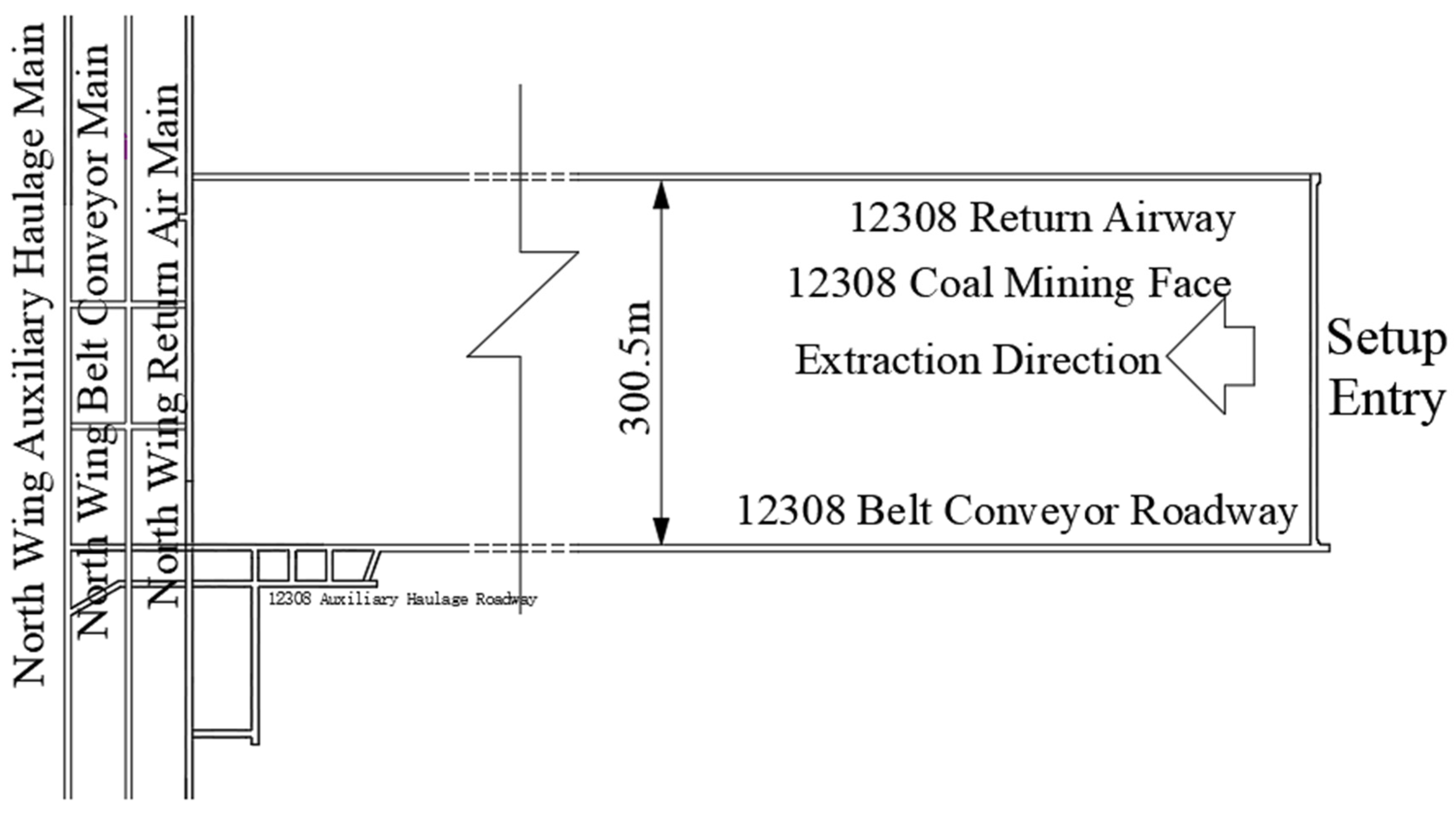
2. Engineering Geological Conditions
2.1. Engineering Geological Profile
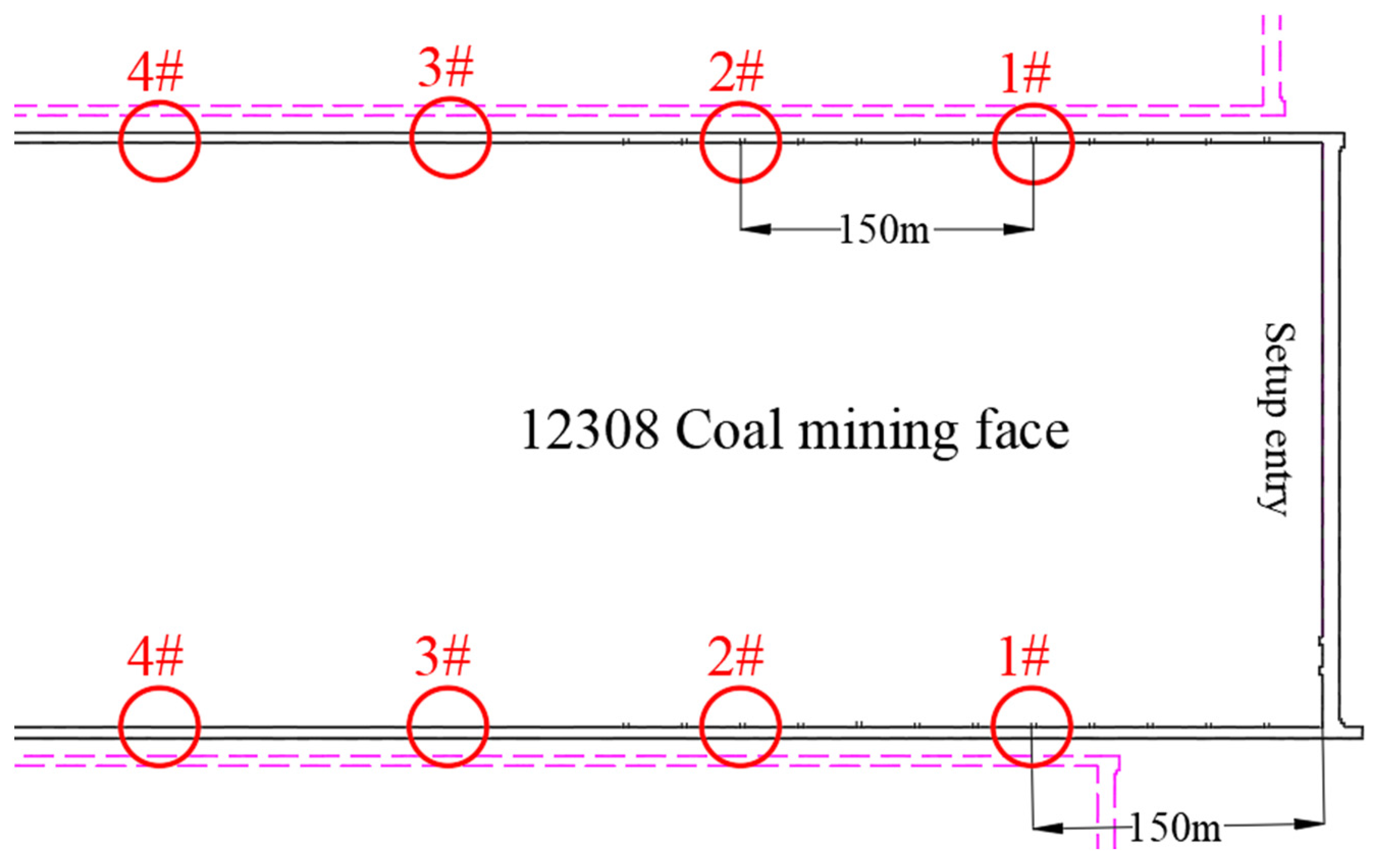
2.2. Support Configuration of the Working Face
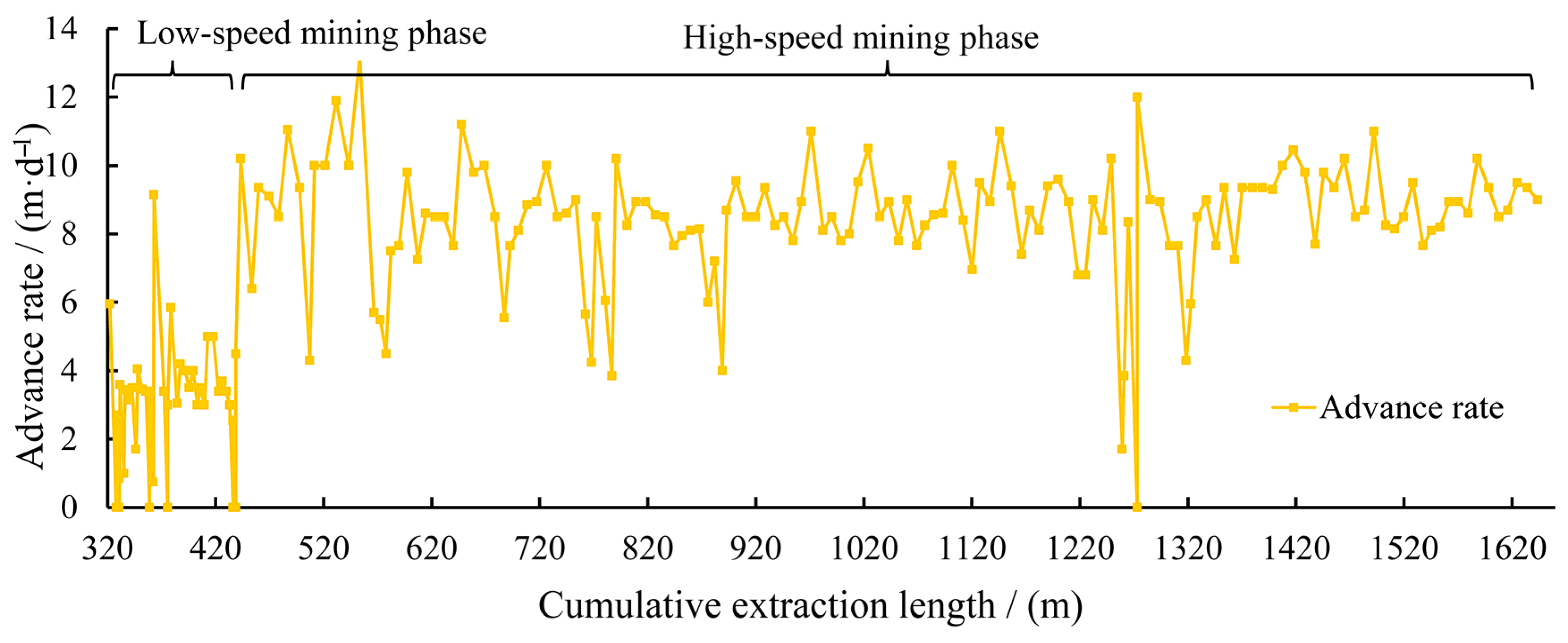
2.3. Advance Rate Conditions of the 12308 Working Face
3. Influence of Face Advancing Rate on Roof Caving Interval
3.1. Establishment and Design of Numerical Model
- (1)
- Numerical Model Construction
- (2)
- Constitutive Models and Mechanical Parameters of Coal–Rock Mass
- (3)
- Numerical Simulation Scheme
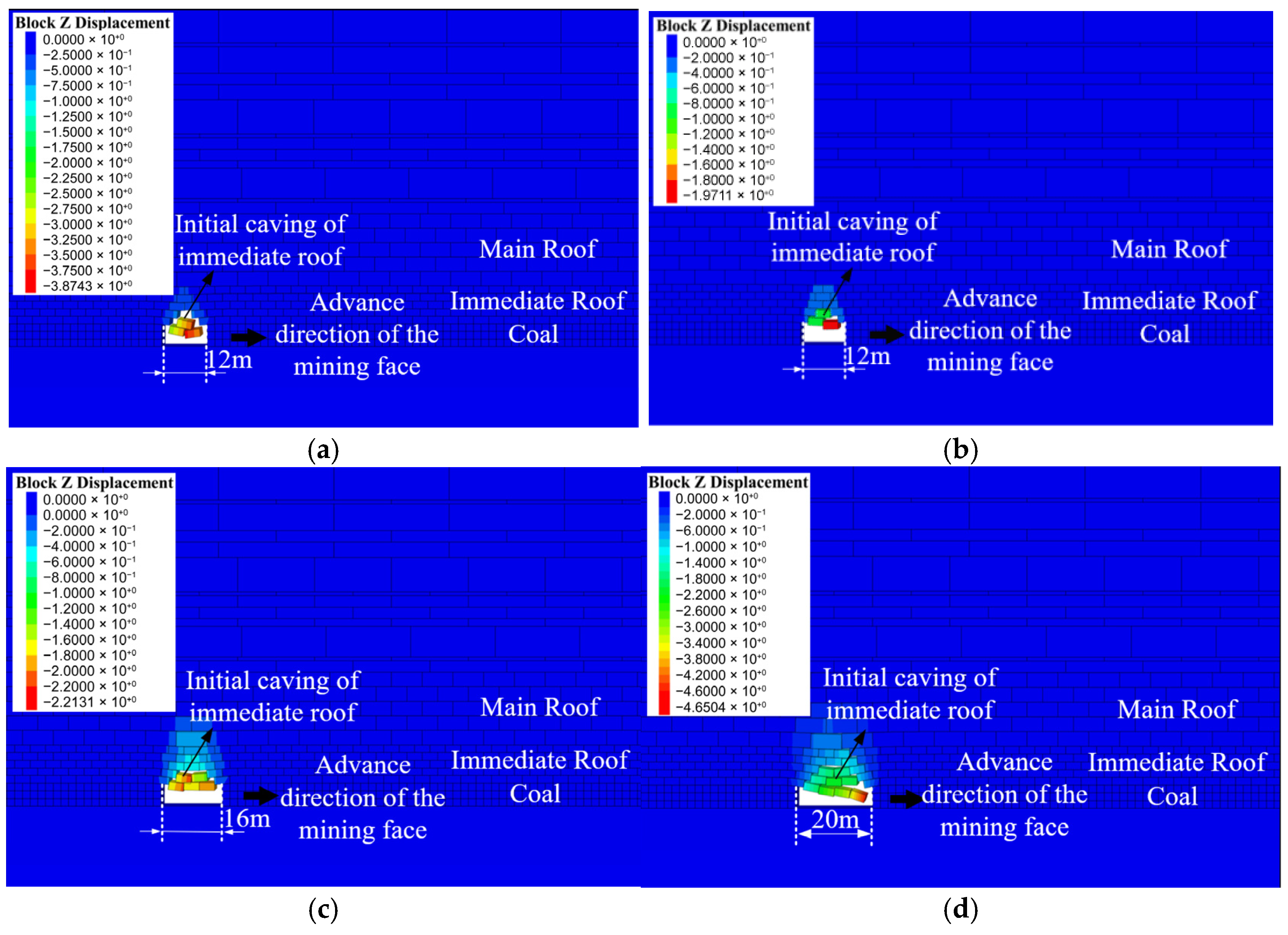
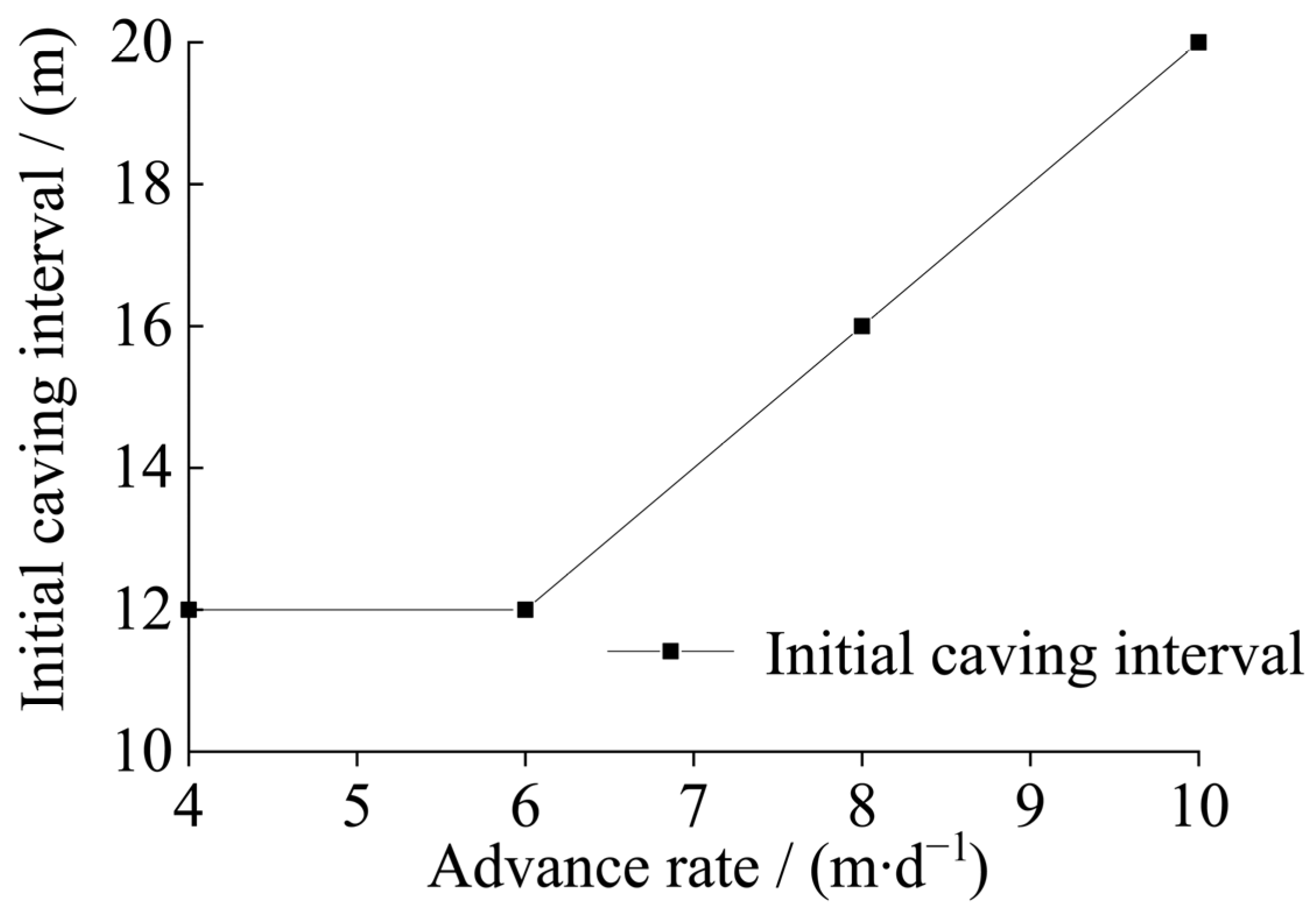
3.2. Simulation of Immediate Roof Initial Caving Intervals Under Different Advance Rates
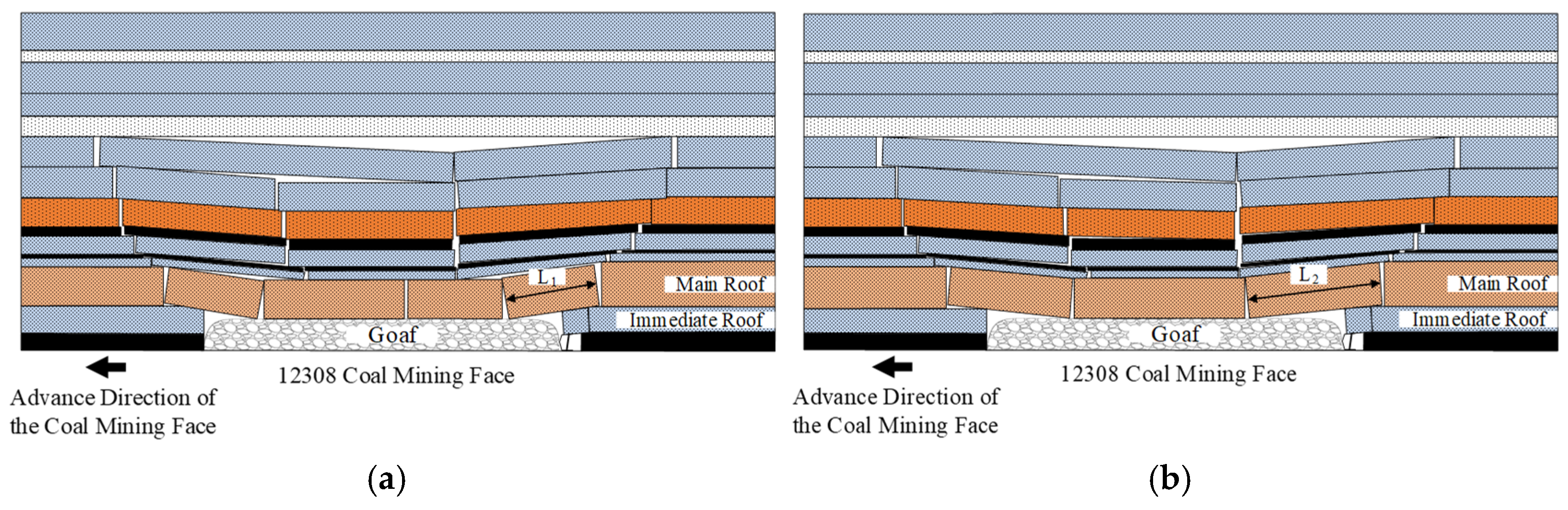
3.3. Simulation of Main Roof Initial Weighting Intervals Under Different Advance Rates·
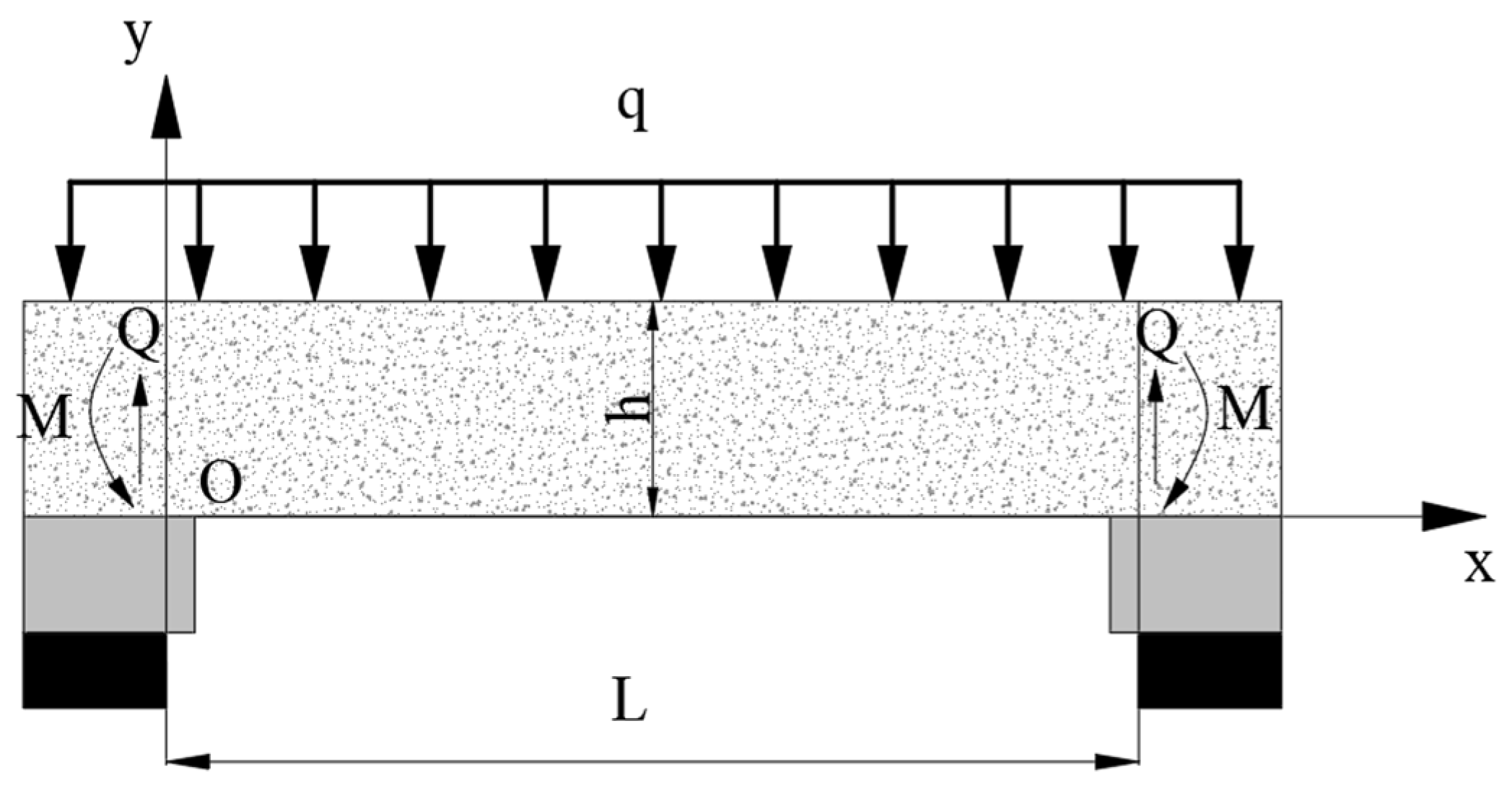
3.4. Theoretical Study on the Influence of Advance Rate on the First Weighting Interval of the Main Roof
4. Influence of Advance Rate on Front Abutment Pressure
4.1. Theoretical Analysis of Front Abutment Pressure
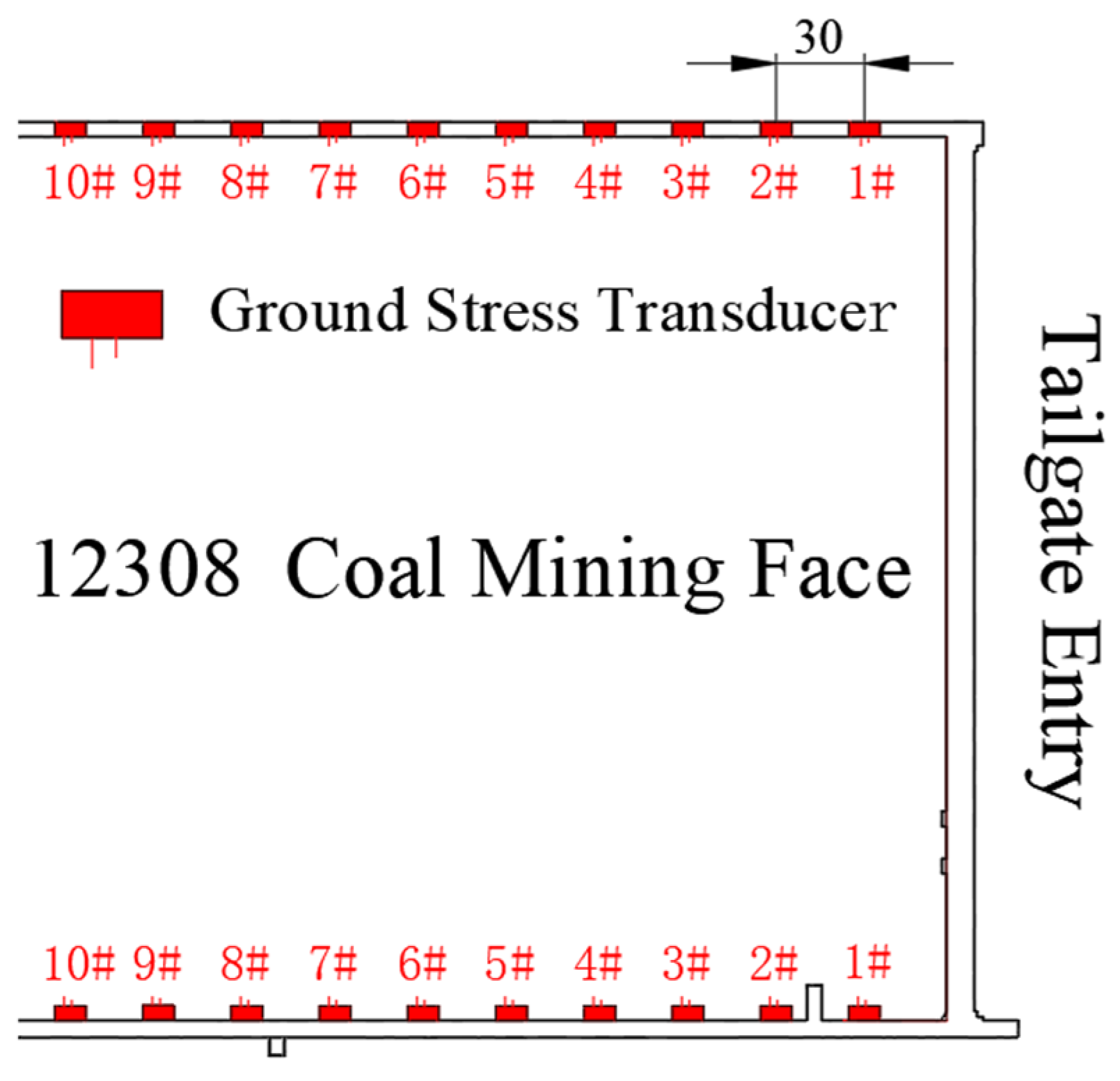
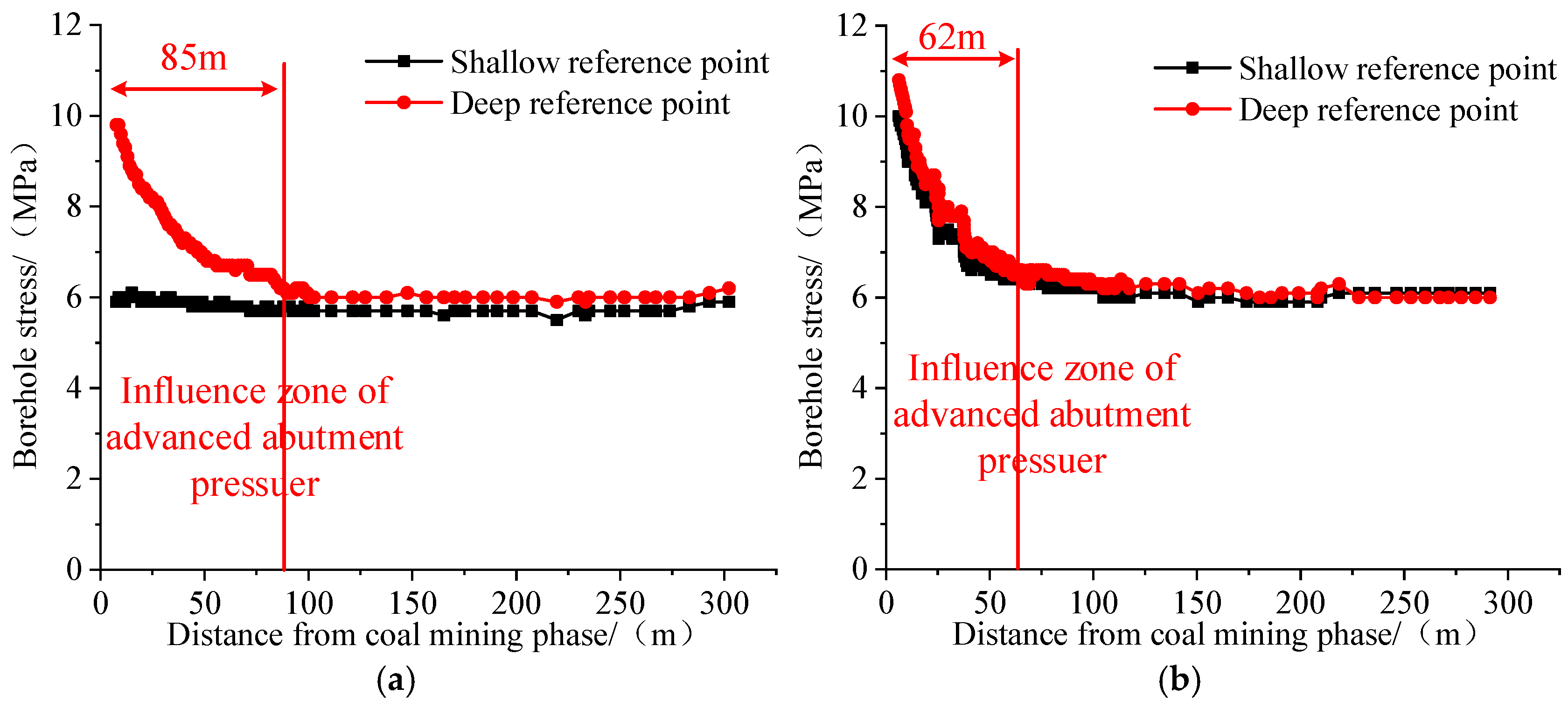
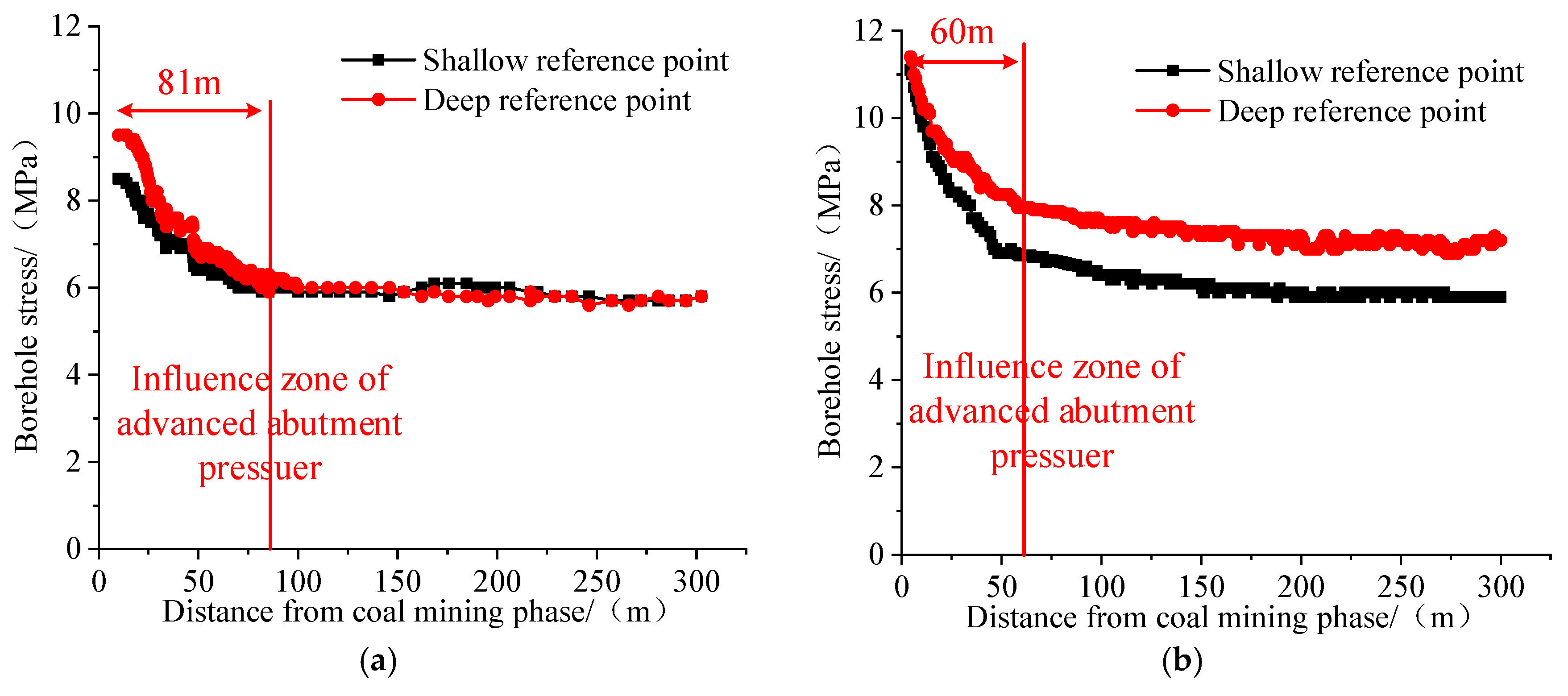
4.2. Field Monitoring of Front Abutment Pressure in the 12308 Working Face
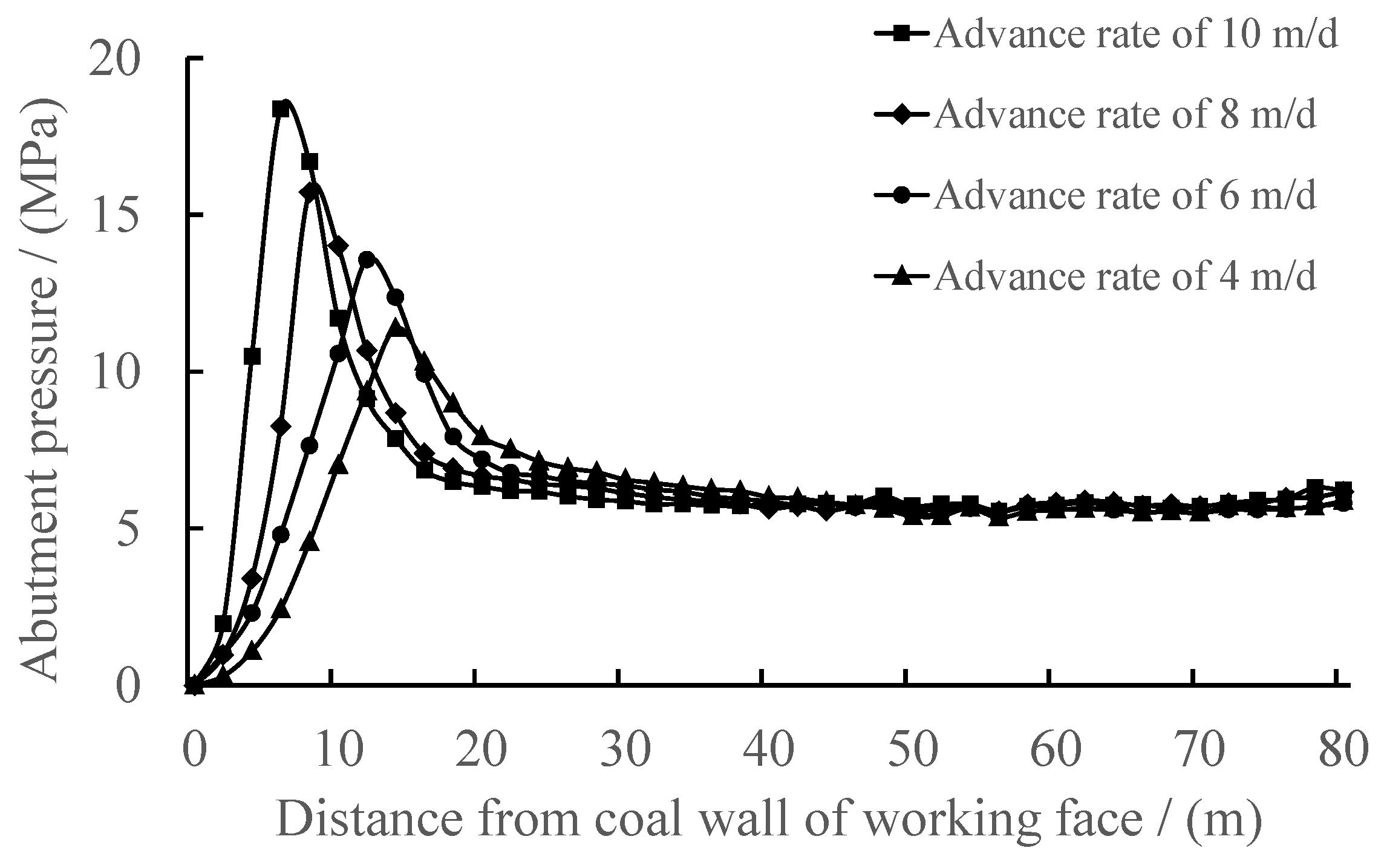
4.3. Numerical Simulation Study of Front Abutment Pressure Under Different Advance Rates
5. Effects of Advance Rate on Shield Resistance and Microseismic Event Distribution
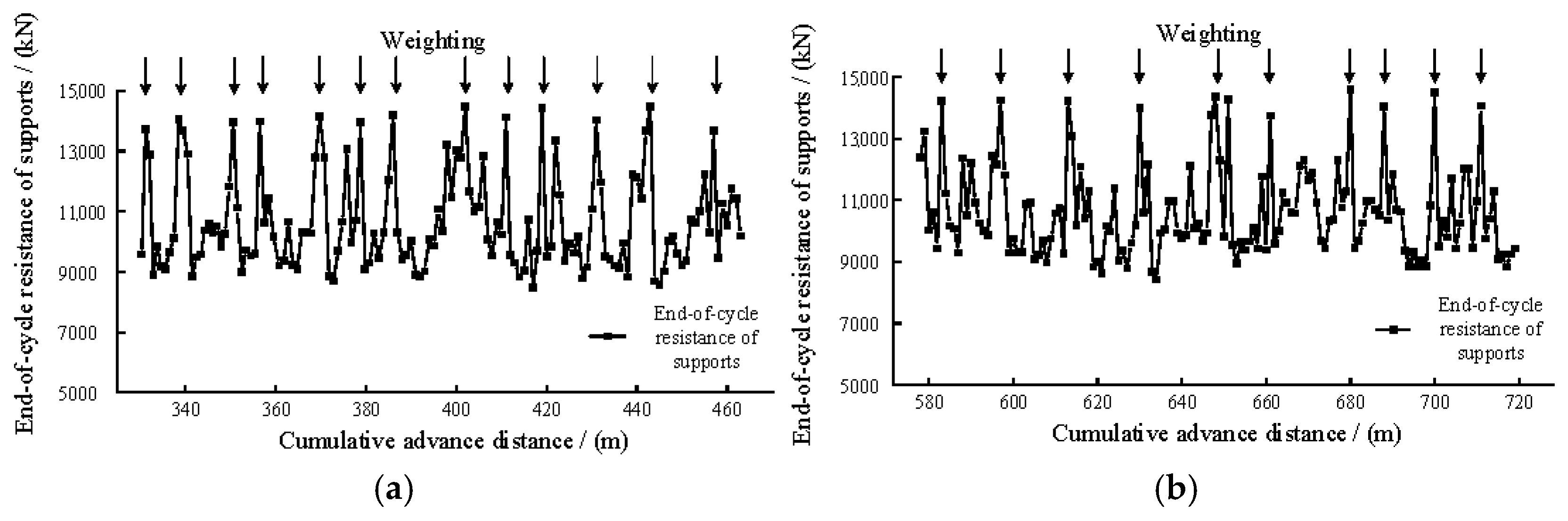
5.1. Field Monitoring of Shield Resistance in the 12308 Working Face
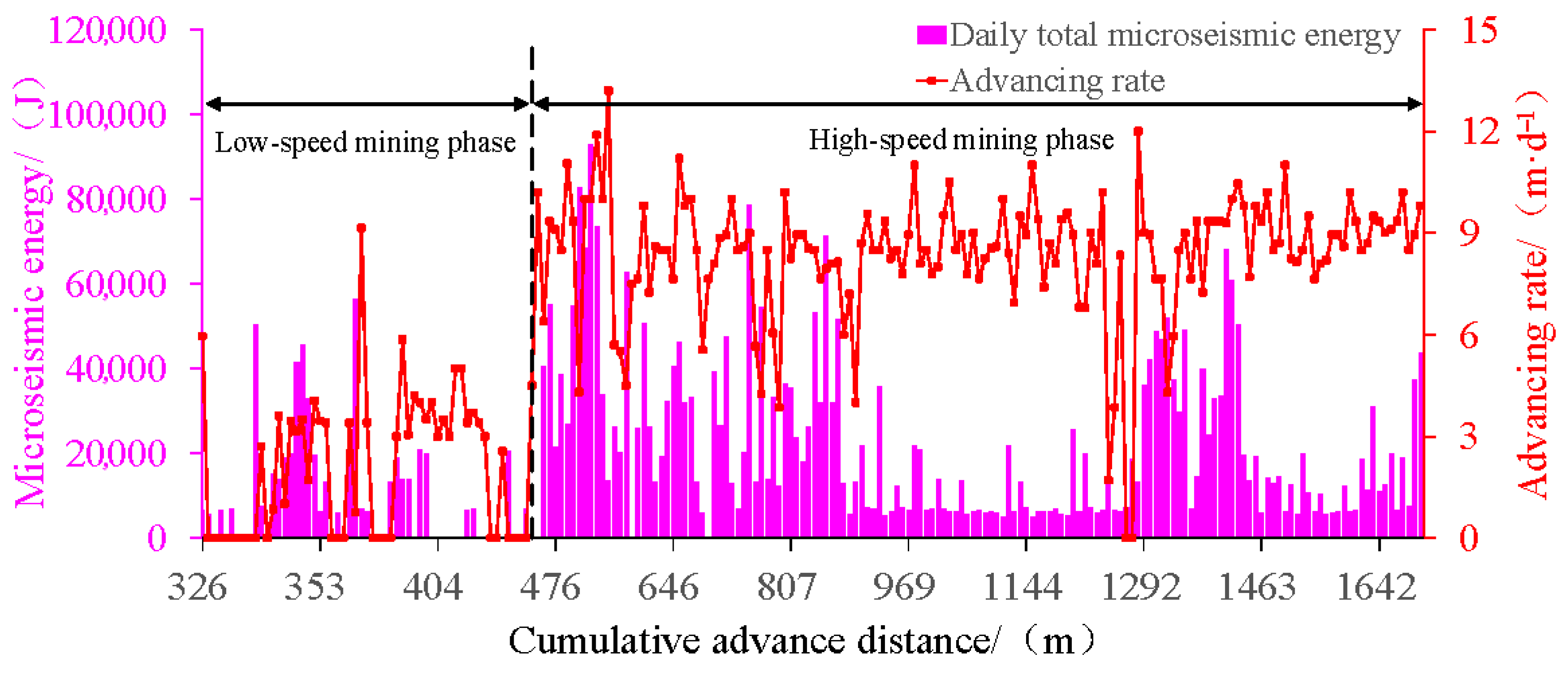
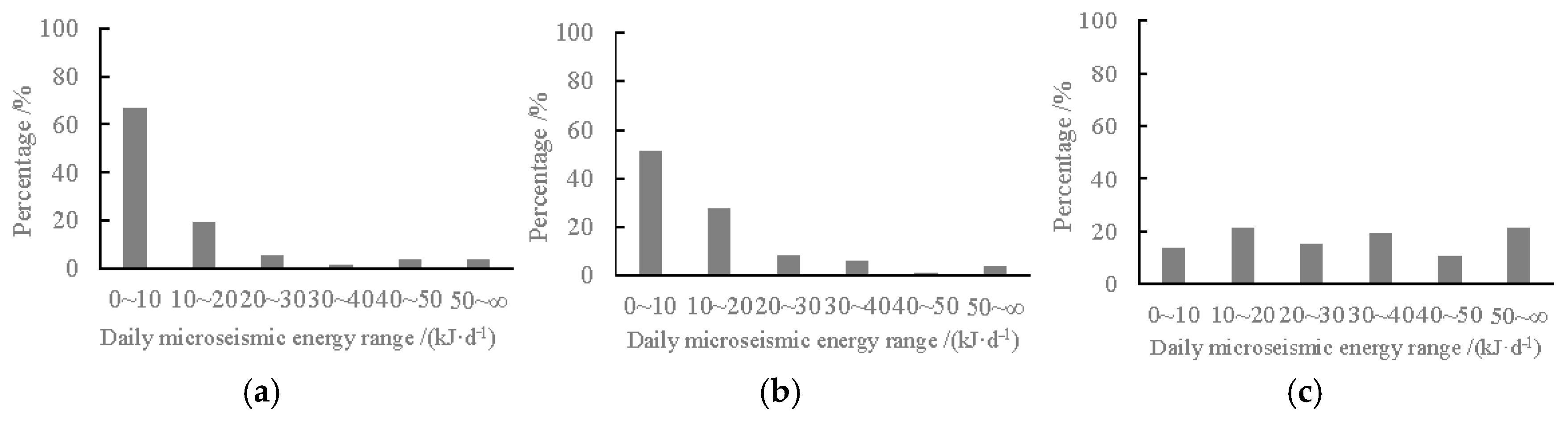
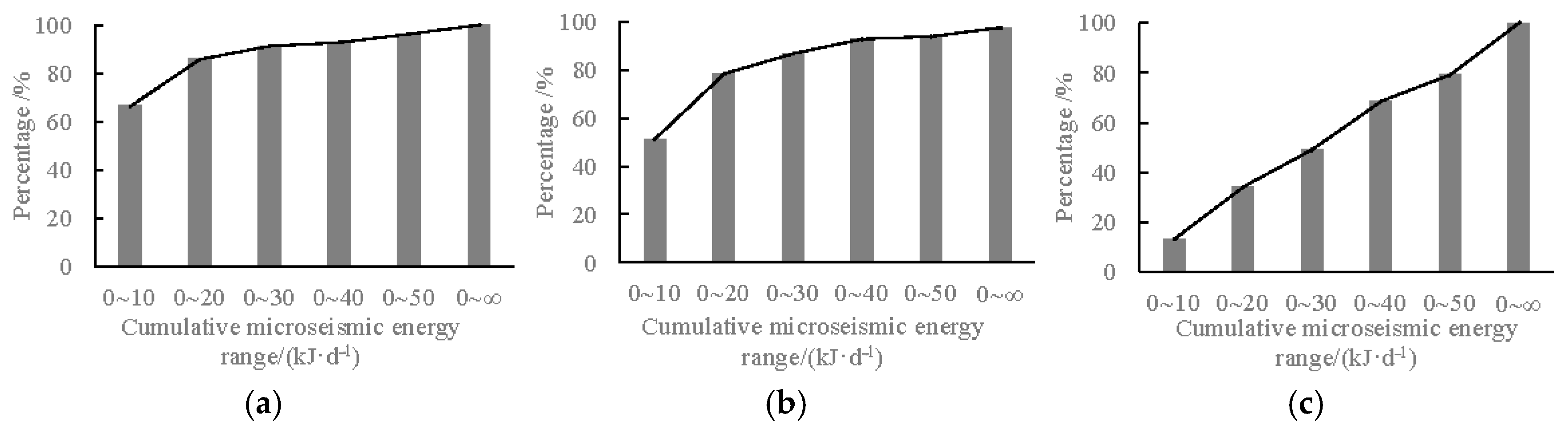
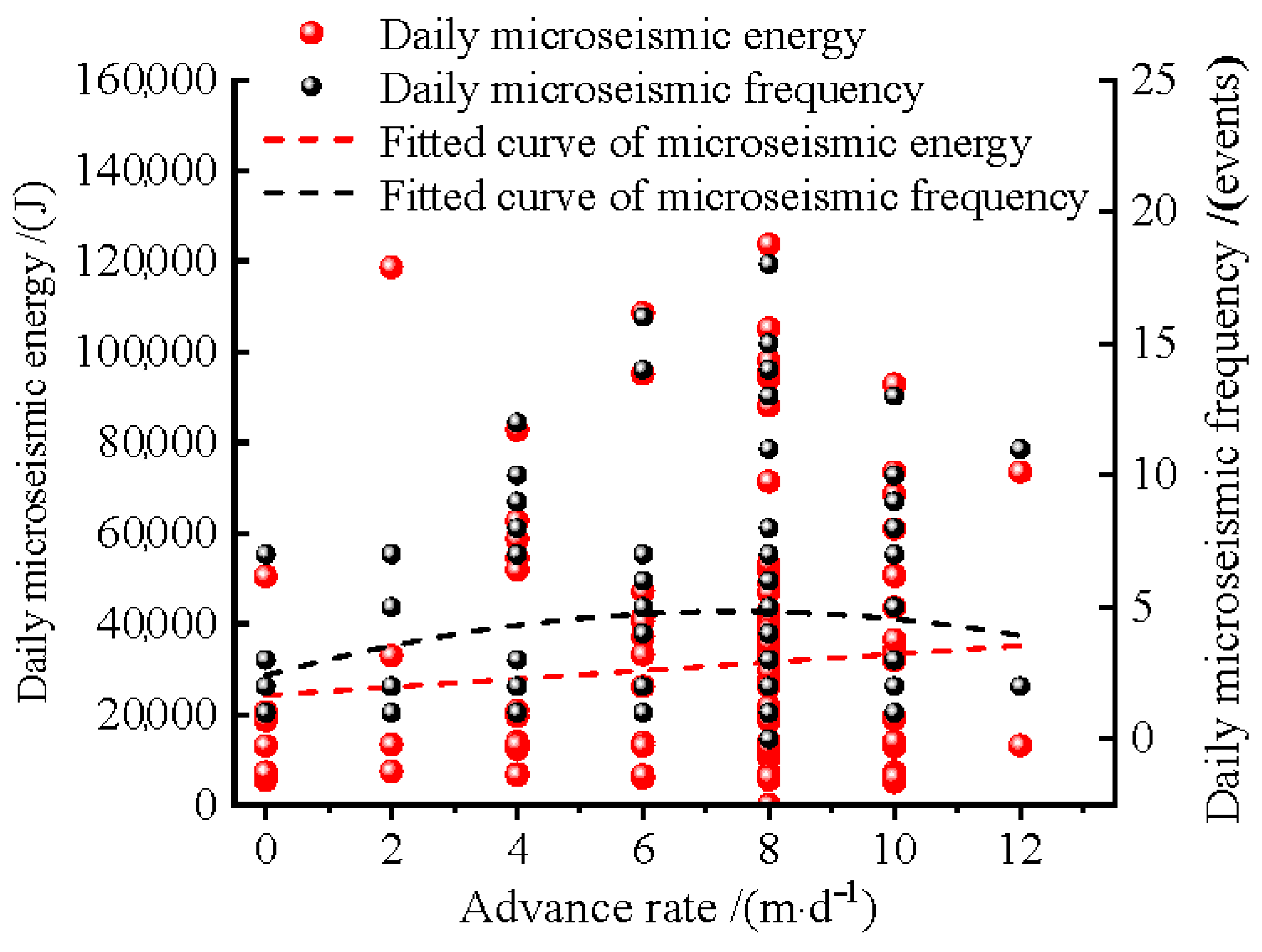
5.2. Field Monitoring of Microseismic Event Distribution in the 12308 Working Face
6. Dynamic Regulation Evaluation Methodology for Strata Pressure Manifestations
- (1)
- Low-speed phase: Cumulative advancement = 126 m;
- (2)
- High-speed steady phase: Cumulative advancement = 742 m;
- (3)
- High-speed unsteady phase: Cumulative advancement = 508 m (total high-speed advancement = 1250 m).
7. Main Conclusions
- (1)
- Research on roof caving intervals under different advancing rates reveals that both the initial caving interval of the immediate roof and the first weighting interval of the main roof exhibit dependence on advancing rates. Specifically, these intervals increase progressively with higher advancing rates.
- (2)
- Through the establishment of a mechanical model for overburden fracture structures, combined with theoretical analysis, field measurements, and numerical simulations, it is demonstrated that abutment pressure ahead of the working face correlates significantly with advancing rates. Increasing advancing rates reduce the influence range of abutment pressure while amplifying its peak magnitude and shifting the peak location toward the coal wall.
- (3)
- An investigation into support resistance under varying advancing rates indicates a clear relationship between the periodic weighting interval of the main roof and advancing rates. Transitioning from low-speed (e.g., 4 m/d) to high-speed advancing (e.g., 10 m/d) increases the periodic weighting interval by 31.8% and intensifies the weighting magnitude by 1%.
- (4)
- Microseismic activity demonstrates a distinct advancing rate effect. Both the daily microseismic event frequency and cumulative energy escalate with increasing advancing rates. During high-speed advancing phases, the average daily event counts rise from 1.4 events/d to 3.4 events/d, while daily energy increases from 9.4 × 103 J to 2.2 × 104 J, representing a 59.3% enhancement.
- (5)
- A critical threshold of 40 kJ/d is established as the production-limiting criteria for microseismic energy during low-speed advancing phases. Similarly, 50 kJ/d serves as the critical threshold for high-speed phases. Upon reaching these thresholds, strategic reduction in advancing rates is recommended, specifically by reducing daily advance distance by two cutting cycles.
- (6)
- A dynamic control methodology for strata pressure manifestations is proposed, centering on advancing rate optimization. By analyzing the relationship between single-event microseismic energy release and advancing rates, the optimal advancing rate for Panel 12308 is determined as 6 m/d, which was validated through practical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, H.; Gao, M.; Zhang, R.; Peng, G.; Wang, W.; Li, A. Study on the Mechanical Properties and Mechanical Response of Coal Mining at 1000 m or Deeper. Rock. Mech. Rock. Eng. 2019, 52, 1475–1490. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Zhao, J.; Ju, M.; De Silva, R.V.S.; Rathnaweera, T.D.; Bandara, A.K.M.S. Opportunities and Challenges in Deep Mining: A Brief Review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Ghorbani, Y.; Nwaila, G.T.; Zhang, S.E.; Bourdeau, J.E.; Canovas, M.; Arzua, J.; Nikadat, N. Moving towards deep underground mineral resources: Drivers, challenges and potential solutions. Resour. Policy 2023, 80, 103222. [Google Scholar] [CrossRef]
- Cao, J.; Dou, L.; Konietzky, H.; Zhou, K.; Zhang, M. Failure mechanism and control of the coal bursts triggered by mining-induced seismicity: A case study. Environ. Earth Sci. 2023, 82, 168. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.; Wang, X.; Liu, Y.; Xie, H.; Du, P. Acoustic Emission Characteristics of Coal Failure Under Triaxial Loading and Unloading Disturbance. Rock Mech. Rock Eng. 2023, 56, 1043–1061. [Google Scholar] [CrossRef]
- Hu, J.; He, M.; Li, H.; Tao, Z.; Liu, D.; Cheng, T.; Peng, D. Rockburst Hazard Control Using the Excavation Compensation Method (ECM): A Case Study in the Qinling Water Conveyance Tunnel. Engineering 2024, 34, 154–163. [Google Scholar] [CrossRef]
- Waqar, M.F.; Guo, S.; Qi, S. A Comprehensive Review of Mechanisms, Predictive Techniques, and Control Strategies of Rockburst. Appl. Sci. 2023, 13, 3950. [Google Scholar] [CrossRef]
- Ordin, A.A.; Timoshenko, A.M. Coalbed methane release as a function of coal breakup. J. Min. Sci. 2016, 52, 524–529. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, G.; Jiang, S.; Fan, Z.; Li, S.; Ni, H. Dual-hazard control mechanism of burst-prone and spontaneous combustion coalface considering effect of retreat speed. Energy Rep. 2021, 7, 278–288. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, X.; Zhang, Z.; Zhang, H.; Gu, Z.; Zhang, S.; Yan, G. Compound disaster characteristics of rock burst and coal spontaneous combustion in island mining face: A case study. Case Stud. Therm. Eng. 2024, 63, 105240. [Google Scholar] [CrossRef]
- Linkov, A. Rockbursts and the instability of rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 727–732. [Google Scholar] [CrossRef]
- Napier, J.; Malan, D. Simulation of tabular mine face advance rates using a simplified fracture zone model. Int. J. Rock Mech. Min. Sci. 2018, 109, 105–114. [Google Scholar] [CrossRef]
- Nawrocki, P.A. One-dimensional, semi-analytical solution for time-dependent behaviour of a seam. Int. J. Numer. Anal. Meth. Geomech. 1995, 19, 59–74. [Google Scholar] [CrossRef]
- Gogolewska, A.; Junik, P. Seismic hazard related to rate of face advance in Lubin copper ore mine. Min. Sci. 2013, 20, 87–99. [Google Scholar] [CrossRef]
- Deng, Z.-G.; Wang, S.; Mo, Y.-L.; Liu, W.-J. Influence of Mining Speed on Stope Energy in Deep Mines. Appl. Geophys. 2024. [Google Scholar] [CrossRef]
- Yu, X.; Gao, M.; Zhao, H.; Zhao, S.; Zhao, H. Research on the Laws of Overlying Rock Fracture and Energy Release under Different Mining Speeds. Appl. Sci. 2024, 14, 3222. [Google Scholar] [CrossRef]
- Li, W.; Tu, S.; Tu, H.; Liu, X.; Miao, K.; Zhao, H.; Ma, J.; Tang, L.; Li, Y. A New Method to Assess Thick, Hard Roof-Induced Rock Burst Risk Based on Mining Speed Effect on Key Energy Strata. Sustainability 2022, 14, 15054. [Google Scholar] [CrossRef]
- Jia, C.; Jia, C.; Lai, X.; Lai, X.; Cui, F.; Cui, F.; Feng, G.; Feng, G.; He, S.; He, S.; et al. Study on Multisize Effect of Mining Influence of Advance Speed in Steeply Inclined Extrathick Coal Seam. Lithosphere 2022, 2022, 9775460. [Google Scholar] [CrossRef]
- Keneti, A.; Sainsbury, B. Review of published rockburst events and their contributing factors. Engineering Geology. 2018, 246, 361–373. [Google Scholar] [CrossRef]
- Prakash, A.; Kumar, A.; Verma, A.; Mandal, S.K.; Singh, P.K. Trait of subsidence under high rate of coal extraction by longwall mining: Some inferences. Sādhanā 2021, 46, 216. [Google Scholar] [CrossRef]
- Eremin, M.O.; Makarov, P.V. Mathematical Modeling of Stress-Strain Evolution in the Rock Mass around a Mine Opening. Evaluation of the Steps of First Roof Caving at Different Thicknesses of the Main Roof. Phys. Mesomech. 2019, 22, 287–295. [Google Scholar] [CrossRef]
- Jooste, Y.; Malan, D.F. Rock engineering aspects of a modified mining sequence in a dip pillar layout at a deep gold mine. J. South. Afr. Inst. Min. Metall. 2015, 115, 1097–1112. [Google Scholar] [CrossRef][Green Version]
- Wang, D.-Y. Study of Impact of Mining Rate on Abutment Pressure of Stope. Coal Technol. 2014, 33, 94–96. (In Chinese) [Google Scholar]
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Jiang, F.-X.; Xun, L.; Yang, S. Study on microseismic monitoring for spatial structure of overlying strata and mining pressure field in longwall face. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2003, 25, 23. [Google Scholar]








| Sequential Strata | Stratigraphic Unit Designation | Density (kg/m3) | Elastic Modulus (GPa) | Cohesion (MPa) | Internal Friction Angle/° | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| 17 | Sandy mudstone | 2120 | 1.76 | 3.41 | 40 | 1.55 |
| 16 | Coal seam 2-1 lower | 1460 | 0.57 | 1.88 | 24 | 0.22 |
| 15 | Sandy mudstone | 2120 | 1.76 | 3.41 | 40 | 1.55 |
| 14 | Siltstone | 1890 | 0.6 | 2.42 | 32 | 0.33 |
| 13 | Medium-grained sandstone | 2350 | 4.21 | 4.7 | 32 | 3.2 |
| 12 | Sandy mudstone | 2120 | 1.12 | 3.41 | 40 | 1.55 |
| 11 | Coal seam 2-2 upper | 1460 | 0.57 | 1.88 | 24 | 0.22 |
| 10 | Sandy mudstone | 2040 | 0.78 | 3.41 | 40 | 1.13 |
| 9 | Siltstone | 1870 | 0.6 | 2.42 | 35 | 0.25 |
| 8 | Coal seam 2-2 middle | 1440 | 0.57 | 1.88 | 24 | 0.22 |
| 7 | Sandy mudstone | 2030 | 0.78 | 3.41 | 40 | 1.11 |
| 6 | Coal seam 2-2 lower | 1460 | 0.57 | 1.88 | 24 | 0.22 |
| 5 | Sandy mudstone | 2040 | 0.78 | 3.41 | 40 | 1.13 |
| 4 | Conglomeratic sandstone | 2450 | 5.4 | 4.5 | 29 | 2.1 |
| 3 | Sandy mudstone | 2070 | 0.78 | 3.41 | 40 | 0.86 |
| 2 | Coal seam 3-1 | 1440 | 0.57 | 2.2 | 24 | 0.3 |
| 1 | Sandy mudstone | 2162 | 1.76 | 3.41 | 30 | 0.92 |
| Sequential Strata | Joint Surface | Normal Stiffness (GPa) | Tangential Stiffness (GPa) | Cohesion (MPa) | Internal Friction Angle/° | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| 17 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 16 | Coal seam 2-1 lower | 3.8 | 2.4 | 3.2 | 24 | 0.25 |
| 15 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 14 | Siltstone | 4.2 | 4.27 | 4.8 | 26 | 0.2 |
| 13 | Medium-grained sandstone | 8.5 | 5.2 | 9.2 | 32 | 1.0 |
| 12 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 11 | Coal seam 2-2 upper | 3.8 | 2.4 | 3.2 | 24 | 0.25 |
| 10 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 9 | Siltstone | 4.2 | 4.27 | 4.8 | 26 | 0.2 |
| 8 | Coal seam 2-2 middle | 3.8 | 2.4 | 3.2 | 24 | 0.25 |
| 7 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 6 | Coal seam 2-2 lower | 3.8 | 2.4 | 3.2 | 24 | 0.25 |
| 5 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 4 | Conglomeratic sandstone | 6.2 | 5.2 | 8.7 | 28 | 1.2 |
| 3 | Sandy mudstone | 5.5 | 4.27 | 4.5 | 25 | 0.6 |
| 2 | Coal seam 3-1 | 3.8 | 2.3 | 3.2 | 24 | 0.23 |
| 1 | Sandy mudstone | 5.5 | 4.27 | 3.5 | 25 | 0.6 |
| Advance Rate/(m∙d−1) | Initial Weighting Interval/(m) | Position Relative to Coal Wall/(m) |
|---|---|---|
| 4 | 52 | 4 |
| 6 | 54 | 2 |
| 8 | 56 | 1 |
| 10 | 60 | 1 |
| Rock Mass Description | RMR Score Range | Q Value Range | Corresponding k Value |
|---|---|---|---|
| Fault influence zone, intensely weathered rock zone | 20–40 (Class IV Rock Mass) | 0.1–1.0 | 0.50~0.65 |
| Crushed limestone with argillaceous infilling | 40–60 (Class III Rock Mass) | 1.0–4.0 | 0.65~0.75 |
| Massive sandstone with closed joint development | 60–80 (Class II Rock Mass) | 4.0–10 | 0.75~0.85 |
| Intact granite with joint spacing > 3 m | 80–100 (Class I Rock Mass) | >10 | 0.85~0.90 |
| Stage | Influence Zone of Advanced Abutment Pressure/(m) | Peak Value of Advanced Abutment Pressure/(MPa) | Distance from Coal Wall to Peak Position/(m) |
|---|---|---|---|
| Low-speed mining phase | 83 | 9.27 | 8.8 |
| High-speed mining phase | 61 | 10.9 | 5.4 |
| Stage | Support Position | Weighting Frequency | Periodic Weighting Interval/(m) | Support Load During Weighting/(kN) | Remarks |
|---|---|---|---|---|---|
| Low-speed mining phase | Upper | 13 | 10.2 | 14,091.6 | |
| Middle | 12 | 10.3 | 14,454.6 | ||
| Lower | 12 | 10.5 | 14,133.9 | ||
| 12.3 | 10.3 | 14,226.7 | Average | ||
| High-speed mining phase | Upper | 9 | 15.4 | 14,235.7 | |
| Middle | 8 | 15.5 | 14,529.4 | ||
| Lower | 9 | 14.4 | 14,231.4 | ||
| 8.7 | 15.1 | 14,332.2 | Average |
| Warning Level | 12308 Coal Mining Face | Response Measures |
|---|---|---|
| A No rockburst risk | Emax ≤ 1.0 × 104 J Frequency ≤ 70/d | Normal production. |
| B Weak rockburst risk | 1.0 × 104 J < Emax ≤ 1.1 × 104 J 70/d < Frequency ≤ 80/d | Normal excavation and mining operations, strengthen monitoring. |
| C Moderate rockburst risk | 1.1 × 104 J < Emax ≤ 1.3 × 104 J 80/d < Frequency ≤ 90/d | Reduce the advancing speed, carry out hazard-relieving measures, and resume the advancing speed after verifying that the hazard is eliminated. |
| D Severe rockburst risk | Emax > 1.3 × 104 J Frequency > 90/d | Stop operations, evacuate personnel from the dangerous area, take hazard-relieving measures after the hazard level drops to the moderate rockburst level, and resume production after verifying that the hazard is eliminated. |
| Stage Name | Advance Rate Range/(m·d−1) | Advance Rate/(m·d−1) | Microseismic Event Count/(Times·d−1) | Total Energy of Microseismic Events/(J·d−1) | Emax/J |
|---|---|---|---|---|---|
| Low-speed mining phase | 2~4 | 3.7 | 1.4 | 9.4 × 103 | 7.7 × 103 |
| High-speed mining stage | 8~10 | 8.4 | 3.4 | 2.2 × 104 | 7.9 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Liu, B.; Yang, J. Research on Advance Rate Effects and Their Regulation of Strata Pressure Behavior in Deeply Buried Weakly Cemented Longwall Panels Under High-Intensity Mining Conditions. Appl. Sci. 2025, 15, 4266. https://doi.org/10.3390/app15084266
Yu F, Liu B, Yang J. Research on Advance Rate Effects and Their Regulation of Strata Pressure Behavior in Deeply Buried Weakly Cemented Longwall Panels Under High-Intensity Mining Conditions. Applied Sciences. 2025; 15(8):4266. https://doi.org/10.3390/app15084266
Chicago/Turabian StyleYu, Fenghai, Baodeng Liu, and Jin Yang. 2025. "Research on Advance Rate Effects and Their Regulation of Strata Pressure Behavior in Deeply Buried Weakly Cemented Longwall Panels Under High-Intensity Mining Conditions" Applied Sciences 15, no. 8: 4266. https://doi.org/10.3390/app15084266
APA StyleYu, F., Liu, B., & Yang, J. (2025). Research on Advance Rate Effects and Their Regulation of Strata Pressure Behavior in Deeply Buried Weakly Cemented Longwall Panels Under High-Intensity Mining Conditions. Applied Sciences, 15(8), 4266. https://doi.org/10.3390/app15084266






