Abstract
Solid waste treatment and resourceization critically depend on waste characterization. Heavy metals and critical raw materials are found as trace elements in solid waste dumps, and their reliable quantification plays a critical role for decision risk regarding effective waste management. The reliable quantification of trace elements is a very challenging issue. Hence, in this study, a new conservative approach for data analysis in screening for trace elements in waste dumps is presented. We propose a theoretical model for statistical data interpretation to overcome the drawbacks of conventional approaches based on unproven hypotheses, such as binomial, Poisson, or Gaussian distributions of the particles carrying the analyte. Our model addresses concentration values close to the limit of quantification (LOQ) of an analytical method. This model fills the gap of data analysis when a set of analytical results are uniformly distributed. Our approach deals with results reported as being lower than the LOQ. The model was applied on XRFS results from studies carried out on tailings to emphasize the differences among classic, robust, and conservative data analyses. Classical analyses overestimate the concentration values and underestimate the associated uncertainties increasing the decision risk. This study demonstrates that a conservative approach is mandatory when screening for trace elements if the concentration values are uniformly distributed. The proposed model can be applied to any solid waste dump, regardless of the analytical method used for trace element screening.
1. Introduction
Secondary resources, mainly solid wastes, are an important part of the circular economy, as they can substitute genuine resources and reduce the carbon footprint caused by genuine resource extraction [1]. The recycling of solid waste streams would be ideal if the recyclers received clean streams of waste products, which would allow them to produce recovered materials of sufficiently high quality for reuse in the same, or similar, products (so-called closed-loop recycling) [1]. However, many solid wastes contain significant amounts of heavy metals (e.g., As, Ba, Cd, Cr, Pb, Hg, and Se) [2,3,4].
The presence of heavy metals in a solid waste stream can limit its potential for recovery. For example, ferrous slag recycling in agriculture (e.g., soil fertilizer, soil amendment, soil pH improvement) or in road and pavement construction can create environmental issues if slag pollutes the soil by leaching toxic elements under rainy conditions [5,6]. Consequently, the Resource Conservation and Recovery Act enforced by the Environmental Protection Agency stated allowable limits for heavy metals in soils [7]. Hence, the reliable measurement of heavy metal contents in a solid waste stream is mandatory for most recovery applications.
Another significant challenge in waste management is the screening for critical raw materials (CRMs) in industrial solid waste dumps, as required by Regulation (EU) 2024/1252 [8]. Notably, this regulation mandates that “By 24 November 2027, Member States shall adopt and implement measures to promote the recovery of critical raw materials from extractive waste, in particular from closed extractive waste facilities”. Additionally, Regulation (EU) 2024/1252 (Article 27) obligates operators of extractive waste facilities in each EU Member State “to provide to the competent authority a preliminary economic assessment study regarding the potential recovery of critical raw materials, from waste stored in their facilities by 24 November 2026. The study shall at least include an estimation of the quantities and concentrations of critical raw materials contained in the extractive waste and in the extracted volume and an assessment of their technical and economic recoverability. Operators shall specify the methods used to estimate those quantities and concentrations”.
The transition of mineral waste to an asset for the re-mining and recovery of CRMs requires representative sampling and appropriate data processing methods to assess its economic potential [9]. Tailing deposits are typically low-grade deposits of CRMs, i.e., CRMs are present at trace levels. In addition, contaminants such as Pb, Hg, and Cd are present at trace levels in tailings. Thus, an accurate estimation of the concentration of CRMs and associated contaminants is crucial for the safe recovery of valuable minerals and for the implementation of a zero-waste approach to enable the proper reclamation of pond sites.
In cases where materials are regulated at low levels, such as heavy metal content, the analyst must establish whether the analytical method is capable of detecting the analyte at all at the regulated level [10]. The officers who evaluate the conformity of the regulated analytes must also differentiate between statements about an analytical result, which is known, and inferences about the true value, which is not known. It is also essential to understand that there are at least two quite different limits involved in analytical measurement, i.e., the limit of detection (LOD) and limit of quantification (LOQ) [10]. In conformity assessment based on upper limits, the challenge is the increased uncertainty associated with low-level concentration values [11]. The reliable assessment of targeted analytes that belong to the CRM list is complicated by the fact that the CRM concentrations in the Earth’s crust are in the parts-per-million (ppm) range [12,13,14]. According to F. Pittard, “There are no areas that are more vulnerable to such misfortune than sampling and assaying for trace amounts of constituents of interest in the environment, in high purity materials, in precious metals exploration, food chain, chemicals, and pharmaceutical products” [15]. Therefore, the accurate evaluation of the concentration value of the targeted analyte at the lot scale and of its uncertainty has two benefits: (1) triggering investment for CRM harvesting from waste streams and (2) preventing decision risk in the mining for precursors of CRMs or precious metals. Additionally, the application of a conservative approach to conformity assessment can mitigate erroneous decisions due to false positives and false negatives when trace element contents are tested [16,17].
Statistical data analysis in the sampling of grained/particulate solid wastes for trace constituents is often based on mass/discrete probability distributions such as Poisson distribution, double Poisson distribution, or binomial distribution [15,18,19,20,21,22]. In the frame of discrete distributions, a granular waste lot is conceptually modeled as a population of particles, with each one having (or not) a targeted property such as a chemical concentration, a nugget mineral, or a generic property. In this context, sampling from a population of discrete materials (e.g., a solid waste lot) is the random selection of a subset (i.e., a “sample”). The sample/subset is representative if it contains reliably similar proportions between particles of interest and the particles occurring in the batch of materials to be characterized. In the case of tailings and other fine-grained substances, this approach has at least three drawbacks:
(i) The concentration of an analyte in a waste particle is a rather continuous function. This contradicts the hypothesis that some particles contain a constant quantity of analyte while others contain none. Accordingly, discrete distributions are unsuitable for the interpretation of statistical data in cases of fine-grained solid wastes.
(ii) An analyte can exist in different particles as part of dissimilar compounds. This contradicts the assumption that a particle contains a constant quantity of analyte, further rendering discrete probability models inappropriate.
(iii) Discrete sampling (particle by particle) is inappropriate in the case of fine-grained wastes such as tailings and bottom ashes. Instead, incremental sampling is the standard approach used when sampling fine-grained waste dumps [14].
The analytical procedures used for trace elements require sample comminution, i.e., crushing, milling, and sometimes analyte extraction through chemical or physical methods [14,23,24]. A well-prepared sample results in a homogenized analyte distribution, meaning that the analytical results reflect the mean concentration of the aliquot. However, even with homogenization, the dependence of analytical results on aliquot size cannot be eliminated.
Our proposed approach aims to eliminate the unproven hypothesis of the granularity of the analyte (nudged distribution) contained in the targeted lot, which was often adopted in previous studies without supporting evidence [15,20]. To overcome the limitations of conventional approaches, we present a new theoretical model designed to enhance data interpretation for the incremental sampling of fine-grained substances, including tailings, pharmaceutical powders, and food [24].
The key concept of the model is assigning a uniform probability density function (pdf) to the analyte mass in an aliquot and a triangular pdf to the aliquot mass. The rationale for assigning a uniform pdf to the mass of the targeted analyte is based on the evidence that 1 g of fine-grained subsample may contain over a million particles of mixed minerals. Further, an analyte may exist as grains or in an atomic state incorporated into different minerals. ISO 98-3 recommends using a uniform pdf when little information is available about an assessed quantity [25]. These considerations support attributing a uniform random variable to the targeted analyte mass.
It is worth noting that the concentration of the analyte, its uncertainty (standard or expanded), and the aliquot mass are the only data that a laboratory can provide for a sample that has undergone a chain of preparatory operations to produce the analytical specimen, also known as the aliquot.
Laboratory practice shows that the aliquot mass is weighed with high accuracy using a calibrated balance, whose uncertainty is certified. Usually, the calibration certificate of a balance does not specify the pdf which is assigned to the measurand. When a calibration certificate specifies the volume of a flask as 1000 ± 5 mL, it is recommended to use a triangular distribution [26]. Therefore, a triangular pdf is the best choice for the aliquot mass when it is considered as a random variable [25,26].
The theoretical model addresses both the ideal measurement case, where the analytical process does not introduce uncertainty, and the practical one, where the analytical process distorts the results through unavoidable LOQ and measurement uncertainty. The model emphasizes the critical role of mass reduction; i.e., the primary sample mass of the order of kilograms is reduced to an aliquot mass of a few grams. Accordingly, the weighing operation plays a critical role in the modeling of the probability distribution function ascribed to the concentration of a trace element.
The conservative approach for data analysis was applied when surveying iron ore tailings for CRMs through incremental sampling. The concentrations of major, minor, and trace elements of the collected samples were measured using energy-dispersive X-ray fluorescence spectrometry (ED-XRFS). Handheld and benchtop ED-XRFS techniques are frequently used for surveying purposes as they are fast, accessible, and reliable for elemental analysis. There are some other X-ray based techniques that can be used for advanced studies of solid waste, such as X-ray absorption spectrometry and total reflection X-ray fluorescence spectrometry, that have the ability to measure trace levels of elements in the ppb range to provide important information on the local state of the atoms, etc. [27,28]. It is beyond the scope of this paper to discuss the advantages offered by recent developments of these techniques. The reader interested in the application of advanced X-ray-based techniques may find valuable information in dedicated literature such as [27,28].
The raw data processing method for each X-ray-based technique depends on the intellectual property of the producer. The statistical analysis of a suite of results provided by an X-ray technique in a laboratory is performed based on the classical statistical approach [26]. The data analysis in the proficiency testing scheme is carried out both on classical and robust statistics [29].
This study contributes novel insights into the statistical analysis of data when surveying for trace elements, including CRMs, by addressing the entire process of data acquisition, i.e., sampling, subsampling, and laboratory analysis. Furthermore, we introduce the novel idea of disregarding the analyte concentration from its specific carriers; for example, analytes can be found in any particle as atoms in compounds or nuggets, among others. This approach avoids the use of discrete distributions of particles carrying the targeted analyte that are unfit for the interpretation of data when screening for trace elements.
The superiority of the proposed conservative approach over classical and robust statistical data analyses is demonstrated in cases where uniform data distribution is found to be close to the detection limit. Additionally, the decision risk associated with solid waste recycling is highlighted, particularly when traditional statistical analyses lead to overestimated analyte concentrations and underestimated uncertainties. The approach proposed here can facilitate a deeper insight into analyte distribution in targeted batches (lot, stockpile) through the statistical modeling of the entire measurement chain, i.e., sampling and analytical measurement. The model is versatile as it can be applied to any incremental sample of fine-grained substances in cases where the distribution of the analyte in the lot is unknown.
2. Materials and Methods
This study is largely theoretical; therefore, the first part of this section is dedicated to deriving the statistical background of the proposed conservative approach. The latter part discusses the SEM-EDS and XRFS investigations, which provide the data necessary to demonstrate the applicability of the conservative approach.
2.1. Derivation of the pdfs Assigned to Aliquot Mass and to Analyte Mass
The mass concentration of an analyte in a subsample is considered a random continuous variable, denoted as R, defined as the ratio of analyte mass, denoted as Y, to the aliquot mass, denoted as X. Both X and Y masses are considered random continuous variables. According to standard laboratory procedures, an aliquot is taken from a comminuted sample and carefully weighed for analytical measurement. The laboratory practice under the ISO EN 17025 standard imposed high exactness for the aliquot mass measurement [30]. The uncertainty of a laboratory weighing is less than 10−2 g for masses of several grams. In such a case, a triangular probability density function (pdf) can be assigned to the X mass [26].
where m is the mean mass of the aliquot and a is the largest weighing error.
The analyte mass Y is considered a random variable whose value in a sample of X mass is unknown and very difficult to establish through experimental trials. The ISO 98-3 standard [25] recommends assigning a uniform pdf in cases where no reliable information about a random variable exists. In this respect, a uniform pdf is assigned to the analyte mass Y contained in an aliquot.
where b is the maximum mass of the analyte in an aliquot.
2.2. Derivation of the pdf Assigned to True Analyte Concentration in the Aliquot
The analyte concentration in an aliquot is the ratio R = Y/X. The cumulative distribution of R is [31]:
where fX(x) and fY(y) are the pdfs assigned to the variables X and Y, respectively.
Based on Equation (3), the pdf of R, fR(r), is derived as follows [31]:
The upper limit of integration in Equation (4) depends on the r value, as shown in Figure 1; i.e., for r < b/(m + a), u belongs to the interval [m − a; m + a]. In cases where r ranges from b/(m + a) to b/(m − a), (green line in Figure 1), the upper limit of integration is b/r. Therefore, is a branched function defined on the intervals [0; b/(m + a)], [b/(m + a); b/m], and [b/m; b/(m − a)].
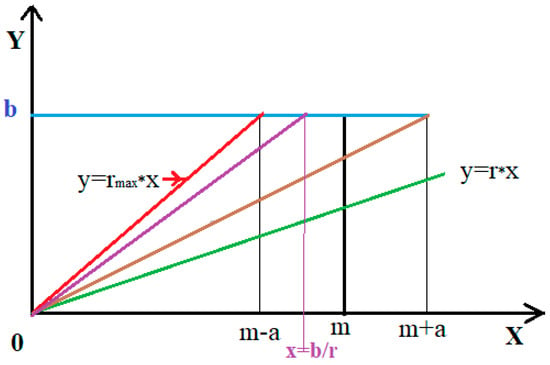
Figure 1.
Schematic drawing of the dependence of the upper limit of integration on the r value.
The value of the R variable assigned to the analyte concentration in a specimen ranges from 0 to b/(m − a). The range [0, b/(m − a)] is divided into 3 intervals—[0; b/(m + a)], [b/(m + a); b/m], and [b/m; b/(m − a)]—because of the different ways of superposing between uniform distribution and triangular distribution. In the range [0; b/(m + a)], R intersects the entire distribution of X, while in the intervals [b/(m + a); b/m] and [b/m; b/(m − a)], R only intersects a part of the triangular distribution of X, as shown in Equations (5)–(7).
In cases where r [0; b/(m + a)], the is calculated as follows:
Equation (5) shows that R is uniformly distributed for r [0; b/(m + a)].
In cases where r [b/(m + a); b/m], the second branch of the pdf of R, denoted as , is calculated as follows:
Respectively,
In cases where r [b/m; b/(m − a)], the third branch of the pdf of R, denoted as , is calculated as follows:
The true analyte concentration is calculated as the mean of R, denoted by , i.e.,
The mathematical expression of the expectance of R is
where ln() is the natural logarithm.
Considering that a/m ≤ 10−2, then the expression of in Equation (10) can be better perceived if its expression is expanded in Maclaurin series depending on the z = a/m variable, respectively:
The expression of the mean value of the analyte concentration in Equation (11) is similar to that of a uniform distribution, i.e., b/(2m), except for a tiny increase of less than 1.7 × 10−5%, depending mainly on the weighing uncertainty.
The variance of the analyte concentration, denoted by σ2, is calculated as
where
The mathematical expression of the variance of the R variable is
Based on the same argument as in Equation (10), we used the Maclaurin series expansion of Equation (14) to obtain a more significant form of , i.e.,
The variance of R is close to the variance in cases where it is uniformly distributed, but it contains a supplementary positive term, which increases its value. The increasing rate is , i.e., in practice, less than 0.05%.
In cases where z ≤ 10−2, the coefficient of variation (CV) of R is
The CV value of R is specific to a uniform pdf in cases where the weighing error is less than 10−2 g. Otherwise, CV will be a function of z = a/m, whose derivative is positive; i.e., CV(z) is the minimum for z = 0 and increases as z increases.
The model described above can be applied in the case of an ideal concentration measurement where the laboratory provides an exact concentration value in the range [0, b/(m − a)]. Laboratory practice shows that any analytical procedure is characterized by a limit of detection (LOD), LOQ, an analytical range, and uncertainty of the result estimated as the standard deviation (SD) or expanded uncertainty [10,32,33]. Therefore, the results obtained using an analytical method will be altered to some extent. Therefore, further considerations are necessary to estimate the effects of the laboratory analysis on the resulting values.
2.3. Derivation of the Analyte Concentration with Laboratory Constraints
When the concentration of a sample is measured using an instrumental or wet chemical procedure, the measured value will differ from the true concentration R due to analytical errors and other uncontrollable factors. To account for measurement uncertainty, one can introduce a random variable (error variable) E, provided that its pdf is known. In the case of instrumental analysis (e.g., XRFS, ICP), E is typically considered to be normally distributed due to many influencing factors that contribute to the measurement uncertainty budget. According to the central limit theorem, when the number of influencing factors exceeds 30, then the convolution of their pdfs results in a normal pdf [34,35]. A measurement procedure cannot tolerate large errors; therefore, a truncated normal pdf must be assigned to E, denoted as fE(e) [34,35], i.e.,
where ε is the largest error and KE is the normalized constant, i.e.,
where Φ() is the cumulative distribution function of the standard normal distribution N(0;1).
The variable assigned to the concentration provided by a laboratory that has an LOQ = 0 is
C = R + E
Assuming that the parameters of the pdf of E are known, i.e., σE and ε, then the calculation of the mathematical expression of fC(c) can be obtained based on the convolution method [31]:
where is the convolution operator.
As is the convolution of fR(r) and fE(e) functions, then its characteristic function CC(t) is the product of the characteristic functions assigned to the pdfs of the variables R and E, respectively [31,35]. The characteristic function of variable R, denoted as , is defined as follows:
The is defined in the same way.
According to the convolution theorem, the characteristic function of the C variable is
Based on , the mean of C, denoted as , and the square mean of C, denoted as , are calculated as follows:
The variance of C is
As can be observed in Equation (25), a measurement process that introduces errors with a truncated normal distribution does not affect the mean value of the true concentration (R), but it increases the variance of the true concentration (.
The measurement process imposes a constraint on the analytical domain [q, Q], where q is the minimum measurable value and Q is the maximum measurable value of the specific procedure. In practice, q can be considered equivalent to the LOQ. Consequently, R values ranging from 0 to LOQ cannot be reported for a given analytical method. When an analyte concentration cannot be quantified with a certain confidence level, it is reported as less than a q value, which is frequently improperly named the “lower limit of detection” [36]. Hence, the measurement procedure implies the truncation of the , i.e., the left side of the distribution is removed in the interval [0, q]. The pdf of the truncated C variable, denoted as g(c), is
The truncation caused by the analytical procedure will alter the mean concentration and variance calculated based on the analytical data. As an example, in cases where is supposed to be uniform in the range [0, b/m], the expectation of g(c) is
Equation (27) shows that the mean value of a trace concentration (some ppm) obtained based on measurement results is greater than its true value with 0.5 x q, which is 0.5 x LOQ. If the LOQ is 4 ppm and the averaged value is 6 ppm, then the true value of the mean is 4 ppm, i.e., the relative error is 50%.
The variance of g(c), denoted as s2, decreases.
The decrease in the variance of g is caused by the cancelation of the very low values of C equivalent to shortening the spreading range of C.
The truncation of C values introduces an additional risk in the decision making regarding CRM recovery, as it creates a positive confidence by falsely increasing the concentration mean and decreasing its uncertainty.
An exact mathematical treatment of the truncation effects caused by the LOQ of the analytical method using the above derived expression is beyond the scope of this study. However, an approach is proposed to overcome this drawback. Suppose a set of N specimens is measured under reproducible conditions in a qualified laboratory and the maximum value, cmax, is obtained. The range [0, cmax] can be divided into n intervals, n = [cmax/q] + 1, where [cmax/q] is the integer part of cmax/q. Subsequently, a histogram of the results should be constructed using n bins, each with a width of q. Data reported as lower than the “limit of detection” are assigned to the first bin. If a statistical test confirms that the data are uniformly distributed, the concentration of the targeted analyte is uniformly distributed in the measured specimens. Therefore, the model proposed in this paper can be applied for conservative data analysis; i.e., the true mean and its standard deviation should be considered as follows:
In cases where the histogram shows data clustering, then another distribution of the analyte should be identified.
2.4. Sample Preparation and Characterization
The old and abandoned Teliuc tailings pond in Romania was explored with the aim of screening for the presence of certain CRMs (Figure 2). The pond is located at 45°44′08″ N 22°53′01″ E and has an area of approximately 35 ha. The Teliuc pond contains approximately 5.0 × 106 m3 waste, resulting from iron ore processing through flotation. A large area of the Teliuc pond surface (Figure 2) is not covered by vegetation. However, this pond still pollutes the surrounding area, at least with flying dust. Additionally, it pollutes the soil and underground water as heavy metals leach into the environment when it rains. Screening for CRMs in the tailings was suggested by previous literature reports [37,38]. We collected 40 samples from across the surface of the dump. The full characterization of the tailings is beyond the scope of this study, as we only address an example of how to apply the proposed data analysis model to the evaluation of CRM content in the pond.

Figure 2.
Representative images collected from Teliuc tailing pond, Romania: (a) access to the pond; (b) edge with boulders and minor rocks; (c) marginal grass and lack of vegetation on the pond; (d) lunar aspect; (e) detail of lunar aspect; (f) solid lumpy waste.
The gross sample of tailings collected weighed approximately 4 kg. The gross sample was crushed, ground, and milled until a powdered state was obtained using home-made laboratory crushers and grinding mills. The fraction that had been sieved using a 1 mm mesh was coned and then quartered, and a subsample weighing approximately 0.5 kg underwent advanced milling using a ball mill (Retsch GmbH, Haan, Germany). The milling process lasted until the residue on the sieve (65 μm mesh) was less than 10%. The powder that passed through a 65 μm mesh sieve underwent subsampling through coning and quartering, and approximately 50 g of the powder was selected for XRFS measurements. Scanning electron microscopy with energy-dispersive spectroscopy (SEM-EDS) was used to evaluate the tailings’ heterogeneity, in terms of both mineralogy and elemental composition. This information is essential for a deeper understanding of the waste condition and to establish the methods for its adequate characterization. The SEM-EDS observations were performed using a Zeiss EVO 50 XVP (Carl Zeiss Microscopy GmbH, Jena, Germany) equipped with an LaB6 electron gun and an EDS accessory from Bruker. The oxide and elemental concentrations were measured through a Xepos ED(P)-XRF spectrometer (SPECTRO Analytical GmbH, Kleve, Germany). The decision to use the ED-XRFS technique was based on its figure of merit, i.e., its cost efficiency ratio. XRFS allows for simple, rapid, and cheap sample preparation, while other approaches such as ICP-MS, ICP-AAS, and AAS require a complicated sample preparation process, such as sample dissolution or digestion, that may introduce a number of additional chemicals [38].
The aliquots for XRFS measurements were prepared as pressed pellets. The pellets contained 7.25 g of tailings. The XRF spectra were processed with the TurboQuant Pellets analytical program.
The pond contains mostly fine-grained tailings and granular and lumpy minerals (Figure 2 and Figure 3).

Figure 3.
Images of incremental sampling: (a) sampling from a depth of 50 cm; (b) fine waste sample; (c) coarse waste sample.
3. Results and Discussion
Assessment of the Tailings’ Heterogeneity at the Micro Scale
The particle size and morphology in the tailings’ body varied in unpredictable ways, as Figure 4 shows.

Figure 4.
Representative SEM images of the sampled tailings: (a) image of fine particles; (b) image of an aggregate of particles; (c) image showing a rugged surface morphology of tailings; (d) image specific to crystalline particles.
The SEM images reveal aggregated particles that appear amorphous (Figure 4a–c). Figure 4d shows the presence of particles with crystalline shapes. The point-specific EDS analysis performed on the tailings depicted in Figure 4 indicates chemical heterogeneity at the micro scale (Figure 5).
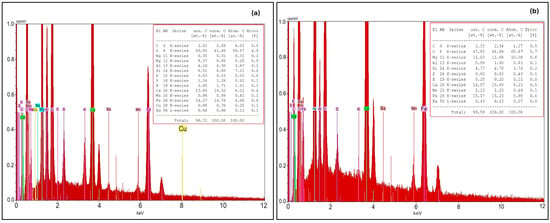
The EDS analysis in Figure 5a shows concentration values that are significantly different from those in Figure 5b. Notably, U is measured in the second specimen (Figure 5b), while in the first one (Figure 5a) it is undetected. These findings from the SEM and EDS investigations support the hypothesis of assigning uniform distribution to the quantities of trace elements in the tailing aliquots.
The XRFS measurements yield results that must be interpreted as mean values at a scale of approximately 1 Kg, as the collected sample was homogenized prior to subsampling the aliquot used for testing. The XRFS results include both major and minor components of the tailings, as presented in Table 1, which lists the results for aliquots no. 1 and no. 22. These aliquots were randomly chosen to ensure that there was no bias regarding the XRFS analyses.

Table 1.
Representative XRFS test report for aliquots no. 1 and no. 22 from the sampling set of 40 samples.
The analytical range of the Xepos instrument covers many of the CRMs (V, Ga, Ge, Rb, Y, Nb, Mo, Ag, Cd, Sb, Te, La, Ce, Hf, Cs, and Bi) as well as heavy metals (As, Cd, Cr, Hg, Pb, and Se). The XRFS results indicate that these elements are at trace levels in these tailings (Table 1).
Given that the analysis of CRMs in the tailings using XRFS is of greater current interest than that of heavy metals, the application of the developed model for statistical data analysis focused on selected CRMs. For instance, the concentrations of La, Te, and Hf are below their respective LOQ values, while those of Ga, Y, and Sr exceed their respective LOQs. Bi and Ge serve as examples of CRMs whose concentrations fluctuate below and above their LOQ values. To better illustrate the data analysis, Y, Ce, Ge, and Bi were selected. Their measured concentration values in the 40 specimens, along with their associated standard deviation, are presented in Table 2.

Table 2.
Concentration (C) and associated standard deviation (SD) of Y, Ce, Ge, and Bi in ppm, measured through ED(P)-XRFS, for the 40 sampled tailing aliquots.
The histograms of Y and Ce (Figure 6) show that their concentration values have a clustering tendency. The absolute frequency values for each bin in Figure 6a,b indicate that the left-side tails of the histograms are heavier than those on the right. This demonstrates that the empirical distributions of Y and Ce concentration values have smaller values due to the prevalence of the aliquots with lower contents of Y and Ce. The theoretical distribution that can be assigned to the empirical distributions shown in Figure 6 can be assumed as normal, but applying statistical inference to demonstrate the adequacy of normal distribution for the data in Figure 6 is beyond the scope of this study. According to the central limit theorem, the arithmetic means of the Y and Ce concentrations follow normal distributions at N(21.5, 0.3) and N(34.6, 1.2), respectively.
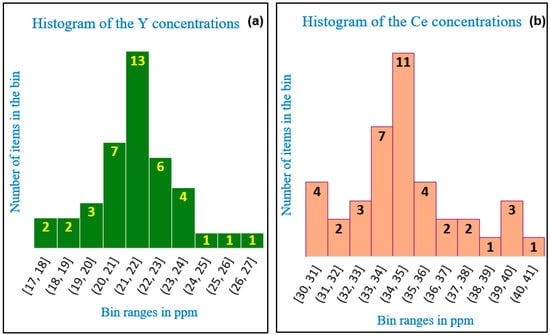
Figure 6.
Histograms of the concentration values in ppm for (a) Y and (b) Ce.
A robust statistical analysis conducted in accordance with ISO 13508 [29] and ISO 5725-5 [39] provided more accurate values for Y (median 21.4, with a standard deviation of 1.3), while for Ce, the median was 34.5 ppm with a standard deviation of 1.8 ppm. The proposed model is not applicable to Y and Ce elemental concentrations, as their concentration values are all above the LOQs and exhibit a clustering tendency. However, for Ge and Bi, the use of the proposed model is mandatory as some of their concentration values fall below their LOQs, and the histograms of the data suggest a uniform distribution of the analytical outcomes (Figure 7).
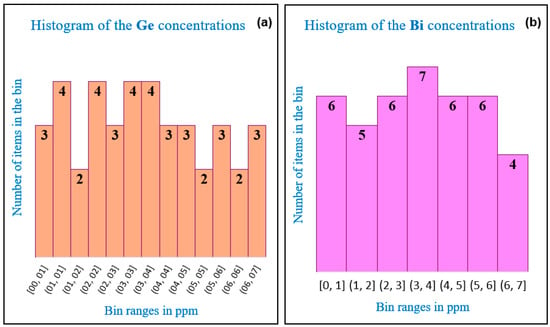
Figure 7.
Histograms of the concentration values in ppm for: (a) Ge and (b) Bi.
The histogram of the concentration values for Ge and Bi do not exhibit a clustering tendency, suggesting that the concentration values are uniformly distributed (Figure 7a,b). Clearly, a larger set of data would better underpin the hypothesis of their uniform distribution, but it would entail a higher cost and significantly more laboratory work.
Investment decisions in the mining of precursors of CRMs and of precious metals are mainly made based on the averaged values of the targeted analyte at the lot scale and on the uncertainty assigned to this value. The averaged value and its assigned uncertainties depend on the statistical approach applied to averaged data, as shown in this paper. Comparative data analyses of the classical, robust, and comprehensive approaches (Table 3) demonstrate that, in the case of uniform distributed entry data, the approach proposed in this paper yields the most reliable values for the concentration mean and its assigned uncertainty. To highlight the differences among the classical and robust statistical analysis approaches and the approach proposed in this paper, we performed classical and robust analyses of the data in Table 2. Classical statistical analysis relies on the arithmetic mean, standard deviation (SD), and relative SD, denoted as RSD, which is akin to the coefficient of variation. Our data analysis approach takes into account a = 0.01 g, m = 7.25 g, and analytical uncertainty equal to the LOQ specified by the TurboQuant analytical software (TurboQuant I version), as specified in Table 3.

Table 3.
The outcomes of statistical data analyses using classical, robust, and conservative approaches.
4. Discussion
The XRFS reported an LOQ = 0.5 ppm for Ge and an LOQ = 1.0 ppm for Bi. Five outcomes were reported to be below the LOQ for Ge, and six for Bi. A robust statistical analysis of the data for Ge yielded a median of 2.2 ppm and a standard deviation of 1.9 ppm, while for Bi, a median of 3.2 ppm was obtained with a standard deviation of 1.9 ppm.
Applying the conservative model proposed in this study, the mean concentration of Ge was calculated as 2.9 ppm, which is higher than that provided by the robust statistical analysis at approximately 0.7 ppm, i.e., approximately 32% greater. For Bi, the conservative approach yielded a mean concentration value of 3.3 ppm, which is very close to the robust estimation value of 3.2 ppm, representing an increase of approximately 3%. The conservative approach revealed higher standard uncertainties in these cases—approximately 3.4 ppm for Ge and 3.9 ppm for Bi—that exceeded the concentration values themselves. In such cases, the data are deemed unreliable for decision making regarding the recovery of Ge and Bi.
The data analysis model we proposed herein produced contradictory results for Y and Ce (Table 3), with their concentrations exhibiting a clustering tendency (Figure 5a,b). This outcome aligns with the limitations of our model, as it is only valid for uniformly distributed data, such as in the cases of Ge and Bi (Figure 6a,b).
Classical statistical analysis overestimates the Ge and Bi concentration values by approximately 59% and 15%, respectively. Similarly, robust statistical analysis overestimates the Ge and Bi concentration values by approximately 43% and 7%, respectively. Additionally, the SDs assigned to the concentration values using classical and robust data analysis are underestimated (Table 3). This evidence demonstrates that both classical and robust statistical analyses of concentration values close to the LOQ of a suite of uniformly distributed results yield higher values than for real (true) ones. Such data analyses may lead to false positive decisions regarding investment in a trace element recovery business. Therefore, when there is evidence that analytical outcomes are uniformly distributed, it is prudent to apply a statistical analysis based on the conservative approach outlined earlier in this paper.
5. Conclusions
A conservative approach was designed for data analysis when surveying for trace elements in fine-grained waste deposits, such as CRMs and heavy metals. Given that even-grained solid wastes are comminuted and milled before chemical and mineralogical analyses, it is evident that discrete distributions are inoperant for statistical data analysis in the screening of solid waste.
The proposed model was designed to cover the gap in statistical data analysis as a fundamental theoretical approach, particularly in cases where the outcomes indicate a uniform distribution of the targeted elemental concentration values.
The theoretical framework encompasses both ideal and practical measurement scenarios. In an ideal measurement case, the analytical process does not introduce uncertainty, while in practical situations, the analytical process distorts the results due to the unavoidable LOQ of the method and measurement uncertainty.
A key finding of this study is the effect of weighing on the derivation of the concentration pdf. The weighing exactness allows a triangular pdf to be assigned to the aliquot mass variable X with a very narrow CV, which effectively behaves as a Dirac distribution relative to the pdf of the analyte mass variable, X.
The conservative approach was applied to a survey of iron ore tailings for CRMs, using incremental sampling followed by XRFS analyses. This application demonstrated the advantages of the conservative approach compared to classical and robust statistical analyses. It was found that classical and robust statistical analyses of concentration values close to the LOQ, for a suite of results that are uniformly distributed, yield higher values and smaller uncertainties. Consequently, classical statistical data analysis may present a false positive picture of a solid waste pile’s contents, potentially leading to an erroneous decision to invest in trace element recovery.
The relative uncertainty in measurement better reflects the precision of the entire analytical chain, including statistical data processing, as its value is smaller as the measurement process works better. Additionally, the relative uncertainties allow measurement procedures to be compared in cases where they are correctly assessed. The data provided in Table 3 highlight situations in which different statistical data processing approaches yield different relative uncertainty values. The proposed approach is deemed the most reliable in cases where the data are uniformly distributed.
The approach we propose offers deeper insight into analyte distribution within a targeted batch (e.g., lot, pile, pond, dump) through the statistical modeling of the entire measurement chain, encompassing both sampling and analytical measurement. The model is versatile and can be applied to any fine-grained substance that is incrementally sampled when the distribution of the analyte in the lot is unknown.
Author Contributions
Conceptualization, A.-L.T., I.P., A.P. and C.U.; methodology, A.-L.T., I.P., A.P., Z.K. and D.F.M.; software, A.P., R.-N.T. and G.I.; validation, I.P., C.U., F.N. and A.C.M.; formal analysis, Z.K., R.-N.T. and D.F.M.; investigation, A.-L.T., I.P., C.U., F.N., G.I. and A.C.M.; resources, A.-L.T., A.P., Z.K., G.I., D.F.M. and A.C.M.; data curation, C.U., F.N., G.I. and A.C.M.; writing—original draft preparation, I.P., C.U., R.-N.T. and G.I.; writing—review and editing, I.P., A.P., R.-N.T. and G.I.; visualization, I.P., Z.K., F.N., R.-N.T. and G.I.; supervision, A.-L.T. and I.P.; project administration, A.-L.T. and A.P.; funding acquisition, A.-L.T., A.P., C.U., Z.K. and D.F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Zbynek Karas was employed by the company DestroKladno s.r.o. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- GACERE. Circular Economy and Solid Waste—Working Paper. 2024. Available online: https://www.unido.org/sites/default/files/unido-publications/2024-06/Working%20Paper_Circular%20Economy%20and%20Solid%20Waste.pdf (accessed on 20 January 2024).
- European Commission DG ENV. E3 Project ENV.E.3/ETU/2000/0058 Heavy Metals in Waste Final Report February 2002. Available online: https://cordis.europa.eu/article/id/15254-heavy-metals-in-waste (accessed on 20 January 2024).
- Document Number C (2009, 3013), (2009/360/EC), Commission Decision, 30 April 2009, Completing the Technical Requirements for Waste Characterisation Laid Down by Directive 2006/21/EC of the European Parliament and of the Council on the Management of Waste from Extractive Industries. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32009D0360 (accessed on 3 March 2024).
- Onwualu-John, J.N.; Uzoegbu, M.U. Physicochemical Characteristics and Heavy Metals Level in Groundwater and Leachate around Solid Waste Dumpsite at Mbodo, Rivers State Nigeria. J. Appl. Sci. Environ. Manag. 2022, 26, 2107–2112. [Google Scholar] [CrossRef]
- Simon, F.G.; Scholz, P. Assessment of the Long-Term Leaching Behavior of Incineration Bottom Ash: A Study of Two Waste Incinerators in Germany. Appl. Sci. 2023, 13, 13228. [Google Scholar] [CrossRef]
- Das, S.; Galgo, S.J.; Aam, M.A.; Lee, J.G.; Hwang, H.Y.; Lee, C.H.; Kim, P.J. Recycling of ferrous slag in agriculture: Potentials and challenges. Crit. Rev. Environ. Sci. Technol. 2020, 52, 1–35. [Google Scholar] [CrossRef]
- United States Department of Agriculture Natural Resources Conservation Service Soil Quality Institute 411, S. Donahue Dr. Auburn, AL 36832 334-844-4741 X-177 Urban Technical Note No. 3 September, 2000. Available online: https://semspub.epa.gov/work/03/2227185.pdf (accessed on 3 March 2024).
- Regulation (EU) 2024/1252 of the European Parliament and of the Council of 11 April 2024 Establishing a Framework for Ensuring a Secure and Sustainable Supply of Critical Raw Materials and Amending Regulations (EU) No 168/2013, (EU) 2018/858, (EU) 2018/1724 and (EU) 2019/1020. Available online: https://eur-lex.europa.eu/eli/reg/2024/1252/oj (accessed on 8 July 2024).
- Dino, G.A.; Rossetti, P.; Perotti, L.; Alberto, W.; Sarkka, H.; Coulon, F.; Wagland, S.; Griffiths, Z.; Rodeghiero, F. Landfill mining from extractive waste facilities: The importance of a correct site characterisation and evaluation of the potentialities. A case study from Italy. Resour. Policy 2018, 59, 50–61. [Google Scholar] [CrossRef]
- Analytical Methods Committee AMCTB No. 92. The edge of reason: Reporting and inference near the detection limit. AMC Technical Brief. Anal. Methods 2020, 12, 401–403. [CrossRef]
- Thompson, M.; Ellison, S.L.R. Towards an uncertainty paradigm of detection capability. Anal. Methods 2013, 5, 5857–5861. [Google Scholar] [CrossRef]
- Wikipedia, Abundance of elements in Earth’s Crust. Available online: https://en.wikipedia.org/wiki/Abundance_of_elements_in_Earth%27s_crust (accessed on 30 March 2024).
- Baldassarre, G.; Fiorucci, A.; Marini, P. Recovery of Critical Raw Materials from Abandoned Mine Wastes: Some Potential Case Studies in Northwest Italy. Mater. Proc. 2023, 15, 77. [Google Scholar] [CrossRef]
- Pencea, I.; Turcu, R.N.; Popescu-Arges, A.C.; Timis, A.L.; Priceputu, A.; Ungureanu, C.; Matei, E.; Nedelcu, L.; Petrescu, M.I.; Niculescu, F. An improved balanced replicated sampling design for preliminary screening of the tailings ponds aiming at zero-waste valorization. A Romanian case study. J. Environ. Manag. 2023, 331, 117260. [Google Scholar] [CrossRef]
- Pitard, F.F. Theoretical, practical, and economic difficulties in sampling for trace constituents. J. S. Afr. Inst. Min. Metall. 2010, 110, 313–321. Available online: https://www.saimm.co.za/Journal/v110n06p313.pdf (accessed on 15 January 2025).
- Araya, N.; Ramirez, Y.; Kraslawski, A.; Cisternas, L.A. Feasibility of re-processing mine tailings to obtain critical raw materials using real options analysis. J. Environ. Manag. 2021, 284, 112060. [Google Scholar] [CrossRef]
- Sarker, S.K.; Haque, N.; Bhuiyan, M.; Bruckard, W.; Pramanik, B.K. Recovery of strategically important critical minerals from mine tailings. J. Environ. Chem. Eng. 2022, 10, 107622. [Google Scholar] [CrossRef]
- Pitard, F.R. Pierre Gy’s Sampling Theory and Sampling Practice: Heterogeneity, Sampling Correctness, and Statistical Process Control, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Minkkinen, P.O.; Esbensen, K.H. Sampling of particulate materials with significant spatial heterogeneity—Theoretical modification of grouping and segregation factors involved with correct sampling errors: Fundamental Sampling Error and Grouping and Segregation Error. Anal. Chim. Acta 2019, 1049, 47–64. [Google Scholar] [CrossRef] [PubMed]
- Hennebert, P. The sorting of waste for a circular economy: Sampling when (very) few particles have (very) high concentrations of contaminant or valuable element. In Proceedings of the 17th International Waste Management and Landfill Symposium, Santa Margherita di Pula, CA, USA, 30 September–4 October 2019; Italy in Proceedings SARDINIA2019. CISA Publisher: Padova, Italy, 2019. Available online: www.cisapublisher.com (accessed on 17 February 2024).
- Hennebert, P.; Beggio, G. Sampling representative waste samples based on particles size. Detritus 2022, 18, 3–11. [Google Scholar]
- Hennebert, P.; Beggio, G. Sampling and sub-sampling of granular waste: Size of a representative sample in terms of number of particles. Detritus 2021, 17, 30–41. [Google Scholar] [CrossRef]
- Ladenberger, A.; Arvanitidis, N.; Jonsson, E.; Arvidsson, R.; Casanovas, S.; Lauri, L. Identification and Quantification of Secondary CRM Resources in Europe, SCRREEN—Contract Number: 730227. Available online: https://scrreen.eu/wp-content/uploads/2018/03/SCRREEN-D3.2-Identification-and-quantification-of-secondary-CRM-resources-in-Europe.pdf (accessed on 19 February 2024).
- Gerlach, R.W.; Nocerino, J.M. Guidance for Obtaining Representative Laboratory Analytical Subsamples from Particulate Laboratory Samples. EPA/600/R-03/027 November 2003, ID: 75176. Available online: https://www.researchgate.net/publication/242671015_Guidance_for_Obtaining_Representative_Laboratory_Analytical_Subsamples_from_Particulate_Laboratory_Samples (accessed on 20 December 2024).
- ISO/IEC 98-3; Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995). ISO: Geneva, Switzerland, 2008.
- Coskun, A.; Oosterhuis, W. Statistical distributions commonly used in measurement uncertainty in laboratory medicine. Biochem. Medica 2020, 30, 010101. [Google Scholar] [CrossRef]
- Terzano, R.; Denecke, M.; Falkenberg, G.; Miller, B.; Paterson, D.; Janssens, K. Recent advances in analysis of trace elements in environmental samples by X-ray based techniques (IUPAC Technical Report). Pure Appl. Chem. 2019, 91, 1029–1063. [Google Scholar] [CrossRef]
- Allegretta, I.; Bilo, F.; Marguí, E.; Pashkova, G.V.; Terzano, R. Development and Application of X-rays in Metal Analysis of Soil and Plants. Agronomy 2023, 13, 114. [Google Scholar] [CrossRef]
- ISO 13528:2015; Statistical Methods for Use in Proficiency Testing by Interlaboratory Comparison, 2nd ed. ISO: Geneva, Switzerland, 2015; pp. 10–12, 32–33, 44–51, 52–62.
- ISO/IEC 17025:2017; General Requirements for the Competence of Testing and Calibration Laboratories. ISO: Geneva, Switzerland, 2017.
- Pencea, I. Multiconvolutional Approach to Treat the Main Probability Distribution Functions Used to Assess the Uncertainties of Metallurgical Tests; InTech, Ed.; Chapter 6 in Metallurgy—Advances in Materials and Processes; IntechOpen: London, UK, 2012; p. 186. ISBN 978-953-51-0736-1. [Google Scholar] [CrossRef]
- Kadachia, A.N.; Al-Eshaikhb, M.A. Limits of detection in XRF spectroscopy. X-Ray Spectrom. 2012, 41, 350–354. [Google Scholar] [CrossRef]
- Badla, C.; Wewers, F. Optimization of X-ray Fluorescence Calibration through the Introduction of Synthetic Standards for the Determination of Mineral Sands Oxides. S. Afr. J. Chem. 2020, 73, 92–102. [Google Scholar] [CrossRef]
- Wikipedia, Truncated Normal Distribution. Available online: https://en.wikipedia.org/wiki/Truncated_normal_distribution (accessed on 25 March 2024).
- Wikipedia, Characteristic Function (Probability Theory). Available online: https://en.wikipedia.org/wiki/Characteristic_function_(probability_theory) (accessed on 25 March 2024).
- Rousseau, R.M. Detection Limit and Estimate of Uncertainty of Analytical XRF Results. Rigaku J. 2001, 18, 33–47. Available online: https://www.researchgate.net/publication/228687395_Detection_limit_and_estimate_of_uncertainty_of_analytical_XRF_results (accessed on 15 January 2025).
- Moran-Palacios, H.; Ortega-Fernandez, F.; Lopez-Castaño, R.; Alvarez-Cabal, J.V. The Potential of Iron Ore Tailings as Secondary Deposits of Rare Earths. Appl. Sci. 2019, 9, 2913. [Google Scholar] [CrossRef]
- Blannin, R.; Frenzel, M.; Tolosana-Delgado, R.; Gutzmer, J. Towards a sampling protocol for the resource assessment of critical raw materials in tailings storage facilities. J. Geochem. Explor. 2022, 236, 106974. [Google Scholar] [CrossRef]
- ISO 5725-5:1998; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 5: Alternative Methods for the Determination of the Precision of a Standard Measurement Method, 1st ed. ISO: Geneva, Switzerland, 1998; pp. 35–36.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).