Study on the Impact of Diaphragm Deformation on Fatigue Performance and Maintenance Strategies in Steel Bridge Decks
Abstract
1. Introduction
2. Real Bridge Test-Based Fatigue Performance Analysis
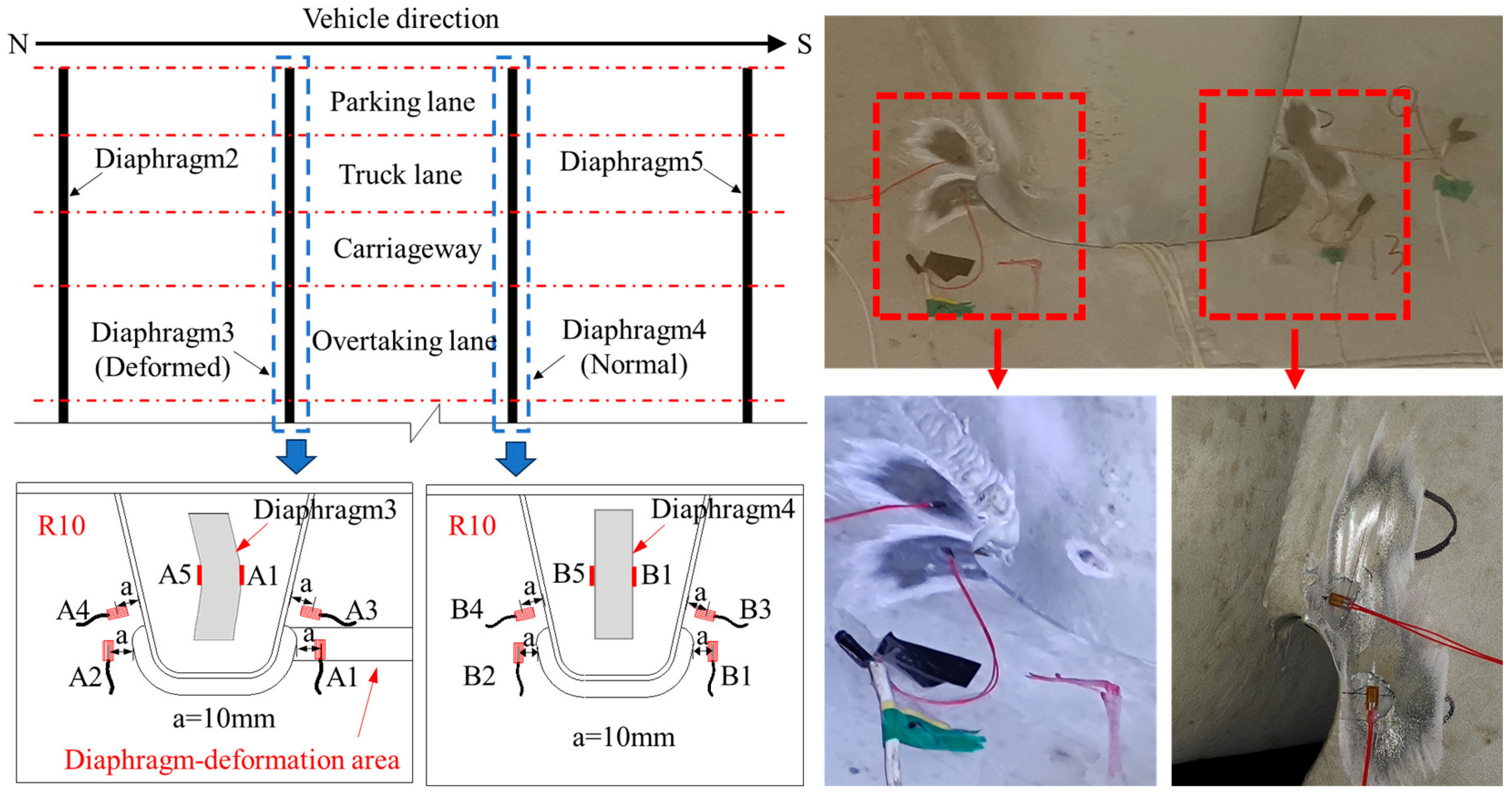
2.1. Type of Diaphragm Deformation
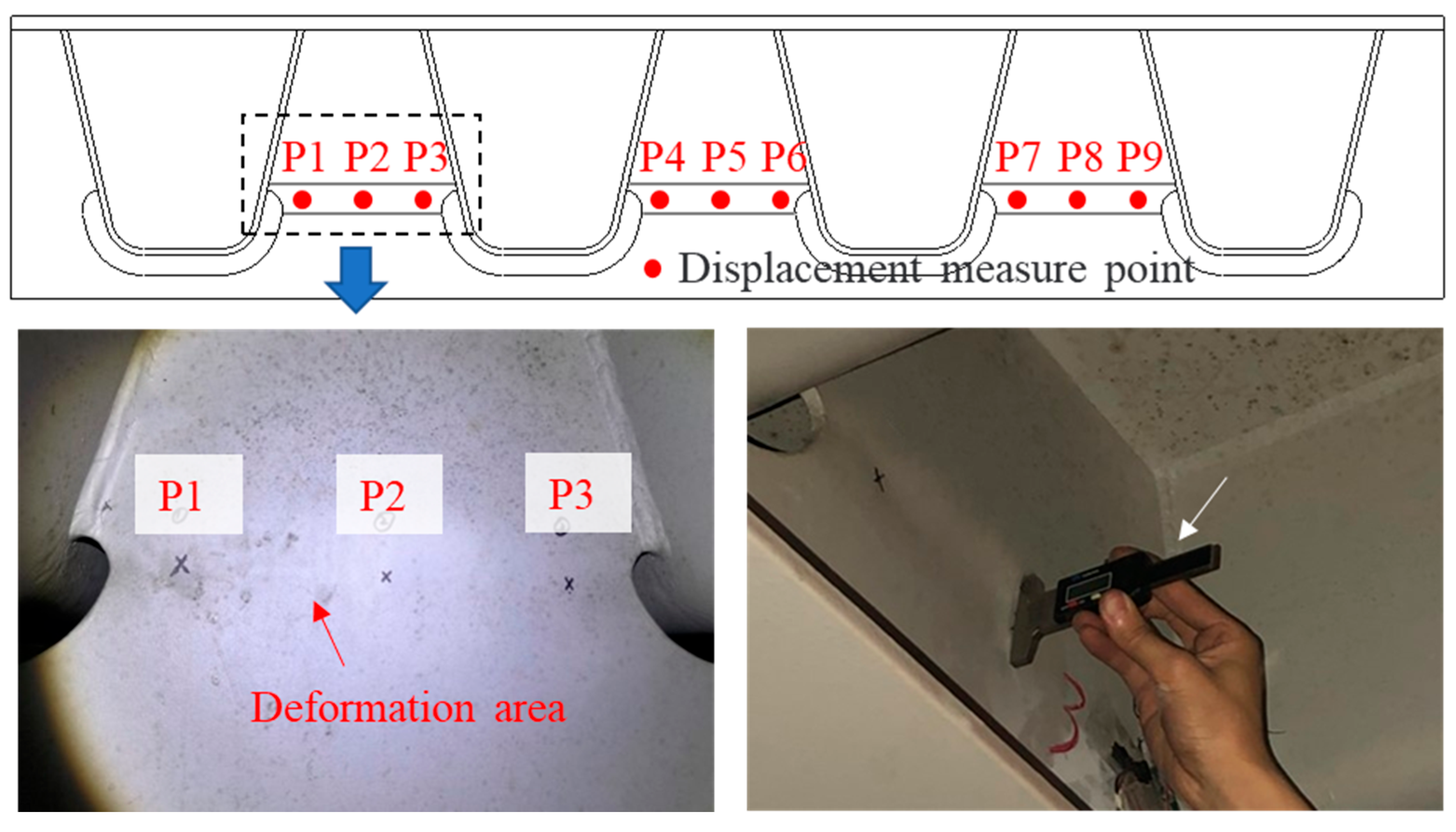
2.2. Stress Test Scheme
2.3. Influence of Fatigue Performance
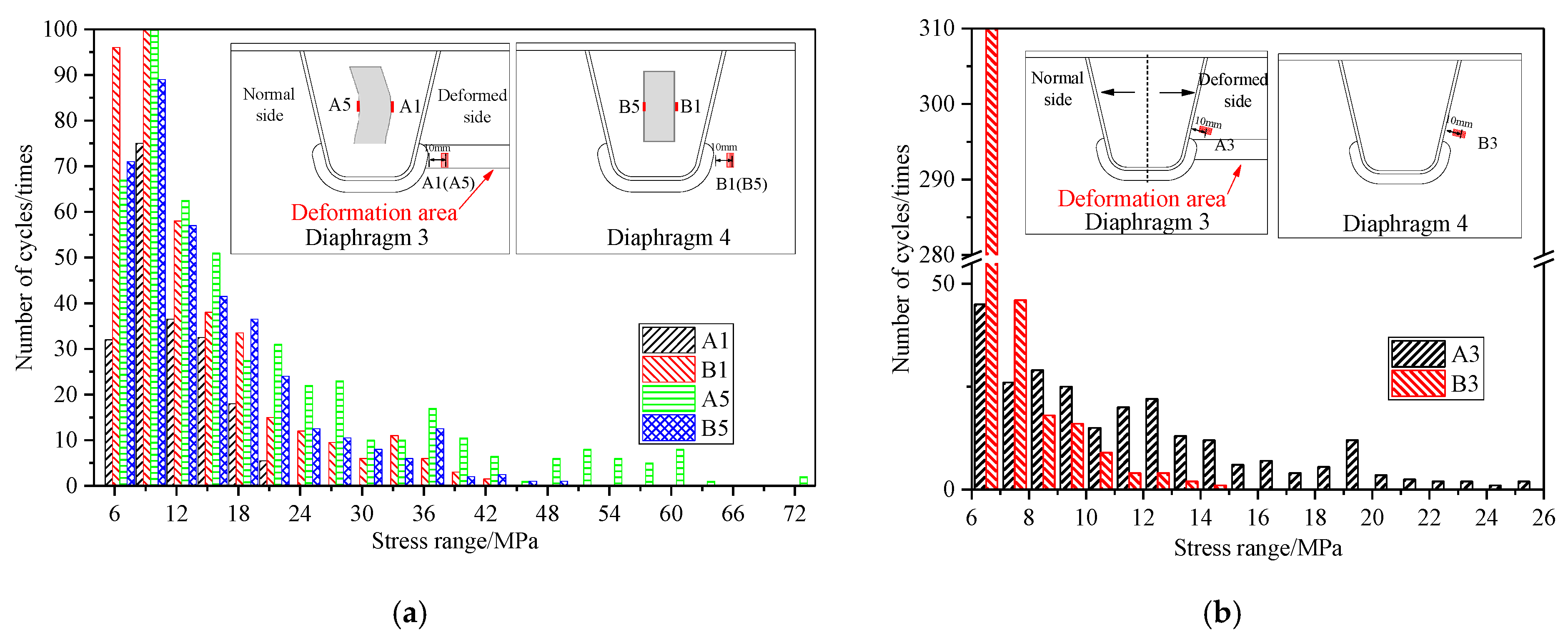
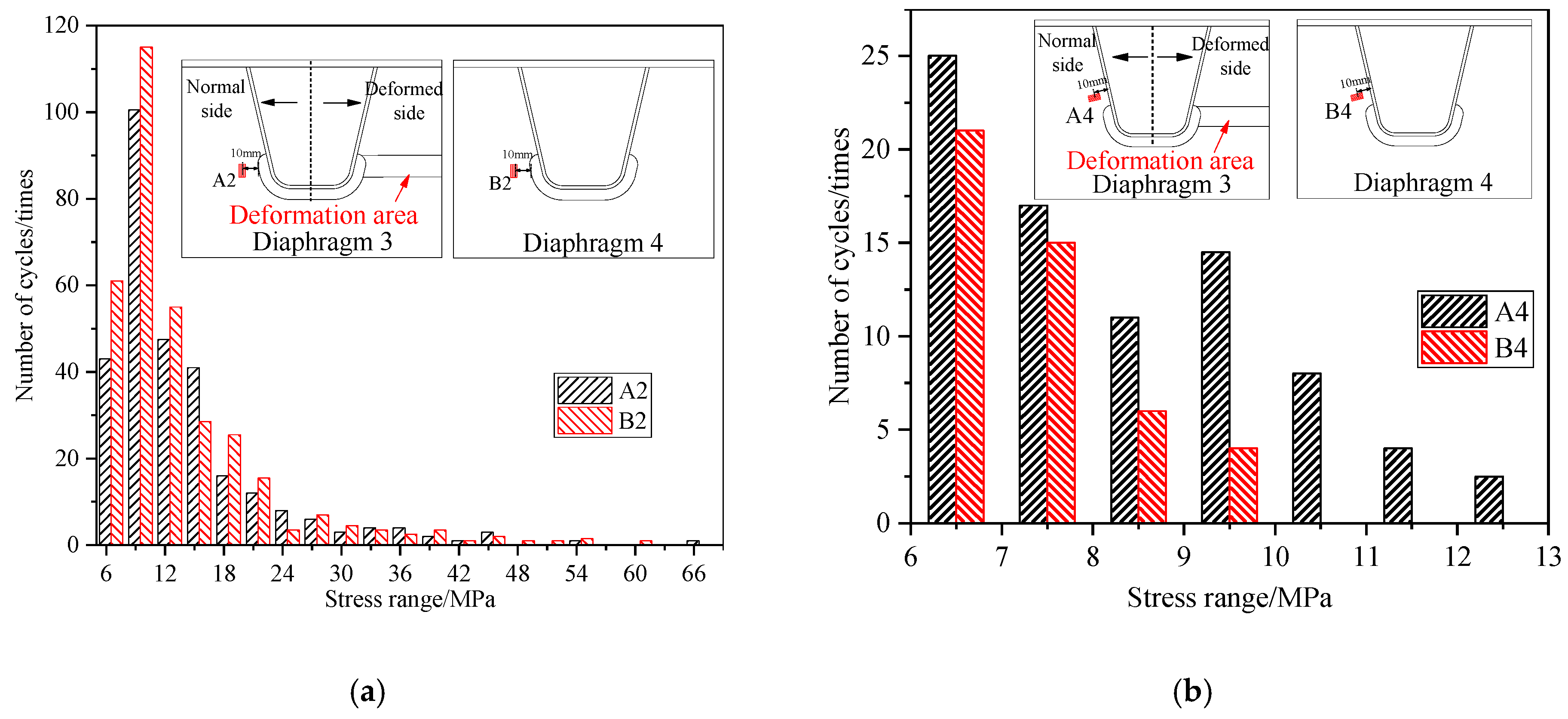
2.3.1. Deformed Region of Diaphragm-3 Collapse
2.3.2. Normal Side of Diaphragm-3
3. Effect on Stress Characteristics by Numerical Simulation
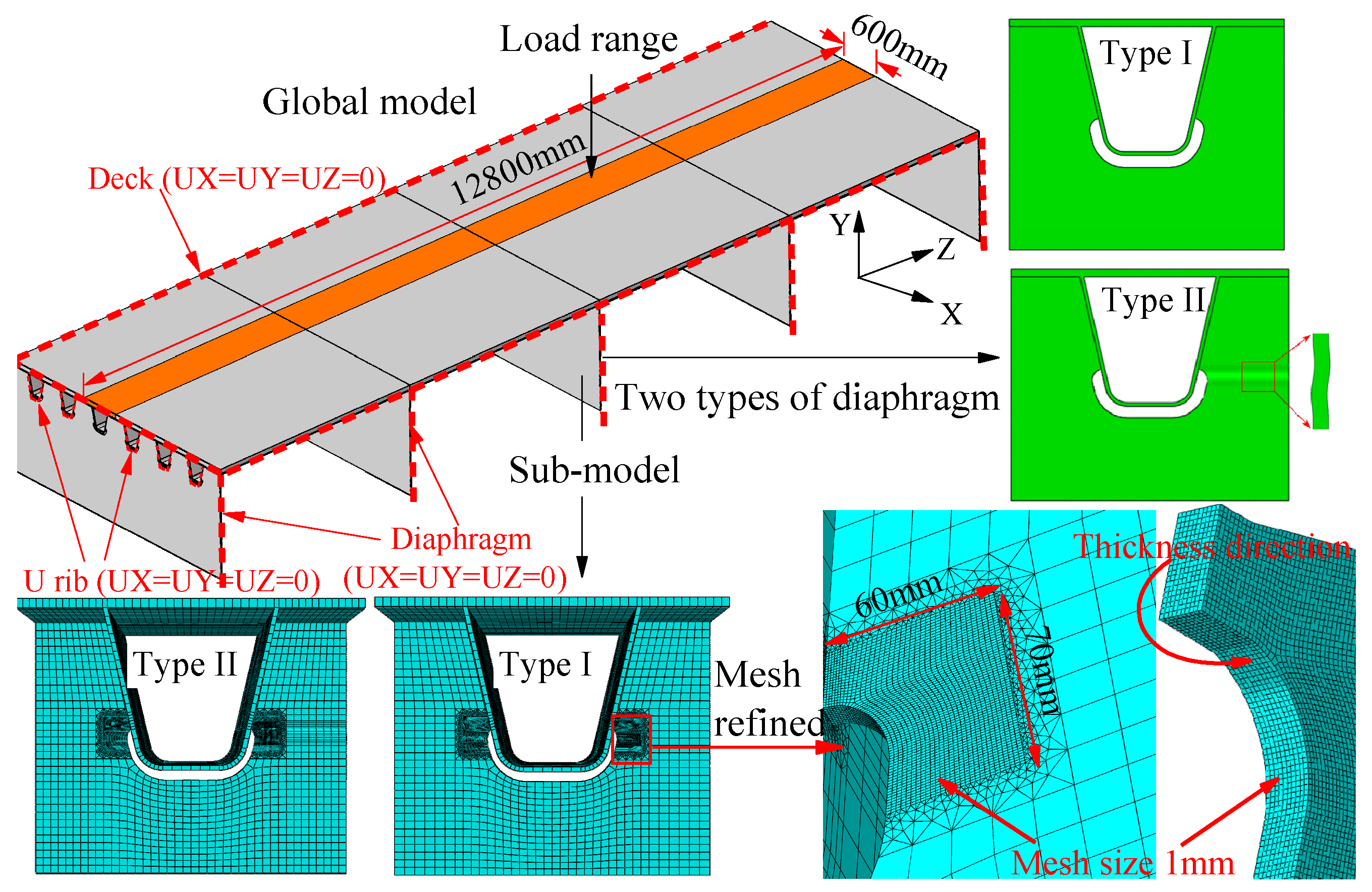
3.1. Finite Element Modeling
3.2. Analysis of the Influence Scope
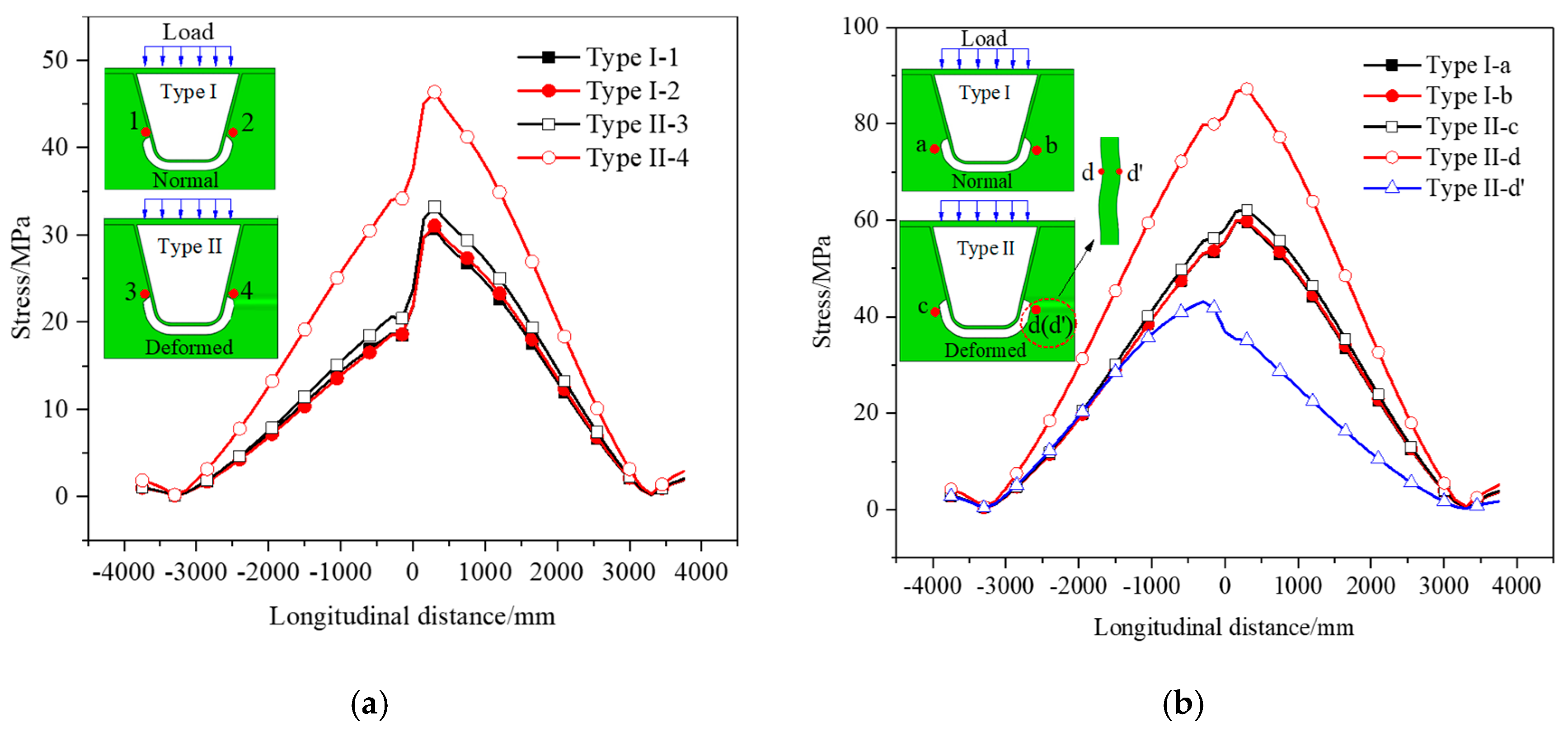
3.3. Analysis of In-Plane and Out-of-Plane Deformation
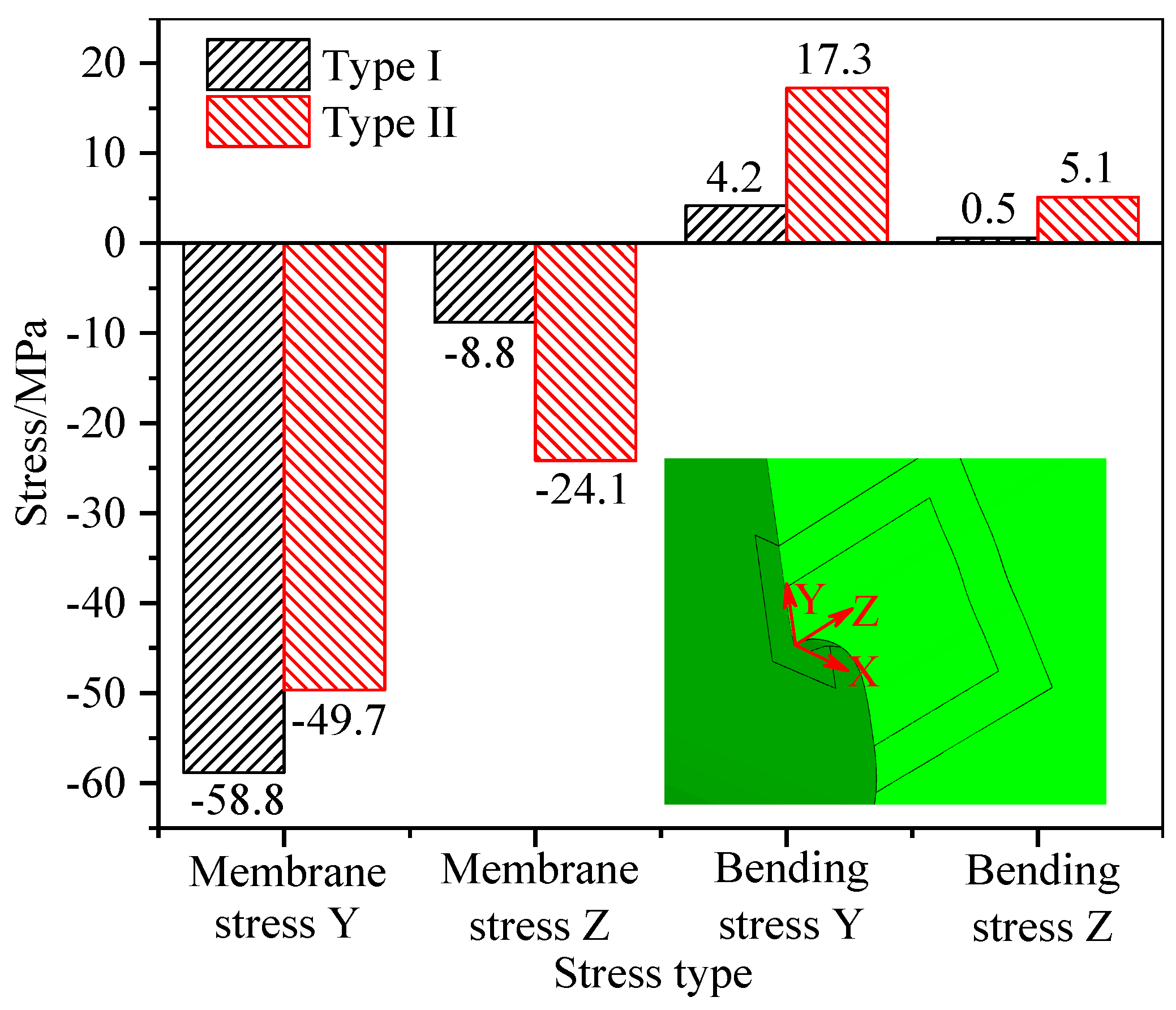
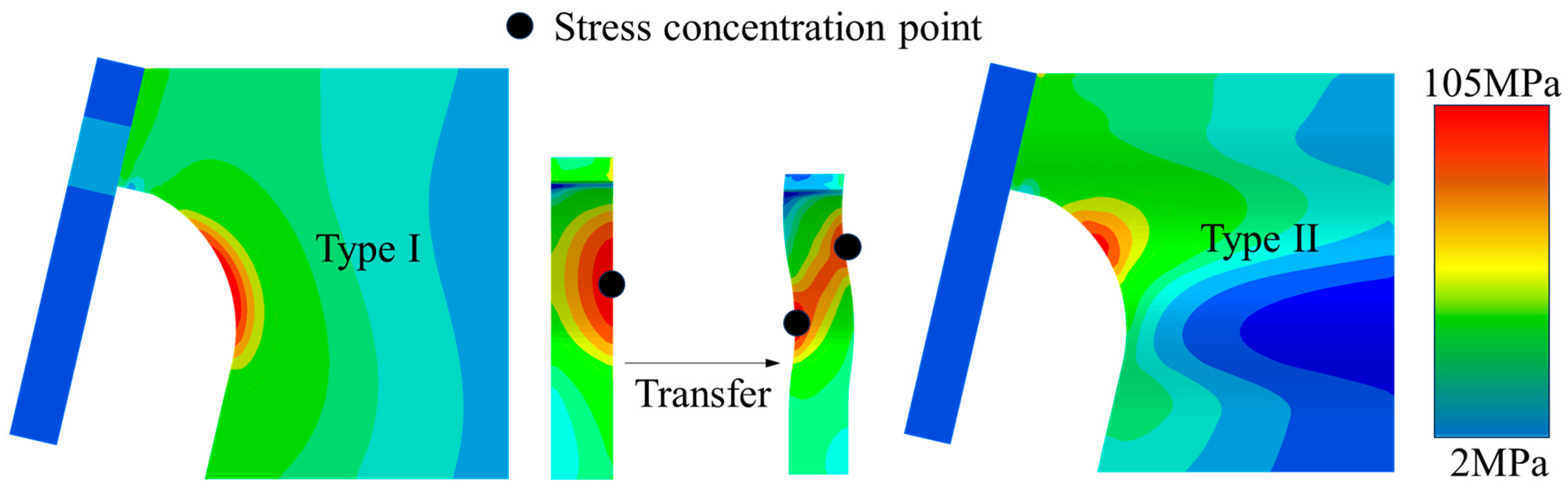
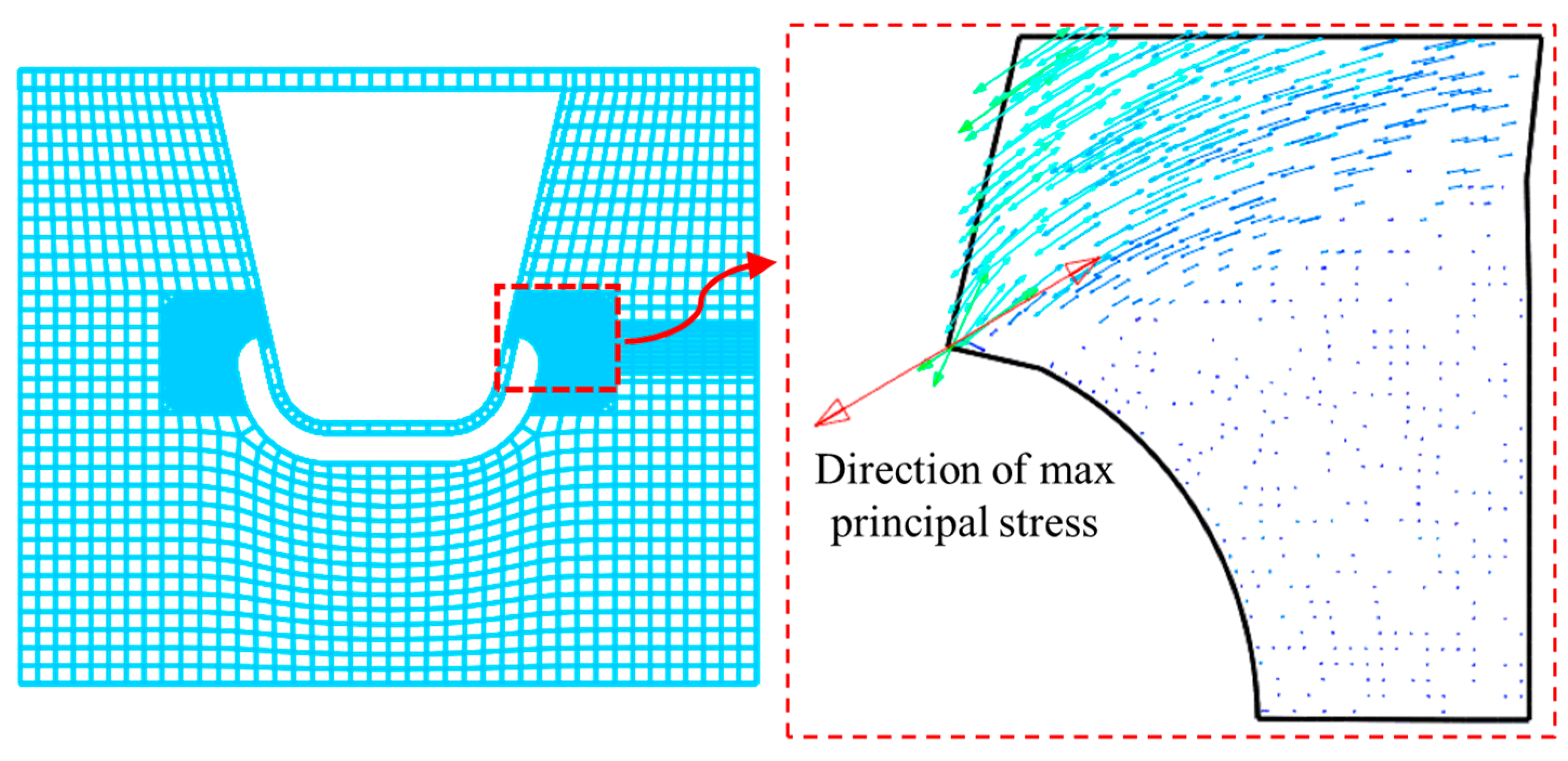
3.4. Analysis of Local Stress Characteristics
4. Maintenance Schemes
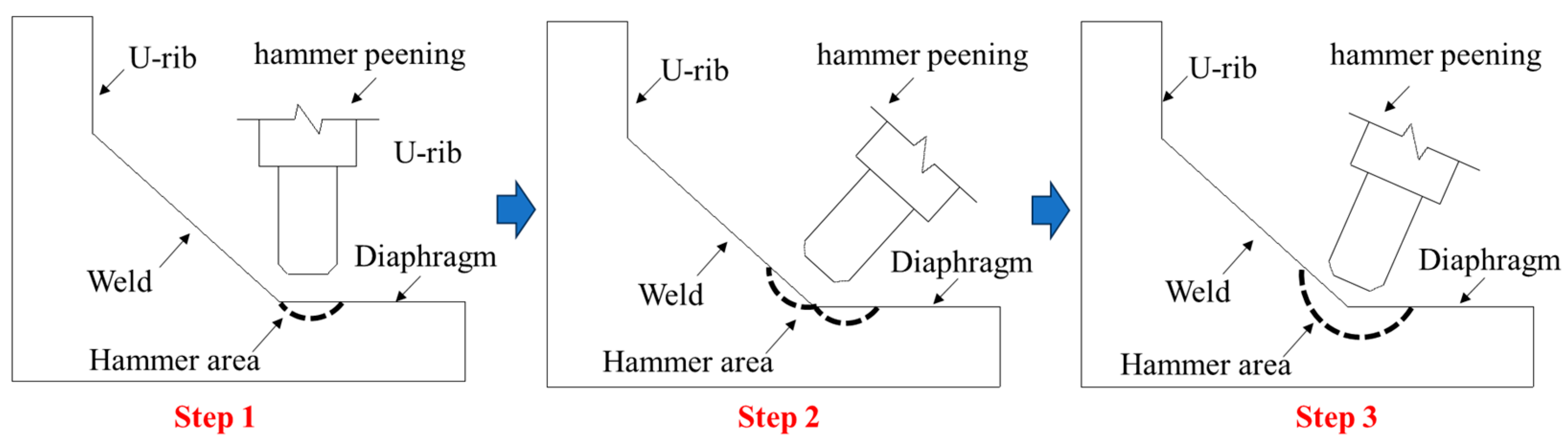
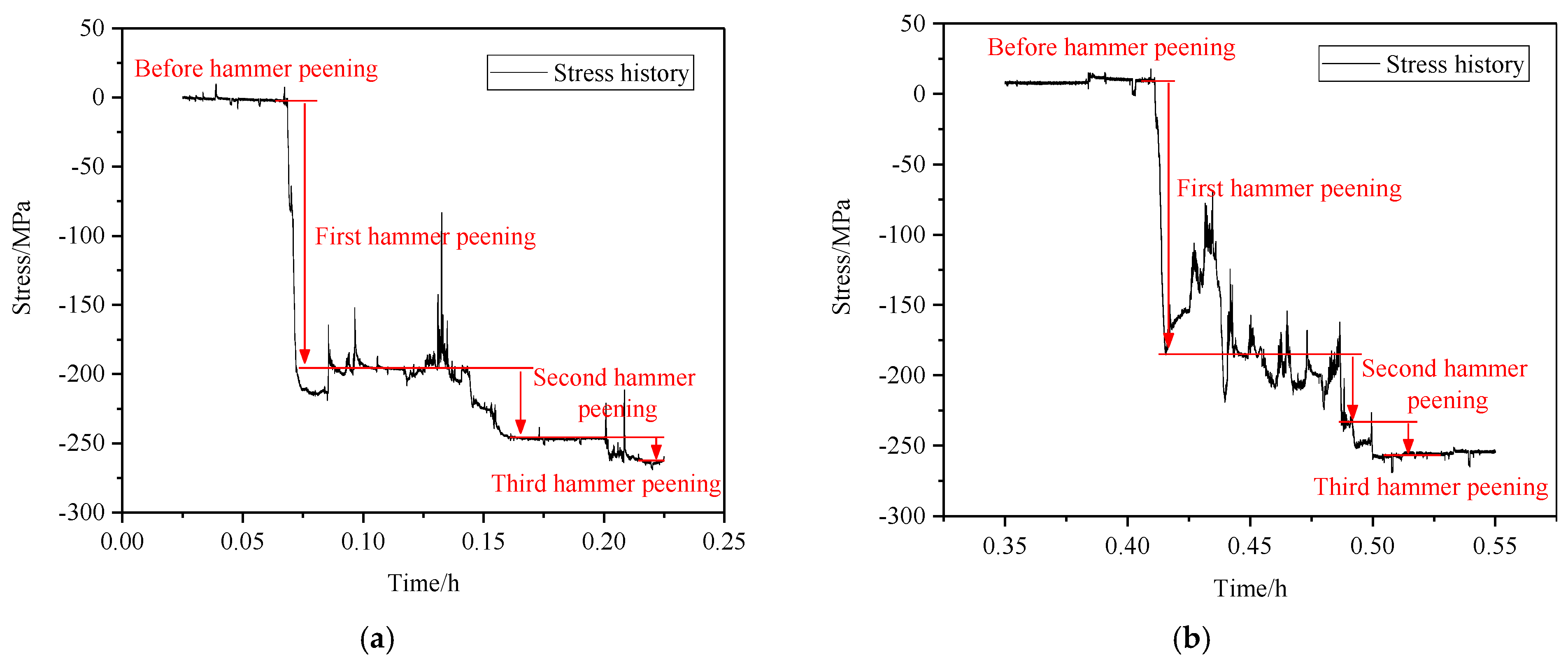
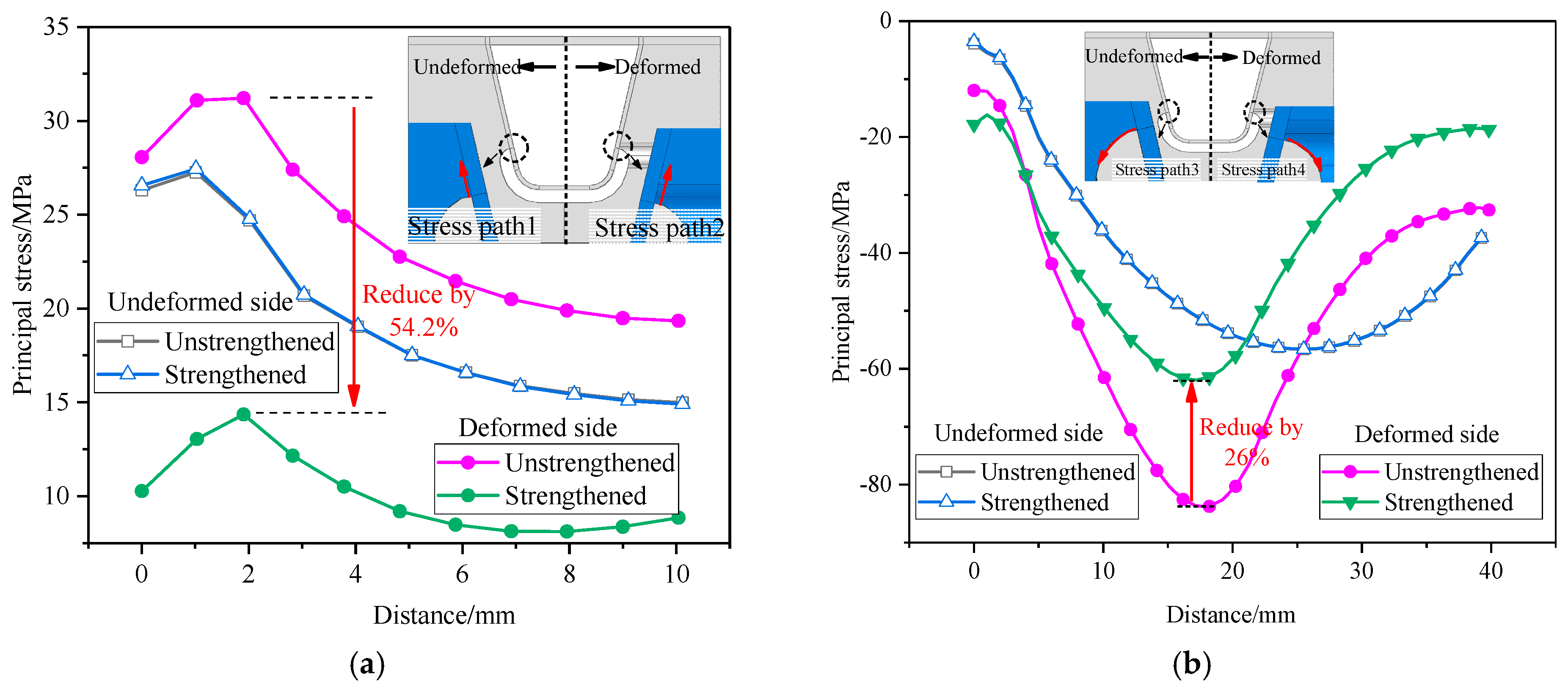
4.1. Hammer Peening Strengthening
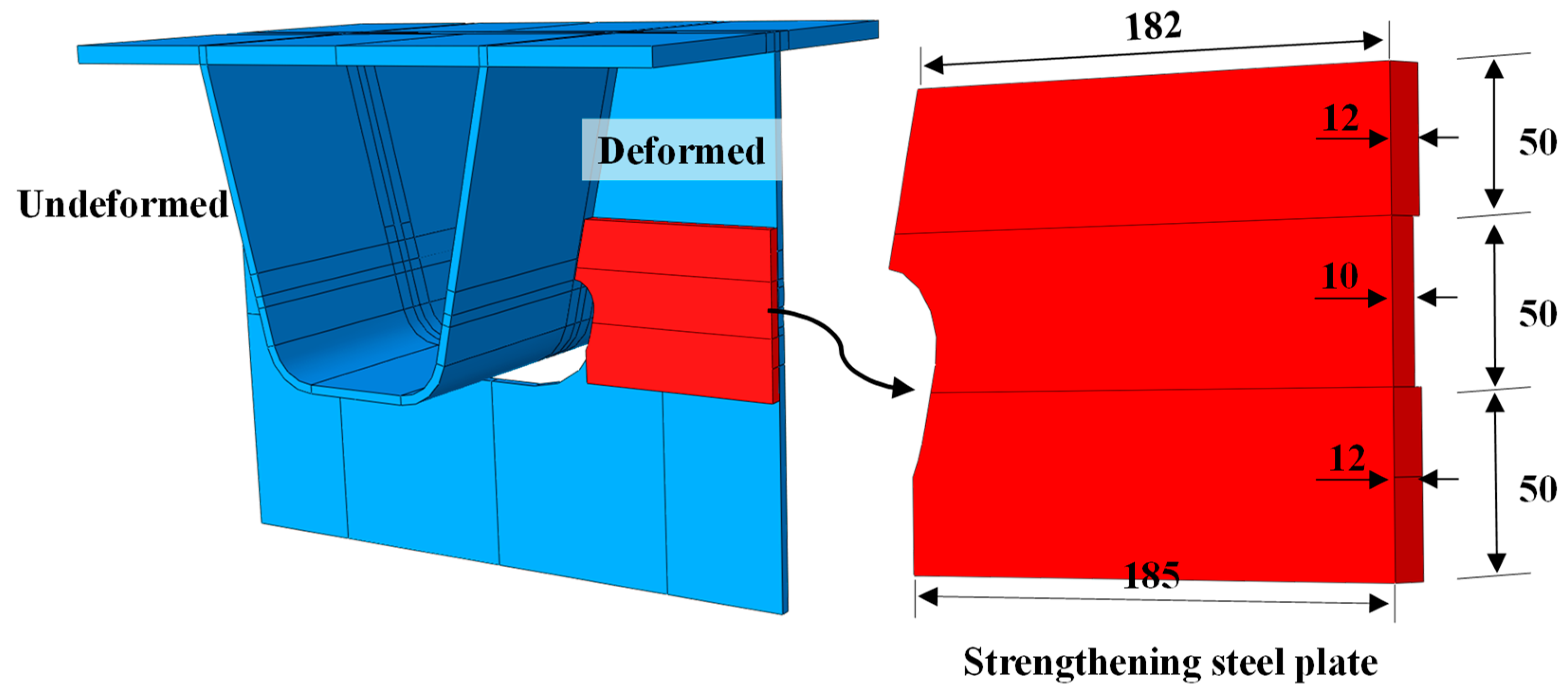
4.2. Steel Plate Strengthening
4.3. Classified Maintenance Suggestions
5. Conclusions
- (1)
- Field measurements reveal distinct stress responses to diaphragm deformation. While the structural stress and fatigue performance at the normal regions of DU welded joints remain largely unchanged, the distorted regions show significant stress amplification, with stress ranges increasing by 50%. These results highlight the importance of prioritizing inspection of distortion-affected areas in operational bridges.
- (2)
- On the distorted side of the diaphragm, stresses in the DU weld and both in-plane and out-of-plane deformations perpendicular to the weld increase significantly. Stress concentrations shift from the arc notch section toward the depressed zone of the diaphragm, accompanied by a rise in both the number of stress concentration points and the simulated stress magnitude, the latter increasing by 72.6%, elevating the risk of DU welded joint cracking.
- (3)
- Based on the mechanical behavior of the deformed region, it is suggested to implement regular inspections and graded maintenance strategies corresponding to the progression of the deformation. For areas exhibiting minor and stable deformation, hammer peening proves effective for enhancing fatigue resistance at this stage. However, steel plate reinforcement is more appropriate when addressing advanced diaphragm deformation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OSD | Orthotropic steel deck |
| DU | Diaphragm-to-U-rib |
Appendix A
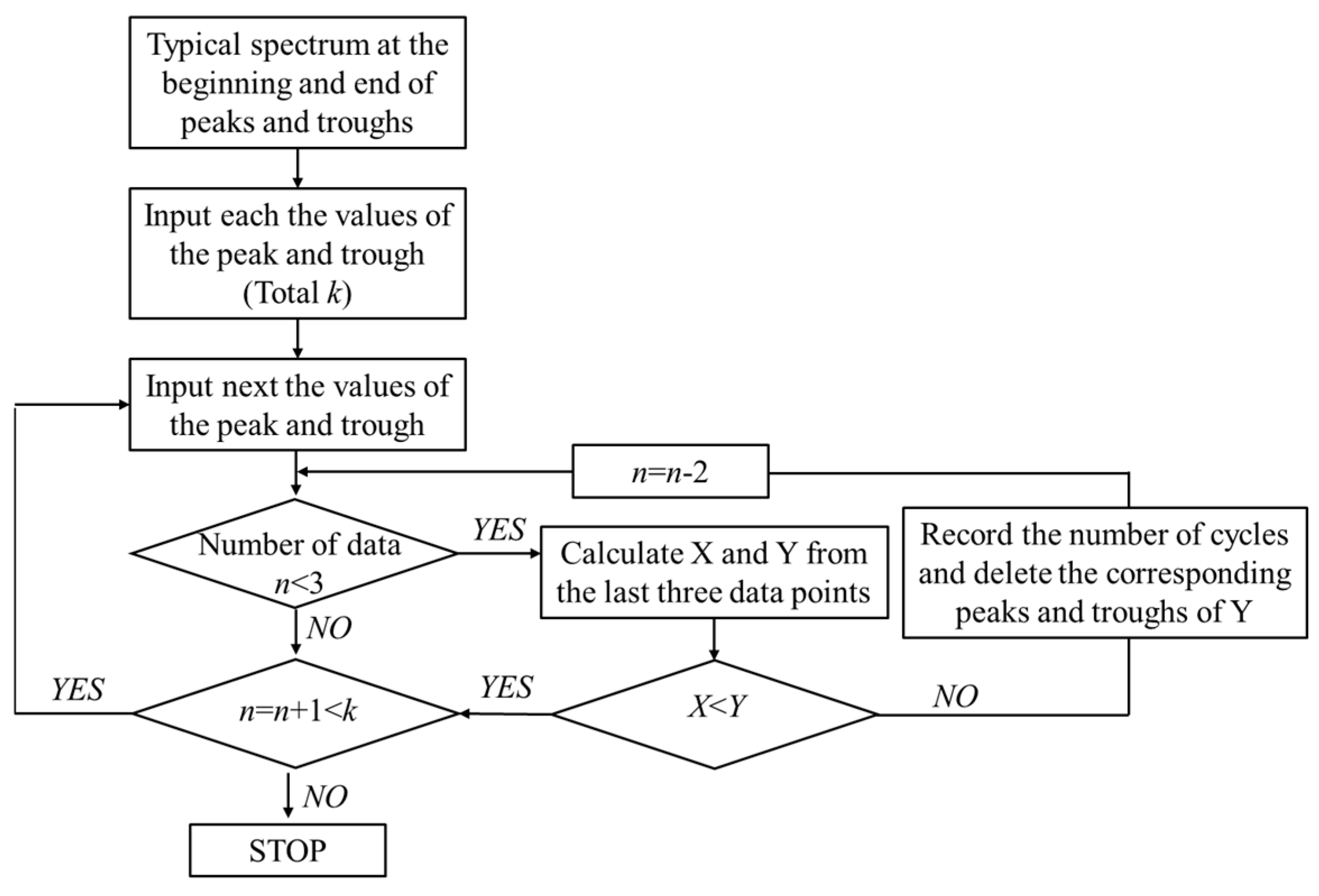
Appendix B
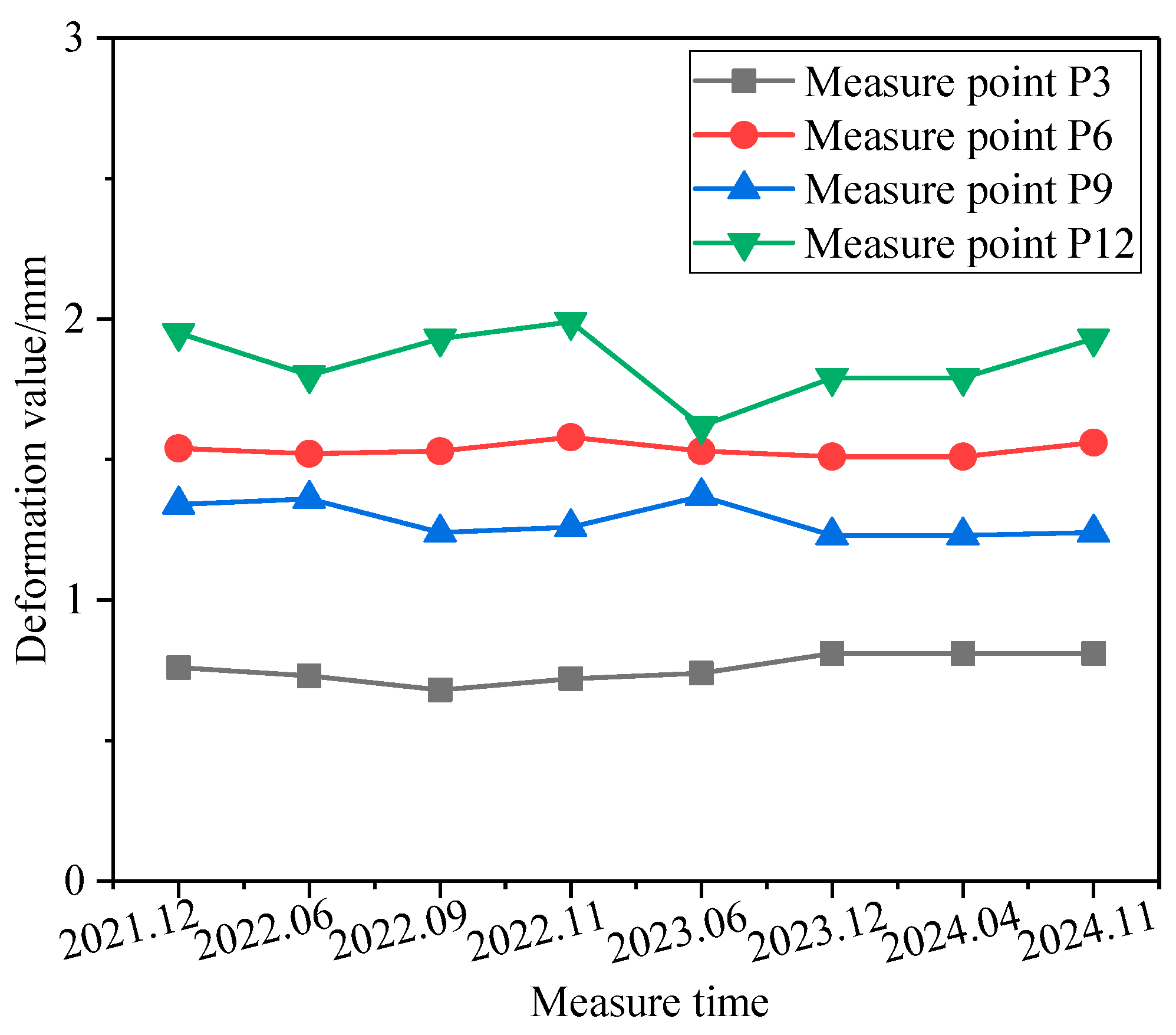
| Displacement Measure Points | Deformation Values/mm | |||||||
|---|---|---|---|---|---|---|---|---|
| 2021.12 | 2022.06 | 2022.09 | 2022.11 | 2023.6 | 2023.12 | 2024.04 | 2024.11 | |
| P1 | 1.28 | 1.26 | 1.30 | 1.32 | 1.36 | 1.30 | 1.30 | 1.36 |
| P2 | 1.42 | 1.28 | 1.62 | - | 1.44 | 1.49 | 1.49 | 1.34 |
| P3 | 0.76 | 0.73 | 0.68 | 0.72 | 0.74 | 0.81 | 0.81 | 0.81 |
| P4 | 1.17 | - | 0.92 | 1.09 | 0.98 | 0.94 | 0.94 | 0.99 |
| P5 | 1.29 | 1.34 | 1.41 | 1.46 | 1.34 | 1.25 | 1.25 | 1.36 |
| P6 | 1.54 | 1.52 | 1.53 | 1.58 | 1.53 | 1.51 | 1.51 | 1.56 |
| P7 | 1.50 | 1.42 | 1.41 | 1.48 | 1.46 | 1.32 | 1.32 | - |
| P8 | - | 1.19 | 1.18 | 1.16 | 1.23 | 1.08 | 1.08 | 1.07 |
| P9 | 1.34 | 1.36 | 1.24 | 1.26 | 1.37 | 1.23 | 1.23 | 1.24 |
| P10 | - | 0.88 | 1.16 | 0.97 | 0.53 | 0.98 | 0.98 | 0.8 |
| P11 | 0.8 | 0.92 | 0.99 | 0.89 | 0.76 | 1.86 | - | 0.82 |
| P12 | 1.95 | 1.80 | 1.93 | 1.99 | 1.62 | 1.79 | 1.79 | 1.93 |
References
- Oh, C.K.; Bae, D. Fatigue test of an advanced orthotropic steel deck system using high performance steel for bridges. Int. J. Steel Struct. 2013, 13, 93–101. [Google Scholar] [CrossRef]
- Liu, J.; Guo, T.; Feng, D.M.; Liu, Z.X. Fatigue performance of rib-to-deck joints strengthened with FRP angles. J. Bridge Eng. 2018, 23, 04018060.1–04018060.14. [Google Scholar] [CrossRef]
- Wang, K.N.; Jie, Z.Y.; Liang, S.D.; Zhuge, P. Fatigue assessment of U-rib full penetration welded joints based on local methods. J. Constr. Steel Res. 2023, 200, 107684. [Google Scholar] [CrossRef]
- Luo, P.J.; Zhang, Q.H.; Bao, Y.; Bu, Y.Z. Fatigue performance of welded joint between thickened-edge U-rib and deck in orthotropic steel deck. Eng. Struct. 2019, 181, 699–710. [Google Scholar] [CrossRef]
- Jiang, F.; Ding, Y.L.; Song, Y.S.; Geng, F.F.; Wang, Z.W. Digital Twin-driven framework for fatigue life prediction of steel bridges using a probabilistic multiscale model: Application to segmental orthotropic steel deck specimen. Eng. Struct. 2021, 241, 112461. [Google Scholar] [CrossRef]
- Srinivasa, C.V.; Kumar, W.P.P.; Kumar, M.T.P.; Bangar, A.R.; Kumar, P.; Rudresh, M.S. Experimental and numerical studies on buckling of laminated composite skew plates with circular holes under uniaxial compression. Mech. Adv. Mater. Struct. 2017, 24, 304–317. [Google Scholar] [CrossRef]
- He, J.X.; Ren, M.F.; Huang, Q.Z.; Shi, S.S.; Chen, H.R. Buckling behavior of compression-loaded advanced grid stiffened composite cylindrical shells with reinforced cutouts. Polym. Polym. Compos. 2011, 19, 357–362. [Google Scholar] [CrossRef]
- Di, Z.; Zheng, X.T.; Wu, T.C. Damage characteristics of open-hole laminated composites subjected to longitudinal loads. Compos. Struct. 2019, 230, 111474. [Google Scholar] [CrossRef]
- Li, X.W. Analysis of Plate Parts Local Damage at the Pivot Point of Steel Box Girder During Construction. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2018. (In Chinese). [Google Scholar] [CrossRef]
- Yan, R.Z.; Zhu, M.H.; Wang, S.; Zhou, J.T.; LIu, X.Y. Damage mechanism analysis for steel box girder of a sea-crossing bridge during temporary storage process and strengthening measures. World Bridges 2019, 47, 80–85. (In Chinese) [Google Scholar] [CrossRef]
- Yao, Y.; Ji, B.H.; Li, Y.F.; Fu, Z.Q.; Chen, Z.Z. Diaphragm splicing deviation in steel bridge deck: Effect on fatigue performance and its preventive measures. J. Perform. Constr. Facil. 2021, 35, 04021008. [Google Scholar] [CrossRef]
- Wang, B.H. Fatigue assessment of the diaphragm-to-rib welded connection in orthotropic steel deck using effective notch stress approach. J. Fail. Anal. Prev. 2015, 15, 65–73. [Google Scholar] [CrossRef]
- Corte, W.D. Parametric study of floorbeam cutouts for orthotropic bridge decks to determine shape factors. J. Bridge Struct. 2009, 5, 75–85. [Google Scholar] [CrossRef]
- Chen, C.Y. Fatigue and Fracture, 1st ed.; Huazhong University of Science & Technology Press: Wuhan, China, 2002; pp. 37–41. (In Chinese) [Google Scholar]
- Amzallag, C.; Gerey, J.P.; Robert, J.L.; Bahuaud, J. Standardization of the rainflow counting method for fatigue analysis. Int. J. Fatigue 1994, 16, 287–293. [Google Scholar] [CrossRef]
- EN 1993-1-9; Eurocode3: Design of Steel Structures, Part 1-9: Fatigue Strength of Steel Structure. European Commission: Brussels, Belgium, 2003.
- Kwon, K.; Frangopol, D.M. Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data. Int. J. Fatigue 2010, 32, 1221–1232. [Google Scholar] [CrossRef]
- Liu, M.; Frangopol, D.M.; Kwon, K. Optimization of retrofitting distortion-induced fatigue cracking of steel bridges using monitored data under uncertainty. Eng. Struct. 2010, 32, 3467–3477. [Google Scholar] [CrossRef]
- Chmelko, V. Cyclic anelasticity of metals. Kov. Mater. Met. Mater. 2014, 52, 353–359. [Google Scholar] [CrossRef][Green Version]
- JTG D64; Specification for Design of Highway Steel Bridge. JTG (Highway China) Transportation: Beijing, China, 2015. (In Chinese)
- Wang, Y.X.; Fu, Z.Q.; Ge, H.B.; Ji, B.H.; Hayakawa, N. Cracking reasons and features of fatigue details in the diaphragm of curved steel box girder. Eng. Struct. 2021, 201, 109767. [Google Scholar] [CrossRef]
- Kainuma, S.; Yang, M.Y.; Jeong, Y.S.; Inokuchi, S.; Kawabata, A.; Uchida, D. Experiment on fatigue behavior of rib-to-deck weld root in orthotropic steel decks. J. Constr. Steel Res. 2016, 119, 113–122. [Google Scholar] [CrossRef]
- Cheng, B.; Cao, X.E.; Ye, X.H.; Cao, Y.S. Fatigue tests of welded connections between longitudinal stringer and deck plate in railway bridge orthotropic steel decks. Eng. Struct. 2017, 153, 32–42. [Google Scholar] [CrossRef]
- Zhu, J.C.; Barsoum, I.; Barsoum, Z.; Khurshid, M. Evaluation of local stress-based fatigue strength assessment methods for cover plates and T-joints subjected to axial and bending loading. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2531–2548. [Google Scholar] [CrossRef]
- Chmelko, V.; Harakal, M.; Žlábek, P.; Margetin, M.; Ďurka, R. Simulation of Stress Concentrations in Notches. Metals 2022, 12, 43. [Google Scholar] [CrossRef]
- Han, T.; He, X.Q.; En, Y.F. Hermetically metal sealing random vibration damage mechanism and fatigue life prediction. Appl. Mech. Mater. 2013, 423–426, 1501–1505. [Google Scholar] [CrossRef]
- Wu, J.; Qiang, B.; Liao, X.X.; Kang, L.; Yao, C.R.; Li, Y.D. Experimental investigation and numerical simulation of welding residual stress in orthotropic steel deck with diaphragm considering solid-state phase transformation. Eng. Struct. 2022, 250, 113415. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, Q.H.; Bao, Y.; Bu, Y.Z.; Luo, Y. Fatigue life evaluation of welded joints in steel bridge considering residual stress. J. Constr. Steel Res. 2019, 153, 509–518. [Google Scholar] [CrossRef]
- Dai, X.H.; Zhang, X.M.; Meng, C.; Guo, Y.W.; Zhu, Y.Y.; Yuanzhou, Z.Y. The Maintenance effect of diaphragm-to-rib fatigue cracks in orthotropic steel deck via steel plate reinforcement. Appl. Sci. 2023, 13, 10368. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Yao, Y.; Li, Z.; Ji, B. Study on the Impact of Diaphragm Deformation on Fatigue Performance and Maintenance Strategies in Steel Bridge Decks. Appl. Sci. 2025, 15, 4245. https://doi.org/10.3390/app15084245
Li C, Yao Y, Li Z, Ji B. Study on the Impact of Diaphragm Deformation on Fatigue Performance and Maintenance Strategies in Steel Bridge Decks. Applied Sciences. 2025; 15(8):4245. https://doi.org/10.3390/app15084245
Chicago/Turabian StyleLi, Chuanxi, Yue Yao, Zhendong Li, and Bohai Ji. 2025. "Study on the Impact of Diaphragm Deformation on Fatigue Performance and Maintenance Strategies in Steel Bridge Decks" Applied Sciences 15, no. 8: 4245. https://doi.org/10.3390/app15084245
APA StyleLi, C., Yao, Y., Li, Z., & Ji, B. (2025). Study on the Impact of Diaphragm Deformation on Fatigue Performance and Maintenance Strategies in Steel Bridge Decks. Applied Sciences, 15(8), 4245. https://doi.org/10.3390/app15084245




