Abstract
Selection bias can cause recommendation systems to over-rely on users’ historical behavior and ignore potential interests, thus reducing the diversity and accuracy of recommendations. Our research on selection bias reveals that the existing literature often overlooks the impact of sentiment factors on selection bias. In recommendation tasks, sentiment bias—stemming from users’ sentiment reactions—can lead to the suggestion of low-quality products to important users and unfair recommendations of niche items (targeted at specific markets or purposes). Addressing sentiment bias and enhancing recommendations for key users could help balance research on selection bias. Sentiment bias is embedded in user ratings and reviews. To mitigate this bias, it is essential to analyze user ratings and comments to uncover genuine sentiments. To this end, we have developed a sentiment analysis module aimed at eliminating discrepancies between reviews and ratings, providing accurate sentiment scores, extracting users’ true opinions, and reducing sentiment bias. Additionally, we have designed a combinatorial function that adapts to three distinct scenarios for bias correction. Moreover, we introduce the concept of dynamic debiasing, where the modeling time is not fixed but varies over time. On this basis, we propose a dynamic selection debiased recommendation method based on sentiment analysis. This paper demonstrates how the three approaches—sentiment analysis for data sparsity, combinatorial functions for dataset optimization, and time-dynamic modeling with inverse propensity weighting—can effectively mitigate selection bias. Our experiments with multiple real-world datasets show that our model can significantly enhance recommendation performance.
1. Introduction
Recommendation systems are essential in addressing the problem of information overload. However, traditional models are susceptible to exposure and selection biases [1], which can lead to suboptimal outcomes. This is due to the limited number of items that users can evaluate and their incomplete understanding of their own preferences. In the context of recommendation systems, selection bias refers to the tendency of users to choose items that do not accurately reflect their true interests or preferences. Importantly, user recommendations may not always be objective and may involve subjective evaluations. Users may exhibit bias toward certain items for various reasons, further influencing the recommendations generated by the system. Consequently, these recommendations may not align with the user’s actual preferences [2,3,4,5].
The presence of selection bias in recommendation systems can lead to several problematic outcomes, negatively affecting their performance. This can result in reduced accuracy and overspecialization of recommendations [6], as they may reflect users’ selection preferences rather than their actual interests. To mitigate selection bias in recommendation systems, we focus on investigating the following three factors influencing selection bias: data sparsity [7], selectivity of user behavior [8], and high demands of IPS methods [9].
First, interaction data in recommendation systems are typically highly sparse because users can only access and interact with a limited number of items. Second, during the process of rating or reviewing a small subset of items, users selectively provide feedback based on their preferences, leading to data imbalance. Due to data sparsity and imbalance, recommendation systems often focus on explicit user ratings while ignoring implicit factors in rating and review data, such as personal sentimental fluctuations, subjective preference differences, and social environmental influences. This directly contributes to the formation of sentiment bias. At present, the utilization of sentiment analysis to remove sentiment bias and alleviate data sparsity represents a promising approach that is unlikely to give rise to modeling difficulties owing to differences in data structures. A subset of researchers categorize reviews into several categories through sentiment analysis (a common method is binary categorization into positive and negative reviews) [10,11]. By analyzing user preferences in this way, more accurate recommendations can be made [12,13]. It is important to ensure that user ratings and reviews of products are obtained simultaneously, as this enables more accurate recommendations to be made on the basis of comprehensive and authentic opinions. However, the current study found the sentiment bias contained in the text, but it is basically in the direction of text processing [14,15], and does not consider that the selection bias in recommendation systems is also affected by the sentiment bias due to data sparsity. Existing studies primarily adopt binary classification methods, which can only coarsely identify positive or negative sentiments and generate labels. These methods fail to align with users’ 0-to-5 rating scales, resulting in poor performance in correcting sentiment bias between ratings and reviews. To address this, we construct a sentiment analysis module that employs dual attention vectors to analyze user reviews and derive fine-grained sentiment scores (0–5) instead of binary labels. This approach more precisely represents the nuanced emotions in user reviews and visually captures sentiment bias between ratings and reviews. Additionally, we design a refined composite function to resolve sentiment bias and alleviate data sparsity.
We then analyze the IPS-based debiasing method. Currently, IPS-based methods have become the cornerstone for selection debiasing. Schnabel et al. [5] introduced the fundamental principle of IPS: reweighting training samples to adjust data distributions and mitigate selection bias. To optimize IPS, researchers commonly apply smoothing techniques and regularization methods [9] to reduce the high variance introduced by IPS, thereby improving model robustness and accuracy. IPS aligns the distribution of offline data with the target learning objective by adjusting sample weights [16]. While existing IPS-based debiasing methods improve recommendation performance compared to approaches ignoring bias, they exhibit significant limitations. These methods often assume the following: (1) selection bias remains static over time and (2) user preferences remain constant despite item usage. However, real-world user data reveal that both selection bias and user preferences are dynamic [8]. When they evolve over time [8], static methods fail to eliminate recommendation bias. To tackle this, researchers have defined dynamic debiasing [2]; as data change over time, models must continuously update to adapt to dynamically shifting user preferences and reflect current bias characteristics. Dynamic debiasing seeks models that explain user behavior across entire time spans, rather than relying solely on current behavior (while considering performance constraints). Previous work, however, assumes static selection bias and only models dynamic user preferences, leading to suboptimal debiasing performance. To address this, some studies enhance factor-based collaborative filtering algorithms by incorporating temporal dynamics [17], arguing that temporal models outperform static ones. Huang et al. [8] theoretically proved that existing debiasing methods become biased when both selection bias and user preferences are dynamic, and introduced a debiasing model under this assumption. A key limitation, however, is that existing collaborative filtering algorithms are static models [18], assuming fixed relationships across time. Moreover, all current IPS-based debiasing studies rely on static IPS methods, which poorly adapt to dynamic scenarios, drastically reducing debiasing effectiveness. Therefore, this work proposes dynamic scene modeling, constructing a dynamic debiasing module that incorporates time-aware inverse propensity scoring to capture dynamically changing user preferences and alleviate the high variance issue of IPS.
Therefore, we propose the design of a debiased recommendation framework (sentiment classification and temporal dynamic debiased recommendation module (SCTD)) on the basis of sentiment analysis and temporal dynamic debiasing. Specifically, the SCTD consists of a sentiment classification scoring module (sentiment classification scoring module, SCS) and a temporal dynamic debiased recommendation module (temporal dynamic debiased recommendation module, TDR).
The main contributions of this paper are as follows:
- (1)
- We propose a recommendation framework based on sentiment bias and temporal dynamic debiasing, namely the SCTD, which utilizes the sentiment scores of reviews and ratings to better capture the user’s true preferences for recommendation.
- (2)
- We focus on capturing dynamic user interests and real-world user behaviors by alleviating data imbalance and sparsity issues through two modules, the SCS and TDR.
- (3)
- We conducted comparative experiments on the Yelp and Jingdong datasets. The experimental results show that our model is optimal in all metrics and has good debiasing performance in the case of sparse data. Meanwhile, it shows that our model is of great significance in alleviating data sparsity in the real world, and provides a concrete implementation solution for solving the problem of dynamic bias in user behavior.
2. Related Work
The selection of debiased recommendations has become a popular research topic. In this section, we review some of the recent literature on selection-biased recommendation methods. This includes how dynamic modeling can mitigate the effects of selection bias and how addressing data sparsity for studying sentiment bias can in turn help mitigate selection bias.
2.1. Dynamic Debiased Recommendation System
To address dynamic scene debiasing, three common methods are typically employed [2]: time window, time decay function, and integration-based learning. The use of time windows and time decay functions for the analysis of recent operations may result in the loss of pertinent information and the introduction of noise. Integration-based learning methods employ a variety of models, each of which considers only a fraction of the total behavioral spectrum. Current studies have improved recommendation accuracy by using multilayer perceptron [19], convolutional neural networks [20], or graph neural networks [21], but all of them ignored the effect of temporal variations on user preferences. To address these issues, one paper introduced a definition of dynamic debiasing [2]. It is essential to recognize that data are subject to change over time and therefore require constant updating with the latest modeling techniques to reflect their current nature. This approach assumes that selection bias is static and that only dynamic user preference scenarios are modeled, which results in the debiasing approach exhibiting suboptimal performance. In response to the aforementioned issue, some researchers have sought to enhance factor-based collaborative filtering algorithms by incorporating temporal features [17]. They proposed that temporal models are more effective than static models. However, a challenge persists, as existing collaborative filtering algorithms are static models, wherein relationships are assumed to be fixed at different times. Relational data, however, evolve over time, exhibiting strong temporal patterns. In a study presented at WSDM ’22 [8], a theoretical assumption was made, and it was proven that existing debiasing methods are no longer unbiased when both selection bias and user preferences are dynamic.
From the above, it follows that the problem we are currently facing is how to mitigate selection bias in recommendation tasks in dynamic scenarios. Currently, methods for solving the problem of selection bias include data filling (data imputation) and reverse tendency weighting (propensity score). The mainstream method for data imputation suffers from empirical errors due to improper designation of the missing data model or inaccurate estimation of the rating value. The performance of IPS-based models depends on the accuracy of their propensities. Therefore, previous studies have used heuristic optimization schemes such as directly populating missing values. These methods are prone to empirical errors due to improperly specified missing data models or inaccurate score estimation. Currently, the use of propensity scores in training recommendation models is a more common method to mitigate selection bias. The challenge with propensity scores is that they directly target IPS-based unbiased estimators and optimize specific losses. Despite this, formulating accurate propensity scores is a rigorous task, and the performance of IPS-based models depends on the accuracy of these scores. Propensity score-based methods have large variances and can lead to nonoptimal results.
To summarize the above, the existing IPS-based dynamic debiasing methods are flawed in that (1) the research hypothesis identifies that the existing selection bias and user preference are static, but in reality both change over time, so the existing debiasing methods are no longer theoretically unbiased, and (2) the IPS-based methods are distorted because of the assumptions of the dynamic scenarios leading to the inability of the static IPS methods to eliminate the recommendation bias, and bring about the high variance problem affecting recommendation model performance. So, in order to improve the accuracy of IPS, we build the TDR module based on dynamic scene modeling to accommodate dynamically changing selection biases and user preferences.
2.2. Sentiment Bias
Sentiment bias refers to the phenomenon where users’ evaluations or ratings deviate from their true feelings due to personal emotions, preferences, or external factors (such as mood fluctuations or social influences). This bias directly impacts the accuracy and fairness of recommendation systems. Therefore, researching how to identify and eliminate sentiment bias from evaluation and review-based models has become a critical topic in the field of recommendation systems [22]. Currently, research on sentiment bias primarily focuses on the following aspects:
- (1)
- Sentiment Analysis and Bias Identification: Using natural language processing (NLP) techniques to analyze user reviews and identify sentiment tendencies and biases. For example, sentiment lexicons, machine learning models (such as SVM or random forests), or deep learning models [23] (such as BERT) are employed to quantify the sentiment intensity in reviews and detect potential over-positive or over-negative biases.
- (2)
- Debiasing Model Construction: Introducing debiasing mechanisms into recommendation models to mitigate the impact of sentiment bias on recommendation results. For instance, causal inference-based methods [24] can separate user emotions from true preferences, thereby generating more objective recommendations. Additionally, some studies attempt to reduce the interference of sentiment bias through adversarial training [25] or multi-task learning [26].
- (3)
- Fairness and Transparency Research: Sentiment bias not only affects recommendation performance but may also lead to unfair recommendations. Therefore, researchers are exploring how to balance fairness and transparency in the debiasing process. For example, explainable AI [27] techniques can be used to show users how recommendations are generated and ensure that different user groups are treated fairly.
Sentiment bias is one of the critical factors affecting the performance of recommendation systems. By gaining a deeper understanding of the current research status of evaluation and review-based models and integrating advanced sentiment analysis and debiasing techniques, the accuracy and fairness of recommendation systems can be significantly improved, providing users with more reliable recommendation services.
Among the methods employed by various recommendation systems, evaluation and rating-based recommendation models have garnered significant attention due to their ability to leverage explicit user feedback. These models primarily rely on user-provided ratings and reviews to predict preferences and suggest relevant items. In general, a rating-based recommendation model describes the attributes and connections between different users and items through a user–item rating matrix in the recommendation system. In the context of large datasets, the user–item rating matrix frequently exhibits characteristics of sparsity and imbalance, a consequence of the selective expression of user preferences. This phenomenon imposes limitations on rating-based models, rendering them susceptible to the cold-start problem and the challenges posed by data sparsity [28]. An area of focus is the incorporation of contextual information into rating-based models. Researchers are increasingly exploring ways to integrate temporal, spatial, and social context to improve recommendation accuracy. For example, temporal dynamics in user preferences are being modeled using recurrent neural networks (RNNs) or attention mechanisms, enabling systems to adapt to evolving user behaviors. In review-based recommendation models, user preferences are usually inferred by methods such as text analysis [29] and sentiment classification [30], and relevant content is recommended based on the user’s review description of the item. A significant direction is the development of hybrid models that combine collaborative filtering (CF) with review-based insights. Traditional CF methods, which rely on user–item interaction matrices, often struggle with data sparsity and cold-start problems. By incorporating textual reviews, these hybrid models can enhance recommendation accuracy and address limitations of pure CF approaches. For instance, neural collaborative filtering (NCF) and attention mechanisms have been integrated to weigh the importance of different review aspects in generating recommendations [13,31].
Based on the above, we can determine that both review-based and rating-based models work well in certain situations, but do not take into account imbalances in real-world review and rating data in uncovering latent sentiment biases [12,13]. Researchers have failed to consider the potential of sentiment analysis to mitigate selection bias. Sentiment analysis used in existing studies all convert user comments into positive or negative labels, with little coupling to the user’s 0-5 rating. And the above models are often based on ratings or comments. The recommendation models based on ratings cannot accurately grasp the real emotions of users through their ratings. And models based on reviews tend to focus only on reviews and lead to the overfitting phenomenon. In the case of sparse user data, the loss of one side of the information in the ratings or reviews will make the model unable to capture the user’s true emotions about the consumer items. Therefore, we construct the SCS module to obtain user sentiment scores with interval values of 0–5 from user comments. We design the combination function and set three operations according to different situations to combine the user sentiment score with the user rating to eliminate the bias between comments and ratings and mine users’ real sentiment opinions, and to alleviate the data sparsity and the resulting selection bias in the data preprocessing stage.
3. Method
3.1. SCTD Framework
The framework consists of two modules, SCS and TDR. SCS is a convolutional neural network used to perform sentiment analysis on imbalanced data to find out the sentiment bias between ratings and reviews and to obtain the sentiment scores. The output of SCS is the sentiment vector from user U. In addition, we use to denote the rating vector, which comes from the columns of the user–item rating matrix. Based on the vectors and derived from the SCS module, we set up a combinatorial function and take and as inputs to obtain an augmented scoring matrix , which is provided to the TDR trainer. The framework diagram of SCTD is shown in Figure 1.
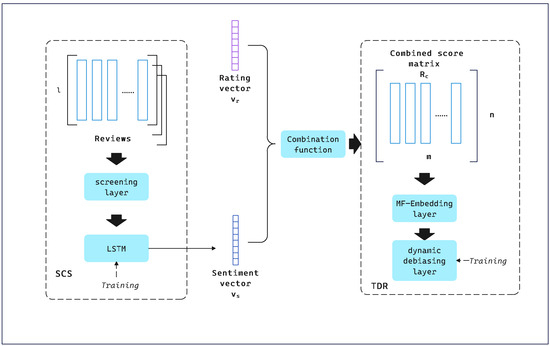
Figure 1.
SCTD framework.
3.2. SCS
Unlike previous dichotomous sentiment analysis tasks, we optimize the output of the sentiment score ratings to fit the scores, ranging from 0 to 5, to fit the corresponding score ratings. Our proposed recommendation system defines U as the set of users and I as the set of items, with U having m elements and I having n elements. There are m users and n items in the user–item matrix . denotes the assessment of item i by user u, while V stands for the complete review text. The set of vectors is the output from the SCS when V is the input.
Our proposal includes four hidden layers within the SCS model. The first of these is the embedding layer, which seeks to translate user comments V into a dense array of feature vectors. The comments of user are arranged into a matrix . Each embedding layer is represented as:
In this context, denotes the count of items evaluated by user u, l signifies the review’s length, and k indicates the latent dimension of the embedded word. Each word in a review is transformed into a K-dimensional vector, and the underlying depiction of user u’s reviews is as follows:
where is an I-dimensional vector and the term of the inner word is a K-dimensional potential vector. represents u’s review of i. ⊙ represents the concatenation operator that combines these vectors into a matrix with dimensions for description. We then input into the second layer, the convolution layer. Attention theory helps us to adjust the weights for each word and each review in the review description matrix differently. g represents the K-dimensional embedding of each word.
and represent the attention vector for each word in the review and the attention vector for each review in the review matrix. First, we denote each word in the review by g and embed an attention factor into g:
where represents the element-wise production of and . The other attention vector focuses on each review in the review matrix:
Subsequently, we feed the output vector from the previous step into the convolution layer to capture contextual features among words. This process can be described as
where and are the weights of the filter function in the CNN. A nonlinear activation function is represented by . The third layer, known as the maximum pooling layer, captures the most crucial information from a variety of contextual features. The max pooling function can be expressed in this way:
The above vectors are resolved to the final layer, the fully connected layer:
The weights in the fully connected neural network are denoted by and , and can serve as either a nonlinear or linear activation function.
Since our goal is to train the network using ratings instead of binary sentiments, we employ softmax as the output function. The SCS process can be outlined as follows:
where consists of .
We use user ratings to train the CNN. The output of the SCS is designed into six classes. The model’s design inherently aligns user ratings (from 0 to 5) with sentiment scores. Finally, the sentiment score vector is calculated, with entries being the sentiment score and a range of (0–5).The specific flow of the SCS is shown in Figure 2.
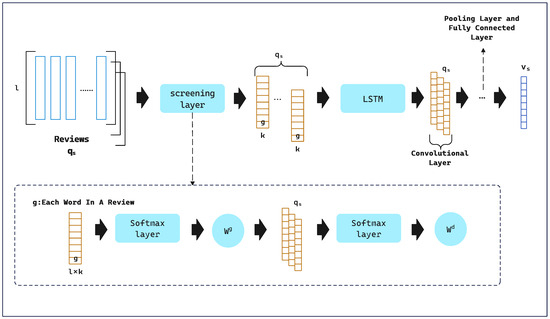
Figure 2.
SCS module.
3.3. Combination Function
Combination function analyzes the rating–comment matrix and captures the sentiment bias between the two by presetting three scenarios. The exact flow of the combinatorial function is shown in the Figure 3.
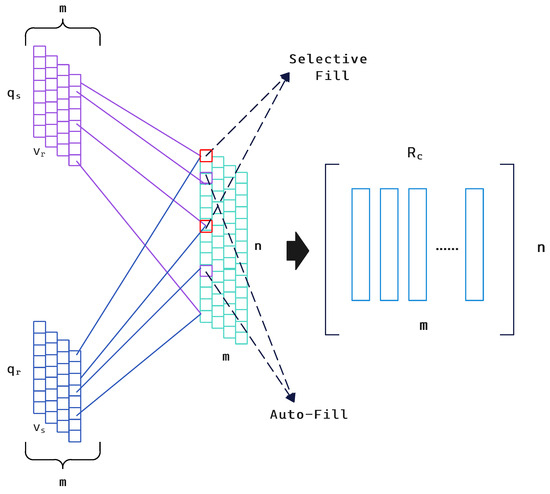
Figure 3.
Combinational function module.
In the combination function, we build the sentiment analysis module and denote each user’s sentiment vector by . We use as the user–item rating matrix, where each column is extracted as a rating vector . We then use a simple but efficient function to build a joint vector with and :
where ⊕ is a combinatorial function of the SCTD. is a -dimensional vector with entry . is a -dimensional vector with entry . is an n-dimensional vector, where equals the number of items evaluated by the user. In practice, ≥ . We assume that = . When a user rates an item and also writes a review, we can obtain the rating via r and calculate the corresponding sentiment score via SCS. We define the difference between and as the opinion bias . We want to enhance expressiveness through reviews and ratings while filtering out useless reviews. Thus, the combinatorial function ⊕ can be generalized to the following three cases.
- Autofill: When the user u only rates or comments one item i, this time can cause gaps in the data and affect the accuracy of the combined function. To avoid this, ⊕ fills or .
- Selective Fill: If the user u has rated and commented on the item i, then a Drop judgment will be made first. If neither the user nor the item is deleted, ⊕ will be filled using a fixed weighted linear function .
- Drop: If , it is not processed. If , ⊕ decreases the user’s sentiment rating for item i. If , the same is not processed. If , ⊕ will remove user u. is the number of deleted comments. and ı are predefined thresholds.
According to the processing corresponding to the above situation, the enhanced rating matrix is constructed, which is expressed by the following formula:
where represents .
3.4. TDR
Traditional debiased recommendation methods are based on static scenarios.
However, traditional recommendation methods with static bias are not unbiased for the current treatment of selection bias in dynamic scenarios. The currently widely used debiasing method uses a static propensity score , which represents the probability that user u observes a particular rating in any time period.
However, this approach ignores the dynamics of selection bias, i.e., these probabilities will vary t in each time period, causing the static IPS estimator to become
Items in collection are recommended to users in the collection . Users have preferences with respect to items, which are generally modeled by a label per user and per item . is a set of time periods. We allow the user’s preferences to change at different time periods . As Equation (12) shows, refers to the static propensity, which refers to the probability that user u observes a particular rating of item i in any time period. In reality, user interaction data are so sparse that it is impossible for all users to rate all items. In Equation (12), the observation metric matrix denotes the ratings recorded for the corresponding time period and the ratings recorded in the interaction data. If , it means that they are missing. When , this means that the ratings of user u for item i in time period t were recorded in the logged data. Compared with Equation (12), the conventional RS debiasing losses are as follows:
where the function L can be chosen according to different RS evaluation metrics. The common mean-squared error (MSE) metric formula is as follows:
In the previous section, we mentioned the standard recommendation loss function and the static IPS-based loss function. Now, we focus on the dynamic selection bias. We set the exact propensity such that the dynamic selection bias can be fully corrected by applying Equation (15) to the evaluation of the predicted scores with reverse weighting:
Equation (15) is applied to the matrix factorization (MF) model. We refer to this method, which combines the MF and time-dynamic debiasing methods, as TDR. Given an observed rating from user u on item i at time t, the MF computes the predicted rating as follows: , where the and are embedding vectors of user u and item i, and , , and are the user, item, and global offsets, respectively. Most importantly, we consider the effect of time on rating prediction and perform dynamic scenario modeling to construct TDR by denoting the time-varying offsets by . In TDR, we construct a dynamic debiasing layer where the number of hidden layers . We use the activation function softmax as the output layer , then the process of TDR can be described as
where represents the tth hidden layer, which is a nonlinear function of the previous hidden layer. represent the parameters of the dynamic debiased layer inside the TDR.
From above, when we train the model, the optimized loss function is as follows:
where G, and H denote the embedding of all items, all offset items, and all users. is the MSE loss function. represents the probability that user u’s rating of item i is observed at time t. We construct the negative log-likelihood (NLL) loss function in order to estimate accurately:
represents the NLL loss for each independent propensity:
4. Experiments
4.1. Datasets
In order to verify the validity of the proposed model, we conducted a number of experiments using datasets from Yelp’s RecSys (https://www.kaggle.com/c/yelp-recsys-2013, accessed on 25 December 2023) and Jingdong (https://re.jd.com/, accessed on 4 January 2024). The Yelp dataset is a comprehensive and widely-used public dataset released by Yelp Inc., designed to support research in areas such as recommendation systems, natural language processing, and data mining. It contains a rich collection of data related to user interactions with businesses, including restaurants, shops, and other services. Its diversity and scale enable researchers to address complex problems and validate models in realistic settings. Because the Yelp dataset is pre-filtered to remove user data with missing ratings or reviews in advance, the sparsity is low. In order to verify the robustness of the SCTD module in the presence of sparse data, we chose the Jingdong dataset for experiments as a supplement to verify the performance of our model. Details of these two datasets are given in Table 1.

Table 1.
The dataset characteristics.
4.2. Parameter Settings
We used 5-fold cross-validation to divide the dataset in the comparison experiments: 80% of the user data are randomly selected as the training set, 10% as the testing set, and 10% as the validation set. We initialized some parameters: word embedding dimension L = 130; learning rate using optimizer Adam = 0.0001; different lengths of filters in SCS (2,3,4); and joint weights in the combinatorial function = 0.6, = 2.0, and = 0.3. The regularization coefficients in the TDR loss function were set to = 0.01 and = 0.001. We also defined a factor of 50 for the fully connected layer in SCS. To reduce overfitting, the fully connected layer uses 0.45. The activation function for the convolutional layer in both SCS and TDR is ReLUs, and the activation function for the output layer and double attention vector computation is softmax.
4.3. Experimental Environment
The specific environment configuration for our experiment is shown in the following Table 2.

Table 2.
Experimental environment.
4.4. Baselines
The following is a description of the models compared in this paper:
- (1)
- Static Average Item Rating (Avg): Avg is a simple recommendation method that calculates the average rating of each item based on historical user ratings.
- (2)
- Time-Aware Average Item Rating (T-Avg): T-Avg extends the traditional average item rating by incorporating temporal dynamics. It calculates item ratings based on recent user interactions, giving higher weight to more recent data.
- (3)
- Static Matrix Factorization (MF): This refers to a conventional matrix factorization model that presumes the selection bias remains constant over time.
- (4)
- Time-Aware Matrix Factorization (TMF) [17]: TMF is an advanced recommendation method that incorporates temporal dynamics into matrix factorization. It models how user preferences and item characteristics evolve over time by assigning time-dependent weights to user–item interactions.
- (5)
- MF-StaticIPS [5]: MF-StaticIPS is a recommendation system approach that combines matrix factorization (MF) with static inverse propensity scoring (Static IPS).
- (6)
- TMF-StaticIPS [32]: TMF-StaticIPS is a recommendation system approach that integrates temporal matrix factorization (TMF) with static inverse propensity scoring (Static IPS).
- (7)
- MF-DANCER [8]: MF-DANCER is a recommendation system method that combines matrix factorization removal and enhanced negative sampling. It corrects selection bias and addresses data sparsity by modeling bias and improving negative sampling.
- (8)
- TMF-DANCER [8]: TMF-DANCER extends MF-DANCER by incorporating temporal dynamics into matrix factorization.
- (9)
- Causal Intervention for Sentiment Debiasing (CISD) [33]: CISD aims to eliminate sentiment bias through causal inference. The model comprises two components: during the training phase, causal intervention is employed to block the influence of sentiment polarity on user and item representations, thereby reducing confounding effects; during the inference phase, adjusted sentiment information is introduced to enhance the personalization and accuracy of recommendations.
4.5. Evaluation Metrics
- (1)
- Mean-Squared Error (MSE): MSE measures the average squared difference between predicted and actual values, emphasizing larger errors and assessing model accuracy in regression tasks.
- (2)
- Mean Absolute Error (MAE): MAE is another metric for assessing regression models. Unlike MSE, MAE is less sensitive to outliers, providing a more robust measure of model accuracy.
- (3)
- Accuracy (ACC): It represents the proportion of correctly classified instances out of the total number of instances.
4.6. Experiment Results
We employ three widely used evaluation metrics, namely MSE, MAE, and ACC, to assess the performance of SCTD and other baseline models. The comparative experimental results are presented in Table 3. As evidenced by the results, SCTD surpasses the state-of-the-art baseline on the Yelp dataset, which unequivocally attests to the efficacy of the proposed model. To gain deeper insights, we further dissect the experimental results. Notably, matrix decomposition-based methods significantly outperform other approaches, underscoring the superiority of leveraging matrix decomposition techniques. Within the realm of matrix decomposition methods, static methods consistently underperform compared to their time-dynamic counterparts. This observation leads us to conclude that in real-world scenarios where user preferences exhibit dynamic biases, static approaches inevitably compromise recommendation performance. Among the time-dynamic methods, TMF-DANCER excels in capturing temporal dynamics, adeptly modeling real-world user attributes. However, in data-scarce environments, SCTD demonstrates superior performance over TMF-DANCER. This is achieved through the construction of the SCS, which effectively mitigates data imbalance and sparsity issues. Furthermore, SCTD integrates the TDR to enhance the representational capacity of the original dataset. It is worth noting that CISD is a model for mitigating sentiment bias, and although CISD introduces causality to address sentiment bias, it is less effective in the comparison of the above assessment metrics because the model does not use the IPS method.

Table 3.
Comparison with different methods on the Yelp dataset.
To rigorously demonstrate that the robustness of SCTD surpasses the aforementioned baseline models, we constructed an imbalanced dataset, Imbalanced-Yelp, designed to simulate real-world data conditions. Specifically, we adopted a node-based approach, systematically deleting 10% of the reviews at each step, and sequentially investigated the impact of deleting reviews ranging from 0% to 100% for each method under study. When 0% of the reviews are deleted, Imbalanced-Yelp is identical to the original Yelp dataset, representing a complete and balanced scenario. Conversely, when 100% of the reviews are deleted, Imbalanced-Yelp is reduced to a ratings-only dataset, simulating an extreme case of data sparsity. The experimental results, illustrated in Figure 4, reveal significant insights. On the Imbalanced-Yelp dataset, the performance of the comparison models TMF-StaticIPS, MF-DANCER, and TMF-DANCER decreases rapidly as the degree of missing user comments continues to increase, while the performance of SCTD as well as MF-StaticIPS remains relatively stable. The performance of TMF-DANCER remains almost the same as that of SCTD when the deleted comments are 0%, but as the degree of missing user comments continues to increase until it reaches 100%, the MSE value of TMF-DANCER improves to 0.1563, while that of SCTD is 0.1379. This highlights the challenges posed by real-world data imbalances and underscores the limitations of TMF-DANCER in such scenarios. In contrast, SCTD maintains robust performance across varying levels of data imbalance, demonstrating its superior adaptability. Additionally, it is noteworthy that MF-StaticIPS, a method based on static IPS, exhibits relatively stable performance throughout the experiments. This stability can be attributed to its static nature, which, while less adaptive to dynamic changes, provides consistent results even under imbalanced conditions. These findings collectively emphasize the advantages of SCTD in handling real-world datasets with inherent imbalances and sparsity, further validating its practical applicability and robustness.
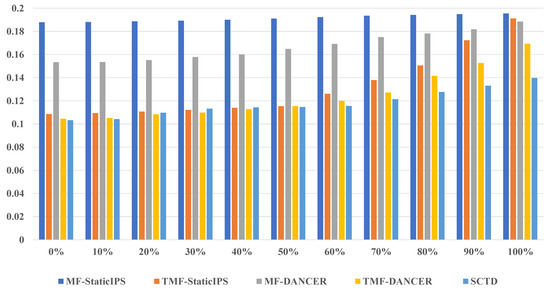
Figure 4.
MSE on Imbalanced-Yelp.
In addition to validating the robustness of the model by constructing the Imbalanced-Yelp dataset, we supplemented our experiments with the Jingdong dataset, which has 25,152 user ratings and only 8310 reviews, and we conducted comparative experiments on such a sparse user ratings–reviews matrix, obtaining the experimental results shown in Table 4. Through the experiments, we could find that SCTD is optimal in all metrics on the Jingdong dataset. It is worth noting that CISD performs causal inference on user reviews to mitigate sentiment bias, and thus, the performance degradation is severe in real scenarios where user reviews are severely missing. While the model TMF-DANCER has less performance degradation, unlike the experiments on the Yelp dataset, the increase in data sparsity causes TMF-DANCER to be worse than our model SCTD in all the metrics. This proves the enhanced robustness of our model in real datasets where data sparsity exists.

Table 4.
Comparison with different methods on the Jingdong dataset.
To rigorously validate the significance of performance improvements, we conducted paired t-tests between SCTD and the best baseline (TMF-DANCER) on the Yelp dataset. We ran each model 10 times with different random seeds and recorded MSE, MAE, and ACC. The results (Table 5) show that SCTD achieves statistically significant improvements in MSE (p = 0.003) and ACC (p = 0.021). This confirms that SCTD’s superiority is not due to random variation.

Table 5.
Statistical significance test on the Yelp dataset (SCTD vs. TMF-DANCER).
The extensive experiments conducted validate that our proposed approach not only adapts well to real-world imbalanced datasets but also consistently outperforms the baseline models, offering a robust solution for practical recommendation scenarios.
4.7. Parameter Analysis
This section focuses on analyzing the parameters in the model on the Yelp dataset and finding the most suitable numerical settings for the model in order to achieve the optimal experimental results and improve the debiasing ability of the model.
The more critical parameters are as follows: sentiment weight , discard threshold , and . The final results of the parameter analysis are shown in Figure 5.
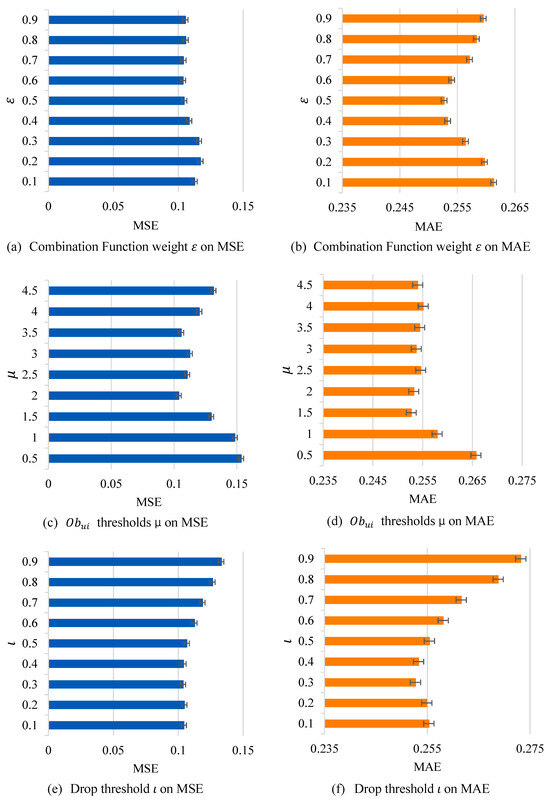
Figure 5.
Parametric analysis of the SCTD model (Yelp).
The tuning experiments reveal that the model reaches the optimal equilibrium on the Yelp dataset when = 0.6. A value that is too high leads to excessive dominance of sentiment scores over the fusion results, weakening the credibility of the original scores; while that is too low fails to fully utilize the fine-grained information in the reviews, leading to a decrease in the model’s generalization ability under sparse data.
The settings of and , on the other hand, directly affect the balance between data quality and integrity. When = 2.0, the system is able to effectively filter out noisy samples with a rating–sentiment deviation of more than 2 points and avoid over-deleting normal users. The setting of user-level discard threshold = 0.3 ensures that only when more than 30% of a user’s reviews are judged to be of low quality will they be removed as a whole. This strategy retains the majority of users’ data while successfully removing about 2% of malicious review-scrubbing accounts, which improves the signal-to-noise ratio of the overall dataset.
5. Conclusions and Future Work
5.1. Conclusions
In this work, we consider selection bias in dynamic scenarios and the impact of sentiment factors on bias. On the basis of the bias caused by sentiment factors, we built the SCS for processing, which solves the problem of sentiment bias between reviews and ratings by filtering bad reviews through a screening layer and then deriving the sentiment score matrix through a training layer. Moreover, we apply a debiased recommendation method based on time-dynamic scenarios to process the enhanced rating matrix obtained from the previous optimization of the sentiment score module to mitigate the influence of selection bias. Our model correctly captures and removes the sentiment bias between user ratings and reviews to improve recommendation performance, which is not considered by other selection bias models. In addition, our model takes into account the dynamic drift of user preferences as well as the dynamic change in selection bias and builds a dynamic debiasing layer to enhance robustness in the presence of highly sparse user data. Experimental results on the Yelp and Jingdong datasets show that our model (1) outperforms the state-of-the-art baseline model in terms of debiasing effect, (2) is more robust than the baseline model in the case of sparse data, (3) removes users’ latent emotional bias between ratings and reviews for fairer recommendations, (4) fully takes into account dynamically biased user preferences, and (5) can better perceive real-world scenarios, which is of great research importance in today’s era of ever-changing user preferences.
5.2. Future Work
The current SCTD model mainly relies on ratings and textual comments, while user behavior data and contextual information also contain rich signals in practical applications. In the future, cross-modal alignment mechanisms can be designed, such as modeling user–item–context heterogeneous relationships through graph neural networks or unifying multimodal feature representations using comparative learning, to further alleviate data sparsity and enhance model generalization capabilities. Second, the refinement of dynamic modeling needs to be enhanced. The existing temporal dynamic module mainly relies on linear assumptions, which makes it difficult to capture nonlinear mutations in user preferences (e.g., sudden hot events). In the future, the interaction effect between short-term fluctuations and long-term trends can be modeled more accurately by introducing a temporal attention mechanism or memory network, combined with external temporal features. In addition, real-time optimization is a key challenge for dynamic recommender systems. Currently, model training relies on offline batch processing, while incremental learning and fast reasoning are required in online scenarios. In the future, lightweight dynamic updating strategies can be explored, such as initializing model parameters through meta-learning, or using a piecewise architecture to separate static and dynamic components to reduce online computation overhead. Finally, dynamic recommender systems need to frequently collect user temporal behavior data, which may lead to the risk of privacy leakage. In the future, decentralized training schemes under the federated learning framework can be explored to combine differential privacy techniques to protect sensitive user information while ensuring that model performance is not significantly affected.
Author Contributions
Conceptualization, F.Z.; methodology, F.Z.; software, F.Z.; validation, F.Z.; formal analysis, F.Z. and W.L.; investigation, F.Z.; resources, F.Z.; data curation, F.Z.; writing—original draft preparation, F.Z.; writing—review and editing, W.L.; visualization, F.Z.; supervision, X.Y.; project administration, W.L.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was inspired by the National Social Science Foundation of China (NSFC) project ‘Research on Data Bias Identification and Governance Mechanisms Based on Digital Twins’, Project No. 22BTQ058.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We are grateful to Hebei University for their cooperation and assistance.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IPS | Inverse Propensity Scoring |
| NLP | Natural Language Processing |
| MF | Matrix Factorization |
| CF | Collaborative Filtering |
| NCF | Neural Collaborative Filtering |
| AVG | Static Average Item Rating |
| SCTD | Sentiment Classification and Temporal Dynamic Debiased Recommendation Module |
| SCS | Sentiment Classification Scoring Module |
| TDR | Temporal Dynamic Debiased Recommendation Module |
| LSTM | Long Short-Term Memory |
References
- SIGIR ’24: Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval; Association for Computing Machinery: New York, NY, USA, 2024.
- Marlin, B.M.; Zemel, R.S. Collaborative prediction and ranking with non-random missing data. In Proceedings of the Third ACM Conference on Recommender Systems, New York, NY, USA, 23–25 October 2009; pp. 5–12. [Google Scholar]
- Ovaisi, Z.; Ahsan, R.; Zhang, Y.; Vasilaky, K.; Zheleva, E. Correcting for selection bias in learning-to-rank systems. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 1863–1873. [Google Scholar]
- Pradel, B.; Usunier, N.; Gallinari, P. Ranking with non-random missing ratings: Influence of popularity and positivity on evaluation metrics. In Proceedings of the Sixth ACM Conference on Recommender Systems, Dublin, Ireland, 9–13 September 2012; pp. 147–154. [Google Scholar]
- Schnabel, T.; Swaminathan, A.; Singh, A.; Chandak, N.; Joachims, T. Recommendations as treatments: Debiasing learning and evaluation. In Proceedings of the International Conference on Machine Learning. PMLR, New York, NY, USA, 19–24 June 2016; pp. 1670–1679. [Google Scholar]
- Adamopoulos, P.; Tuzhilin, A. On over-specialization and concentration bias of recommendations: Probabilistic neighborhood selection in collaborative filtering systems. In Proceedings of the 8th ACM Conference on Recommender Systems, Silicon Valley, CA, USA, 6–10 October 2014; pp. 153–160. [Google Scholar]
- Li, H.; Zheng, C.; Wang, W.; Wang, H.; Feng, F.; Zhou, X.H. Debiased Recommendation with Noisy Feedback. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 25–29 August 2024; KDD ’24; pp. 1576–1586. [Google Scholar] [CrossRef]
- Huang, J.; Oosterhuis, H.; De Rijke, M. It is different when items are older: Debiasing recommendations when selection bias and user preferences are dynamic. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Virtual Event, 21–25 February 2022; pp. 381–389. [Google Scholar]
- Lin, A.; Wang, J.; Zhu, Z.; Caverlee, J. Quantifying and Mitigating Popularity Bias in Conversational Recommender Systems. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, New York, NY, USA, 17–21 October 2022; CIKM ’22; pp. 1238–1247. [Google Scholar] [CrossRef]
- Rubens, N.; Elahi, M.; Sugiyama, M.; Kaplan, D. Active learning in recommender systems. In Recommender Systems Handbook; Springer: Berlin/Heidelberg, Germany, 2015; pp. 809–846. [Google Scholar]
- Zhang, F.; Yuan, N.J.; Lian, D.; Xie, X.; Ma, W.Y. Collaborative knowledge base embedding for recommender systems. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 353–362. [Google Scholar]
- Panniello, U.; Tuzhilin, A.; Gorgoglione, M. Comparing context-aware recommender systems in terms of accuracy and diversity. User Model. User-Adapt. Interact. 2014, 24, 35–65. [Google Scholar] [CrossRef]
- Champiri, Z.D.; Shahamiri, S.R.; Salim, S.S.B. A systematic review of scholar context-aware recommender systems. Expert Syst. Appl. 2015, 42, 1743–1758. [Google Scholar] [CrossRef]
- Yang, X.; Guo, Y.; Liu, Y.; Steck, H. A survey of collaborative filtering based social recommender systems. Comput. Commun. 2014, 41, 1–10. [Google Scholar] [CrossRef]
- Beel, J.; Gipp, B.; Langer, S.; Breitinger, C. Paper recommender systems: A literature survey. Int. J. Digit. Libr. 2016, 17, 305–338. [Google Scholar] [CrossRef]
- Cai, Y.; Guo, J.; Fan, Y.; Ai, Q.; Zhang, R.; Cheng, X. Hard Negatives or False Negatives: Correcting Pooling Bias in Training Neural Ranking Models. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; CIKM ’22; pp. 118–127. [Google Scholar] [CrossRef]
- Koren, Y. Collaborative filtering with temporal dynamics. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 447–456. [Google Scholar]
- Ren, Y.; Tang, H.; Zhu, S. Unbiased Learning to Rank with Biased Continuous Feedback. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; CIKM ’22; pp. 1716–1725. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Hidasi, B. Deep Learning for Recommender Systems. In Proceedings of the Eleventh ACM Conference on Recommender Systems, Como, Italy, 27–31 August 2017; RecSys ’17; pp. 396–397. [Google Scholar] [CrossRef]
- Saelim, A.; Kijsirikul, B. A Deep Neural Networks model for Restaurant Recommendation systems in Thailand. In Proceedings of the 2022 14th International Conference on Machine Learning and Computing, Guangzhou, China, 18–21 February 2022; ICMLC ’22; pp. 103–109. [Google Scholar] [CrossRef]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 25–30 July 2020; SIGIR ’20; pp. 639–648. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Y.; Han, J.; Wang, E.; Zhuang, F.; Yang, J.; Xiong, H. NeuO: Exploiting the sentimental bias between ratings and reviews with neural networks. Neural Netw. 2019, 111, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Da, Y.; Bossa, M.N.; Berenguer, A.D.; Sahli, H. Reducing Bias in Sentiment Analysis Models Through Causal Mediation Analysis and Targeted Counterfactual Training. IEEE Access 2024, 12, 10120–10134. [Google Scholar] [CrossRef]
- Zhu, Y.; Yi, J.; Xie, J.; Chen, Z. Deep Causal Reasoning for Recommendations. ACM Trans. Intell. Syst. Technol. 2024, 15. [Google Scholar] [CrossRef]
- He, X.; He, Z.; Du, X.; Chua, T.S. Adversarial Personalized Ranking for Recommendation. In Proceedings of the The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; SIGIR ’18; pp. 355–364. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.; Zhao, M.; Li, W.; Xie, X.; Guo, M. Multi-Task Feature Learning for Knowledge Graph Enhanced Recommendation. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; WWW ’19; pp. 2000–2010. [Google Scholar] [CrossRef]
- Abusitta, A.; Li, M.Q.; Fung, B.C. Survey on Explainable AI: Techniques, challenges and open issues. Expert Syst. Appl. 2024, 255, 124710. [Google Scholar] [CrossRef]
- Koren, Y.; Rendle, S.; Bell, R. Advances in collaborative filtering. In Recommender Systems Handbook; Springer: Berlin/Heidelberg, Germany, 2021; pp. 91–142. [Google Scholar]
- Rosenthal, S.; Farra, N.; Nakov, P. SemEval-2017 task 4: Sentiment analysis in Twitter. arXiv 2019, arXiv:1912.00741. [Google Scholar]
- Han, J.; Zuo, W.; Liu, L.; Xu, Y.; Peng, T. Building text classifiers using positive, unlabeled and ‘outdated’examples. Concurr. Comput. Pract. Exp. 2016, 28, 3691–3706. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, S.; Wang, L. Cot: Contextual operating tensor for context-aware recommender systems. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Zhang, Y.; Yin, C.; Lu, Z.; Yan, D.; Qiu, M.; Tang, Q. Recurrent Tensor Factorization for time-aware service recommendation. Appl. Soft Comput. 2019, 85, 105762. [Google Scholar] [CrossRef]
- He, M.; Chen, X.; Hu, X.; Li, C. Causal Intervention for Sentiment De-biasing in Recommendation. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; CIKM ’22; pp. 4014–4018. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).