Abstract
The development of rotordynamic systems with reduced energy dissipation is a key challenge in modern applications, such as Flywheel Energy Storage Systems. This paper investigates a fully passive vertical rotor system supported by two passive magnetic bearings whose configuration provides radial stability while minimising power losses due to their thrust effect. A numerical model describes the forces and stiffness of the magnetic bearings, identifying the operational range of the thrust–radial support configuration. A test rig is developed for the experimental characterisation of the rotor and passive magnetic bearings in both static and dynamic conditions. Different magnetic thrust force levels are tested by varying the axial distance between the rotor and stator magnetic rings of the bearings. Static tests are performed to measure the weight force compensation corresponding to the different bearing configurations, validating the numerical model. Dynamic tests analyse the rotor power losses with a non-invasive approach via optical sensor measurements.
1. Introduction
Magnetic bearings have been the subject of scientific research in recent decades due to their advantages over traditional mechanical bearings, such as their lack of contact friction, lower maintenance, and no lubrication requirements [1,2]. These advantages have led to a growing interest in rotating systems with magnetic supports [3,4,5]. Moreover, Permanent Magnetic Bearings (PMBs) are the only fully passive magnetic supports allowing for levitation without energy consumption [6], making them the ideal solution for environmentally sustainable energy storage and conversion applications such as Flywheel Energy Storage Systems (FESSs) [7]. Instead, in Active Magnetic Bearings (AMBs) [8], the stator conductive coils are supplied with current to allow for rotor position control, thus requiring continuous power supply and feedback control logic [9]. Electro-Dynamic Bearings (EDBs) [10] exploit the electromagnetic forces generated by eddy currents into a conductor moving in a magnetic field [11], causing power losses. Finally, Superconductive Magnetic Bearings (SMBs) [1] require a low temperature, with the drawback of the cooling system energy consumption.
According to Earnshaw’s Theorem [12], stable levitation cannot be achieved using only permanent magnets; additional bearings are needed to stabilise the system. Consequently, hybrid solutions, which exploit PMBs and other support typologies, are used to obtain stable levitation and the reduction in energy consumption. In [13], Fang et al. analyse a hybrid AMB–PMB system whose radial behaviour is controlled by the active bearing, while the passive support provides the axial levitation. The passive support is composed of a thrust PMB and a passive damper with a Halbach magnet array, which provides both stiffness and damping. In [14], Filatov and Maslen describe a rotating system whose levitation is achieved by a radial EDB and a thrust PMB made of two coaxial disc-shaped permanent magnets to compensate for the rotor axial load. A further passive hybrid configuration is described in [15], where Dergachev et al. exploit an SMB to provide the stable levitation of an FESS, compensating for its weight using a PMB as thrust bearing. In [16], a PMB is used to partially compensate the weight of a vertical axis wind turbine to limit the axial load and the resulting friction at the carbide tip sharp point base constraint. Further passive hybrid configurations in which PMBs are used both as thrust and as radial bearings are found in literature. In [17], Van Verdeghem and Dehez propose a hybrid EDB–PMB system and investigate the functioning of a rotating machine in which PMB supports are used as centring bearings with a partial compensation of the rotor weight. In [18], Filion et al. analyse a PMB used as a radial and thrust bearing with a ball thrust bearing for the rotor axial stability; the axial force and the radial stiffness and damping are evaluated with tests performed at null angular speed.
This paper introduces a configuration of a fully passive magnetic rotor that exploits the intrinsic radial and thrust effects of the PMBs.
The proposed solution does not require any power supply or control system, thus being more cost-effective and easier to implement compared to the hybrid systems analysed in the state of the art.
The PMB thrust–radial configuration is analysed, and a dedicated test rig is developed for static and dynamic experimental characterisation. The article is organised as follows. First, the model describing the PMB characterisation and the identification of the working range of the support in the thrust–radial configuration is presented. Then, the experimental setup consisting of rotor, bearings, actuation, and measurement systems is described. Finally, the experimental outcomes concerning static and dynamic tests, for the thrust force and power loss investigation, are discussed.
2. PMB Model
A test rig of a fully passive vertical rotor equipped with two PMB supports is developed to analyse a configuration of the bearings as both radial and thrust supports.
The analysis of the PMB axial and radial forces as functions of the magnetic rings’ relative position is necessary for identifying the conditions where the bearings operate as thrust–radial supports providing upward axial force, which partially compensates for the rotor weight and stabilises the system in the radial direction. The numerical evaluation of the magnetic forces is performed with the Coulomb surface charge density method used in [19], where magnets are modelled as equivalent surface distributions of fictitious charges.
According to [20], it is possible to use the charge density method considering the boundary conditions of Equations (1) and (2) at the material interfaces:
Equation (1) implies that the tangential component of the magnetic field intensity is continuous at each material interface. Equation (2) implies that the normal component of the magnetic flux density is continuous at each material interface.
Equation (3) defines the surface charge density of the equivalent fictitious charges located in the plane surfaces of the magnetic rings.
where is the ring magnetisation and is the outward unit normal to the ring surfaces. According to [21], under the hypotheses of linear isotopic homogeneous magnetic material, rare earth material with relative permeability and uniform magnetisation, the modulus of can be expressed by Equation (4).
where is the ring magnetisation and is the outward unit normal to the ring surfaces. Equation (5) expresses the fictitious infinitesimal charge , located on an infinitesimal plane surface of a magnet, in terms of surface charge density.
Thus, the force exchanged between two fictitious infinitesimal charges and placed in two different infinitesimal plane surfaces and of two magnets is calculated with Equation (6).
where the relative position vector is equal to the difference between the position vectors and of the charges and , respectively. Therefore, considering Equation (5) and expressing in terms of and , Equation (6) can be rewritten as Equation (7)
If a PMB, as the one shown in Figure 1, is considered, then the force of the stator ring on the rotor ring is calculated with Equation (8). The total force exchanged between the charges of two plane surfaces of the stator and rotor rings, respectively, is computed by integrating Equation (7) over the respective areas. Finally, the magnetic interactions between the two plane surfaces of the stator ring and the two plane surfaces of the rotor ring are summed, resulting in .
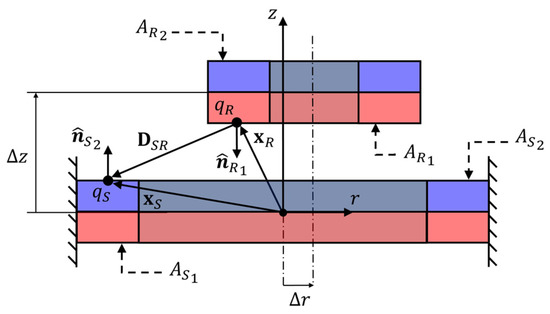
Figure 1.
Surface charge interaction between two PMB rings (with blue and red colours identifying the magnetic north and south poles, respectively).
The integral of Equation (8) can be numerically solved by discretising the surfaces of the magnets and expressing and in Cartesian or cylindrical coordinates [20]. Thus, Equation (8) is a geometric problem where the only variables are the coordinates of the charges and the sign of the surface charge density . Consequently, the force depends on the radial and axial offsets of the PMB rings.
The force is a function of the magnetic ring residual induction and the PMB geometry, and its axial component can be exploited to partially compensate for the rotor weight. Consequently, the required trend of the axial force, necessary for rotor weight compensation, can be achieved by selecting the proper , magnetic ring dimensions and stacking magnetic rings.
Figure 2 shows an example of the axial force , evaluated with Equation (8) in the case of PMB rings with axial magnetisation with the same direction. The values of are evaluated at different configurations of the PMB, changing the position of the rotor magnet while keeping the stator magnet fixed. The rotor magnet position is changed in radial and axial directions, thus varying the PMB ring radial and axial offsets and . The resulting force is normalised with respect to its maximum value and plotted versus the radial and axial offsets and , normalised considering the PMB radial airgap and axial thickness , respectively.
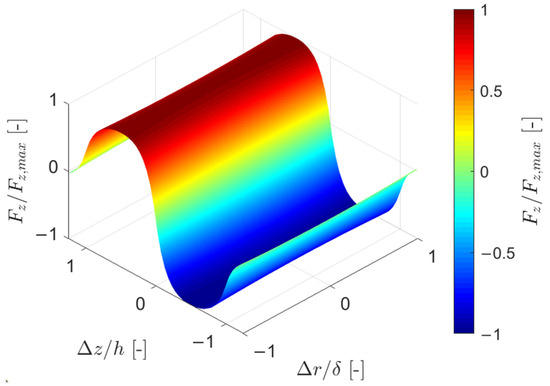
Figure 2.
Normalised axial force as function of the normalised radial and axial offsets.
In the case shown in Figure 2, the axial force strongly depends on the axial offset , while it remains almost constant with respect to the radial offset , because the air gap between the stator and rotor PMB rings is small.
The axial force can be directed either upwards or downwards according to the position and the magnetisation directions of the rotor and stator rings. Only the axial offset range where the axial force is directed upwards and the PMB functions as a thrust bearing is considered to achieve a partial compensation of the rotor weight.
The radial stiffness , as the axial force, assumes both positive and negative values [22,23], corresponding to stable and unstable behaviour in the radial direction, respectively, depending on the PMB axial offset. Therefore, the range of a second axial offset where radial stiffness is positive and the PMB works as a radial bearing must be identified. The radial stiffness , linearised about the rotor centred position, is expressed in Equation (9) as the derivative of the radial force :
An alternative approach for the evaluation of with the derivative of is proposed. According to Equation (10), which is related to the Earnshaw theorem and derived from the steps detailed in Appendix B, the sum of PMB stiffnesses in the -directions of a Cartesian reference system is zero.
Consequently, if a Cartesian reference system is considered with its -axis aligned with the axis of the PMB, then under the hypothesis of null radial displacement of the floating ring, both stiffness and are equal to due to the bearing axial symmetry and depending only on , resulting in Equation (11):
where
This approach avoids the evaluation of and requires only for the calculation of both axial force and radial stiffness; requiring only one of the components of decreases the computational time associated with the demanding numerical solution of the integral in Equation (8) for each axial offset.
Furthermore, Equation (11) highlights that the bearing is always unstable since a positive radial stiffness corresponds to a negative axial stiffness and vice versa. Thus, a rotor with PMBs used in the thrust–radial configuration needs an auxiliary bearing to stabilise the axial degree of freedom. The values of the axial force from Figure 2 are considered at the null radial offset as functions of the PMB ring axial offset, and the corresponding radial stiffness is calculated as a function of the axial offset with Equations (11) and (12). Both and are normalised with respect to their maximum value, respectively, and plotted in Figure 3 as functions of the axial offset.
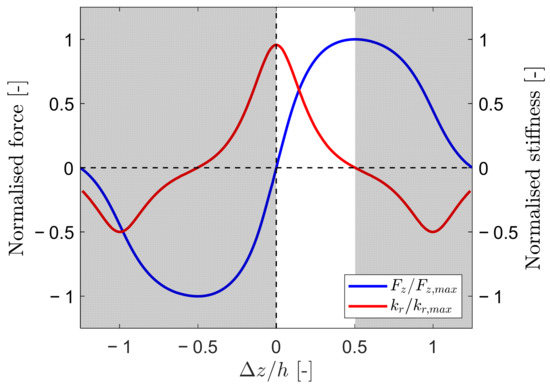
Figure 3.
Identification of the axial offset range for the PMB thrust–radial configuration through the analysis of axial force and stiffness.
The intersection of the two axial offset ranges with upward axial force and positive stiffness, respectively, is equal to and corresponds to the condition where the PMB works in the thrust–radial configuration.
Finally, the trends of and in Figure 3 highlight that in the PMB thrust–radial configuration, the higher the thrust axial force for the rotor weight compensation, the lower the radial stiffness.
3. Experimental Setup
The test rig consists of a fully passive vertical rotor, supported by two thrust–radial PMBs and a ball bearing to stabilise the system in the axial direction; it is designed to investigate the thrust–radial support configuration, allowing for the variation of the relative position of the rings of the magnetic bearings. Figure 4 shows the overview of the system and a sketch of its components.
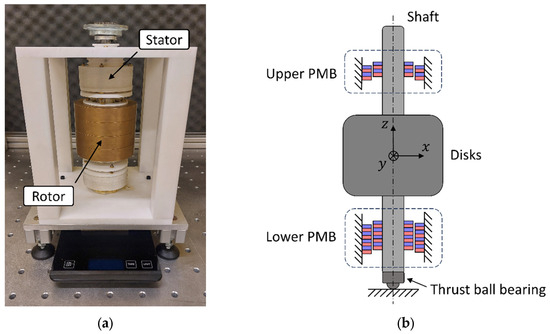
Figure 4.
(a) Test rig of the rotor with PMB supports; (b) rotor component sketch.
The stator and the structure around the rotor are made of Teflon to avoid interactions with the PMBs owing to their diamagnetic behaviour. The rotor consists of four brass disks mounted on an aluminium shaft. The rotor is always kept in contact with the base constraint since its full vertical levitation would lead the system to instability. Therefore, a thrust ball bearing is mounted at the bottom of the shaft to reduce the contact friction losses. The thrust ball bearing is in contact with an aluminium base support placed on a scale (precision N) that measures the downward force, which is given by the sum of the rotor weight and the PMB axial forces. The lower and the upper PMBs consist of four and two stacked magnetic ring pairs made of an alloy of neodymium, iron, and boron (NdFeB). Every magnetic ring is mounted with the same upward magnetisation direction (the blue and red colours of the PMB rings in Figure 4 and Figure 5 identify the north and south magnetic poles, respectively). The PMB stator rings are housed inside two hollow cylindrical supports that are placed above and under the brass disks. These cylindrical supports are mounted on the stator structure via threaded connections; their rotation allows for the variation in the PMB stator ring axial position, as shown in Figure 5. The variation of the support axial position causes a variation of the magnetic axial force, and consequently the rotor weight can be partially compensated for. The rotor and the PMB ring properties are listed in Appendix A, in Table A1.

Figure 5.
Axial position variation of the PMB stator rings.
Figure 6 shows the rotor test bench with the actuation and measuring systems.
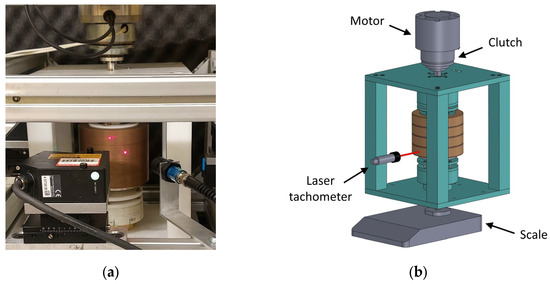
Figure 6.
(a) Rotor test rig; (b) test rig CAD model.
The actuation system consists of a DC brushless motor (Northrop Grumman BN34-25EN-02LH, Falls Church, VA, USA) controlled by an external driver (Litton SCA-B4-70-10, Beverly Hills, CA, USA) and an electromagnetic clutch (MWM EMS-60, Mannheim, Germany). The motor maximum rated torque and speed are Nm and rpm, while the clutch maximum transmitted torque and speed are Nm and rpm, respectively.
The rotor angular speed data are detected by a laser tachometer (LaserTach LT2 ICP, Centennial, CO, USA) and acquired at Hz by means of a Siemens SCADAS Mobile acquisition system.
4. Results and Discussion
In this section, the experimental tests and their outcomes are analysed. The experimental campaign consists of two types of tests: static tests aimed at studying the PMB axial force and dynamic tests to investigate the effect of the partial rotor weight compensation on the power losses.
4.1. Static Tests
The static tests involve adjusting the PMB configuration by varying the axial offset between the rotor and stator rings through the rotation of the stator supports. The contact reaction force , equal to the downward force measured by the scale, and the axial displacement are recorded at each support rotation step, thus allowing for the evaluation of the corresponding magnetic force . Centring bushes are used at both the lower and upper supports to keep the rotor radial offset null during the tests. The lower bearing axial force is evaluated at different ring axial offsets. Each test is performed according to the following procedure:
- The starting position of the tests corresponds to axial position of the stator ring at which is null; is set equal to zero and the scale measures a force equal to the rotor weight force;
- The stator support is progressively rotated to vary its vertical position, moving downward by steps of , up to the maximum upward value, corresponding to the condition where a further rotation of the stator support causes a decrease in .
The experimental axial force of the lower PMB is compared to the force estimated with Equation (8) in Figure 7. The relative error between the experimental measurements and the model force at the corresponding axial offsets are listed in Table 1. The maximum relative error is equal to 5%, according to the experimental characterisation of the .
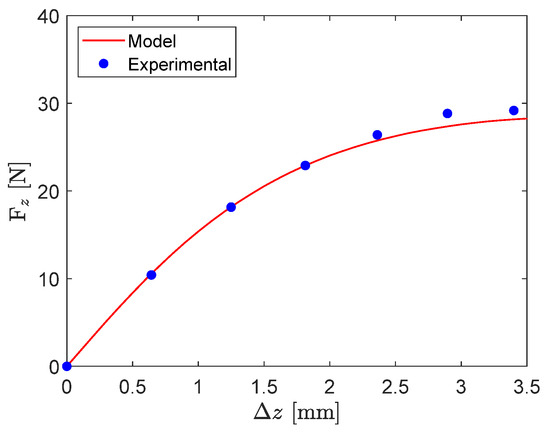
Figure 7.
Axial force as a function of the PMB ring axial offset.

Table 1.
Relative error between the experimental measurements and the model.
4.2. Dynamic Tests
The dynamic tests consist of angular speed sweep down runs, performed at three PMB configurations (named A, B, and C, as shown in Table 2, where refers to both the upper and the lower magnetic supports), with the aim of analysing the relation between the PMB ring offset and the system power loss reduction. Configuration A corresponds to a pure radial bearing with null axial offset and null rotor weight compensation, while the B and C configurations belong to the thrust–radial configuration offset range. Each test is performed according to the following procedure:

Table 2.
Dynamic test PMB configurations.
- The rotor is accelerated, then it is decoupled from the actuation system and left freely rotating, so that its angular speed progressively decreases;
- The angular speed is acquired from rad/s until the rotor stops.
The angular speeds measured during three sets of tests performed for each PMB configuration listed in Table 2 are shown in Figure 8a. The evaluation of the rotor angular acceleration during the sweep down tests is a common practise to estimate the power losses [24]. Therefore, the angular accelerations in Figure 8b are obtained by computing the time derivative of the experimental angular speeds. The time history regions where the angular speed rapidly changes due to contacts between the rotor and the stator (clearly visible in Conf. C), e.g., caused by critical speeds, superharmonic and subharmonic resonances [25,26], are not considered. In fact, under these conditions the acceleration has high peaks, as shown in Figure 8b, that are not related only to Coulomb friction or aerodynamic drag losses.
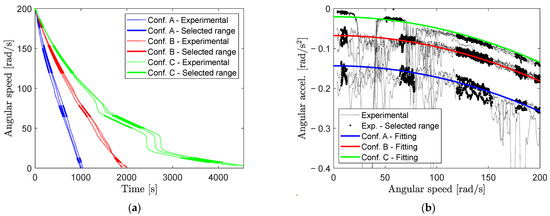
Figure 8.
(a) Angular speed time histories; (b) angular acceleration fitting.
The torque equilibrium related to the rotation the rotor about its axis is considered in Equation (13).
where and are the resisting and driving torques, respectively.
The driving torque is null during the angular speed sweep down tests since the rotor is uncoupled from the motor. Thus, Equation (13) is rewritten in terms of powers as Equation (14) by multiplying both terms by the angular speed , obtaining the expression of the total power loss .
A polynomial fitting of the acceleration data of Figure 8b is performed in the selected ranges to evaluate the total power loss, with Equation (14), as a function of the angular speed excluding the stator–rotor contact effects. Figure 9a shows the total power loss for each configuration, while Figure 9b shows the percentage reduction in the total power loss of PMB configurations B and C, with respect to configuration A with null weight compensation, as a function of the angular speed.
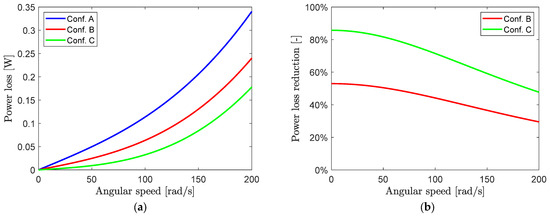
Figure 9.
(a) Total power loss in A, B, and C configurations; (b) power loss percentage reduction due to the partial weight compensation in B and C configurations.
The aerodynamic and friction effects are the two main sources of system power loss, as expressed in Equation (15):
where the aerodynamic losses are
and the friction losses are
where the contact reaction force is
The aerodynamic power loss is expressed in Equation (16), according to [27], as a sum of terms that are functions of the angular speed to the power, with . The friction power loss expressed in Equation (17) is linear with respect to the angular speed and proportional to the contact reaction force (see Table 2). The aerodynamic effect is considered equal in the three configurations under the assumption that small PMB axial offsets do not significantly affect the airgaps between the stator and the rotor. Therefore, PMB configurations with different values cause a variation of the rotor acceleration proportional to the variation of , visible in Figure 8b and independent of the angular speed. Consequently, the power loss reduction of Figure 9b is totally addressed to the change in the friction loss due to the PMB thrust effect:
- At low speed, the power loss percentage reduction tends to the values of the weight percentage compensation listed in Table 2 because the aerodynamic effect tends to zero;
- At high speed, the aerodynamic losses are the most relevant; the percentage reduction in configuration C is still high and equal to 47.7% at 200 rad/s.
The reduction in power losses results in a decrease in the energy required to operate the rotating system. From the perspective of energy storage applications, the power loss reduction improves the FESS discharge time performance.
5. Conclusions
In this research work, a thrust–radial PMB configuration is presented. This architecture also allows for the use of radial PMBs for partial rotor weight compensation, thus reducing the power losses due to friction in the mechanical thrust bearing used for axial stabilisation. A numerical model is presented to evaluate the bearing forces and stiffness and the possible axial offset range of the thrust–radial configuration.
An experimental test rig is developed to analyse the thrust–radial PMBs with different offset configurations, measuring the magnetic axial forces by means of static tests and the rotor power losses with angular speed sweep down tests.
The experimental model comparison between the axial forces measured with the static tests and the numerical values shows compliant results, validating the PMB force model.
The reduction in power losses is shown by the increased rotation time before the system stops, which is proportional to the weight compensation achieved in the three PMB configurations.
The percentage reduction in total power losses, achieved in the PMB configuration with higher rotor weight compensation, varies from 84.9% to 47.7% in the range of 0 ÷ 200 rad/s, and it would increase in the case of operation in low pressure environments, such as FESSs.
Author Contributions
Conceptualization, A.V. and S.P.C.; methodology, A.V. and S.P.C.; software, S.P.C. and S.V.; validation, A.V., S.P.C. and S.V.; formal analysis, S.P.C., A.V. and S.V.; investigation, S.P.C.; resources, A.V.; data curation, S.P.C.; writing—original draft preparation, S.P.C.; writing—review & editing, A.V., S.V. and S.P.C.; visualization, S.P.C.; supervision, A.V and S.V.; project administration, A.V.; funding acquisition, A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This publication is part of the project PNRR-NGEU which has received funding from the MUR–DM 351/2022. This research was developed within the “Network 4 Energy Sustainable Transition–NEST” project. The “NEST” project is funded under the Italian National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.3—Call for tender No. 1561 of 11 October 2022 of Ministero dell’Università e della Ricerca (MUR) and the European Union—NextGenerationEU consortium.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol | Description |
| rotor mass [kg] | |
| polar moment of inertia [kg m2] | |
| gravitational acceleration [m/s2] | |
| rotor angular speed [rad/s] | |
| PMB ring residual magnetic induction [T] | |
| vacuum permeability [H/m] | |
| magnet infinitesimal surface [m2] | |
| magnet infinitesimal surface charge [C] | |
| surface charge density [A/m] | |
| outward unit normal to the PMB ring plane surfaces [-] | |
| outward unit normal to the lower and upper surfaces of the PMB stator ring [-] | |
| outward unit normal to the lower and upper surfaces of the PMB rotor ring [-] | |
| position vector of an infinitesimal surface charge [m] | |
| relative position vector between two infinitesimal surface charges [m] | |
| , | axial and radial offsets between the PMB rotor and stator rings [m] |
| , | lower and upper plane surface of the PMB stator ring [m2] |
| , | lower and upper plane surface of the PMB rotor ring [m2] |
| overall force between PMB stator and rotor rings [N] | |
| , | PMB axial and radial force components [N] |
| axial forces of the lower and upper PMB [N] | |
| magnetic flux density [T] | |
| , , | magnetic flux density in -, -, and - directions [T] |
| magnetisation [A/m] | |
| m | magnetic moment [A m2] |
| , , | magnetic moment in -, -, and - directions [A m2] |
| magnetic field intensity [A/m] | |
| electric field [V/m] | |
| current density [A/m-2] | |
| vacuum permittivity [F/m] | |
| , | PMB axial and radial stiffness [N/m] |
| PMB thickness [m] | |
| PMB radial airgap [m] | |
| Coulomb rolling contact friction coefficient [-] | |
| ball radius of the ball thrust bearing [m] | |
| contact reaction force [N] | |
| k | angular speed exponent for aerodynamic power loss terms [-] |
| aerodynamic power loss coefficients [Nm sk] | |
| total power losses [W] | |
| resisting torque [Nm] | |
| driving torque [Nm] | |
| power losses due to contact friction effect [W] | |
| power losses due to aerodynamic effect [W] | |
| magnetic potential energy [J] |
Appendix A

Table A1.
Rotor and PMB properties.
Table A1.
Rotor and PMB properties.
| Characteristic | Property | Value |
|---|---|---|
| Rotor | m, mass [kg] | |
| l, length [mm] | ||
| It, transversal moment of inertia [kg m2] | ||
| Ip, polar moment of inertia [kg m2] | ||
| Stator magnets | dint, internal diameter [mm] | |
| dext, external diameter [mm] | ||
| hr, ring height z [mm] | ||
| Br, residual magnetic induction [T] | ||
| Rotor magnets | dint, internal diameter [mm] | |
| dext, external diameter [mm] | ||
| hr, ring height z [mm] | ||
| Br, residual magnetic induction [T] |
Appendix B
The magnetic potential energy of a dipole is expressed in a Cartesian reference system with Equation (A1) as a function of the magnetic moment and of the magnetic flux density .
Under the assumption of constant magnetic moment , Equation (A2) is derived.
Since the divergence and the curl of the magnetic field are null, due to Equation (2) and Maxwell’s Equation (A3) in the absence of current or changing electric field , respectively, each component of the Laplacian of B is null according to Equation (A4).
The substitution of Equation (A4) into (A2) leads to Equation (A5), which corresponds to an implication of the Earnshaw’s theorem to the magnetostatic case [28].
The interaction force between a magnet and a magnetic field is given by Equation (A6).
By substituting Equation (A6) into Equation (A5), Equation (A7) is obtained, leading to the magnetic stiffness equation used in [23,29].
References
- Slininger, T.S.; Chan, W.; Severson, E.L.; Jawdat, B. An Overview on Passive Magnetic Bearings. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CN, USA, 17–20 May 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Maslen, E.H.; Schweitzer, G. Magnetic Bearings; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ebrahimi, R.; Ghayour, M.; Khanlo, H.M. Nonlinear dynamic analysis and experimental verification of a magnetically supported flexible rotor system with auxiliary bearings. Mech. Mach. Theory 2018, 121, 545–562. [Google Scholar] [CrossRef]
- Bonisoli, E.; Venturini, S.; Cavallaro, S.P. Nonlinear characterisation of a rotor on passive magnetic supports. Int. J. Mech. Control 2022, 23, 121–128. [Google Scholar]
- Zhou, J.; Fang, Z.; He, S.; Zhang, Q. Modelling and stability analysis of the permanent magnetic bearing-rotor system under base excitation. Arch. Appl. Mech. 2025, 95, 29. [Google Scholar] [CrossRef]
- Safaeian, R.; Heydari, H. Comprehensive comparison of different structures of passive permanent magnet bearings. IET Electr. Power Appl. 2018, 12, 179–187. [Google Scholar] [CrossRef]
- Li, X.; Palazzolo, A. A review of flywheel energy storage systems: State of the art and opportunities. J. Energy Storage 2022, 46, 103576. [Google Scholar] [CrossRef]
- Schweitzer, G. Applications and Research Topics for Active Magnetic Bearings. IUTAM Bookser. 2010, 1011, 263–273. [Google Scholar] [CrossRef]
- Roy, H.K.; Das, A.S.; Dutt, J.K. An efficient rotor suspension with active magnetic bearings having viscoelastic control law. Mech. Mach. Theory 2016, 98, 48–63. [Google Scholar] [CrossRef]
- Supreeth, D.K.; Bekinal, S.I.; Chandranna, S.R. An Overview on Electrodynamic Bearings. IEEE Access 2022, 10, 57437–57451. [Google Scholar] [CrossRef]
- Amati, N.; De Leépine, X.; Tonoli, A. Modeling of Electrodynamic Bearings. J. Vib. Acoust. 2008, 130, 061007. [Google Scholar] [CrossRef]
- Earnshaw, S. On the nature of the molecular forces which regulate the constitution of the luminiferous ether. Trans. Camb. Philos. Soc. 1848, 7, 97–112. [Google Scholar]
- Fang, J.; Le, Y.; Sun, J.; Wang, K. Analysis and Design of Passive Magnetic Bearing and Damping System for High-Speed Compressor. IEEE Trans. Magn. 2012, 48, 2528–2537. [Google Scholar] [CrossRef]
- Filatov, A.V.; Maslen, E.H. Passive Magnetic Bearing for Flywheel energy storage systems. IEEE Trans. Magn. 2001, 37, 3913–3924. [Google Scholar] [CrossRef]
- Dergachev, P.; Kosterin, A.; Kurbatova, E.; Kurbatov, P. Flywheel energy storage system with magnetic hts suspension and embedded in the flywheel motor-generator. In Proceedings of the IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016. [Google Scholar] [CrossRef]
- Premkumar, T.M.; Mohan, T.; Sivamani, S. Design and Analysis of a Permanent Magnetic Bearing for Vertical Axis Small Wind Turbine. Energy Procedia 2017, 117, 291–298. [Google Scholar] [CrossRef]
- Van Verdeghem, J.; Dehez, B. Fully Passively Levitated Self-Bearing Machine Implemented Within a Reaction Wheel. IEEE Trans. Ind. Appl. 2021, 57, 5782–5795. [Google Scholar] [CrossRef]
- Filion, G.; Ruel, J.; Dubois, M.R. Reduced-Friction Passive Magnetic Bearing: Innovative Design and Novel Characterization Technique. Machines 2013, 1, 98–115. [Google Scholar] [CrossRef]
- Bekinal, S.I.; Anil, T.R.; Jana, S. Analysis of axially magnetized permanent magnet bearing characteristics. Prog. Electromagn. Res. B 2012, 44, 327–343. [Google Scholar] [CrossRef]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Santra, T.; Roy, D.; Yamada, S. Calculation of Force between Two Ring Magnets Using Adaptive Monte Carlo Technique with Experimental Verification. Prog. Electromagn. Res. 2016, 49, 181–193. [Google Scholar] [CrossRef]
- Chalageri, G.R.; Bekinal, S.I.; Doddamani, M. Dynamic Analysis of 650 W Vertical-Axis Wind Turbine Rotor System Supported by Radial Permanent Magnet Bearings. Eng. Proc. 2023, 59, 56. [Google Scholar] [CrossRef]
- Dagnaes-Hansen, N.A.; Santos, I.F. Permanent magnet thrust bearings for flywheel energy storage systems: Analytical, numerical, and experimental comparisons. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5280–5293. [Google Scholar] [CrossRef]
- Popescu, A.; Houpert, L.; Olaru, D.N. Four approaches for calculating power losses in an angular contact ball bearing. Mech. Mach. Theory 2020, 144, 103669. [Google Scholar] [CrossRef]
- Cavallaro, S.P.; Venturini, S.; Bonisoli, E. Nonlinear dynamics of a horizontal rotor with asymmetric magnetic supports. Int. J. Non-Linear Mech. 2024, 165, 104764. [Google Scholar] [CrossRef]
- Chen, H.; Zhong, S.; Lu, Z.; Chen, Y.; Han, J.; Wang, C. Analysis on multi-mode nonlinear resonance and jump behavior of an asymmetric rolling bearing rotor. Arch. Appl. Mech. 2021, 91, 2991–3009. [Google Scholar] [CrossRef]
- Venturini, S.; Cavallaro, S.P.; Vigliani, A. Windage loss characterisation for flywheel energy storage system: Model and experimental validation. Energy 2024, 307, 132641. [Google Scholar] [CrossRef]
- Bassani, R. Earnshaw (1805–1888) and Passive Magnetic Levitation. Meccanica 2006, 41, 375–389. [Google Scholar] [CrossRef]
- Bassani, R. Magnetoelastic Stability of Magnetic Axial Bearings. Tribol. Lett. 2013, 49, 397–401. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).