Advancement of the DRPE Encryption Algorithm for Phase CGHs by Random Pixel Shuffling
Abstract
1. Introduction
- From a complex virtual scene, designed by means of computer graphics (CGs), we generate a CGH in which relevant scene information such as luminosity, depth, and occlusion is stored.
- To encrypt this information, we present an evolution of the DRPE algorithm by incorporating random pixel shuffling. This significantly increases the robustness of the encryption against brute force attacks.
- Two keys are defined: one for the pixel shuffling process and one for the random mask phase modification process.
- The proposal allows these keys to be generated from a single key or to be independent in order to improve the level of encryption security.
- The decrypted scene is obtained by simulation or in the laboratory.
2. Preliminaries
2.1. Number and Text Encryption Methods
2.2. Image Encryption Methods
CGH Encryption Methods: DRPE Encryption
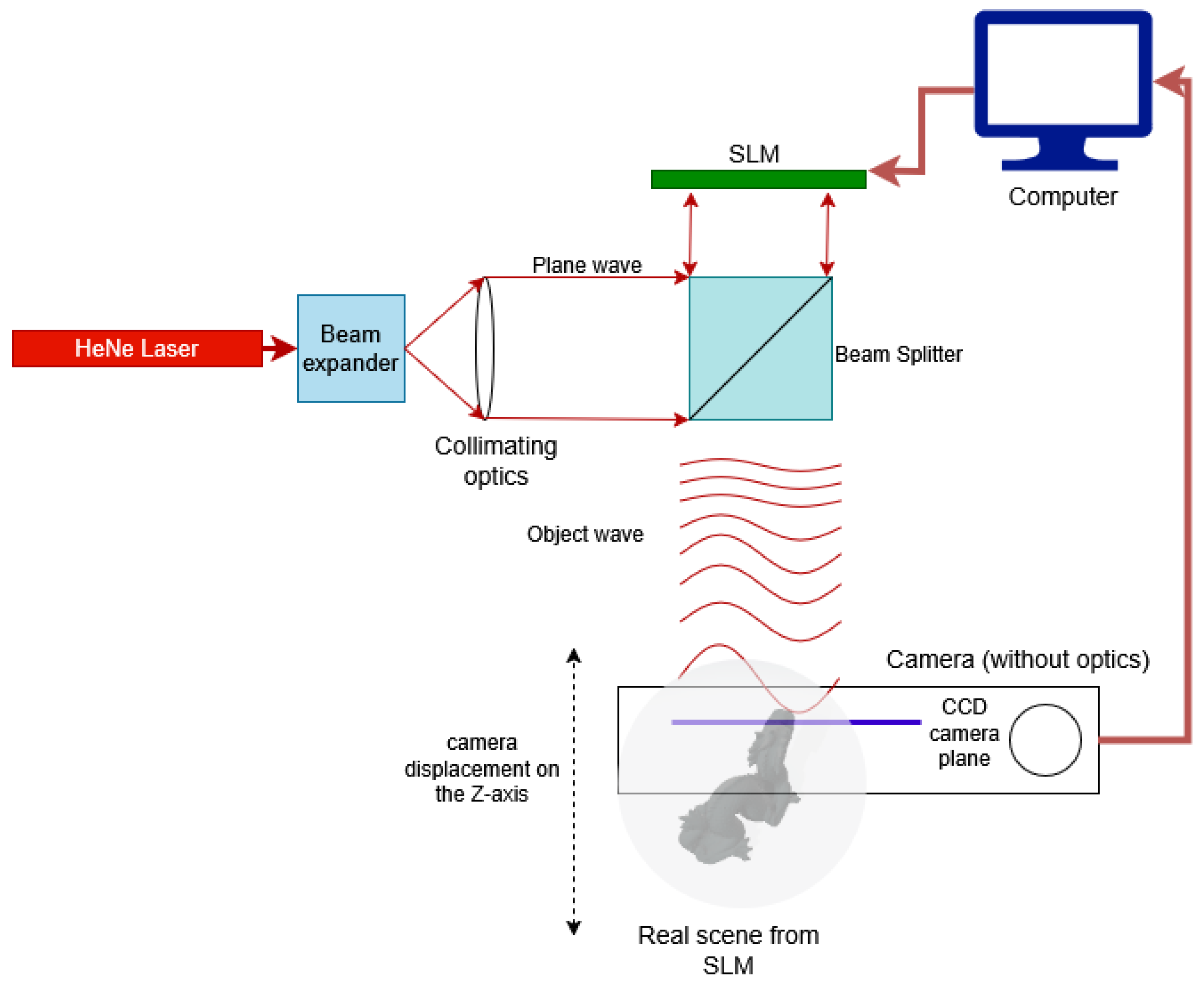
3. From the Synthesis of a 3D Scene to Its Safe Reception: Process Description
3.1. Scene and CGH Synthesis
3.2. Encryption of the CGH
3.3. Decryption and Visualization of the Scene Stored in the CGH
3.4. Visualization
4. Results Discussion and Performance Analysis
- CGH Storage: The 3D scene is stored within a CGH. Vulnerability to Statistical Analysis is avoided since methods such as intensity histograms cannot reveal patterns or facilitate partial image reconstruction. It is also resistant to partial transformations, as modifying a subset of pixels in the CGH does not compromise the integrity of the stored information.
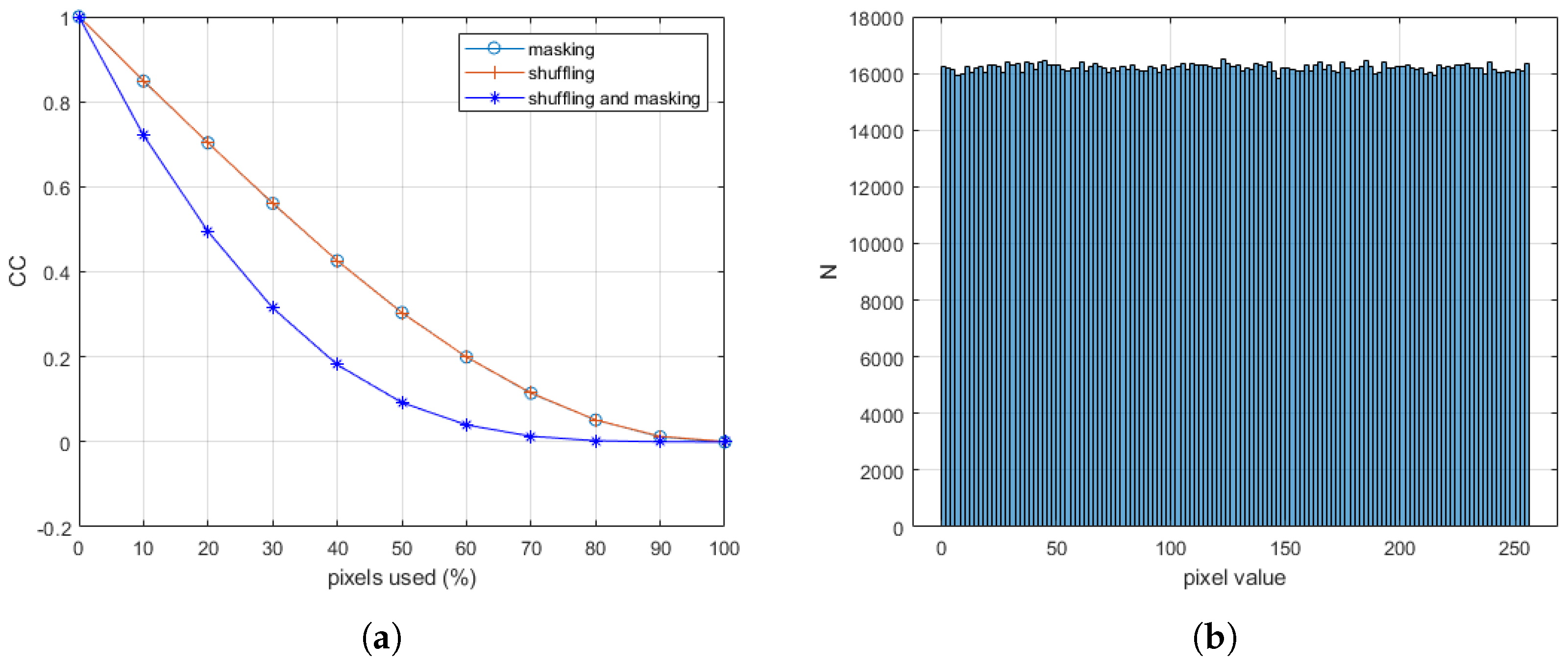
- Pixel Shuffling: As will be shown next, pixel shuffling can be robust against brute force attacks when the number of possible pixel permutations is sufficiently large.
- Random Phase Modification: This adds an additional layer of complexity to the encryption, as it modifies the phase disturbance that each pixel of the CGH presents to the reconstruction wavefront. It also alters the phase histogram of the ciphertext, further complicating attacks using statistical tools.
4.1. Visual Assessment
4.2. Key Space
4.2.1. Remarks on Pixel Shuffling
- Probability that the first selected pixel matches the first pixel of the image: Suppose the first pixel has the value j within the range [0–255], and it appears times; then
- Probability that the second extraction matches the second pixel of the image: Suppose the second pixel has the value k within the range [0–255], and it appears times; thenHowever, it is also possible that it has the value j, in which case, the probability would be
- Following this reasoning, the probability that the L-th extraction matches the L-th pixel of the image: Suppose the L-th pixel has the value m within the range [0–255], and it appears times but has already appeared n times previously; then
4.2.2. Key Size Issues
4.2.3. Remarks on DRPE Phase Mask
4.3. Key Sensitivity
4.4. Sensitivity vs. Robustness of Information
4.5. Pixel Correlation
4.6. Pixel Distribution
4.6.1. Information Entropy
4.6.2. Efficiency Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Co. Publishers: Englewood, CO, USA, 2017; Volume 1. [Google Scholar]
- Singh, M.; Singh, A.K. A comprehensive survey on encryption techniques for digital images. Multimed. Tools Appl. 2023, 82, 11155–11187. [Google Scholar] [CrossRef]
- SaberiKamarposhti, M.; Ghorbani, A.; Yadollahi, M. A comprehensive survey on image encryption: Taxonomy, challenges, and future directions. Chaos Solitons Fractals 2024, 178, 114361. [Google Scholar] [CrossRef]
- Javidi, B.; Carnicer, A.; Yamaguchi, M.; Nomura, T.; Pérez-Cabré, E.; Millán, M.S.; Nishchal, N.K.; Torroba, R.; Barrera, J.F.; He, W.; et al. Roadmap on optical security. J. Opt. 2016, 18, 083001. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Xu, B.; Chen, J. Optical image encryption and authentication using phase-only computer-generated hologram. Opt. Lasers Eng. 2021, 146, 106722. [Google Scholar] [CrossRef]
- Daemen, J.; Rijmen, V. The Design of Rijndael; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Memiş, S.; Lai, Q.; Hu, G. An image encryption method based on multi-space confusion using hyperchaotic 2D Vincent map derived from optimization benchmark function. Nonlinear Dyn. 2023, 111, 20377–20405. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Paul, G.; Maitra, S. RC4 Stream Cipher and Its Variants; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. Fully Homomorphic Encryption without Bootstrapping. ACM Trans. Comput. Theory 2014, 6, 1–36. [Google Scholar] [CrossRef]
- Research, M. Microsoft SEAL (Simple Encrypted Arithmetic Library). 2020. Available online: https://github.com/microsoft/SEAL (accessed on 10 February 2025).
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Bernstein, D.J.; Lange, T.; Peters, C. Post-Quantum Cryptography. Nature 2017, 549, 188–195. [Google Scholar] [CrossRef]
- Bos, J.W.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Kyber: A CCA-Secure Module-Lattice-Based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar] [CrossRef]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A Ring-Based Public Key Cryptosystem. In Algorithmic Number Theory; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Lepoint, T.; Seiler, G. CRYSTALS-Dilithium: Digital Signatures from Module Lattices. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 356–373. [Google Scholar] [CrossRef]
- Zhang, L.; Liao, X.; Wang, X. An image encryption approach based on chaotic maps. Chaos Solitons Fractals 2005, 24, 759–765. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A Novel Multi-Channel Image Encryption Algorithm Leveraging Pixel Reorganization and Hyperchaotic Maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Qian, K.; Xiao, Y.; Wei, Y.; Liu, D.; Wang, Q.; Feng, W. A Robust Memristor-Enhanced Polynomial Hyper-Chaotic Map and Its Multi-Channel Image Encryption Application. Micromachines 2023, 14, 2090. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Tamaki, K. Secure Quantum Key Distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Hao, W.; Zhang, T.; Chen, X.; Zhou, X. A hybrid NEQR image encryption cryptosystem using two-dimensional quantum walks and quantum coding. Signal Process. 2023, 205, 108890. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Bao, X. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Meng, F.; Gu, Z. A Color Image-Encryption Algorithm Using Extended DNA Coding and Zig-Zag Transform Based on a Fractional-Order Laser System. Fractal Fract. 2023, 7, 795. [Google Scholar] [CrossRef]
- Cheng, L.; Yu, W.; Zhang, Z.; Zhang, Y. Image encryption using deep learning. Neurocomputing 2019, 338, 144–152. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. A novel image encryption algorithm with deep neural network. Signal Process. 2022, 196, 108536. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, X.; Jin, M.; Zhang, L.; Xu, B. Optical image encryption based on two-channel detection and deep learning. Opt. Lasers Eng. 2023, 162, 107415. [Google Scholar] [CrossRef]
- Chen, W.; Javidi, B.; Chen, X. Advances in optical security systems. Adv. Opt. Photon. 2014, 6, 120–155. [Google Scholar] [CrossRef]
- Nishchal, N.K. Optical Cryptosystems; IOP Publishing Ltd.: Bristol, UK, 2019; pp. 1–180. [Google Scholar] [CrossRef]
- Singh, H.; Yadav, A.K.; Vashisth, S.; Singh, K. Double phase-image encryption using gyrator transforms, and structured phase mask in the frequency plane. Opt. Lasers Eng. 2015, 67, 145–156. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef]
- Tajahuerce, E.; Javidi, B. Encrypting three-dimensional information with digital holography. Appl. Opt. 2000, 39, 6595–6601. [Google Scholar] [CrossRef]
- Takeda, M.; Nakano, K.; Suzuki, H.; Yamaguchi, M. Encrypted imaging based on algebraic implementation of double random phase encoding. Appl. Opt. 2014, 53, 2956–2963. [Google Scholar] [CrossRef]
- Carnicer, A.; Montes-Usategui, M.; Arcos, S.; Juvells, I. Vulnerability to chosen-cyphertext attacks of optical encryption schemes based on double random phase keys. Opt. Lett. 2005, 30, 1644–1646. [Google Scholar] [CrossRef]
- Hamadi, I.A.; Jamal, R.K.; Mousa, S.K. Image encryption based on computer generated hologram and Rossler chaotic system. Opt. Quantum Electron. 2022, 54, 33. [Google Scholar] [CrossRef]
- Hu, T.; Ying, Y.; Sun, X.; Jin, W. The recovery scheme of computer-generated holography encryption–hiding images based on deep learning. Opt. Commun. 2023, 529, 129100. [Google Scholar] [CrossRef]
- Nomura, T.; Javidi, B. Optical encryption based on the input phase mask designed for the space bandwidth of the optical system. In Optical Information Systems III; Javidi, B., Psaltis, D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2005; Volume 5908, p. 59080B. [Google Scholar] [CrossRef]
- Kajiya, J.T. The rendering equation. SIGGRAPH Comput. Graph. 1986, 20, 143–150. [Google Scholar] [CrossRef]
- PLUTO-2 Phase Only Spatial Light Modulator (Reflective) | HOLOEYE Photonics AG. Available online: https://holoeye.com/products/spatial-light-modulators/pluto-2-1-lcos-phase-only-refl/ (accessed on 10 February 2025).
- Magallón, J.A.; Blesa, A.; Serón, F.J. Monte–Carlo Techniques Applied to CGH Generation Processes and Their Impact on the Image Quality Obtained. Eng. Rep. 2025, 7, e13109. [Google Scholar] [CrossRef]
- Durstenfeld, R. Algorithm 235: Random permutation. Commun. ACM 1964, 7, 420. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Pi, D.; Liu, J.; Wang, Y. Review of computer-generated hologram algorithms for color dynamic holographic three-dimensional display. Light. Sci. Appl. 2022, 11, 231. [Google Scholar] [CrossRef] [PubMed]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for reducing speckle noise in digital holography. Light. Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef]
- Blinder, D.; Birnbaum, T.; Ito, T.; Shimobaba, T. The state-of-the-art in computer generated holography for 3D display. Light. Adv. Manuf. 2022, 3, 572–600. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for Chaos-Based Cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming, Volume 1: Fundamental Algorithms, 3rd ed.; Includes discussion on Stirling’s approximation in combinatorial analysis; Addison-Wesley: Boston, MA, USA, 1997. [Google Scholar]
- Witten, I.H.; Neal, R.M.; Cleary, J.G. Arithmetic coding for data compression. Commun. ACM 1987, 30, 520–540. [Google Scholar] [CrossRef]





| Description | Figure | Entropy H(X) |
|---|---|---|
| Image from 3D scene 1 | Figure 2a | 7.067178 |
| CGH | Figure 2b | 7.994257 |
| Encrypted CGH | Figure 4a | 7.994281 |
| Image from recovered scene (simulation) | Figure 5a | 5.389448 |
| Image from recovered scene (lab) 1 | Figure 5b | 6.072168 |
| Process | t(s.) |
|---|---|
| (a) Scene synthesis | 26.55 |
| (b) CGH synthesis | 1600.37 1 |
| (c) Encryption | 0.32 |
| (d) Decryption | 0.32 |
| (e) Scene simulation | 0.78 |
| CGH Size (in Pixels) | t(s.) |
|---|---|
| 1600.37 | |
| 809.08 | |
| 204.27 | |
| 56.06 | |
| 16.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blesa, A.; Serón, F.J. Advancement of the DRPE Encryption Algorithm for Phase CGHs by Random Pixel Shuffling. Appl. Sci. 2025, 15, 4120. https://doi.org/10.3390/app15084120
Blesa A, Serón FJ. Advancement of the DRPE Encryption Algorithm for Phase CGHs by Random Pixel Shuffling. Applied Sciences. 2025; 15(8):4120. https://doi.org/10.3390/app15084120
Chicago/Turabian StyleBlesa, Alfonso, and Francisco J. Serón. 2025. "Advancement of the DRPE Encryption Algorithm for Phase CGHs by Random Pixel Shuffling" Applied Sciences 15, no. 8: 4120. https://doi.org/10.3390/app15084120
APA StyleBlesa, A., & Serón, F. J. (2025). Advancement of the DRPE Encryption Algorithm for Phase CGHs by Random Pixel Shuffling. Applied Sciences, 15(8), 4120. https://doi.org/10.3390/app15084120






