1. Introduction
Although significant efforts are ongoing in construction projects using project management methods to have them completed within their budgets and schedules, construction is characterized by delays and overrun costs. Delayed projects and over-run costs greater than 100% of the initially planned project duration and cost are common in developing countries, and, usually, the contractors and the project owners are in disagreement [
1].
Schedule compression in the construction sector has received consideration as an initiative to address these challenges from the academic research and professional practice points of view. Both project owners and contractors gain benefits in reducing the project length for different reasons. Therefore, contractors speed up the completion of the project to fulfil contracted items, to avoid delays in the project, and use the least time possible to complete the projects. Project owners wants to speed up project delivery so that the project meets the needs of the market conditions and stakeholders. The time–cost problem, which what this process is known as in the academic literature, involves selecting the minimum cost duration so any project can be implemented with a given duration [
2]. Thus, decreasing the project schedule duration leads to increases in the direct and decrements in the indirect costs. The expenses incurred for all resources utilized in the project execution phase form a part of the direct costs, and indirect costs and are spent even without the work being performed. Shortening the schedule necessitates hiring additional resources to accelerate individual activities, which gradually raises direct costs while steadily decreasing indirect costs. In view of this, academics and industry experts have been interested in the reduction in these supplementary direct expenses and the identification of the best minimum cost duration.
Resource planning, allocation, and leveling are major challenges for executing compressed construction projects. Researchers and industry experts have devised various techniques so that they can optimize scheduling and minimize the project duration at the minimum cost. The critical path method (CPM) has been one of the most used methods for scheduling in construction. CPM scheduling was introduced in the late 1950s by Morgan Walker and James Kelley to minimize the expenses resulting from the interruption and subsequent resumption of project operations when scheduling is not effective. CPM works very well in identifying the critical duration of a project and reducing the overall duration of a project. However, this is not a part of resource planning in the scheduling process, and substantial expenses as the result of disproportionately allocating a certain resource have been pointed out and called resource leveling [
3]. In order to meet the continuous and variable demands for resources over time, the amendment of these resources to meet these needs requires additional cost, which includes the cost of hiring and termination, which is called acquisition and releasing.
In the problem of resource planning, contending with the uncertainty around activity duration and cost adds to the complexity, making this an inherently hard combinatorial problem. Project management is complex because it is based on the unrealistic expectation that project managers know the exact duration and cost of each activity in advance. In truth, construction projects are inherently unique, as no two projects are the same in any manner. Such uncertainty in project execution is influenced by the combined effects of many internal and external factors (e.g., economic and social pressure, work risks, and climatic changes). To deal with these uncertainties, a framework that can consider these factors properly is probability theory, which has been adopted by researchers dealing with this type of project. It is difficult to store, record, and analyze historical construction data; thus, cost and time data are not easy to use and have not been frequently used to solve this problem in the past [
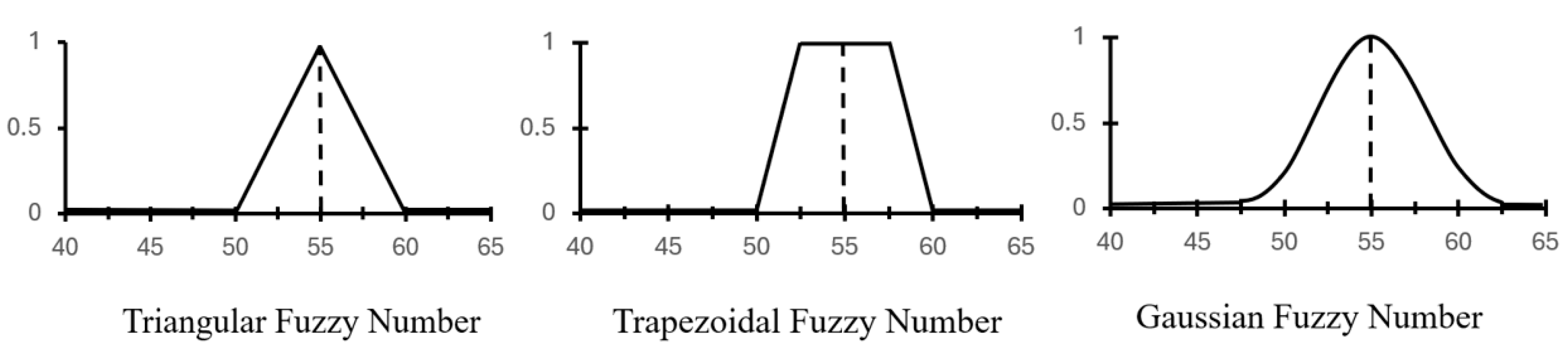
4]. Therefore, the probabilistic distributions for different project activities cannot be accurately determined. To address the challenges mentioned above, FST, which analyzes uncertainty-related factors, is a more promising way. Unsurprisingly, the membership of an element in a fuzzy set is any real value between 0 and 1, and so, it is much more suitable for representing uncertainty if the numerical boundaries of element membership cannot be associated accurately. Once fuzzy models are properly used, then construction projects can be more accurately scheduled, such that, at the same time, we can achieve accuracy and efficiency in production planning.
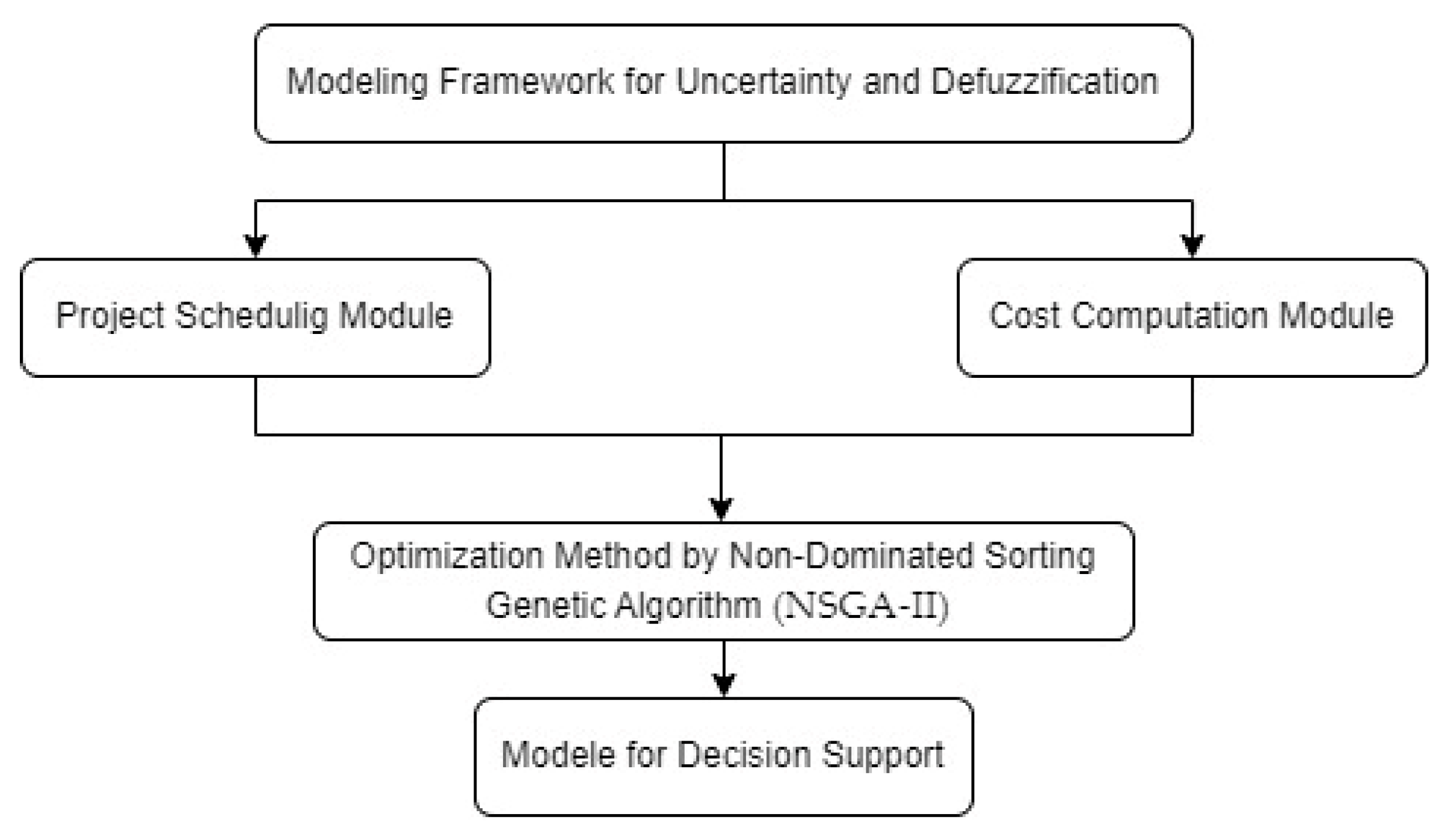
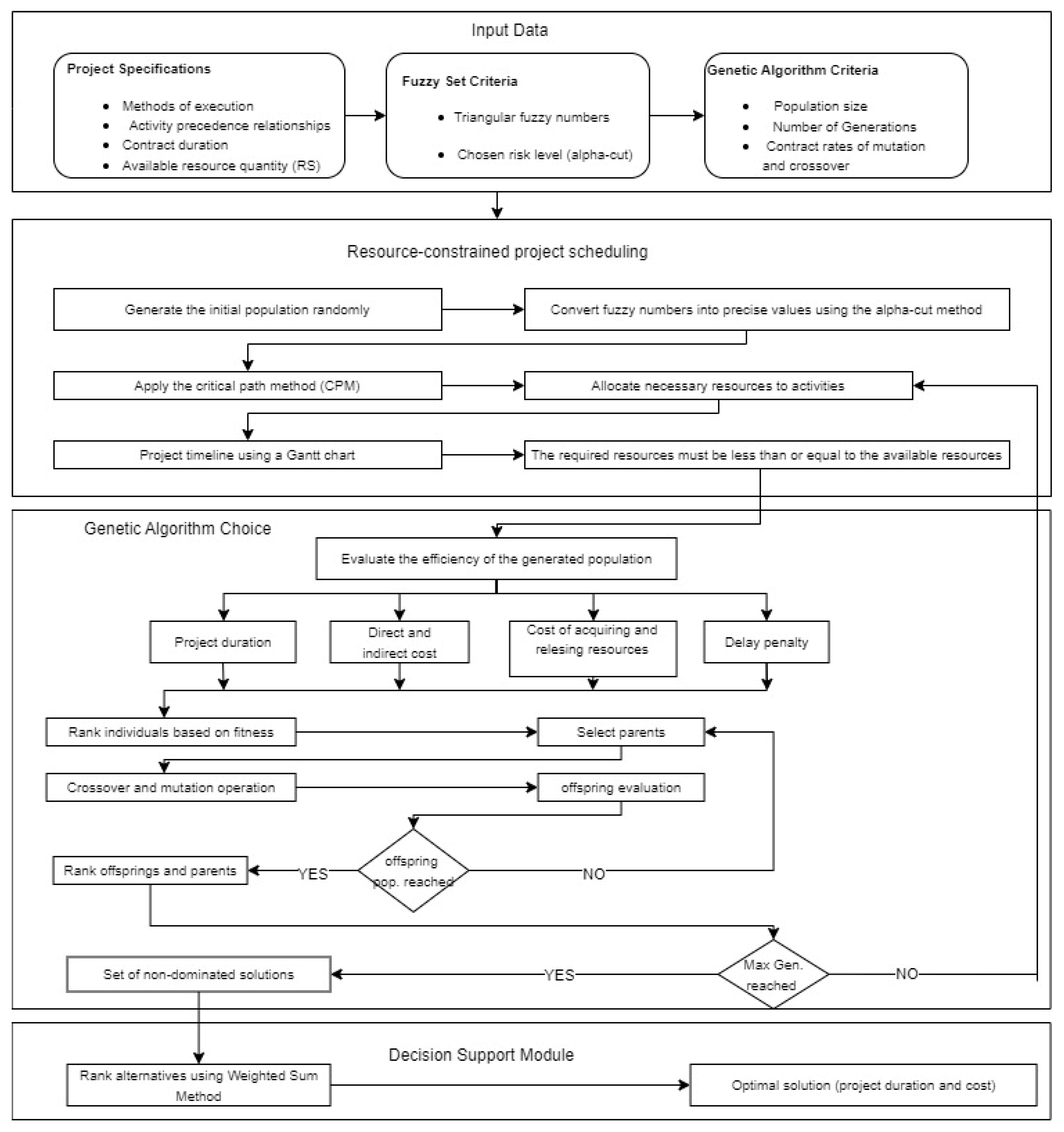
The purpose of this research was to find a model for compressing construction schedules under resource constraints, while taking into account resource leveling as well as the uncertainty related to both the cost of the activity and its duration. In order to achieve this goal, there were subobjectives we fulfilled, which were
Determining model uncertainties related to activity duration and cost.
Optimizing resource allocation and leveling.
Developing a fully automated and efficient computational tool.
By fulfilling these objectives, this study aimed to bridge the gaps in construction scheduling methodologies and provide a more effective framework for project acceleration while maintaining cost efficiency and resource optimization.
2. Literature Review
The available literature provides various approaches and algorithms for optimizing project scheduling by leveraging well-defined objective functions aligned with decision-makers’ goals. These methods aim to enhance the efficiency of planning for resource-limited projects and reduce project duration.
Exact, heuristic, and metaheuristic or evolutionary methods are some of these algorithms. Methods are used with these algorithms for finding the optimal solution, but they can be computationally expensive for large problems. Heuristic methods are suitable for complex problems due to their ability to give good (not optimal) solutions quickly. A set of more technologically advanced methodologies based on metaheuristic and evolutionary methods, which have been largely inspired by natural phenomena, have been refined, leading to the search for high-quality solutions within a reasonable time. For objective functions, time, and cost, or quality-based classification is performed. Mathematical models for establishing relationships between objective functions and problem constraints are exact methods to determine the optimal solution exactly. These methods use different optimization techniques like linear programming, which is used when the relation between variables is linear, to help improve problem-solving processes.
Dynamic programming is also used as it allows problems to be broken down into smaller subproblems whose solutions are combined to solve the overall problem, and this helps reduce computational complexity and tends to improve performance. On the other hand, these methods are being very accurate in solving optimal solutions, so they are very reasonable in solving complex problems that need exact and reliable results [
5]. Rules are used for solving complex problems, which involve heuristic methods; that is, heuristic methods use rules in order to select good solutions and discard the ones that are unacceptable, quickly jumping to a near or an optimal solution. The most used technique is branch and bound, which divides the problem and excludes unpromising solutions systematically based on estimated bounds, which enhances search efficiency. However, it is an effective technique for solving the traveling salesperson problem )TSP), for which the boundedness and branching algorithms can be used, but no single algorithm is suitable for all problems because the appropriate strategy depends upon the type of problem [
6].
Advanced approaches, typically called metaheuristic and evolutionary algorithms, are applied to find solutions for complex problems such as total cost optimization (TCO). Despite computational constraints, the strategies used for finding solutions that are high quality are heuristic. The methods include genetic algorithms (GAs), which are inspired by natural evolution by selection, crossover, and mutation; ant colony optimization (ACO), which imitates the behavior of ants when searching for food to improve search efficiency; and particle swarm optimization (PSO), which uses swarm intelligence to obtain a fast and efficient solution. On the contrary, while the GA relies on natural selection, ACO and PSO utilize collective knowledge to enhance the search for solutions. At the same time, these algorithms are very powerful tools for speeding up and facilitating the finding of solutions to complex optimization problems that most traditional methods struggle to deal with.
The research on resource-constrained project scheduling and schedule compression can be divided into four categories: time cost optimization models, deterministic scheduling, scheduling under uncertainty, and resource allocation models. The objectives of the TCO model are minimizing project duration while following budget constraints [
7]. Schedules based on resource availability and deadlines are optimized in deterministic models [
8]. These concepts are applied to scheduling under uncertainty, which is related to unpredictable project conditions. Equations that are NP-hard problems include resource allocation models for optimizing project duration and cost, to ensure project resource usage is balanced and sound.
Different approaches to tackling the time–cost in project scheduling have been developed by researchers. The multiple binary decision method (MBDM) was suggested to minimize project duration at the minimum cost, and Ref [
9] sed fuzzy cost analysis and expert judgment to optimize schedule compression. Ref. [
10] applied a convex hull method and genetic algorithms in order to obtain optimal solutions, while [
11] proposed an adaptive weight method for improving the search for superior solutions. Ref. [
12] used an ant colony optimization (ACO) algorithm to solve time–cost trade-off problems [
13]. A particle swarm optimization (PSO) algorithm was proposed to achieve superior solution quality and computational efficiency for large-scale projects. Researchers [
14] used TLBO with a modified adaptive weight method to find better Pareto front solutions than the previous metaheuristic methods used in construction engineering and project management.
The resource-constrained project scheduling problem (RCPSP) is a major challenge since its basic form assumes that each activity is executed within a single mode within a single processing time using one unit of a single renewable resource. The one-mode resource-constrained project scheduling problem has been extended to the, mode resource-constrained project scheduling problem (MMRCPSP) where activities can be accomplished in different execution modes with different durations and resource requirements [
15]. Several methods have been proposed to solve the MMRCPSP. A branch-and-bound method, developed by [
16], and a global optimization algorithm for balancing [
17] have been applied to deal with the among time, cost, and quality in this problem. Heuristic approaches have also been developed to solve this problem with better efficiency, including the multi-pass priority approach with backward planning [
18]. Metaheuristic algorithms have recently been used in optimization studies. CP was applied to optimize schedule compression by [
19,
20], who developed a two-phase genetic algorithm to deal with the time–cost trade-off as well. The proposed multi-objective model for both renewable and non-renewable resources to maximize the net present value and minimize project duration is based on the genetic algorithm and simulated annealing [
21]. This idea was first proposed by [
22], namely, a classification of renewable and non-renewable resources. Similarly, Ref. [
23] proposed an ant colony optimization (ACO) algorithm to deal with resource constraints, and other authors [
24] utilized linear programming to determine the best way to execute activities while releasing the resources in predetermined quantities at predetermined times. Finally, Ref. [
25] examined the multi-project scheduling problem, proposing resource-sharing policies to minimize deviations between planned and actual project completion times.
Project scheduling success relies on the amount of accurate information that can be collected before project initiation. However, data availability is limited to the estimation of the duration, costs, and resource availability. Because of these problems, researchers have chosen to adopt fuzzy set (FS) theory instead of stochastic models. Mathematical and metaheuristic models have been adopted. Risk levels [
26] were defined with time–cost optimization with the use of the α-cut method; Ref. [
27] integrated scheduling and resource allocation under uncertainty. Ref. [
28] applied the ant colony optimization (ACO) algorithm to facilitate the time–cost trade-off decision-making process. Later, these inefficiencies were reduced using metaheuristic models. To perform scheduling, Ref. [
29] applied a particle swarm optimization algorithm operating with a genetic algorithm. At the same time, Ref. [
30] created a comprehensive model based on repetitive scheduling, fuzzy set theory, and genetic algorithms to optimize cost, delays, and scheduling.
Distributing resources according to constraints and leveling is a very complex problem that falls under the category of resource allocation scheduling problems in project management. The numbers of resources, activities, and execution modes make it a complex problem. Genetic-algorithm-based models [
31] and NSGA-II applications have been developed extensively for different multi-mode project scheduling and resource leveling problems [
32]. Recent research emphasizes incorporating resource allocation into time buffering via robust scheduling methods, which aim to increase efficiency between cost and quality in dynamic project environments.
Through a comprehensive review of the literature on schedule compression and project scheduling, several observations (gaps) were identified, along with potential improvements that could enhance the efficiency and accuracy of project schedules.
Table 1 provides a summary of the capabilities and limitations of the methods found in the most recent and relevant references in this field.
The gaps identified in previous research can be summarized as follows:
Resource scheduling methods that are unconstrained by available resources.
Deterministic scheduling methods under resource constraints.
Scheduling methods that ignore delay penalties.
Scheduling methods that do not consider the additional costs associated with resource management, whether during resource acquisition (hiring) or release (firing).
To address these research gaps, this paper presents a comprehensive approach that advances project scheduling models and schedule compression methodologies. The proposed framework effectively balances project duration, cost, and resource constraints, making it more applicable to real-world scenarios. This approach enhances execution efficiency and reduces overall project costs, providing an innovative model that surpasses the traditional scheduling methods in this field.
5. Results of NSGA-II Optimization Approach
As shown in
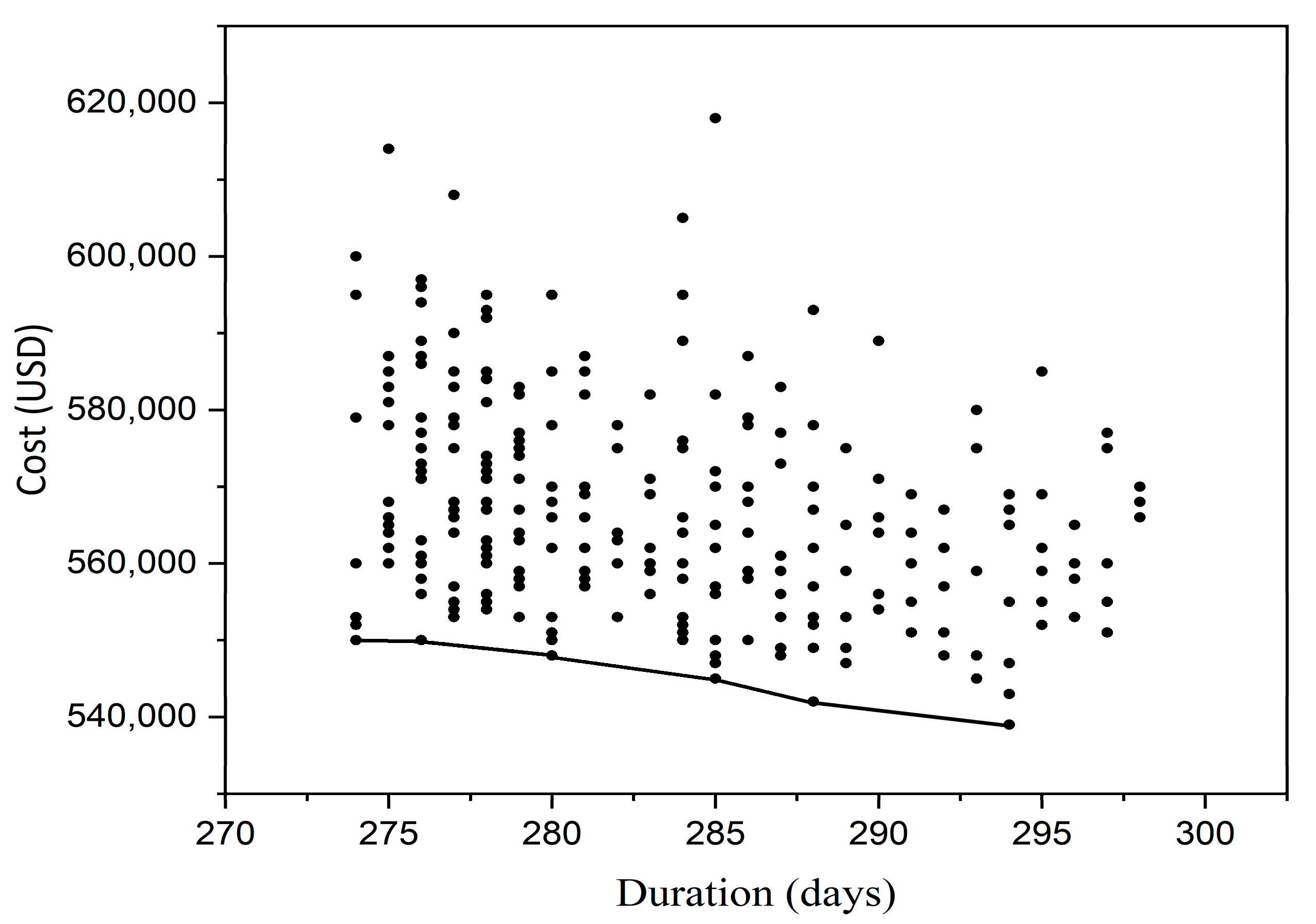
Table 6, the non-dominated set of solutions was generated after executing 200 generations in an optimized NSGA-II with population size = 50, crossover rate = 0.4, and mutation rate = 0.6. The optimal solution among them was identified using the weighted sum technique. The optimal choice was determined as the solution with the smallest preference index (PI), since the problem was solved using the minimization approach. The penultimate solution was the optimum, i.e., the PI value was 0.16549756, duration of implementation was 274 days and cost was USD 550,000. The solutions obtained after executing 200 generations using the optimization algorithm are presented in
Figure 7. The curve illustrates the relationship between cost and time, representing the non-dominated set of solutions that reflects the best achievable balance between these two factors. This set comprises the most efficient solutions, where no single criterion can be improved without compromising the other.
Table 7 represents the appropriate implementation mode for each of the activities in the project; it illustrates the execution mode for each project activity after applying the optimal solution identified through the optimization algorithm. This selection was made by achieving the optimal balance between cost, time, and resources based on the optimization criteria adopted in this study.
Based on
Table 6, the selected execution mode for each project activity was determined.
Table 8 presents the optimal duration, cost, and resource allocation for each project activity. Furthermore,
Figure 8 presents the project network, illustrating the execution time for each activity, the earliest start and finish times, the latest start and finish times, as well as the floating period duration.
The project cost distribution for the project using the method proposed in this study is presented in
Table 9. By comparing the obtained results (274 days and USD 632,200) with the contracted project duration and cost (285 days and USD 660,500), it is obvious that applying the method will lead to the project being completed in shorter time and at a lesser cost. We found that the proposed method is capable of finding a globally optimal solution and avoid entrapment in local minima. And, the main advantage of the method used for scheduling optimization is the implementation of the NSGA-II algorithm and its capability of reassigning resources for noncritical activities within their floating periods. This results in effective monitoring of constraints to resource without exceeding cost or duration of project activities.
Summary of Results
The optimization approach using the NSGA-II algorithm successfully identified an optimal project schedule by balancing cost, time, and resource constraints. After 200 generations, the best solution was determined using the weighted sum technique, with an optimal preference index (PI) of 0.16549756, a project duration of 274 days, and a total direct cost of USD 550,000. The analysis of the non-dominated set of solutions demonstrates that no single criterion (cost or time) could be improved without negatively impacting the other. By applying the optimal execution mode for each project activity (as detailed in
Table 7 and
Table 8), resources for noncritical activities within their floating periods are redistributed effectively using our method. Comparing the obtained results (274 days and USD 632,200) with the contracted project duration and cost (285 days and USD 660,500), using the proposed method achieved a shorter project duration and lower cost. This confirms the effectiveness of NSGA-II in avoiding local minima and identifying a globally optimal solution. The method’s ability to dynamically allocate resources while maintaining project constraints ensures an efficient and feasible scheduling solution.