Genetic Algorithm-Based Model Updating in a Real-Time Digital Twin for Steel Bridge Monitoring

Abstract

The integration of digital twin technology with structural health monitoring (SHM) is revolutionizing the assessment and maintenance of critical infrastructure, particularly bridges. Digital twins—virtual, data-driven replicas of physical structures—enable real-time monitoring by continuously synchronizing sensor data with computational models. This study presents the development of a real-time digital twin for a three-span steel railway bridge, utilizing a high-fidelity finite element (FE) model built using OpenSeesPy v 3.5 and instrumented with 18 strategically placed accelerometers. The dynamic properties of the bridge are extracted using Stochastic Subspace Identification (SSI), enabling an accurate estimation of modal parameters. To enhance the fidelity of the digital twin, a genetic algorithm-based model-updating strategy is implemented, optimizing the steel elastic modulus to minimize discrepancies between measured and simulated frequencies and mode shapes. The results demonstrate a remarkable reduction in frequency errors (below 5%) and a significant improvement in modal shape correlation (MAC > 0.93 post-calibration), confirming the model’s ability to reflect the bridge’s true condition. This work underscores the potential of digital twins in predictive maintenance, early damage detection, and life-cycle management of bridge infrastructure, offering a scalable framework for real-time SHM in complex structural systems.

1. Introduction

The aging global infrastructure, particularly with regard to bridges, demands innovative approaches to ensure structural integrity, safety, and longevity. Structural Health Monitoring (SHM) has emerged as a critical tool for early damage detection and preventive maintenance, yet traditional methods often rely on periodic inspections or offline analyses, which lack real-time insights. The introduction of digital twin technology—dynamic, virtual replicas of physical systems—has revolutionized SHM by enabling continuous, data-driven monitoring and predictive analytics. Digital twins integrate real-time sensor data, physics-based models, and machine learning to mirror a structure’s behavior, offering unprecedented capabilities to predict failures, optimize maintenance, and extend service life.

The inherent challenges in predicting structural behavior under dynamic loads requires the development of accurate numerical models, predominantly constructed using the finite element method (FEM) [1,2,3]. These models serve as critical tools for simulating a structure’s real-world conditions, enabling predictions of its dynamic response (e.g., resonance frequencies, displacement patterns, and stress distributions) under operational or extreme loading scenarios [4]. Recent studies have highlighted the application of FEM in analyzing composite steel-UHTCC (Ultra-High Toughness Cementitious Composite) bridge structures, offering valuable insights into their mechanical performance. For instance, Chen et al. [5] investigated the local instability and interactive mechanisms of UHTCC-encased rectangular steel tubular columns, demonstrating the material’s ability to enhance structural stability under compressive loads. Similarly, Tong et al. [6] explored the flexural performance and crack width prediction of steel-UHTCC composite bridge decks with wet joints, emphasizing the importance of accurate FEM modeling for predicting serviceability limits. Additionally, Chen et al. [7] examined the flexural behavior of novel profiled steel-UHTCC assembled composite bridge decks, showcasing the potential of FEM in optimizing design parameters for improved load-bearing capacity.

Such simulations are indispensable for optimizing maintenance strategies and ensuring long-term structural integrity. However, constructing reliable numerical models is often hindered by severe data limitations: historical records of material properties (e.g., concrete compressive strength, steel yield stress), boundary conditions (e.g., foundation rigidity, joint fixity), and damage states (e.g., crack propagation, corrosion) are frequently incomplete, outdated, or absent entirely [8,9]. Consequently, engineers must rely on idealized assumptions about material behavior, structural connectivity, and degradation mechanisms—factors that profoundly influence model accuracy but rarely reflect real-world complexities. For instance, simplifications in modeling aging concrete’s time-dependent stiffness loss or poorly documented retrofit interventions can lead to significant discrepancies between simulated and observed behavior. To address these limitations, structural health monitoring (SHM) systems have emerged as a cornerstone of modern infrastructure management [10]. By deploying sensor networks (e.g., accelerometers, strain gauges, temperature sensors) to collect real-time data on structural responses—such as vibration modes, load distributions, and environmental effects—SHM provides empirical insights into a structure’s operational state. These datasets are pivotal for diagnosing anomalies (e.g., localized stiffness reduction, unbalanced loads) and informing data-driven model calibration. For example, SHM-derived modal parameters (e.g., natural frequencies, damping ratios) can be used to iteratively refine FEM assumptions through optimization algorithms (e.g., genetic algorithms, Bayesian inference), minimizing the gap between simulated and measured behavior [11,12]. This synergy between experimental observation and computational modeling not only enhances predictive accuracy but also enables adaptive maintenance planning, ensuring interventions are prioritized based on quantifiable risk rather than heuristic judgment.

Digital twins originated in the manufacturing and aerospace industries but have gained traction in civil engineering over the past decade. Pioneering studies by Grieves [13] and Tao et al. [14] established their potential for infrastructure monitoring, emphasizing the synergy between sensors and computational models. For bridges, digital twins have been applied to track dynamic responses, assess load capacities, and simulate extreme-event scenarios [12,15,16,17,18,19]. Key challenges include achieving model fidelity, handling sensor noise, and ensuring computational efficiency for real-time updates.

A critical component of digital twins is operational modal analysis (OMA), which extracts modal parameters (natural frequencies, damping ratios, mode shapes) from ambient or operational vibrations. Techniques like Stochastic Subspace Identification (SSI) have become cornerstones of OMA due to their robustness in output-only scenarios [20]. Recent advancements integrate SSI with finite element (FE) models to calibrate digital twins [21,22], though discrepancies between numerical and experimental results persist due to material variability and modeling assumptions.

Model updating—a process to align FE models with real-world data—has been addressed through optimization algorithms. Genetic algorithms (GA) and Bayesian inference are widely used to minimize errors in frequencies and mode shapes [23,24,25,26]. However, few studies have combined high-density sensor networks, SSI-based modal identification, and multi-objective optimization in a unified digital twin framework, particularly for steel-truss railway bridges with complex dynamic behavior.

This study advances digital twin technology for bridge SHM by developing a real-time monitoring system that integrates (a) high-resolution sensor data from 18 accelerometers strategically placed to capture modal shapes; (b) SSI-based OMA to extract free-vibration responses and identify physical modes using stabilization diagrams; and (c) finite element model calibration via a genetic algorithm, optimizing steel elastic modulus to align numerical and experimental frequencies and mode shapes.

The methodology’s efficiency is demonstrated through a case study on a three-span steel-truss railway bridge, showcasing how real-time data and model updating enhance predictive maintenance. The integration of OpenSeesPy [27] for FE modeling and PyGAD [28] for optimization underscores the practicality of the approach for field applications.

Following this, Section 2 details the bridge’s geometry and sensor configuration. Section 3 outlines the SSI methodology and modal identification process. Section 4 presents the FE model development and calibration results, and Section 5 discusses implications for SHM. The conclusions highlight the twin’s role in transforming bridge maintenance paradigms.

By bridging gaps between sensor data, computational models, and real-world behavior, this work provides a scalable blueprint for digital twin deployment in critical infrastructure.

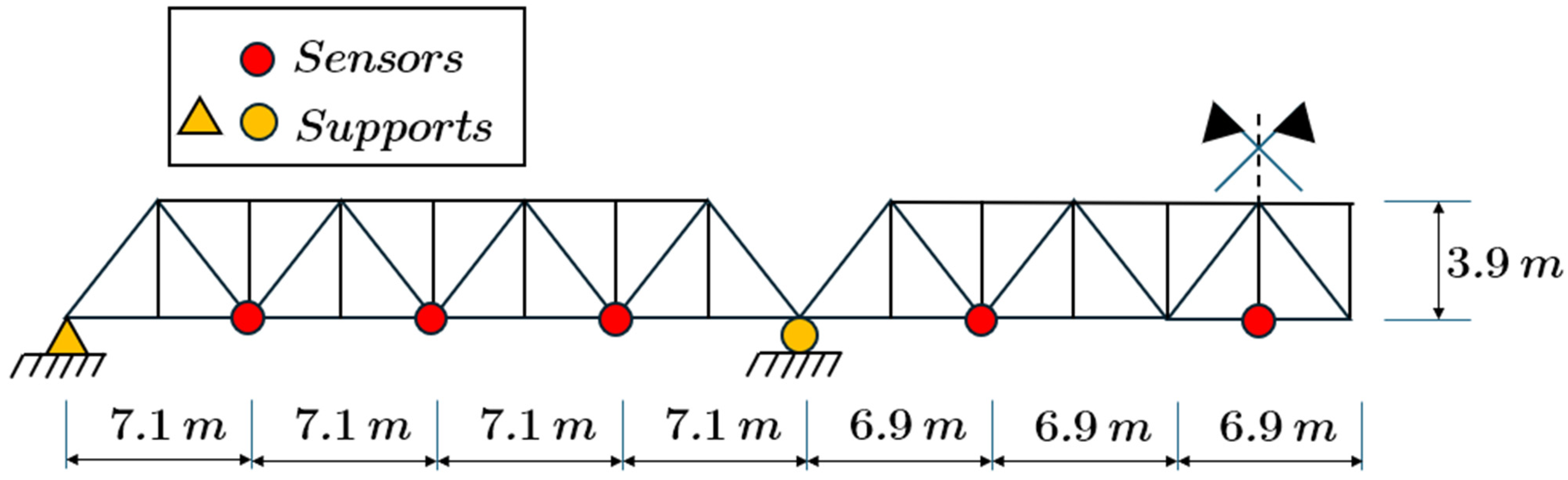
2. Case Study

The bridge shown in Figure 1 consists of three simply supported spans constructed with steel trusses, featuring a closed triangular mesh design. The side spans measure 28.54 m each, while the central span is slightly longer, at 34.72 m. The bridge rests on piers made of masonry, which have a width of 7.23 m, a height of 4.90 m, and a minimum thickness of 2.26 m. Each pier is capped with a cement conglomerate top cap for added structural integrity.

The lateral and central spans that are subject to monitoring exhibit highly regular modal behavior. Consequently, the placement of the accelerometer sensors was strategically designed to capture these modal shapes accurately. Figure 2 shows the placement of sensors across the bridge. For each monitored span, six sensors were installed on the lower chord of the truss: two sensors at the centerline (one on each side) and two sensors (one on each side) at each quarter-span. This configuration ensures comprehensive monitoring and effective modal shape representation.

3. Real Bridge: Dynamic Identification

3.1. Extraction of Free Vibrations

An accelerogram recorded by a sensor can be segmented into three distinct phases based on the following vibration characteristics: (1) ambient vibrations (low-amplitude background noise); (2) train-induced vibrations (high-amplitude pseudo-stationary signals during train transit); (3) free vibrations (decaying oscillations post-train passage).

The effective duration of an accelerometric signal is defined as the time interval $t_{eff}=t_2-t_1$ between two instants $t_1$ and $t_2$ during which the central 90% fraction of the total Arias energy develops, defined as:

$$A_{tot}={\displaystyle \frac{\pi }{2g}}{\int }_0^T{a}^2\left(t\right)dt$$

(1)

where $a\left(t\right)$ is the acceleration time history, $g$ is the gravity acceleration and $T$ is the total duration of the signal.

The acceleration signal is then divided into three segments: ambient vibrations ($t<t_1$), high-amplitude pseudo-stationary vibrations from the passing train ($t_1\le t\le t_2$), and free vibrations ($t>t_2$).

As illustrated in Figure 3 the proposed method effectively identifies the three phases. The free vibration segment $t>t_2$ is particularly critical for analyzing structural damping and natural frequencies, as it represents the system’s unforced response.

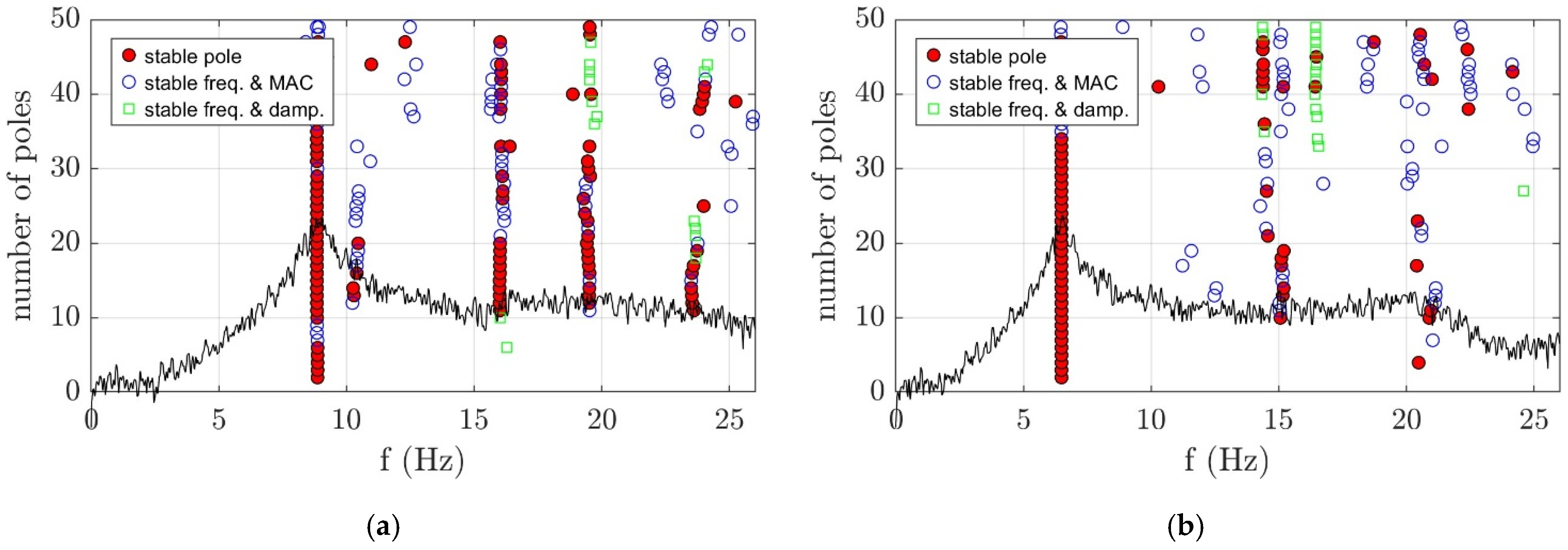
3.2. Operational Modal Analysis Using SSI

The Stochastic Subspace Identification (SSI) procedure is a widely used operational modal analysis (OMA) technique for extracting the modal characteristics (natural frequencies, damping ratios, and mode shapes) of structures, such as bridges, using output-only data from accelerometers. Unlike traditional methods that require input excitation measurements, SSI relies solely on the response data (e.g., accelerations) recorded by sensors installed on the structure.

To obtain the modal parameters, a discrete-time state-space representation is used:

$${\widehat{x}}_{k+1}=\left[A\right]\cdot {\widehat{x}}_k+\left[B\right]\cdot u_k$$

(2)

$$y_k=\left[C\right]\cdot {\widehat{x}}_k+\left[D\right]\cdot u_k$$

(3)

where $x_k=x_k\left({\Delta }_t\right)$ is the discrete-time state vector containing displacement and velocities of the system, $y_k$ is the vector of system response, $u_k$ is the vector of input, $\left[A\right]$ and $\left[B\right]$ are the matrices of input that contain, respectively, the physical information and the statistical parameters, $\left[C\right]$ is the output matrix, and $\left[D\right]$ is the direct transmission matrix in discrete time.

The primary challenge in estimating this parametric model lies in the uncertainty of the true model order, which is influenced by the presence of noise in the recorded signals or the limited availability of recordings. To address this, a strategy is employed where multiple models of increasing order are evaluated to capture all physical modes within the frequency range of interest. However, this approach also introduces numerous numerical modes (spurious modes) that lack physical significance and arise solely from the noise in the recordings.

The SSI method is applied to the free vibration segments extracted from six accelerometers strategically positioned on each span of the bridge. This approach utilizes the free vibrations of the structure to accurately estimate its dynamic properties. To differentiate between physical modes (true structural dynamics) and spurious modes (numerical artifacts or noise), a stabilization diagram (Figure 4) is employed. This diagram serves as a powerful visualization tool, plotting the system’s natural frequencies across multiple model orders. Stable modes, representing consistent physical behavior, appear as vertically aligned points, while spurious modes scatter randomly. Through this analysis, two dominant frequencies associated with the vertical modes of the bridge were identified. These frequencies correspond to the fundamental dynamic characteristics of the structure, providing critical insights into its vibrational behavior.

The identified frequencies are further validated by examining their corresponding modal shapes, as illustrated in Figure 5. These shapes depict the spatial deformation patterns of the bridge at each natural frequency, offering a deeper understanding of the structure’s dynamic response. For instance, the first mode typically represents the global bending or sway of the bridge, and the second mode often captures higher order bending or torsional behavior. By correlating the frequencies from the stabilization diagram with their respective modal shapes, the analysis confirms the physical significance of the identified modes. This step is crucial for ensuring that the results align with the expected dynamic behavior of the bridge. The identified frequencies and modal shapes serve as baseline data for structural health monitoring, enabling the detection of changes in the bridge’s dynamic properties that may indicate damage or degradation.

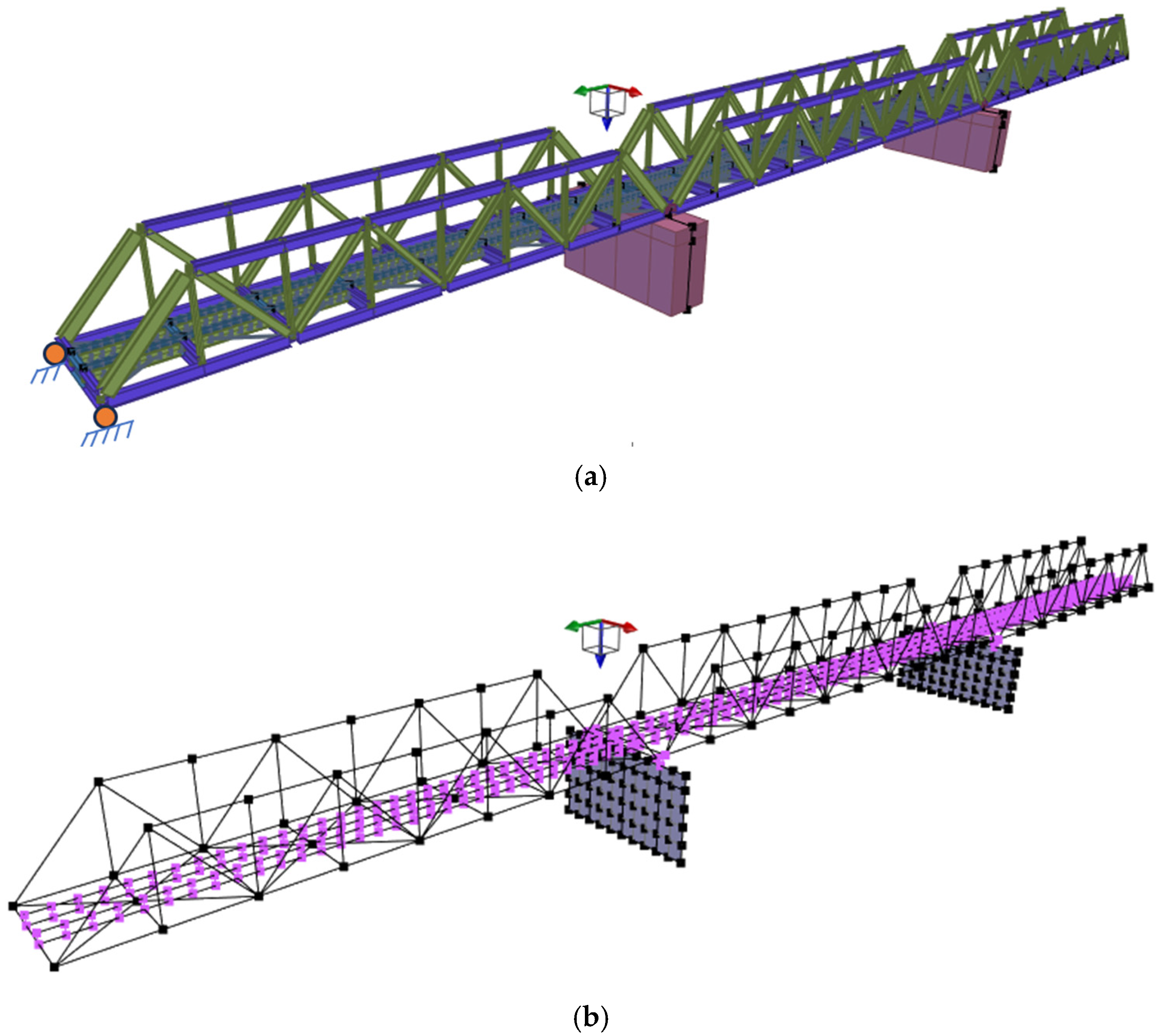
4. FE Modeling

The numerical model of the bridge was developed using the STKO [29] interface for OpenSees v 3.5 [27]. The model accurately represents a steel truss railway bridge with riveted connections, featuring three spans, as illustrated in Figure 6.

Table 1. Sectional details of the bridge elements.

Element	Profile
Braces	T 100 × 10 mm
Tracks	I 200 × 150 × 20 mm
Top chords	T 400 × 10 mm
Bottom chords	T 400 × 32 mm
Verticals	IPE300
Rail support beam	IPE500

summarizes various sectional details of the bridge. The elastic modulus ($E_s$) of all steel members is $200\mathrm{G}\mathrm{P}\mathrm{a}$. Below is a detailed description of the model’s components and their respective modeling approaches:

(1)

Braces: Modeled using T-profile truss elements to capture their axial load-bearing behavior.

(2)

Piers: Represented using 4-node shell elements (ASDShellQ4) to simulate their bending and shear resistance.

(3)

Ballast: Modeled as a series of springs to account for its elastic support and damping effects on the bridge structure.

(4)

Track Support Beams: Simulated using IPE beam elements to replicate their flexural and torsional stiffness.

(5)

Top and Bottom Chords: Modeled with double-T beam elements to accurately reflect their combined axial and bending capacities.

(6)

Verticals: Represented using IPE300 beam elements to capture their structural role in transferring loads between the chords and the diagonals.

(7)

Diagonals: Modeled using double-C beam elements to simulate their ability to withstand both tension and compression forces.

(8)

Boundary Conditions: The boundary conditions of the model were carefully defined to reflect real-world constraints: (1) the piers were fixed at their base to simulate their rigid connection to the foundation; (2) one abutment was constrained to block linear displacements along the x-, y-, and z-axes, as well as rotations about the x-axis, to represent a fixed support condition; (3) the other abutment was constrained to block linear displacements along the y and z axes, allowing for potential thermal expansion along the x-axis; (4) the spans were connected to the piers using rigidLink elements in OpenSees, ensuring a rigid connection that transfers forces and moments effectively.

The bridge is equipped with a monitoring system consisting of 12 triaxial accelerometric sensors. The sensors operate at a sampling rate of 1 kHz, providing high-resolution data for detailed analysis of the bridge’s behavior. This setup enables the detection of subtle vibrations, modal properties, and potential anomalies in the structure’s response.

Figure 7 illustrates the deformed shapes of the dominant vibration modes identified through modal analysis for spans 1 and 2 of the bridge.

Table 2. Comparison between the frequencies of the real bridge ($f_{real}$) and the uncalibrated finite element model ($f_{FE}$).

	Mode	${\mathit{f}}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}} \mathbf{\left(}\mathbf{H}\mathbf{z}\mathbf{\right)}$	${\mathit{f}}_{\mathit{F}\mathit{E}} \mathbf{(}\mathbf{H}\mathbf{z}$)	${\Delta }_{\mathit{f}} \mathbf{(}\mathbf{\%}\mathbf{)}$
Span 1	1	8.85	10.86	18.51
	2	16.03	19.50	17.79
Span 2	1	6.48	7.48	13.37
	2	14.38	17.98	20.02

compares the corresponding natural frequencies obtained from operational modal analysis (OMA) of the real structure with those derived from the numerical model. A significant discrepancy (${\Delta }_f$) is observed between the experimental and computational results, with frequency differences reaching as high as 20% for certain modes. This substantial deviation underscores the necessity of calibrating the finite element model (FEM) to align its dynamic behavior with real-world measurements. The calibration methodology, focused on adjusting material properties via genetic algorithms, will be detailed in the subsequent section. This detailed modeling approach, combined with the advanced monitoring system, ensures the generation of high-quality synthetic data that can be used for structural health monitoring, performance assessment, and further research on steel truss railway bridges.

5. Model Updating and Results

The optimization of the bridge model is performed by systematically adjusting the elastic modulus of steel components within the finite element (FE) framework to minimize discrepancies between the numerical model and the real-world structural behavior. This calibration process focuses on steel properties. The elastic modulus of steel $\left(E_s\right)$, a key parameter governing material stiffness, is iteratively modified across the various members of the bridge—such as the diagonals, verticals, upper and lower currents, etc.—to reflect potential material degradation, manufacturing variability, or operational aging.

The baseline mechanical properties of the bridge, including the elastic modulus of steel ($E_s=200\mathrm{G}\mathrm{P}\mathrm{a}$), were derived from material certificates and design specifications, representing the undamaged state of the structure. To account for aging and localized defects, the elastic modulus was allowed to vary within a ±30% range during the GA-based optimization. This range reflects potential variability in material properties due to factors such as corrosion, fatigue, and joint loosening. The GA-based approach uses the global dynamic response of the structure (e.g., natural frequencies and mode shapes) to infer changes in material properties, providing a practical and efficient method for model updating. This approach is consistent with established practices in SHM literature [22,23] and ensures that the numerical model accurately reflects the current condition of the bridge.

The optimization focuses on adjusting the steel elastic modulus $E_s$ of members because it serves as a practical and effective parameter to capture the global effects of localized phenomena such as joint degradation, fatigue, and stress redistribution. In typical finite element (FE) models of steel truss bridges, connections and joints are often idealized, making it challenging to explicitly model their complex behavior. By calibrating the elastic modulus, these localized effects are synthetized into a single parameter that governs the overall stiffness of the structural members. This approach allows the digital twin to identify members exhibiting anomalous behavior, which may indicate potential damage. Once identified, detailed inspections can determine the specific nature of the damage.

The objective function is formulated as a multi-criteria error metric that quantifies the alignment between the experimentally measured dynamic properties of the real bridge and the numerically simulated results. Specifically, the function incorporates two principal components:

(1)

Natural Frequency Error: The relative difference between the first $n$ natural frequencies ($f_{real,i}$) obtained from OMA using accelerometer data and the corresponding FEM-derived frequencies ($f_{FE,i}$):

$$E_{freq}=\sum _{i=1}^n{\left({\displaystyle \frac{f_{real,i}-f_{FE,i}}{f_{real,i}}}\right)}^2$$

(4)

This term ensures the model replicates the global vibrational characteristics of the structure.

(2)

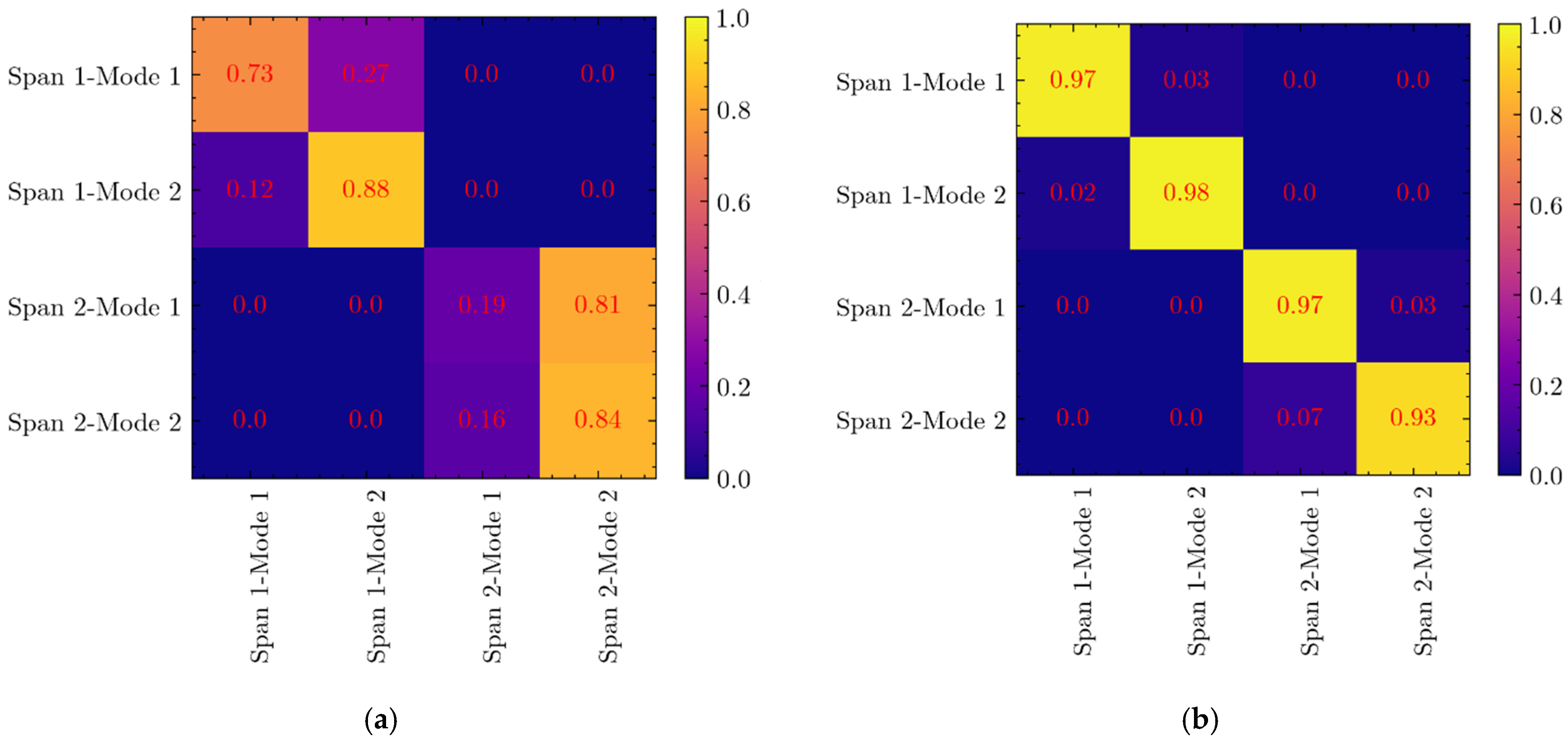
Modal Shape Correlation: The modal assurance criterion (MAC) is employed to evaluate the consistency between real and numerical mode shapes (${\varphi }_{real,i},{\varphi }_{FE,i}$):

$$MA{C}_i={\displaystyle \frac{{\left|{\varphi }_{real,i}^T\cdot {\varphi }_{FE,i}\right|}^2}{\left({\varphi }_{real,i}^T\cdot {\varphi }_{FE,i}\right)\cdot \left({\varphi }_{FE,i}^T\cdot {\varphi }_{FE,i}\right)}}$$

(5)

A penalty term $E_{MAC}={\sum }_{i=1}^n\left(1-MA{C}_i\right)$ is then added to the objective function to enforce spatial agreement in mode shapes, preventing erroneous mode-swapping issues common in modal analysis.

The combined objective function is expressed as:

$$J=\alpha \cdot E_{freq}+\beta \cdot E_{MAC}$$

(6)

where $\alpha$ and $\beta$ are weighting coefficients that prioritize frequency matching versus modal shape fidelity. The weighting coefficients $\alpha$ and $\beta$ in the multi-objective fitness function (Equation (6)) were determined through a sensitivity analysis evaluating different $\alpha :\beta$ ratios (1:1, 2:1, and 1:2). The 1:1 ratio ($\alpha =0.5$, $\beta =0.5$) minimized both frequency errors ($RMSE<0.5\mathrm{H}\mathrm{z}$) and modal assurance criterion ($MAC>0.95$) errors, providing the best balance between frequency matching and modal shape fidelity. This ratio ensured that neither objective was overemphasized, avoiding overfitting to either frequencies or mode shapes. Consequently, $\alpha =0.5$ and $\beta =0.5$ were used for the results presented in this study.

The genetic algorithm implementation employs the PyGAD library [28] to drive the optimization process, utilizing its customizable operators for selection, crossover, and mutation to evolve candidate solutions, where each solution represents a unique set of elastic modulus values assigned to predefined bridge components. The hyperparameters used during optimization via PyGAD are reported in

Table 3. Hyperparameters adopted in PyGAD application for model updating.

Number of generations	1000
Population size	20
Number of genes	6
Parent selection type	Tournament
K tournament	3
Cross over type	Two points
Mutation type	Random
Mutation probability	0.1
Stop criteria	“Saturate 50” or “reach 1000”

.

To enhance computational efficiency, the finite element (FE) model in OpenseesPy [27] is automated via scripting: for each candidate solution, the updated elastic modulus values are assigned to relevant bridge elements, a modal analysis is executed, and the resulting natural frequencies and modal assurance criterion (MAC) values are extracted to compute the objective function $J$. Constraints are imposed to restrict the steel elastic modulus variations to $\pm 30\%$, ensuring material properties remain physically realistic. This process is further accelerated through parallel computation, which evaluates the fitness of population members across multiple concurrent FE model instances, drastically reducing optimization runtime while maintaining accuracy. The model updating procedure is illustrated in the flowchart in Figure 8.

Table 4. Initial and calibrated elastic modulus of various structural members of the bridge.

	Initial ${\mathit{E}}_{\mathit{s}}\mathbf{\left(}\mathbf{G}\mathbf{P}\mathbf{a}\mathbf{\right)}$	Calibrated ${\mathit{E}}_{\mathit{s}}$$\mathbf{(}\mathbf{G}\mathbf{P}\mathbf{a}$)
Braces	200	186
Tracks		205
Top and bottom chords		178
Verticals		191

reports the initial and calibrated elastic modulus of various members of the steel bridge obtained from the model updating procedure using PyGAD v 3.4.0.

Table 5. Comparison of modal data from the FEMs and the real bridge.

	Mode	Real Bridge	Initial FE Model			Updated FE Model
		${\mathit{f}}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}\mathbf{\left(}\mathbf{H}\mathbf{z}\mathbf{\right)}$	${\mathit{f}}_{\mathit{F}\mathit{E}}\mathbf{\left(}\mathbf{H}\mathbf{z}\mathbf{\right)}$	${\Delta }_{\mathit{f}}\mathbf{(}\mathbf{\%}\mathbf{)}$	$\mathit{M}\mathit{A}\mathit{C}$	${\mathit{f}}_{\mathit{F}\mathit{E}}\mathbf{(}\mathbf{\%}\mathbf{)}$	${\Delta }_{\mathit{f}}\mathbf{(}\mathbf{\%}\mathbf{)}$	$\mathit{M}\mathit{A}\mathit{C}$
Span 1	1	8.85	10.86	18.51	0.73	8.85	0.00	0.97
	2	16.03	19.50	17.79	0.88	16.50	2.85	0.98
Span 2	1	6.48	7.48	13.37	0.19	6.49	0.15	0.97
	2	14.38	17.98	20.02	0.84	14.88	3.36	0.93

summarizes the comparative analysis of modal parameters—natural frequencies and modal assurance criterion (MAC) values—derived from experimental measurements and finite element models (FEMs) before and after calibration. Post-calibration results demonstrate strong alignment between the updated FEM and experimental data, with frequency discrepancies reduced to less than 5% and MAC values substantially enhanced across all modes. Figure 9 shows the comparison of the MAC values between the initial and calibrated FE models. It highlights a substantial improvement in the accuracy of the numerical model after the updating process. Initially, the MAC values were relatively low, particularly for the first mode of Span 2, where the initial correlation was only 0.19. This indicated a significant discrepancy between the numerical and experimental modal shapes. After the calibration process, which involved optimizing the elastic modulus of the steel components using a genetic algorithm, the MAC values increased significantly across all modes, with a minimum value reaching 0.93. This improvement confirms that the updated model better captures the true dynamic behavior of the bridge, ensuring a more reliable digital twin representation for structural health monitoring applications. The enhanced correlation underscores the effectiveness of the model updating approach in refining both global and local structural response characteristics.

6. Conclusions

This study demonstrates the development and implementation of a real-time digital twin for a steel-truss railway bridge, integrating sensor-based structural health monitoring (SHM), operational modal analysis (OMA), and finite element (FE) model updating. By leveraging Stochastic Subspace Identification (SSI) for modal parameter extraction and genetic algorithm-based optimization for model calibration, the digital twin accurately captures the bridge’s dynamic behavior and provides an effective tool for real-time condition assessment.

The key findings of this study are as follows:

(1)

Accurate modal parameter identification: the SSI method effectively extracted the bridge’s natural frequencies and mode shapes from free vibration responses, demonstrating its reliability for real-world structural monitoring.

(2)

High-fidelity digital twin calibration: by optimizing the elastic modulus of steel components, the model updating process reduced frequency errors to below 5% and significantly improved modal assurance criterion (MAC) values (>0.93), ensuring strong alignment between numerical predictions and experimental data.

(3)

Scalable and practical digital twin framework: the integration of OpenSeesPy for FE modeling and PyGAD for optimization proves to be an efficient approach for real-time SHM applications, making this methodology adaptable to other bridge structures and critical infrastructure systems.

(4)

Enhanced predictive maintenance and damage detection: the validated digital twin provides a reliable baseline for monitoring structural changes over time, enabling early damage detection and data-driven maintenance decisions to improve bridge safety and service life.

While the proposed framework demonstrates significant advancements, certain limitations must be acknowledged, as follows: (1) Sensor noise sensitivity: modal parameters derived via SSI may be influenced by ambient noise, particularly in low-amplitude free vibration segments, potentially affecting calibration accuracy. (2) Environmental effects: temperature fluctuations and humidity, which can alter material properties and boundary conditions, were not explicitly modeled, limiting the framework’s ability to distinguish between environmental and damage-induced changes. (3) Simplified material calibration: the optimization focused solely on adjusting the elastic modulus of steel, neglecting localized effects such as joint degradation or fatigue-induced micro-cracks.

To address these limitations and further enhance the digital twin’s robustness, future research will focus on the following: (a) The integration of multi-sensor data: incorporating strain gauges and displacement sensors to capture localized deformations and reduce reliance on accelerometer-derived modal data. (b) Environmental coupling: developing hybrid models that account for temperature, humidity, and operational load variations to isolate structural degradation from external influences. (c) Advanced optimization algorithms: implementing hybrid genetic algorithms with machine learning to refine parameter adjustments and reduce computational costs. (d) Localized damage modeling: extending the calibration process to include joint stiffness, connection looseness, and fatigue effects for holistic structural assessment.

In summary, this research highlights the transformative potential of digital twins in structural engineering, providing a foundation for next-generation smart infrastructure solutions. By bridging the gap between real-world sensor data and computational models, digital twins can revolutionize SHM, ensuring the safety, resilience, and longevity of critical transport infrastructure.