Filtered Operator-Based Nonlinear Control for DC–DC Converter-Driven Triboelectric Nanogenerator System
Abstract
1. Introduction
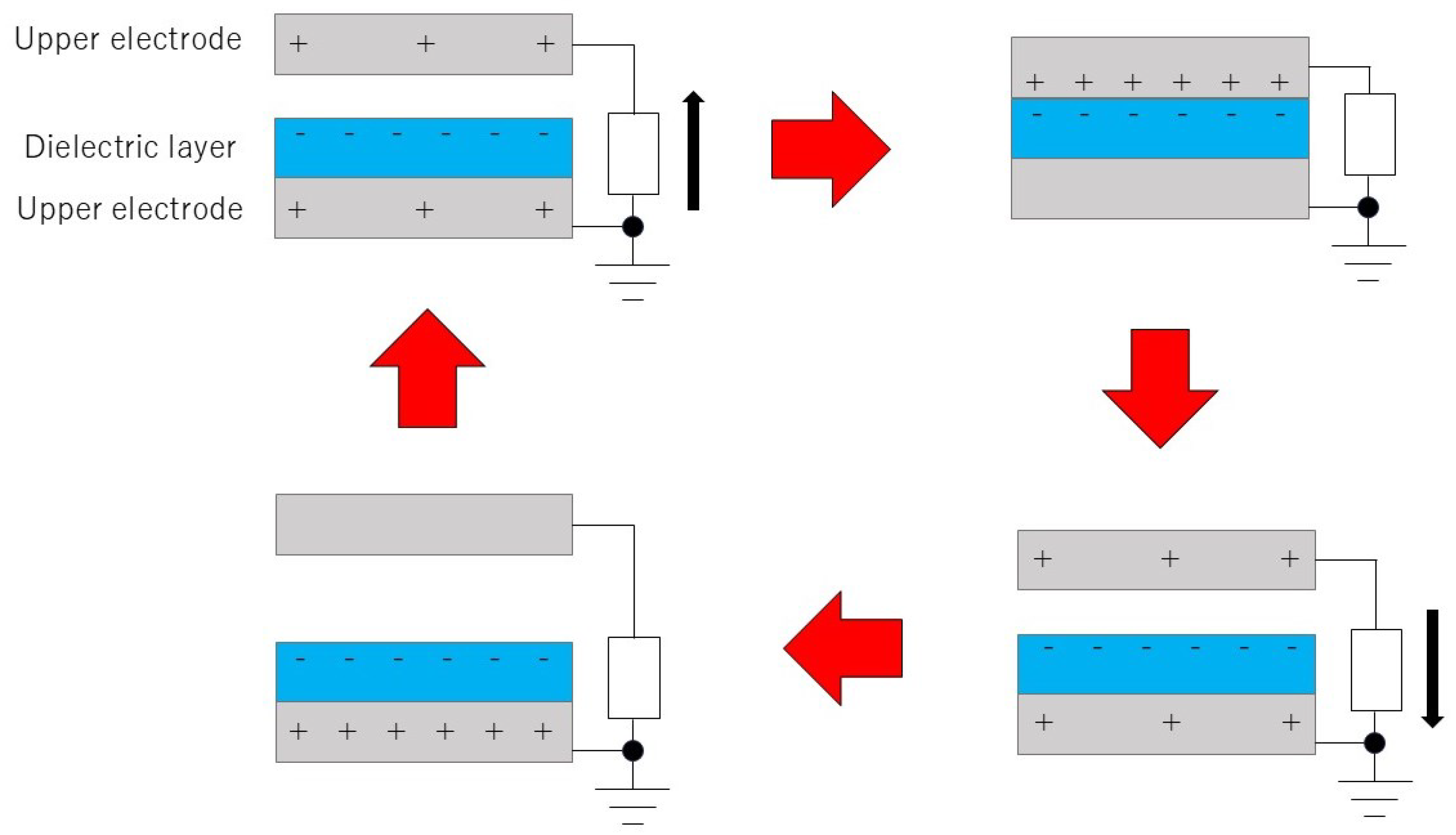
2. Operating Principle of the TENG
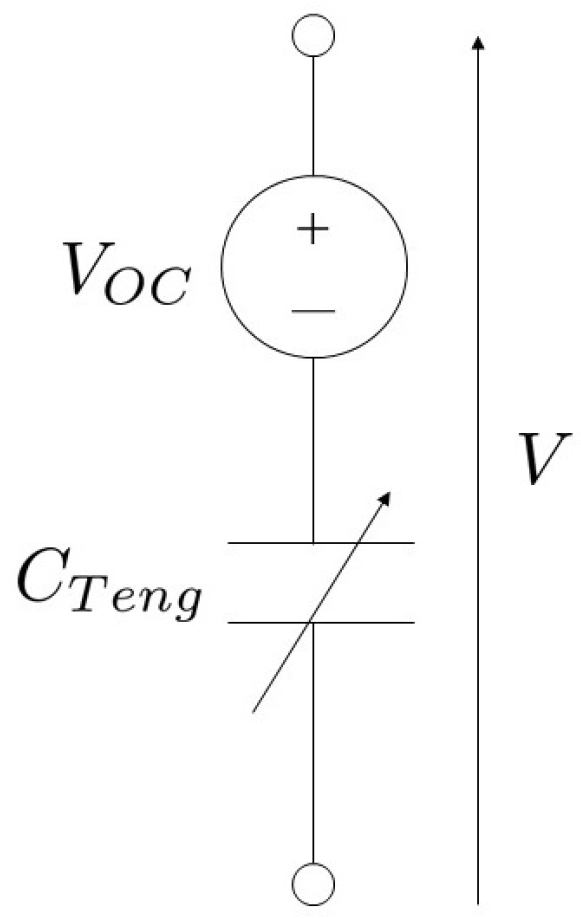
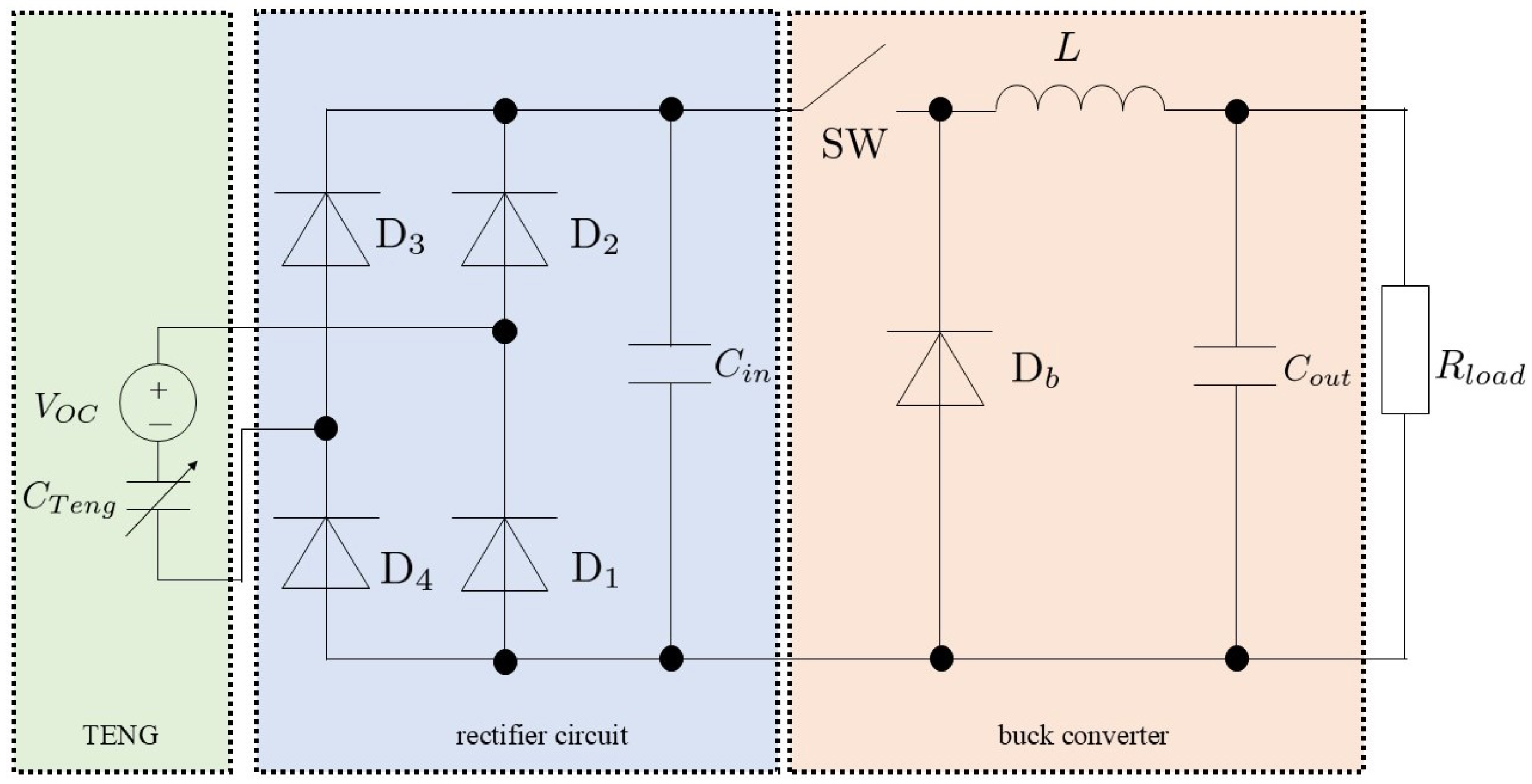
3. Modeling of the TENG System
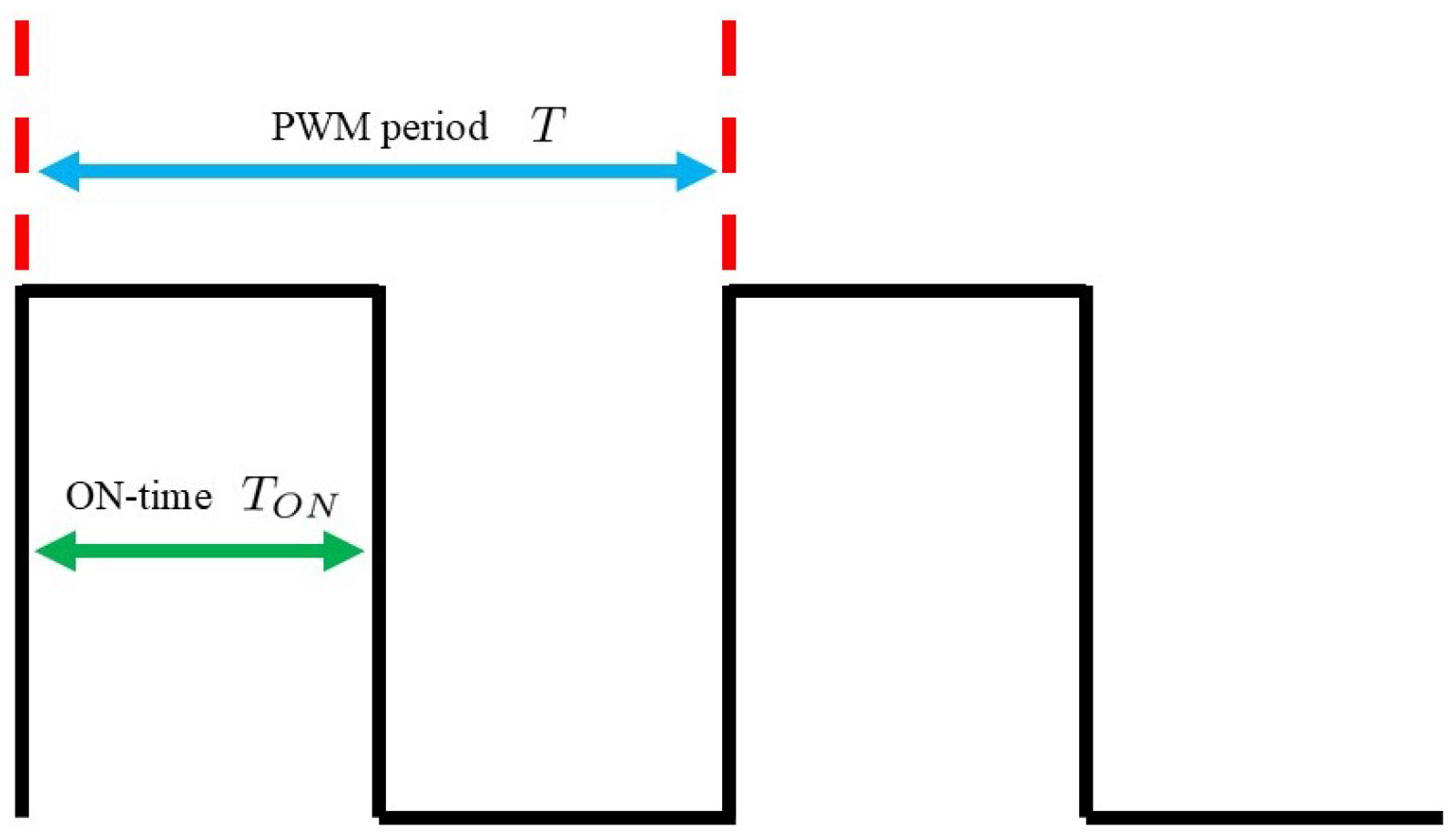
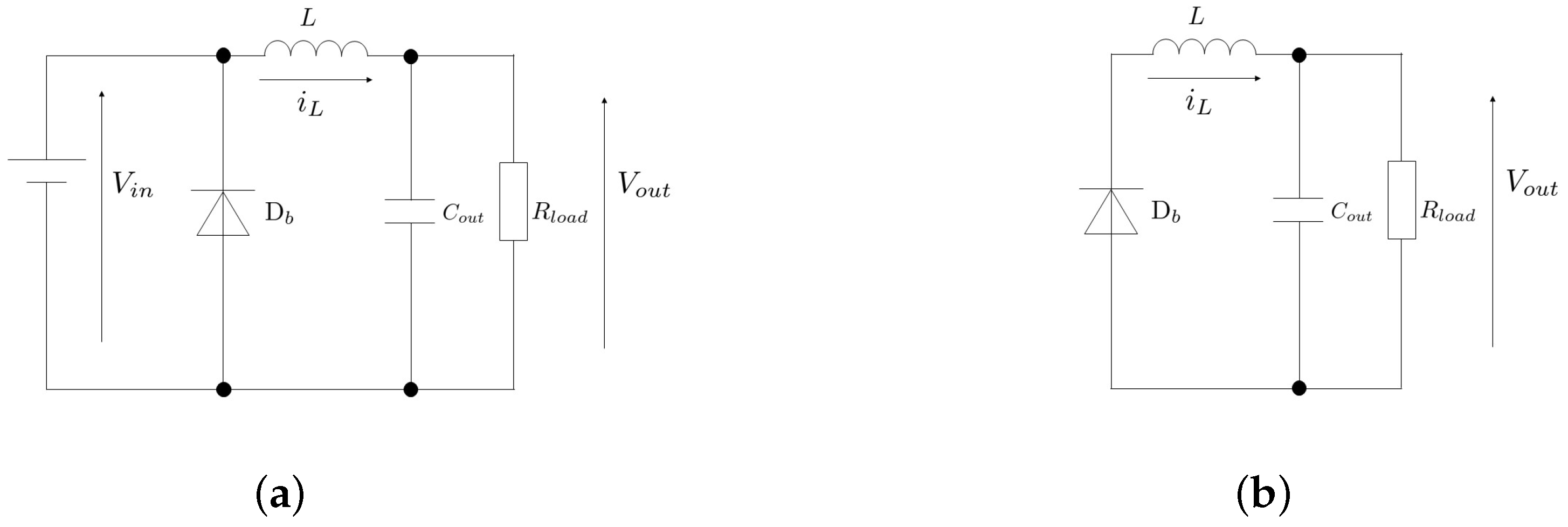
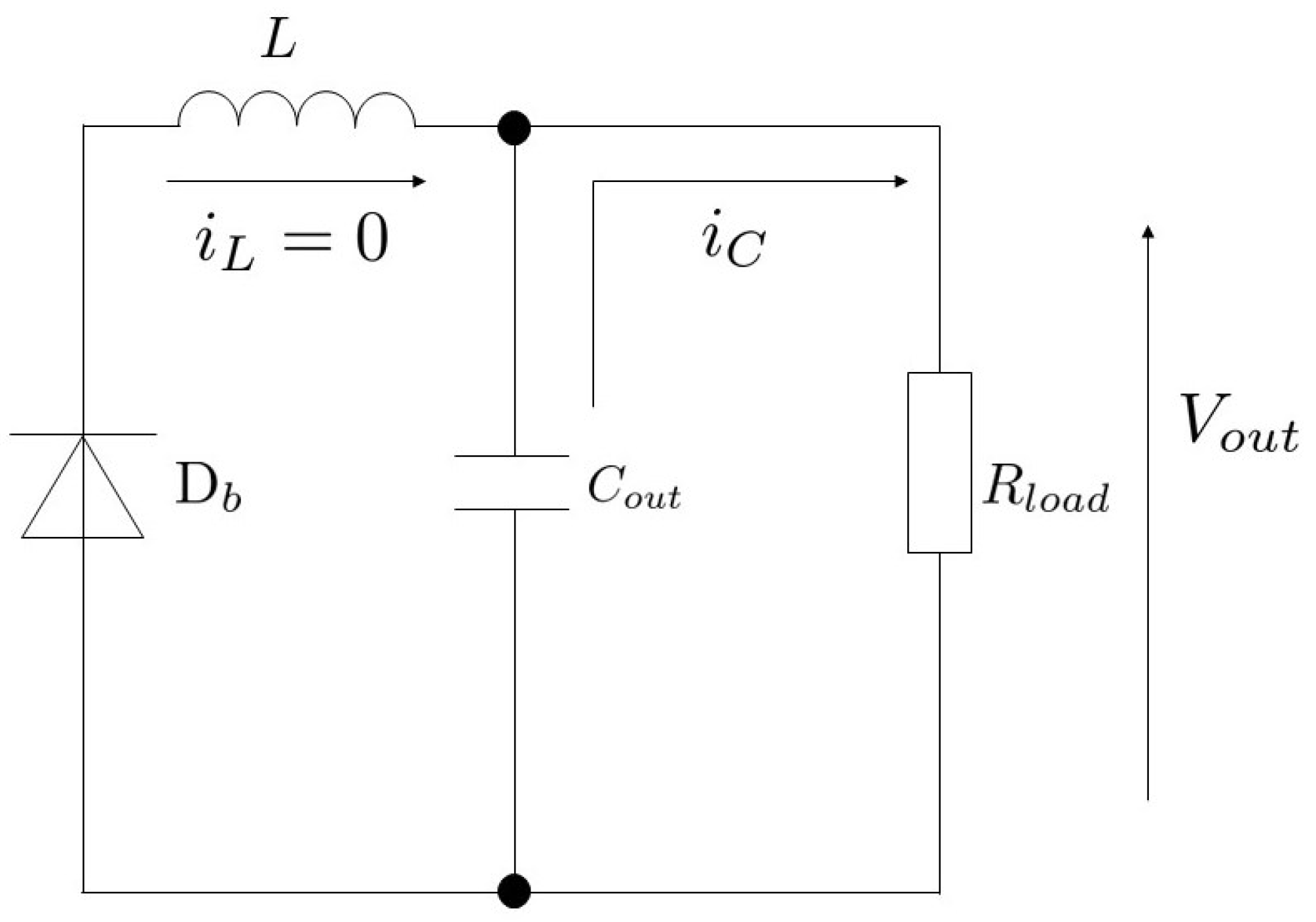
3.1. Buck Converter
3.2. Problem Statement
4. Control System Design
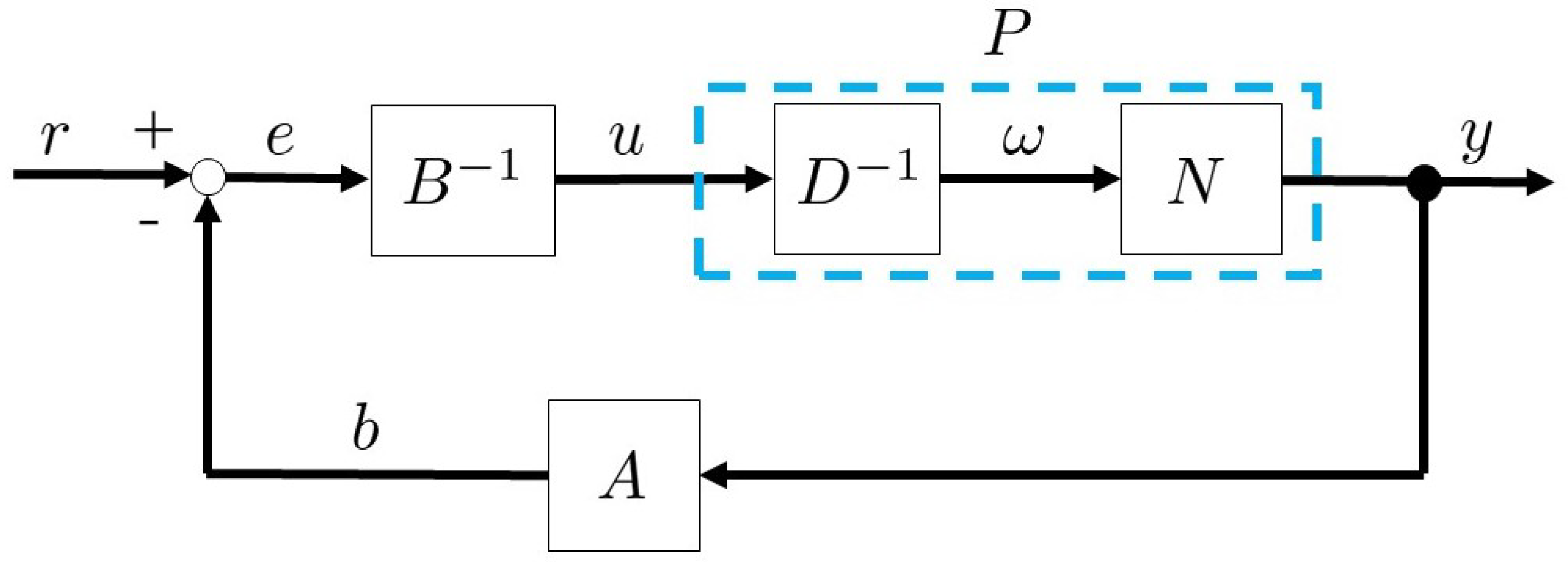
4.1. Right Factorization
4.2. Operator Theory
4.3. Proof of Stability of Control System
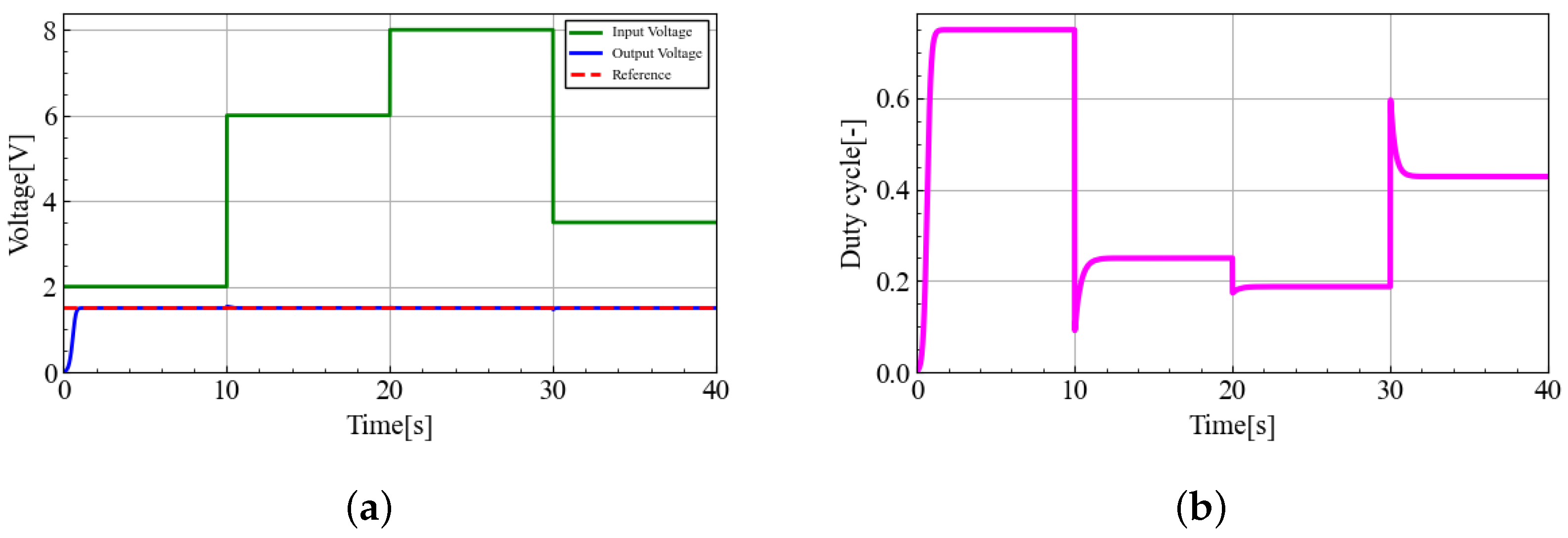
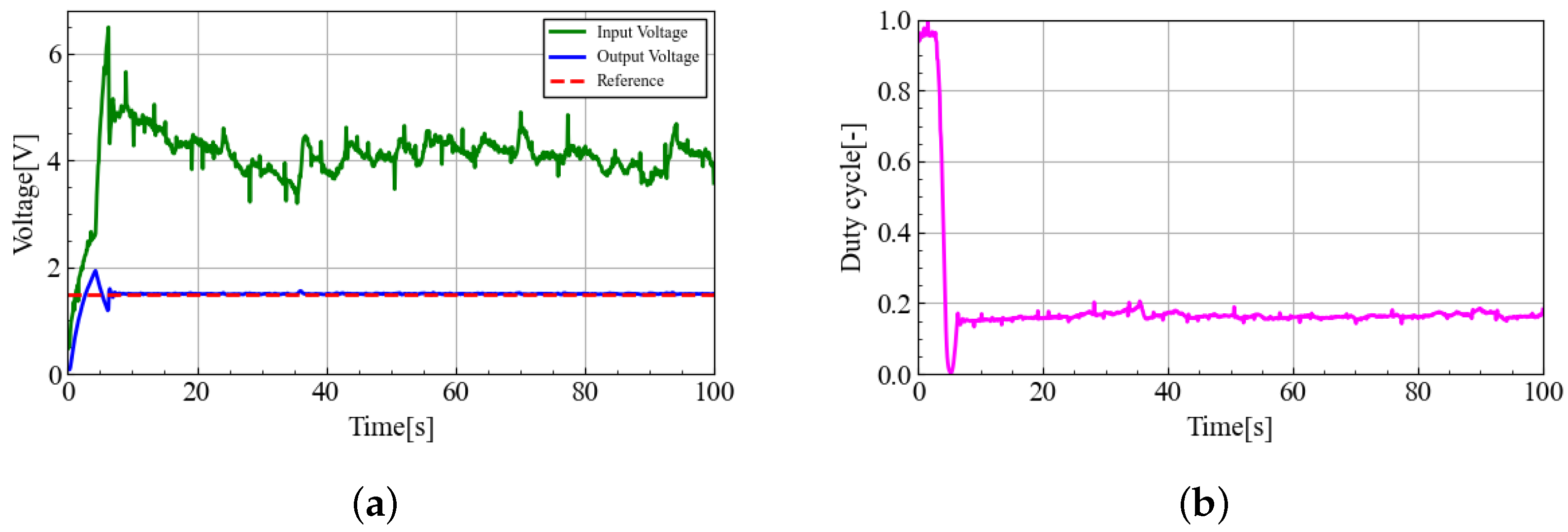
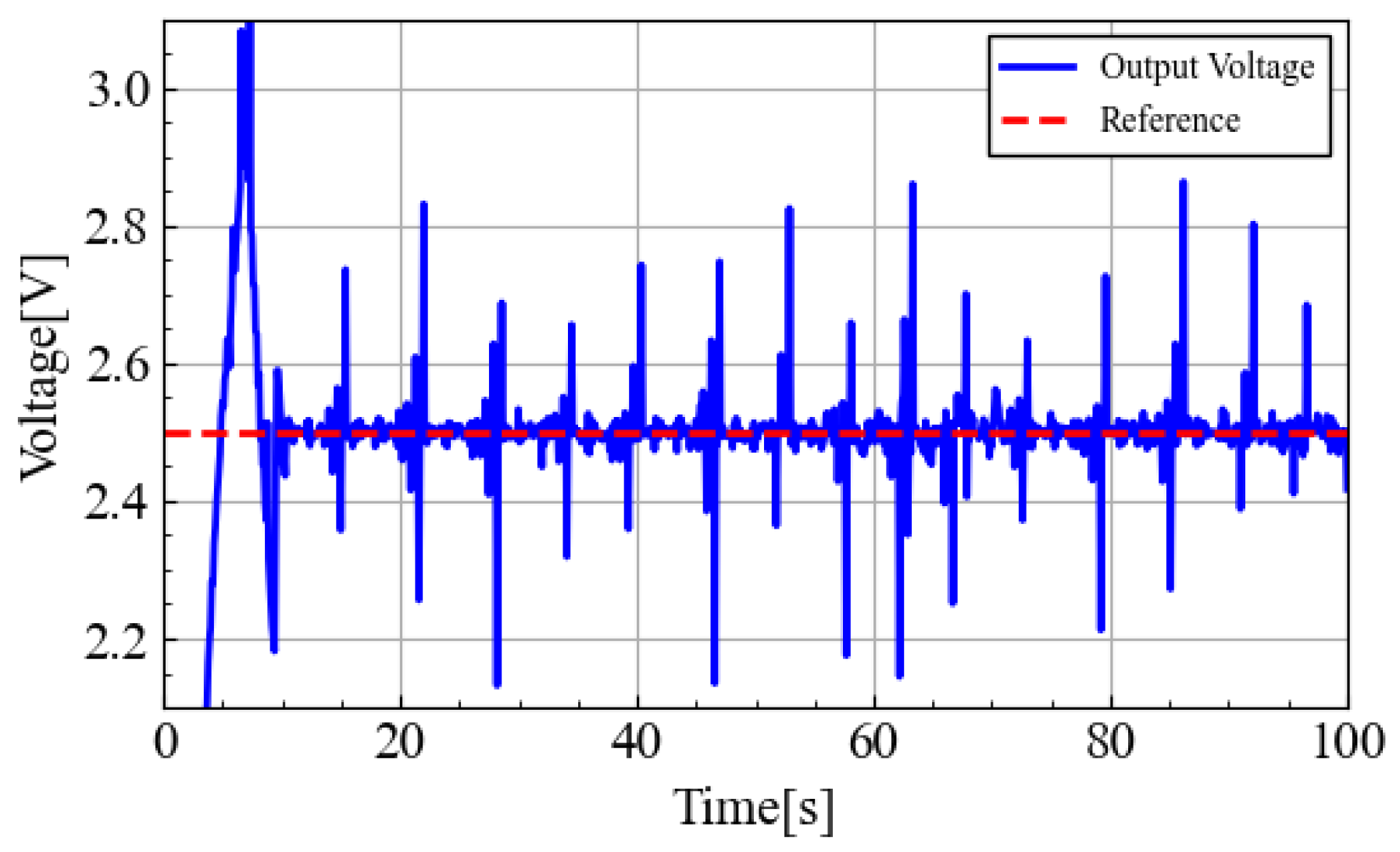
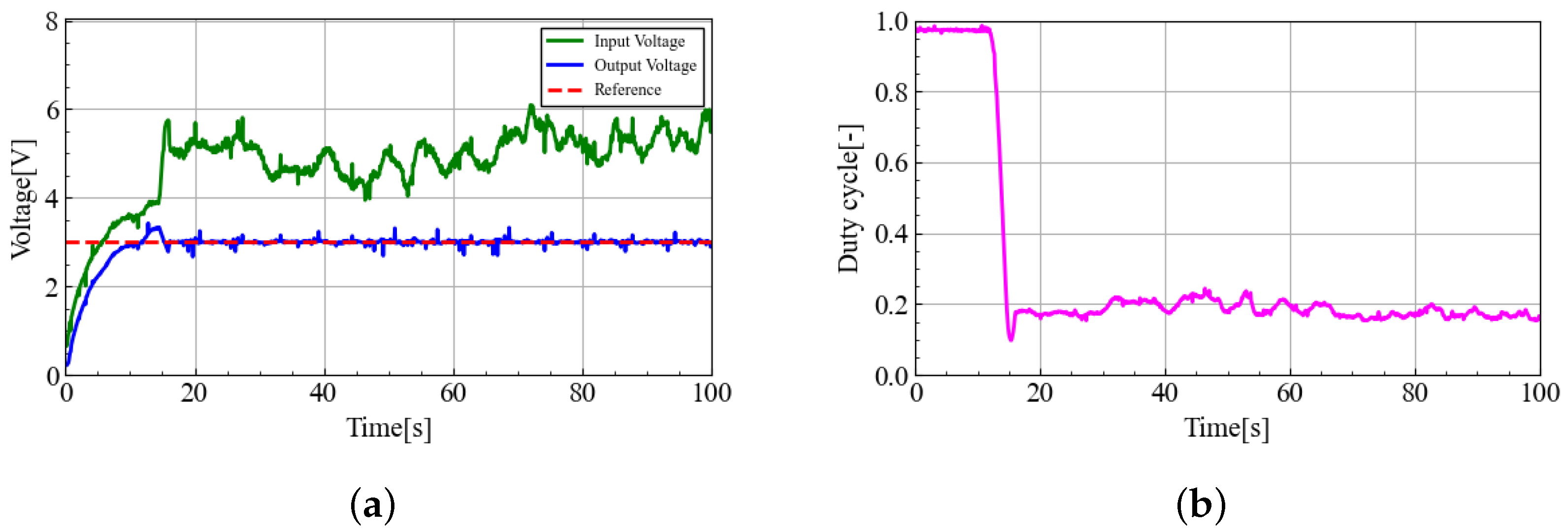
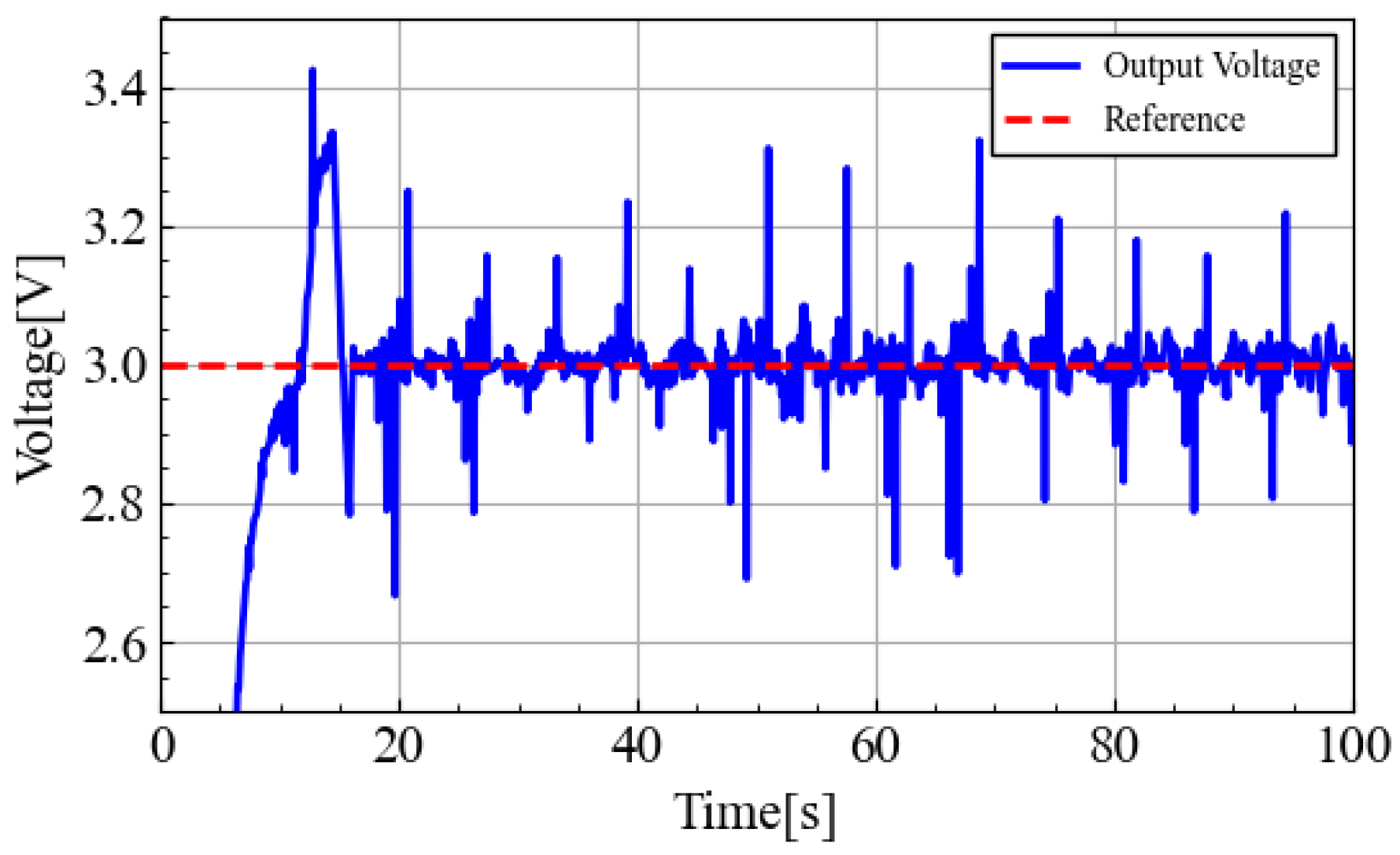
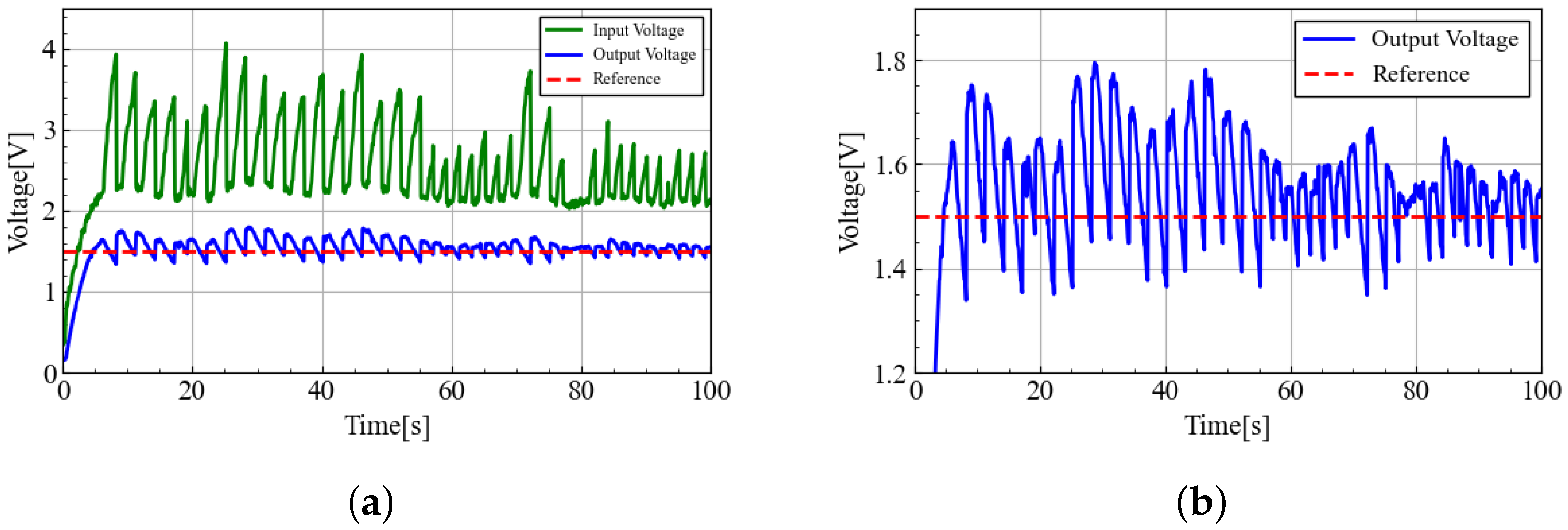
5. Simulation and Experiment
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Yang, Y.; Wang, Z.L. Triboelectric Nanogenerators as Flexible Power Sources. NPJ Flex. Electron. 2017, 1, 10. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, Y.S.; Zhang, H.; Liu, Y.; Lee, S.; Wang, Z.L. A Single-Electrode Based Triboelectric Nanogenerator as Self-Powered Tracking System. Adv. Mater. 2013, 25, 6594–6601. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Lin, L.; Xie, Y.; Jing, Q.; Niu, S.; Wang, Z. Sliding-Triboelectric Nanogenerators Based on In-Plane Charge-Separation Mechanism. Nano Lett. 2013, 13, 2226–2233. [Google Scholar] [CrossRef]
- Zhang, H.; Yao, L.; Quan, L.; Zheng, X. Theories for Triboelectric Nanogenerators: A Comprehensive Review. Nanotechnol. Rev. 2020, 9, 610–625. [Google Scholar] [CrossRef]
- Cui, X.; Yu, C.; Wang, Z.; Wan, D.; Zhang, H. Triboelectric Nanogenerators for Harvesting Diverse Water Kinetic Energy. Micromachines 2022, 13, 1219. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, N.; Liu, J.; Wen, Z.; Sun, X.; Lee, S.T.; Sun, B. Integrating a Silicon Solar Cell with a Triboelectric Nanogenerator via a Mutual Electrode for Harvesting Energy from Sunlight and Raindrops. ACS Nano 2018, 12, 2893–2899. [Google Scholar] [CrossRef]
- Ahmed, A.; Hassan, I.; Mosa, M.I.; Elsanadidy, E.; Phadke, S.G.; El-Kady, F.M.; Rusling, F.J.; Selvaganapathy, R.P.; Kaner, B.R. All Printable Snow-Based Triboelectric Nanogenerator. Nano Energy 2019, 60, 17–25. [Google Scholar] [CrossRef]
- Luo, J. Recent Progress of Triboelectric Nanogenerators: From Fundamental Theory to Practical Applications. EcoMat 2020, 2, e12059. [Google Scholar] [CrossRef]
- Wu, C.; Wang, A.C.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric Nanogenerator: A Foundation of The Energy for The New Era. Adv. Energy Mater. 2019, 9, 1802906. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric Nanogenerators as New Energy Technology for Self-Powered Systems and as Active Mechanical and Chemical Sensors. ACS Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef]
- Kawaguchi, A.; Uchiyama, H.; Matsunaga, M.; Ohno, Y. Simple and Highly Efficient Intermittent Operation Circuit for Triboelectric Nanogenerator Toward Wearable Electronic Applications. Appl. Phys. Express 2021, 14, 057001. [Google Scholar]
- Huang, Y.-J.; Chung, C.-K. Research on Performance Enhancement, Output Regulation, and the Applications of Nanogenerators. Micromachines 2025, 16, 208. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Wang, H.; Harmon, W.; Bamgboje, D.; Wang, L. Current Progress on Power Management Systems for Triboelectric Nanogenerators. IEEE Trans. Power Electron. 2022, 37, 9850–9864. [Google Scholar]
- Li, X.; Zhang, C.; Gao, Y.; Zhao, Z.; Hu, Y.; Yang, O.; Liu, L.; Zhou, L.; Wang, J.; Wang, Z.L. A Highly Efficient Constant-Voltage Triboelectric Nanogenerator. Energy Environ. Sci. 2022, 15, 1334–1345. [Google Scholar]
- Huang, Y.-J.; Chung, C.-K. Design and Fabrication of Polymer Triboelectric Nanogenerators for Self-Powered Insole Applications. Polymers 2023, 15, 4035. [Google Scholar] [CrossRef]
- Endo, H.; Deng, M. Electric Power Control of Thermoelectric Generation System. In Proceedings of the International Conference on Power, Energy and Electrical Engineering, Shiga, Japan, 26–28 February 2021; pp. 215–219. [Google Scholar]
- Singh, G.; Kundu, S. An Efficient DC-DC Boost Converter for Thermoelectric Energy Harvesting. AEU-Int. J. Electron. Commun. 2020, 118, 153132. [Google Scholar]
- Liu, C.; Shimane, R.; Deng, M. Operator-Based Triboelectric Nanogenerator Power Management and Output Voltage Control. Micromachines 2024, 15, 1114. [Google Scholar] [CrossRef]
- Wen, N.; Liu, Z.; Wang, W.; Wang, S. Feedback Linearization Control for Uncertain Nonlinear Systems Via Generative Adversarial Networks. ISA Trans. 2024, 146, 555–566. [Google Scholar]
- Yu, X.; Okyay, K. Sliding-Mode Control with Soft Computing: A Survey. IEEE Trans. Ind. Electron. 2009, 56, 3275–3285. [Google Scholar]
- Rigatos, G.; Siano, P.; Melkikh, A.; Zervos, N. A Nonlinear H-Infinity Control Approach to Stabilization of Distributed Synchronous Generators. IEEE Syst. J. 2018, 12, 2654–2663. [Google Scholar]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-Based Nonlinear Feedback Control Design Using Robust Right Coprime Factorization. IEEE Trans. Autom. 2006, 51, 645–648. [Google Scholar]
- Deng, M.; Saijo, N.; Gomi, H.; Inoue, A. A Robust Real Time Method for Estimating Human Multijoint Arm Viscoelasticity. Int. J. Innov. Comput. Control 2006, 2, 705–721. [Google Scholar]
- Zenteno-Torres, J.; Cieslak, J.; Dávila, J.; Henry, D. Sliding Mode Control with Application to Fault-Tolerant Control: Assessment and Open Problems. Automation 2021, 2, 1–30. [Google Scholar] [CrossRef]
- Utkin, V.; Lee, H. Chattering Problem in Sliding Mode Control Systems. IFAC Proc. Vol. 2006, 39, 1. [Google Scholar]
- Deng, M.; Inoue, A.; Goto, S. Operator Based Thermal Control of an Aluminum Plate with a Peltier Device. Int. J. Innov. Comput. Inf. Control 2008, 4, 3219–3229. [Google Scholar]
- Cho, S.; Jang, S.; La, M.; Yun, Y.; Yu, T.; Park, J.S.; Choi, D. Facile Tailoring of Contact Layer Characteristics of the Triboelectric Nanogenerator Based on Portable Imprinting Device. Materials 2020, 13, 872. [Google Scholar] [CrossRef]
- Wang, H.; Funaki, H.; Noge, Y.; Shoyama, Y. Widely Applicable Statespace Average Method. Tech. Comm. Energy Eng. Electron. Commun. 2023, 122, 418. (In Japanese) [Google Scholar]
- Tanabata, Y.; Deng, M. Filtered Right Coprime Factorization and Its Application to Control a Pneumatic Cylinder. Processes 2024, 12, 1475. [Google Scholar] [CrossRef]
- Chen, G.; Han, Z. Robust Right Coprime Factorization and Robust Stabilization of Nonlinear Feedback Control Systems. IEEE Trans. Autom. Control 1998, 43, 1505–1509. [Google Scholar]
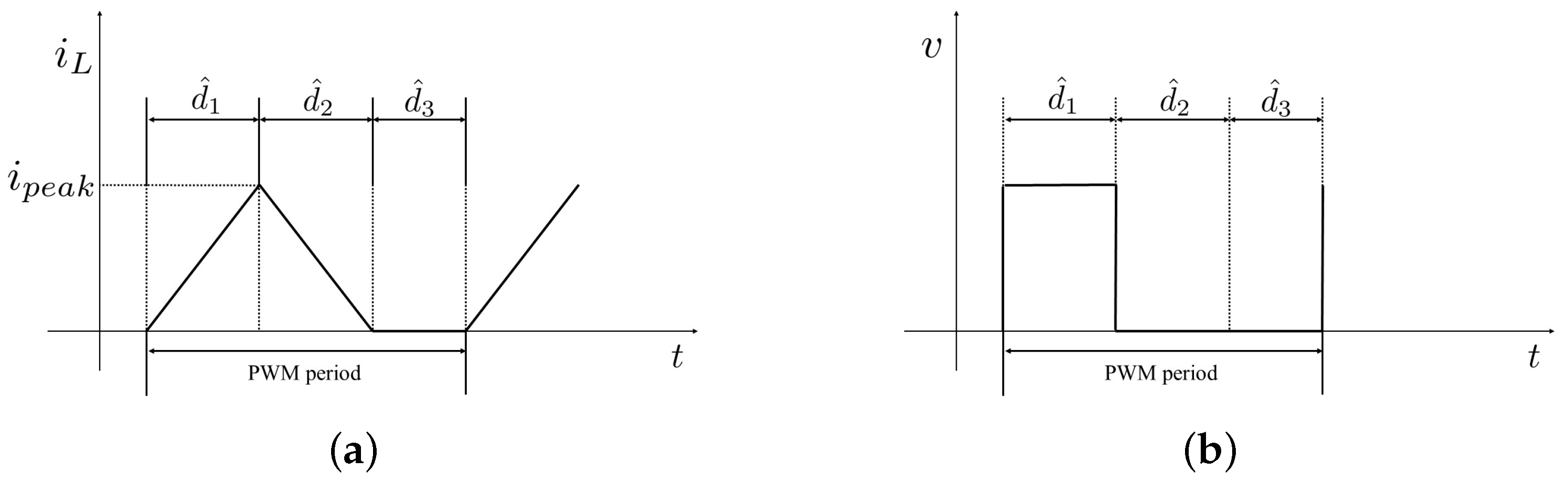





| Parameter | Definition | Value |
|---|---|---|
| f | Sampling Frequency | |
| Reference Voltage | ||
| Load Resistance | ||
| L | Inductance | |
| Output Capacitor | ||
| Switching Frequency | ||
| Time Constant |
| Parameter | Definition | Value |
|---|---|---|
| f | Sampling Frequency | |
| The Thickness of the Dielectric | ||
| Reference Voltage | ||
| Load Resistance | ||
| L | Inductance | |
| Input Capacitor | ||
| Output Capacitor | ||
| Switching Frequency | ||
| Maximum Distance Between the Layers | 25 | |
| S | Electrode’s Area | |
| Vibration Period | ||
| Time Constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimane, R.; Liu, C.; Deng, M. Filtered Operator-Based Nonlinear Control for DC–DC Converter-Driven Triboelectric Nanogenerator System. Appl. Sci. 2025, 15, 4054. https://doi.org/10.3390/app15074054
Shimane R, Liu C, Deng M. Filtered Operator-Based Nonlinear Control for DC–DC Converter-Driven Triboelectric Nanogenerator System. Applied Sciences. 2025; 15(7):4054. https://doi.org/10.3390/app15074054
Chicago/Turabian StyleShimane, Ryusei, Chengyao Liu, and Mingcong Deng. 2025. "Filtered Operator-Based Nonlinear Control for DC–DC Converter-Driven Triboelectric Nanogenerator System" Applied Sciences 15, no. 7: 4054. https://doi.org/10.3390/app15074054
APA StyleShimane, R., Liu, C., & Deng, M. (2025). Filtered Operator-Based Nonlinear Control for DC–DC Converter-Driven Triboelectric Nanogenerator System. Applied Sciences, 15(7), 4054. https://doi.org/10.3390/app15074054







