Optimization Algorithm for Cutting Masonry with a Robotic Saw
Abstract
Featured Application
Abstract
1. Introduction
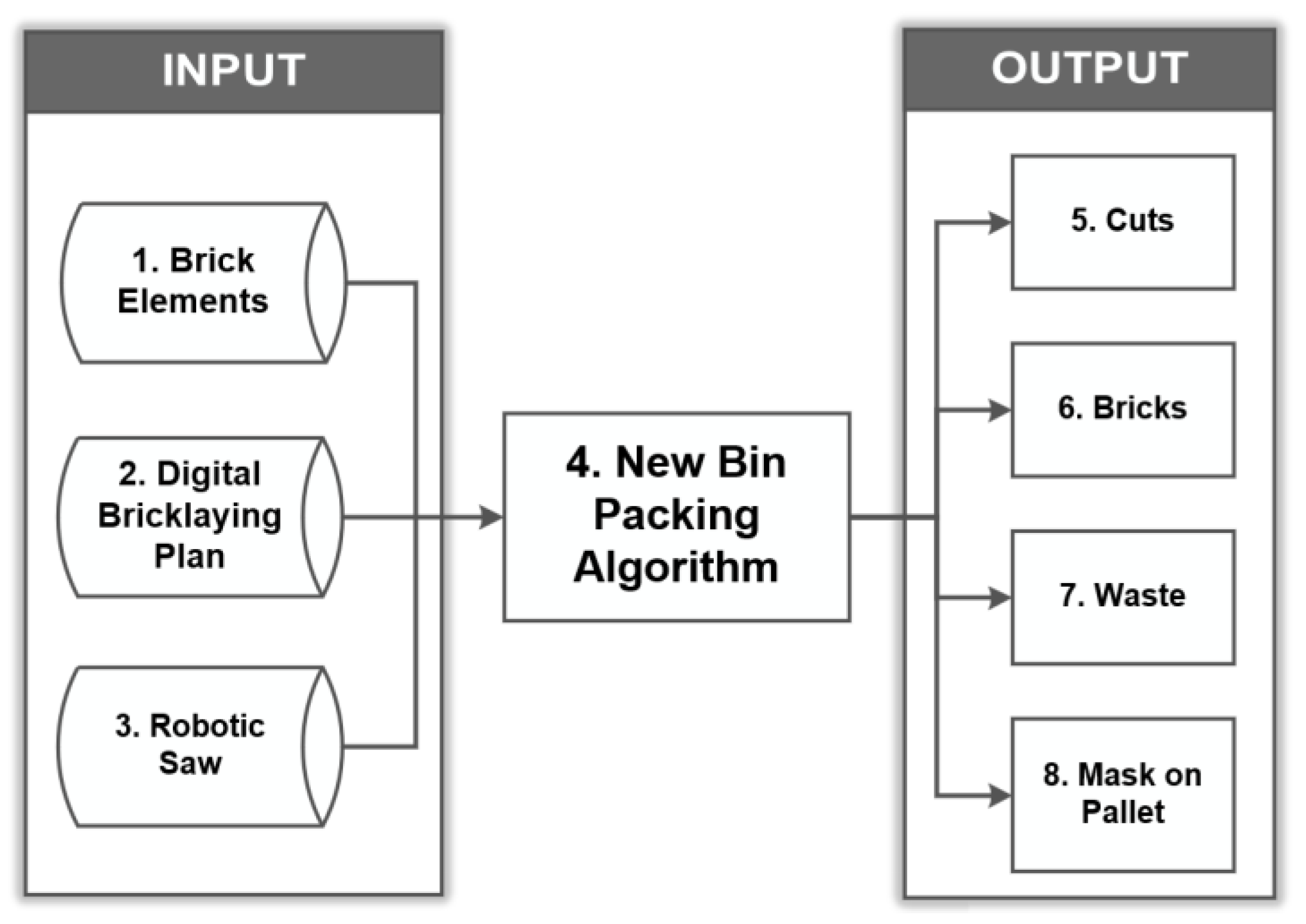
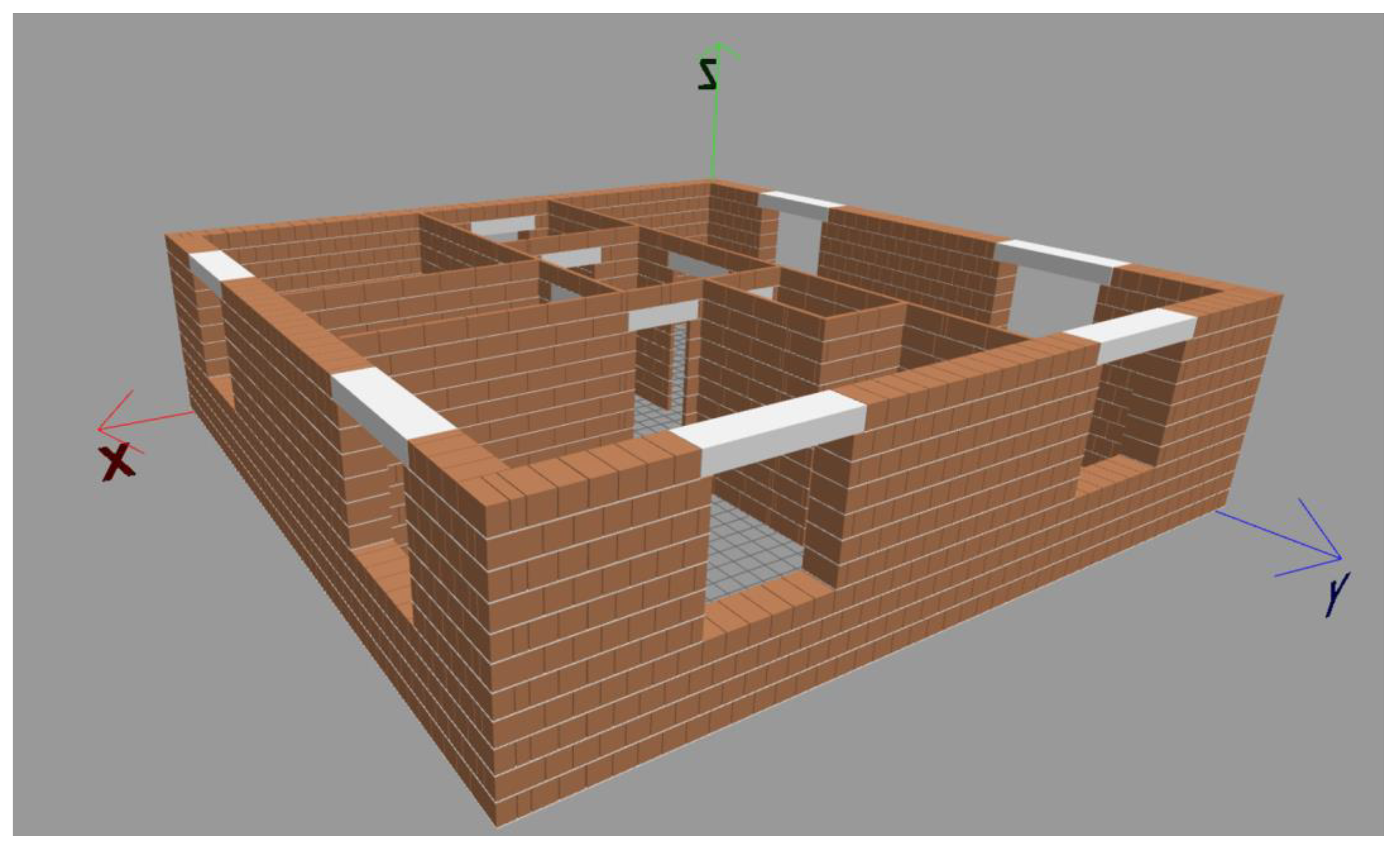
2. Materials and Methods
- The number of whole masonry elements is minimal: , where for the containers used.
- The condition of the minimal number of cuttings can be formulated as minimizing the number of wasted pieces: , where for containers with unused space. A fully filled container reduces the number of cuts by 1.
- Other constraints can be formulated as:where .where .
- —array of objects to pack into container ( is the number of elements in a group t, is the size of an element).
- —container size.
- —maximum possible number of objects in container.
- Listing the array of elements in the form: .
- Random ordering of elements in the array: .
- Copying the first elements to the work area: .
- Each container combination must meet the condition:where is the number of objects in a container assembly.
- Used space and unused space are calculated for each container combination.
- Container combination is sorted into an array according to increasing unused space .
- The combination containing a smaller number of elements with the same unused space receives negative penalty points and is placed lower in order.
- The best combination is determined by the condition for the best variant:
- Step 2 is repeated. To converge the algorithm successfully, the iteration must be performed at most times.
- Container is filled:where is the used space of the container.
- Unused space of the container is calculated: .
- The array of element is reduced by the elements occupied in the optimal container: .
- Steps 2 to 4 are repeated for .
- Total used space: , where is the optimal number of containers (maximization problem).
- Unused total space (CDW): , where is the optimal number of containers (minimization problems).
- The total number of cuts for the entire set of elements (minimization problems).
- The container combination (minimization problems).
- The multi-objective optimization problem can be formulated as:
- Multicriteria analysis is performed by assigning a weight to each criterion.
- List optimal containers K_opt.
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDW | construction and demolition waste |
| IFCs | Industry Foundation Classes |
| BIM | Building Information Model |
| PHP | Personal Home Page |
| NP-hard | nondeterministic polynomial time problem |
| NF | Next-Fit packing algorithm |
| FF | First-Fit packing algorithm |
| BF | Best-Fit packing algorithm |
| FFD | First-Fit Decreasing packing algorithm |
| FCB | fired clay brick |
Appendix A
| //This program will find optimal masonry cutting with a robotic saw: START SET container_size, number_of_elements SET minimal_length_of_cut, random_first_elements SET Array[element] of number_of_elements SET Array[container] of number_of_elements SET Array[result] COMPUTE max_objects = container_size/minimal_length_of_cut COMPUTE number_of_groups = all_combinations(Array[element], container_size, max_objects) WHILE Array[element] NOT EQUAL [] Array[element] = random sort Array[element] SET work_area TO random_first_elements FROM Array[element] COMPUTE used_space, unused_space FOR each Array[container] COMPUTE number_cuts FOR each Array[container] Array[container] = SORT Array[container] (DESC unused_space, ASC number_cuts) IF unused_space in first Array[container] ≥ min(Array[work_area]) COMPUTE used_space += min(Array[work_area]) FOR first Array[container] COMPUTE unused_space − = min(Array[work_area]) FOR first Array[container] REMOVE min(Array [element]) FROM Array[element] ELSE Array[result].APPEND(first Array[container]) END IF ENDWHILE COMPUTE multi_criterial_score FOR each Array[result] Array[result] = SORT Array[result] (DESC multi_criterial_score) PRINT Array[result] //Function for computation all possible cuts combinations in container FUNCTION all_combinations(element, container_size, n) SET number_group = 0 FOR each possible value v_1 in element FOR each possible value v_2 in element … FOR each possible value v_n in element SET tmp = 0 FOR i = 1 TO n tmp = tmp + v_i IF tmp ≥ container_size number_group = number_group + 1 BREAK END IF END FOR i END FOR v_n … END FOR v_2 END FOR v_1 RETURN number_group END FUNCTION END |
Appendix B
| ID | Elements | Container, [mm] | Min Cut, [mm] | Total Combs | Set of Elements (Size [mm], Number) |
|---|---|---|---|---|---|
| 1 | 426 | 500 | 100 | 121 | (480, 70), (360, 20), (320, 72), (290, 95), (250, 9), (150, 73), (130, 34), (120, 1), (110, 27), (100, 25) |
| 2 | 529 | 500 | 100 | 65 | (450, 76), (440, 82), (380, 85), (300, 13), (260, 24), (210, 16), (170, 94), (160, 36), (140, 4), (110, 99) |
| 3 | 616 | 500 | 100 | 15 | (470, 78), (450, 70), (380, 33), (370, 60), (350, 23), (330, 85), (300, 11), (270, 89), (240, 92), (180, 75) |
| 4 | 455 | 500 | 100 | 34 | (470, 52), (460, 9), (430, 70), (390, 83), (350, 38), (320, 26), (280, 12), (270, 33), (130, 90), (100, 42) |
| 5 | 556 | 500 | 100 | 39 | (420, 23), (390, 69), (370, 77), (320, 7), (290, 79), (260, 94), (220, 56), (180, 83), (160, 51), (140, 17) |
| 6 | 591 | 500 | 100 | 46 | (480, 61), (360, 2), (310, 63), (280, 91), (270, 54), (250, 75), (240, 63), (190, 20), (180, 75), (110, 87) |
| 7 | 582 | 500 | 100 | 24 | (400, 35), (390, 88), (360, 69), (340, 79), (300, 80), (270, 44), (260, 64), (230, 1), (210, 95), (150, 27) |
| 8 | 621 | 500 | 100 | 48 | (480, 97), (460, 80), (430, 34), (300, 76), (290, 80), (250, 86), (200, 30), (180, 98), (150, 25), (110, 15) |
| 9 | 291 | 500 | 100 | 25 | (490, 33), (470, 42), (460, 43), (330, 13), (320, 35), (280, 35), (270, 48), (190, 25), (180, 15), (170, 2) |
| 10 | 533 | 500 | 100 | 62 | (480, 59), (470, 70), (430, 43), (400, 10), (310, 19), (250, 79), (180, 45), (160, 100), (120, 64), (100, 44) |
| 11 | 536 | 600 | 200 | 26 | (560, 25), (520, 64), (440, 75), (420, 32), (350, 43), (340, 76), (270, 72), (250, 74), (230, 43), (210, 32) |
| 12 | 575 | 600 | 200 | 21 | (580, 94), (480, 14), (400, 87), (370, 47), (360, 85), (350, 73), (330, 4), (300, 23), (250, 98), (240, 50) |
| 13 | 529 | 600 | 200 | 13 | (560, 26), (550, 72), (540, 54), (510, 48), (490, 53), (480, 33), (430, 65), (390, 40), (270, 65), (250, 73) |
| 14 | 548 | 600 | 100 | 84 | (540, 8), (460, 89), (440, 32), (350, 19), (300, 99), (270, 63), (250, 90), (190, 76), (140, 9), (100, 63) |
| 15 | 483 | 600 | 100 | 71 | (590, 34), (580, 47), (540, 38), (510, 13), (420, 18), (350, 100), (220, 52), (160, 85), (140, 17), (100, 79) |
| 16 | 352 | 400 | 50 | 186 | (360, 22), (330, 26), (320, 39), (230, 1), (190, 24), (160, 100), (120, 53), (110, 27), (60, 35), (50, 25) |
| 17 | 380 | 400 | 50 | 130 | (390, 14), (370, 76), (330, 29), (300, 25), (260, 37), (180, 33), (130, 8), (110, 20), (70, 40), (50, 98) |
| 18 | 446 | 400 | 50 | 49 | (380, 87), (350, 99), (310, 37), (270, 1), (260, 44), (250, 62), (220, 21), (140, 58), (110, 14), (70, 23) |
| 19 | 387 | 400 | 100 | 25 | (340, 53), (310, 20), (300, 48), (290, 9), (270, 18), (250, 28), (240, 30), (230, 40), (130, 51), (120, 90) |
| 20 | 612 | 400 | 100 | 13 | (370, 63), (330, 86), (310, 92), (280, 57), (270, 51), (260, 76), (250, 96), (240, 15), (200, 8), (190, 68) |
| ID | New Bin Packing Algorithm | First-Fit Decreasing Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Containers | Cuts | Combs | Usage | Unused Space, [mm] | Containers | Cuts | Combs | Usage | Unused Space, [mm] | |
| 1 | 273 | 393 | 12 | 83.96% | 21,900 | 262 | 397 | 11 | 87.48% | 16,400 |
| 2 | 340 | 469 | 10 | 87.81% | 20,730 | 321 | 492 | 10 | 93.00% | 11,230 |
| 3 | 495 | 616 | 10 | 81.58% | 45,590 | 495 | 616 | 10 | 81.58% | 45,590 |
| 4 | 324 | 421 | 11 | 86.94% | 21,160 | 323 | 455 | 10 | 87.21% | 20,660 |
| 5 | 383 | 515 | 12 | 79.61% | 39,050 | 358 | 549 | 11 | 85.17% | 26,550 |
| 6 | 340 | 491 | 12 | 88.43% | 19,670 | 340 | 492 | 12 | 88.43% | 19,670 |
| 7 | 459 | 581 | 10 | 77.02% | 52,730 | 459 | 581 | 10 | 77.02% | 52,730 |
| 8 | 425 | 548 | 11 | 91.54% | 17,980 | 413 | 548 | 10 | 94.20% | 11,980 |
| 9 | 249 | 274 | 10 | 81.71% | 22,770 | 249 | 274 | 10 | 81.71% | 22,770 |
| 10 | 311 | 423 | 13 | 93.59% | 9970 | 307 | 477 | 15 | 94.81% | 7970 |
| 11 | 366 | 493 | 10 | 86.14% | 30,440 | 366 | 493 | 10 | 86.14% | 30,440 |
| 12 | 426 | 441 | 11 | 83.84% | 41,300 | 426 | 441 | 11 | 83.84% | 41,300 |
| 13 | 460 | 529 | 11 | 82.95% | 47,040 | 460 | 529 | 11 | 82.95% | 47,040 |
| 14 | 295 | 431 | 14 | 88.81% | 19,800 | 290 | 471 | 12 | 90.34% | 16,800 |
| 15 | 295 | 438 | 11 | 86.07% | 24,650 | 273 | 472 | 13 | 93.01% | 11,450 |
| 16 | 177 | 300 | 17 | 88.21% | 8350 | 176 | 351 | 11 | 88.71% | 7950 |
| 17 | 212 | 309 | 14 | 90.98% | 7650 | 204 | 331 | 11 | 94.54% | 4450 |
| 18 | 352 | 389 | 11 | 86.85% | 18,520 | 351 | 402 | 10 | 87.09% | 18,120 |
| 19 | 267 | 369 | 11 | 81.39% | 19,880 | 255 | 369 | 11 | 85.22% | 15,080 |
| 20 | 501 | 535 | 9 | 76.71% | 46,680 | 574 | 608 | 10 | 74.83% | 57,780 |
| ID | Weight Set 1 | Weight Set 2 | ||||
|---|---|---|---|---|---|---|
| Score NBPA | Score FFD | Diff | Score NBPA | Score FFD | Diff | |
| 1 | 54.43 | 55.92 | −1.50 | 46.64 | 47.46 | −0.82 |
| 2 | 54.87 | 55.98 | −1.11 | 48.44 | 47.58 | 0.85 |
| 3 | 33.64 | 33.64 | 0.00 | 26.91 | 26.91 | 0.00 |
| 4 | 47.71 | 46.70 | 1.01 | 41.16 | 37.36 | 3.80 |
| 5 | 46.83 | 48.46 | −1.63 | 40.42 | 39.27 | 1.15 |
| 6 | 55.43 | 55.39 | 0.04 | 51.11 | 51.01 | 0.10 |
| 7 | 39.17 | 39.17 | 0.00 | 31.40 | 31.40 | 0.00 |
| 8 | 52.98 | 54.65 | −1.67 | 47.09 | 48.42 | −1.33 |
| 9 | 40.50 | 40.50 | 0.00 | 34.73 | 34.73 | 0.00 |
| 10 | 58.73 | 55.88 | 2.85 | 55.24 | 48.91 | 6.33 |
| 11 | 46.85 | 46.85 | 0.00 | 40.69 | 40.69 | 0.00 |
| 12 | 45.17 | 45.17 | 0.00 | 45.46 | 45.46 | 0.00 |
| 13 | 27.84 | 27.84 | 0.00 | 22.28 | 22.28 | 0.00 |
| 14 | 59.92 | 59.30 | 0.62 | 56.47 | 53.06 | 3.41 |
| 15 | 54.71 | 55.11 | −0.41 | 47.49 | 45.00 | 2.49 |
| 16 | 60.89 | 58.27 | 2.62 | 54.62 | 46.73 | 7.89 |
| 17 | 60.78 | 61.32 | −0.55 | 56.09 | 54.22 | 1.88 |
| 18 | 49.56 | 49.46 | 0.10 | 44.76 | 43.52 | 1.25 |
| 19 | 43.26 | 44.99 | −1.73 | 36.47 | 37.86 | −1.39 |
| 20 | 34.55 | 26.19 | 8.36 | 32.67 | 21.22 | 11.46 |
| 7 | 7 | 11 | 3 | |||
References
- Construction and Demolition Waste. Available online: https://environment.ec.europa.eu/topics/waste-and-recycling/construction-and-demolition-waste_en (accessed on 13 January 2025).
- Moschen-Schimek, J.; Kasper, T.; Huber-Humer, M. Critical Review of the Recovery Rates of Construction and Demolition Waste in the European Union—An Analysis of Influencing Factors in Selected EU Countries. Waste Manag. 2023, 167, 150–164. [Google Scholar] [CrossRef] [PubMed]
- Waste Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Waste_statistics (accessed on 20 January 2025).
- Distribution of Waste Generation in the United Kingdom in 2020, by Economic Activity. Available online: https://www.statista.com/statistics/1317719/waste-generation-split-uk-by-source/ (accessed on 20 January 2025).
- U.S. Industrial Waste Production in 2011, by Sector. Available online: https://www.statista.com/statistics/249121/breakdown-of-the-us-industrial-waste-market-by-sector/ (accessed on 20 January 2025).
- Construction Producer Price and Construction Cost Indices Overview. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Construction_producer_price_and_construction_cost_indices_overview (accessed on 13 January 2025).
- Construction Building Materials: Commentary, March 2024. Available online: https://www.gov.uk/government/statistics/building-materials-and-components-statistics-march-2024/construction-building-materials-commentary-march-2024 (accessed on 13 January 2025).
- Building Materials Price Growth Plummets in 2023. Available online: https://www.nahb.org/blog/2024/01/building-materials-prices-plummet-in-2023 (accessed on 13 January 2025).
- Olsson, J.A.; Hafez, H.; Miller, S.A.; Scrivener, K.L. Greenhouse Gas Emissions and Decarbonization Potential of Global Fired Clay Brick Production. Environ. Sci. Technol. 2025, 59, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Popowicz, M.; Katzer, N.J.; Kettele, M.; Schöggl, J.-P.; Baumgartner, R.J. Digital technologies for life cycle assessment: A review and integrated combination framework. Int. J. Life Cycle Assess. 2024, 30, 405–428. [Google Scholar] [CrossRef]
- Banihashemi, S.; Meskin, S.; Sheikhkhoshkar, M.; Mohandes, S.R.; Hajirasouli, A.; LeNguyen, K. Circular Economy in Construction: The Digital Transformation Perspective. Clean. Eng. Technol. 2024, 18, 100715. [Google Scholar] [CrossRef]
- Akbari, S.; Sheikhkhoshkar, M.; Pour Rahimian, F.; El Haouzi, H.B.; Najafi, M.; Talebi, S. Sustainability and Building Information Modelling: Integration, Research Gaps, and Future Directions. Autom. Constr. 2024, 163, 105420. [Google Scholar] [CrossRef]
- Liu, Y.; Alias, A.H.; Haron, N.A.; Bakar, N.A.; Wang, H. Robotics in the Construction Sector: Trends, Advances, and Challenges. J. Intell. Robot. Syst. 2024, 110, 72. [Google Scholar] [CrossRef]
- Sawhney, A.; Riley, M.; Irizarry, J. Construction 4.0: An Innovation Platform for the Built Environment, 1st ed.; Routledge: New York, NY, USA, 2020. [Google Scholar]
- Bock, T.; Linner, T. Construction Robots: Elementary Technologies and Single-Task Construction Robots, 1st ed.; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Liu, Y.; Belousov, B.; Schneider, T.; Harsono, K.; Cheng, T.-W.; Shih, S.-G.; Tessmann, O.; Peters, J. Advancing Sustainable Construction: Discrete Modular Systems & Robotic Assembly. Sustainability 2024, 16, 6678. [Google Scholar] [CrossRef]
- Porotherm Products. Available online: https://porothermuk.co.uk/products/ (accessed on 31 March 2025).
- Cavity Best Practice Guide. Available online: https://www.wienerberger.co.uk/content/dam/wienerberger/united-kingdom/marketing/documents-magazines/brochures/UK_MKT_DOC_POR_Porotherm_Cavity_Best_Practice_Guide.pdf (accessed on 31 March 2025).
- Usmanov, V.; Illetško, J.; Šulc, R. Digital Plan of Brickwork Layout for Robotic Bricklaying Technology. Sustainability 2021, 13, 3905. [Google Scholar] [CrossRef]
- Borges, Y.G.F.; Schouery, R.C.S.; Miyazawa, F.K. Mathematical Models and Exact Algorithms for the Colored Bin Packing Problem. Comput. Oper. Res. 2024, 164, 106527. [Google Scholar] [CrossRef]
- Fleszar, K. A MILP Model and Two Heuristics for the Bin Packing Problem with Conflicts and Item Fragmentation. Eur. J. Oper. Res. 2022, 303, 37–53. [Google Scholar] [CrossRef]
- Coffman, E.G., Jr.; Csirik, J.; Galambos, G.; Martello, S.; Vigo, D. Bin Packing Approximation Algorithms: Survey and Classification. In Pardalos Handbook of Combinatorial Optimization; Pardalos, P., Du, D.Z., Graham, R., Eds.; Springer: New York, NY, 2021; pp. 455–531. [Google Scholar]
- Ekici, A. Bin Packing Problem with Conflicts and Item Fragmentation. Comput. Oper. Res. 2021, 126, 105113. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, F.; Huang, H.; Huang, G.; Cui, C. An Industrial Robot-Based Sawing Method for Natural Stone Sculpture. J. Comput. Des. Eng. 2024, 11, 75–85. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Fierro, G.; Man, C.; So, P.; Leung, K. Developing an Automatic Integration Approach to Generate Brick Model from Imperfect Building Information Modelling. J. Build. Eng. 2024, 97, 110697. [Google Scholar] [CrossRef]
- IFC 4.3.2.0 (IFC4X3_ADD2) Official. Available online: https://standards.buildingsmart.org/IFC/RELEASE/IFC4_3/ (accessed on 27 February 2025).
- Borges, Y.; de Lima, V.; Miyazawa, F.; Pedrosa, L.; de Queiroz, T.; Schouery, R. Algorithms for the Bin Packing Problem with Scenarios. J. Comb. Optim. 2024, 48, 34. [Google Scholar] [CrossRef]
- Quesada, J.; Gil-Gala, F.; Durasevic, M.; Sierra, M.; Varela, R. Evolutionary Algorithms for Bin Packing Problem with Maximum Lateness and Waste Minimization. In University of Oviedo; Vicente, J., Calvo, M., Adeli, H., Eds.; Springer: Cham, Switzerland, 2024; Volume 14675. [Google Scholar] [CrossRef]
- Jena, S.; Subramani, K.; Velasquez, A. A Differential Approach for Several NP-Hard Optimization Problems. In West Virginia University; Barneva, R., Brimkov, V., Gentile, C., Pacchiano, A., Eds.; Springer: Cham, Switzerland, 2024; Volume 14494. [Google Scholar] [CrossRef]
- da Silva, R.; Borges, Y.; Schouery, R. Fast Neighborhood Search Heuristics for the Colored Bin Packing Problem. Ann. Oper. Res. 2024, 343, 125–152. [Google Scholar] [CrossRef]
- Mommessin, C.; Erlebach, T.; Shakhlevich, N. Classification and Evaluation of the Algorithms for Vector Bin Packing. Comput. Oper. Res. 2025, 173, 106860. [Google Scholar] [CrossRef]
- Martello, S.; Toth, P. Knapsack Problems: Algorithms and Computer Implementations; Wiley-Interscience Series in Discrete Mathematics and Optimization; J. Wiley & Sons: Chichester, UK; New York, NY, USA, 1990. [Google Scholar]
- Vázquez-Aguirre, J.; Carmona-Arroyo, G.; Quiroz-Castellanos, M.; Cruz-Ramírez, N. Causal Analysis to Explain the Performance of Algorithms: A Case Study for the Bin Packing Problem. Math. Comput. Appl. 2024, 29, 73. [Google Scholar] [CrossRef]
- PHP Documentation. Available online: https://www.php.net/download-docs.php (accessed on 25 February 2025).
- Math Library for PHP. Available online: https://github.com/markrogoyski/math-php (accessed on 25 February 2025).
- Optimization Algorithm for Cutting Masonry with Robotic Saw. Available online: https://github.com/UsmanovSla/NewBinPackingAlgorithm (accessed on 26 February 2025).
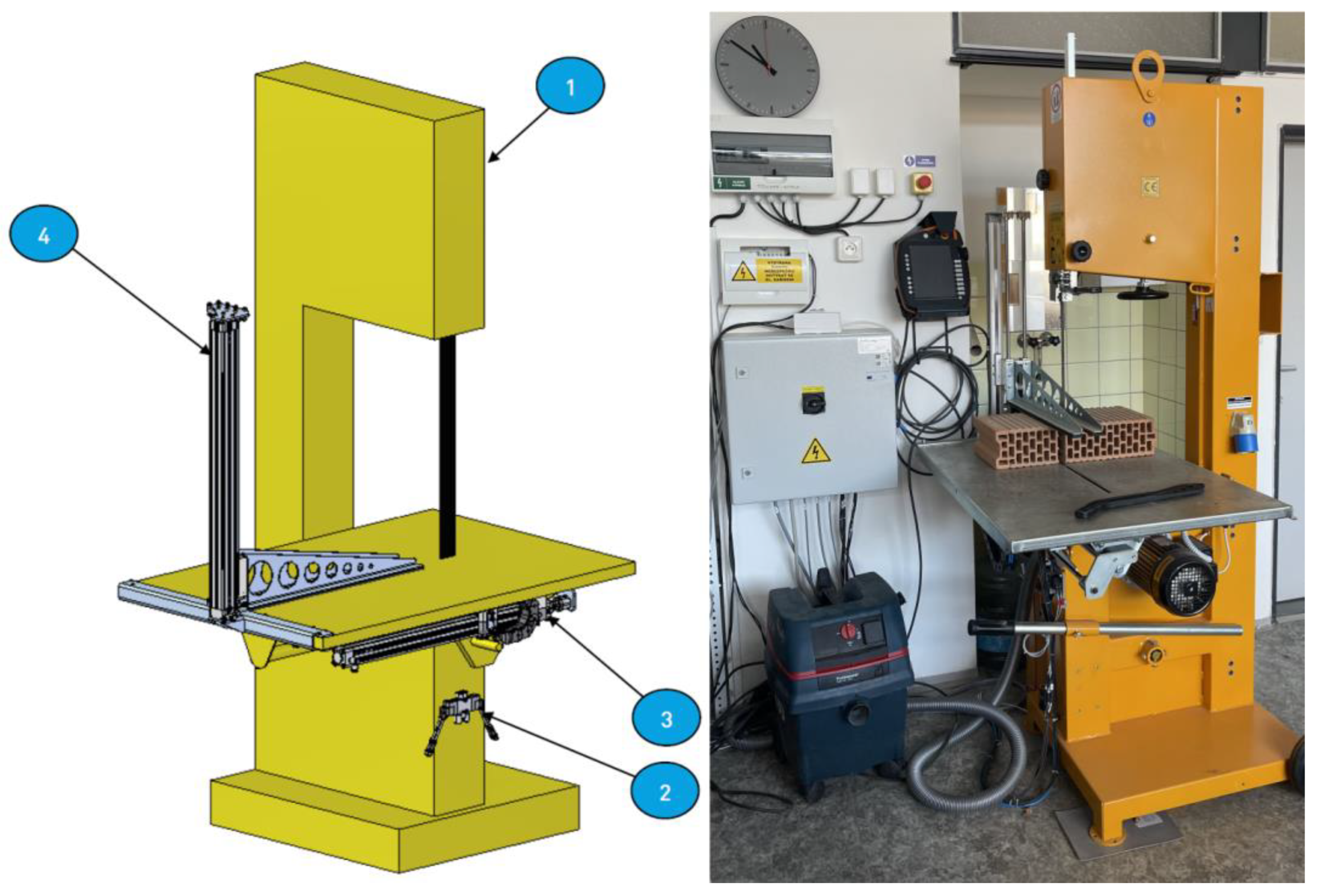
- 400 CCE H47 Band Saw. Available online: https://www.eurotsc.com/en/products/400-cce-h47-band-saw/ (accessed on 20 February 2025).
- Al, B.; Alkan, M. Compositions of Integers And Fibonacci Numbers. Communications Faculty of Sciences University Of Ankara-Series A1. Math. Stat. 2024, 73, 178–191. [Google Scholar] [CrossRef]
- Sgall, J. Online Bin Packing: Old Algorithms and New Results. In Language, Life, Limits; Beckmann, A., Csuhaj-Varjú, E., Meer, K., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2014; Volume 8493. [Google Scholar] [CrossRef]
- Test Quality of Bin-Packing Algorithms. Available online: https://github.com/tahoe01/Bin-Packing (accessed on 25 February 2025).
- New Bin Packing Algorithm for Robotic Saw. Available online: http://www.robostav.cz/new-bin-packing-algorithm-on-line (accessed on 28 February 2025).
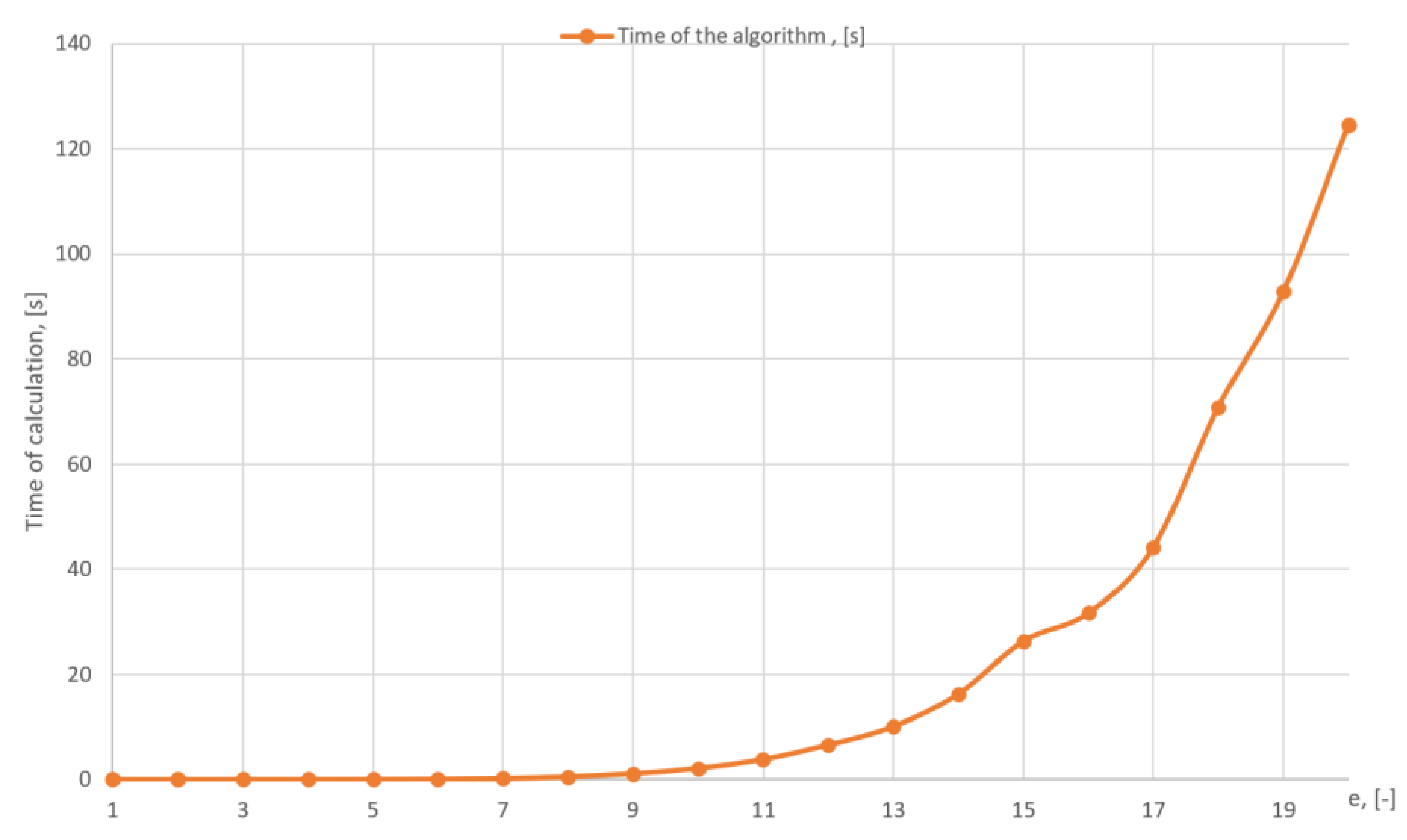
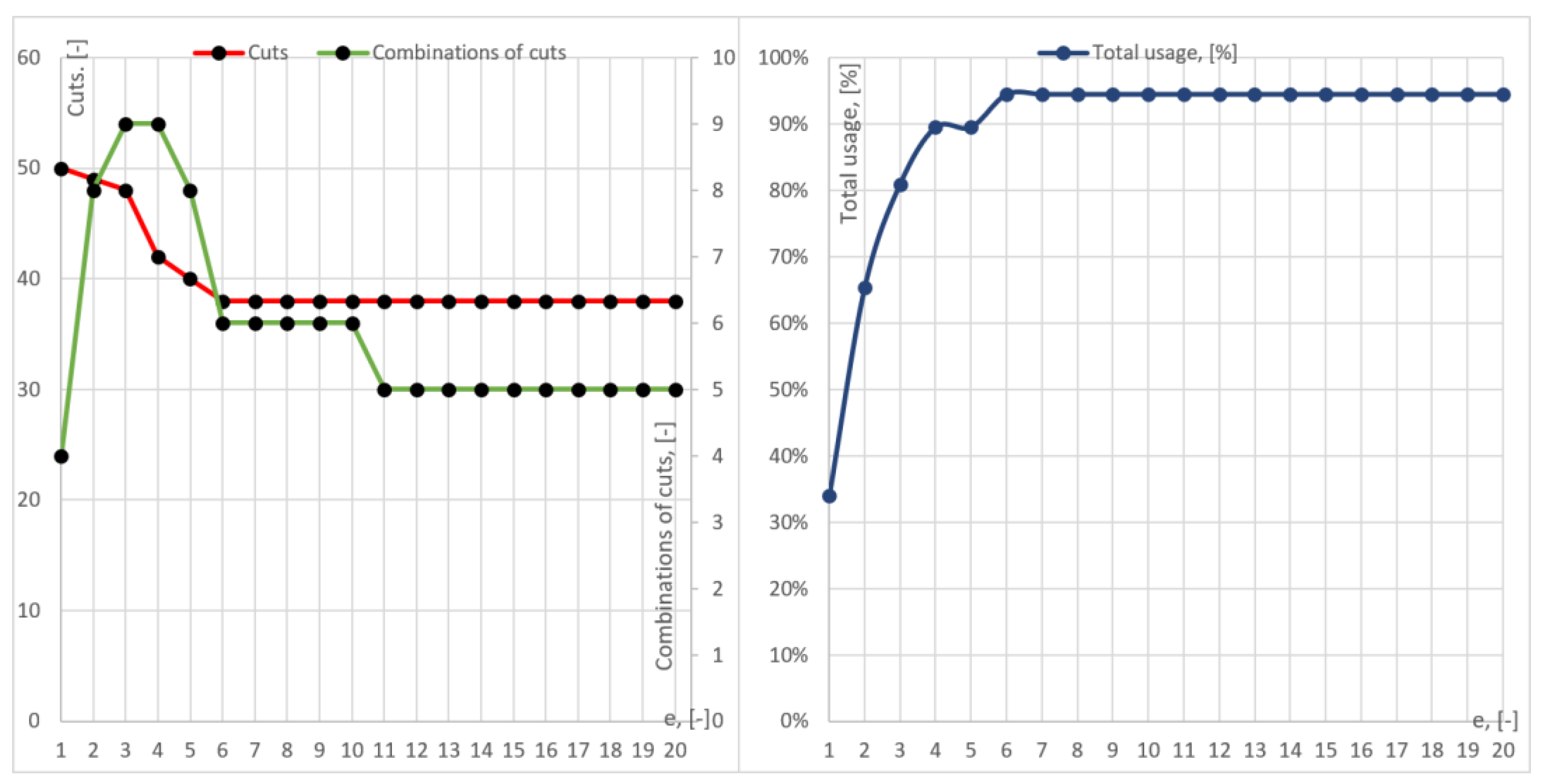
| e | Number of Containers | Number of Groups | Number of Cuts | Unused Space, [mm] | Time, [s] | Total Usage, [%] |
|---|---|---|---|---|---|---|
| 1 | 50 | 4 | 50 | 16,500 | 0.003076 | 34.000% |
| 2 | 26 | 8 | 49 | 4500 | 0.002287 | 65.385% |
| 3 | 21 | 9 | 48 | 2000 | 0.003186 | 80.952% |
| 4 | 19 | 9 | 42 | 1000 | 0.006804 | 89.474% |
| 5 | 19 | 8 | 40 | 1000 | 0.023867 | 89.474% |
| 6 | 18 | 6 | 38 | 500 | 0.077412 | 94.444% |
| 7 | 18 | 6 | 38 | 500 | 0.214188 | 94.444% |
| 8 | 18 | 6 | 38 | 500 | 0.530642 | 94.444% |
| 9 | 18 | 6 | 38 | 500 | 1.135994 | 94.444% |
| 10 | 18 | 6 | 38 | 500 | 2.128886 | 94.444% |
| 11 | 18 | 5 | 38 | 500 | 3.856181 | 94.444% |
| 12 | 18 | 5 | 38 | 500 | 6.596284 | 94.444% |
| 13 | 18 | 5 | 38 | 500 | 10.123138 | 94.444% |
| 14 | 18 | 5 | 38 | 500 | 16.274853 | 94.444% |
| 15 | 18 | 5 | 38 | 500 | 26.315432 | 94.444% |
| 16 | 18 | 5 | 38 | 500 | 31.709445 | 94.444% |
| 17 | 18 | 5 | 38 | 500 | 44.169316 | 94.444% |
| 18 | 18 | 5 | 38 | 500 | 70.867784 | 94.444% |
| 19 | 18 | 5 | 38 | 500 | 92.810268 | 94.444% |
| 20 | 18 | 5 | 38 | 500 | 124.552543 | 94.444% |
| Iteration | Combination | Number of Cuts | Used Part, [mm] | Unused Snippet, [mm] | Container Usage, [%] | Time, [s] |
|---|---|---|---|---|---|---|
| 1 | 300 + 150 | 2 | 450 | 50 | 90% | 0.287428 |
| 2 | 250 + 150 + 100 | 2 | 500 | 0 | 100% | 0.246005 |
| 3 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.269982 |
| 4 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.264411 |
| 5 | 250 + 150 + 100 | 2 | 500 | 0 | 100% | 0.254247 |
| 6 | 250 + 150 + 100 | 2 | 500 | 0 | 100% | 0.265522 |
| 7 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.255779 |
| 8 | 250 + 150 + 100 | 2 | 500 | 0 | 100% | 0.260728 |
| 9 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.266978 |
| 10 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.258111 |
| 11 | 250 + 150 + 100 | 2 | 500 | 0 | 100% | 0.276104 |
| 12 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.259949 |
| 13 | 300 + 100 + 100 | 2 | 500 | 0 | 100% | 0.257400 |
| 14 | 300 + 150 | 2 | 450 | 50 | 90% | 0.257507 |
| 15 | 300 + 150 | 2 | 450 | 50 | 90% | 0.141309 |
| 16 | 150 + 150 + 150 | 3 | 450 | 50 | 90% | 0.033435 |
| 17 | 150 + 150 + 150 | 3 | 450 | 50 | 90% | 0.000960 |
| 18 | 150 + 100 | 2 | 250 | 250 | 50% | 0.000041 |
| w = 18 | Combinations: 5 | 38 | 8500 | 500 | 94.444% | 3.856181 |
| Parameters | New Bin Packing Algorithm | Next-Fit Decreasing | First-Fit Decreasing | Worst-Fit Decreasing | Best-Fit Decreasing |
|---|---|---|---|---|---|
| Total usage, [%] | 94.44% | 77.27% | 89.474% | 89.474% | 89.474% |
| Number of containers, [-] | 18 | 22 | 19 | 19 | 19 |
| Number of cuts, [-] | 38 | 44 | 43 | 44 | 44 |
| Unused space, [mm] | 500 | 2500 | 1000 | 1000 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usmanov, V.; Kovářík, M.; Šulc, R.; Jarský, Č. Optimization Algorithm for Cutting Masonry with a Robotic Saw. Appl. Sci. 2025, 15, 4015. https://doi.org/10.3390/app15074015
Usmanov V, Kovářík M, Šulc R, Jarský Č. Optimization Algorithm for Cutting Masonry with a Robotic Saw. Applied Sciences. 2025; 15(7):4015. https://doi.org/10.3390/app15074015
Chicago/Turabian StyleUsmanov, Vjačeslav, Michal Kovářík, Rostislav Šulc, and Čeněk Jarský. 2025. "Optimization Algorithm for Cutting Masonry with a Robotic Saw" Applied Sciences 15, no. 7: 4015. https://doi.org/10.3390/app15074015
APA StyleUsmanov, V., Kovářík, M., Šulc, R., & Jarský, Č. (2025). Optimization Algorithm for Cutting Masonry with a Robotic Saw. Applied Sciences, 15(7), 4015. https://doi.org/10.3390/app15074015







