Damage Recovery Method for Air–Sea Cross-Domain Communication Network Based on Improved Dijkstra and Load Balancing
Abstract
1. Introduction
- We propose a multi-node failure recovery method that integrates link quality prediction with minimum communication cost, leveraging an improved Dijkstra algorithm and load-balancing strategy to achieve more efficient network recovery.
- Considering the characteristics of air–sea cross-domain communication networks, we develop an objective function that balances load distribution and communication cost and solve it using the whale optimization algorithm to optimize path selection and load allocation during the recovery process.
- Through simulation analysis, we validate the effectiveness of the proposed algorithm, particularly by comparing its performance with traditional recovery strategies in two scenarios: random node failures and deliberate attacks. The results further demonstrate the superior performance of our algorithm in network recovery.
- This study provides a novel approach and solution for damage recovery in air–sea cross-domain communication networks, significantly contributing to the enhancement of network reliability and stability.
2. Related Work
2.1. Topology Reconstruction
2.2. Swarm Intelligence
3. Methodology
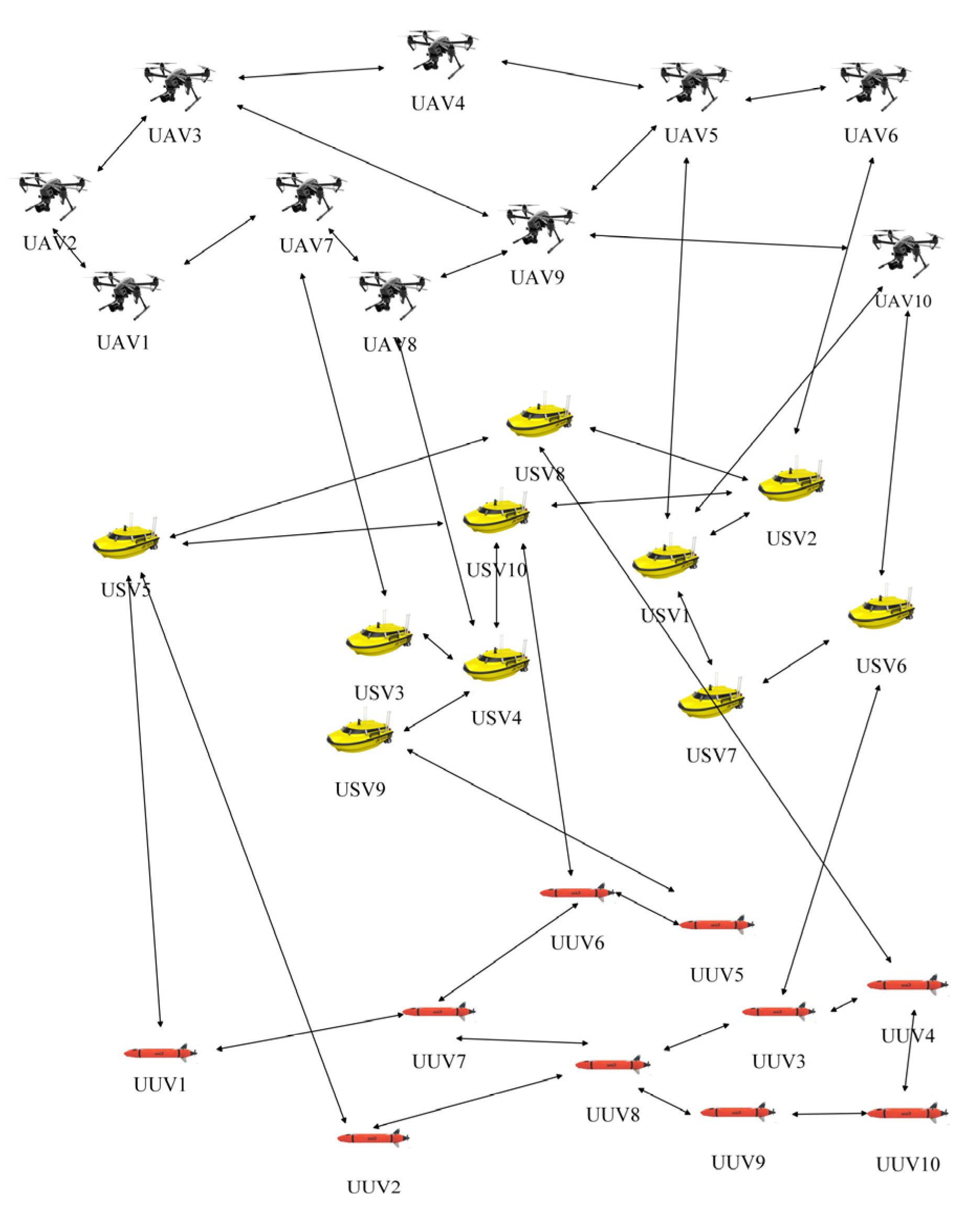
3.1. Air–Sea Cross-Domain Communication Network Model
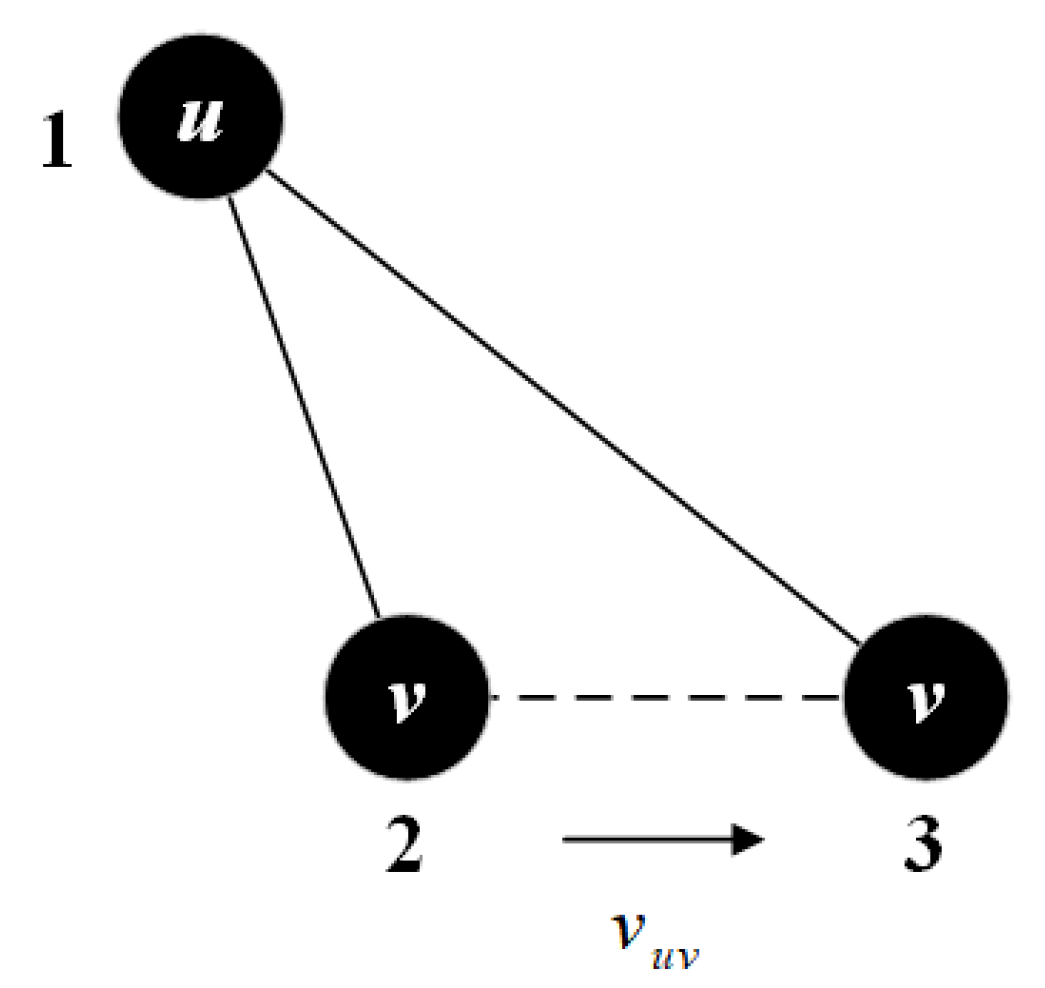
3.2. Link Quality Prediction Algorithm
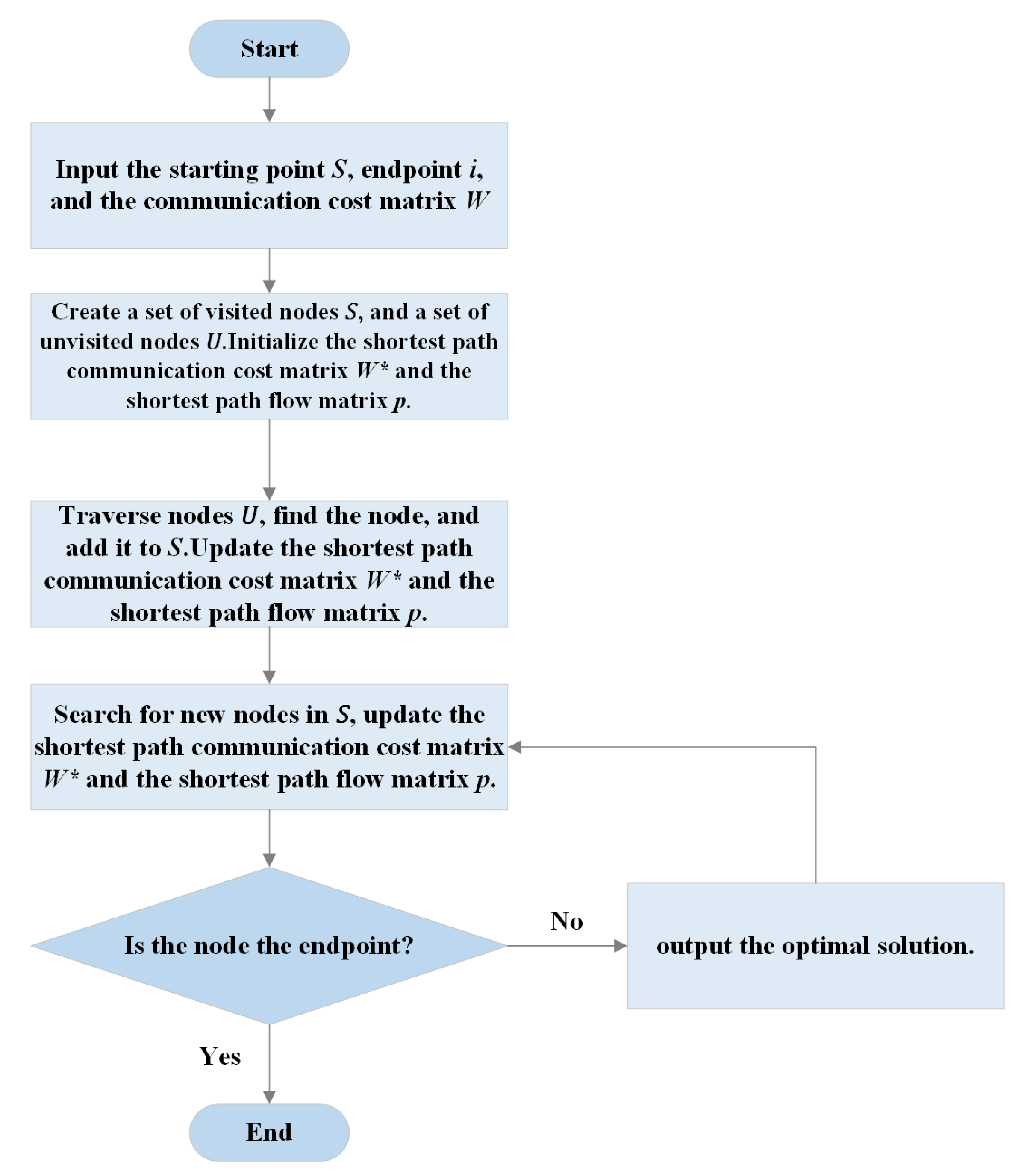
3.3. Path Selection Strategy Based on Improved Dijkstra and Load Balancing
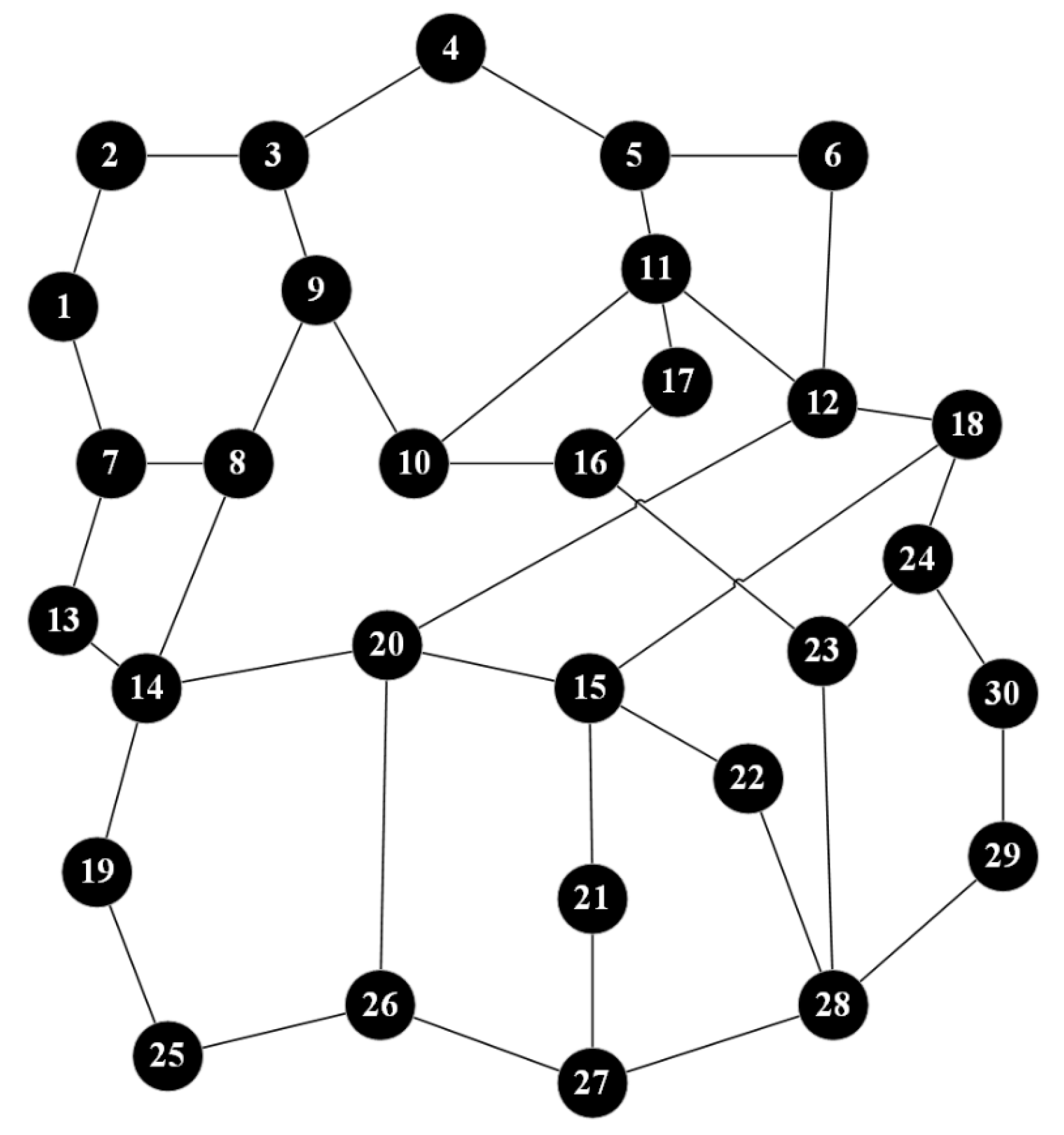
4. Validation of Algorithm Effectiveness
5. Comparison of Algorithm Performance
5.1. Random Failure Scenario
5.2. Deliberate Attack Scenario
5.3. Performance Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| USV | unmanned surface vessels |
| UUV | unmanned underwater vehicles |
References
- Shang, Z.G.; Zhang, H.Y.; Liu, S.Z.; Qiao, G.; Yu, H.; Miao, B.; Ma, L.; Wang, Z. Research Progress and Development Trend of Air-Sea Cross-domain Communication. J. Unmanned Undersea Syst. 2024, 32, 592–610. [Google Scholar]
- Xing, M.H.; Shang, Z.G.; Qiao, G.; Zhou, F.; Nie, D.; Zhang, T.; Li, T.; Xie, J. Cross-Domain Communication Buoy System Based on Optimal Communication Link Selection. J. Unmanned Undersea Syst. 2024, 32, 650–658. [Google Scholar]
- Yazıcıoğlu, A.Y.; Egerstedt, M.; Shamma, J.S. Formation of robust multi-agent networks through self-organizing random regular graphs. IEEE Trans. Netw. Sci. Eng. 2015, 2, 139–151. [Google Scholar] [CrossRef]
- Zhang, J. Multi-UAV Collaborative Surveillance Network Recovery via Deep Reinforcement Learning. IEEE Internet Things J. 2024, 11, 34528–34540. [Google Scholar] [CrossRef]
- Xing, M.; Deng, H.; Han, R. ICN-Oriented Mobility Support Method for Dynamic Allocation of Mobile Data Flows. Electronics 2023, 12, 1701. [Google Scholar] [CrossRef]
- Vijaya Vardan Reddy, S.P.; Kishore, V.V.; Diwakaran, S.; Sujatha, V.; Jayakumar, T. A Robust Design of Fault Nodes Identification and Recovery Model Over Wireless Sensor Network. In Proceedings of the Ninth International Conference on Science Technology Engineering and Mathematics (ICONSTEM), Chennai, India, 4–5 April 2024; pp. 1–7. [Google Scholar]
- Caleb, S.; Thangaraj, S.J.J. Enhancing Fault Tolerance in Wireless Mesh Networks through Adaptive and Resilient Routing Protocols. In Proceedings of the 2023 International Conference on Data Science, Agents & Artificial Intelligence (ICDSAAI), Chennai, India, 21–23 December 2023; pp. 1–6. [Google Scholar]
- Hu, P.; Xue, H.; Wu, C.; Guo, M.; Li, J.; Chen, X.; Liu, S.; Zhou, L.; Xie, S. HGR: A Hybrid Global Graph-Based Recovery Approach for Cloud Storage Systems with Failure and Straggler Nodes. In Proceedings of the 44th International Conference on Distributed Computing Systems (ICDCS), Jersey City, NJ, USA, 23–26 July 2024; pp. 750–761. [Google Scholar]
- Wójcik, R.; Domżał, J.; Duliński, Z. Flow-aware multi-topology adaptive routing. IEEE Commun. Lett. 2014, 18, 1539–1542. [Google Scholar] [CrossRef]
- Menth, M.; Martin, R. Network resilience through multi-topology routing. In Proceedings of the Fifth International Workshop on Design of Reliable Communication Networks, Naples, Italy, 16–19 October 2005; pp. 271–277. [Google Scholar]
- Gardner, M.T.; May, R.; Beard, C.; Medhi, D. Using multi-topology routing to improve routing during geographically correlated failures. In Proceedings of the 2014 10th International Conference on the Design of Reliable Communication Networks (DRCN), Ghent, Belgium, 1–3 April 2014; pp. 1–8. [Google Scholar]
- Cevher, S.; Ulutas, M.; Altun, S.; Hokelek, I. Multi topology routing based IP fast re-route for software defined networks. In Proceedings of the 2016 IEEE Symposium on Computers and Communication (ISCC), Messina, Italy, 27–30 June 2016; pp. 1224–1226. [Google Scholar]
- Zhang, R.Y.; Xiao, G.Y.; Shan, Q.H.; Zou, T.; Li, D.; Teng, F. Communication topology reconstruction method for multi-agent cooperative control in polymorphic networks. J. Commun. 2022, 43, 50–59. [Google Scholar]
- Qin, N.N.; Wu, D.E.; Yu, Y.H. A double connectivity recovery algorithm in partition based on backbone polygon in sensor networks. Comput. Eng. Sci. 2017, 39, 673. [Google Scholar]
- Ma, G.Z. Fault-Tolerant Topology Control and Connectivity Restorantion in Wireless Sensor Networks. Ph.D. Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2017. [Google Scholar]
- Kang, Z.; Zeng, H.; Hu, H.; Xiong, Q.; Xu, G. Multi-objective optimized connectivity restoring of disjoint segments using mobile data collectors in wireless sensor network. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 65. [Google Scholar] [CrossRef]
- Du, R.; Fei, H.; W Zhang, W. Research and Design of a SpaceWire Network Dynamic Reconfiguration Method Based on Dijkstra Algorithm. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; pp. 168–173. [Google Scholar]
- Jabarulla Mohammed, M.; Asim Basha, M. Shortest Path Problem under Pythagorean Fuzzy Network Using Dijkstra’s Algorithm. Asian Res. J. Math. 2024, 10, 47–57. [Google Scholar] [CrossRef]
- Wang, N.; Ho, K.H.; Pavlou, G. AMPLE: An adaptive traffic engineering system based on virtual routing topologies. IEEE Commun. Mag. 2012, 50, 185–191. [Google Scholar] [CrossRef]
- Altenhofen, K.; Zobel, J.; Scheuermann, B. Increasing Network Resilience Through Dynamic Routing with Disjoint Paths. In Proceedings of the 2024 IFIP Networking Conference (IFIP Networking), Thessaloniki, Greece, 3–6 June 2024; pp. 23–31. [Google Scholar]
- Willis, P.; Shenoy, N.; Hamilton, J.; Pan, Y. Resiliency in Networks Through Meshed Trees. In Proceedings of the 15th International Conference on Network of the Future (NoF), Castelldefels, Spain, 2–4 October 2024; pp. 45–53. [Google Scholar]
- Zuo, J.X. Research on Topological Reconstruction of UAV Swarm Network and Key Technology. Master’s Thesis, Xi’an Technological University, Xi’an, China, 2022. [Google Scholar]
- Chen, M.; Wang, H.; Chang, C.Y.; Wei, X. SIDR: A swarm intelligence-based damage-resilient mechanism for UAV swarm networks. IEEE Access 2020, 8, 77089–77105. [Google Scholar] [CrossRef]
- Cui, Y.N.; Ren, J.; Du, W.C. Network topology optimization control algorithm for multiple unmanned surface vehicle. Control Theory Appl. 2016, 33, 1639–1649. [Google Scholar]
- Chouikhi, S.; El Korbi, I.; Ghamri-Doudane, Y.; Saidane, L.A. Distributed connectivity restoration in multichannel wireless sensor networks. Comput. Netw. 2017, 127, 282–295. [Google Scholar] [CrossRef]
- Pliatsios, D. Comparison of Swarm Intelligence Methods for Joint Resource Orchestration in Open Radio Access Network. In Proceedings of the 14th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Rome, Italy, 17–19 July 2024; pp. 632–637. [Google Scholar]
- Volovoda, T. Swarm Intelligence for UAV. In Proceedings of the 7th International Conference on Actual Problems of Unmanned Aerial Vehicles Development (APUAVD), Kyiv, Ukraine, 22–24 October 2024; pp. 313–316. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Xie, N.; Wang, R. A historic Review of Grey Forecasting Models. J. Grey Syst. 2017, 29, 1–29. [Google Scholar]
- Gharehchopogh, F.S.; Gholizadeh, H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]
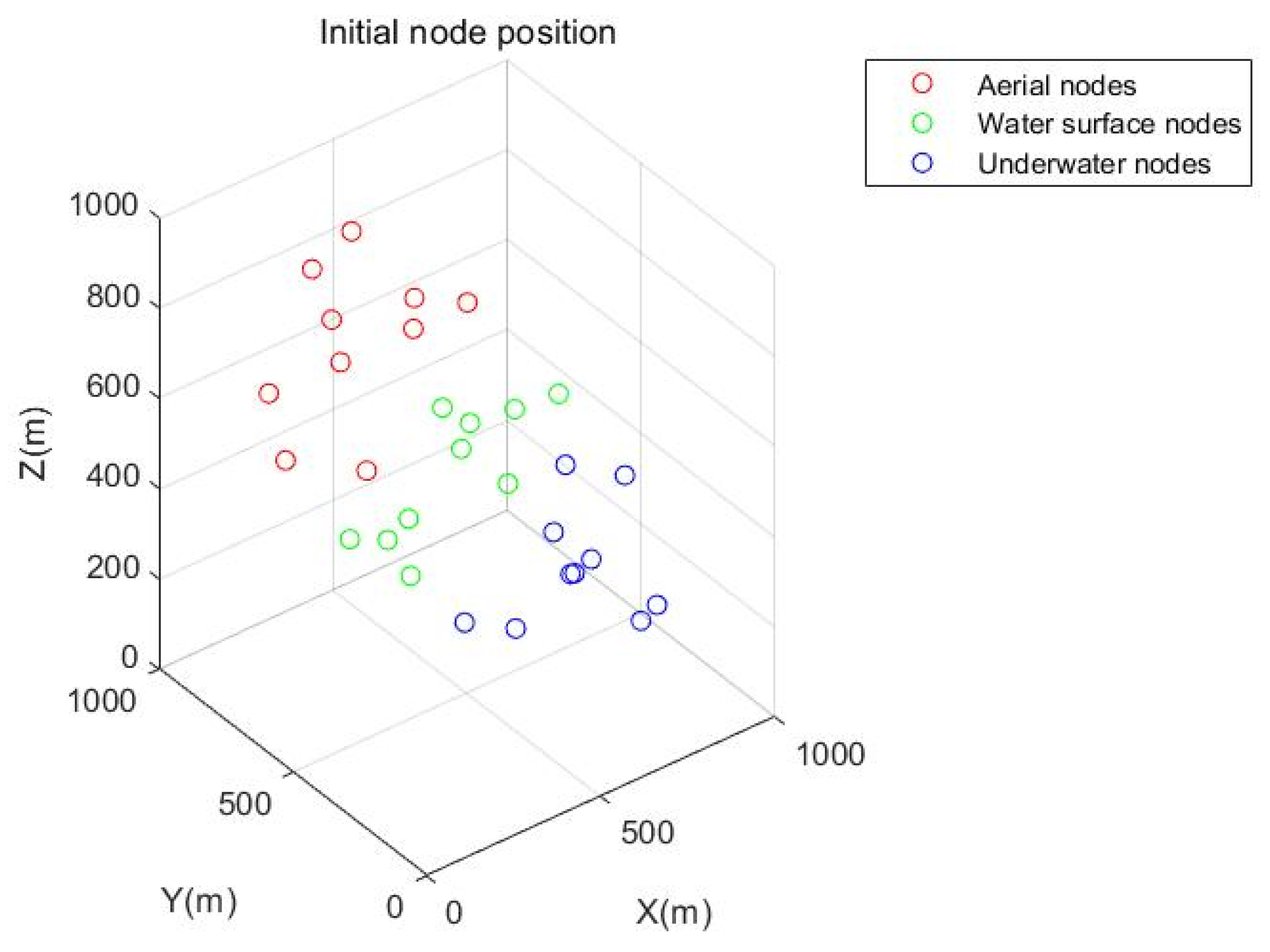
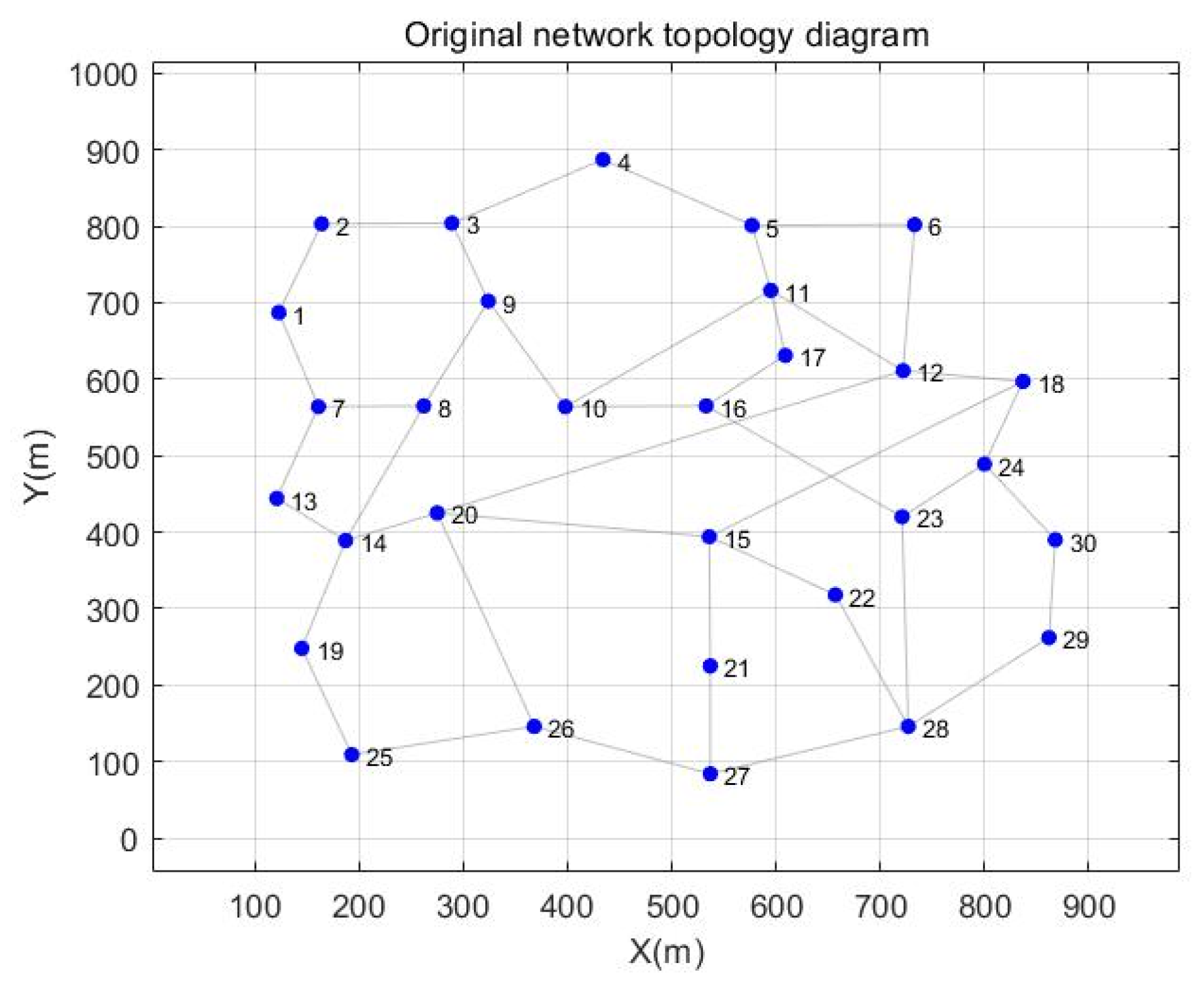
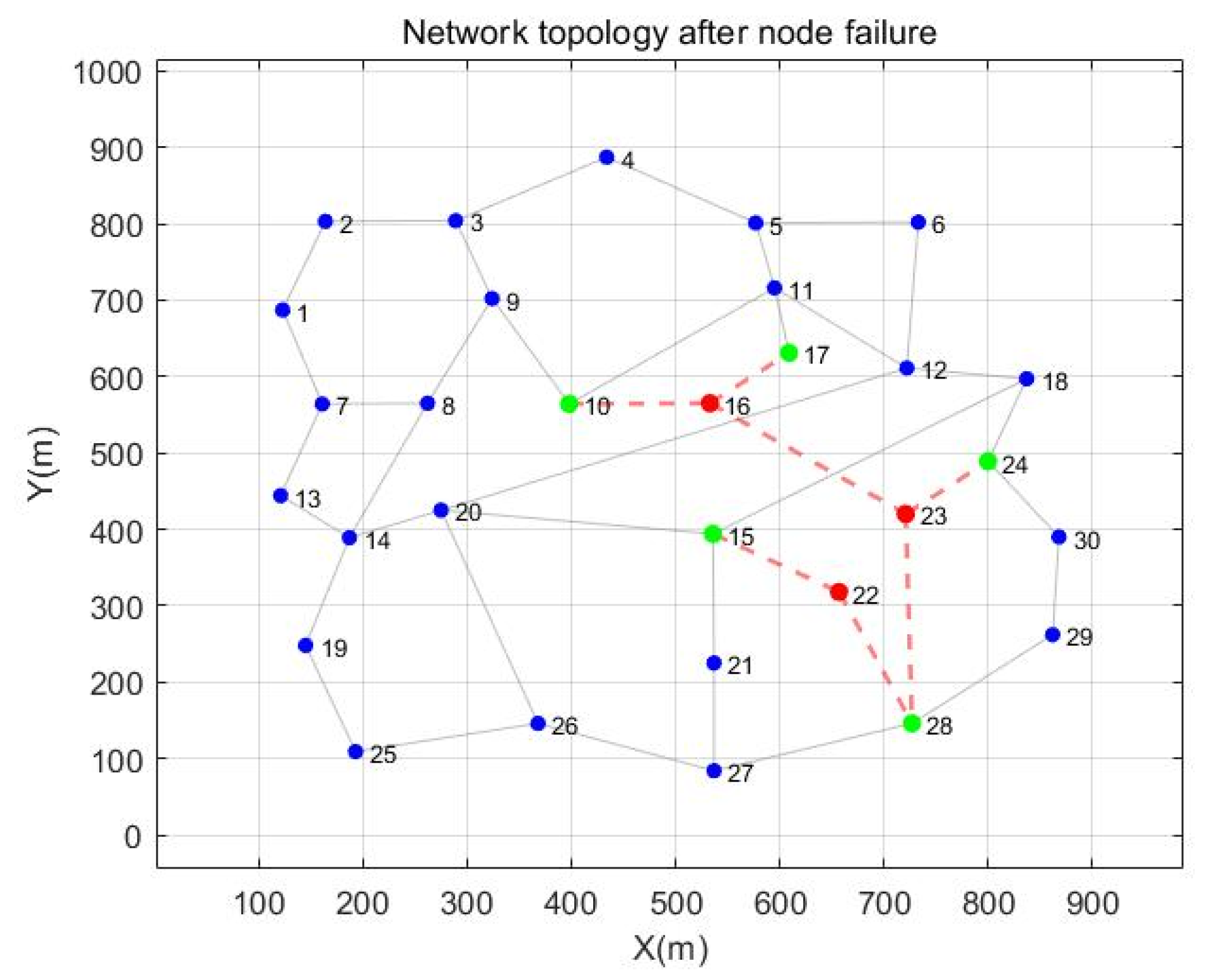
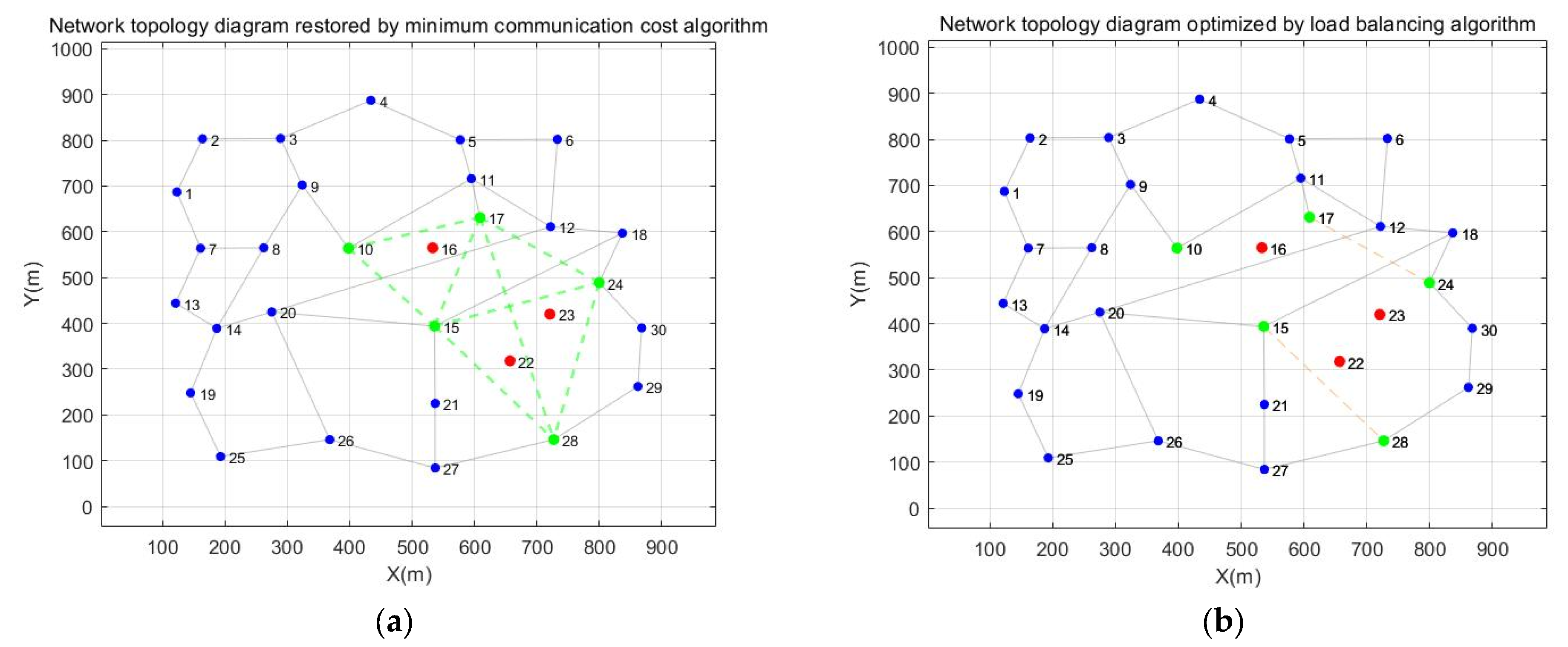
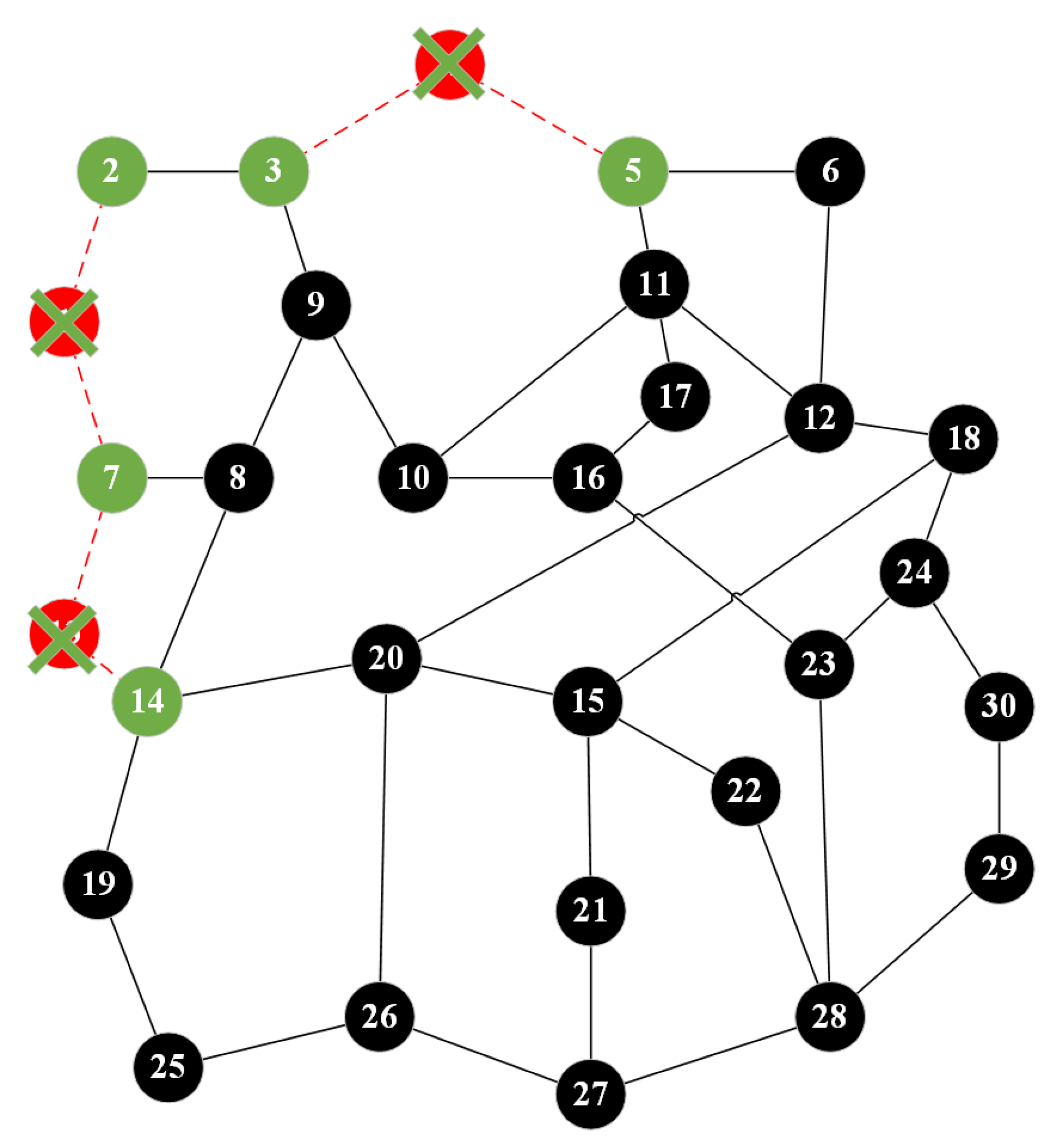
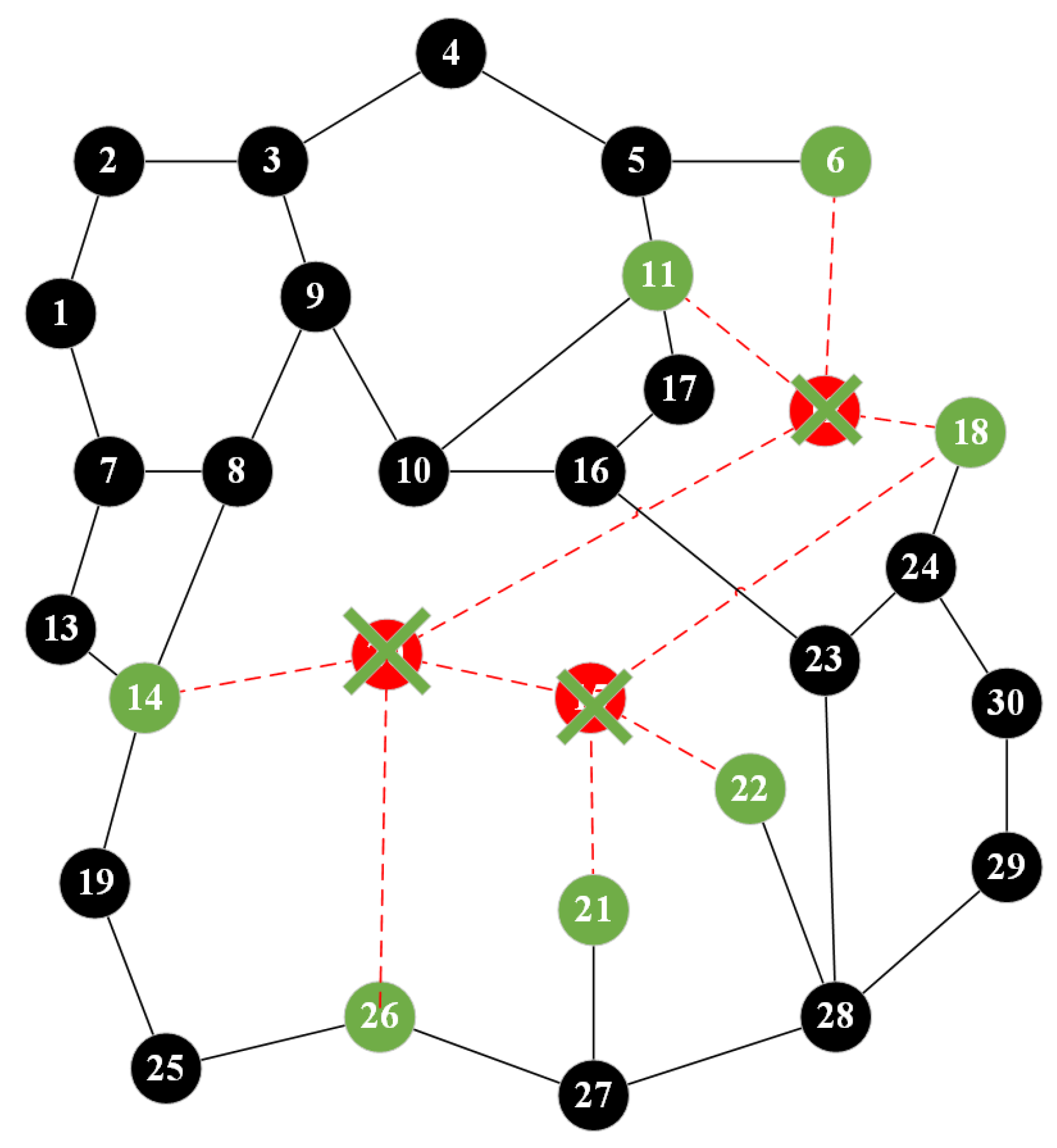

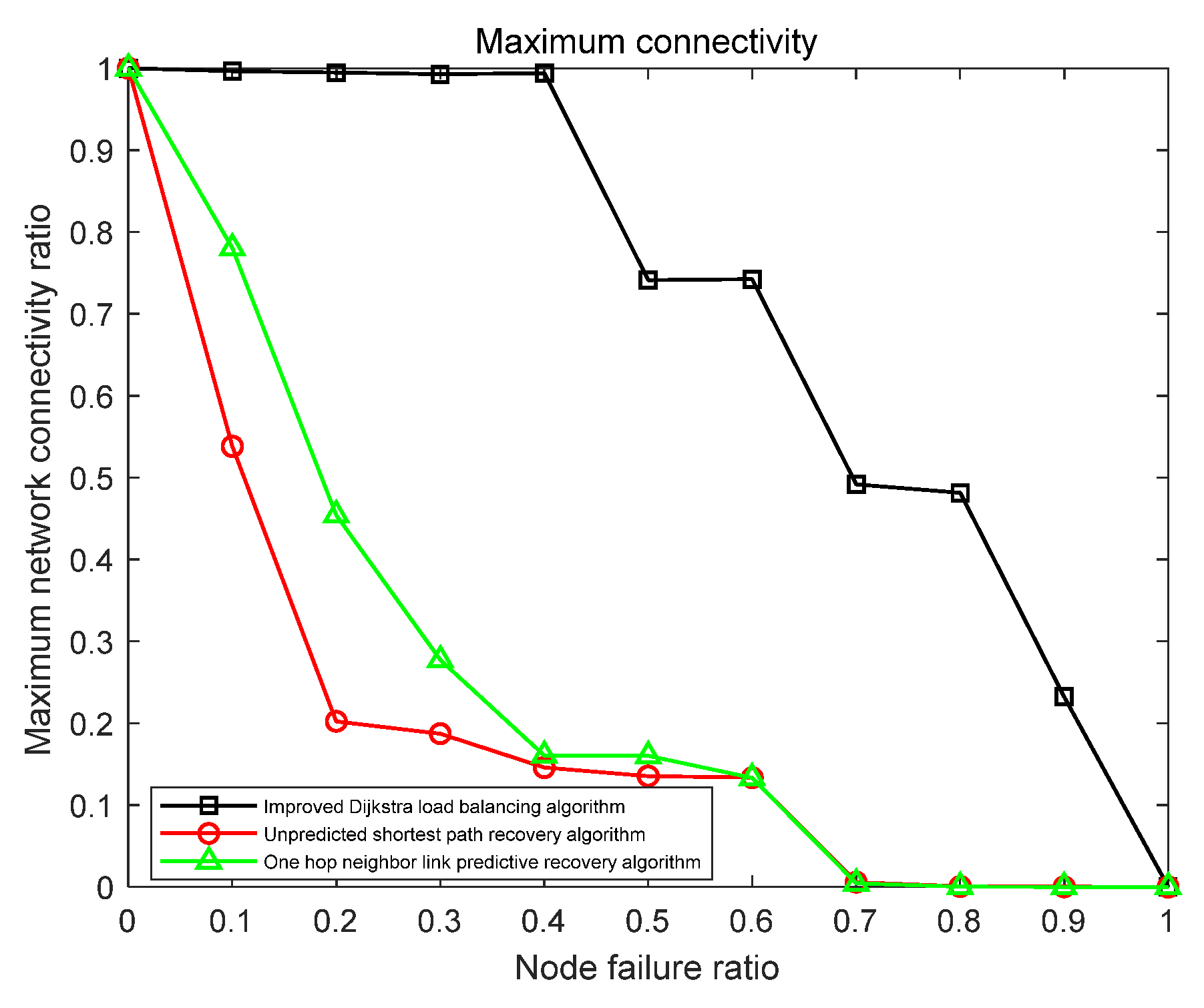
| Start | End | Shortest Path | Path Quality |
|---|---|---|---|
| 10 | 15 | 10→15 | 17.33 |
| 10 | 17 | 10→17 | 10.40 |
| 10 | 24 | 10→17→24 | 20.28 |
| 10 | 28 | 10→17→28 | 26.99 |
| 15 | 17 | 15→17 | 11.92 |
| 15 | 24 | 15→24 | 20.04 |
| 15 | 28 | 15→28 | 16.35 |
| 17 | 24 | 17→24 | 9.88 |
| 17 | 28 | 17→28 | 16.59 |
| 24 | 28 | 24→28 | 16.21 |
| Number of Links | Average Load | Load Variance | |
|---|---|---|---|
| Minimum communication cost algorithm | 16 | 3.2 | 0.675 |
| Load-balancing optimization algorithm | 4 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Z.; Zhang, H.; Yang, J. Damage Recovery Method for Air–Sea Cross-Domain Communication Network Based on Improved Dijkstra and Load Balancing. Appl. Sci. 2025, 15, 3956. https://doi.org/10.3390/app15073956
Shang Z, Zhang H, Yang J. Damage Recovery Method for Air–Sea Cross-Domain Communication Network Based on Improved Dijkstra and Load Balancing. Applied Sciences. 2025; 15(7):3956. https://doi.org/10.3390/app15073956
Chicago/Turabian StyleShang, Zhigang, Hongyu Zhang, and Jing Yang. 2025. "Damage Recovery Method for Air–Sea Cross-Domain Communication Network Based on Improved Dijkstra and Load Balancing" Applied Sciences 15, no. 7: 3956. https://doi.org/10.3390/app15073956
APA StyleShang, Z., Zhang, H., & Yang, J. (2025). Damage Recovery Method for Air–Sea Cross-Domain Communication Network Based on Improved Dijkstra and Load Balancing. Applied Sciences, 15(7), 3956. https://doi.org/10.3390/app15073956





