Maintenance Method for Rail Corrugation Considering Wheel–Rail Interaction Force
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview
2.2. Rail Surface Roughness
2.3. Results for Surface Roughness
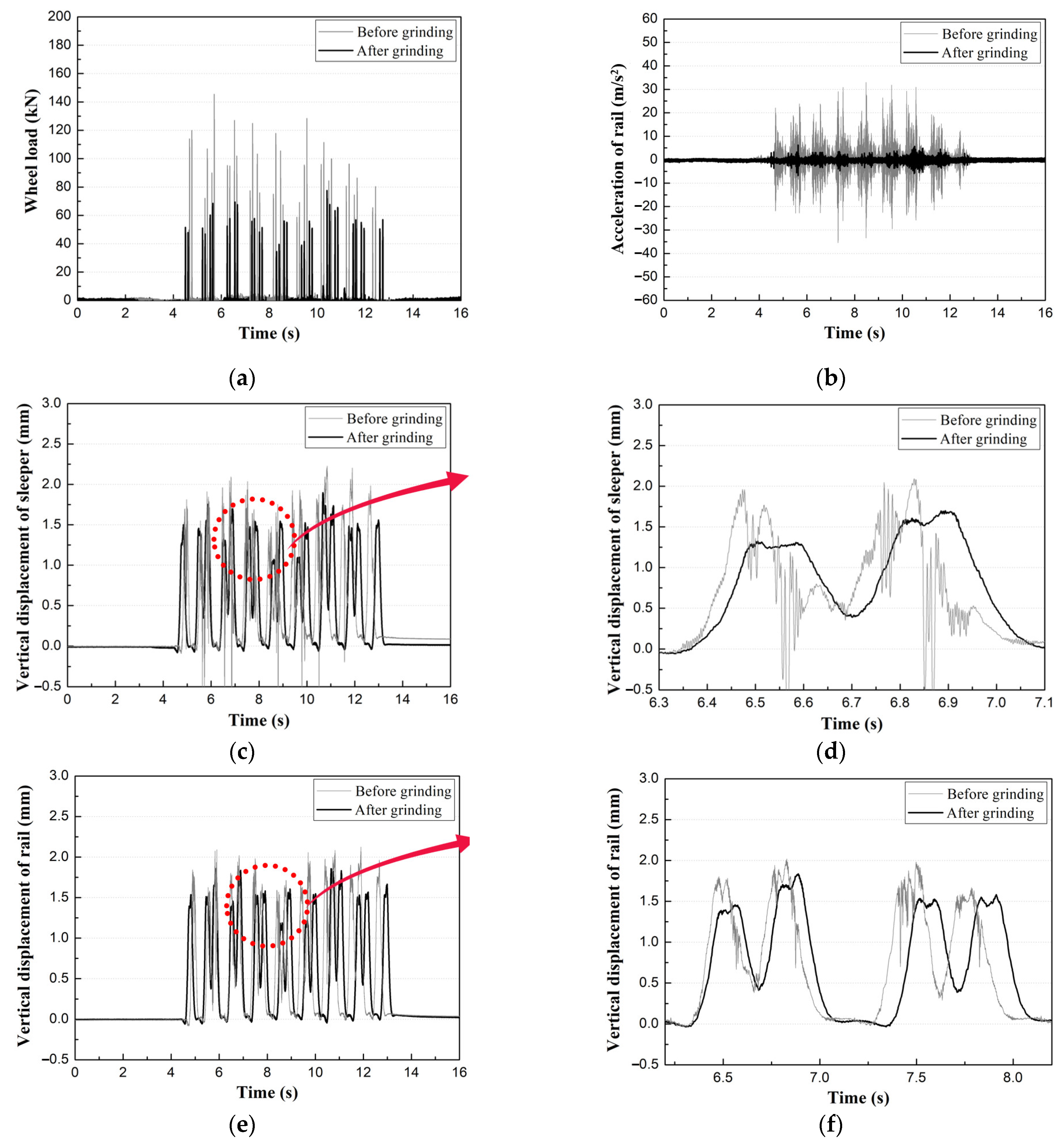
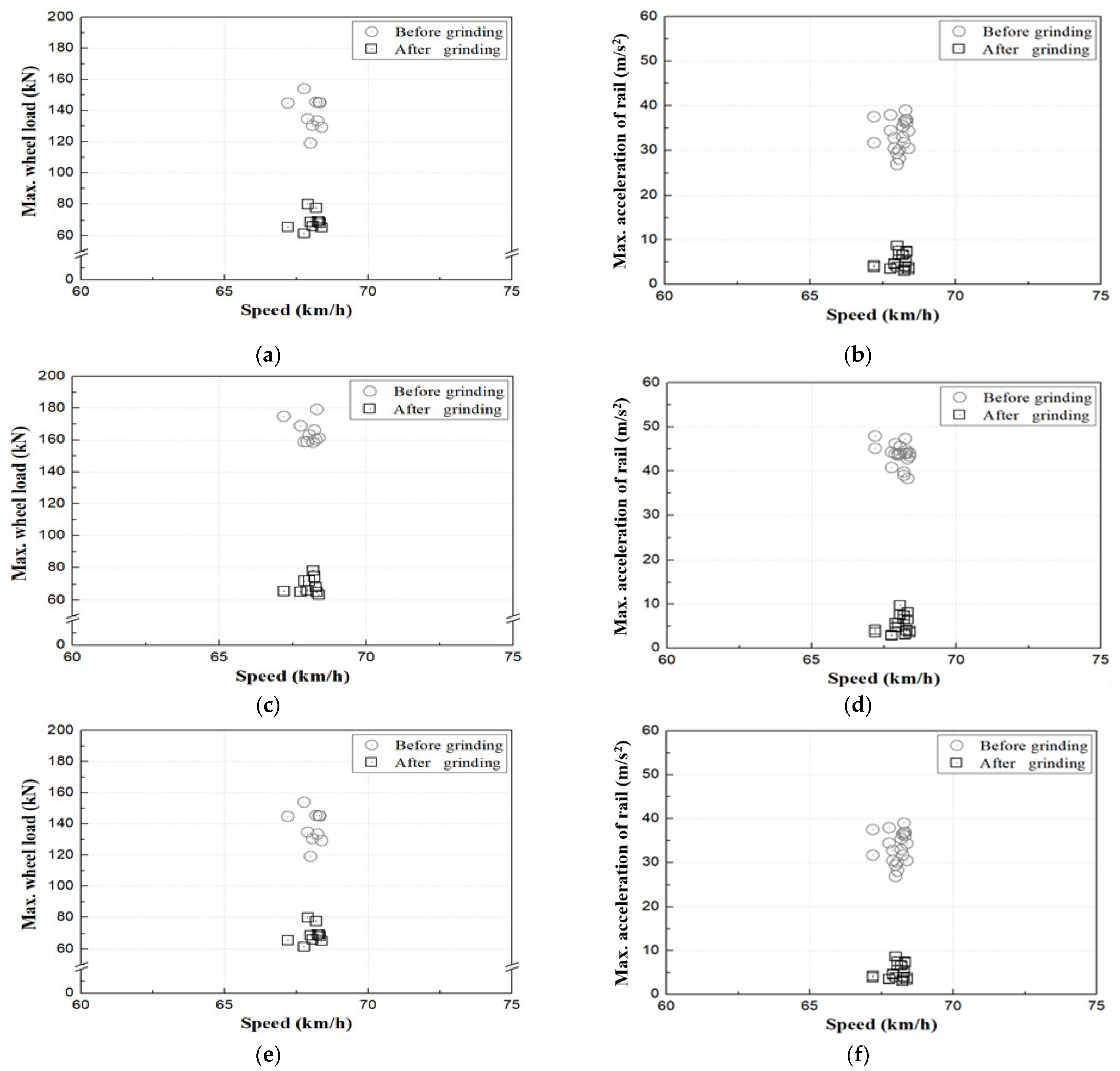
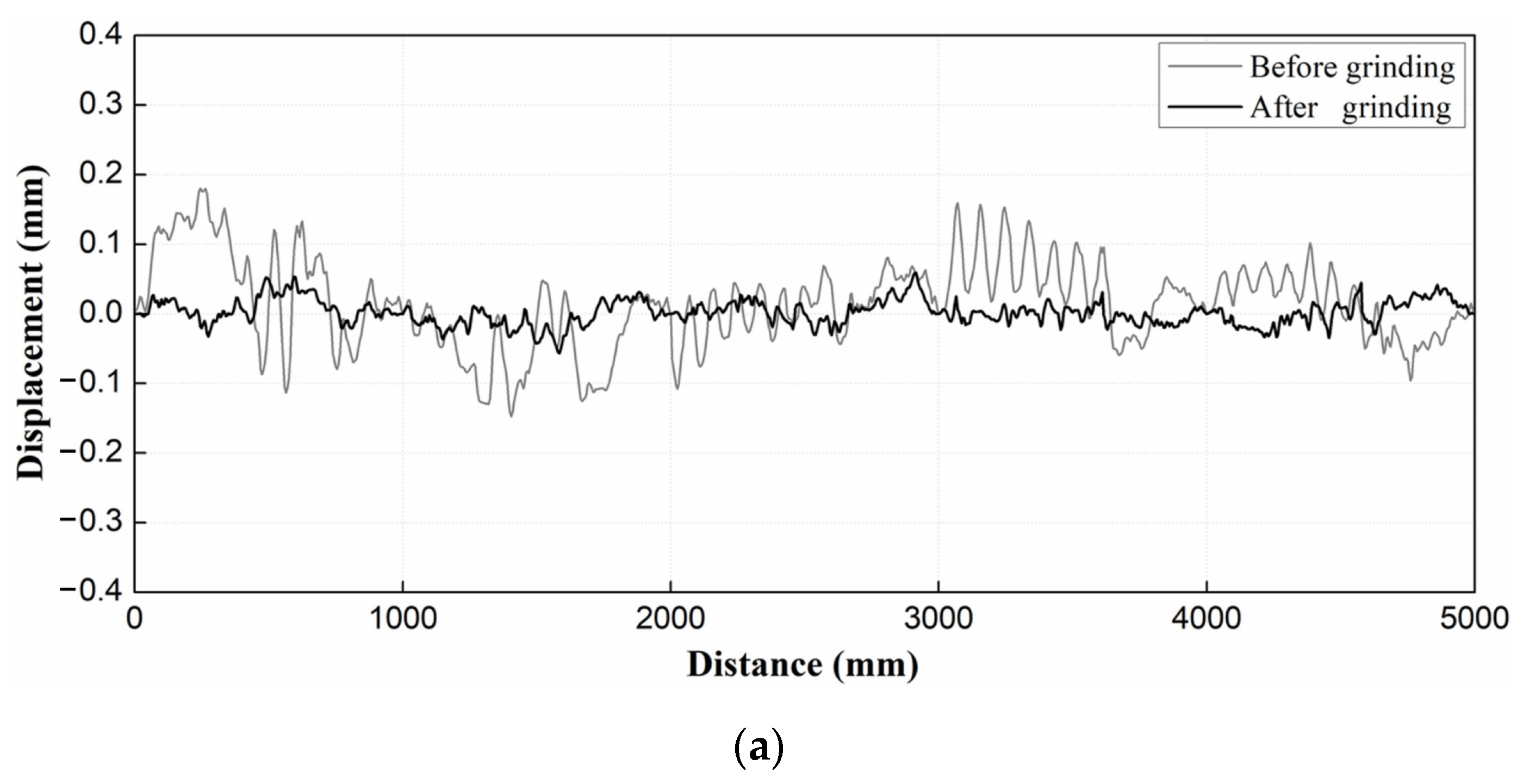
2.4. Effect of Rail Grinding on Dynamic Track Response
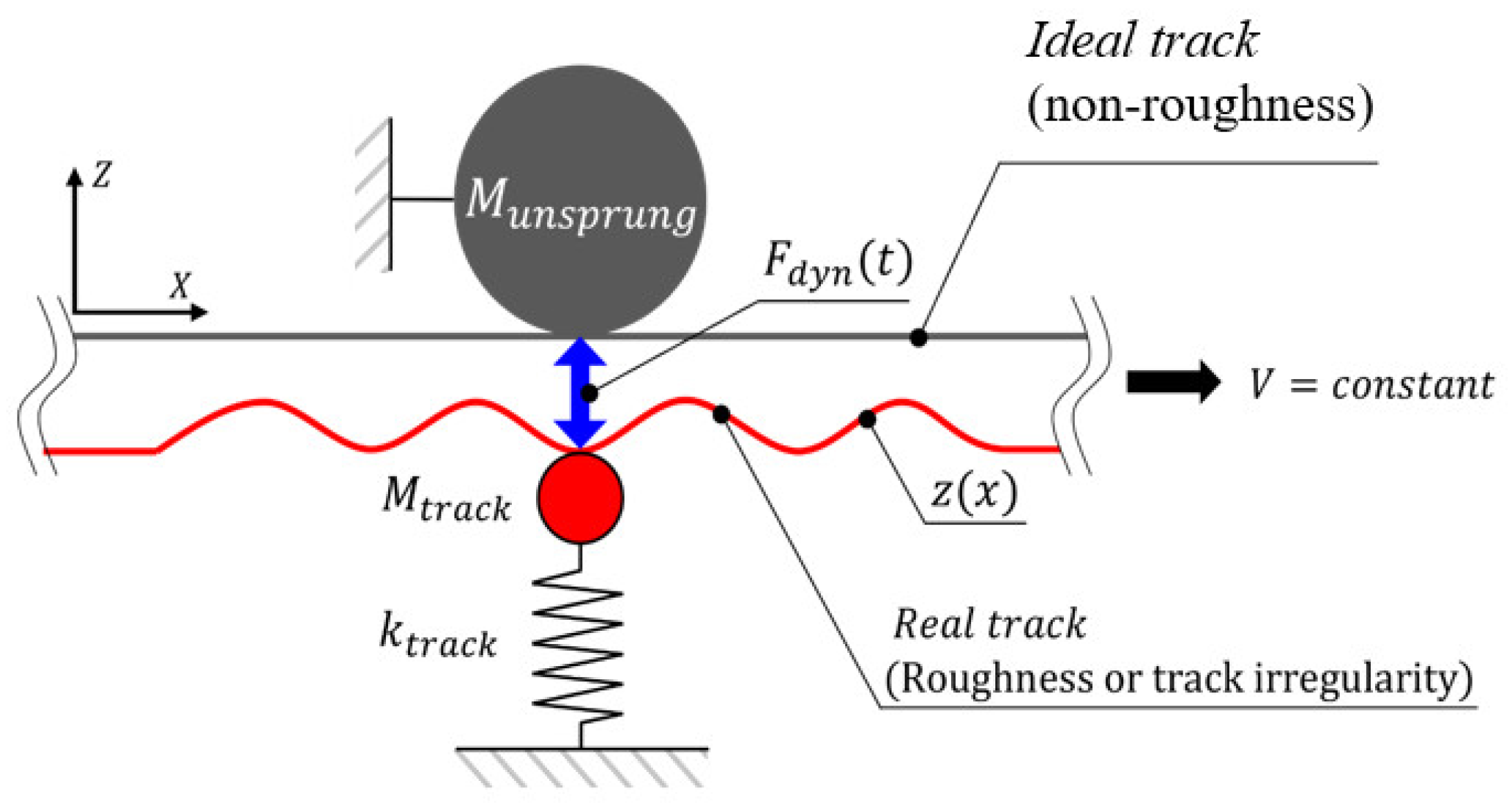
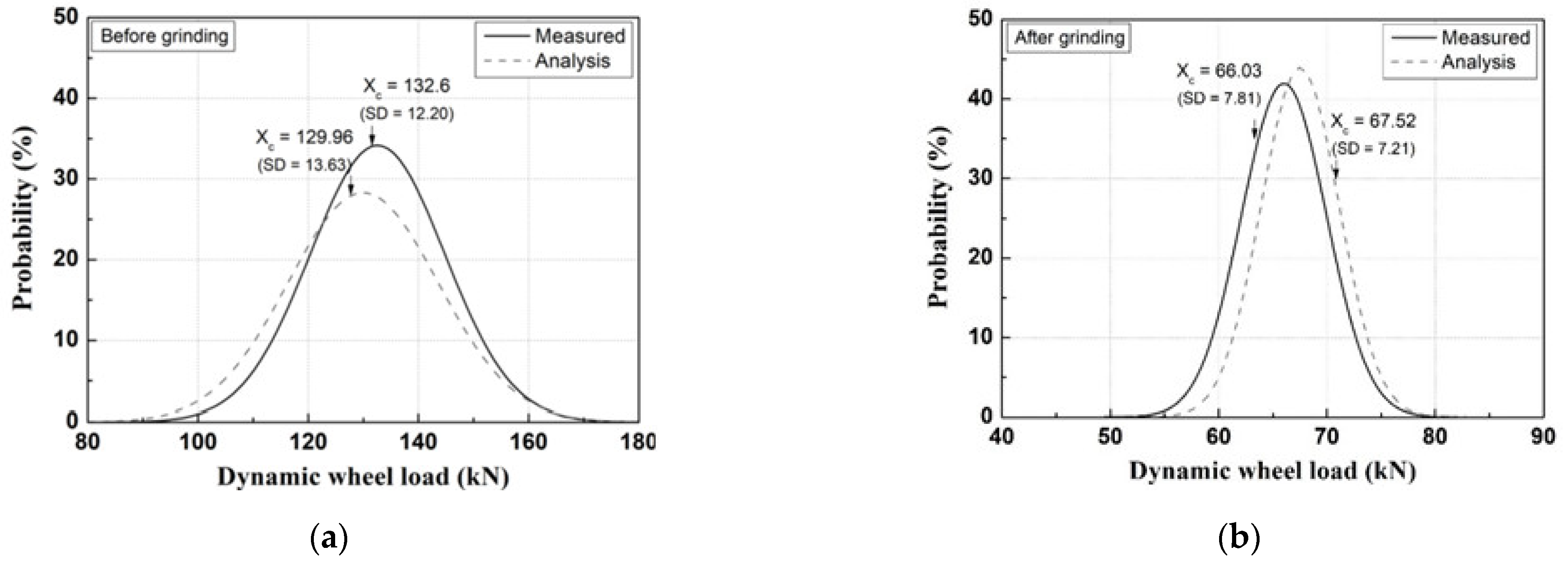
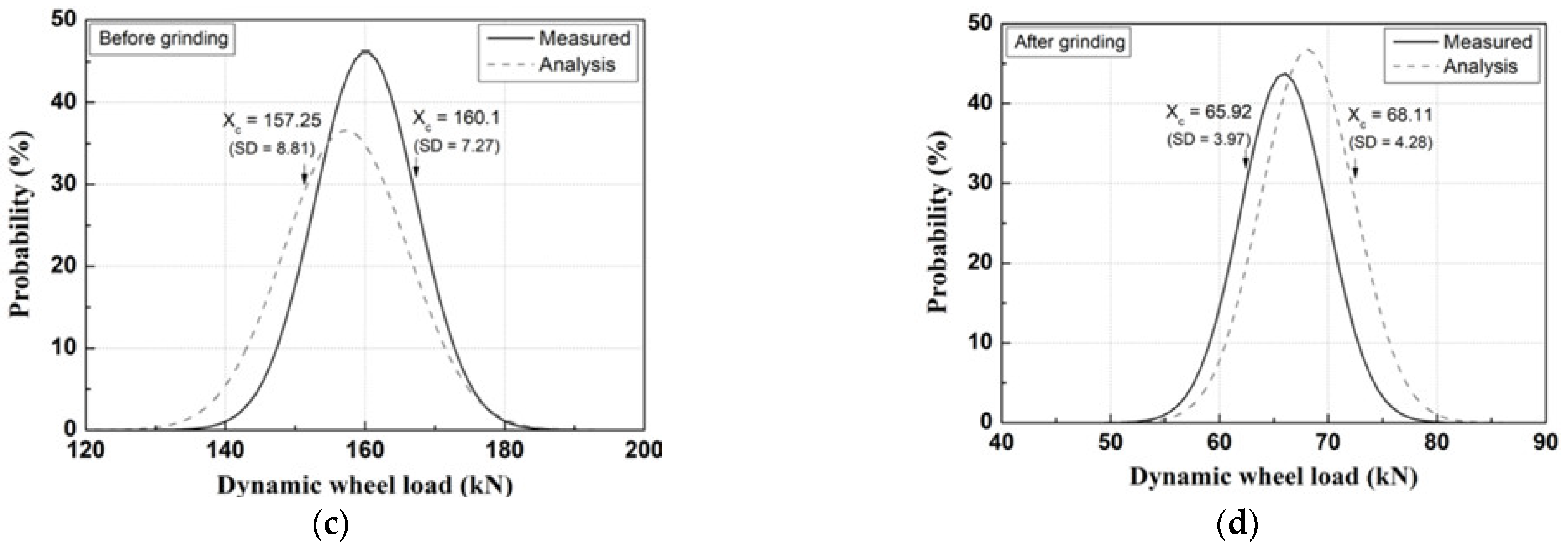
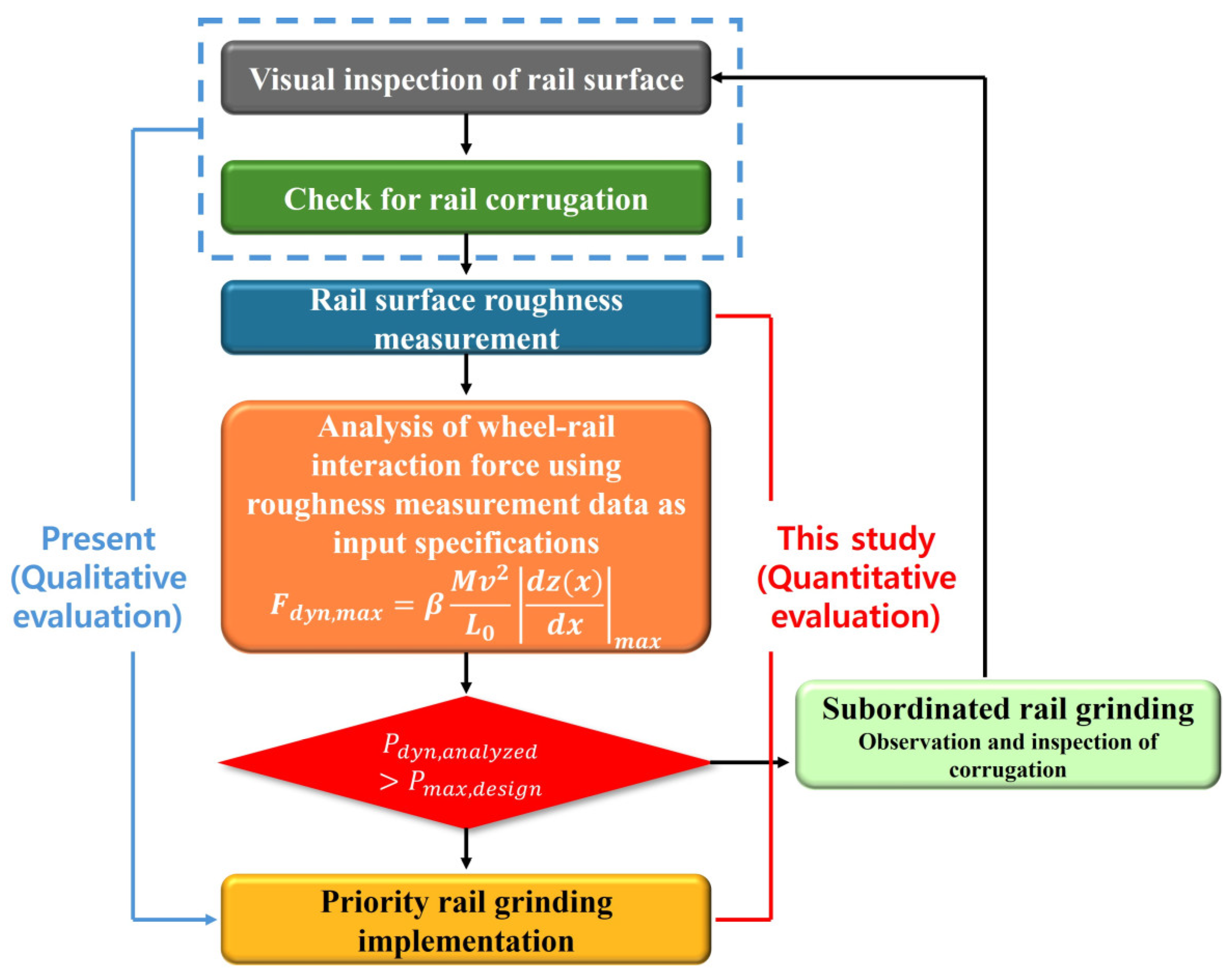
3. Wheel–Rail Interaction Force
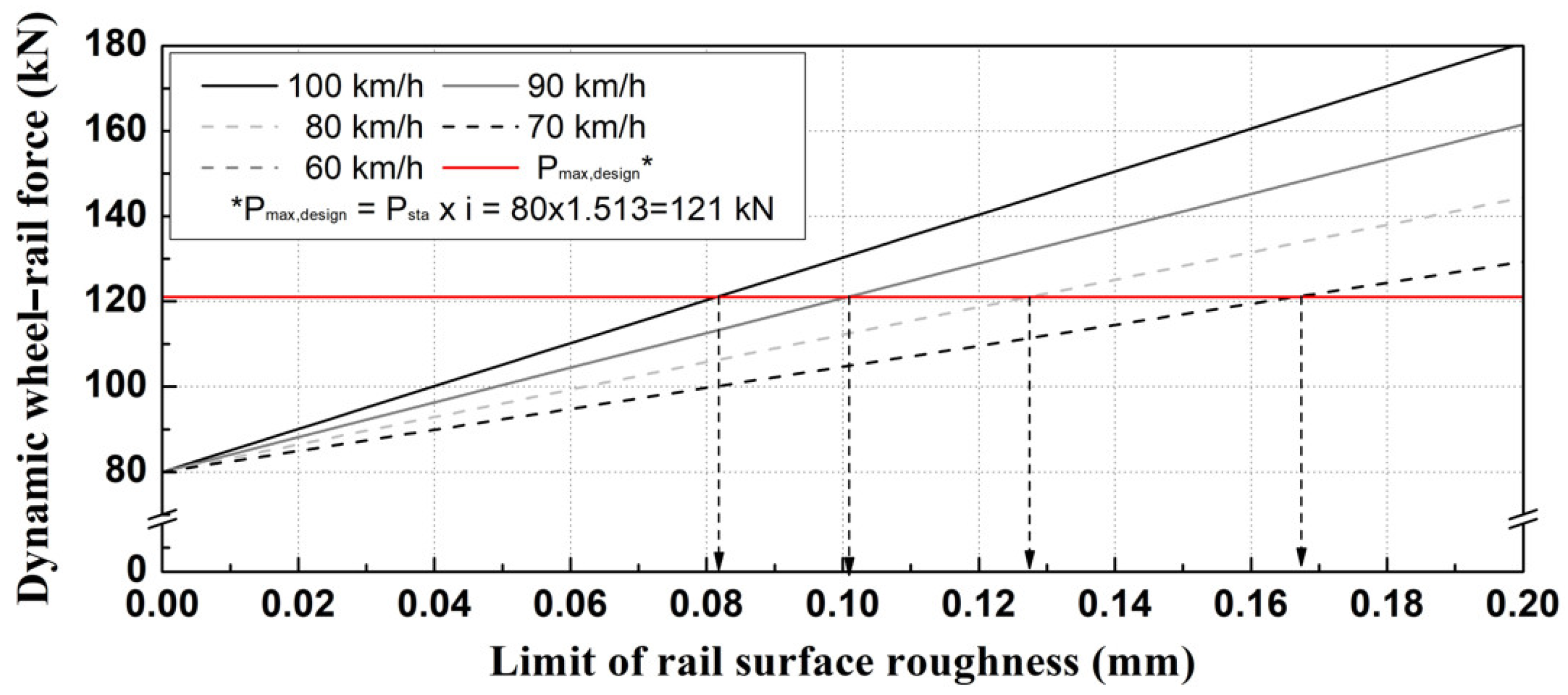
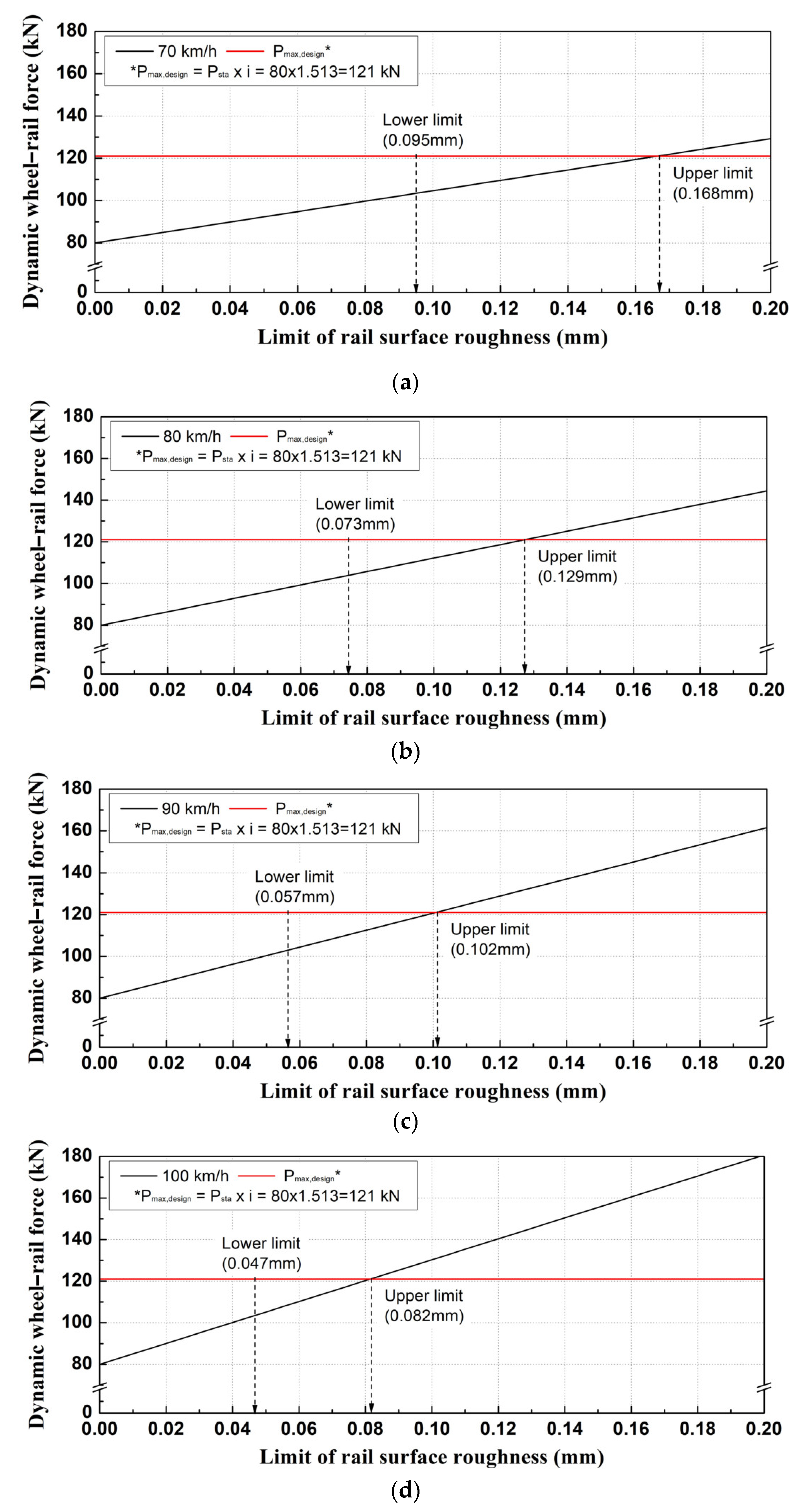
4. Criteria of Rail Surface Roughness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, H.S. Cause Analysis and Avoiding Measures of Rail Corrugation for Sleeper Floating Track in Urban Transit. Ph.D. Dissertation, Dongyang University, Yeongju-si, Republic of Korea, 2021. [Google Scholar]
- Seo, J.M. An Optimum Maintenance for Rail Surface Considering Dynamic Wheel-Rail Force. Master’s Thesis, Seoul National University of Science and Technology, Seoul, Republic of Korea, 2015. [Google Scholar]
- Park, J.W. Optimum Quality Index by Rail Grinding Based on Rail Surface Degradation and Dynamic Wheel-Rail Force. Ph.D. Dissertation, Seoul National University of Science and Technology, Seoul, Republic of Korea, 2017. [Google Scholar]
- Yang, S.C.; Jang, S.Y. Investigation of the maintenance criteria for the rail surface defects in high-speed railways. J. Korean Soc. Railw. 2011, 14, 535–544. [Google Scholar]
- Chae, K.H. A Study on the Characteristics of Rail Corrugation on the Gyongbu High Speed Railway. Master’s Thesis, Woosong University, Daejeon, Republic of Korea, 2014. [Google Scholar]
- Ha, K.Y.; Kim, H. A study of rail wear by change of acceleration and deceleration. J. Korean Soc. Railw. 2007, 10, 607–612. [Google Scholar]
- Hwang, Y.T. A Study on Force-Based Rail Surface Quality Maintenance Method. Ph.D. Dissertation, Woosong University, Daejeon, Republic of Korea, 2019. [Google Scholar]
- Lee, C.W.; Choi, J.Y.; Kim, J.C. Characterization in high speed rail corrugation. In Proceedings of the Korean Society for Precision Engineering, JeJu, Republic of Korea, 1–3 June 2011. [Google Scholar]
- Go, D.C.; Sugn, D.Y.; King, S.Y.; Park, Y.G. The laboratory study for establishing rail grinding period in underground railway. In Proceedings of the Korean Society for Railway, Gyeongju, Republic of Korea, 21–23 May 2009. [Google Scholar]
- Park, J.H. Development of Rail Corrugation Measurement System. Master’s Thesis, Chosun University, Gwangju, Republic of Korea, 2016. [Google Scholar]
- Seo, J.; Kwon, S.; Park, Y. A study on the effect analysis of rail grinding in highspeed railway considering dynamic wheel-rail force. J. Korean Soc. Railw. 2019, 22, 494–503. [Google Scholar]
- Grassie, S.L. Rail corrugation: Characteristics, cause and treatments. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 581–596. [Google Scholar]
- Collettea, C.; Vanhonacker, P.; Bastaits, R.; Levy, D. Comparison between time and frequency studies of a corrugated curve of RER paris network. Eng. Fract. Mech. 2008, 265, 1249–1258. [Google Scholar]
- Meehan, P.A.; Daniel, W.J.T.; Campey, T. Prediction of the Growth of Wear-Type Rail Corrugation. Eng. Fract. Mech. 2005, 258, 1001–1013. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Huang, J.; Ji, Y.; Li, D.; Wu, S. Dynamic wheel-rail adhesion characteristics on wet curved tracks considering surface roughness. Phys. Fluids 2025, 37, 022104. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y.; Long, X.; Wang, Y. Optimizing rail profiles to improve metro vehicle-rail dynamic performance considering worn wheel profiles and curved tracks. Struct. Multidiscip. Optim. 2020, 63, 419–438. [Google Scholar]
- Ma, C.; Gao, L.; Xin, T.; Cai, X.; Nadakatti, M.M.; Wang, P. The dynamic resonance under multiple flexible wheelset-rail interactions and its influence on rail corrugation for high-speed railway. J. Sound Vib. 2021, 498, 115968. [Google Scholar] [CrossRef]
- Jung, C.M. Maintenance Strategy for Rail Corrugation Considering Wheel-Rail Interaction Force. Ph.D. Dissertation, Dongyang University, Yeongju-si, Republic of Korea, 2022. [Google Scholar]
- Choi, J.Y.; Yun, S.W.; Chung, J.S.; Kim, S.H. Comparative study of wheel-rail contact impact force for jointed rail and continuous welded rail on light-rail transit. Appl. Sci. 2020, 10, 2299. [Google Scholar] [CrossRef]
- Steenbergen, M.J.M.M.; Esveld, C. Rail weld geometry and assessment concepts. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2006, 220, 257–271. [Google Scholar]
- Hwang, S.K. A Study on Application of Force-Based Track Irregularity Analysis Method. Master’s Thesis, Dongyang University, Yeongju-si, Republic of Korea, 2021. [Google Scholar]
- Wang, K.Y.; Liu, P.F.; Zhai, W.M.; Huang, C.; Chen, Z.G.; Gao, J.M. Wheel/rail dynamic interaction due to excitation of rail corrugation in high-speed railway. Sci. China Technol. Sci. 2015, 58, 226–235. [Google Scholar]
- Niu, L.; Yang, F.; Deng, X.; Zhang, P.; Jing, G.; Qiang, W.; Guo, Y. An assessment method of rail corrugation based on wheel-rail vertical force and its application for rail grinding. J. Civ. Struct. Health Monit. 2023, 13, 1131–1150. [Google Scholar] [CrossRef]
- Du, L.; Liu, W. Study on wheel-rail interaction based on rail roughness. Vibroeng. Procedia 2015, 5, 475–480. [Google Scholar]
- Nielsen, J.C.O.; Ekberg, A. Acceptance criterion for rail roughness level spectrum based on assessment of rolling contact fatigue and rolling noise. Wear 2011, 271, 319–327. [Google Scholar]
- Keropyan, A.; Gorbatyuk, S. Impact of roughness of interacting surfaces of the wheel-rail pair on the coefficient of friction in their contact area. Procedia Eng. 2016, 150, 406–410. [Google Scholar] [CrossRef]
- Nielsen, J.C.O. Rail roughness level assessment based on high-frequency wheel-rail contact force measurements. In Proceedings of the 9th International Workshop on Railway Noise, Munich, Germany, 4–8 September 2007; pp. 355–362. [Google Scholar]
- Jaramillo, J.A.A.; Sánchez, J.C.; Santa, J.F.; Palacio, M.E.; Toro, A. Roughness evolution of wheel surface in a simulated wheel-rail contact. Tribol.-Mater. Surf. Interfaces 2022, 16, 188–201. [Google Scholar]
- Grassie, S.L.; Saxon, M.J.; Smith, J.D. Measurement of longitudinal rail irregularities and criteria for acceptable grinding. J. Sound Vib. 1999, 227, 949–964. [Google Scholar]
- Choi, J.Y.; Park, Y.G.; Lee, S.M. The evaluation of track impact factor on the various track type in urban transit. J. Korean Soc. Railw. 2011, 14, 248–255. [Google Scholar] [CrossRef]



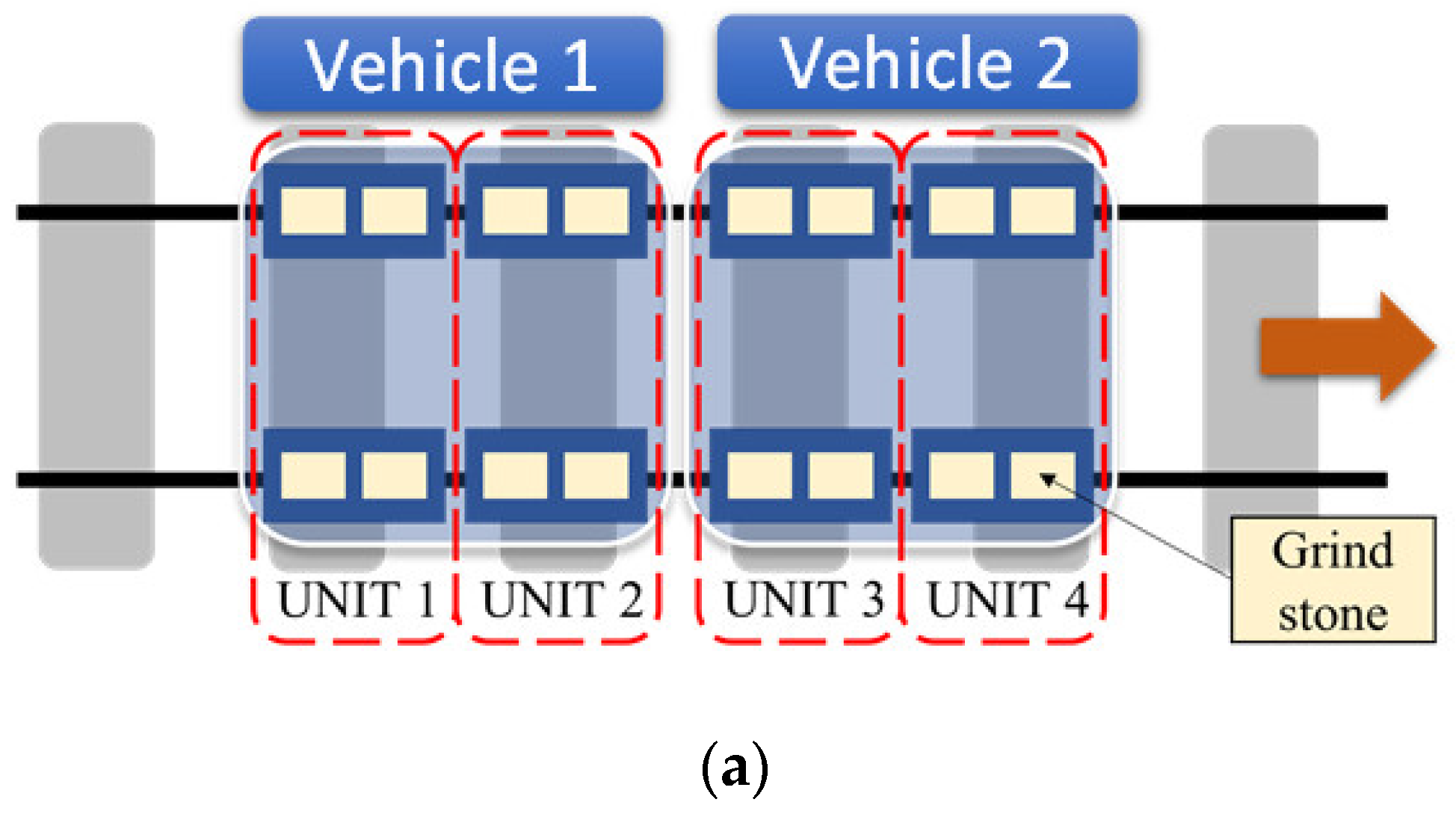




| Items | Details |
|---|---|
| Substructure | Data |
| Alignment | Straight |
| Track type | STEDEF (sleeper floating track) |
| Sleeper spacing (mm) | 625 |
| Rail (kg/m) | 60 |
| Location | Nearby station (deceleration section) |
| Operation speed (km/h) | 68~70 |
| Annual tonnage (megaton) | About 18 |
| Items | Details |
|---|---|
| Size (length × width × height) | 27.1 m × 2.4 m × 3.7 m |
| Weight | 76 tons |
| Engine spec. | 205 kw, 1800 RPM × 2 each |
| Number of grinding stones | 16 |
| Diameter of grinding stones | Stone A: 180 mm × 12 each |
| Stone B: 260 mm × 4 each | |
| Grinding motor type | Rotary wheel type, electric type |
| Grinding motor rotation speed | 3600 RPM |
| Grinding motor power | 11 kw × 16 each |
| Grinding angle | Stone A: (−)20–(+)15° |
| Stone B: (−)70–(−)5° | |
| Grinding head control | 2 stones 1 set, independent control |
| Normal running speed | 60 km/h |
| Grinding speed | 2–8 km/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.-Y.; Jeong, C.M.; Kim, S.-H. Maintenance Method for Rail Corrugation Considering Wheel–Rail Interaction Force. Appl. Sci. 2025, 15, 3915. https://doi.org/10.3390/app15073915
Choi J-Y, Jeong CM, Kim S-H. Maintenance Method for Rail Corrugation Considering Wheel–Rail Interaction Force. Applied Sciences. 2025; 15(7):3915. https://doi.org/10.3390/app15073915
Chicago/Turabian StyleChoi, Jung-Youl, Cheon Man Jeong, and Sun-Hee Kim. 2025. "Maintenance Method for Rail Corrugation Considering Wheel–Rail Interaction Force" Applied Sciences 15, no. 7: 3915. https://doi.org/10.3390/app15073915
APA StyleChoi, J.-Y., Jeong, C. M., & Kim, S.-H. (2025). Maintenance Method for Rail Corrugation Considering Wheel–Rail Interaction Force. Applied Sciences, 15(7), 3915. https://doi.org/10.3390/app15073915







