Joint Optimization Algorithm for UAV-Assisted Caching and Charging Based on Wireless Energy Harvesting
Abstract
1. Introduction
2. Problem Statement
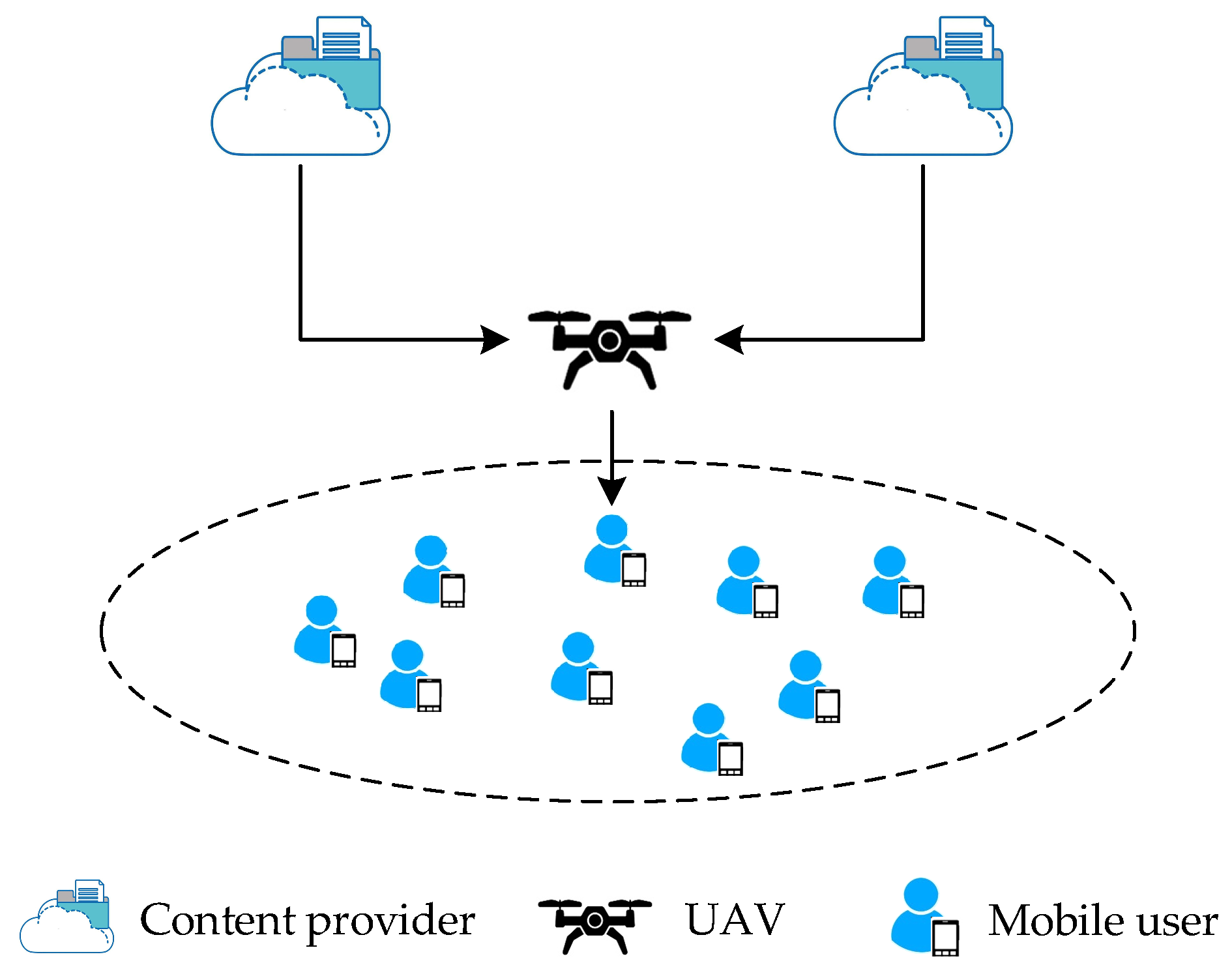
2.1. Network Model
2.2. Channel Model
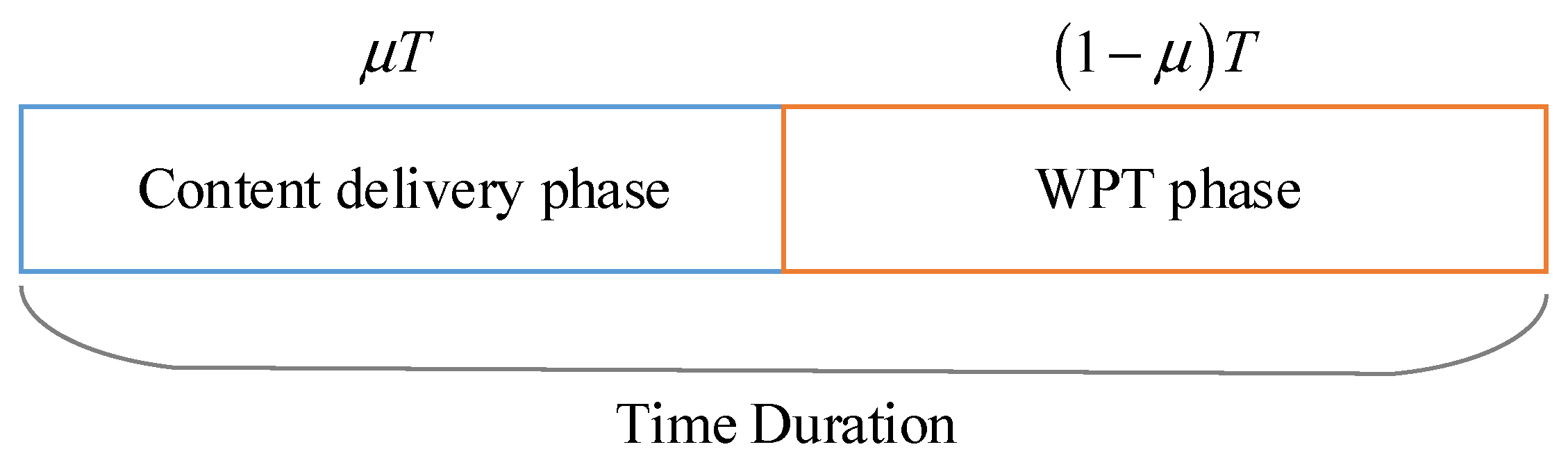
2.3. Transmission Model
2.4. Cache Placement Model
2.5. Problem Formulation
3. Cache Strategy Formulation Based on Stackelberg Game
| Algorithm 1 Content Provider Pricing and UAV Cache Placement Algorithm |
| Input Output
|
4. Combined Optimization of UAV Location, User Pairing, and Power Allocation
4.1. UAV Transmission Power Optimization
4.2. User Pairing Optimization
4.3. UAV Location Optimization
| Algorithm 2 Joint Optimization Algorithm for UAV Cache and Charging Services |
| Input, initial location of all users, Output: Total Revenue of UAV
|
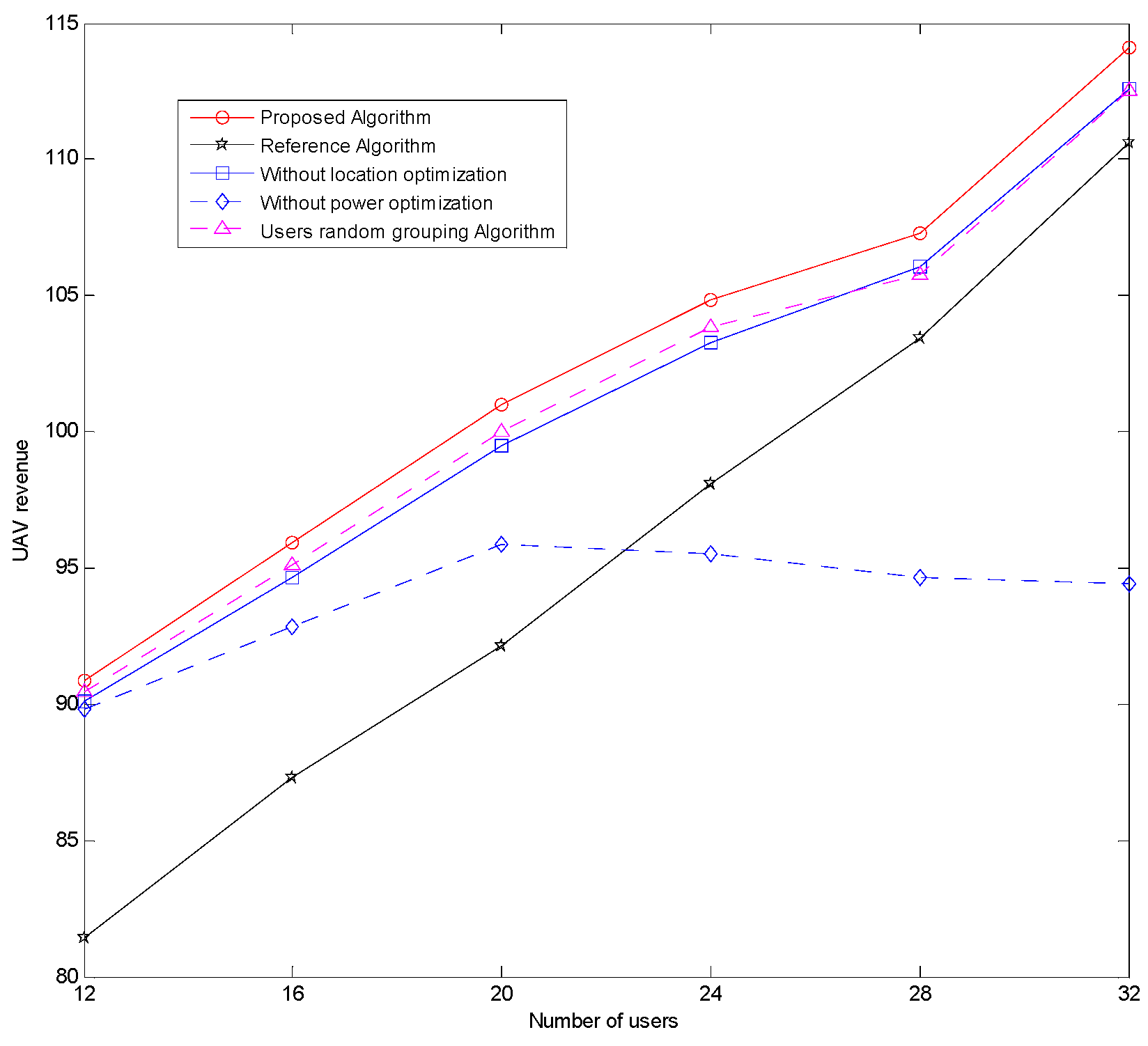
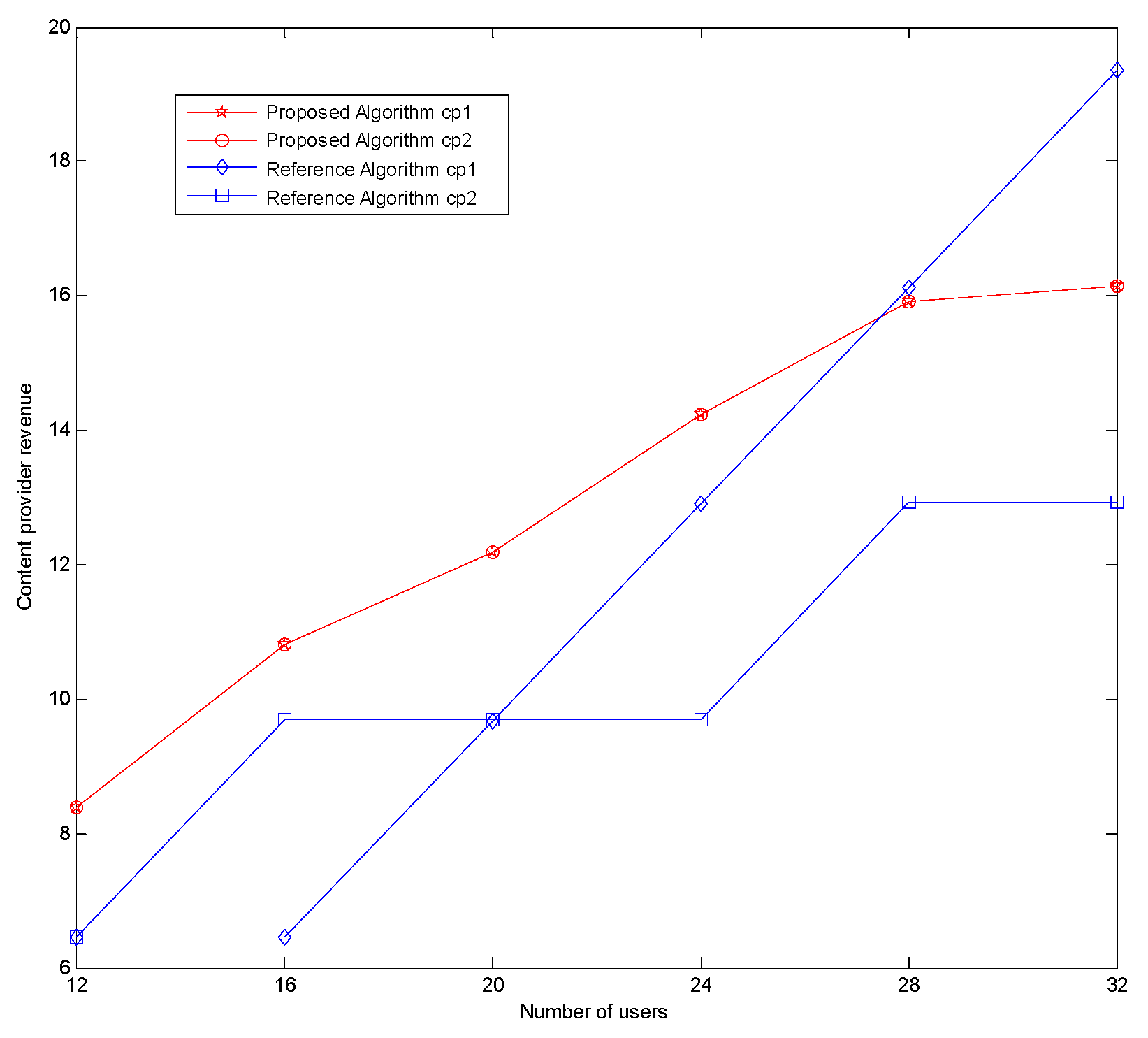
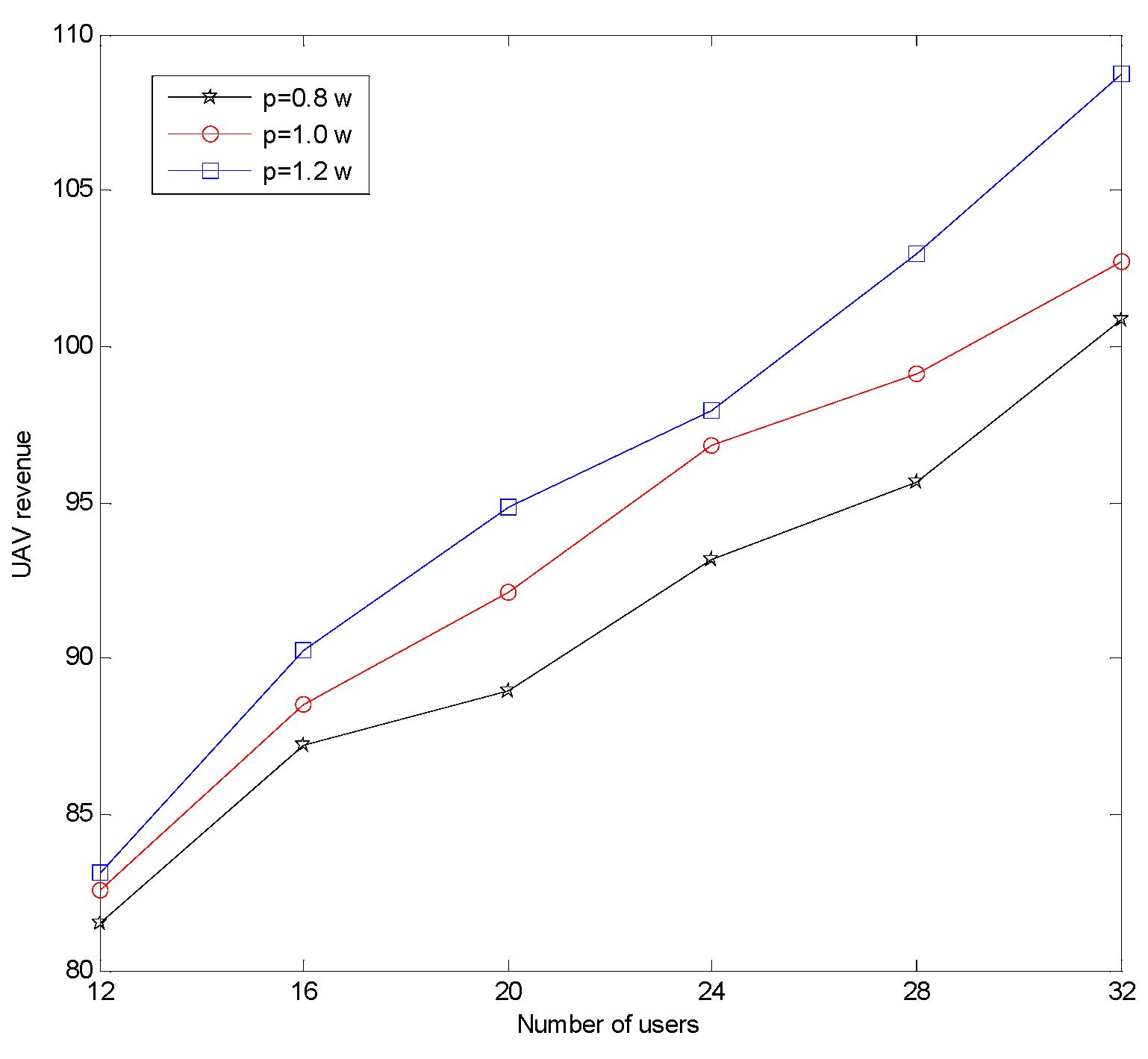
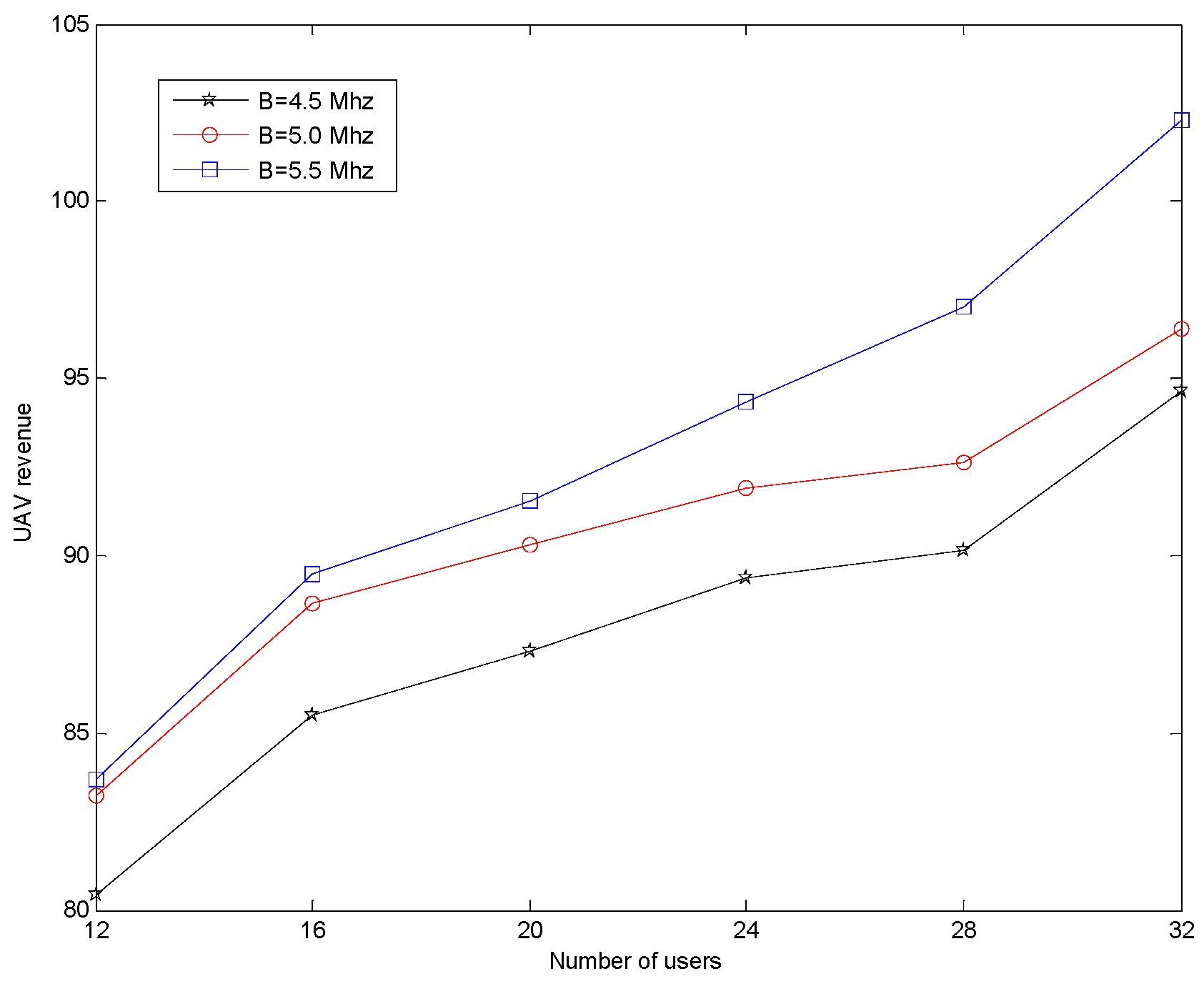
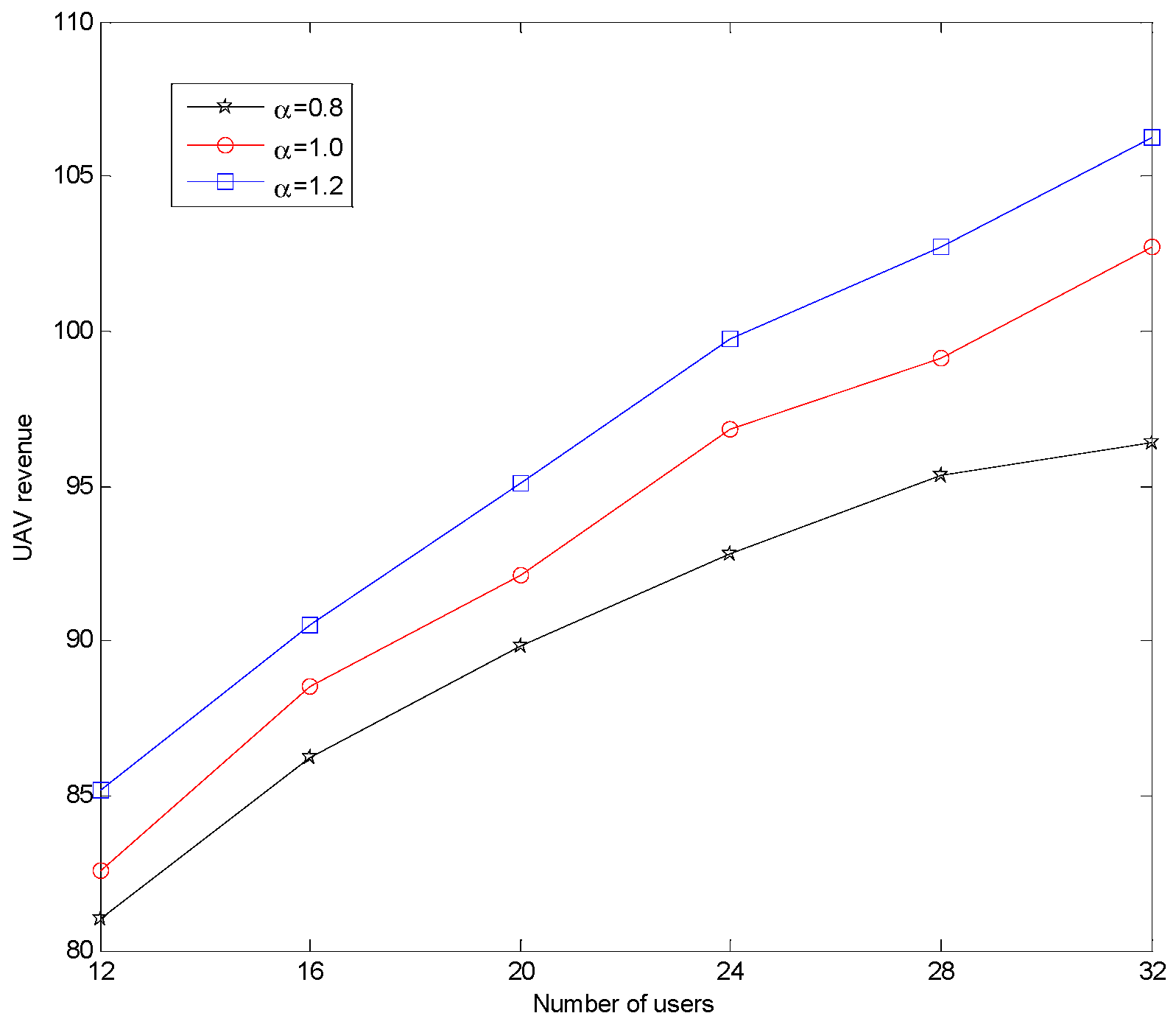
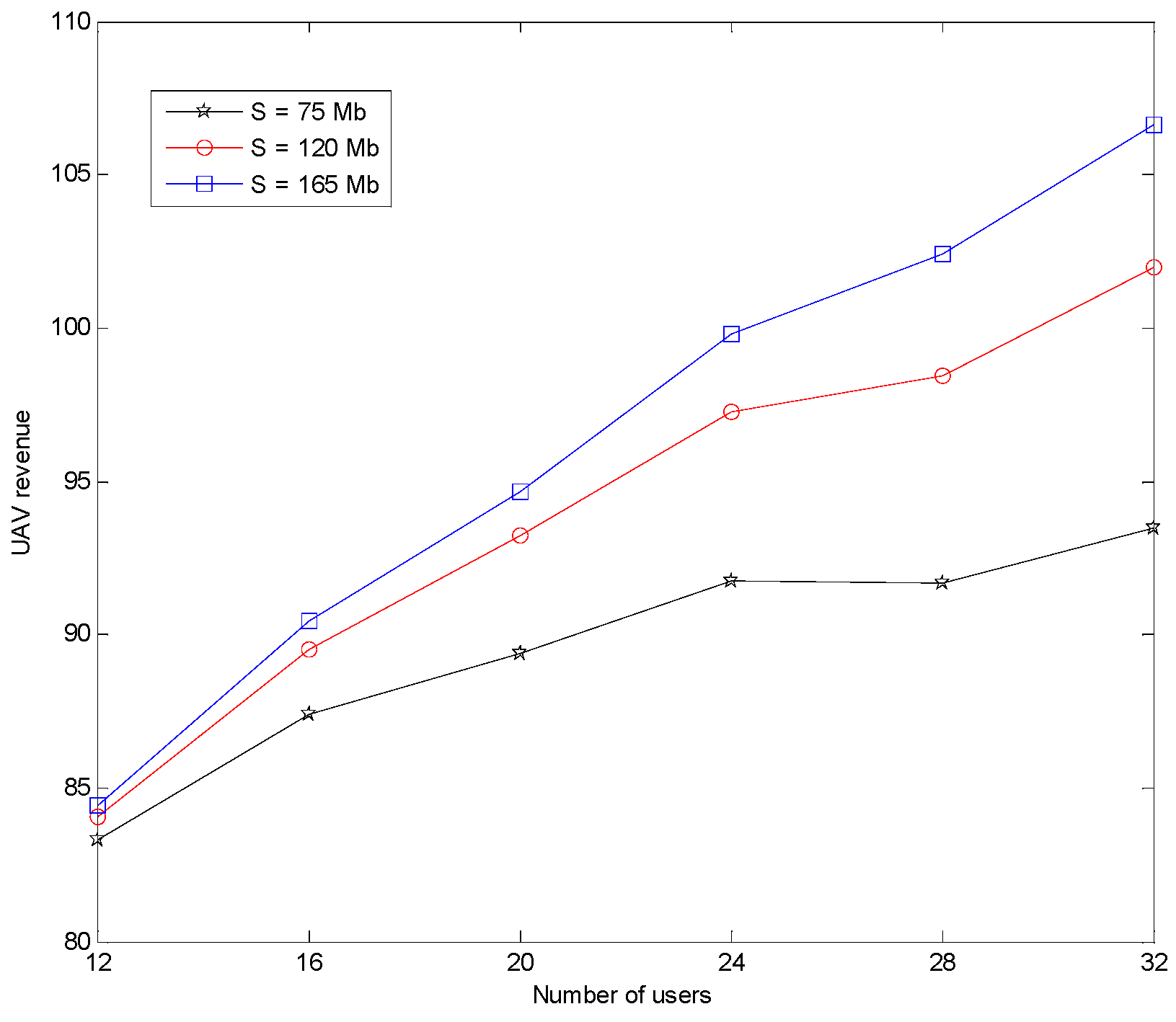
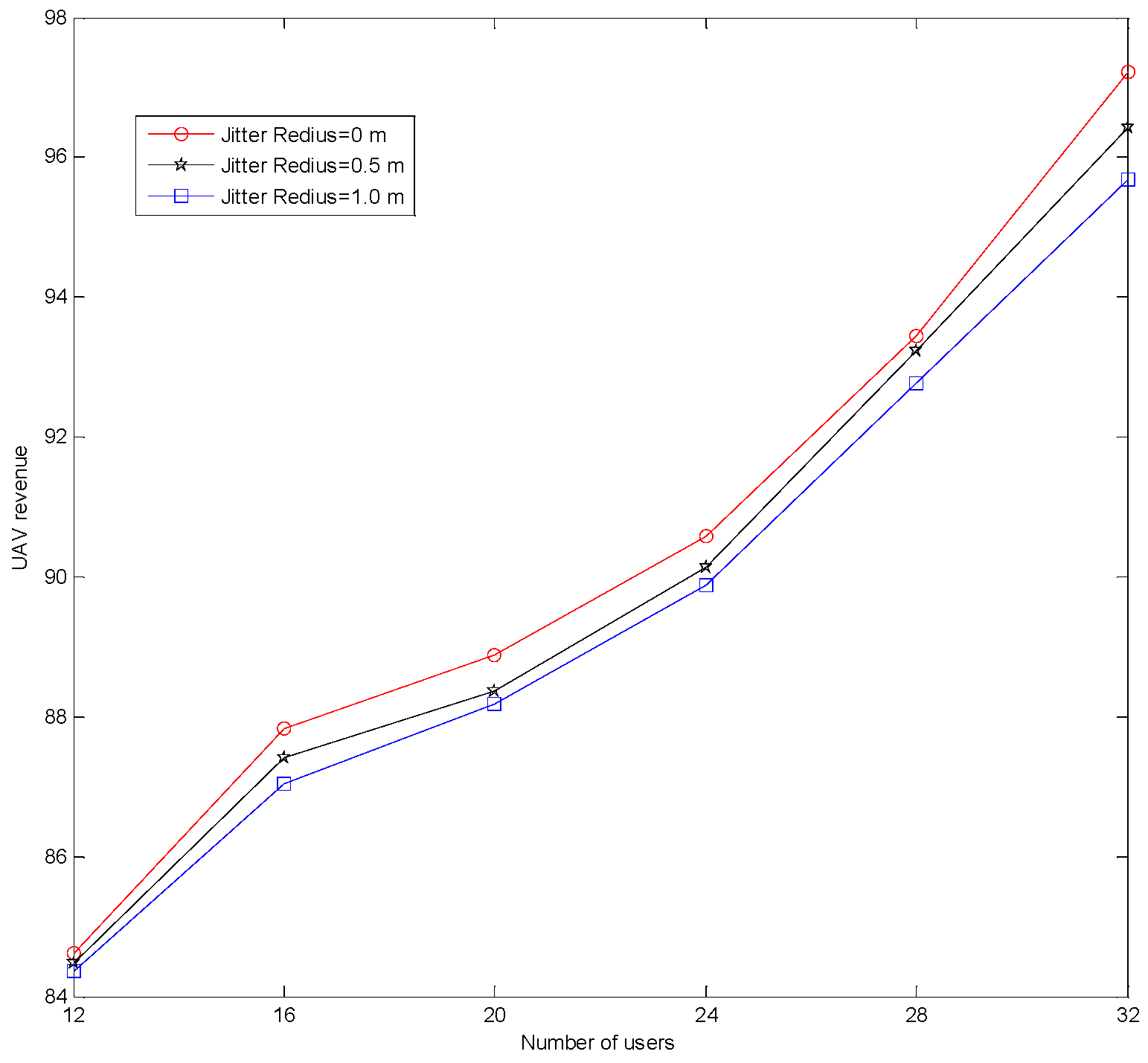
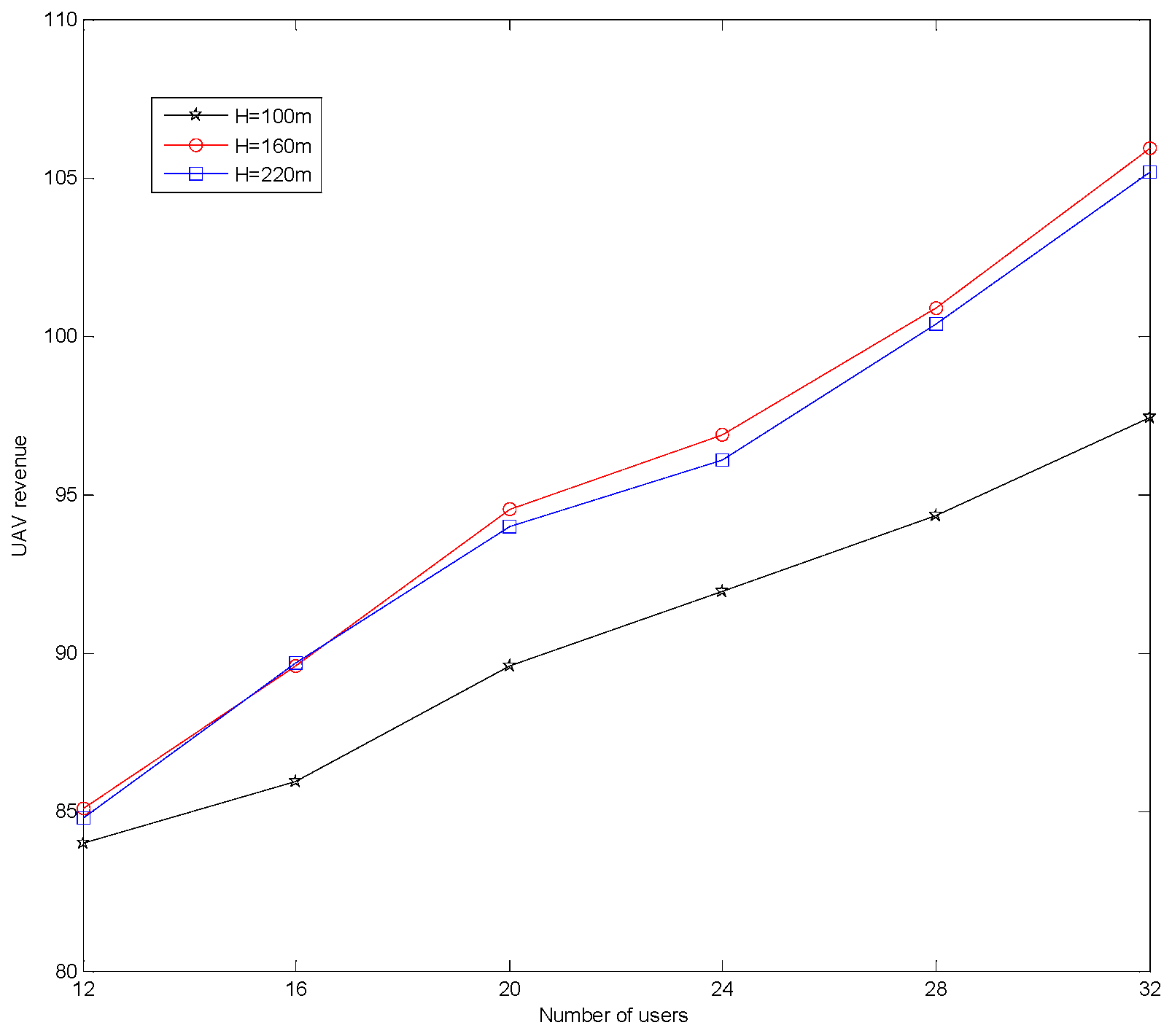
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lopez-Perez, D.; Ding, M.; Claussen, H.; Jafari, A.H. Towards 1 Gbps/UE in Cellular Systems: Understanding Ultra-Dense Small Cell Deployments. IEEE Commun. Surv. Tutor. 2015, 17, 2078–2101. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.-C.; Schneckenburger, N. A Survey of Air-to-Ground Propagation Channel Modeling for Unmanned Aerial Vehicles. IEEE Commun. Surv. Tutor. 2019, 21, 2361–2391. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, H.; Peng, J. Performance Analysis of Cooperative Caching and Transmission Diversity in Cache-Enabled UAV Networks. IEEE Trans. Wirel. Commun. 2023, 23, 4411–4423. [Google Scholar] [CrossRef]
- Chen, M.; Saad, W.; Yin, C. Liquid State Machine Learning for Resource and Cache Management in LTE-U Unmanned Aerial Vehicle (UAV) Networks. IEEE Trans. Wirel. Commun. 2019, 18, 1504–1517. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Z.; Liu, Y.; Xu, W.; Nallanathan, A. Caching Placement and Resource Allocation for Cache-Enabling UAV NOMA Networks. IEEE Trans. Veh. Technol. 2020, 69, 12897–12911. [Google Scholar] [CrossRef]
- Zhou, R.; Huang, Y.; Wang, Y.; Jiao, L.; Tan, H.; Zhang, R.; Wu, L. User Preference Oriented Service Caching and Task Offloading for UAV-Assisted MEC Networks. IEEE Trans. Serv. Comput. 2025, 1–12. [Google Scholar] [CrossRef]
- Ji, J.; Zhu, K.; Niyato, D.; Wang, R. Joint Cache Placement, Flight Trajectory, and Transmission Power Optimization for Multi-UAV Assisted Wireless Networks. IEEE Trans. Wirel. Commun. 2020, 19, 5389–5403. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, C.; Hu, X.; He, J.; Peng, M.; Ng, D.W.K.; Quek, T.Q.S. Joint Content Caching, Service Placement, and Task Offloading in UAV-Enabled Mobile Edge Computing Networks. IEEE J. Sel. Areas Commun. 2024, 43, 51–63. [Google Scholar] [CrossRef]
- Xie, L.; Cao, X.; Xu, J.; Zhang, R. UAV-Enabled Wireless Power Transfer: A Tutorial Overview. IEEE Trans. Green Commun. Netw. 2021, 5, 2042–2064. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, J.; Zhang, Y.; Nie, J.; Lim, W.Y.B.; Zhang, H.; Xiong, Z. Aerial Refueling: Scheduling Wireless Energy Charging for UAV Enabled Data Collection. IEEE Trans. Green Commun. Netw. 2022, 6, 1494–1510. [Google Scholar] [CrossRef]
- Hu, X.; Wen, P.; Xiao, H.; Wang, W.; Wong, K.-K. Maximizing Energy Charging for UAV-Assisted MEC Systems With SWIPT. IEEE Trans. Veh. Technol. 2025, 1–6. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, H.; Yao, H.; Wang, S. A Blockchain-Enabled Energy-Efficient Data Collection System for UAV-Assisted IoT. IEEE Internet Things J. 2020, 8, 2431–2443. [Google Scholar] [CrossRef]
- Qi, H.; Li, Y.; Xu, Y.; Quek, T.Q.S. UAV-Assisted Mobile Crowdsensing Systems Empowered by Wireless Power Transfer and Adaptive Compression Techniques. IEEE Wirel. Commun. Lett. 2024, 13, 2487–2491. [Google Scholar] [CrossRef]
- Zhao, M.-M.; Shi, Q.; Zhao, M.-J. Efficiency Maximization for UAV-Enabled Mobile Relaying Systems With Laser Charging. IEEE Trans. Wirel. Commun. 2020, 19, 3257–3272. [Google Scholar]
- Yin, Y.; Gui, G.; Liu, M.; Gacanin, H.; Sari, H.; Adachi, F. Joint User Pairing and Resource Allocation in Air-to-Ground Communication-Caching-Charging Integrated Network Based on NOMA. IEEE Trans. Veh. Technol. 2023, 72, 15819–15828. [Google Scholar] [CrossRef]
- Chai, S.; Lau, V.K.N. Multi-UAV Trajectory and Power Optimization for Cached UAV Wireless Networks With Energy and Content Recharging-Demand Driven Deep Learning Approach. IEEE J. Sel. Areas Commun. 2021, 39, 3208–3224. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Unmanned Aerial Vehicle With Underlaid Device-to-Device Communi-cations: Performance and Tradeoffs. IEEE Trans. Wirel. Commun. 2016, 15, 3949–3963. [Google Scholar]
- Yaliniz, R.I.B.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an Aerial Base Station in Next Generation Cellular Networks. In Proceedings of the 2016 IEEE International Conference on Communications, Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Breslau, L.; Cao, P.; Fan, L.; Phillips, G.; Shenker, S. Web caching and Zipf-like distributions: Evidence and implications. In Proceedings of the IEEE INFOCOM ‘99, Conference on Computer Communications, Proceedings, Eighteenth Annual Joint Conference of the IEEE Computer and Communications Societies, The Future is Now (Cat. No.99CH36320), New York, NY, USA, 21–25 March 1999; Volume 1, pp. 126–134. [Google Scholar]
- Hong, M.; Razaviyayn, M.; Luo, Z.-Q.; Pang, J.-S. A Unified Algorithmic Framework for Block-Structured Optimization Involving Big Data: With applications in machine learning and signal processing. IEEE Signal Process. Lett. 2016, 33, 57–77. [Google Scholar]
- Cui, J.; Ding, Z.; Fan, P. A Novel Power Allocation Scheme Under Outage Constraints in NOMA Systems. IEEE Signal Process. Lett. 2016, 23, 1226–1230. [Google Scholar] [CrossRef]
- Choi, J. Power Allocation for Max-Sum Rate and Max-Min Rate Proportional Fairness in NOMA. IEEE Commun. Lett. 2016, 20, 2055–2058. [Google Scholar] [CrossRef]
- Timotheou, S.; Krikidis, I. Fairness for Non-Orthogonal Multiple Access in 5G Systems. IEEE Signal Process. Lett. 2015, 22, 1647–1651. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, J.; Huang, Y.; He, S.; You, X.; Yang, L. On Optimal Power Allocation for Downlink Non-Orthogonal Multiple Access Systems. IEEE J. Sel. Areas Commun. 2017, 35, 2744–2757. [Google Scholar] [CrossRef]
- Do, N.T.; Da Costa, D.B.; Duong, T.Q.; An, B. A BNBF User Selection Scheme for NOMA-Based Cooperative Relaying Systems With SWIPT. IEEE Commun. Lett. 2016, 21, 664–667. [Google Scholar] [CrossRef]
| Parameter | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|
| UAV bandwidth | 5 Mhz | 3 dB | |
| Transmission | 1 W | 23 dB | |
| Time duration | 60 s | Content size | 15 Mbit |
| 2 Ghz | Content numbers | 20 | |
| −114 dBm | Charging | 1 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhu, Q. Joint Optimization Algorithm for UAV-Assisted Caching and Charging Based on Wireless Energy Harvesting. Appl. Sci. 2025, 15, 3908. https://doi.org/10.3390/app15073908
Zhu Y, Zhu Q. Joint Optimization Algorithm for UAV-Assisted Caching and Charging Based on Wireless Energy Harvesting. Applied Sciences. 2025; 15(7):3908. https://doi.org/10.3390/app15073908
Chicago/Turabian StyleZhu, Yumeng, and Qi Zhu. 2025. "Joint Optimization Algorithm for UAV-Assisted Caching and Charging Based on Wireless Energy Harvesting" Applied Sciences 15, no. 7: 3908. https://doi.org/10.3390/app15073908
APA StyleZhu, Y., & Zhu, Q. (2025). Joint Optimization Algorithm for UAV-Assisted Caching and Charging Based on Wireless Energy Harvesting. Applied Sciences, 15(7), 3908. https://doi.org/10.3390/app15073908






