Enhancing the Anti-Interference Capability of Orbital Angular Momentum Beams Generated by an Ultra-Large-Scale Metasurface
Abstract
1. Introduction
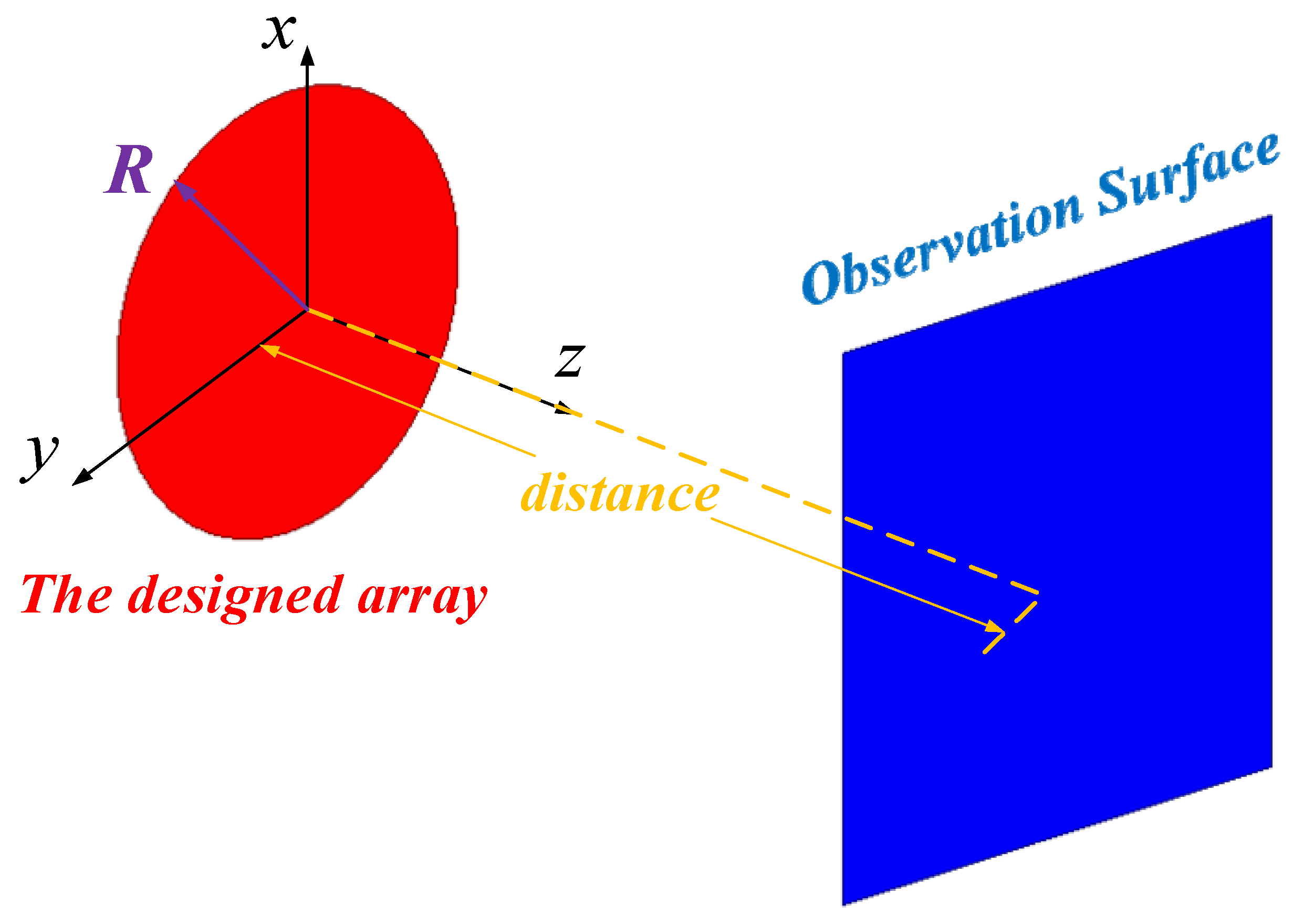
2. Theoretical Analysis of the near Field of an Ultra-Large-Scale Metasurface
2.1. Calculation of a Noiseless Near-Field Metasurface
2.2. Calculation of Noisy Near-Field Metasurface
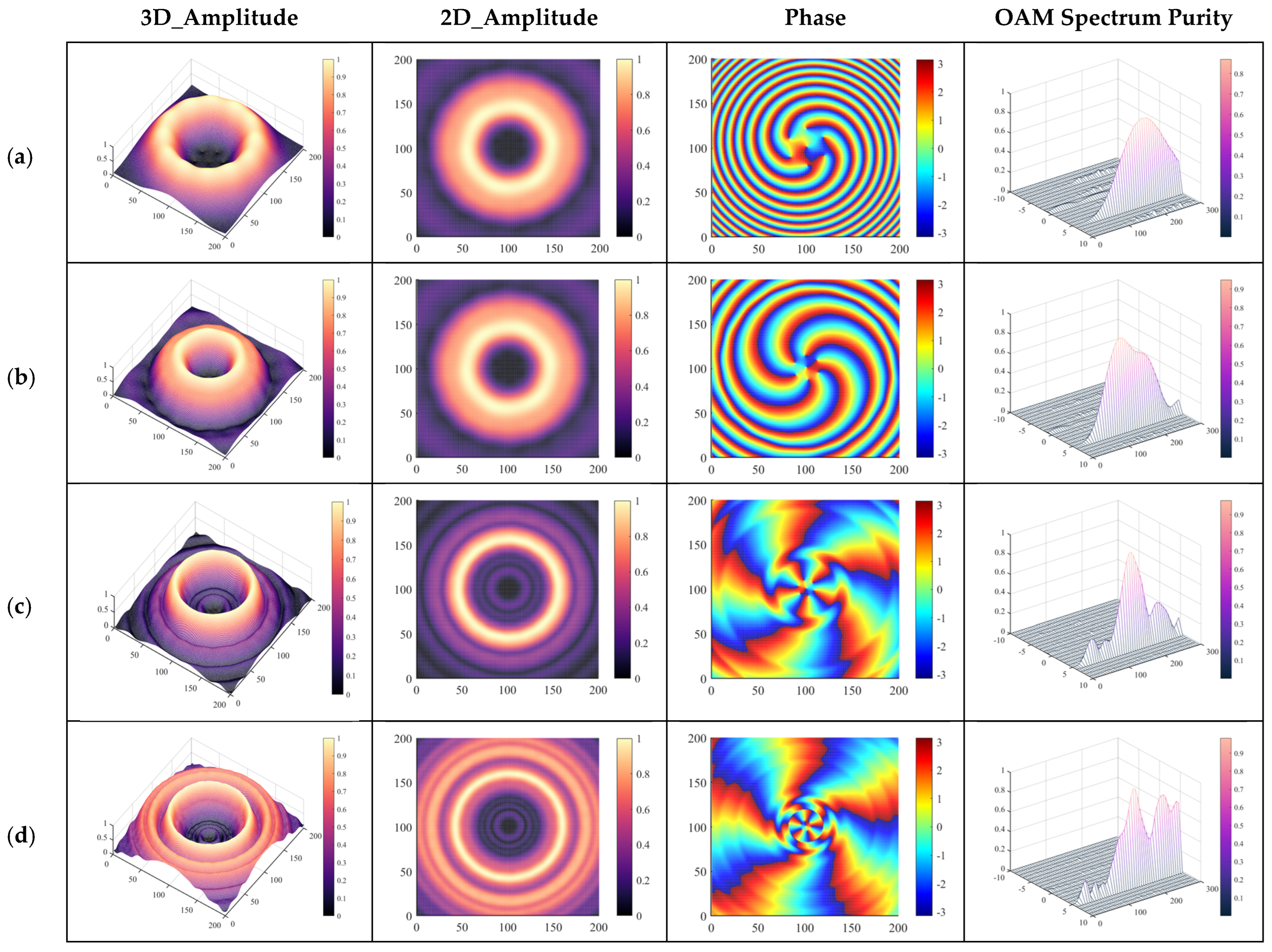
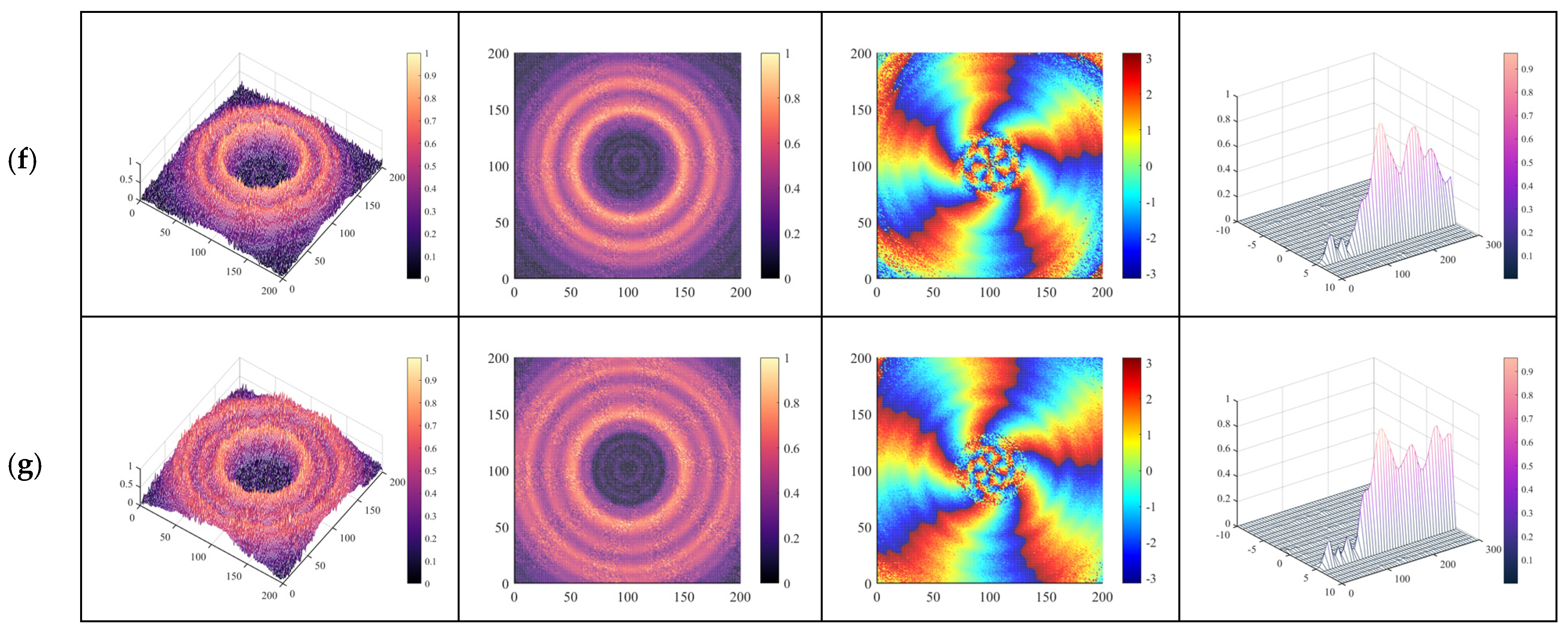
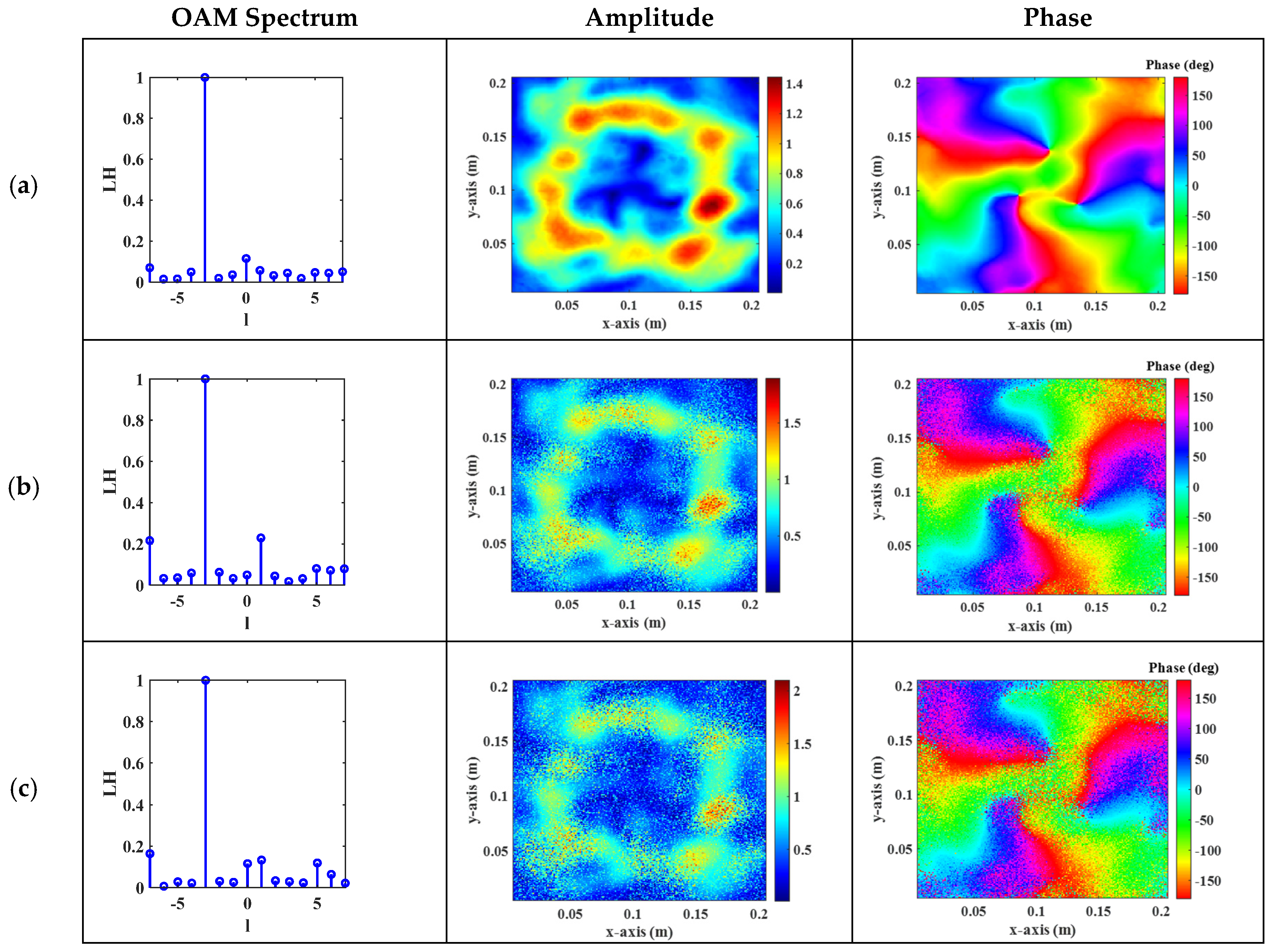
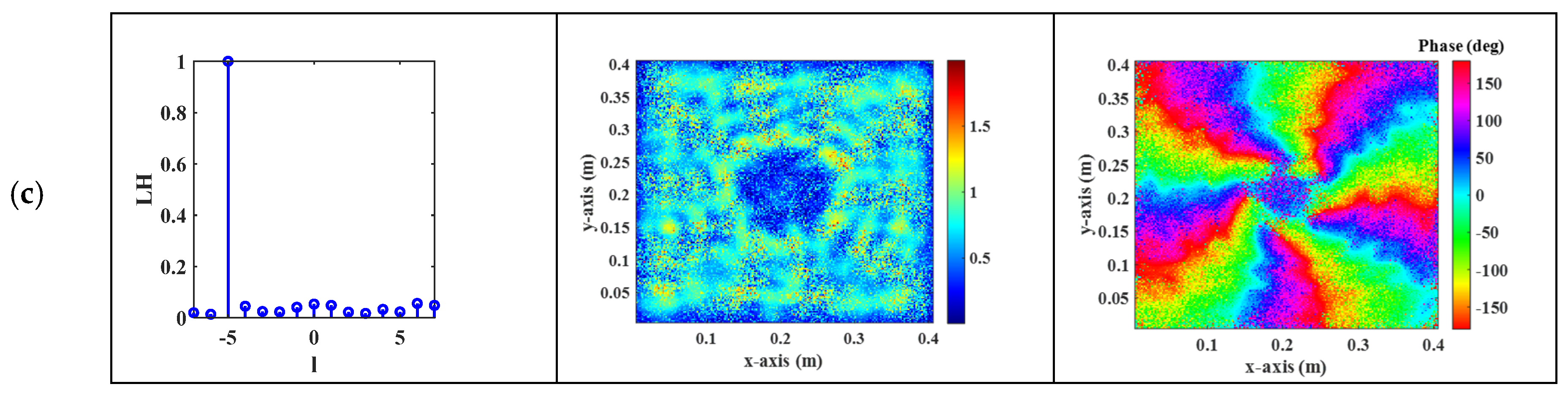
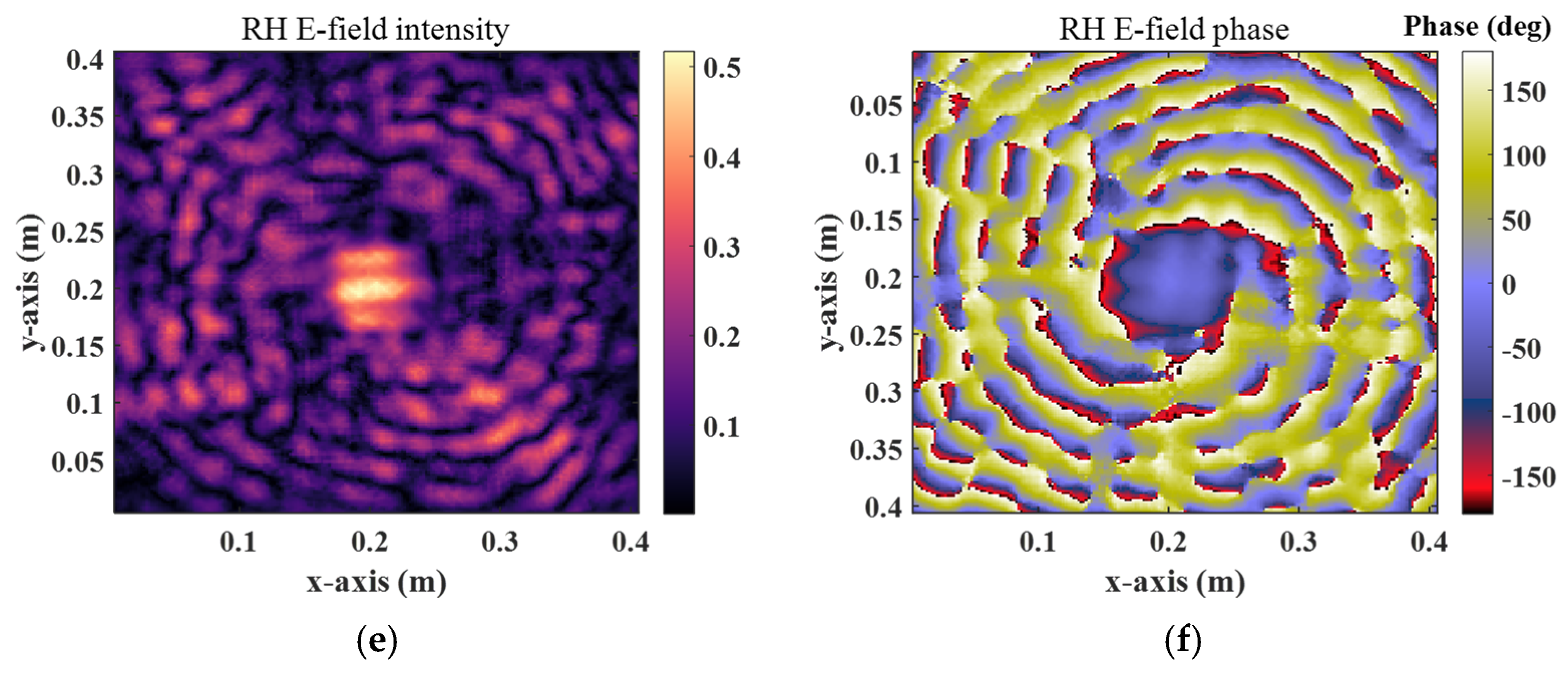
2.2.1. Observation Surface Distance Is 0.9 m
2.2.2. Observation Surface Distance of 1.2 m
3. Near-Field Simulation of Metasurfaces with Varying Dimensions
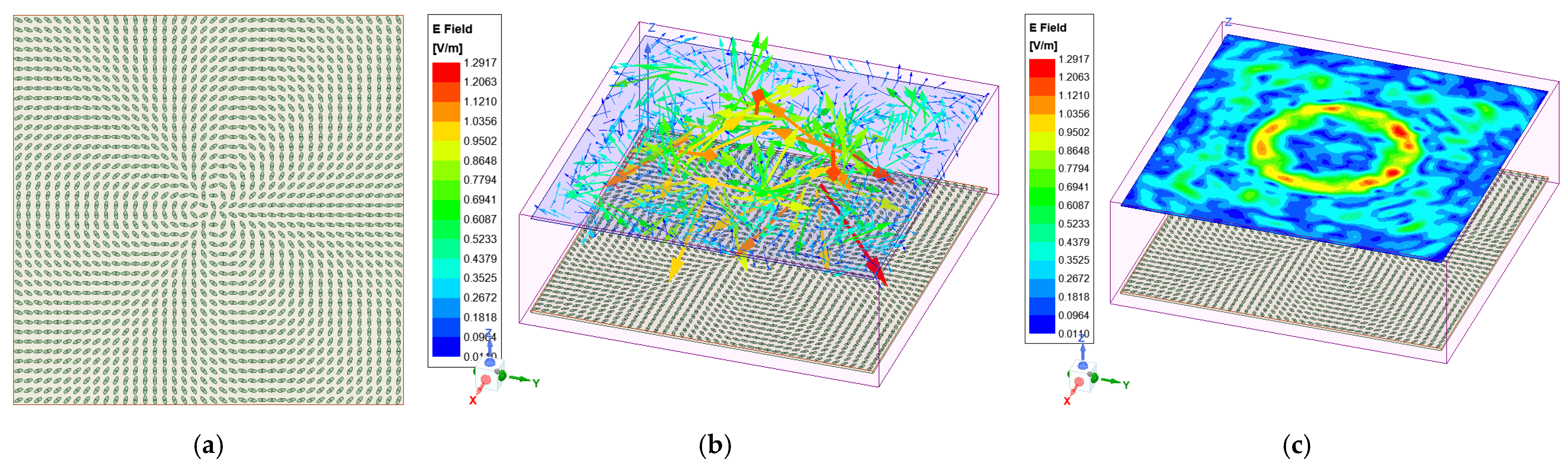
3.1. EE Unit Cell Design
3.2. Near-Field Simulation of the Compact Metasurface
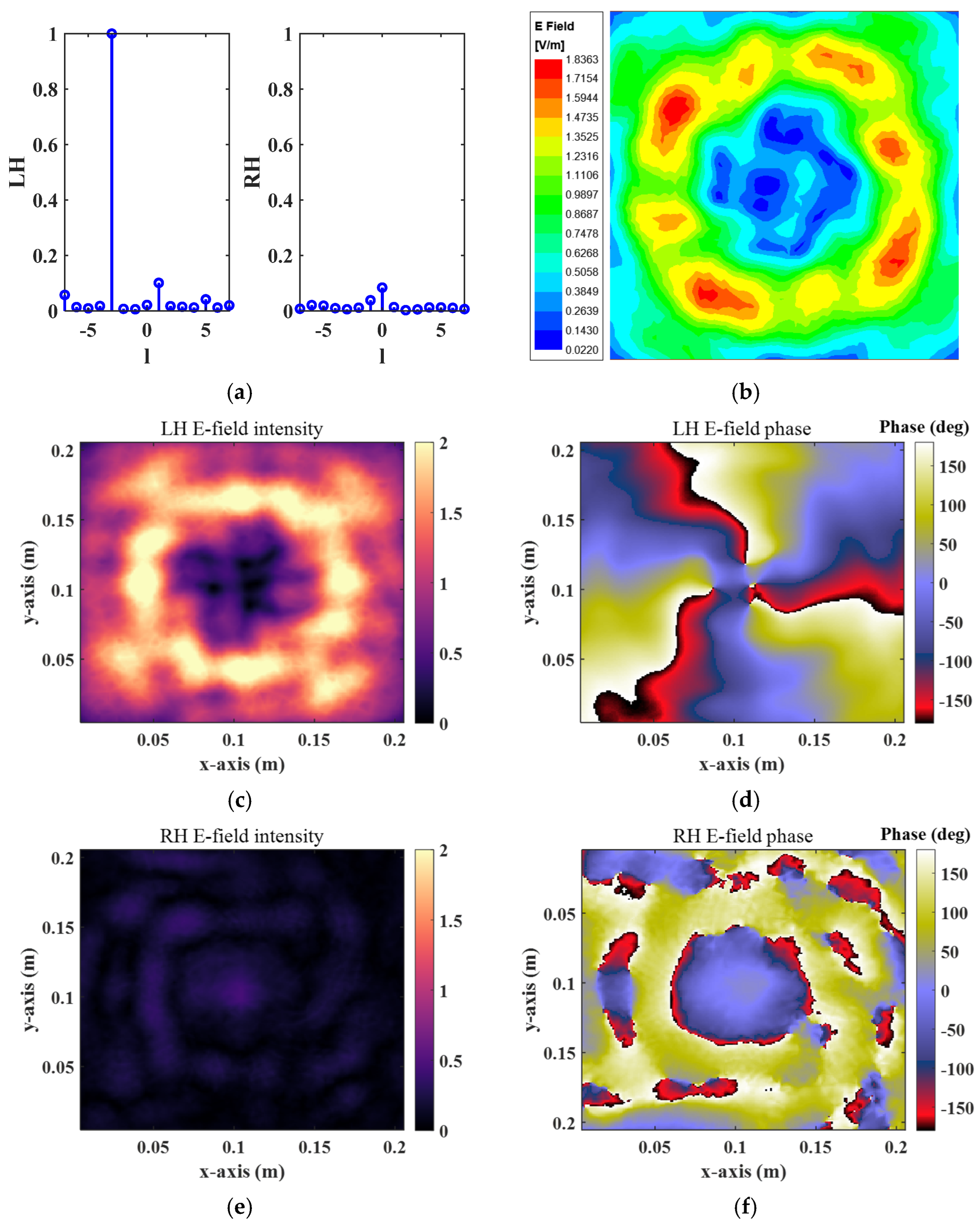
3.2.1. Normal Incidence of a Linearly Polarized Plane Wave on a Compact Metasurface
3.2.2. Normal Incidence of a Circularly Polarized Plane Wave on a Compact Metasurface
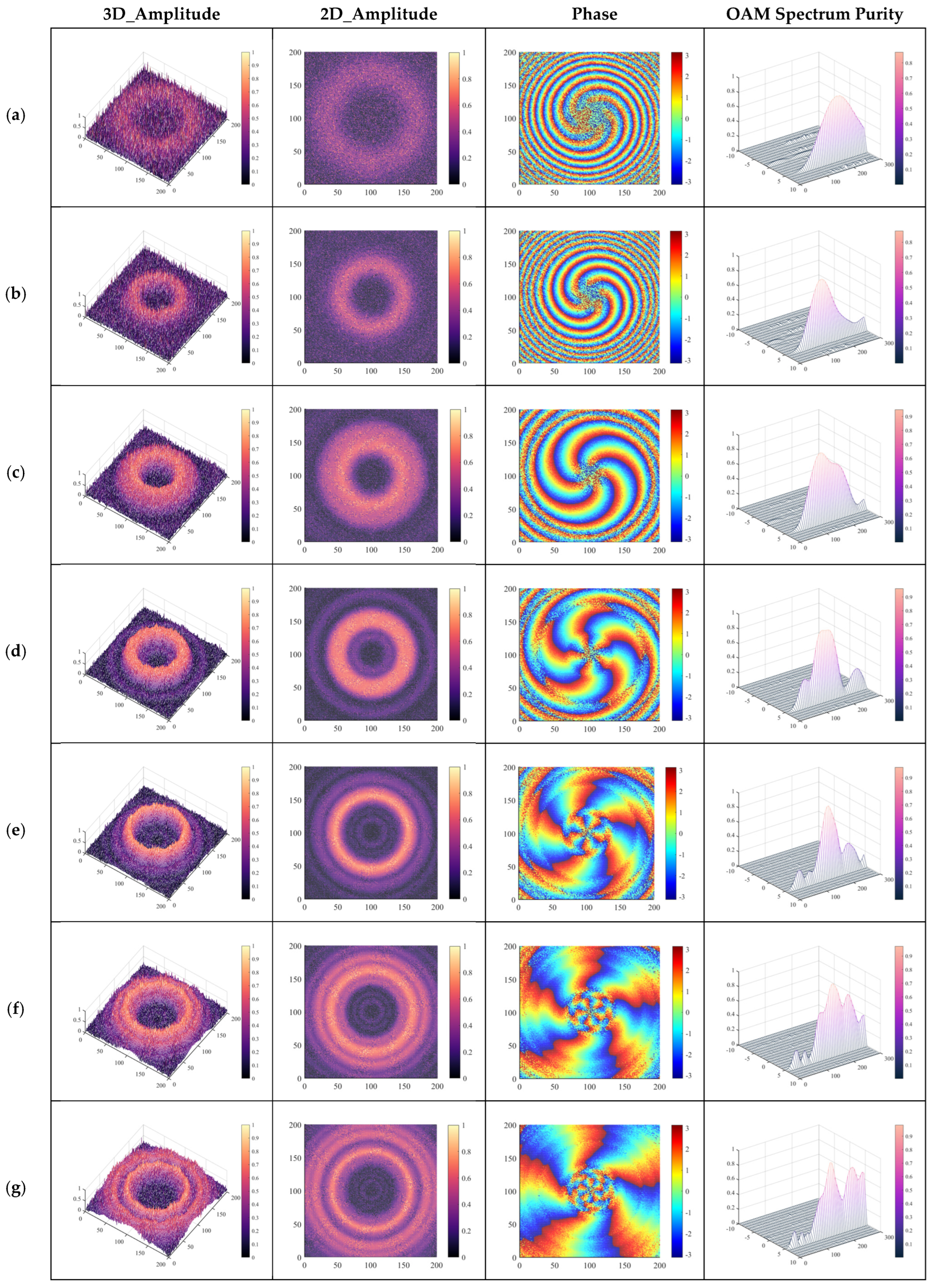
3.3. Near-Field Simulation of Large-Scale Metasurfaces
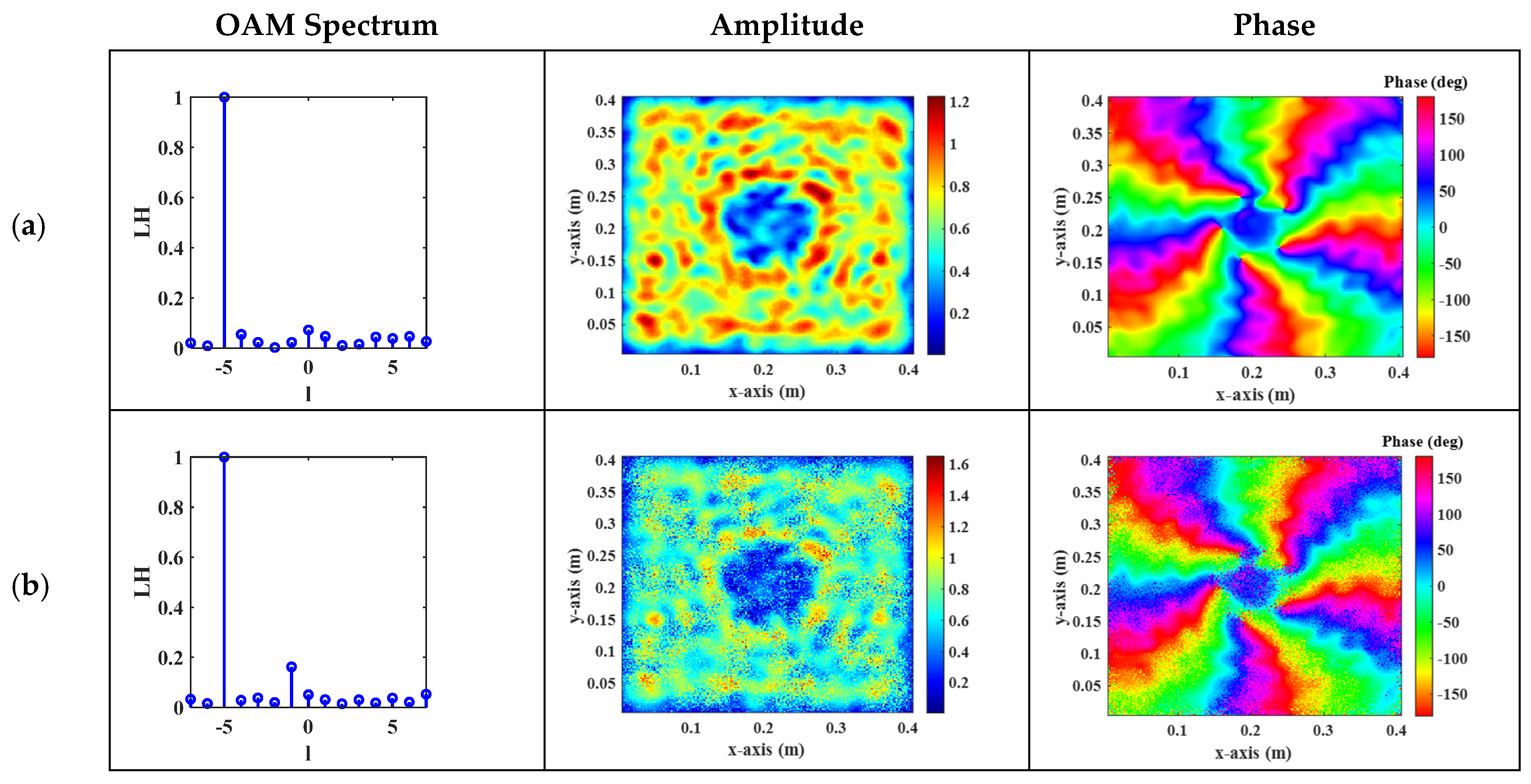
3.3.1. Normal Incidence of a Linearly Polarized Plane Wave on a Large-Scale Metasurface
3.3.2. Normal Incidence of a Circularly Polarized Plane Wave on a Large-Scale Metasurface
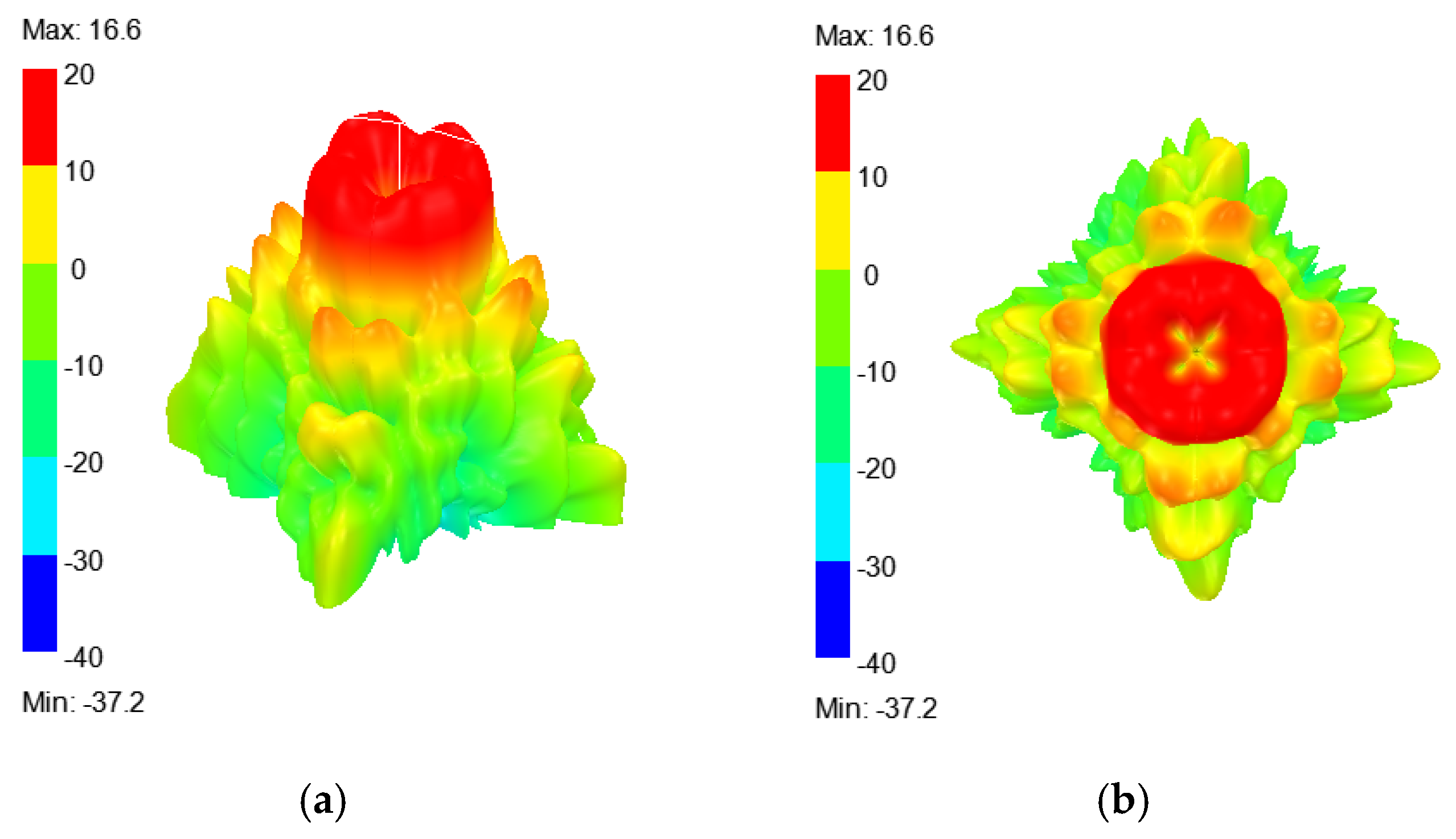
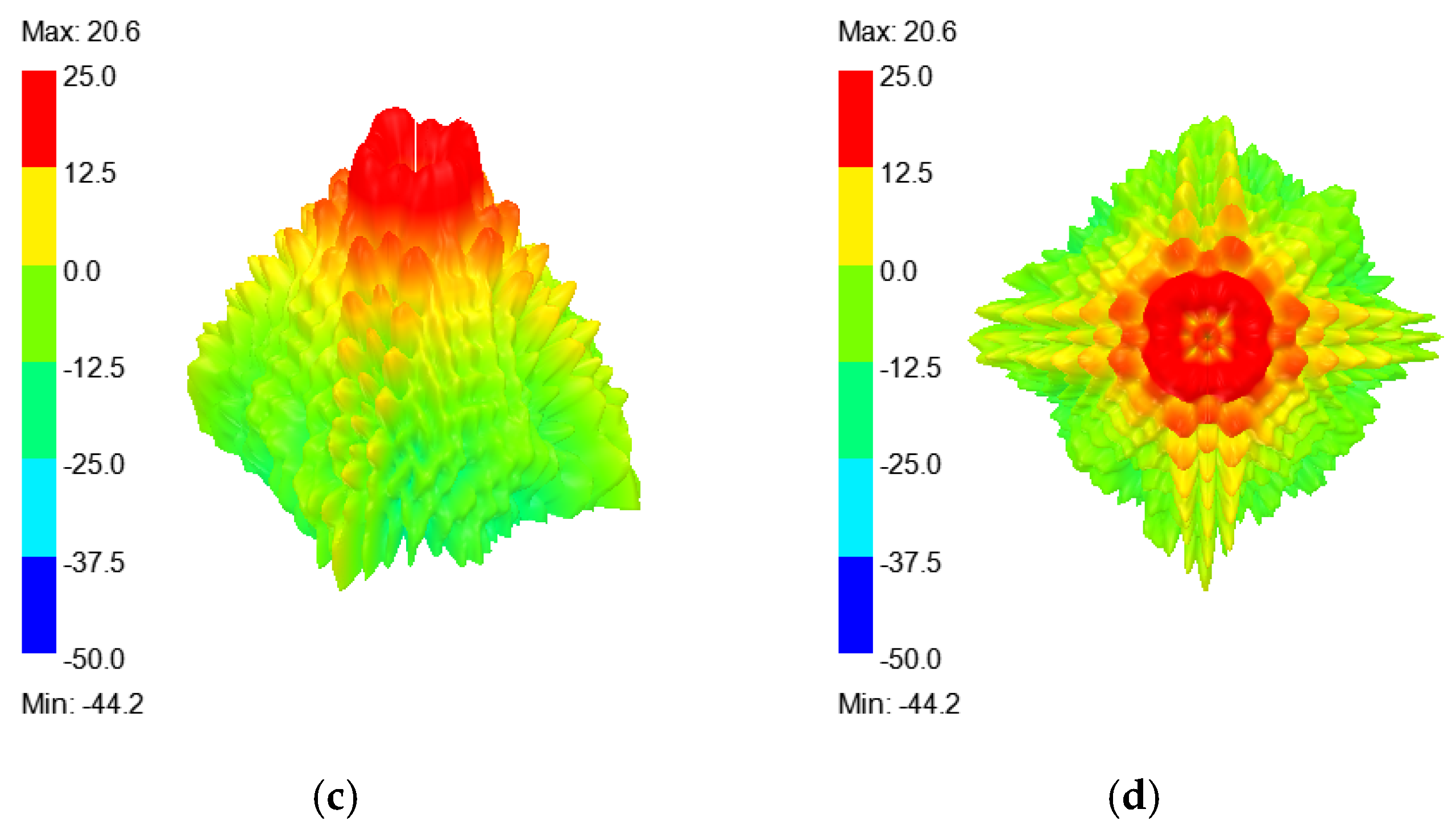
4. Discussion of Far-Field Patterns with Varying Dimensions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, K.; Cheng, Y.; Gao, Y.; Li, X.; Qin, Y.; Wang, H. Super-resolution radar imaging based on experimental OAM beams. Appl. Phys. Lett. 2017, 110, 164102. [Google Scholar] [CrossRef]
- Bu, X.; Zhang, Z.; Liang, X.; Chen, L.; Tang, H.; Zeng, Z.; Wang, J. A Novel Scheme for MIMO-SAR Systems Using Rotational Orbital Angular Momentum. Sensors 2018, 18, 3511. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, D. Large-Scale Orbital Angular Momentum Radar Pulse Generation with Rotational Antenna. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2316–2319. [Google Scholar] [CrossRef]
- Grier, D.G.; Han, Y. Erratum: Vortex rings in a constant electric field. Nature 2003, 424, 267–268. [Google Scholar] [CrossRef] [PubMed]
- Herring, R.A. Physics. A new twist for electron beams. Science 2011, 331, 155–156. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Xie, G.; Lavery, M.P.J.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. [Google Scholar] [CrossRef]
- Barbuto, M.; Miri, M.A.; Alù, A.; Bilotti, F.; Toscano, A. A Topological Design Tool for the Synthesis of Antenna Radiation Patterns. IEEE Trans. Antennas Propag. 2020, 68, 1851–1859. [Google Scholar] [CrossRef]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhu, G.; Zhang, J.; Zhu, J.; Zhang, Y.; Liu, J.; Yu, S. Compact and high-performance mode sorter enabling a multi-dimensional multiplexed 50-km vortex fiber communication system. Optica 2020, 7, 254–262. [Google Scholar] [CrossRef]
- Yang, L.J.; Sun, S.; Sha, W.E.I. Ultrawideband Reflection-Type Metasurface for Generating Integer and Fractional Orbital Angular Momentum. IEEE Trans. Antennas Propag. 2020, 68, 2166–2175. [Google Scholar] [CrossRef]
- Yang, L.J.; Sun, S.; Sha, W.E.I.; Huang, Z.; Hu, J. Arbitrary Vortex Beam Synthesis With Donut-Shaped Metasurface. IEEE Trans. Antennas Propag. 2021, 70, 573–584. [Google Scholar] [CrossRef]
- Yang, L.J.; Sun, S.; Xu, H.X.; Qiu, C.W. Broadband Amplitude–Phase Metasurface for Generating Crosstalk-Free Amplitude-Modulated Vortex Beams. IEEE Trans. Antennas Propag. 2025, 73, 421–431. [Google Scholar] [CrossRef]
- Tao, K.; Sun, S.; Chen, P.Y.; Yang, L.J.; Yang, Y.; Hu, J. A Novel Method for Controlling the Divergence Angle of Multimode Vortex Beams. IEEE Antennas Wirel. Propag. Lett. 2025, 24, 344–348. [Google Scholar] [CrossRef]
- Bao, Y.; Ni, J.; Qiu, C.W. A Minimalist Single-Layer Metasurface for Arbitrary and Full Control of Vector Vortex Beams. Adv. Mater. 2020, 32, 1905659. [Google Scholar] [CrossRef]
- Liu, H.; Teng, C.; Yang, H.; Deng, H.; Xu, R.; Deng, S.; Chen, M.; Yuan, L. Proposed phase plate for superimposed orbital angular momentum state generation. Opt. Express 2018, 26, 14792–14799. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, S.; Chen, Y.; Zhang, K.; Ding, X.; Ratni, B.; Wu, Q.; Burokur, S.N.; Qiu, C.-W. A Fully Phase-modulated Metasurface as An Energy Controllable Circular Polarization Router. Adv. Sci. 2020, 7, 2001437. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Kang, L.; Yue, T.; Xu, H.X.; Yang, Y.; Jin, Z.; Yu, C.; Hong, W.; Werner, D.H.; Qiu, C.W. A Single Noninterleaved Metasurface for High-Capacity and Flexible Mode Multiplexing of Higher-Order Poincaré Sphere Beams. Adv. Mater. 2020, 32, e1903983. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, K.; Ratni, B.; Song, Q.; Ding, X.; Wu, Q.; Burokur, S.N.; Genevet, P. Independent phase modulation for quadruplex polarization channels enabled by chirality-assisted geometric-phase metasurfaces. Nat. Commun. 2020, 11, 4186. [Google Scholar] [CrossRef]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to-orbital angular momentum conversion of light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef]
- Sun, J.J.; Sun, S.; Yang, L.J.; Hu, J. Enhanced Misalignment Estimation of Orbital Angular Momentum Signal Based on Deep Recurrent Neural Networks. IEEE Trans. Antennas Propag. 2023, 71, 5522–5527. [Google Scholar] [CrossRef]
- Xu, H.X.; Liu, H.; Ling, X.; Sun, Y.; Yuan, F. Broadband vortex beam generation using multimode Pancharatnam–Berry metasurface. IEEE Trans. Antennas Propag. 2017, 65, 7378–7382. [Google Scholar]
- Akram, M.R.; Ding, G.; Chen, K.; Feng, Y.; Zhu, W. Ultrathin single layer metasurfaces with ultra-wideband operation for both transmission and reflection. Adv. Mater. 2020, 32, e1907308. [Google Scholar] [PubMed]
- Luo, W.; Sun, S.; Xu, H.X.; He, Q.; Zhou, L. Transmissive ultrathin pancharatnam-berry metasurfaces with nearly 100% efficiency. Phys. Rev. Appl. 2017, 7, 044033. [Google Scholar]
- Tang, S.; Cai, T.; Liang, J.-G.; Xiao, Y.; Zhang, C.-W.; Zhang, Q.; Hu, Z.; Jiang, T. High-efficiency transparent vortex beam generator based on ultrathin Pancharatnam–Berry metasurfaces. Opt. Express 2019, 27, 1816–1824. [Google Scholar] [PubMed]
- Jeong, J.; Kim, Y.-D. Analysis of Near-Field EM Energy Densities for UCA-OAM Wave Based on Infinitesimal Dipoles. IEEE Acess 2024, 12, 81518–81526. [Google Scholar]
- He, D.; Guan, K.; Yan, D.; Yi, H.; Zhang, Z.; Wang, X. Physics and AI-based digital twin of multi-spectrum propagation characteristics for communication and sensing in 6G and beyond. IEEE J. Sel. Areas Commun. 2023, 41, 3461–3473. [Google Scholar] [CrossRef]
- He, D.; Ai, B.; Guan, K.; Wang, L.; Zhong, Z.; Kürner, T. The Design and Applications of High-Performance Ray-Tracing Simulation Platform for 5G and Beyond Wireless Communications: A Tutorial. IEEE Commun. Surv. Tutor. 2019, 21, 10–27. [Google Scholar]
- Cicchetti, R.; Faraone, A.; Testa, O. Near Field Synthesis Based on Multi-Port Antenna Radiation Matrix Eigenfields. IEEE Access 2019, 7, 62184–62197. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, B.; Guan, K.; Qian, A. Enhancing the Anti-Interference Capability of Orbital Angular Momentum Beams Generated by an Ultra-Large-Scale Metasurface. Appl. Sci. 2025, 15, 3900. https://doi.org/10.3390/app15073900
Su B, Guan K, Qian A. Enhancing the Anti-Interference Capability of Orbital Angular Momentum Beams Generated by an Ultra-Large-Scale Metasurface. Applied Sciences. 2025; 15(7):3900. https://doi.org/10.3390/app15073900
Chicago/Turabian StyleSu, Boli, Ke Guan, and An Qian. 2025. "Enhancing the Anti-Interference Capability of Orbital Angular Momentum Beams Generated by an Ultra-Large-Scale Metasurface" Applied Sciences 15, no. 7: 3900. https://doi.org/10.3390/app15073900
APA StyleSu, B., Guan, K., & Qian, A. (2025). Enhancing the Anti-Interference Capability of Orbital Angular Momentum Beams Generated by an Ultra-Large-Scale Metasurface. Applied Sciences, 15(7), 3900. https://doi.org/10.3390/app15073900







