Fast Temperature Field Extrapolation Under Non-Periodic Boundary Conditions
Abstract
1. Introduction
2. Methodology
2.1. POD Reduced-Order Method
2.2. FVM for Unstructured Grid
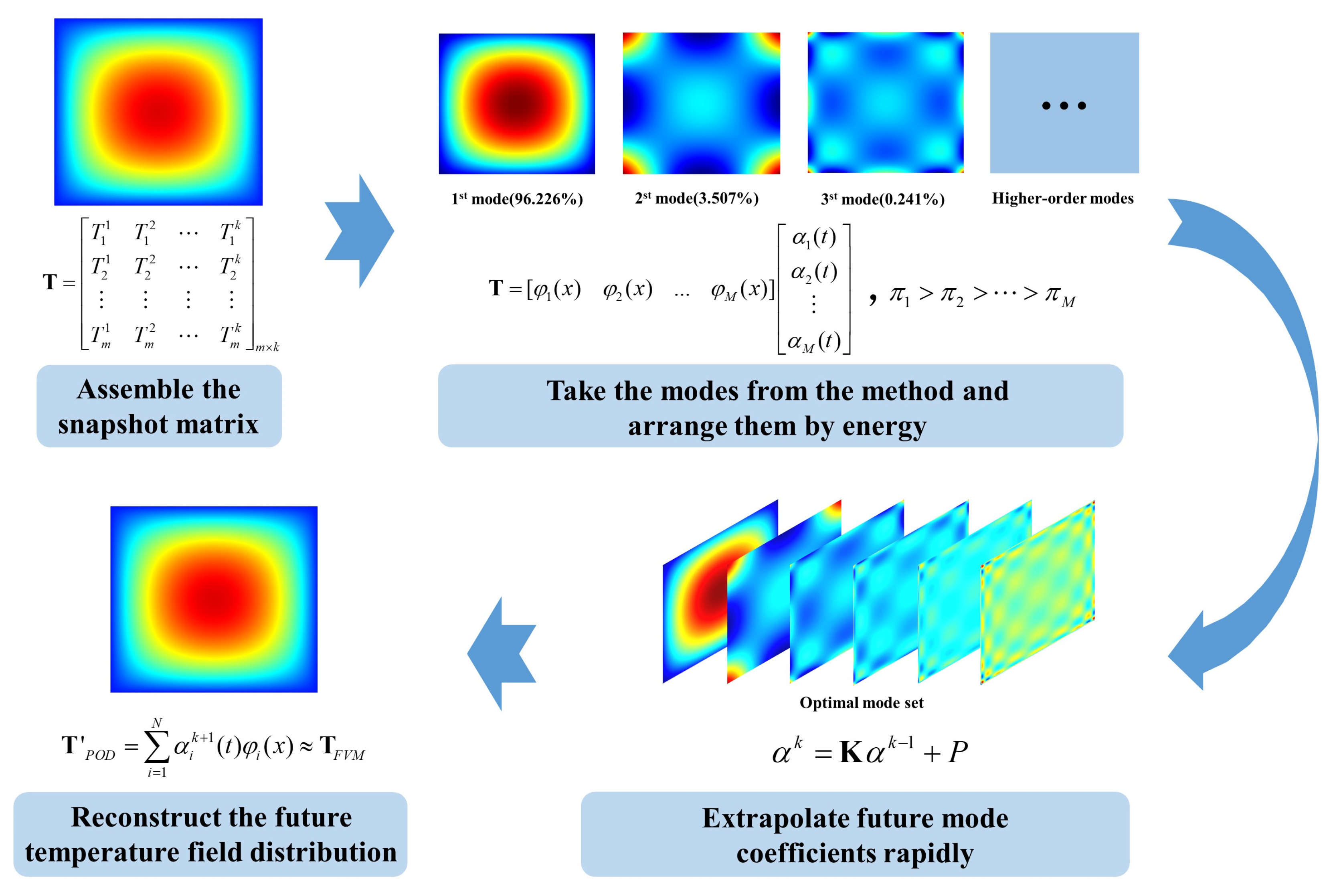
2.3. POD-FVM Reduced-Order Extrapolation Method
- According to the calculation results of FVM, select the beginning temperature field to assemble the temperature transient matrix.
- Decompose the temperature transient matrix with the SVD method to obtain the POD modes, mode coefficients, and eigenvalue of the matrix. POD modes are ranked according to the eigenvalue size.
- Select the first N modes according to Equation (6) to form the optimal POD mode set and then bring them into step 3 in Figure 1 to obtain the POD-FVM reduced-order extrapolation format, which can solve the mode coefficients for a future time.
- Reconstruct the temperature field with Equation (1) to obtain the POD solution of the temperature field in the future.
3. Model Description
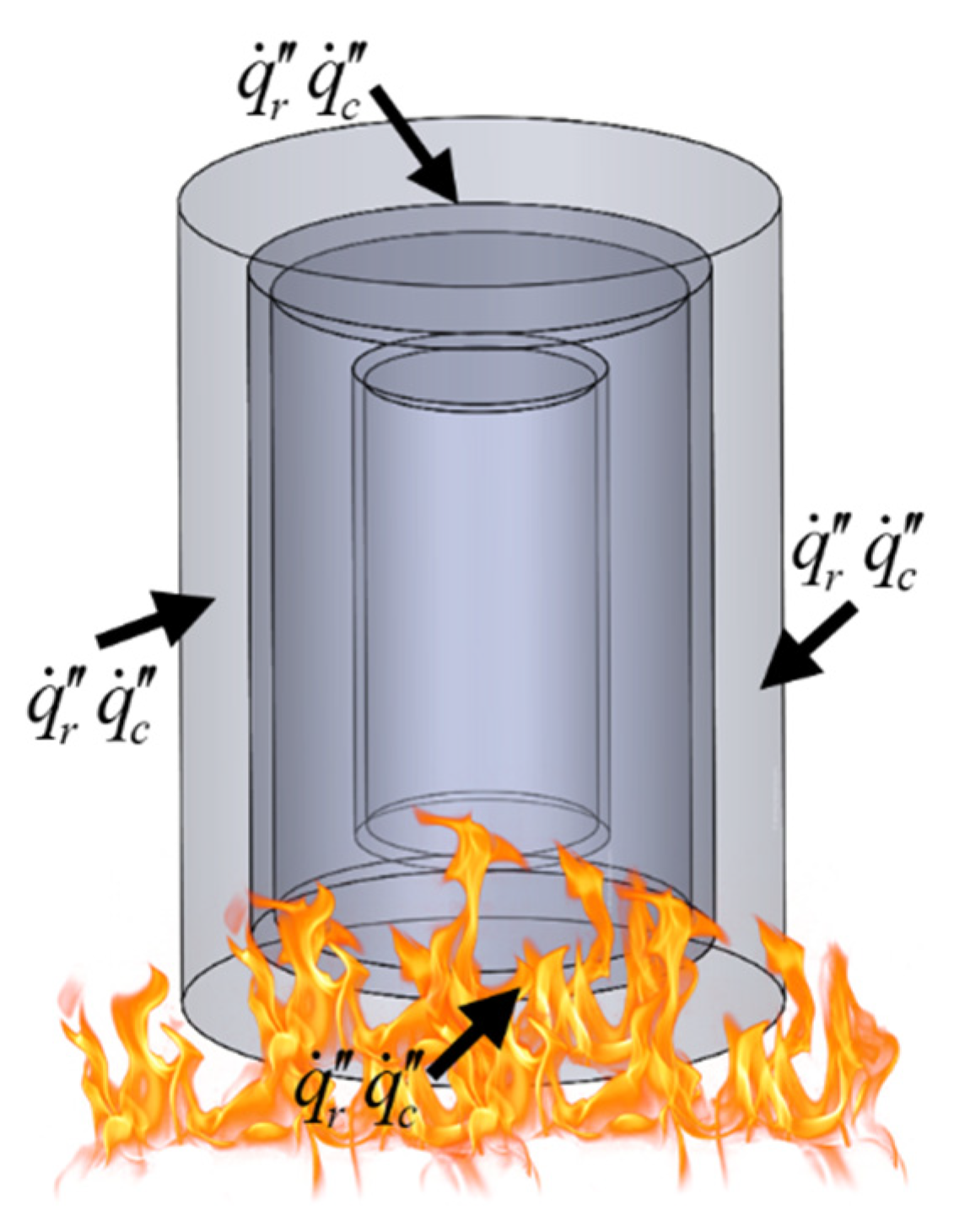
3.1. Complex Structure with Explosives
3.2. Non-Periodic Thermal Boundary
4. Results and Discussions
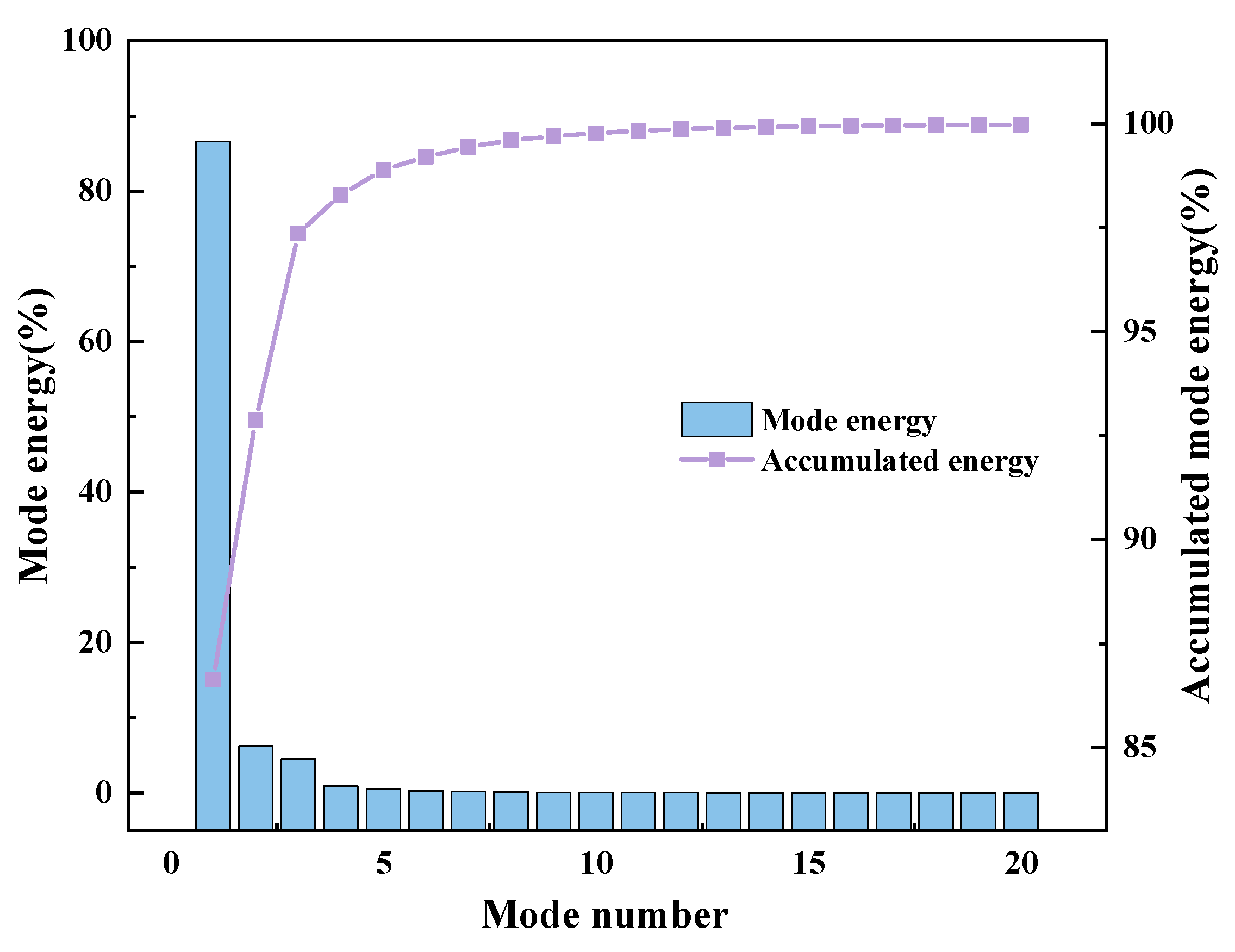
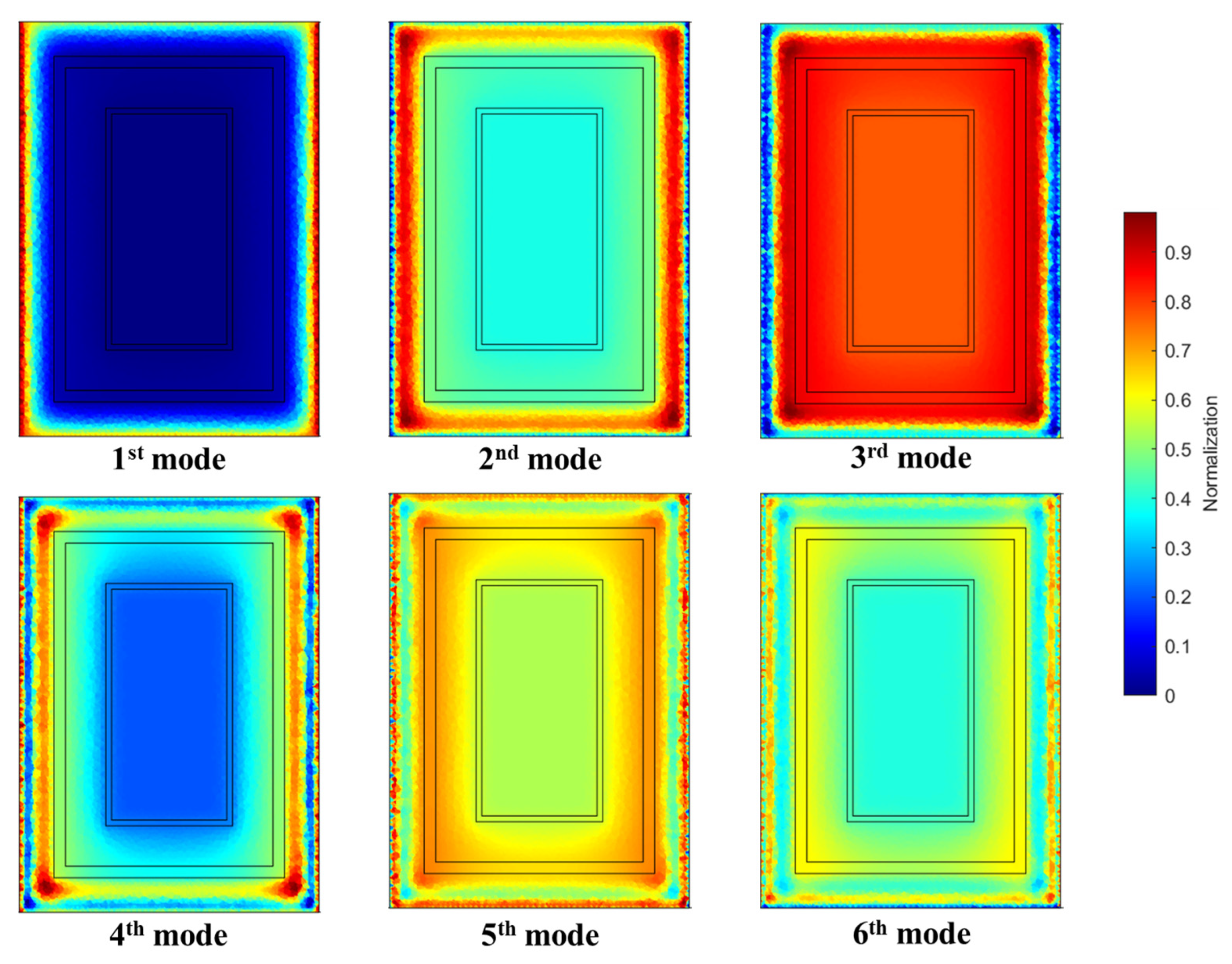
4.1. Selection of POD Mode
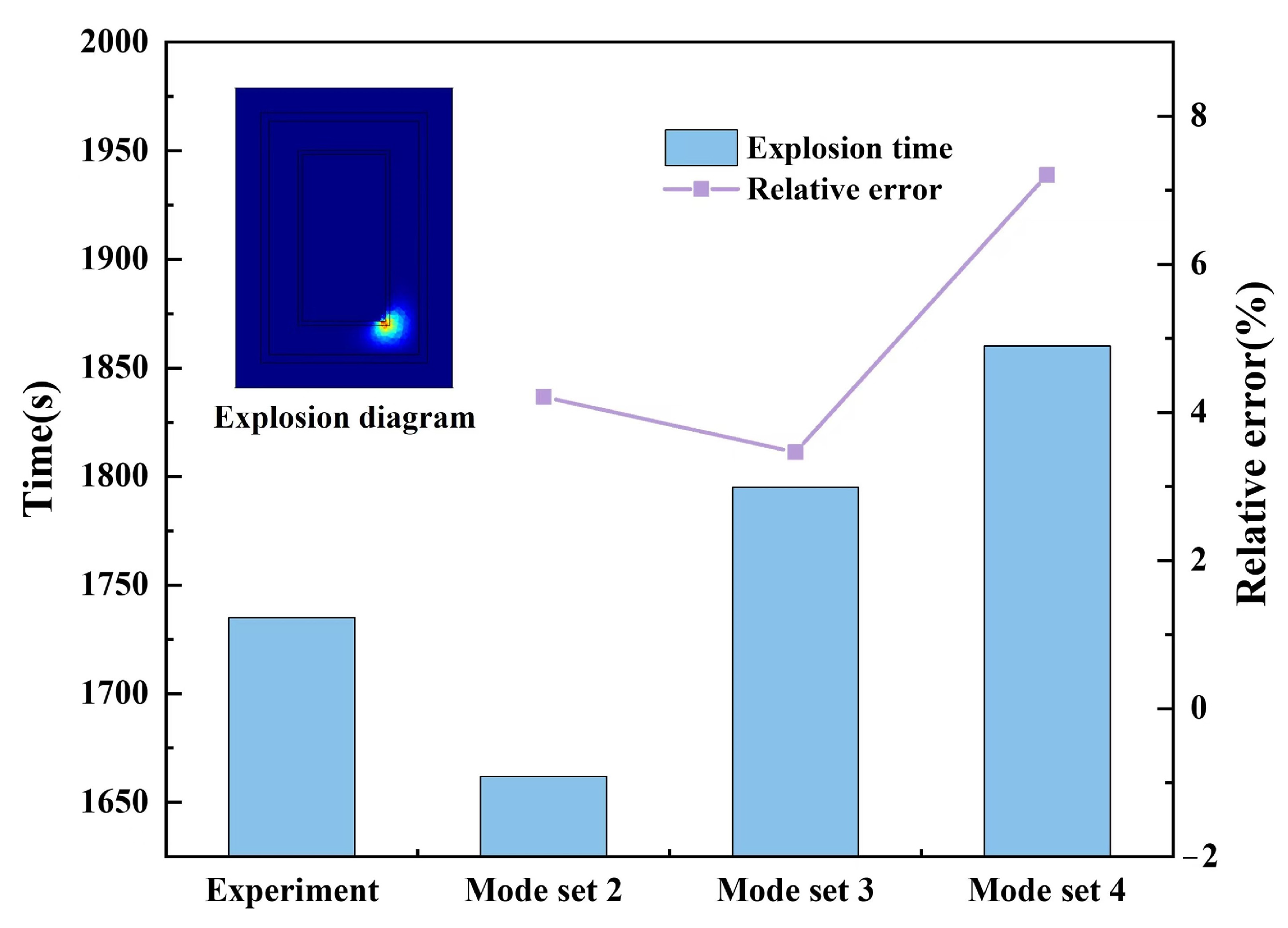
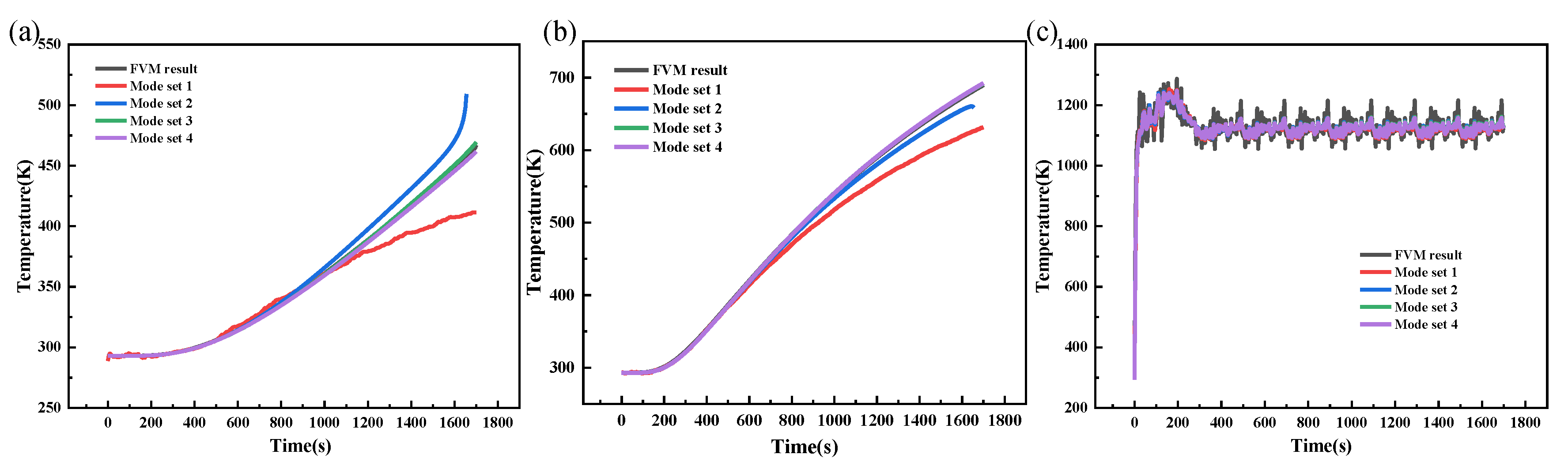
4.2. Accuracy Analysis of POD-FVM Reduced-Order Extrapolation
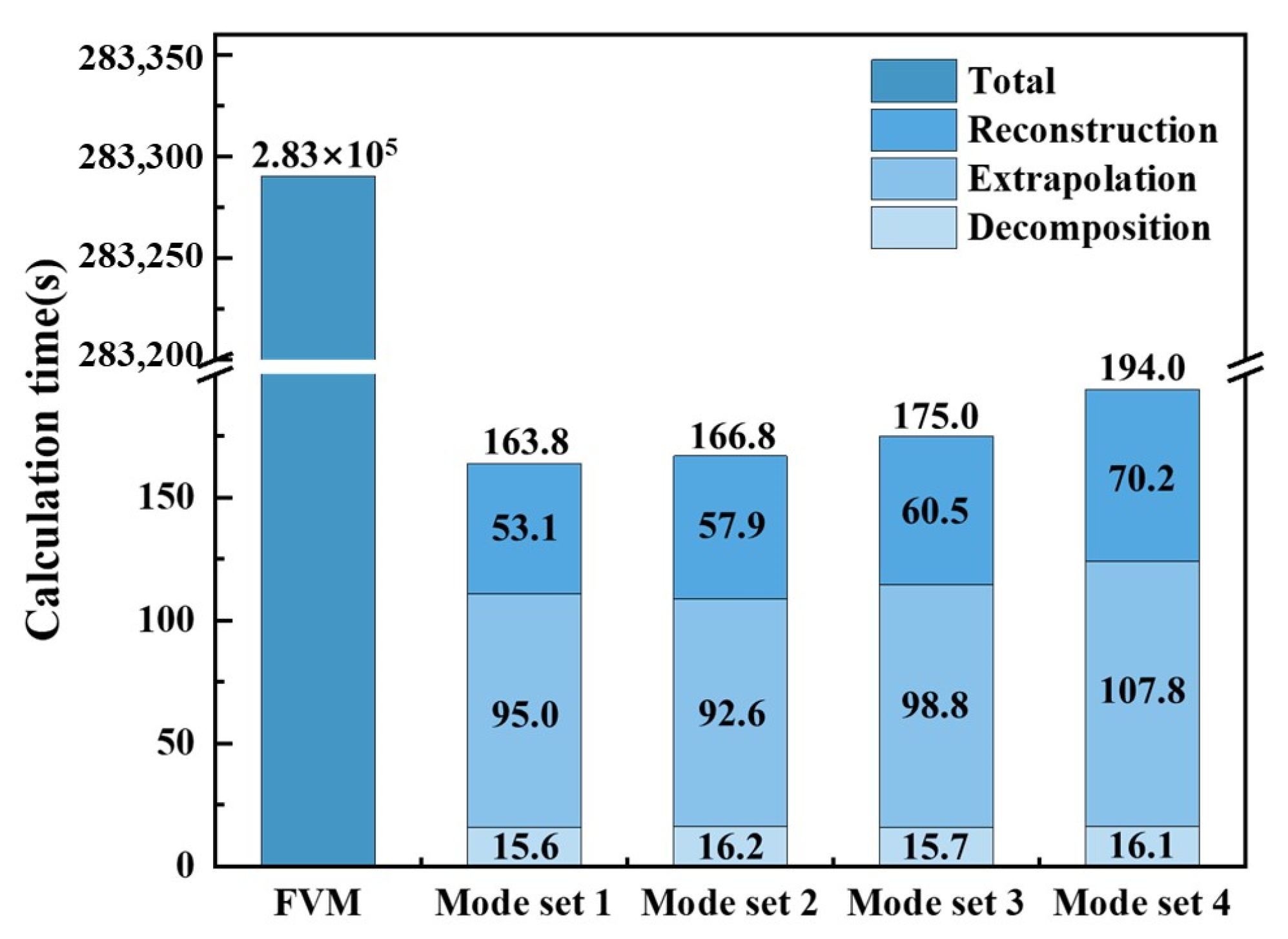
4.3. Computational Cost of the FVM and POD-FVM Reduced-Order Extrapolation Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute | ||
| DOAJ | Directory of open-access journals | ||
| TLA | Three-letter acronym | ||
| LD | Linear dichroism | ||
| Nomenclature | |||
| c | heat capacity | Greek symbols | |
| d | distance of grid centroid | α | coefficient of POD modes |
| E | reaction energy | γ | accumulated mode energy |
| vertical interface vector | δ | relative error | |
| unit vector | ε | emissivity | |
| F | angle of view coefficient | θ | grid angle |
| FoΔ | grid Fourier number | λ | thermal conductivity |
| h | heat transfer coefficient | π | eigenvalue |
| I | proportion of eigenvalues | ρ | density |
| i | one unit in the modes | σ | Steffen–Boltzmann constant |
| M | total number of modes | φ | POD mode |
| N | number of modes selected | ||
| Q | reaction heat | Subscripts and superscript | |
| heat flux | c | convection | |
| R | gas constant | E | grid point |
| surface vector | f | grid interface | |
| s | generalized heat source | g | flame gas |
| T | temperature | k | time |
| thermal diffusion vector | P | grid point | |
| T(x,t) | temperature field matrix | r | flame radiation |
| T′(x,t) | approximate temperature field matrix | s | spray |
| ∇T | temperature gradient | w | wall |
| Δt | time step | X | adjacent grid point |
| V | volume of the grid | ||
| Z | pre-factor | Abbreviations | |
| FVM | finite volume method | ||
| POD | proper orthogonal decomposition | ||
References
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar]
- Luo, X.B.; Hu, R.; Liu, S.; Wang, K. Heat and fluid flow in high-power LED packaging and applications. Prog. Energy Combust. Sci. 2016, 56, 1–32. [Google Scholar]
- Xing, G.Y.; Xue, S.; Han, J.C.; Zuo, H.Y.; Hu, R.; Tu, Z.K.; Luo, X.B. Turbulent lubrication model for journal-axial coupled hydrodynamic bearings without grooves. Tribol. Int. 2023, 190, 109036. [Google Scholar]
- Xiang, L.Y.; Yu, X.J.; Hong, T.; Yang, X.; Xie, B.; Hu, R.; Luo, X.B. Performance of spray cooling with vertical surface orientation: An experimental investigation. Appl. Therm. Eng. 2023, 219, 119434. [Google Scholar]
- Khandekar, S.; Sahu, G.; Muralidhar, K.; Gatapova, E.Y.; Kabov, O.A.; Hu, R.; Luo, X.B.; Zhao, L. Cooling of high-power LEDs by liquid sprays: Challenges and prospects. Appl. Therm. Eng. 2021, 184, 115640. [Google Scholar]
- Xiang, L.Y.; Hu, R. Liquid directional steering. Matter 2022, 5, 13–15. [Google Scholar] [CrossRef]
- Samadiani, E.; Joshi, Y. Multi-parameter model reduction in multi-scale convective systems. Int. J. Heat Mass Transf. 2010, 53, 2193–2205. [Google Scholar]
- Xiang, L.Y.; Cheng, Y.H.; Yu, X.J.; Fan, Y.W.; Yang, X.; Zhang, X.F.; Xie, B.; Luo, X.B. High-performance thermal management system for high-power LEDs based on double-nozzle spray cooling. Appl. Therm. Eng. 2023, 231, 121005. [Google Scholar] [CrossRef]
- Ostoich, C.M.; Bodony, D.J.; Geubelle, P.H. Fluid-thermal response of spherical dome under a Mach 6.59 laminar boundary layer. AIAA J. 2012, 50, 2791–2808. [Google Scholar]
- Wang, Y.; Yu, B.; Cao, Z.Z.; Zou, W.Z.; Yu, G.J. A comparative study of POD interpolation and POD projection methods for fast and accurate prediction of heat transfer problems. Int. J. Heat Mass Transf. 2012, 55, 4827–4836. [Google Scholar]
- Lu, K.; Zhang, K.Y.; Zhang, H.P.; Gu, X.H.; Jin, Y.L.; Zhao, S.B.; Fu, C.; Yang, Y.F. A review of model order reduction methods for large-scale structure systems. Shock Vib. 2021, 2021, 6631180. [Google Scholar] [CrossRef]
- Lohrasbi, S.; Hammer, R.; Eßl, W.; Reiss, G.; Defregger, S.; Sanz, W. A modification to extended proper orthogonal decomposition-based correlation analysis: The spatial consideration. Int. J. Heat Mass Transf. 2021, 175, 121065. [Google Scholar]
- Alonso, D.; Velazquez, A.; Vega, J.M. Robust reduced order modeling of heat transfer in a back step flow. Int. J. Heat Mass Transf. 2009, 52, 1149–1157. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Benner, P.; Gugercin, S.; Willcox, K. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 1988, 57, 483–531. [Google Scholar] [CrossRef]
- Nikolaidis, M.-A.; Ioannou, P.J.; Farrell, B.F.; Lozano-Durán, A. POD-based study of turbulent plane Poiseuille flow: Comparing structure and dynamics between quasi-linear simulations and DNS. J. Fluid Mech. 2023, 962, A16. [Google Scholar]
- Wang, L.; Pan, C.; Wang, J.; Gao, Q. Statistical signatures of u component wall-attached eddies in proper orthogonal decomposition modes of a turbulent boundary layer. J. Fluid Mech. 2022, 944, A26. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation; Nauka: Moscow, Russia, 1967; pp. 166–178. [Google Scholar]
- Sirovich, L. Turbulence and the Dynamics of Coherent Structures Part II: Symmetries and Transformations. Q. Appl. Math. 1987, 45, 573–582. [Google Scholar]
- Hazenberg, M.; Astrid, P.; Weiland, S. Low order modeling and optimal control design of a heated plate. In Proceedings of the 2003 European Control Conference, Cambridge, UK, 1–4 September 2003; pp. 1240–1245. [Google Scholar]
- Raghupathy, A.P.; Ghia, U.; Ghia, K.; Maltz, W. Boundary-condition-independent reduced-order modeling of complex 2D objects by POD-Galerkin methodology. In Proceedings of the 2009 25th Annual IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 15–19 March 2009; pp. 208–215. [Google Scholar]
- Georgaka, S.; Stabile, G.; Rozza, G.; Bluck, M.J. Parametric POD-Galerkin model order reduction for unsteady-state heat transfer problems. Commun. Comput. Phys. 2019, 27, 1–32. [Google Scholar] [CrossRef]
- Hu, H.M.; Du, X.Z.; Yang, L.J.; Yang, Y.P.; Cheng, T.R. Cross scale simulation on transport phenomena of direct air-cooling system of power generating units based on reduced order modeling. Int. J. Heat Mass Transf. 2014, 75, 156–164. [Google Scholar]
- He, S.P.; Wang, M.J.; Zhang, J.; Tian, W.X.; Qiu, S.Z.; Su, G.H. A deep-learning reduced-order model for thermal hydraulic characteristics rapid estimation of steam generators. Int. J. Heat Mass Transf. 2022, 198, 123424. [Google Scholar]
- Han, D.X.; Yu, B.; Yu, G.J.; Zhao, Y.; Zhang, W.H. Study on a BFC-based POD-Galerkin ROM for the steady-state heat transfer problem. Int. J. Heat Mass Transf. 2014, 69, 1–5. [Google Scholar] [CrossRef]
- Jiang, W.W.; Pan, T.; Jiang, G.H.; Sun, Z.Y.; Liu, H.Y.; Zhou, Z.Y.; Ruan, B.; Yang, K.; Gao, X.W. Data-driven physical fields reconstruction of supercritical-pressure flow in regenerative cooling channel using POD-AE reduced-order model. Int. J. Heat Mass Transf. 2023, 217, 124699. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, H.; Sun, P.; An, J.; Navon, I.M. A reduced-order finite volume element formulation based on POD method and numerical simulation for two-dimensional solute transport problems. Math. Comput. Simulat. 2012, 42, 1263–1280. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, H.; Sun, P.; Gao, J.Q. A reduced-order finite difference extrapolation algorithm based on POD technique for the non-stationary Navier–Stokes equations. Appl. Math. Model. 2013, 37, 5464–5473. [Google Scholar]
- Luo, Z.D.; Nie, S.; Li, H. A reduced order extrapolated difference algorithm for parabolic equations based on POD method. Math. Pract. Cogn. 2013, 43, 161–167. [Google Scholar]
- Vuppula, V.K.R.; Ramanujam, M.; Runkana, V. Reduced-order modeling of conjugate heat transfer in lithium-ion batteries. Int. J. Heat Mass Transf. 2024, 227, 125537. [Google Scholar] [CrossRef]
- Teng, F.; Luo, Z.D.; Yang, J. A reduced-order extrapolated natural boundary element method based on POD for the parabolic equation in the 2D unbounded domain. Comput. Appl. Math. 2019, 38, 102. [Google Scholar]
- Frey, P.J.; George, P.L. Mesh Generation Application to Finite Elements, 2nd ed.; ISTE Ltd.: London, UK; John Wiley & Sons Publishing: Indianapolis, IN, USA, 2008. [Google Scholar]
- Wu, S.; Li, M.H.; Zhang, Z.L. Thermal protection design and analysis of complex explosive structures in fire environment. Acta Ordnance Eng. 2014, 35, 1275–1280. [Google Scholar]
- Jiang, C.Y.; Soh, Y.C.; Li, H. Two-stage indoor physical field reconstruction from sparse sensor observations. Energy Build. 2017, 151, 548–563. [Google Scholar]
- Azzouz, M.S.; Guo, X.; Przekop, A.; Mei, C. Comparison of PDE/Galerkin and FEM for nonlinear aerospace structures analyses. In Proceedings of the 44th Structures, Structural Dynamics and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Xing, G.Y.; Xue, S.; Hong, T.; Zuo, H.Y.; Luo, X.B. A Novel Hydrodynamic Suspension Micropump Using Centrifugal Pressurization and the Wedge Effect. Sci. China Technol. Sci. 2023, 66, 2047–2058. [Google Scholar]
- Carere, G.; Strazzullo, M.; Ballarin, F.; Rozza, G.; Stevenson, R. A weighted POD-reduction approach for parametrized PDE-constrained optimal control problems with random inputs and applications to environmental sciences. Comput. Math. Appl. 2021, 102, 261–276. [Google Scholar]
- Yang, X.; Zhang, X.F.; Zhang, T.X.; Xiang, L.Y.; Xie, B.; Luo, X.B. Paving continuous heat dissipation pathways for quantum dots in polymer with orange-inspired radially aligned UHMWPE fibers. Opto-Electron. Adv. 2024, 7, 240036. [Google Scholar]
- Li, T.Y.; Gao, Y.Q.; Han, D.X.; Yang, F.S.; Yu, B. A novel POD reduced-order model based on EDFM for steady-state and transient heat transfer in fractured geothermal reservoir. Int. J. Heat Mass Transf. 2020, 146, 118783. [Google Scholar]
- Souza, Y.P.; Loureiro, F.S.; Mansur, W.J.; Ferreira, W.G.; Camargo, R.S. A time-domain POD approach based on numerical implicit and explicit Green’s functions for 3D elastodynamic analysis. Comput. Struct. 2023, 275, 106921. [Google Scholar]
- Zhang, X.; Xiang, H. A fast meshless method based on proper orthogonal decomposition for the transient heat conduction problems. Int. J. Heat Mass Transf. 2015, 84, 729–739. [Google Scholar]
- Zhu, Q.H.; Liang, Y.; Gao, X.W. A proper orthogonal decomposition analysis method for transient nonlinear heat conduction problems. Part 1 Basic Algorithm. Numer. Heat Transf. Part B Fundam. 2019, 77, 87–115. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Wu, S.; Li, M.H.; Zhang, Z.L. Numerical Simulation of Heat Transfer Problems in Structure with Explosive under Fire. Chin. J. Energ. Mater. 2014, 22, 617–623. [Google Scholar]
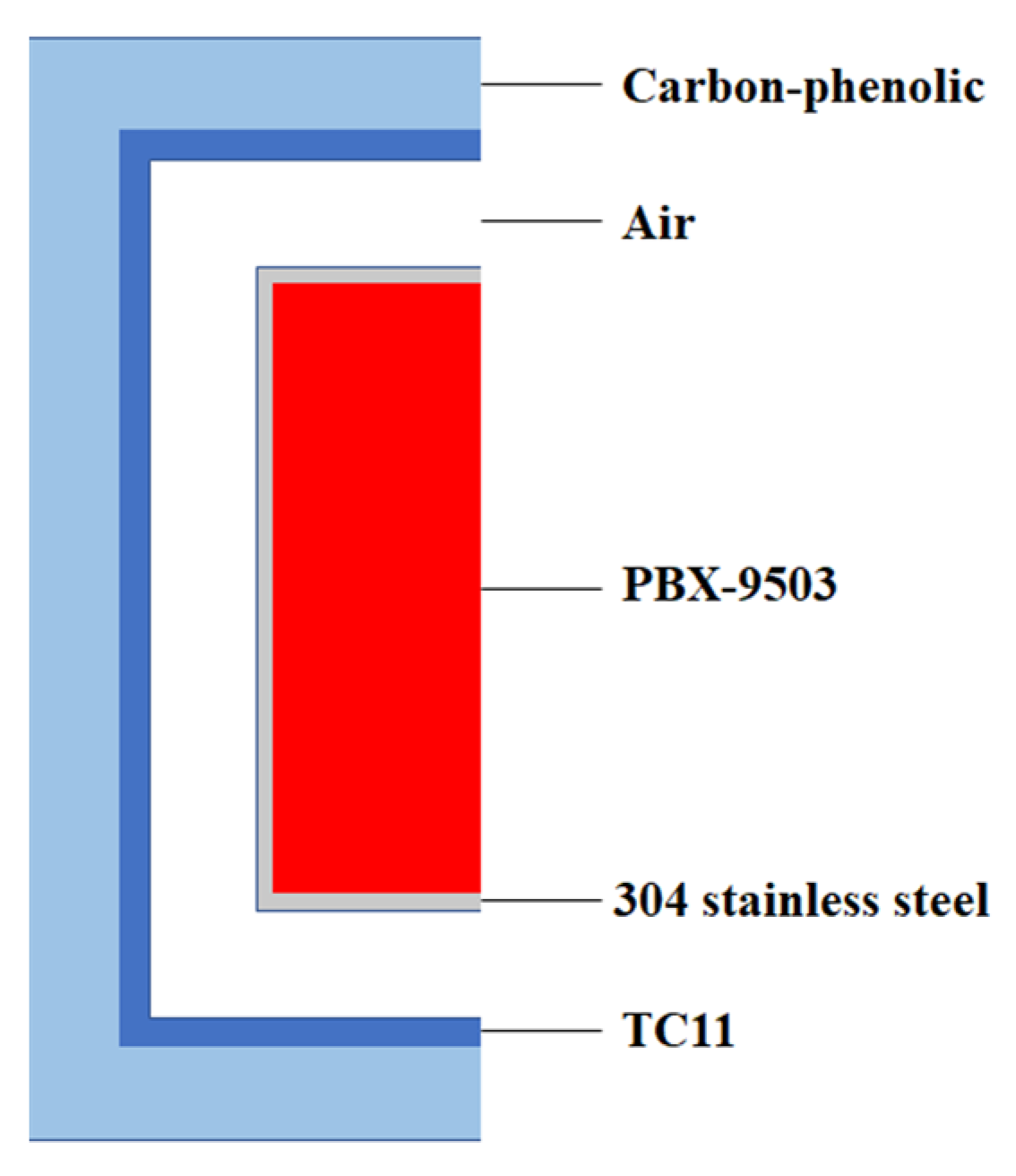
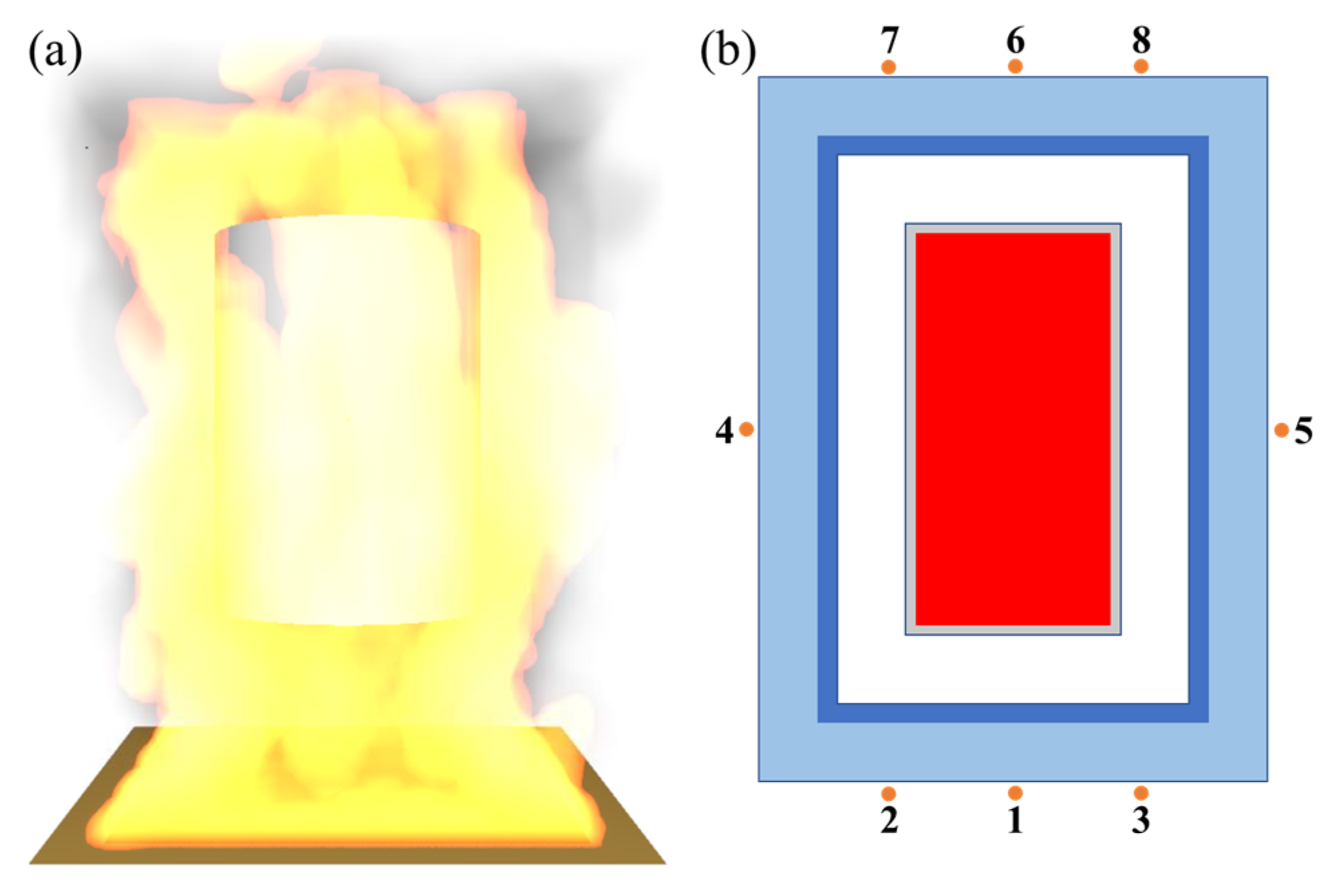
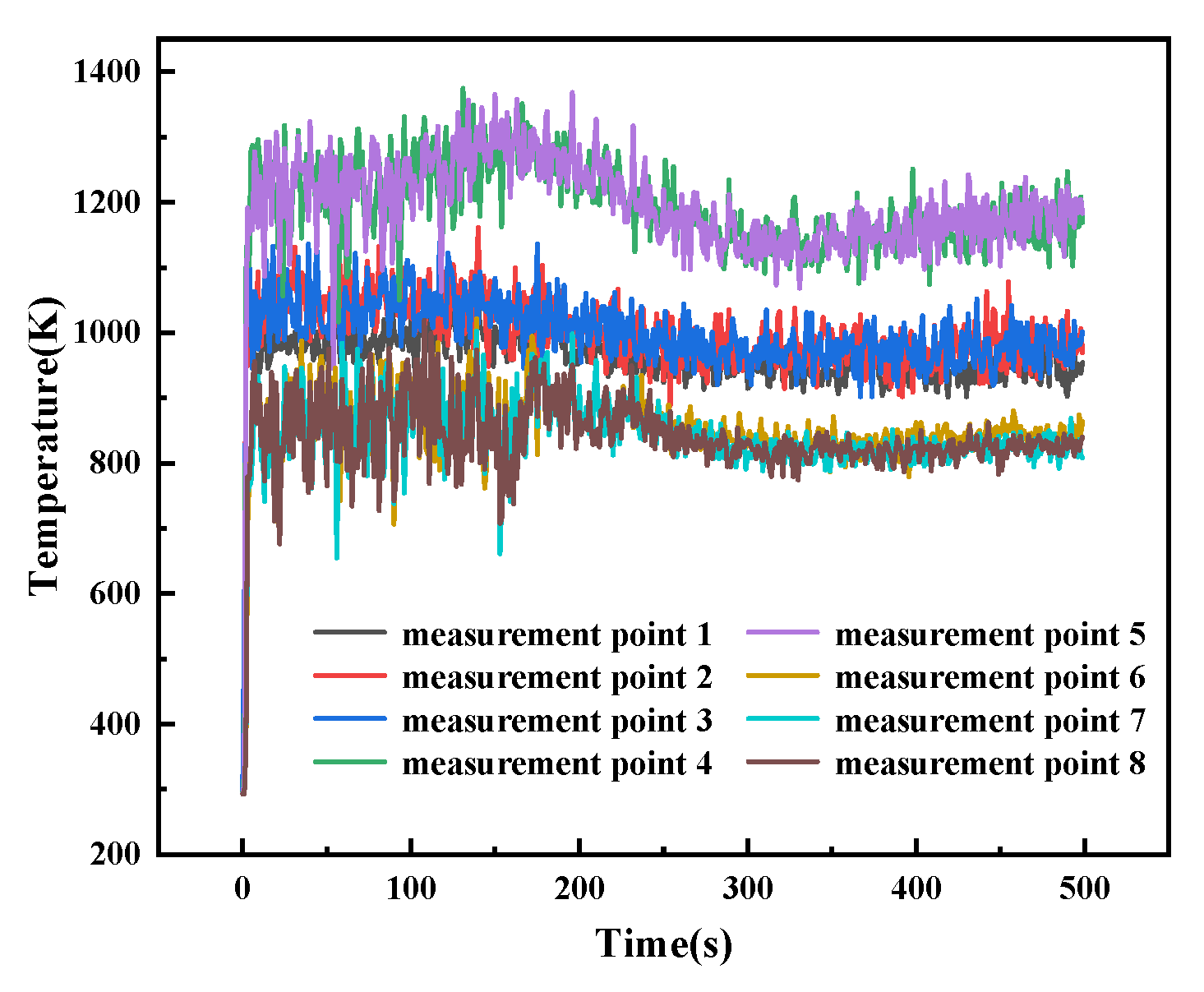

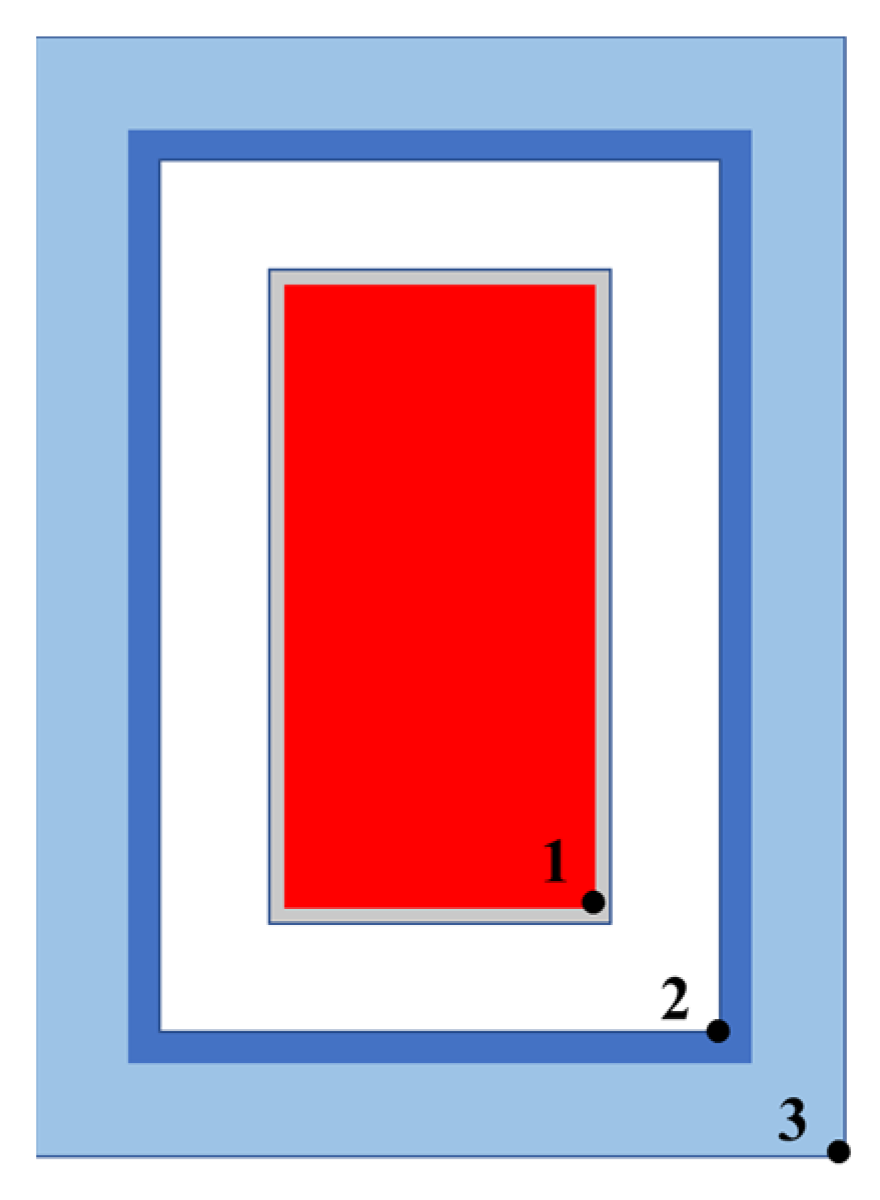


| Material | Thickness/mm | Thermal Conductivity/(W/m·K) |
|---|---|---|
| Carbon-phenolic | 30 | 0.48 |
| TC11 | 10 | 7.5 |
| Air | 35 | 0.038 |
| 304 stainless steel | 5 | 19.5 |
| PBX-9503 | 0.302 |
| Parameter | Value |
|---|---|
| 4.78 × 105 | |
| 4780/s | |
| Mode Set | γ Value | Number of POD Modes | Energy Ratio |
|---|---|---|---|
| 1 | 99% | 6 | 99.2004% |
| 2 | 99.9% | 13 | 99.9029% |
| 3 | 99.99% | 26 | 99.9906% |
| 4 | 99.999% | 55 | 99.9990% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Hu, Y.; Zhang, B.; Zha, Y.; Luo, X. Fast Temperature Field Extrapolation Under Non-Periodic Boundary Conditions. Appl. Sci. 2025, 15, 3895. https://doi.org/10.3390/app15073895
Wang F, Hu Y, Zhang B, Zha Y, Luo X. Fast Temperature Field Extrapolation Under Non-Periodic Boundary Conditions. Applied Sciences. 2025; 15(7):3895. https://doi.org/10.3390/app15073895
Chicago/Turabian StyleWang, Fengjun, Yupeng Hu, Bisheng Zhang, Yuntao Zha, and Xiaobing Luo. 2025. "Fast Temperature Field Extrapolation Under Non-Periodic Boundary Conditions" Applied Sciences 15, no. 7: 3895. https://doi.org/10.3390/app15073895
APA StyleWang, F., Hu, Y., Zhang, B., Zha, Y., & Luo, X. (2025). Fast Temperature Field Extrapolation Under Non-Periodic Boundary Conditions. Applied Sciences, 15(7), 3895. https://doi.org/10.3390/app15073895





