Three-Dimensional Inversion of the Time-Lapse Resistivity Method on the MPI Parallel Algorithm
Abstract
:1. Introduction
2. Rationale and Theory
2.1. Three-Dimensional Forward Modeling Algorithm
2.2. Time-Lapse Function
2.3. Three-Dimensional Time-Lapse Inversion Objective Function
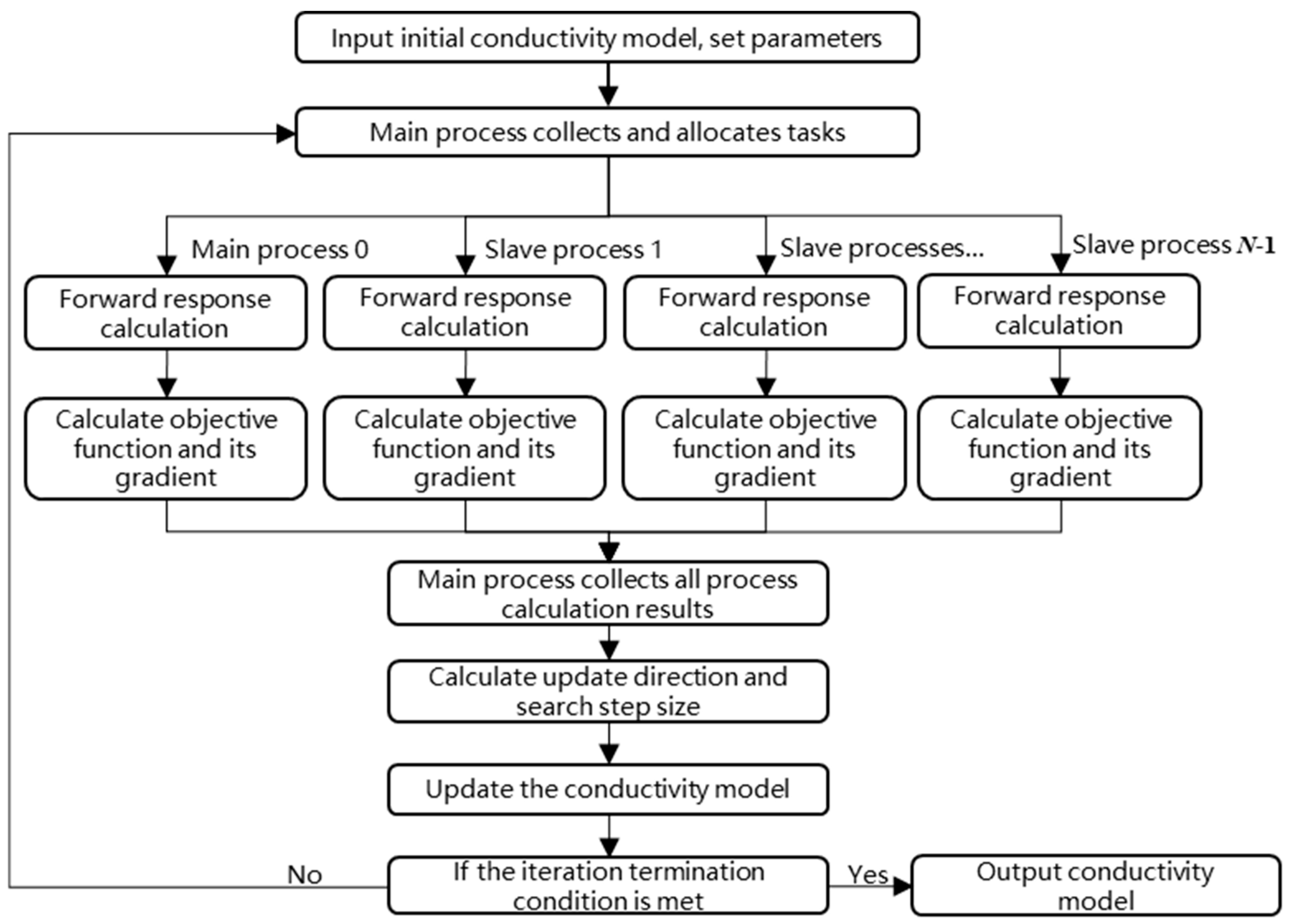
2.4. MPI Parallel Inversion Algorithm
3. Synthetic Example Tests
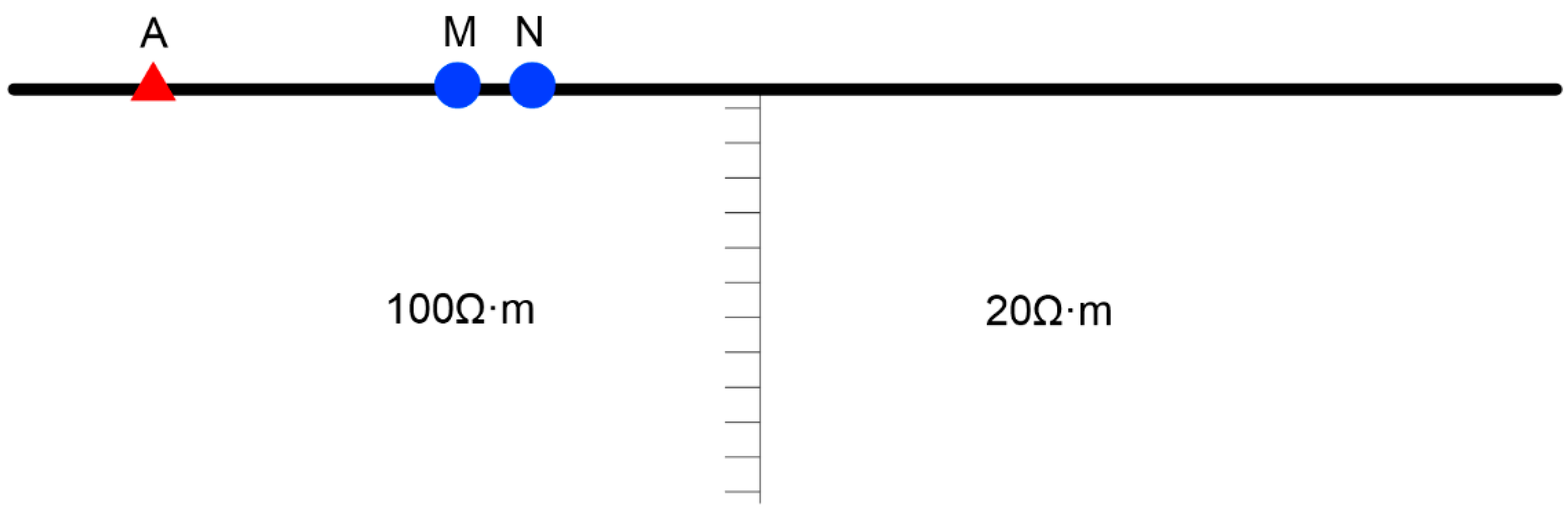
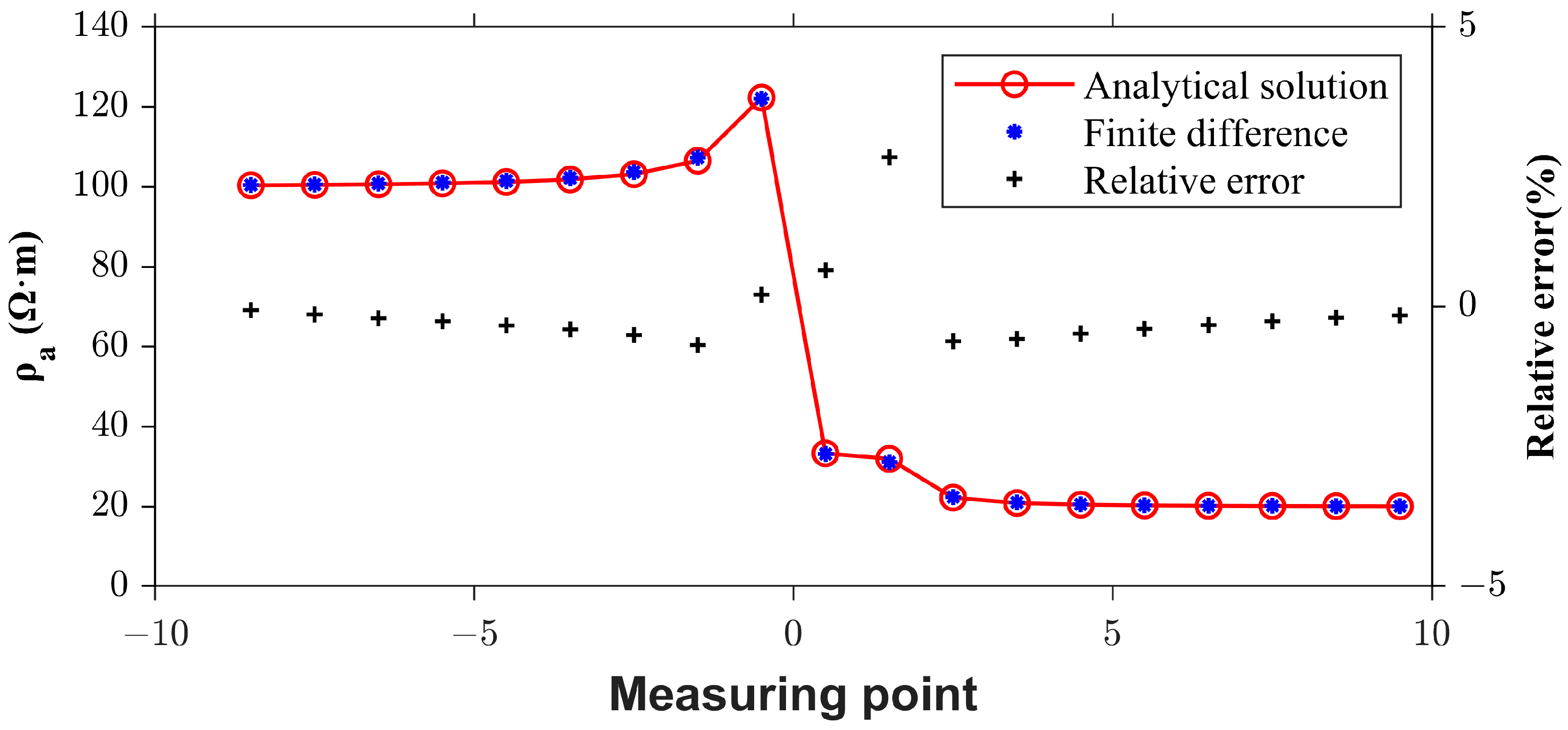
3.1. Theoretical Model and Forward Modeling Response
3.2. MPI Parallel Calculation Efficiency
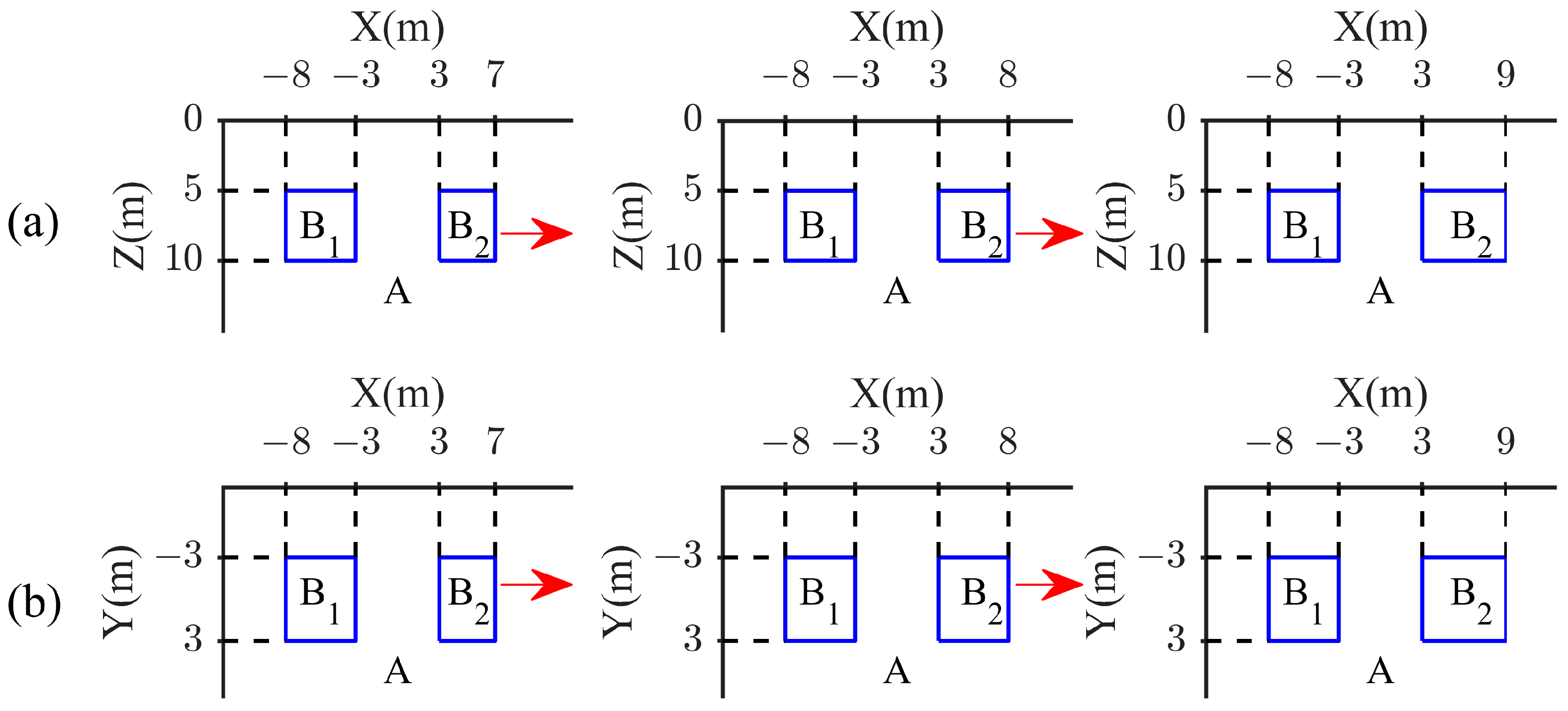
3.3. Analysis of the Inversion Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Attwa, M.; Günther, T.; Grinat, M.; Binot, F. Evaluation of DC, FDEM and IP resistivity methods for imaging perched saltwater and a shallow channel within coastal tidal flat sediments. J. Appl. Geophys. 2011, 75, 656–670. [Google Scholar] [CrossRef]
- López-González, A.E.; Tejero-Andrade, A.; Hernández-Martínez, J.L.; Prado, B. Induced Polarization and Resistivity of Second Potential Differences (SPD) with Focused Sources Applied to Environmental Problems. J. Environ. Eng. Geophys. 2019, 24, 49–61. [Google Scholar] [CrossRef]
- Douglas, Y.; Oldenburg, D. DC resistivity and IP methods in acid mine drainageproblems results from the Copper Cliff mine tailings impoundments. J. Appl. Geophys. 1996, 34, 187–198. [Google Scholar]
- Robinson, J.; Buda, A.; Collick, A.; Shober, A.; Ntarlagiannis, D.; Bryant, R.; Folmar, G.; Andres, S.; Slater, L. Electrical monitoring of saline tracers to reveal subsurface flow pathways in a flat ditch-drained field. J. Hydrol. 2020, 586, 124862. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A.; LaBrecque, D.; Nitao, J. Electrical resistivity tomography of vadose water movement. Water Resour. Res. 1992, 28, 1429–1442. [Google Scholar] [CrossRef]
- Cassiani, G.; Bruno, V.; Villa, A.; Fusi, N.; Binley, A.M. A saline trace test monitored via time-lapse surface electrical resistivity tomography. J. Appl. Geophys. 2006, 59, 244–259. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Yang, X. Difference Inversion of ERT Data:a Fast Inversion Method for 3-D In Situ Monitoring. J. Environ. Eng. Geophys. 2001, 6, 83–89. [Google Scholar] [CrossRef]
- Oldenborger, G.A.; Knoll, M.D.; LaBrecque, D.J. Time-lapse ERT monitoring of an injection/withdrawal experiment in a shallow unconfined aquifer. Geophysics 2007, 72, 177–187. [Google Scholar] [CrossRef]
- Miller, C.R.; Routh, P.S.; Brosten, T.R.; McNamara, J.P. Application of Time-Lapse ERT Imaging to Watershed Characterization. Geophysics 2008, 73, 7–17. [Google Scholar]
- Kim, K.J.; Cho, I.K. Time-lapse inversion of 2D resistivity monitoring data with a spatially varying cross-model constraint. J. Appl. Geophys. 2011, 74, 114–122. [Google Scholar]
- Zhu, D.; Tan, H.; Peng, M.; Wang, T. Three-Dimensional Joint Inversion of the Resistivity Method and Time-Domain-Induced Polarization Based on the Cross-Gradient Constraints. Appl. Sci. 2023, 13, 8145. [Google Scholar] [CrossRef]
- Ma, H.; Guo, Y.; Wu, P.; Tan, H. 3-D joint inversion of multi-array data set in the resistivity method based on MPI parallel algorithm. Chin. J. Geophys. 2018, 61, 5052–5065. [Google Scholar]
- Ma, H. Study of DC and IP 3-D Nonlinear Conjugate Gradients Parallel Inversion Algorithm for the Different Record Layouts Combined Data. Ph.D. Thesis, China University of Geosciences (Beijing), Beijing, China, 2015. [Google Scholar]
- Kim, J.H.; Supper, R.; Tsourlos, P.; Yi, M.J. Four-dimensional inversion of resistivity monitoring data through Lp norm minimizations. Geophys. J. Int. 2013, 195, 1640–1656. [Google Scholar] [CrossRef]
- Loke, M.H.; Dahlin, T.; Rucker, D.F. Smoothness-constrained time-lapse inversion of data from 3D resistivity surveys. Near Surf. Geophys. 2013, 12, 5–24. [Google Scholar]
- Farquharson, C.G.; Oldenburg, D.W. Non-linear inversion using general measures of data misfit and model structure. Geophys. J. Int. 1998, 134, 213–227. [Google Scholar]
- Xu, Y.; Yang, P.; Dong, F. An extended L-curve method for choosing a regularization parameter in electrical resistance tomography. Meas. Sci. Technol. 2016, 27, 114002. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational recipes for electromagnetic inverse problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef]
- Moorkamp, M.; Heincke, B.; Jegen, M.; Roberts, A.W. A framework for 3-D joint inversion of MT, gravity and seismic refraction data. Geophys. J. Int. 2011, 184, 477–493. [Google Scholar]





| Function Name | Functions |
|---|---|
| MPI_INIT | Initializes all MPI programs. |
| MPI_FINALIZE | Finalizes all MPI programs. |
| MPI_COMM_RANK | Returns the identification number for calling a process in a given communication domain, distinguishing different processes from other processes. |
| MPI_COMM_SIZE | Returns the number of included processes in a given communication domain. |
| Function Name | Functions |
|---|---|
| MPI_SEND | Sends the data in the buffer to the destination child process. |
| MPI_RECV | Receives information from the specified process. |
| MPI_BCAST | Sends a message from the main process to all child processes in the group that includes itself. |
| MPI_ ALLGATHER | Make each child process collect data from all other processes. |
| Type of Program | Number of Processes | Running Time /Minutes | Acceleration Ratio |
|---|---|---|---|
| Serial program | 1 | 487.26 | 1 |
| MPI parallel program | 5 | 124.3 | 3.92 |
| 10 | 64.62 | 7.54 | |
| 20 | 36.77 | 12.98 | |
| 30 | 32.46 | 15.04 | |
| 40 | 31.32 | 15.56 |
| Parameter | Model | Separate Inversion | Time-Lapse Inversion |
|---|---|---|---|
| T1 | 6.15 | 5.95 | |
| T2 | 5.41 | 5.48 | |
| T3 | 5.35 | 4.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Yang, Y.; Wen, L. Three-Dimensional Inversion of the Time-Lapse Resistivity Method on the MPI Parallel Algorithm. Appl. Sci. 2025, 15, 3885. https://doi.org/10.3390/app15073885
Zhu D, Yang Y, Wen L. Three-Dimensional Inversion of the Time-Lapse Resistivity Method on the MPI Parallel Algorithm. Applied Sciences. 2025; 15(7):3885. https://doi.org/10.3390/app15073885
Chicago/Turabian StyleZhu, Depeng, Youxing Yang, and Lei Wen. 2025. "Three-Dimensional Inversion of the Time-Lapse Resistivity Method on the MPI Parallel Algorithm" Applied Sciences 15, no. 7: 3885. https://doi.org/10.3390/app15073885
APA StyleZhu, D., Yang, Y., & Wen, L. (2025). Three-Dimensional Inversion of the Time-Lapse Resistivity Method on the MPI Parallel Algorithm. Applied Sciences, 15(7), 3885. https://doi.org/10.3390/app15073885





