Numerical Investigation of Axial Velocity Uniformity in Porous Medium of Gasoline Particulate Filters
Abstract
1. Introduction
2. Physical and Mathematical Model
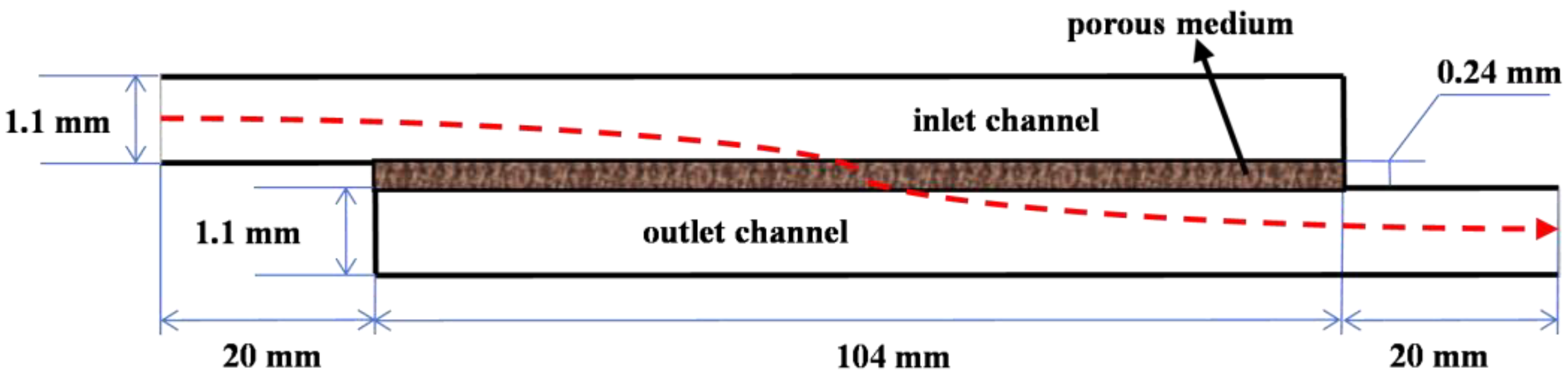
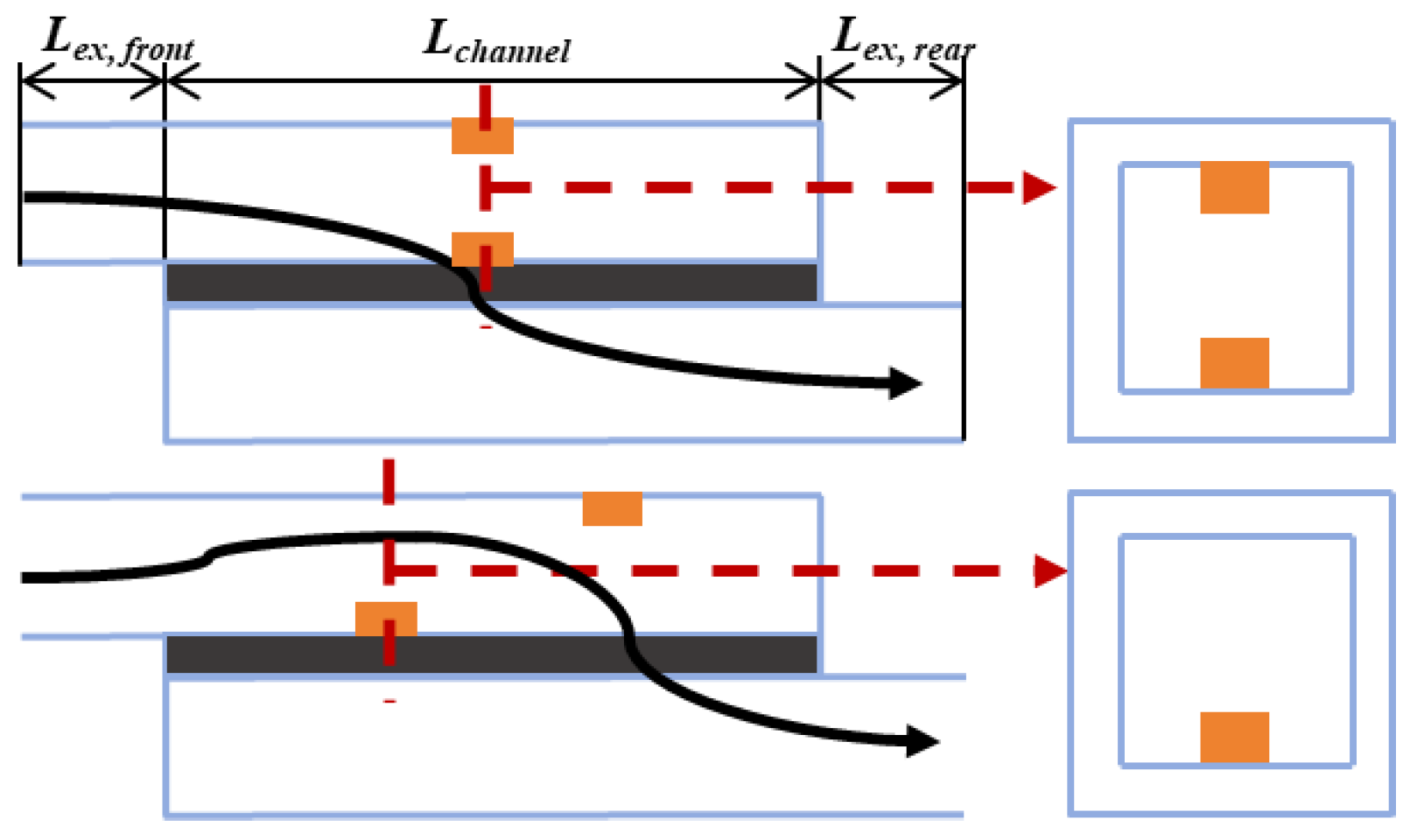
2.1. Channel Model
2.2. Simulation Details
2.2.1. Physical Parameters
2.2.2. Boundary Conditions
3. Results and Discussion
3.1. Feasibility Analysis of the Model
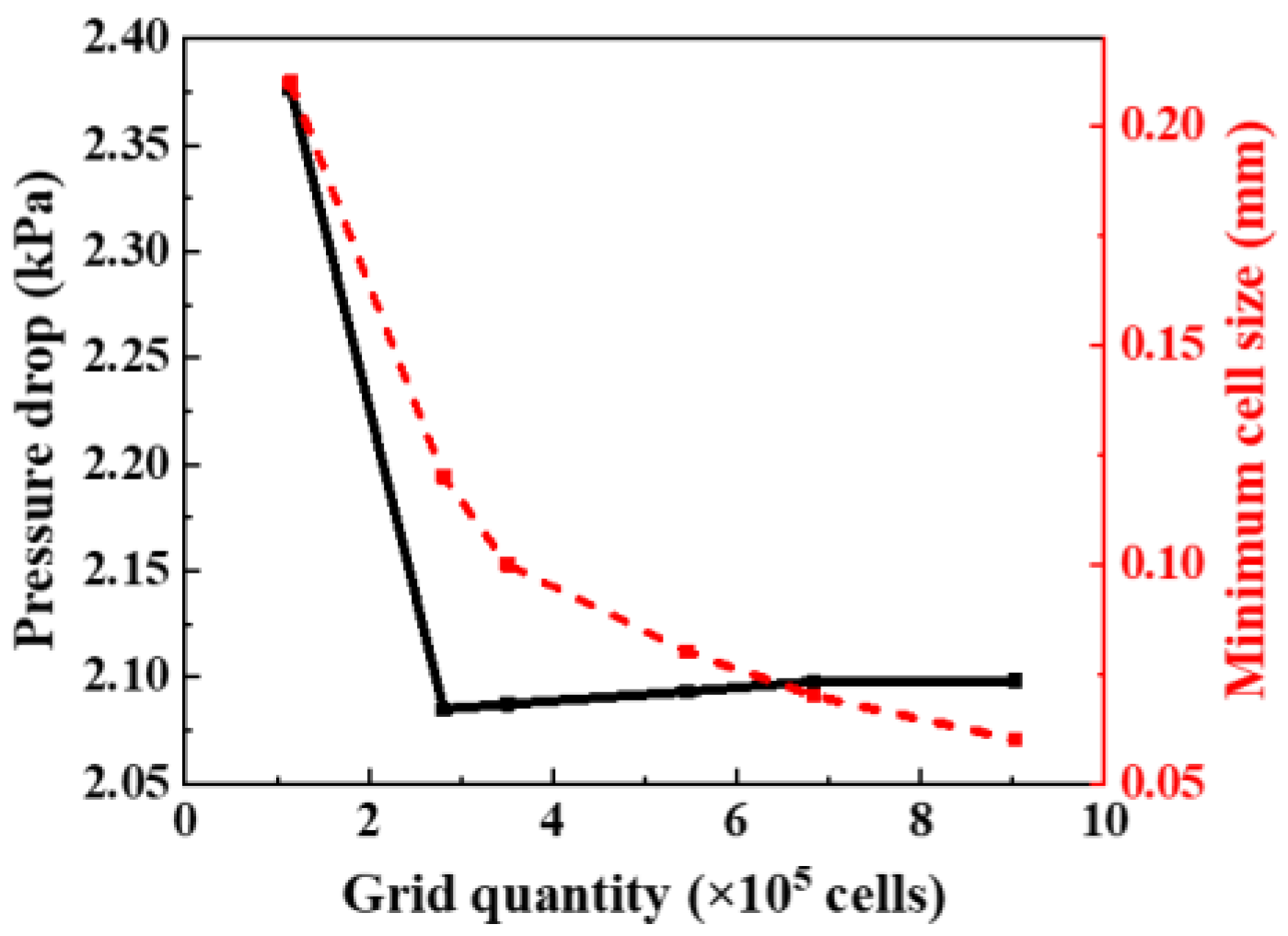
3.1.1. Analysis of Grid Independence
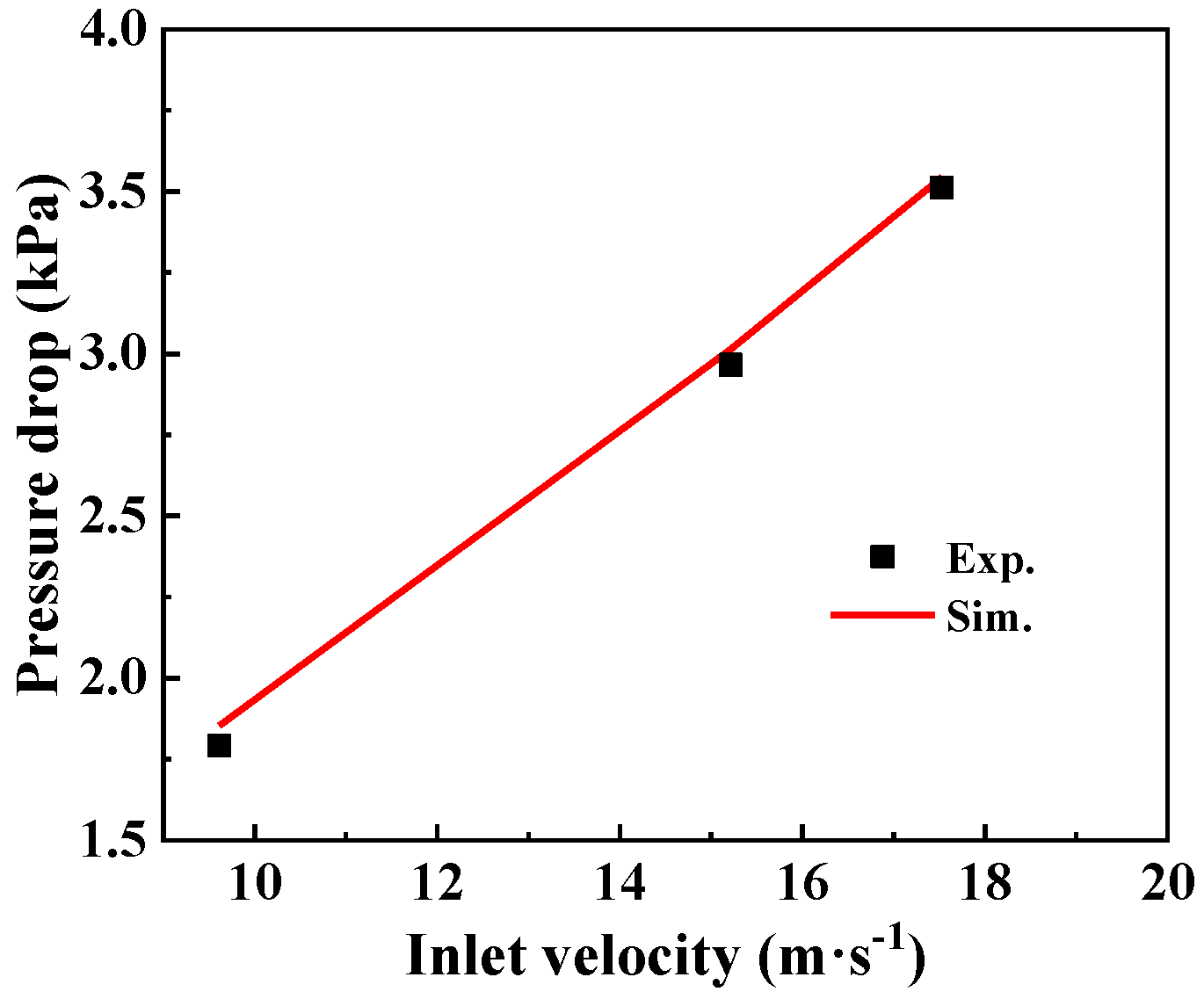
3.1.2. Model Validation
3.2. Zoned Washcoat
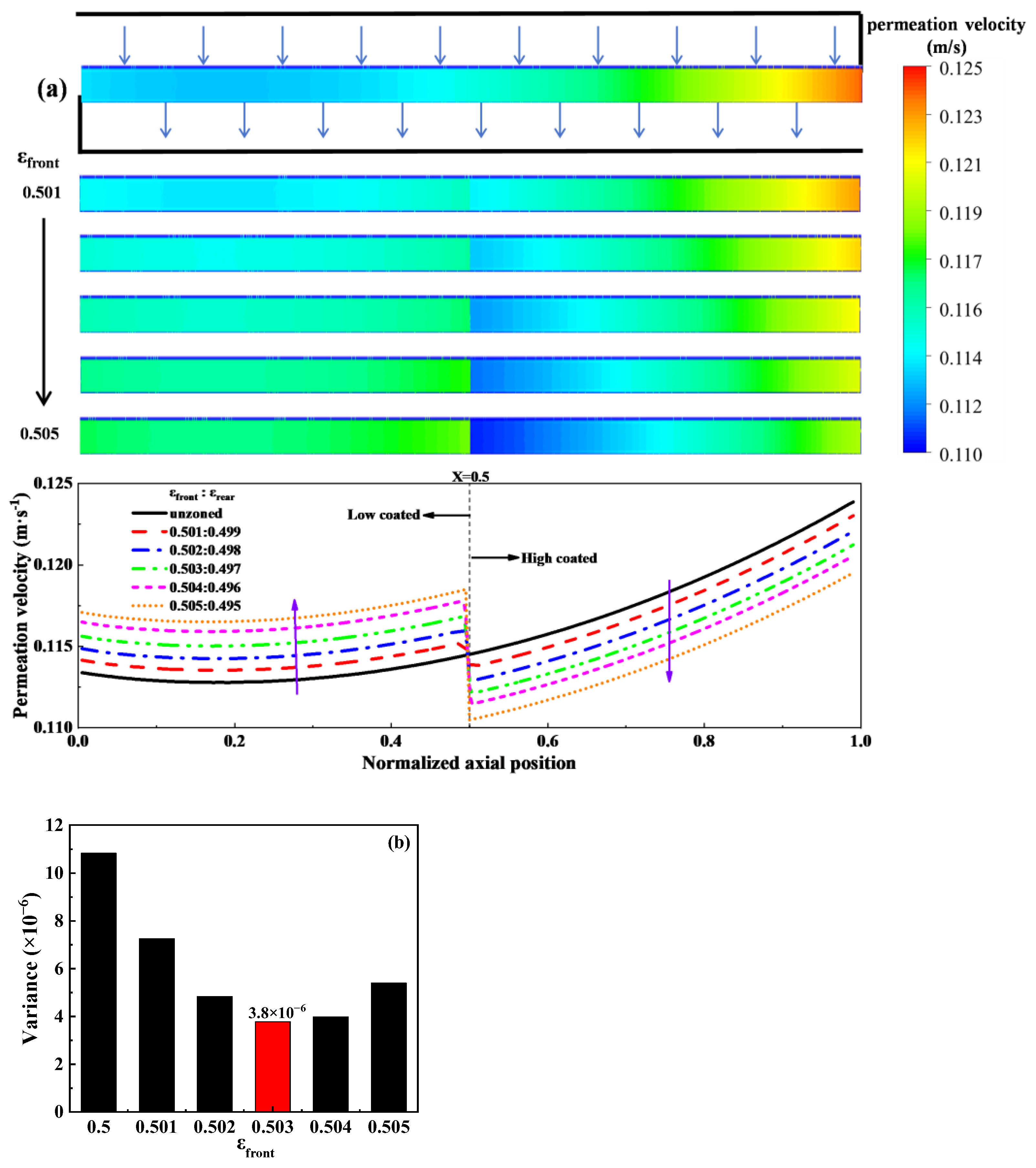
3.2.1. Average Partition
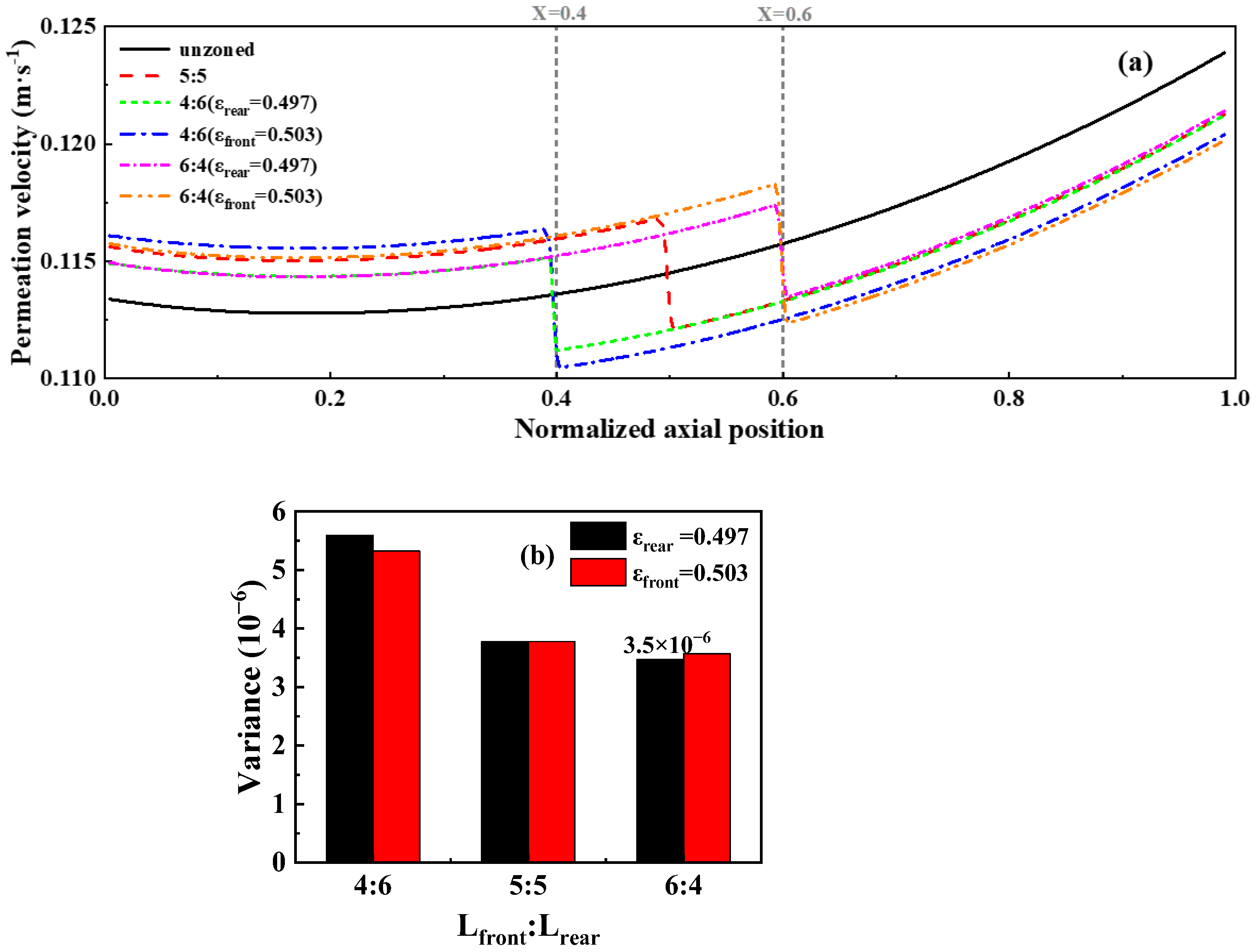
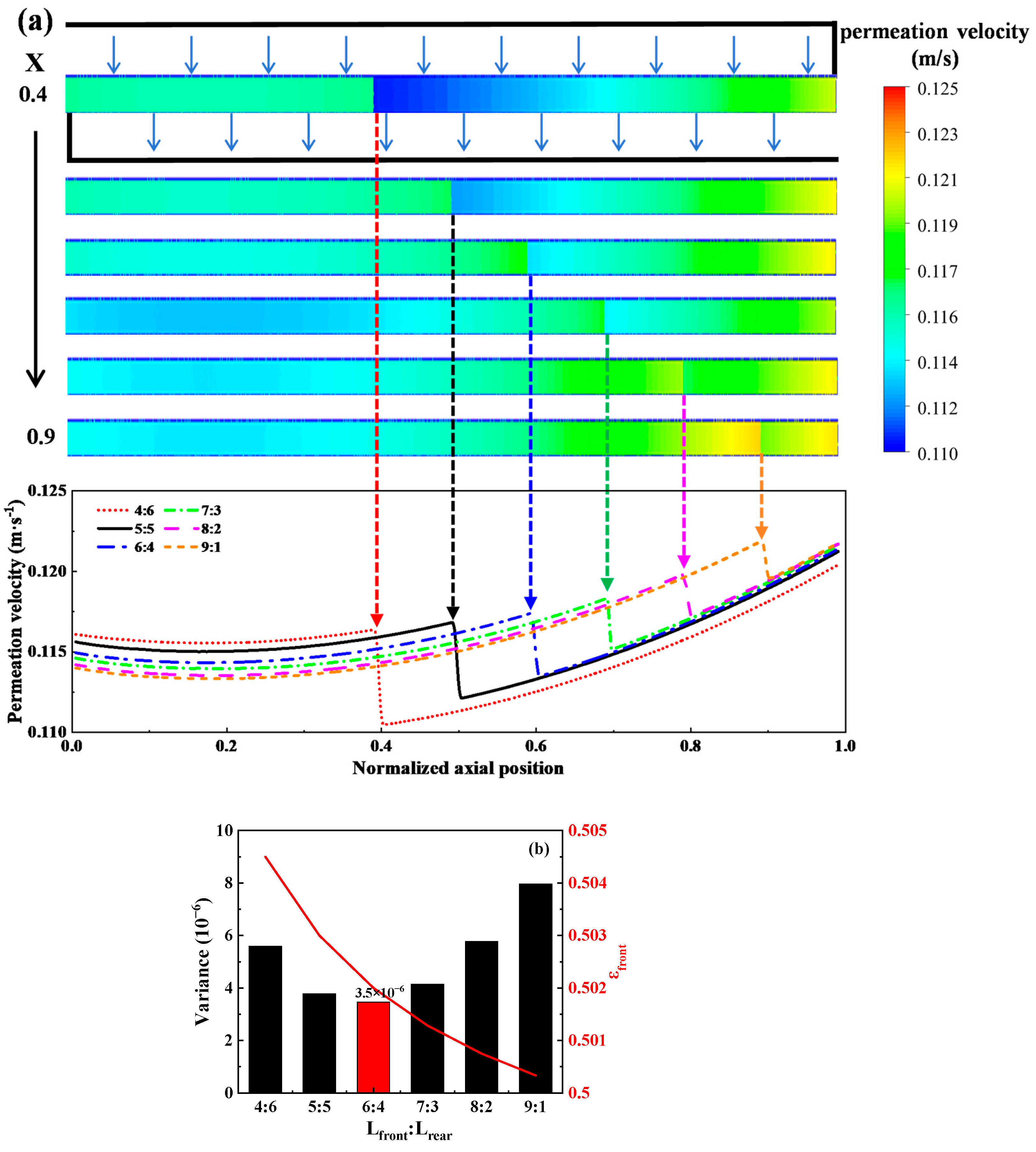
3.2.2. Different Length Proportion and Porosity Configuration
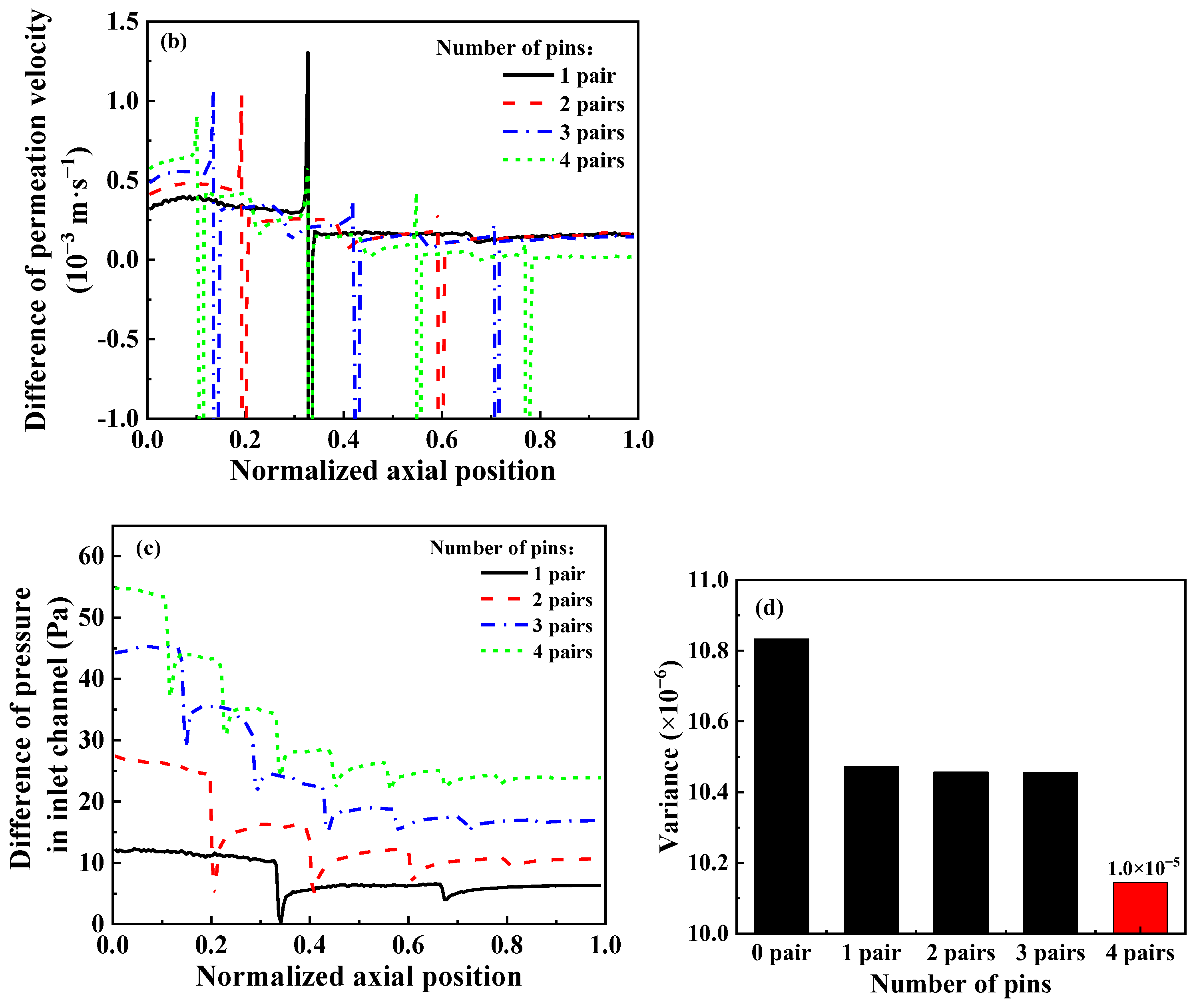
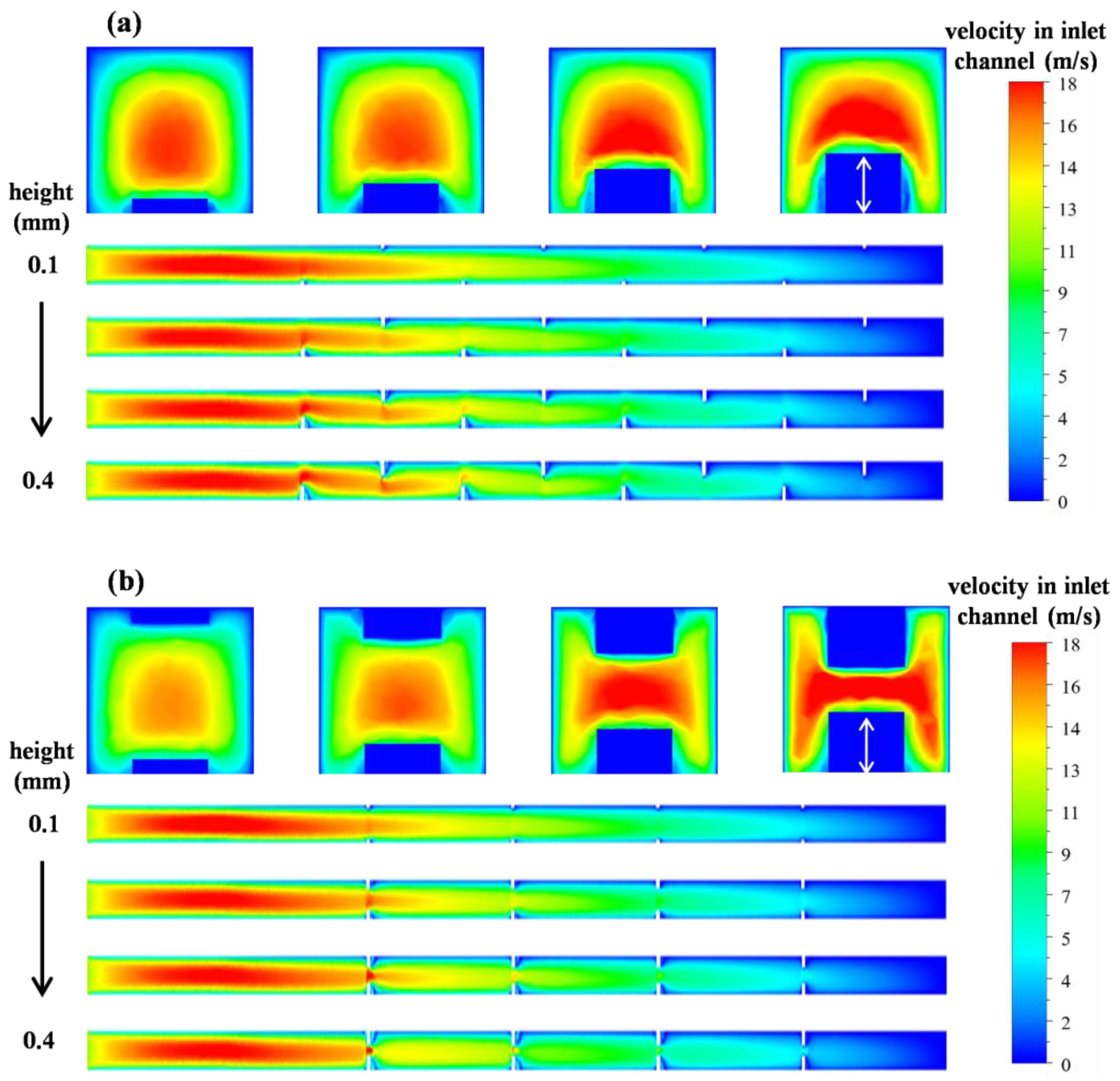
3.3. Pins in Inlet Channel
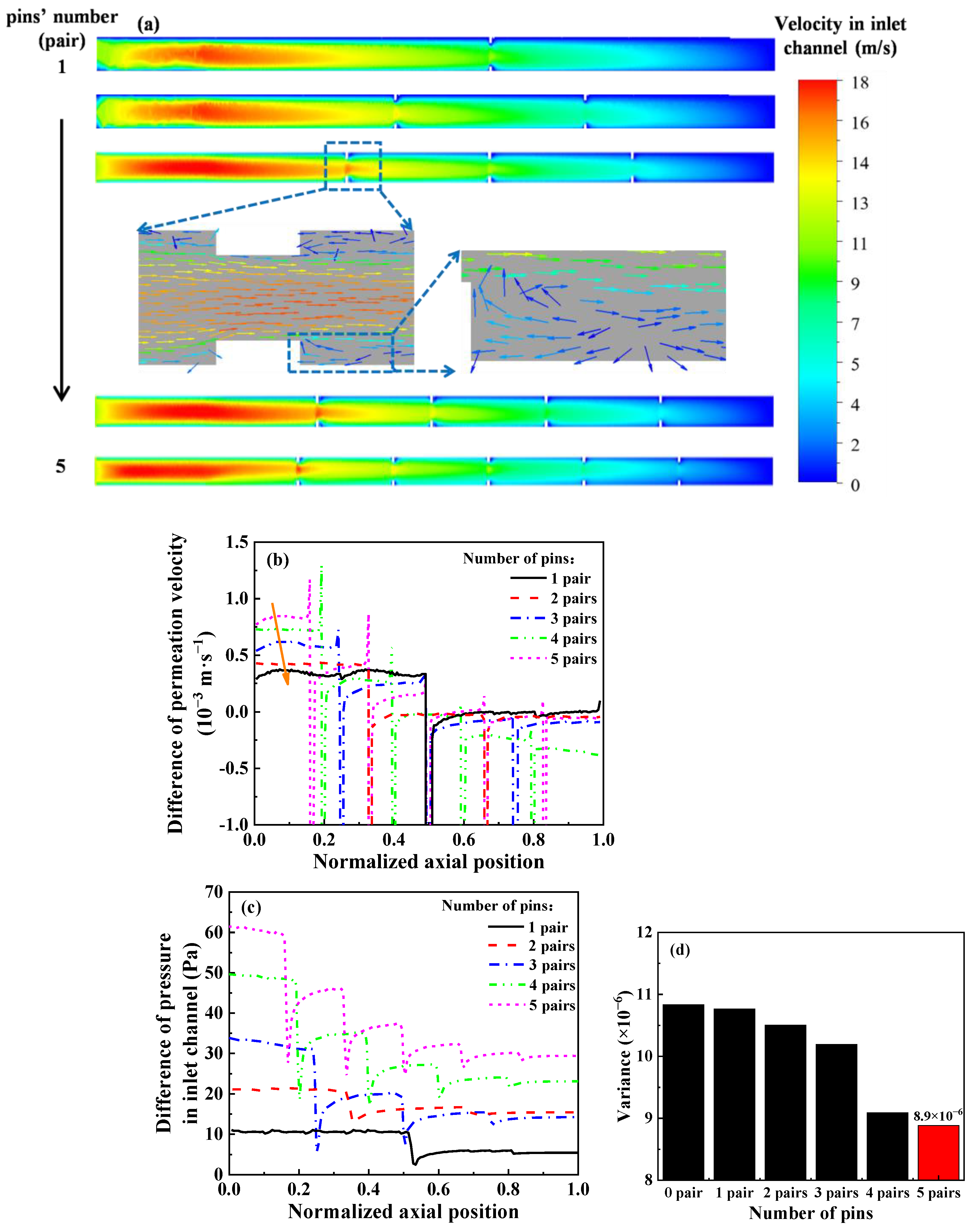
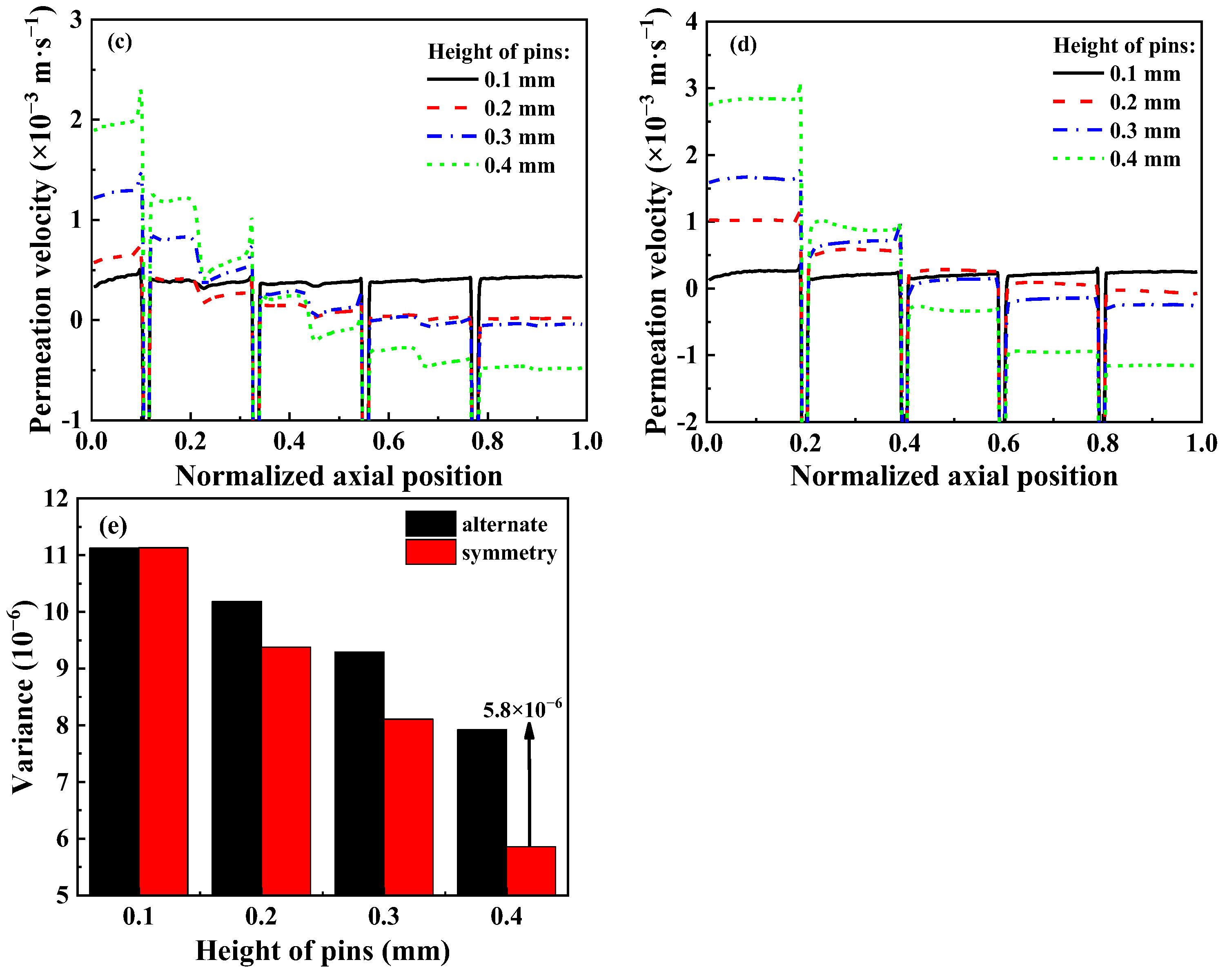
3.3.1. Symmetrical Arrangement
3.3.2. Alternate Arrangement
3.3.3. Different Height
3.4. Combination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation | |
| GPF | gasoline particulate filter |
| Symbols | |
| fluid density | |
| time | |
| velocity components in the x, y, and z directions | |
| P | pressure |
| viscosity | |
| magnitude of the velocity | |
| L | length |
| momentum source term | |
| vw | wall velocity |
| Subscripts | |
| front | porous medium’s low coated parts |
| rear | porous medium’s high coated parts |
| ave | average |
References
- Yanzhao, A. Experimental and Numerical Studies on the Soot Particle Formation Mechanism in the Gasoline Direct Injection Engine D. Ph.D. Thesis, Tianjin University, Tianjin, China, 2016. [Google Scholar]
- Pope Iii, C.A.; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung Cancer, Cardiopulmonary Mortality, and Long-Term Exposure to Fine Particulate Air Pollution. J. Am. Med. Assoc. 2002, 287, 1132–1141. [Google Scholar] [CrossRef]
- Gong, J.; Rutland, C. A Quasi-Dimensional NOx Emission Model for Spark Ignition Direct Injection (SIDI) Gasoline Engines; SAE: Melbourne, Australia, 2013. [Google Scholar]
- Zhang, J.; Wong, V.W.; Shuai, S.; Chen, Y.; Sappok, A. Quantitative Estimation of the Impact of Ash Accumulation on Diesel Particulate Filter Related Fuel Penalty for a Typical Modern on-Road Heavy-Duty Diesel Engine. Appl. Energy 2018, 229, 1010–1023. [Google Scholar] [CrossRef]
- Nakamura, K.; Sugaya, Y.; Yamaguchi, K.; Kusaka, J.; Arndt, M.; Dardiotis, C. Characterization of Soot Loading and Filtration Efficiency of a Gasoline Particulate Filter with Photoacoustic Sensor and Particle Number Counting Systems. Atmosphere 2023, 14, 476. [Google Scholar] [CrossRef]
- Johnson, T. Vehicular Emissions in Review. SAE Int. J. Engines 2016, 9, 1258–1275. [Google Scholar] [CrossRef]
- Park, G.; Park, S.; Hwang, T.; Oh, S.; Lee, S. A Study on the Impact of DPF Failure on Diesel Vehicles Emissions of Particulate Matter. Appl. Sci. 2023, 13, 7592. [Google Scholar] [CrossRef]
- Cho, I.; Moon, I.; Kim, D.; Park, T.; Lee, D.; Lee, J. Experimental Investigation on OBD Signal and PN Emission Characteristics by Damaged-DPF Types of 2.0 L Diesel Vehicle. Appl. Sci. 2022, 12, 7853. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A. Using CFD Simulation as a Tool to Identify Optimal Operating Conditions for Regeneration of a Catalytic Diesel Particulate Filter. Appl. Sci. 2019, 9, 3453. [Google Scholar] [CrossRef]
- Richter, J.M.; Klingmann, R.; Spiess, S.; Wong, K.-F. Application of Catalyzed Gasoline Particulate Filters to GDI Vehicles. SAE Int. J. Engines 2012, 5, 1361–1370. [Google Scholar] [CrossRef]
- Prikhodko, V.Y.; Curran, S.J.; Barone, T.L.; Lewis, S.A.; Storey, J.M.; Cho, K.; Wagner, R.M.; Parks, J.E. Emission Characteristics of a Diesel Engine Operating with In-Cylinder Gasoline and Diesel Fuel Blending. SAE Int. J. Fuels Lubr. 2010, 3, 946–955. [Google Scholar] [CrossRef]
- Sirignano, M.; D’Anna, A. Filtration and Coagulation Efficiency of Sub-10 nm Combustion-Generated Particles. Fuel 2018, 221, 298–302. [Google Scholar] [CrossRef]
- Yu, M.; Luss, D.; Balakotaiah, V. Regeneration modes and peak temperatures in a diesel particulate filter. Chem. Eng. J. 2013, 232, 541–554. [Google Scholar] [CrossRef]
- Mamakos, A.; Steininger, N.; Martini, G.; Dilara, P.; Drossinos, Y. Cost Effectiveness of Particulate Filter Installation on Direct Injection Gasoline Vehicles. Atmos. Environ. 2013, 77, 16–23. [Google Scholar] [CrossRef]
- Gong, J.; Stewart, M.L.; Zelenyuk, A.; Strzelec, A.; Viswanathan, S.; Rothamer, D.A.; Foster, D.E.; Rutland, C.J. Importance of Filter’s Microstructure in Dynamic Filtration Modeling of Gasoline Particulate Filters (GPFs): Inhomogeneous Porosity and Pore size Distribution. Chem. Eng. J. 2018, 338, 15–26. [Google Scholar] [CrossRef]
- Chan, T.W.; Meloche, E.; Kubsh, J.; Rosenblatt, D.; Brezny, R.; Rideout, G. Evaluation of a Gasoline Particulate Filter to Reduce Particle Emissions from a Gasoline Direct Injection Vehicle. SAE Int. J. Fuels Lubr. 2012, 5, 1277–1290. [Google Scholar] [CrossRef]
- Lambert, C.; Chanko, T.; Dobson, D.; Liu, X.; Pakko, J. Gasoline Particle Filter Development. Emiss. Control Sci. Technol. 2017, 3, 105–111. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z.; Zhang, M.; Xu, H.; Ma, X.; Shuai, S. Exhaust Non-Volatile Particle Filtration Characteristics of Three-Way Catalyst and Influencing Factors in a Gasoline Direct Injection Engine Compared to Gasoline Particulate Filter. Fuel 2021, 290, 120065. [Google Scholar] [CrossRef]
- Jang, J.; Lee, J.; Choi, Y.; Park, S. Reduction of Particle Emissions from Gasoline Vehicles with Direct Fuel Injection Systems Using a Gasoline Particulate Filter. Sci. Total Environ. 2018, 644, 1418–1428. [Google Scholar] [CrossRef]
- Gong, J.; Viswanathan, S.; Rothamer, D.A.; Foster, D.E.; Rutland, C.J. Dynamic Heterogeneous Multiscale Filtration Model: Probing Micro- and Macroscopic Filtration Characteristics of Gasoline Particulate Filters. Environ. Sci. Technol. 2017, 51, 11196–11204. [Google Scholar] [CrossRef]
- Gong, J.; Rutland, C.J. PDF-Based Heterogeneous Multiscale Filtration Model. Environ. Sci. Technol. 2015, 49, 4963–4970. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.; Rutland, C.J. Filtration Characteristics of Fuel Neutral Particulates Using a Heterogeneous Multiscale Filtration Model. J. Eng. Gas Turbines Power 2015, 137, 111507. [Google Scholar] [CrossRef]
- Viswanathan, S.; Rothamer, D.; Sakai, S.; Hageman, M.; Foster, D.; Fansler, T.; Andrie, M. Effect of Particle Size Distribution on the Deep-Bed Capture Efficiency of an Exhaust Particulate Filter. J. Eng. Gas Turbines Power 2015, 137, 101504. [Google Scholar] [CrossRef]
- Cooper, J.D.; Liu, L.; Ramskill, N.P.; Watling, T.C.; York, A.P.E.; Stitt, E.H.; Sederman, A.J.; Gladden, L.F. Numerical and Experimental Studies of Gas Flow in a Particulate Filter. Chem. Eng. Sci. 2019, 209, 115179. [Google Scholar] [CrossRef]
- Kong, X.; Li, Z.; Shen, B.; Wu, Y.; Zhang, Y.; Cai, D. Simulation of Flow and Soot Particle Distribution in Wall-Flow DPF Based on Lattice Boltzmann Method. Chem. Eng. Sci. 2019, 202, 169–185. [Google Scholar] [CrossRef]
- Zou, J.; Chen, X.; Song, B.; Cui, Y. Bionic Spider Web Flexible Strain Sensor Based on CF-L and Machine Learning. ACS Appl. Mater. Interfaces 2024, 16, 23761–23770. [Google Scholar] [CrossRef] [PubMed]
- Onori, S.; Korneev, S. Modeling the Flow and Transport Dynamics in Gasoline Particulate Filters to Improve Filtration Efficiency. J. Dyn. Syst. Meas. Control 2020, 142, 061006. [Google Scholar] [CrossRef]
- Walter, R.; Neumann, J.; Hinrichsen, O. A Model-Based Analysis of Washcoat Distribution on Zoned Coated Gasoline Particulate Filters. Chem. Eng. J. 2022, 441, 135615. [Google Scholar] [CrossRef]
- Thorsten Boger, W.C. Reducing Particulate Emissions in Gasoline Engines; SAE: Melbourne, Australia, 2018. [Google Scholar]
- Yang, S.; Liu, K.-b.; Yi, S.; Ye, S.; Li, J.; Yuan, H.; Zhao, G.; Pei, S.; He, L.; Ding, X.; et al. Distribution and Provenance of Modern Pollen and Spores in the Surface Sediments of Liaodong Bay, China. Mar. Geol. 2016, 376, 1–14. [Google Scholar] [CrossRef]
- Bissett, E.J. Mathematical Model of the Thermal Regeneration of a Wall-Flow Monolith Diesel Particulate Filter. Chem. Eng. Sci. 1984, 39, 1233–1244. [Google Scholar] [CrossRef]
- Gomez-Flores, A.; Hwang, G.; Ilyas, S.; Kim, H. A CFD study of the transport and fate of airborne droplets in a ventilated office: The role of droplet-droplet interactions. Front. Environ. Sci. Eng. 2021, 16, 31. [Google Scholar] [CrossRef]
- Peters, B.J. Numerical Simulation of a Diesel Particulate Filter during Loading and Regeneration. In Proceedings of the ASME 2003 Internal Combustion Engine Division Spring Technical Conference, Salzburg, Austria, 11–14 May 2003. [Google Scholar]
- Xiao, G.; Li, B.; Tian, H.; Leng, X.; Long, W. Numerical Study on Flow and Pressure Drop Characteristics of a Novel Type Asymmetric Wall-Flow Diesel Particulate Filter. Fuel 2020, 267, 117148. [Google Scholar] [CrossRef]
- Zhang, X.; William Ruona, P.T. 3D Numerical Study of Pressure Loss Characteristics and Filtration Efficiency through a Frontal Unplugged DPF. SAE Int. J. Fuels Lubr. 2010, 3, 177–193. [Google Scholar]
- Li, Y. GPF Capture and Regeneration Characteristics of GDI Engine under Typical Working Conditions. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Wang, X.; Deng, Y.; Yan, T.; Liu, Y. Numerical Investigation on the Progressive Evolution of Regeneration Pattern with Feed Temperature in a Wall-Flow-Catalyzed Diesel Particulate Filter. Ind. Eng. Chem. Res. 2022, 61, 10736–10746. [Google Scholar] [CrossRef]
- Chiavola, O.; Chiatti, G.; Sirhan, N. Impact of Particulate Size During Deep Loading on DPF Management. Appl. Sci. 2019, 9, 3075. [Google Scholar] [CrossRef]
- Özşimşek, A.O.; Omar, M.A. A numerical study on the effect of employing porous medium on thermal performance of a PV/T system. Renew. Energy 2024, 226, 120327. [Google Scholar] [CrossRef]
- Jahangir, S.; Hogendoorn, W.; Poelma, C. Dynamics of Partial Cavitation in an Axisymmetric Converging-Diverging Nozzle. Int. J. Multiph. Flow. 2018, 106, 34–45. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Y.; Su, C.; Srinivasan, A.; Gong, J.; Kamp, C.J. Performance of Asymmetric Particulate Filter with Soot and Ash Deposits: Analytical Solution and Its Application. Ind. Eng. Chem. Res. 2018, 57, 15846–15856. [Google Scholar] [CrossRef]
- Opitz, B.; Votsmeier, M. A Simulation Study on the Conversion Efficiency of Catalytically Active Particulate Filters. Chem. Eng. Sci. 2016, 149, 117–128. [Google Scholar] [CrossRef]
- Zuo, Q.; Xie, Y.; Zhu, G.; Wei, K.; Zhang, B.; Chen, W.; Tang, Y.; Wang, Z. Investigations on a New C-GPFs with Electric Heating for Enhancing the Integrated Regeneration Performance under Critical Parameters. Energy 2021, 225, 120265. [Google Scholar] [CrossRef]
- Belot, I.; Vidal, D.; Votsmeier, M.; Hayes, R.E.; Bertrand, F. Numerical Investigation of the Impact of Washcoat Distribution on the Filtration Performance of Gasoline Particulate Filters. Chem. Eng. Sci. 2020, 221, 115656. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A. Modeling and Simulation of Soot Combustion Dynamics in a Catalytic Diesel Particulate Filter. Chem. Eng. Sci. 2015, 137, 69–78. [Google Scholar] [CrossRef]
- Boger, T.; Cutler, W. Reducing Particulate Emission in Gasoline Engines; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Bres, G.A.; Ham, F.E.; Nichols, J.W.; Lele, S.K. Unstructured Large-Eddy Simulations of Supersonic Jets. AIAA J. 2017, 55, 1164–1184. [Google Scholar]
- Kai, C. Numerical Investigation on Heat Transfer Performance and Flow Behavior of Special-Shaped Pipe. Master’s Thesis, Tianjin University, Tianjin, China, 2006. [Google Scholar]
- Bensaid, S.; Marchisio, D.L.; Fino, D.; Saracco, G.; Specchia, V. Modelling of Diesel Particulate Filtration in Wall-Flow Traps. Chem. Eng. J. 2009, 154, 211–218. [Google Scholar] [CrossRef]


| Initial Parameters | Number |
|---|---|
| Inlet velocity (m·s−1) | 11 |
| Outlet pressure | Atmospheric pressure |
| Porosity | 0.5 |
| Viscous resistance (m−2) | 6.5 × 1012 |
| Inertial resistance (m−1) | 2 × 108 |
| Exhaust density (kg·m−3) | 1 |
| Dynamic viscosity (Pa·s) | 2.9 × 10⁻⁵ |
| Re | 417 |
| Parameters | Value |
|---|---|
| Diameter (mm) | 330.2 |
| Length (mm) | 177.8 |
| Thickness (mm) | 0.31 |
| Inlet volume flow rate (m3·s−1) | 0.2–0.8 |
| Cell density (cpsi) | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Zhang, F.; Pei, Y. Numerical Investigation of Axial Velocity Uniformity in Porous Medium of Gasoline Particulate Filters. Appl. Sci. 2025, 15, 3854. https://doi.org/10.3390/app15073854
Hu Y, Zhang F, Pei Y. Numerical Investigation of Axial Velocity Uniformity in Porous Medium of Gasoline Particulate Filters. Applied Sciences. 2025; 15(7):3854. https://doi.org/10.3390/app15073854
Chicago/Turabian StyleHu, Yuxin, Fan Zhang, and Yiqiang Pei. 2025. "Numerical Investigation of Axial Velocity Uniformity in Porous Medium of Gasoline Particulate Filters" Applied Sciences 15, no. 7: 3854. https://doi.org/10.3390/app15073854
APA StyleHu, Y., Zhang, F., & Pei, Y. (2025). Numerical Investigation of Axial Velocity Uniformity in Porous Medium of Gasoline Particulate Filters. Applied Sciences, 15(7), 3854. https://doi.org/10.3390/app15073854







