Abstract
The particle filter (PF) algorithm has found widespread application in navigation multipath estimation. However, it exhibits significant limitations in complex multipath environments. Its state prediction relies heavily on particle distribution and is prone to particle degeneracy, where the weights of most particles approach zero, and only a few particles contribute significantly to state estimation. These issues result in an inadequate number of effective samples, degrading multipath estimation performance. Therefore, a navigation multipath estimation method based on an EKF-GAPF (Extended Kalman Filter–Genetic Algorithm Particle Filter) algorithm is proposed in this paper. This method utilizes the EKF to calculate the mean and covariance of samples using the latest observation information, providing a more reasonable proposal density for particle filtering and enhancing the accuracy of state prediction. Simultaneously, by introducing the crossover and mutation mechanisms of the adaptive genetic algorithm, particles are continuously evolved during the resampling process, preventing them from falling into local extrema. Experimental results show that EKF-GAPF outperforms EKF, EPF, and PF in amplitude and delay estimation. Under the condition of random initial values, the multipath signal amplitude estimation error converges to 0.002, and the multipath signal time delay estimation error converges to 0.006 (approximately 1.8 m). This method enables high-precision parameter estimation for both direct and multipath signals.
1. Introduction
Multipath interference is a primary source of positioning errors in satellite navigation systems [1,2]. This phenomenon occurs when a satellite signal is reflected by the ground or obstacles during propagation, resulting in multiple signal paths reaching the receiver. These reflected signals cause delays, attenuation, and distortion, which degrade the receiver’s signal acquisition and tracking performance. Consequently, the accuracy of positioning and timing for the user is significantly compromised. The positioning error caused by multipath signals can be as high as hundreds of meters [3]. In severe cases, it may cause the receiver to lose lock on the satellite signal and be unable to complete the positioning function. With the increasing demand for new applications of the Global Navigation Satellite System (GNSS) in complex environments such as urban canyons [4], and the heavy reliance on the pseudo-code phase in the implementation of the Low Orbit Navigation Satellite Networking Program pseudo-code [5,6], the study of efficient mitigation technology for multipath errors in navigation signals is particularly important and has become a research hotspot in the field of navigation signal processing [7]. Approaches for mitigating multipath signals can be classified into three categories: measurement-domain processing techniques [8,9], hardware-based design methods [10,11], and baseband signal processing techniques [12,13]. Measurement-domain processing techniques usually rely on external support or require long-term static observations, limiting their applicability in dynamic environments. Hardware-based methods are constrained by equipment design and cost considerations. In contrast, baseband signal processing techniques have emerged as the most widely adopted approach due to their flexibility and practical implementation potential.
Data processing-based methods enable more accurate estimation of multipath parameters by extracting and analyzing signal features. Liu et al. [12] employed the particle filter (PF) to track the evolution parameters of both the direct signal and its multipath signal. However, its calibration accuracy and efficiency are influenced by the a priori distribution of the initial values [13]. Qin et al. [14] proposed a resampling strategy to mitigate particle degradation and missing issues, resulting in higher multipath estimation accuracy compared to conventional methods such as the adaptive multipath estimating delay lock loop (MEDLL) and the Teager–Kaiser–MEDLL approaches. Wang et al. [15] introduced an adaptive difference evolution-based particle filtering algorithm, which can improve accuracy, but requires more priori information than other multipath parameter estimation algorithms. Similarly, the Genetic Algorithm Particle Filter (GAPF) algorithm proposed in [16] integrates genetic algorithm (GA) into the PF framework to address pseudo-code correlation function distortions. However, the GAPF algorithm suffers from premature convergence and only estimates the time delay, and the amplitude of the multipath signal still needs to be estimated separately through Kalman Filtering (KF). Jee et al. [17] and Siebert et al. [18] proposed multipath estimation methods based on the Extended Kalman Filter (EKF), effectively reducing the influence of multipath signals on localization error using multiple correlator structures. Meanwhile, Mu et al. [19] employed the Least Squares (LS) method to correct EKF observation points, achieving higher pseudo-code tracking accuracy. However, both LS and EKF rely on linearization to handle nonlinear systems, which may introduce linearization errors and consequently reduce estimation accuracy. To address the sensitivity of the EKF algorithm to initial values, Lai et al. [20] combined PF and EKF, but the constructed estimation exhibits obvious fluctuations. Subsequently, Zhang et al. [21] introduced the adaptive maximum correlation entropy Unscented Kalman Filter algorithm, which improved localization accuracy by incorporating the maximum correlation entropy criterion and recursively updating the noise covariance. However, its high computational complexity imposes significant challenges for real-time applications.
To address the issue of particle degradation in PF and the limitations of EKF in handling highly nonlinear distributions, a novel algorithm called EKF-GAPF (Extended Kalman Filter–Genetic Algorithm Particle Filter) is proposed in this paper, which integrates EKF, PF, and the adaptive genetic algorithm (AGA). First, to enhance the accuracy of state prediction and estimation, the state prediction and updating mechanism of EKF is utilized to provide more accurate state estimation and transfer models for particles in PF, which combines the local linearization capability of EKF and the nonparametric advantages of PF. Second, to mitigate the issue of particle degradation, AGA is introduced to improve the importance sampling process. By dynamically adjusting the importance weights and state update strategies of particles, the global search capabilities of EKF-GAPF are enhanced and the possibility of particles falling into local optima is reduced.
2. Signal Model
The multipath suppression algorithm aims to improve signal quality and reduce the impact of multipath effects on signal transmission. The core idea is to analyze the IF data received by the receiver, apply suitable algorithms to estimate the parameters of the multipath signals, identify and suppress the interference caused by different propagation paths, and ultimately enhance the accuracy of signal synchronization. When multipath signals exist, the signal received by the GNSS receiver can be modeled as follows [22]:
where a0 and ai are the amplitudes of the direct signal and the multipath signal, respectively, c(t) is the pseudo-code sequence, w is the carrier angular frequency, M is the number of multipath routes, and and are the code delays of the direct signal and the multipath signal, respectively. Additionally, and represent the carrier phases, n(t) is Gaussian white noise, and the navigation message is ignored. Due to the loss of power caused by signal reflection, the amplitude of the multipath signal is weaker than that of the direct signal, i.e., a0 > ai. Furthermore, the transmission delay of the multipath signal is longer, denoted as [23].
Assuming the received signal contains only one direct signal and one in-phase multipath signal, the correlation peaks of the direct and multipath signals overlap due to the receiver’s inability to distinguish between the direct signal and the reflected signal, leading to a distortion in the shape of the autocorrelation function [24]. As shown in Figure 1, the reflected signal has an amplitude of 0.5 and a delay of 0.4, causing the correlation function curve of the received signal to lose symmetry about the center. This distortion results in the code loop locking to the incorrect phase during subsequent code tracking, which introduces errors in the pseudo-code discriminator.
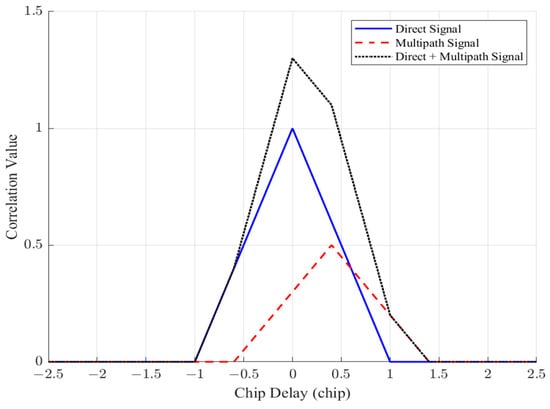
Figure 1.
Effect of multipath signals on correlation results.
Multipath interference affects both the carrier tracking loop and the code tracking loop. The impact of multipath on the carrier tracking loop is relatively small, typically within a few centimeters, and can generally be ignored. However, the effect of pseudo-code tracking errors on receiver positioning is more significant. Since each GPS C/A code consists of 1023 chips, with a code rate of 1.023 MHz and a chip duration of slightly less than 1 microsecond (approximately 300 m) [25], severe multipath interference can cause substantial errors in the code tracking loop’s estimation. This can result in positioning errors of several hundred meters. Figure 2 illustrates the relationship between the receiver’s pseudo-code phase tracking error and the multipath parameters [26].
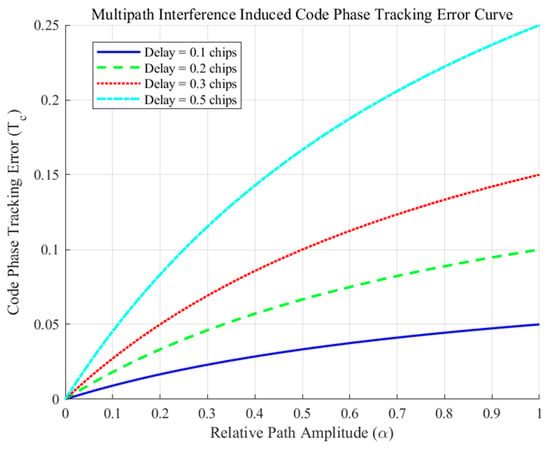
Figure 2.
Code phase tracking error curves due to multipath interference.
After digitizing the received signal and performing correlation with the local pseudo--code generator, the output of the j-th correlator can be expressed as follows:
where C represents the autocorrelation function of the current satellite’s C/A code, is the direct signal delay, is the interval between the j-th correlator and the direct signal, ki is the code chip delay of the i-th multipath signal relative to the direct signal, and n(k) stands for Gaussian white noise.
When the correlator interval is known, the correlation output value is related to the amplitude, time delay and noise of the direct and multipath signals. Therefore, the state space of the system can be modeled as follows:
The state model is expressed as follows:
where is the state matrix, and is the process noise.
The observation model is expressed as follows:
where is the observation matrix, and is the observation noise.
3. EKF-GAPF-Based Method for Multipath Parameter Estimation
As shown in Figure 3, the implementation process of EKF-GAPF is as follows: First, model and sample the signal received by the receiver, and initialize the parameters required by the algorithm. Second, utilize EKF to preliminarily identify signal parameters and provide reasonable prior probability distribution suggestions for PF, thereby improving the state prediction of particles, making it more in line with actual system dynamics, reducing randomness and error accumulation. Third, use PF to sample and update the state of the particle set, and calculate the normalized weights of particles. Fourth, introduce GA to optimize the resampling process of PF [27], which gradually evolves particles to high-probability regions of posterior probability distribution through elite preservation, adaptive crossover, and mutation operations. Fifth, after multiple iterations, the parameter estimation results are output, achieving high-precision optimization of state estimation.
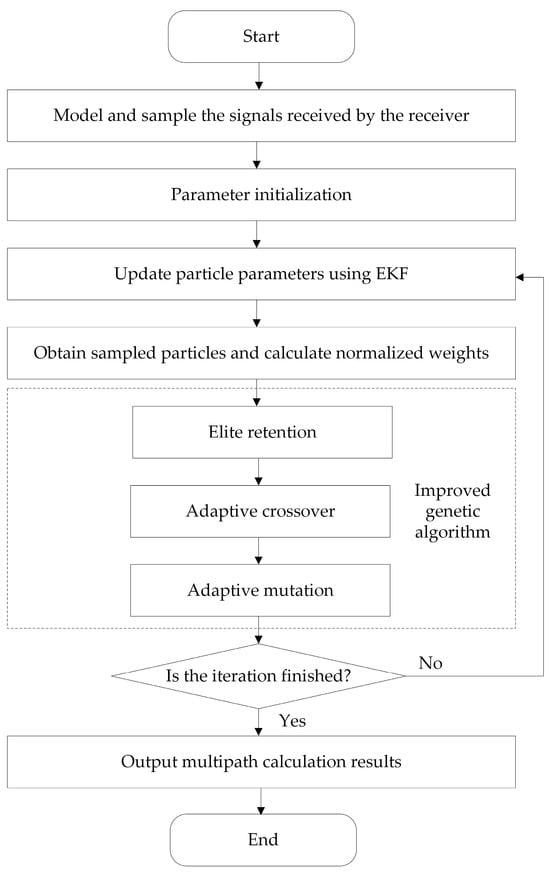
Figure 3.
Flowchart for implementing multipath estimation.
3.1. Preliminary Identification of Parameters
The EKF is utilized to provide a reasonable suggested density for PF. The basic steps of EKF include initialization and updating of predictions and measurements. The implementation process of multipath estimation based on EKF is as follows:
- Initialization:
When k = 0, the initial state estimate is x0|0, the initial error covariance matrix is P0|0, the process noise covariance is Q, and the measurement noise covariance is R.
- Prediction update:
Predict the multipath estimate at the current moment based on the value at the previous moment, expressed as follows:
Simultaneously, the prior error covariance is updated, expressed as follows:
Observation matrix calculation: Calculate the observation matrix, expressed as follows:
Assuming that the autocorrelation function has the desired self-precedence property, a partial derivation of can be obtained:
According to Formulas (2), (8) and (9), H can be obtained from (10).
- Kalman gain calculation:
Calculate the Kalman gain, expressed as follows:
- State estimate update
Update the state based on the Kalman gain and the actual measurements, expressed as follows:
Error covariance matrix update, expressed as follows:
The calibration values from EKF are used as initial values, and then, a set of random samples are generated in the state space based on the prior distribution of the system state. These samples can be used as the initial value of PF, which can improve its convergence speed and efficiency.
3.2. Accurate Identification Based on PF
3.2.1. Accurate Identification Process
- Initialize the particle set:
The particle set is initialized, where N represents the total number of particles. Since PF uses multiple particles to approximate the state distribution, it is less sensitive to a single initial condition, making it more robust.
- Perform importance sampling:
After sampling with EKF, the initial predictions from EKF are employed to obtain predicted measurement values and the measurement noise covariance matrix. A multivariate normal distribution model is then constructed based on these predictions. The initial estimate of the particles suggested by EKF can be expressed as follows:
where XK follows a normal distribution with mean and covariance R, that is,
- Calculate and normalize weights:
Under the assumptions outlined in this model, the particle weights are calculated based on the probability density function of particles and normalized, as shown below:
where n is the dimension of the state vector, is the predicted measurement value, and x is the actual measurement value.
- Resample and state estimation:
Based on the normalized particle weights, GA is applied to resample the new particle set and obtain the estimated result of the system state.
3.2.2. Enhancing the Optimization Capability of PF with AGA
A common problem with PF is that after several iterations, the variance of particles increases due to the presence of process noise, meaning that the weights of many particles are close to zero and have little contribution to the posterior estimation. To address this issue, the GAPF [16] introduced GA to improve the resampling process of PF, which mitigates particle degradation to some extent. However, GA is prone to fall into local optimal solutions [28], resulting in limited performance of multipath estimation.
The three crucial steps of GA are selection, crossover, and mutation [29]. In the selection phase, elite individuals are preserved and directly passed to the next generation, ensuring that optimal solutions are not lost. Then, selection is performed, and individuals with high fitness are more likely to be selected and spread their genes. During crossover, genetic recombination swaps partial genes between two individuals, generating new offspring that explore a broader solution space. A higher crossover probability aids in increasing population diversity, but an excessively high probability may affect the convergence of the algorithm. Mutation increases the diversity of the solution space by randomly changing the genes of individuals, preventing early convergence to the local optimum [30]. A mutation rate that is too high will destroy the existing excellent solutions, while a mutation rate that is too low may limit the global search ability of the algorithm.
Therefore, reasonable settings of crossover and mutation factors are crucial to ensure the effectiveness of GA and to balance global search and local exploitation. An adaptive adjustment strategy is proposed in this paper to dynamically set these factors, and combined with an elite retention strategy to ensure that the best individuals are preserved and passed to the next generation. This dual strategy not only enhances the algorithm’s search efficiency but also improves the stability and quality of the final solution. The above process can be expressed as follows:
where CR1 is the maximum crossover rate, CR1 − CR2 is the minimum crossover rate, I is the current number of iterations, M is the maximum number of iterations, G is the initial crossover probability, g is the average fitness, and gi is the fitness of the current particle. Pc gradually decreases with the increase in the number of iterations to enhance the stability of the population. Meanwhile, Pm is flexibly adjusted based on the number of iterations and particle fitness to avoid falling into local optimal solutions.
4. Simulation and Analysis of EKF-GAPF
To validate the effectiveness of EKF-GAPF, this section conducts verification and comparison from three aspects: the optimization capability of AGA, particle diversity, and the accuracy of multipath parameter estimation. Before the experiment, a signal model needs to be constructed. Since only one dominant multipath is received in signal propagation studies, and considering multiple multipaths does not significantly improve multipath elimination performance [21], a detailed analysis is initially conducted for the single multipath signal. In the simulation, a satellite C/A code signal is used, with a sampling interval of Ts = Tc/10. It is assumed that there are six correlators, with spacing between each branch and the correlators set to ±0.5Tc, ±0.3Tc, and ±0.1Tc. The characteristic parameters of the direct signal and the multipath signal are set as follows: the amplitude of the direct signal is 1, the amplitude of the multipath signal is 0.7, the time delay of the direct signal is 0.1, and the time delay of the multipath signal is 0.3. Under these conditions, the real values of the estimated parameters can be expressed as x = [1; 0.7; 0.1; 0.3]. In Equation (10), the number of multipath signals is set to M = 1, leading to an updated measurement matrix H. For all algorithms, the state transition matrix F is a fourth-order identity matrix, and the system noise Q is set to diag(0.0001, 0.0001, 0.0001, 0.0001). R is calculated from the square of the standard deviation of the normalized correlation between the received signal and the local signals. The number of iterations is 500, and the number of particles used in PF, EPF, GAPF, and EKF-GAPF is 40. Additionally, for GAPF and EKF-GAPF, the parameters CR1, CR2, and G are set to 0.9, 0.4, and 0.2, respectively.
4.1. Optimization Capability of AGA
To verify the optimization performance of AGA, two test functions with distinct characteristics are selected. Test function 1 is a simple quadratic function, as shown in Formula (20), which aims to find parameters a, b, and c by fitting a given set of data points, thereby minimizing the error between the predicted values of the fitting function and the actual values. This function has a regular shape with only one extreme point, making it suitable for evaluating the fitting accuracy of algorithms under ideal conditions. As shown in Formula (21), test function 2 is a complex multi-peak function with numerous local extreme points, easily trapping optimization algorithms in local optimal solutions. By optimizing this function, the global optimization capability of the algorithm can be effectively evaluated. A comparison of the performance between AGA and traditional GA is illustrated in Figure 4 Specifically, Figure 4a shows the performance comparison of AGA and traditional GA in handling minimization problems, and Figure 4b shows their performance comparison in handling maximization problems.
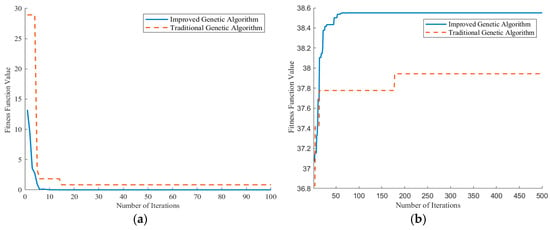
Figure 4.
Performance comparison between AGA and traditional GA: (a) Results for test function 1; (b) results for test function 2.
As can be seen from Figure 4a, the initial convergence speed of AGA is significantly better than that of traditional GA, and it can quickly approach the optimal solution within almost 10 iterations. In contrast, traditional GA requires more iterations to obtain the same result. From Figure 4b, it can be seen that AGA also rapidly improves the objective function value in the early iterations, and approaches the global optimal solution after 50 iterations, while traditional GA easily falls into local optimal solutions at the same number of iterations. In summary, whether for minimization or maximization problems, the improved AGA significantly outperforms traditional GA in terms of convergence speed, global search ability, and resistance to local optima.
4.2. Comparison of Particle Diversity
To verify the advantage of EKF-GAPF in particle weight distribution, this paper conducted a comparative experiment between PF and EKF-GAPF, and statistically analyzed the particle weight distribution. Figure 5 shows the weight distribution of the two algorithms after 500 iterations, where Figure 5a shows the particle weight distribution of PF, and Figure 5b shows the particle weight distribution of EKF-GAPF.
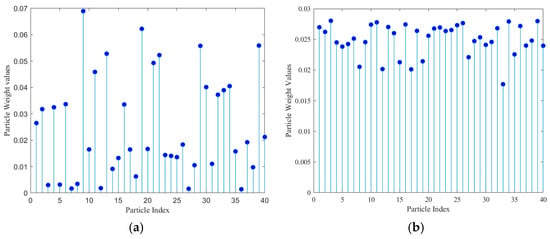
Figure 5.
Distribution of particle weights after 500 iterations: (a) Particle weight distribution using the particle filter (PF); (b) particle weight distribution using the EKF-GAPF.
In Figure 5a, the particle weight distribution is extremely uneven, with a few particles having very high weights and most particles having weights close to zero. This phenomenon indicates that the diversity of particles decreases, that is, a serious particle degradation problem occurs, which will make only a small number of particles able to effectively contribute to the posterior probability distribution, while most particles have minimal impact on the estimation results. In other words, the filtering process mainly relies on a small number of high-weight particles. As the number of iterations increases, errors may gradually accumulate, ultimately reducing filtering accuracy and robustness. In contrast, the weight distribution in Figure 5b is relatively uniform, and the difference in particle weights is not significant, indicating that EKF-GAPF significantly alleviates particle degradation through global optimization of GA during the particle resampling stage and maintains particle diversity. This results in most particles making a relatively balanced contribution to the posterior probability distribution, thereby improving the accuracy and stability of filtering.
4.3. Comparison of Signal Estimation Accuracy
To verify the performance of EKF-GAPF in signal estimation, under the condition that the power of the received signal and the noise signal are equal and the initial value is true, that is, x2 = [1; 0.7; 0.1; 0.3], the estimation results of EKF-GAFF are compared with those of PF, EKF, and EPF proposed in the previous literature and GAPF derived by AGA introduced in this paper.
In the experiment, the Root Mean Square Error (RMSE) [31] is used to evaluate the accuracy of algorithms in signal estimation, which is calculated as follows:
where denotes the number of iterations, is the estimated value, and is the true value.
Figure 6 shows the comparison of estimation results for direct and multipath signals, Figure 7 shows the absolute error of estimations, and Table 1 shows the RMSEs of estimations. These results correspond to a single run of the experiment. Compared with GAPF proposed in [16], which can only estimate signal delay, the signal model proposed in this paper can not only accurately estimate signal delay but also estimate amplitude. As shown in Figure 6 and Figure 7, estimations of EKF-GAPF have smaller fluctuations and is closest to the true value, indicating that EKF-GAPF performs well. From Table 1, it can be seen that EKF-GAPF performs best on all four evaluations metrics, followed by EPF and GAPF, while EKF and PF perform relatively poorly. In the estimation of the direct signal amplitude, the EKF-GAPF outperforms PF, EKF, GAPF, and EPF by 85.8%, 39.3%, 33.9%, and 41.2%, respectively. For the amplitude of multipath signal, EKF-GAPF shows improvements of 86.0%, 44.9%, 37.1%, and 40.5%, respectively. In terms of direct signal delay estimation, EKF-GAPF improves by 81.0%, 45.4%, 50%, and 31.6%, with the RMSE of the direct signal delay reduced to 0.0065, corresponding to about 1.95 m. For the multipath signal delay estimation, EKF-GAPF achieves improvements of 88.0%, 73.1%, 54.6%, and 68.3%, with the RMSE of multipath signal delay reduced to 0.0064, or approximately 1.92 m. These results clearly demonstrate the exceptional performance of EKF-GAPF in estimating both signal amplitude and delay.
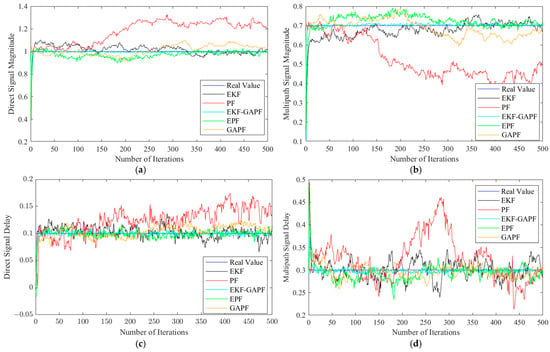
Figure 6.
Comparison of estimation results for direct and multipath signals: (a) Estimated amplitude of the direct signal; (b) estimated amplitude of the multipath signal; (c) estimated delay of the direct signal; (d) estimated delay of the multipath signal.
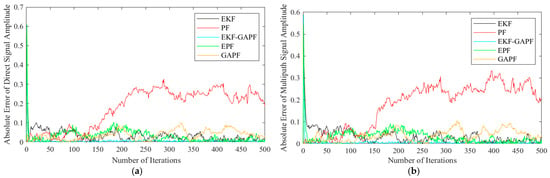
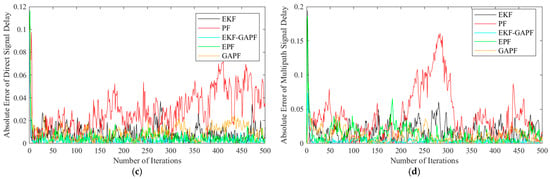
Figure 7.
Absolute error of estimation for direct and multipath signals (under true initial values): (a) Absolute error of amplitude estimation for direct signals; (b) absolute error of amplitude estimation for multipath signals; (c) absolute error of delay estimation for direct signals; (d) absolute error of delay estimation for multipath signals.

Table 1.
RMSEs of estimation for direct and multipath signals.
To verify the convergence and parameter estimation capabilities of different algorithms in the absence of known true signal parameters, this study randomly selects an initial value and conducts 1000 Monte Carlo simulations under the same initial conditions for each algorithm. The mean and standard deviation of the RMSE are computed to evaluate the estimation accuracy and stability of the algorithms. In the experiment, the selected initial value is x2 = [ 0.7415; 0.0529; 0.4197; 0.5240], which deviates from the real state value, thereby better reflecting the uncertainty conditions commonly encountered in practical applications. Figure 8 shows the estimated absolute error of the direct signal and multipath signal with a randomly set initial value. These figures present the run that is closest to the average performance, representing the typical behavior of the algorithm. It can be seen that in terms of amplitude estimation, EKF-GAPF performs well throughout the entire iterative process, with estimation errors continuously decreasing and eventually reaching the minimum value (the estimation error of direct signal amplitude can converge to 0.011, and the estimation error of multipath signal amplitude can converge to 0.002). The initial estimation error of EKF decreases rapidly, but the convergence effect is limited in the later period, and it fails to reach the minimum error. The overall performance of PF is poor. Although the initial error has decreased, its convergence speed is significantly lower than other algorithms. In terms of delay estimation, PF and EKF perform poorly and fluctuate significantly. In comparison, EKF-GAPF has the smallest estimation error in the entire iterative process and obtains the best convergence result. Specifically, the estimation errors for the delays of the direct and multipath signals converge to 0.004, corresponding to approximately 1.2 m, and 0.006, corresponding to approximately 1.8 m. Table 2 shows the mean and standard deviation of the RMSE of five algorithms under this randomly set initial value, where EKF-GAPF outperforms the other algorithms across all evaluation metrics. In the estimation of the direct signal amplitude, EKF-GAPF improves upon PF, EKF, GAPF, and EPF by 69.7%, 51.9%, 52.2%, and 51.8%, respectively. For the amplitude of multipath signal, EKF-GAPF shows improvements of 70.3%, 37.8%, 62.0%, and 53.7%, respectively. In terms of direct signal delay estimation, EKF-GAPF achieves improvements of 65.3%, 21.5%, 58.8%, and 33.7% over the other four algorithms. For the multipath signal delay estimation, EKF-GAPF shows improvements of 77.1%, 42.9%, 71.0%, and 69.1%. Moreover, the RMSE standard deviation of EKF-GAPF is significantly lower than that of other algorithms, indicating greater stability under random initial conditions. Additionally, a similar performance trend is observed under different initial value conditions. Therefore, EKF-GAPF proposed in this paper outperforms the other four algorithms in both estimation accuracy and stability.
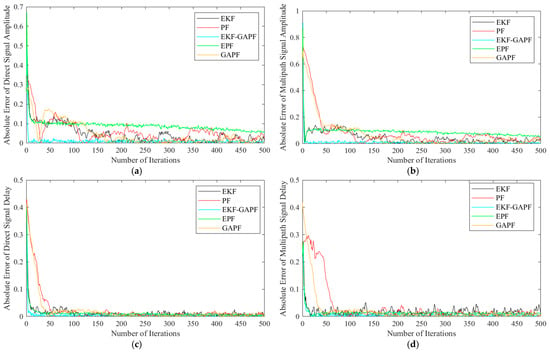
Figure 8.
Absolute error of estimation for direct and one multipath signal (under random initial values): (a) Absolute error of amplitude estimation for direct signals; (b) absolute error of amplitude estimation for multipath signals; (c) absolute error of delay estimation for direct signals; (d) absolute error of delay estimation for multipath signals.

Table 2.
RMSE mean and standard deviation statistics for direct signal and one multipath signal based on 1000 Monte Carlo experiments.
4.4. Parameter Estimation for Two Multipath Signals
To further verify the feasibility of the experiment, the scenario is extended to include two multipath signals. The direct signal is assumed to have an amplitude of 1 and a delay of 0.1, while the two multipath signals have amplitudes of 0.7 and 0.5, with delays of 0.3 and 0.5, respectively. Under these conditions, the real values of the estimated parameters can be expressed as x = [1; 0.7; 0.5; 0.1; 0.3; 0.5]. Accordingly, modifications to certain experimental parameters are required compared to the single multipath scenario. In Equation (10), the number of multipath signals is set to M = 2, leading to an updated measurement matrix. For all algorithms, the state transition matrix is defined as F = eye(6), the system noise covariance Q is set to 0.0001 × eye(6). All other experimental conditions remain unchanged. Similarly to the experiment with only a single multipath, this experiment randomly sets an initial value different from the true value and performs 1000 Monte Carlo simulations to comprehensively evaluate the algorithm’s convergence speed and stability. The selected initial value is x3 = [0.96; 0.52; 0.41; 0.09; 0.21; 0.45]. Figure 9 displays the run closest to the average performance, representing the typical behavior of the algorithms. Table 3 presents the RMSE mean and standard deviation statistics for the direct signal and two multipath signals, based on 1000 Monte Carlo experiments. The results include both the mean and the standard deviation, offering a comprehensive evaluation of the algorithms’ performance under the given experimental conditions. Additionally, similar performance trend is observed under different initial value conditions.
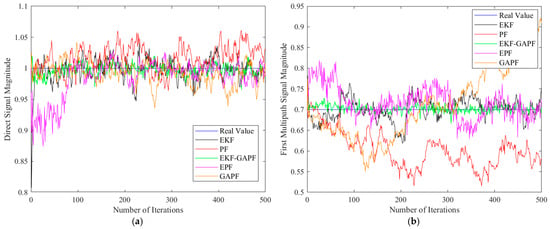
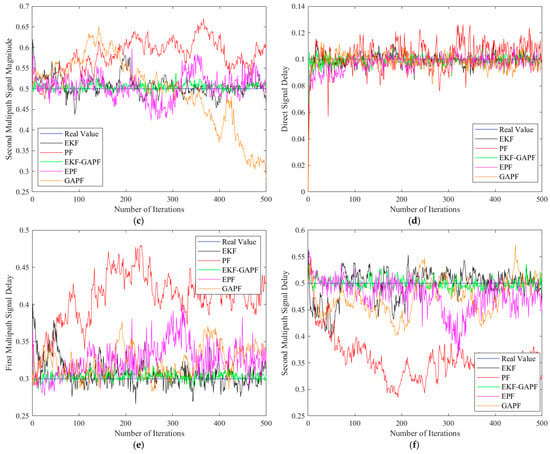
Figure 9.
Comparison of estimation results for direct signal and two multipath signals: (a) Estimated amplitude of the direct signal; (b) estimated amplitude of the first multipath signal; (c) estimated amplitude of the second multipath signal; (d) estimated delay of the direct signal; (e) estimated delay of the first multipath signal; (f) estimated delay of the second multipath signal.

Table 3.
RMSE mean and standard deviation statistics for the direct signal and two multipath signals based on 1000 Monte Carlo experiments.
As shown in Figure 9 and Table 3, EKF-GAPF maintains good parameter estimation performance even as the number of multipath components increases. Compared to the other algorithms, EKF-GAPF exhibits the smallest average RMSE, indicating better parameter estimation accuracy. Moreover, it has the smallest standard deviation, highlighting its greater stability in multiple parameter estimation runs. These results demonstrate that the proposed algorithm outperforms others in multipath signal estimation.
5. Conclusions
By combining EKF, PF, and AGA, a novel EKF-GAPF algorithm is proposed in this paper to improve the estimation performance of navigation signals. This algorithm effectively overcomes the particle degradation problem in PF as well as the limitations of EKF when dealing with highly nonlinear distributions. First, EKF-GAPF provides more accurate state estimation and transition models for particles in PF through the state prediction and update mechanisms of EKF. This approach fully utilizes the local linearization ability of EKF and the nonparametric advantages of PF, thereby enhancing the accuracy of state prediction, reducing dependence on the number of particles, and improving the distribution of particle weights in complex multipath environments. To address the particle degradation problem, the algorithm introduces AGA to optimize the importance sampling process, which enhances global search capability and avoids the risk of falling into local optima by dynamically adjusting the weights of particles and the state update strategy. Experimental results show that EKF-GAPF outperforms traditional EKF, EPF, and PF algorithms in both the magnitude and delay estimation of multipath parameters.
Future research will focus on real-time applications, including tests in dynamic environments to evaluate the performance of EKF-GAPF in real navigation systems. Additionally, a real-time multipath estimation system based on EKF-GAPF will be developed to validate its effectiveness in complex scenarios.
Author Contributions
Conceptualization, J.L. (Jie Li) and X.S.; methodology, Y.J.; software, J.L. (Jie Li) and J.L. (Jingjing Li); validation, X.S., J.L. (Jingjing Li) and L.L.; formal analysis, J.L. (Jie Li); investigation, Y.J.; resources, J.L. (Jingjing Li); data curation, L.L.; writing—original draft preparation, J.L. (Jie Li); writing—review and editing, L.L. and J.L. (Jingjing Li); visualization, Y.J.; supervision, J.L. (Jingjing Li); funding acquisition, X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Guangxi Science and Technology Project (AA24263010, AA23062038, ZY23055048, AB23026120, ZY22096026, AA24206043, AB24010085), the National Natural Science Foundation of China (U23A20280, 62462019, 62161007, 62471153), the Guangdong Basic and Applied Basic Research Foundation (2023A1515012846), the Guangxi Key Laboratory of Precision Navigation Technology and Application (DH202230), the Basic Scientific Research Ability Improvement Project for Young and Middle-aged Teachers of Guangxi Higher Education Institutions (2024KY0233, 2025KY0243), the Guangxi Major Talent Project, and the Project of the Collaborative Innovation Center for BeiDou Location Service and Border and Coastal Defense Security Application.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Xiyan Sun was employed by the GUET-Nanning E-Tech Research Institute Co., Ltd., The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Peppa, I.; Psimoulis, P.A. Detection of GNSS Antenna Oscillatory Motion and Multipath Conditions via Exploitation of Multipath-Induced SNR Variations. GPS Solut. 2023, 27, 117. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, J.; Liu, Y.; Zhu, Q. Variable Projection Algorithm for GPS Positioning in Multipath Environments Based on Aitken Acceleration Method. IEEE Trans. Ind. Inform. 2024, 20, 6404–6412. [Google Scholar] [CrossRef]
- Lee, Y.; Wang, P.; Park, B. Nonlinear Regression-Based GNSS Multipath Dynamic Map Construction and Its Application in Deep Urban Areas. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5082–5093. [Google Scholar] [CrossRef]
- Lee, Y.; Hwang, Y.; Ahn, J.Y.; Seo, J.; Park, B. Seamless Accurate Positioning in Deep Urban Area Based on Mode Switching between DGNSS and Multipath Mitigation Positioning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5856–5870. [Google Scholar] [CrossRef]
- Yan, T.; Wang, Y.; Li, T.; Tian, Y.; Qu, B.; Bian, L. MCSK Signal for LEO Satellite Constellation Based Navigation Augmentation System. In Proceedings of the China Satellite Navigation Conference, Jinan, China, 22–24 May 2023; pp. 295–304. [Google Scholar]
- Chen, Y.; Cheng, J.; Li, X.; Bai, X.; Nie, Z. Research on Tracking Technique Based on BPSK-CSK Signals. Electronics 2024, 13, 1517. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Sun, A.; Meng, X.; Zhao, D.; Hancock, C. GNSS Carrier-Phase Multipath Modeling and Correction: A Review and Prospect of Data Processing Methods. Remote Sens. 2024, 16, 189. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, L.; Zhang, G.; Xu, B.; Hsu, L.-T. Characterization and Validation of GNSS Multipath-Induced Doppler Measurement Error. IEEE Trans. Aerosp. Electron. Syst. 2024; Early Access. [Google Scholar] [CrossRef]
- Wen, W.; Zhang, G.; Hsu, L.-T. Object-Detection-Aided GNSS and Its Integration with Lidar in Highly Urbanized Areas. IEEE Intell. Transp. Syst. Mag. 2020, 12, 53–69. [Google Scholar] [CrossRef]
- Taghdisi, E.; Ghaffarian, M.S.; Mirzavand, R. Low-Profile Substrate Integrated Choke Rings for GNSS Multipath Mitigation. IEEE Trans. Antennas Propag. 2022, 70, 1706–1718. [Google Scholar] [CrossRef]
- Lau, L. GNSS Multipath Errors and Mitigation Techniques. In GPS and GNSS Technology in Geosciences; Elsevier: Amsterdam, The Netherlands, 2021; pp. 77–98. [Google Scholar]
- Liu, X.; Closas, P.; Liu, J.; Hu, X. Particle Filtering and Its Application for Multipath Mitigation with GNSS Receivers. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 1168–1173. [Google Scholar]
- Jiang, Z.; Zhou, W.; Li, H.; Mo, Y.; Ni, W.; Huang, Q. A New Kind of Accurate Calibration Method for Robotic Kinematic Parameters Based on the Extended Kalman and Particle Filter Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 3337–3345. [Google Scholar] [CrossRef]
- Qin, H.; Xue, X.; Yang, Q. GNSS Multipath Estimation and Mitigation Based on Particle Filter. IET Radar Sonar Navig. 2019, 13, 1588–1596. [Google Scholar]
- Zhiyuan, W.; Lan, C.; Gang, X. An Improved Particle Filtering Algorithm and Its Application in Multipath Estimation. Comput. Eng. 2017, 43, 289–295. [Google Scholar]
- Tian, L.; Sun, X.; Ji, Y. Multipath Signal Estimation Algorithm Based on Genetic Particle Filter. Comput. Simul. 2017, 34, 36–40. [Google Scholar]
- Jee, G.-I.; Kim, H.S.; Lee, Y.J.; Park, C.G. A GPS C/A Code Tracking Loop Based on Extended Kalman Filter with Multipath Mitigation. In Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2002), Portland, OR, USA, 24–27 September 2002; pp. 446–451. [Google Scholar]
- Siebert, C.; Konovaltsev, A.; Meurer, M. Development and Validation of a Multipath Mitigation Technique Using Multi-Correlator Structures. Navig. J. Inst. Navig. 2023, 70, 609. [Google Scholar] [CrossRef]
- Mu, X.; Guo, J.; Song, Y.; Sha, Q.; Jiang, J.; He, B.; Yan, T. Application of Modified EKF Algorithm in AUV Navigation System. In Proceedings of the OCEANS 2017, Aberdeen, UK, 19–22 June 2017; pp. 1–4. [Google Scholar]
- Lai, X.; Huang, Y.; Han, X.; Gu, H.; Zheng, Y. A Novel Method for State of Energy Estimation of Lithium-Ion Batteries Using Particle Filter and Extended Kalman Filter. J. Energy Storage 2021, 43, 103269. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, L.; Zhang, J.; Ni, Z.; Yan, G. Multipath Estimation Algorithm Based on Improved Unscented Kalman Filter. J. Taiyuan Univ. Technol. 2023, 54, 877–884. [Google Scholar] [CrossRef]
- Li, H.; Borhani-Darian, P.; Wu, P.; Closas, P. Deep Neural Network Correlators for GNSS Multipath Mitigation. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1249–1259. [Google Scholar] [CrossRef]
- Wang, P.; Morton, Y.J. Multipath Estimating Delay Lock Loop for LTE Signal TOA Estimation in Indoor and Urban Environments. IEEE Trans. Wirel. Commun. 2020, 19, 5518–5530. [Google Scholar] [CrossRef]
- Suzuki, T.; Amano, Y. NLOS Multipath Classification of GNSS Signal Correlation Output Using Machine Learning. Sensors 2021, 21, 2503. [Google Scholar] [CrossRef]
- Jin, R.; Cui, X.; Yan, J.; Xiong, H.; Yang, H.; Gu, M.; Zhen, W. Small Delay GNSS Forwarding Spoofing Detection in Multipath Environment Based on Convolutional Neural Network. IEEE Sens. J. 2024, 24, 24070–24085. [Google Scholar] [CrossRef]
- Chen, J.; Cheng, L.; Gan, M. Modeling of GPS Code and Carrier Tracking Error in Multipath. Chin. J. Electron. 2012, 21, 78–84. [Google Scholar]
- Zhang, J.; Huang, C.; Chow, M.-Y.; Li, X.; Tian, J.; Luo, H.; Yin, S. A Data-Model Interactive Remaining Useful Life Prediction Approach of Lithium-Ion Batteries Based on PF-BiGRU-TSAM. IEEE Trans. Ind. Inform. 2024, 20, 1144–1154. [Google Scholar] [CrossRef]
- Zhou, M.; Long, Y.; Zhang, W.; Pu, Q.; Wang, Y.; Nie, W.; He, W. Adaptive Genetic Algorithm-Aided Neural Network with Channel State Information Tensor Decomposition for Indoor Localization. IEEE Trans. Evol. Comput. 2021, 25, 913–927. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic Algorithms: Theory, Genetic Operators, Solutions, and Applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar]
- Li, Y.; Wu, H.; Sun, Y. Improved Adaptive Genetic Algorithm Based RFID Positioning. J. Syst. Eng. Electron. 2022, 33, 305–311. [Google Scholar] [CrossRef]
- Gao, X.; He, D.; Wang, P.; Yu, W. Signal Parameter Estimation Based on ESPRIT with State Space Model for 5 G NR Signals in Indoor and Urban Environments. IEEE Trans. Veh. Technol. 2024, 74, 2276–2291. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).