Research on Springback Compensation Method of Roll Forming Based on Improved Fuzzy PID Control

Abstract

To enhance the forming accuracy of circular rolling, this paper proposes a control strategy for compensating the springback of sheet metals by altering the rolling angle. A kinematic model for circular rolling springback compensation is established to monitor the forming radian of the sheet metal in real time. The motor is then controlled to adjust the rolling angle of the sheet metal through a mechanical structure, thereby achieving springback compensation. To realize the precise control required by the springback compensation control strategy, a fuzzy PID controller strategy optimized by the coupled whale particle (CWP) algorithm is designed. The research results indicate that the error between the formed radius and the desired radius in a normal circular rolling experiment is 5.4%, 5.32%, and 5.52%. However, after applying the springback compensation strategy, the error in the circular rolling experiment is reduced to 1.6%, 1.55%, and 1.72%. This demonstrates that the proposed springback compensation strategy for circular rolling effectively improves the accuracy of circular rolling.

1. Introduction

Circular roll forming of metal sheets is extensively employed in industries such as aerospace, construction, automotive manufacturing, shipbuilding, and electronics [1,2,3,4]. Plate-rolling machines play a pivotal role in the circular roll forming of metal sheets. Among them, three-roll plate-rolling machines are widely utilized in the industrial field. The precision of circular roll forming is subject to the influence of numerous factors. Notably, the continuous springback generated during the rolling process of metal sheets stands as the most substantial interfering factor [5,6].

Regarding the circular roll forming of metal sheets, scholars from around the globe have carried out extensive research efforts. Zhao [7] conducted a study on the springback and stress distribution characteristics of 316 L austenitic stainless-steel sheets after JCOE bending and unloading. By implementing corresponding compensation for the pre-bending amount, the bending forming accuracy was enhanced. The model constructed by Zhao can provide a theoretical foundation for actual production. Yu and Zhao [8] explored the ellipticity issue in three-roll bending and established a quantitative relationship between the reduction amount and the elastic area. Yu and Huang [9] proposed a continuous compound straightening process for three-roll bending of large-diameter longitudinal-seam welded pipes and developed experimental equipment. The feasibility of the new process was experimentally verified. Wang et al. [10], by means of a model prediction error classification model and a model prediction correction method considering error compensation, constructed a prediction–correction model for elongation after fracture considering error compensation. This model enabled the prediction accuracy of elongation after fracture within an absolute error range of ±0.9% to reach 94.63%. Cheng Jiao-Jiao et al. [11] developed an angle compensation method based on the UDT-type angle adjustment method. High-precision springback control was achieved through finite element analysis simulation, providing a new approach for effective springback control during the roll forming process of high-speed steel with complex cross-sections. Paralikas J et al. [12] proposed an experimental model for the roll forming process of a symmetric U-shaped cross-section of advanced high-strength steel (AHSS) material (DP600 type). The optimal values of process parameters for the minimum elastic longitudinal strain at each rolling station and the shear strain at the strip edge were calculated. This led to a reduction of 20–35% in the elastic longitudinal strain and 30–50% in the shear strain at all rolling stations, thereby improving the rolling quality. Zhen and Guo et al. [13] took into account the mechanical problems in the three-roll bending forming process, established a mechanical model for the upper roll, and analyzed the method of using deflection compensation to improve the circular rolling quality. JAMEL S [14] considered the influence of bending force and residual stress in the asymmetric roll bending forming process, established theoretical models for predicting bending force and residual stress, and analyzed the causes of residual stress. GAVRILESCU I et al. [15] established a hybrid numerical analysis method to study the influence of bending force and bending radius on the displacement of the upper roll. LIU and CAO [16] considered the influence of the non-linear elastic modulus on the springback prediction of high-strength steel roll forming. Through experiments and simulations, it was demonstrated that the variable elastic modulus model is more accurate than the constant elastic modulus model in predicting springback problems. Xing and Liu [17] studied the surface wear depth of pipes and explored the influence of forming process parameters on wear. Although the above-mentioned scholars have proposed corresponding control schemes and compensation methods for sheet springback, these are all for the advanced prediction of springback amounts and do not respond to the real-time changing springback amounts of sheets. Therefore, there still exists a certain degree of forming error, and there is a lack of high-precision control methods [18]. It is also difficult to guarantee the control accuracy during the circular rolling process.

Zhang et al. [19] established a finite element model for the radial–axial rolling of super-large ring components integrated with a fuzzy control algorithm for ring center offset. They investigated the variation laws of the ring center offset under conventional control with the optimal speed-matching coefficient and adaptive fuzzy control. Qian and Tian [20] proposed a method for measuring the real-time dimensions of ring components during the rolling process to achieve real-time monitoring of the growth rate. They also established a design-driven control method for the growth rate of ring components (the ideal-state control method). Through a real-time error–feedback regulation strategy, small-scale errors caused by dynamic defects were eliminated, enabling the growth rate to precisely approach the target value. TIAN and HONG [21] designed a fuzzy self-adaptive PID controller for a cold bending machine for profiles. Based on conventional PID control, this controller uses fuzzy logic to adjust PID parameters online according to the deviation and its rate of change, further improving the performance of the PID controller and enhancing the accuracy of the position control system. GAO et al. [22] adopted a Siemens S7-200 SMART programmable logic controller (PLC) as the slave station controller. They used an acquisition module to collect the position data of magnetic grid rulers and encoders and a proximity switch for zero-point calibration. The improved system features good stability and easy operation, and the adjustment accuracy of the roll position can reach ±1 mm with less time consumption, meeting the requirements for automatic adjustment of the roll position and improving the production efficiency of enterprises. Although the above-mentioned control systems have established corresponding control models, proposed new control methods, and improved control accuracy and anti-interference capabilities, etc., during the control process, they are still unable to respond promptly to the springback of metal sheets. The errors caused by springback during the sheet forming process are still difficult to reduce. To design a reliable and efficient control strategy suitable for circular roll forming, it is essential to simultaneously consider the influence of sheet springback during the circular rolling process and the control accuracy of the circular rolling process.

In this paper, the gap between the working roll and the driven rolls is adjusted by means of sheet springback feedback, thereby achieving the control of sheet circular roll forming. The main contributions lie in the proposal of a kinematic model for circular rolling springback compensation and an improved fuzzy PID controller based on the CWP optimization algorithm. The proposed kinematic model for circular rolling springback compensation effectively reduces the circular roll forming error caused by sheet springback.

2. System Modeling Based on Springback Compensation Strategy

By establishing the kinematic model of the circular rolling mechanism, the relationship between the motor rotation angle and the distance fed back by the sensor is deduced. The circuit current, motor rotation speed, and motor rotation angle are taken as inputs, and the association between the feedback distance and the motor rotation angle is realized in the form of a control model, enabling the motor rotation angle to approach the desired value.

2.1. Kinematic Model of Rolls

Take a horizontally adjusted three-roll circular rolling machine as an example. As shown in Figure 1, the lead screw is fixed to the output shaft of the motor (labeled “1”). The slider (labeled “2”) is sleeved on the lead screw through a lead screw nut. The upper surface of the slider (2) is inclined at a certain angle. The bottom of the wedge (labeled “3”) is in contact with the upper surface of the slider (2). Two driven rolls (labeled “4”), spaced a certain distance apart, are located on the top of the wedge (3). The working roll (labeled “5”) is positioned above the middle of the two driven rolls (4) and is driven to move up and down by a hydraulic mechanism. The circular rolled sheet is placed between the driven rolls (4) and the working roll (5). A distance sensor is installed on the driven rolls (4) to measure the desired distance and the actual forming distance.

The rotation of the lead screw is driven by the motor (1), enabling the slider (2) to move on the lead screw. Since the upper surface of the slider (2) is inclined at a certain angle and the bottom of the wedge (3) is in contact with the upper surface of the slider (2), when the slider (2) moves forward on the lead screw, it can drive the wedge (3) to move upward, thereby bringing the driven rolls (4) closer to the working roll (5) and shaping the radius of the circular rolled sheet. Conversely, when the slider (2) moves backward on the lead screw, it can drive the wedge (3) to move upward, thus moving the driven rolls (4) away from the working roll (5).

Among them, the motor (1) controls the horizontal movement of the slider (2). Through the wedge (3), the horizontal motion of the slider (2) is transformed into the vertical movement of the driven rolls (4). By adjusting the vertical displacement of the driven rolls (4), the contact position between the sheet and the roll is altered. The rotation of the working roll (5) causes the sheet to undergo continuous elastic plastic deformation.

Figure 2 presents a schematic diagram of circular roll forming. The distance sensor therein can measure the distance between the sheet and the sensor, enabling real-time monitoring of the changes in springback. Based on the feedback from the distance sensor, the rotation angle of the motor is adjusted to change the rolling angle of the sheet, thereby correcting the springback that occurs in the sheet. A kinematic model for circular rolling springback compensation is established [23,24]. Based on the desired forming radius $R_q$, the desired distance $L_q$, and the sheet thickness $D_0$, the relationship between the distance $D$ from the distance sensor to the midline is obtained:

$$D^2+{R_q}^2={\left(R_q+L_q+D_0\right)}^2$$

(1)

Based on the actual forming radius $R_s$, the actual distance $L_s$, and the sheet thickness $D_0$, the relationship between the distance $D$ from the distance sensor to the midline is obtained as follows:

$$R_s={\displaystyle \frac{D^2}{2\left(L_s+D_0\right)}}-{\displaystyle \frac{{\left(L_s+D_0\right)}^2}{2}}$$

(2)

Then, the mathematical relationships among the desired forming radius $R_q$, the radius of the driven rolls $R_1$, the center-to-center distance of the driven rolls $D_1$, the sheet thickness $D_0$, and the upper-pressing amount $h$ are as follows:

$${\left({\displaystyle \frac{D_1}{2}}\right)}^2+{\left(R_q+R_1+D_0-h\right)}^2={\left(R_q+R_1+D_0\right)}^2$$

(3)

$D_3$ is the pitch on the screw, and $D_2$ is the horizontal displacement of the slider. Herein, the upper-pressing amount $h$ represents the upward displacement of the driven roll starting from the moment when the working roll, the driven roll, and the sheet come into contact.

$$h=D_2\tan \alpha$$

(4)

In Figure 3, relationship among the rotation angle $\theta$ of the motor, the pitch $D_3$, of the screw rod 1, and the horizontal displacement $D_2$ of the slider 2 is as follows:

$$\theta =2\pi {\displaystyle \frac{D_2}{D_3}}$$

(5)

The slider is set to move to the position corresponding to the desired forming radius. During the circular roll forming process, the motor rotation angle difference $\mathsf{\Delta }\theta$ is adjusted according to the forming radius of the sheet fed back by the distance sensor, that is,

$$\mathsf{\Delta }\theta =2\pi {\displaystyle \frac{\frac{D^2}{2\left(L_s-L_q+D_0\right)}-\frac{{\left(L_s-L_q+D_0\right)}^2}{2}+R_1+D_0}{D_3\tan \alpha }}-2\pi {\displaystyle \frac{\sqrt{{\left(\frac{D^2}{2\left(L_s-L_q+D_0\right)}-\frac{{\left(L_s-L_q+D_0\right)}^2}{2}+R_1+D_0\right)}^2-{\left(\frac{D_1}{2}\right)}^2}}{D_3\tan \alpha }}$$

(6)

2.2. Electromechanical Control Model

To effectuate the control of the motor rotation angle difference, an electromechanical control model for the circular rolling mechanism is established. The armature circuit of the circular roll forming mechanism is depicted in Figure 4.

Let $u$ denote the voltage, $E$ the back electromotive force, $L$ the inductance, $R$ the resistance, $J$ the moment of inertia of the mechanical rotating part of the motor (1), $B$ the viscous friction coefficient of the rotating part of the motor (1), $K_a$ the torque constant, and $K_b$ the back electromotive force constant. The current $i$, the rotational speed $\omega$, and the rotation angle $\theta$ of the motor (1) are selected as state variables:

$$\left\{\begin{array}{l}{x}_1=i\\ x_2=\omega \\ x_3=\theta \end{array}\right.$$

(7)

The derivatives with respect to time are as follows:

$$\left\{\begin{array}{l}{\displaystyle \frac{d{x}_1}{dt}}={\displaystyle \frac{di}{dt}}\\ {\displaystyle \frac{d{x}_2}{dt}}={\displaystyle \frac{d\omega }{dt}}\\ {\displaystyle \frac{d{x}_3}{dt}}={\displaystyle \frac{d\theta }{dt}}\end{array}\right.$$

(8)

From the armature circuit equation, we have

$$L{\displaystyle \frac{di}{dt}}+Ri+E=u$$

(9)

From the dynamic equation, we have

$$J{\displaystyle \frac{d\omega }{dt}}+B\omega =K_{a}i$$

(10)

From the electromagnetic induction relationship, we have

$$E=K_b\omega$$

(11)

Sorting out the above formula, we obtain

$$\left\{\begin{array}{l}{\displaystyle \frac{di}{dt}}=-{\displaystyle \frac{R}{L}}i-{\displaystyle \frac{K_b}{L}}\omega +{\displaystyle \frac{1}{L}}u\\ {\displaystyle \frac{d\omega }{dt}}={\displaystyle \frac{K_a}{J}}i-{\displaystyle \frac{B}{J}}\omega \\ {\displaystyle \frac{d\theta }{dt}}=\omega \end{array}\right.$$

(12)

By substituting $x_1=i$, $x_2=\omega$, and $x_3=\theta$ into the equation, we obtain

$$\left(\begin{array}{c}\stackrel{·}{x_1}\\ \stackrel{·}{x_2}\\ \stackrel{·}{x_3}\end{array}\right)=\left(\begin{array}{ccc}-{\displaystyle \frac{R}{L}}& -{\displaystyle \frac{K_b}{L}}& 0\\ {\displaystyle \frac{K_a}{J}}& -{\displaystyle \frac{B}{J}}& 0\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)+\left(\begin{array}{c}{\displaystyle \frac{1}{L}}\\ 0\\ 0\end{array}\right)u$$

(13)

The output equation is obtained:

$$y=x_3=\left(\begin{array}{ccc}0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)$$

(14)

Assume that the parameter values in the state equation are as shown in

Table 1. Equation of state parameters.

Parameter	Numerical Value
$R$	$50\mathsf{\Omega }$
$L$	$1\mathrm{H}$
$K_a$	$5.0$
$K_b$	$2.5$
$J$	$2.5\mathrm{kg}\cdot {\mathrm{m}}^2$
$B$	$2.5$

.

3. Springback Compensation Control Algorithm

To address the issue that the springback of the sheet during the circular rolling process affects the final forming accuracy, an improved fuzzy PID controller based on the springback compensation strategy is designed. This controller modifies the springback of the sheet by adjusting the rolling angle in real time. A block diagram of its control algorithm is shown in Figure 5.

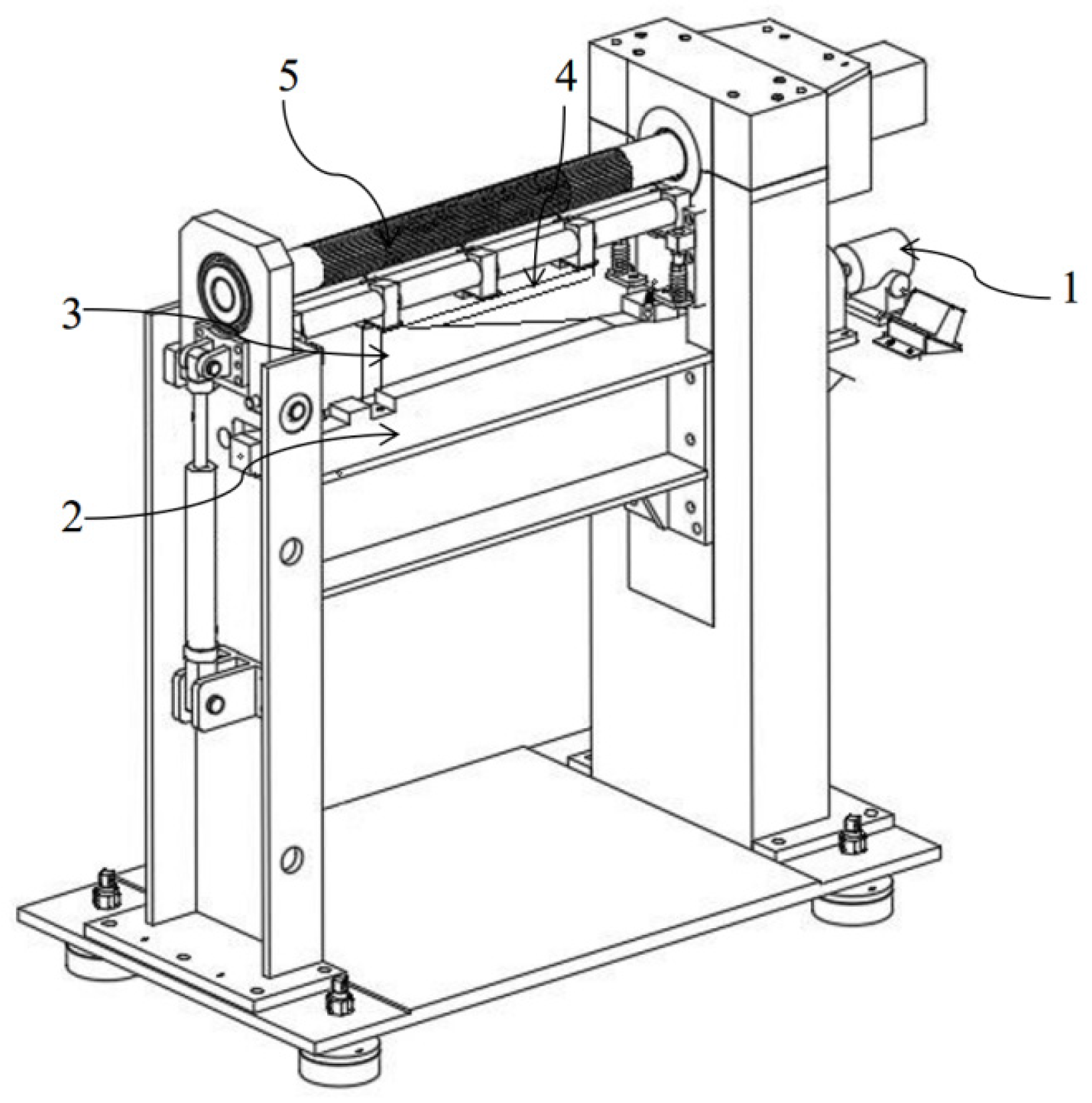
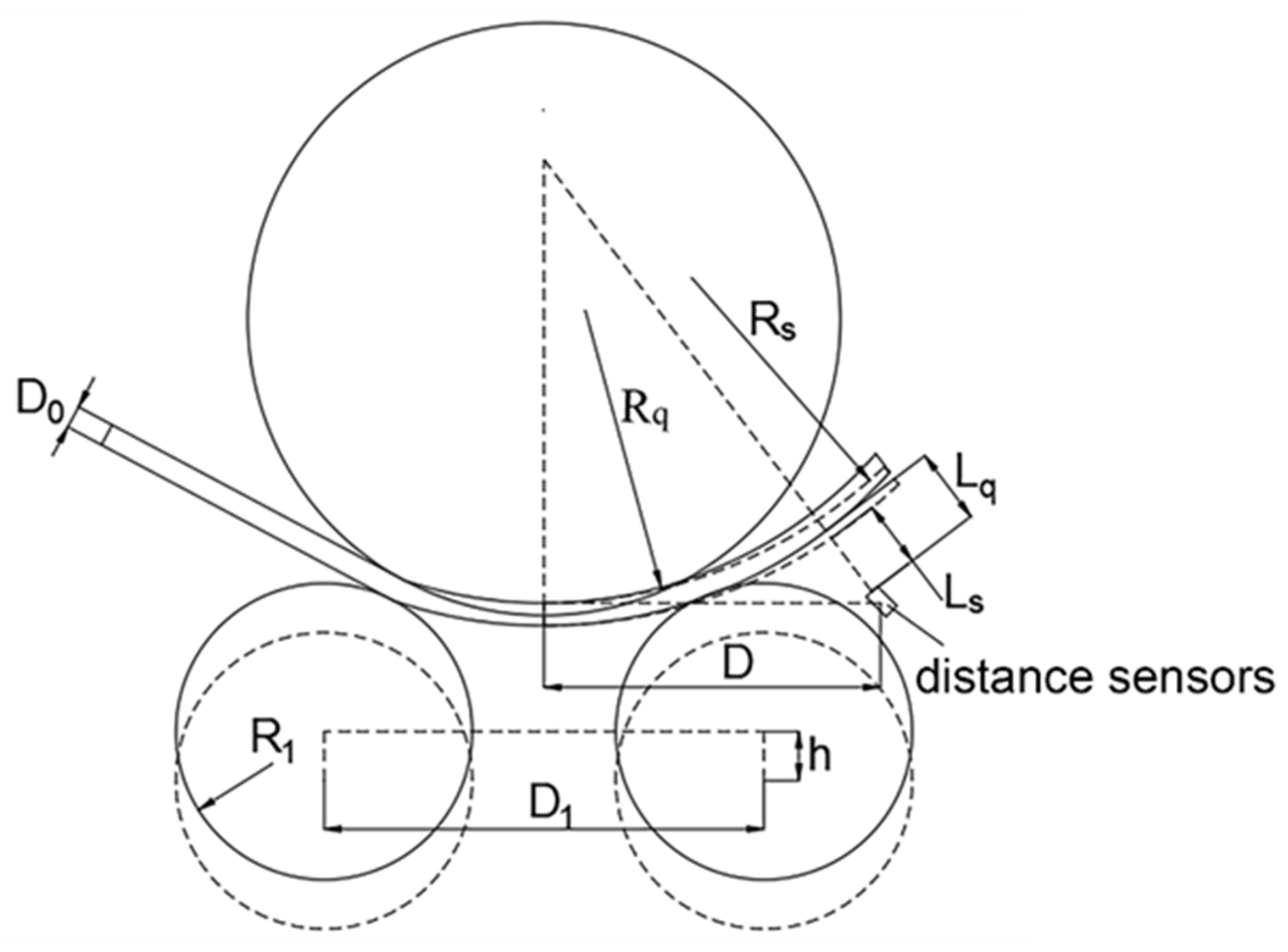
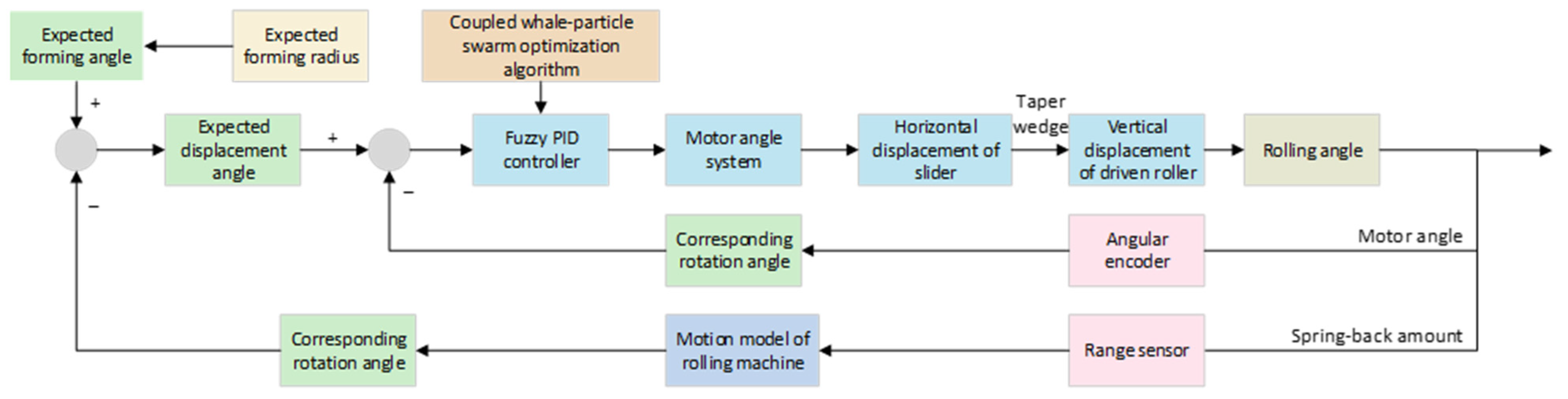
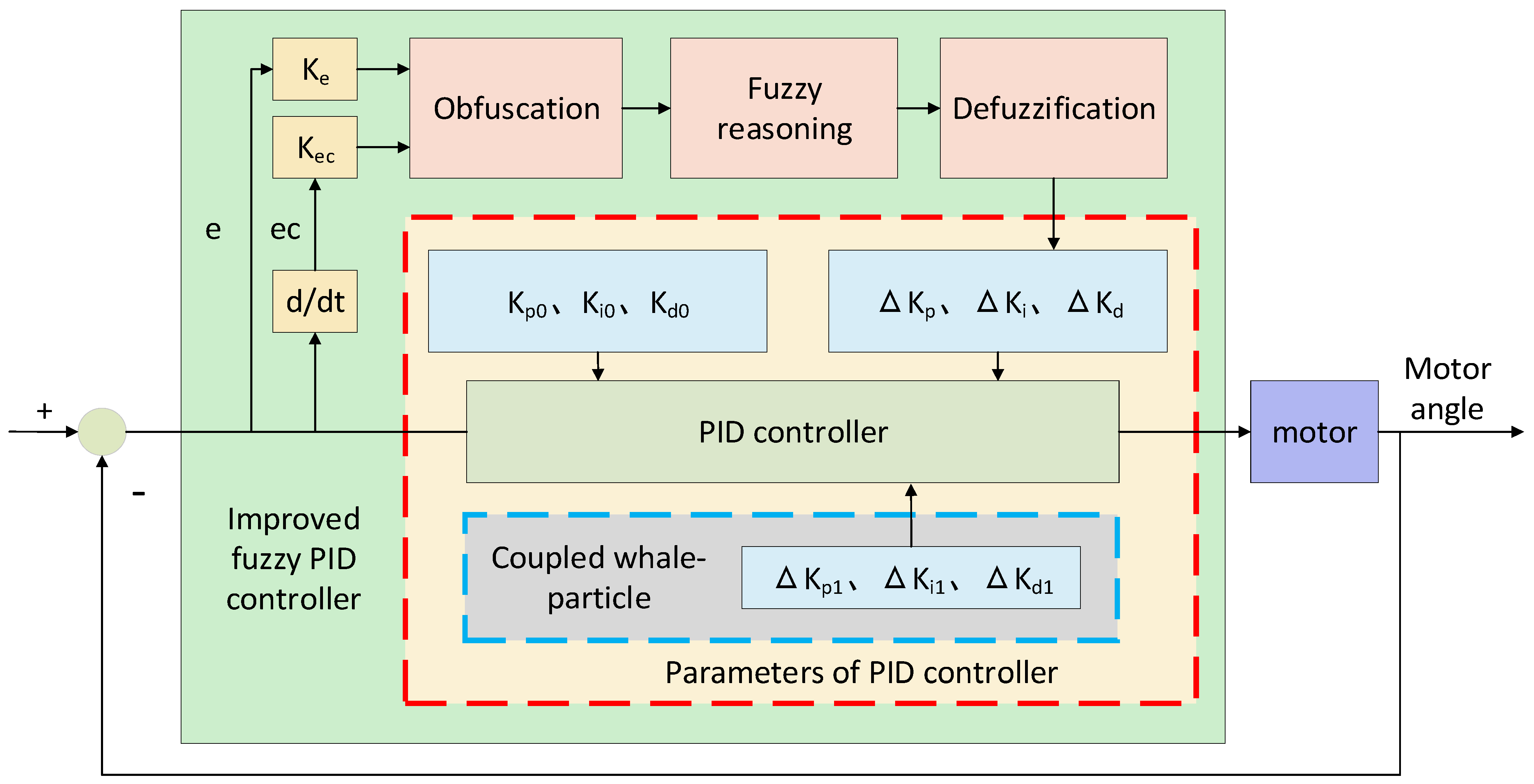
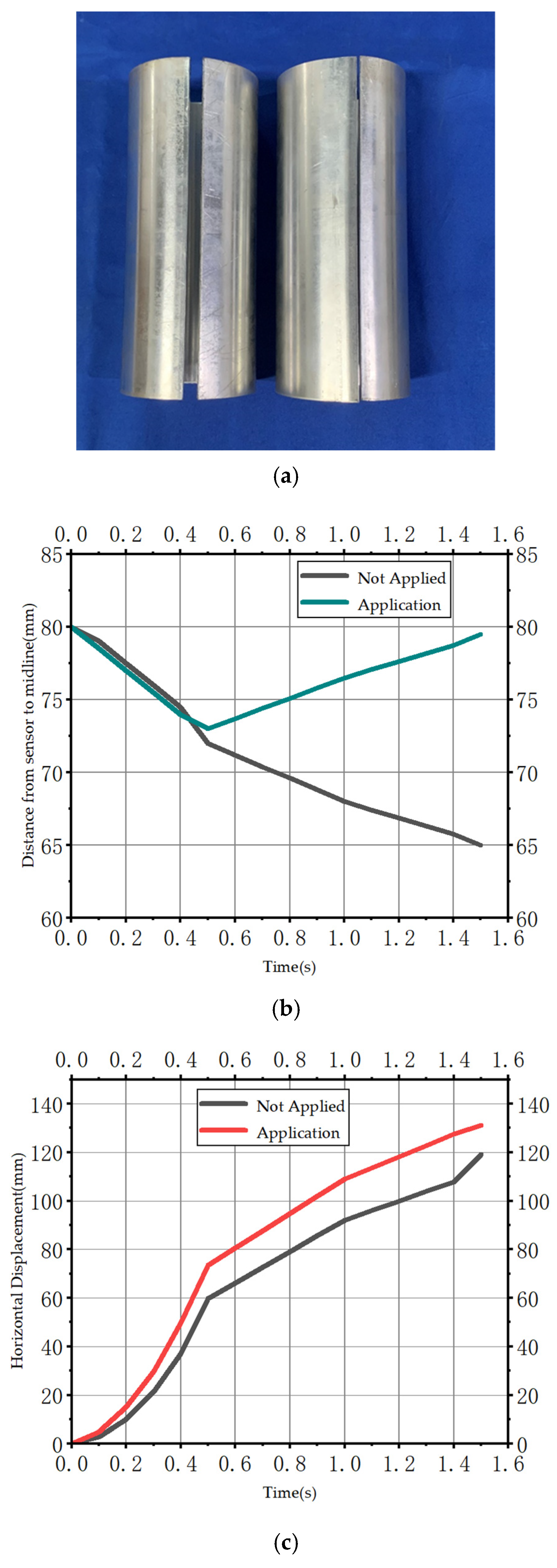
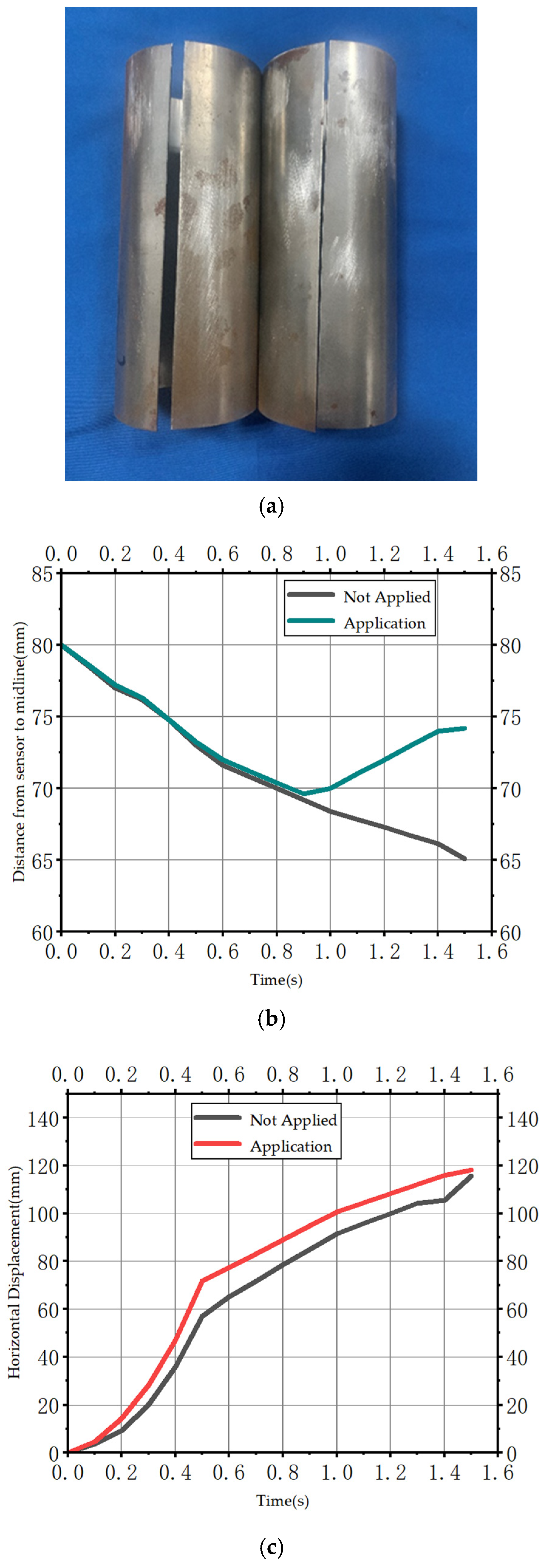
Within a circular rolling cycle, the desired motor rotation angle corresponding to the desired forming radius is input into the improved fuzzy PID controller. The horizontal displacement of the slider is achieved by controlling the motor rotation angle. The wedge then transforms the horizontal displacement of the slider into the vertical displacement of the driven roll, thereby altering the gap between the driving roll and the driven roll to attain the desired rolling angle. To ensure the accuracy and precision of the circular rolling process, an angle encoder is employed to monitor the motor rotation angle and feed it back to the controller. Additionally, a distance sensor is utilized to monitor the springback amount. The fuzzy PID controller is optimized through the CWP algorithm proposed in this paper. This enables real-time reduction in the motor rotation angle difference and correction of the generated springback, ultimately achieving an accurate rolling angle.

3.1. Design of the Fuzzy PID Controller

3.1.1. Input and Output Functions

The improved fuzzy PID control structure is depicted in Figure 6. Through the utilization of Gaussian-type and triangular membership functions for fuzzification, the fuzzy subsets of the fuzzy input variables, namely, the error e, the rate of change in error $ec$, and the fuzzy output variables $\mathsf{\Delta }{K}_p$, $\mathsf{\Delta }{K}_i$, and $\mathsf{\Delta }{K}_d$ are defined as {NB, NM, NS, Z0, PS, PM, PB}. The basic domain of discourse for both the error and the rate of change in error is set to [−30, 30]. Finally, the output variables $\mathsf{\Delta }{K}_p$, $\mathsf{\Delta }{K}_i$, and $\mathsf{\Delta }{K}_d$ are obtained through fuzzification inference using the centroid method. The membership functions of the inputs and outputs are presented in Figure 7.

Furthermore, the initial assigned values of the PID parameters, namely $K_{p0}$, $K_{i0}$, and $K_{d0}$ were obtained through the trial-and-error methodology. The specific parameter values are presented in

Table 2. Controller parameters.

Parameter	Numerical Value
$K_e$	0.1
$K_{ec}$	0.1
$K_{p0}$	50
$K_{i0}$	1
$K_{d0}$	10

. Subsequently, the CWP optimization algorithm is employed to iteratively seek the optimal values of the PID parameters, resulting in the final values $K_{p1}$, $K_{i1}$, and $K_{d1}$. The final PID parameter values of the controller are derived by means of the following equations, thereby ultimately achieving the control of the motor rotation angle:

$$\left\{\begin{array}{c}P=Kp0+\mathsf{\Delta }Kd+\mathsf{\Delta }Kp1\\ I=Ki0+\mathsf{\Delta }Ki+\mathsf{\Delta }Ki1\\ D=Kd0+\mathsf{\Delta }Kd+\mathsf{\Delta }Kd1\end{array}\right.$$

(15)

3.1.2. Fuzzy Control Rules

Through the Mamdani algorithm and the establishment of fuzzy rules, fuzzy inference is implemented to achieve fuzzy control. This enables precise regulation between the error e and the rate of change in error $ec$, ultimately fulfilling the objective of system adjustment. The formulated fuzzy rules are presented in

Table 3. Fuzzy rules.

$\mathit{e}$	$\mathit{e}\mathit{c}$
	NB	NM	NS	Z0	PS	PM	PB
NB	PB/PB/PB	PB/PB/PB	PB/PB/PB	PB/PB/NB	PS/NS/NB	Z0/NM/NM	NS/NB/NS
NM	PB/PB/PB	PB/PB/PB	PM/PM/PM	PM/PM/NM	Z0/NM/Z0	NS/NB/PS	NM/NB/PM
NS	PB/PB/PB	PM/PM/PM	PM/PS/PM	PS/PS/NS	NS/NB/PM	NM/NB/PB	NB/NB/PB
Z0	Z0/Z0/Z0	Z0/Z0/Z0	Z0/Z0/Z0	Z0/Z0/Z0	Z0/Z0/Z0	Z0/Z0/Z0	Z0/Z0/Z0
PS	NB/NB/PB	NM/NB/PB	NS/NB/PM	PS/PS/NS	PM/PS/PM	PM/PM/PM	PB/PB/PM
PM	NM/NB/PM	NS/NB/PS	Z0/NM/Z0	PM/PM/NM	PB/PM/PM	PB/PB/PB	PB/PB/PB
PB	NS/NB/NS	Z0/NM/NM	PS/NS/NB	PB/PB/NB	PB/PB/PB	PB/PB/PB	PB/PB/PB

, and the relationships between the fuzzy output variables $\mathsf{\Delta }{K}_p$, $\mathsf{\Delta }{K}_i$, $\mathsf{\Delta }{K}_d$ and $e$, $ec$ are depicted in Figure 8.

3.2. CWP Algorithm Optimization

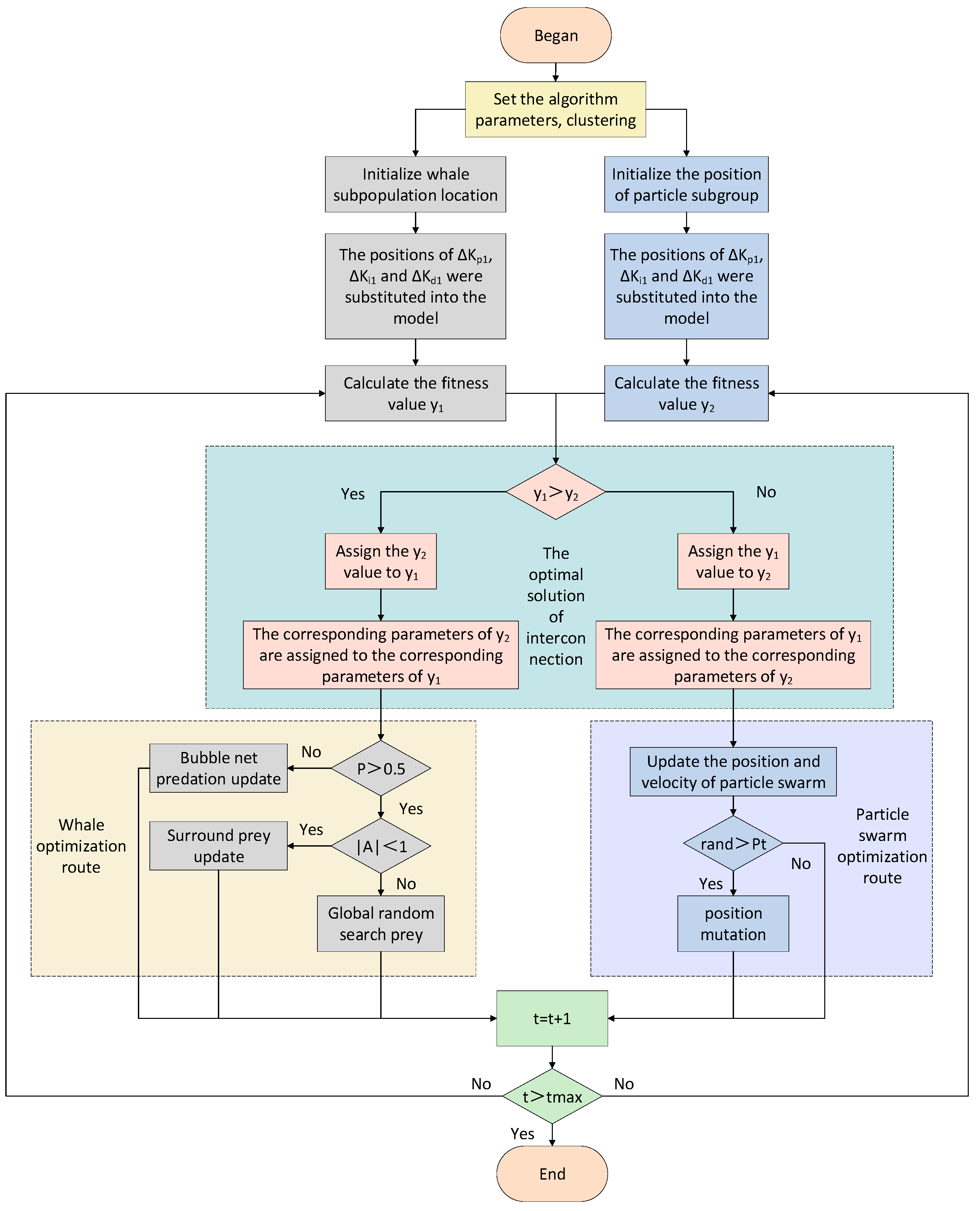
The coupled whale particle (CWP) algorithm integrates the rapid convergence property of the whale optimization algorithm (WOA) and the global search characteristic of the particle swarm optimization (PSO). It is designed to identify the optimal solution in a more expeditious and precise manner, thereby reducing the search space and curbing the consumption of computational resources. By minimizing the convergence deviation, it enhances the overall accuracy of the algorithm. Moreover, this algorithm can be applied to a diverse range of scenarios, circumventing the ineffectiveness of a single algorithm in certain specific situations. In the CWP algorithm, particles are partitioned into two independent search groups. The random parameters of these two groups are initialized, and their corresponding fitness values are computed. Subsequently, the smaller (i.e., superior) fitness value is extracted, which serves as the optimal solution for the current parameters. The optimal solutions are shared among the groups, and the next iteration commences. This process persists until the iteration terminates, at which point the optimal parameter results are output. Figure 9 illustrates the overall procedure of the CWP algorithm for optimizing the parameters of the fuzzy PID controller.

Initially, prior to the commencement of the CWP algorithm, parameters are set, and particles are divided into two sub-populations as required. The positions of the two sub-populations are initialized. The integral of time-multiplied absolute error (ITAE) is adopted as the fitness value, which serves as the criterion for determining the optimization process. Assuming the simulation time is 1 s, the corresponding fitness value y is expressed by the following formula:

$$y={\displaystyle {\int }_0^1\left|e\right|}dt\mathrm{a}=1,$$

(16)

The positions of the two sub-populations are substituted into the model to calculate their respective fitness values. These two fitness values are then compared, and the smaller one is taken as the optimal solution for the current iteration. This optimal solution is assigned to the other sub-population. Meanwhile, the two sub-populations continue to search for the optimal solution along their own trajectories.

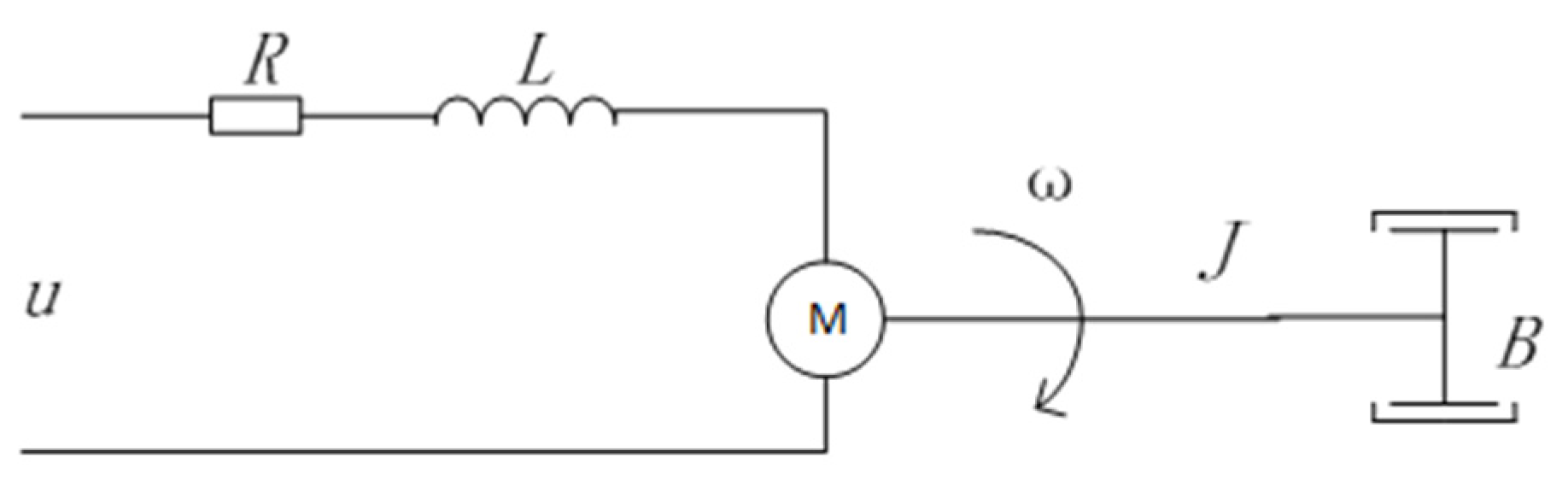
In the electromechanical control model, the system state variable x selects the current $i$, the rotational speed $\omega$, and the rotation angle $\theta$ of the motor (1), that is, $x=\left[i,\omega ,\theta \right]$. Combined with the display relationship $\overrightarrow{X}=D_2={\displaystyle \frac{\theta D_3}{2\pi }}$ between the position vector $\overrightarrow{X}$ and the system state $x$, the control of $D_2$ is achieved by adjusting $\omega$ to find the optimal state.

In the whale optimization route, it is necessary to determine whether the predation probability p > 0.5. If not, the bubble-net predation update is carried out. The updated formula and the expressions of the relevant parameters are as follows [25]:

$$\left\{\begin{array}{l}\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{best}\left(t\right)+\omega \cdot |{\overrightarrow{X}}_{best}\left(t\right)-\overrightarrow{X}\left(t\right)|\cdot e^l\cdot cos\left(2\pi l\right)\\ l=1+rand\cdot \left(-2-{\displaystyle \frac{t}{t_{\max }}}\right)\\ \omega =1-{\displaystyle \frac{t}{t_{\max }}}\end{array}\right.$$

(17)

If the predation probability is p > 0.5, then it is necessary to further determine whether |A| < 1. If so, the update is carried out in accordance with the prey-encircling method. The updated formula and the expressions of the relevant parameters are as follows:

$$\left\{\begin{array}{l}\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{best}\left(t\right)-\omega \cdot \overrightarrow{A}\cdot \left|\overrightarrow{C}\cdot {\overrightarrow{X}}_{best}\left(t\right)-\overrightarrow{X}\left(t\right)\right|\\ \overrightarrow{A}=2a\cdot \overrightarrow{r_1}-a\\ \overrightarrow{C}=2\overrightarrow{r_2}\end{array}\right.$$

(18)

$$a=2-2\sin \left({\displaystyle \frac{t}{2t_{\max }}}\pi \right)$$

(19)

If not |A| < 1, the prey is updated according to the global random search. The formula is as follows:

$$\overrightarrow{X}\left(t+1\right)=\overrightarrow{X_r}\left(t\right)-\overrightarrow{A}\cdot \left|\overrightarrow{C}\cdot \overrightarrow{X_r}\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$

(20)

Among them, $\overrightarrow{A}$ and $\overrightarrow{C}$ are coefficient vectors, and |A| represents the absolute value of the coefficient vector $\overrightarrow{A}$, which indicates the optimization speed and magnitude of encircling the prey and random search. ${\overrightarrow{X}}_{best}\left(t\right)$ is the position vector of the best solution obtained so far, $\overrightarrow{X}$ is the current position vector, and $\overrightarrow{X}\left(t+1\right)$ is the updated position vector. Here, $a$ decreases from 2 to 0 during the iterative process, $\overrightarrow{r_1}$ and $\overrightarrow{r_2}$ are random vectors within the range of [0, 1], $l$ is a random number uniformly distributed in the range of [−1, 1], and $\overrightarrow{X_r}\left(t\right)$ is the position of the current random individual.

In the other optimization route, the positions and velocities of the sub-populations are first updated according to the particle swarm optimization approach [26,27]. The relevant expressions are as follows:

$$v_{ij}={\omega }_{PSO}\cdot v_{ij}+c_1\cdot rand\cdot \left(X_{pb}-X_{ij}\right)+c_2\cdot rand\cdot \left(X_{gb}-X_{ij}\right)$$

(21)

$$X_{ij}=X_{ij}+V_{ij}$$

(22)

$${\omega }_{PSO}=\left({\omega }_{\max }-{\omega }_{\min }\right)\cdot {\left({\displaystyle \frac{t_{\max }-t}{t_{\max }}}\right)}^2+{\omega }_{\min }$$

(23)

$$c_1=\left(c_{1\max }-c_{1\min }\right){\left({\displaystyle \frac{t}{t_{\max }}}\right)}^2+\left(c_{1\min }-c_{1\max }\right){\displaystyle \frac{2t}{t_{\max }}}+c_{1\max }$$

(24)

$$c_2=\left(c_{2\min }-c_{2\max }\right){\left({\displaystyle \frac{t}{t_{\max }}}\right)}^2+\left(c_{2\max }-c_{2\min }\right){\displaystyle \frac{2t}{t_{\max }}}+c_{2\min }$$

(25)

Next, it is necessary to determine whether the current random number rand is greater than the mutation probability Pt. If so, position mutation is carried out; if not, the next step is carried out. The mutation probability and the expressions for position mutation are as follows:

$$Pt=\left(P_{\max }-P_{\min }\right)-\left(P_{\max }-P_{\min }\right)\cdot \cos \left(\pi \cdot {\displaystyle \frac{t}{t_{\max }}}\right)$$

(26)

$$j=ceil(3\cdot rand)$$

(27)

$$X_{ij}\left(t\right)=X_{ij}\left(t\right)+\left(1-{\displaystyle \frac{t}{t_{\max }}}\right)\cdot rand\cdot X_{ij}\left(t\right)$$

(28)

Here, $v_{ij}$ represents the updated velocity of the particle swarm, $X_{ij}$ is the updated position of the particle swarm, $X_{pb}$ denotes the individual optimal extreme value, and $X_{gb}$ represents the global optimal extreme value. $rand\in \left[0,1\right]$ is a random number. ${\omega }_{pso}$ is the PSO inertia weight, ${\omega }_{\max }$ is the maximum PSO inertia weight, and ${\omega }_{\min }$ is the minimum PSO inertia weight. $c_{1\max }$ is the maximum value of the learning factor $c_1$, $c_{1\min }$ is the minimum value of the learning factor $c_1$, $c_{2\max }$ is the maximum value of the learning factor $c_2$, and $c_{2\min }$ is the minimum value of the learning factor $c_2$. $p_{\max }$ is the maximum mutation probability, $p_{\min }$ is the minimum mutation probability, $P_t$ is the current mutation probability, $X_{ij}\left(t\right)$ is the current position of the particle, $rand$ is a random number between 0 and 1, and ceil indicates rounding up.

Finally, it is determined whether the number of iterations has been reached. If it has been reached, the process ends; if not, the updated positions are substituted into the model to calculate the fitness value, and the next cycle is entered.

To ensure a reasonable optimization range, the optimization parameters ΔKp1, ΔKi1, and ΔKd1 are, respectively, set to take values within the intervals [−50, 50], [−5, 5], and [−50, 50]. The parameters of each algorithm are configured as presented in

Table 4. Parameters of each algorithm.

Parameter	Numerical Value
${\omega }_{\max }$	0.9
${\omega }_{\min }$	0.2
$c_{1\max }$	2
$c_{1\min }$	1.3
$c_{2\max }$	1.7
$c_{2\min }$	0.6
$p_{\max }$	0.5
$p_{\min }$	0.1
Population size	20
$t_{\max }$	10

.

3.3. Simulation Analysis of CWP

To further verify the superiority of the springback compensation control strategy using the CWP optimization algorithm, under the same conditions, MATLAB/Simulink (Version R2021b) was employed to simulate the control effects of the circular roll forming process with and without the springback compensation control strategy, as well as with and without CWP optimization.

To simulate the springback of the sheet metal during the circular rolling process, a springback interference quantity is added in the simulation. When the springback of the sheet metal is detected by the distance sensor, the controller adopting the springback compensation strategy will adjust the motor rotation angle to change the gap between the working roll and the driven roll, ultimately correcting the springback of the sheet metal. In contrast, the controller without the springback compensation strategy only adjusts the motor rotation angle based on the feedback from the encoder.

The simulation results of the circular roll forming control are shown in Figure 10 (all three curves use the encoder as feedback). The curve without the springback compensation strategy fails to respond to the springback during the forming process and ultimately cannot reach the desired forming value. The curve that adopts the springback compensation and is controlled by the traditional fuzzy PID can eventually reach the expected value, yet the response during the control process is too slow, the overshoot is excessive, and the robustness is low, which is not conducive to actual production forming. The control strategy using springback compensation and the fuzzy PID controller optimized by CWP has higher control accuracy. It can not only ensure control precision but also maintain relatively stable operation during the control process, with a small overshoot and a fast response speed, meeting the requirements of the actual production process. The specific numerical values of various parameters for the three curves are presented in

Table 5. Control result parameter values.

Control Simulation	Rise Time, t/s	Peak Time, t/s	Overshoot, δ/%	Control Error, e/%
Without CWP optimization	0.5087	0.86	23.04	0.162
After CWP optimization	0.2139	0.31	0.99	0.004

.

The core of this research focuses on the construction of the system architecture and the verification of basic functions. For Figure 8 and Figure 10, our main concern is the impact of springback interference on the performance of the controller. By simulating the springback phenomenon of sheet metal in actual production, we incorporate the key factor of springback interference into the model. Although some preliminary explorations have been conducted regarding measurement noise or control delays, they have not reached a stage where they can be comprehensively and systematically presented. Currently, our emphasis is on establishing a fundamental understanding of the controller’s performance under idealized conditions.

To validate the core functions of the proposed roll bending process control scheme, regarding the performance of the optimization algorithm, our primary objective is to demonstrate the effectiveness of the entire control system in achieving precise roll bending results. Our work mainly revolves around the roll bending results, and using the proposed method, we have significantly improved the forming quality in these results.

Compared with the fuzzy PID control without CWP optimization, the response speed of the optimized fuzzy PID control has increased by 57.95%, the overshoot has decreased by 22.05%, and the control error has decreased by 0.158%.

4. Experimental Verification

The equipment utilized in the experiment is a prototype of a horizontal upward-adjusting three-roll plate bending machine (Wuhan, China). In order to verify the universality of the kinematic model for circular rolling springback compensation, the horizontal upward-adjusting three-roll plate bending machine was used to carry out roll bending experiments on aluminum alloy plates, Q235 steel plates, and 20 steel plates. The desired radius was set at 40 mm. The results are presented in

Table 6. Roll forming results.

Material	Expected Radius	Not Applying the Springback Compensation Strategy to Roll Radius	Applying the Springback Compensation Strategy to Roll Radius
Aluminum alloy	40 mm	42.16 mm	40.64 mm
Q235 Steel	40 mm	42.13 mm	40.62 mm
20 Steel	40 mm	42.21 mm	40.69 mm

, and the forming effects are shown in Figure 11, Figure 12 and Figure 13. When the springback compensation strategy was not applied, the errors between the circular roll forming radii and the desired radius for the aluminum alloy plate, Q235 steel plate, and 20 steel plate were 5.40%, 5.32%, and 5.52%, respectively. After the implementation of the springback compensation strategy, the errors between the circular roll forming radii and the desired radius for the aluminum alloy plate, Q235 steel plate, and 20 steel plate were reduced to 1.60%, 1.55%, and 1.72%, respectively. This demonstrates that the kinematic model for circular rolling springback compensation can effectively predict the circular roll forming radius.

Figure 11a shows the effect of the circular roll forming of the aluminum alloy sheet metal. In the figure, for the cylinder on the left during the rolling process, the springback compensation strategy was not applied, while for the cylinder on the right during the rolling process, the springback compensation strategy was applied. In Figure 11b,c, “Not Applied” indicates that the springback compensation strategy was not applied, and “Application” indicates that the springback compensation strategy was applied.

5. Conclusions

This paper addresses the issue of metal sheet springback affecting the accuracy of circular roll forming and proposes a springback compensation control strategy. Through theoretical analysis and experimental research, the following conclusions are drawn:

(1)

Based on the mechanical principle of sheet springback during the circular roll forming process, a kinematic model for circular rolling springback compensation is established. This model, relying on the principle of the linkage between motor drive and mechanical structure, adjusts the gap between the working roll and the driven roll by controlling the rotation angle of the motor, thereby adjusting the rolling angle of the bending roll to achieve springback compensation and real-time adjustment of the forming radian of the sheet.

(2)

Comparative experimental results show that, after applying the springback compensation strategy, the errors between the circular roll forming radii and the desired radius for aluminum alloy, Q235 steel plate, and 20 steel plate are reduced to 1.60%, 1.55%, and 1.72%, respectively, effectively reducing the forming errors caused by sheet springback.

Although certain achievements have been made in this study, there are still some limitations. Currently, this research only focuses on the relationship between springback and rolling angle. In the follow-up, it is possible to conduct an in-depth exploration of the influence laws of various factors such as the material, temperature, and rolling speed of the sheet on springback, providing a more comprehensive theoretical basis for the optimization of the control strategy.