Optimizing Screw Fixation in Total Hip Arthroplasty: A Deep Learning and Finite Element Analysis Approach
Abstract
1. Introduction
2. Design and Methods
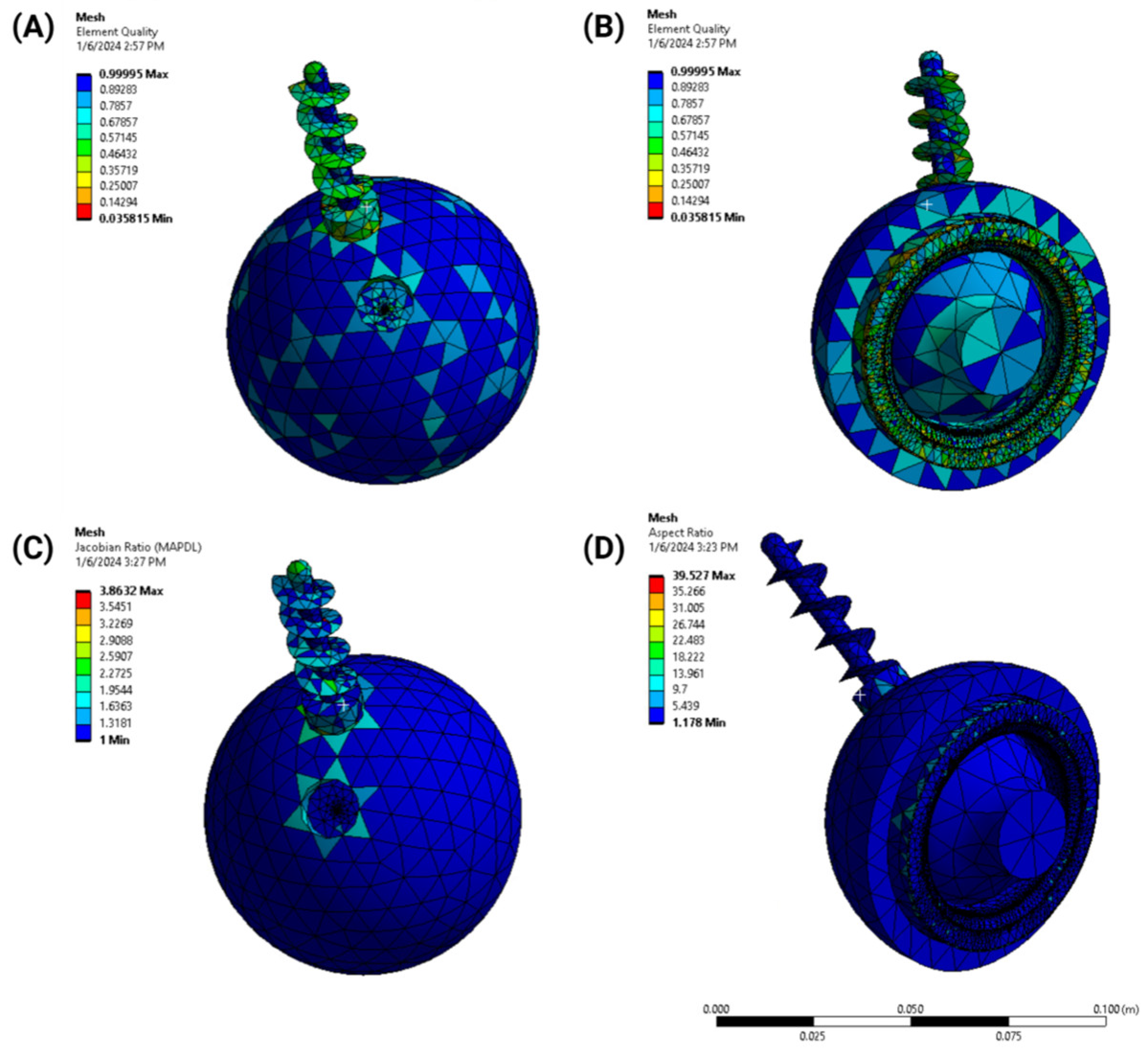
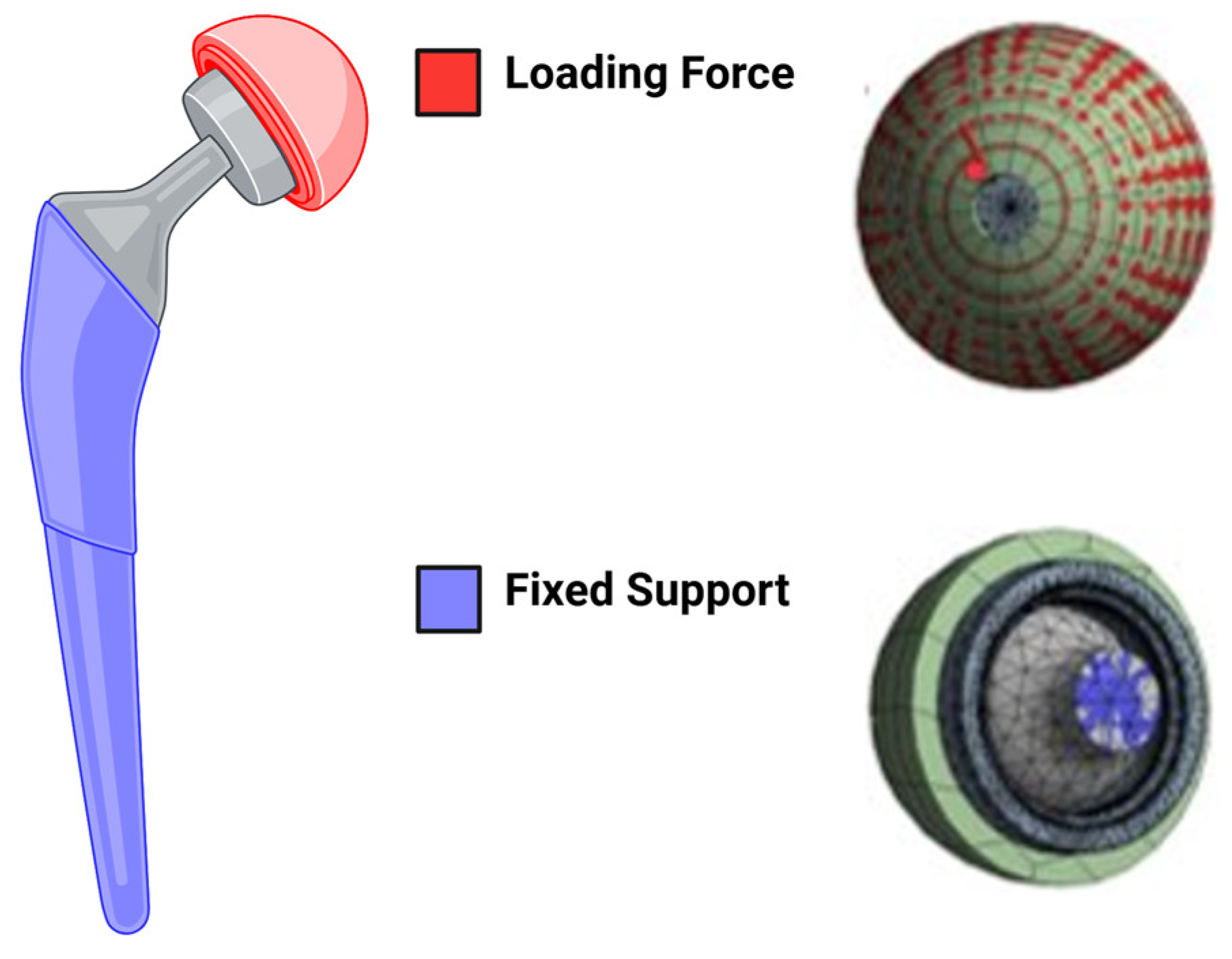
2.1. Finite Element Analysis Set Up
- Element quality: the aspect ratio and skewness of elements were analyzed to maintain numerical stability;
- Jacobian ratio: this was used to evaluate the geometric distortion of elements;
- Aspect ratio: the mesh was optimized to balance computational efficiency and accuracy, ensuring a high-quality representation of the implant geometry.
2.2. Design Optimization
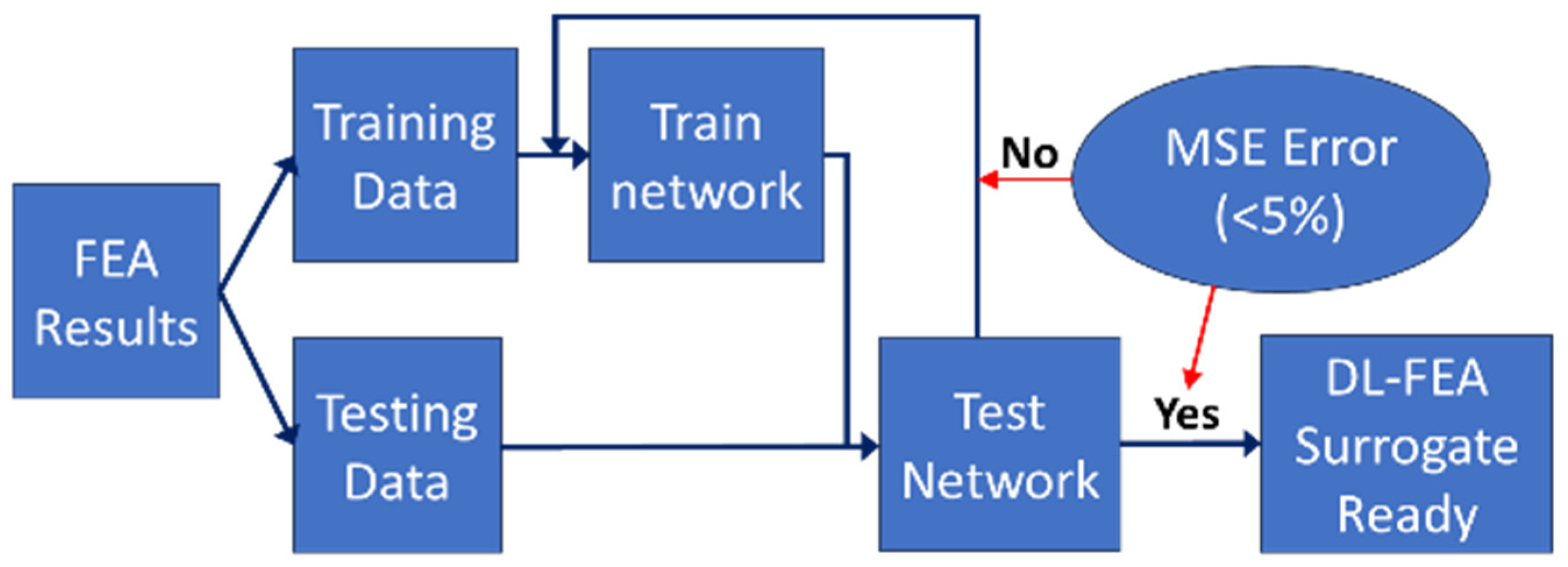
2.3. Deep Learning Surrogate Model
- Input: X-, Y-, Z-coordinates of the mesh;
- Hidden layers: fully connected layers with ReLU activation;
- Output: predicted stress values;
- Training: 80% of the data were used for training, 10% for validation, and 10% for testing.
2.4. Comparative Analysis
- Accuracy assessment: The DL-FEA model’s predictions were compared against traditional FEA results to evaluate stress–strain distributions. Mean squared error (MSE) and correlation coefficients were computed to quantify deviations in predicted deformation patterns.
- Computational efficiency evaluation: The processing times required for both traditional FEA and DL-FEA were recorded and compared. This involved measuring the computation time for multiple loading scenarios and assessing efficiency gains from using the DL-based surrogate model.
- Empirical validation: The DL-FEA model’s stress distribution outputs were cross-referenced with published experimental data on acetabular cup fixation. This comparison ensured that simulation outputs aligned with real-world implant behavior and failure mechanisms.
- Robustness and sensitivity analysis: The model’s response to variations in input parameters, such as material properties and boundary conditions, was analyzed. Sensitivity testing was performed to determine the stability of predictions under different simulation settings.
3. Results
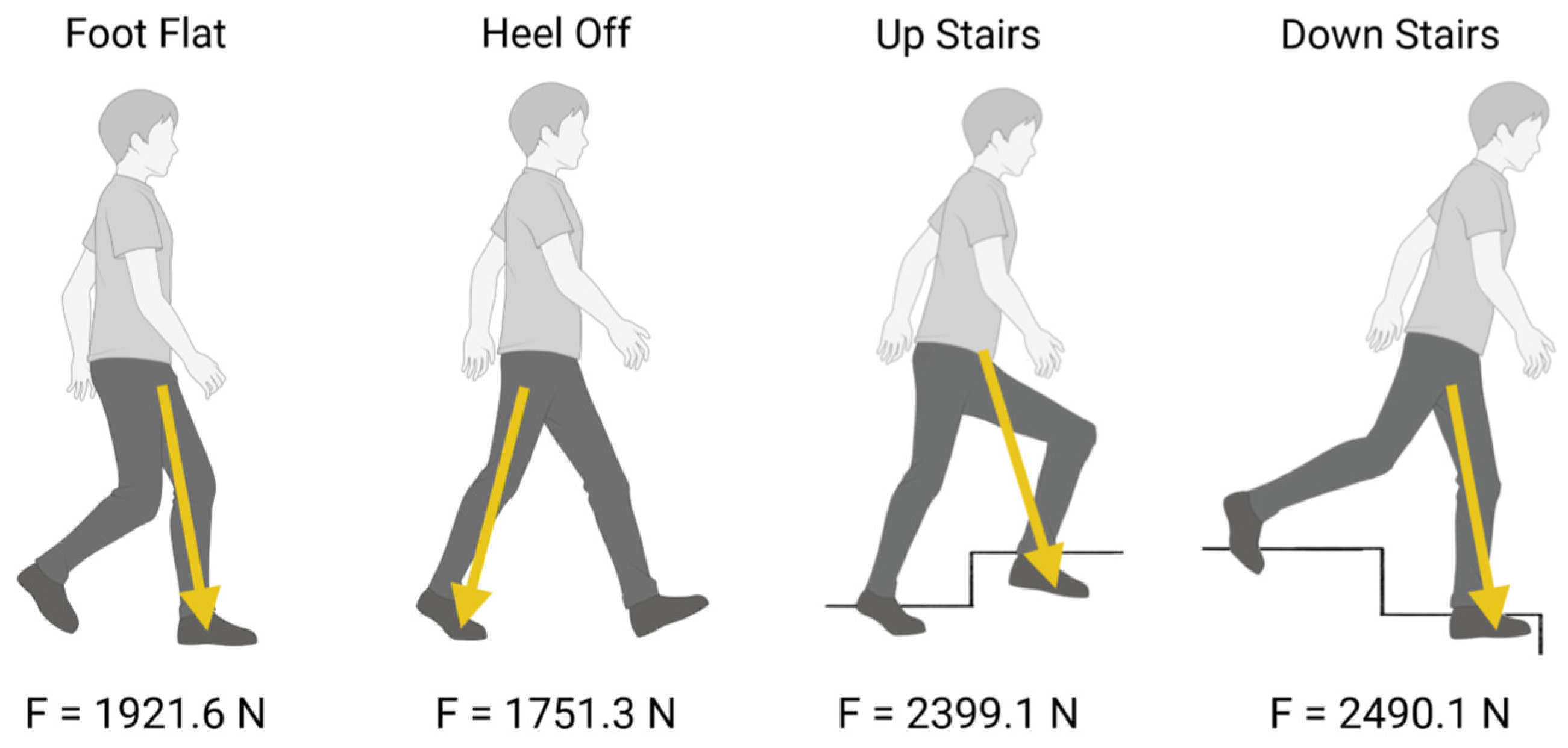
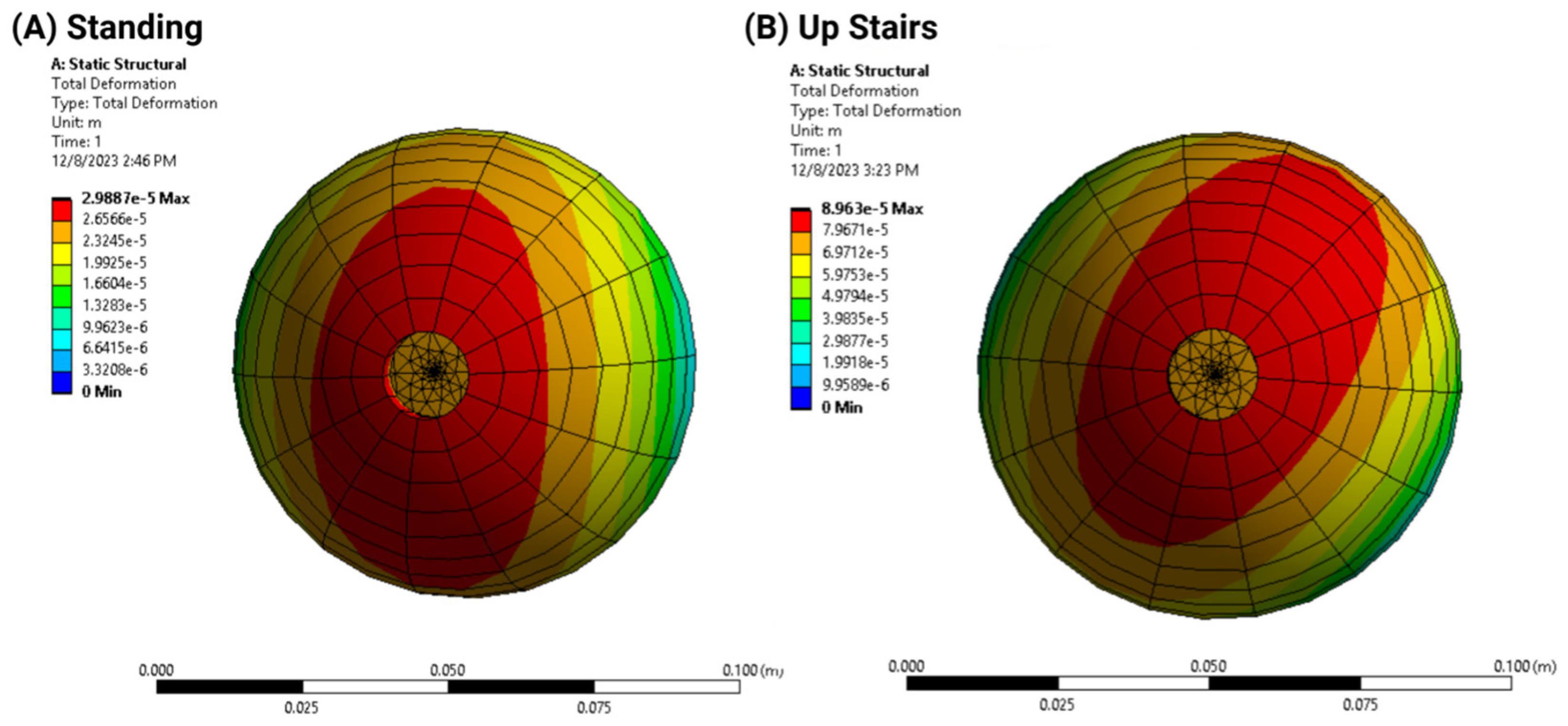
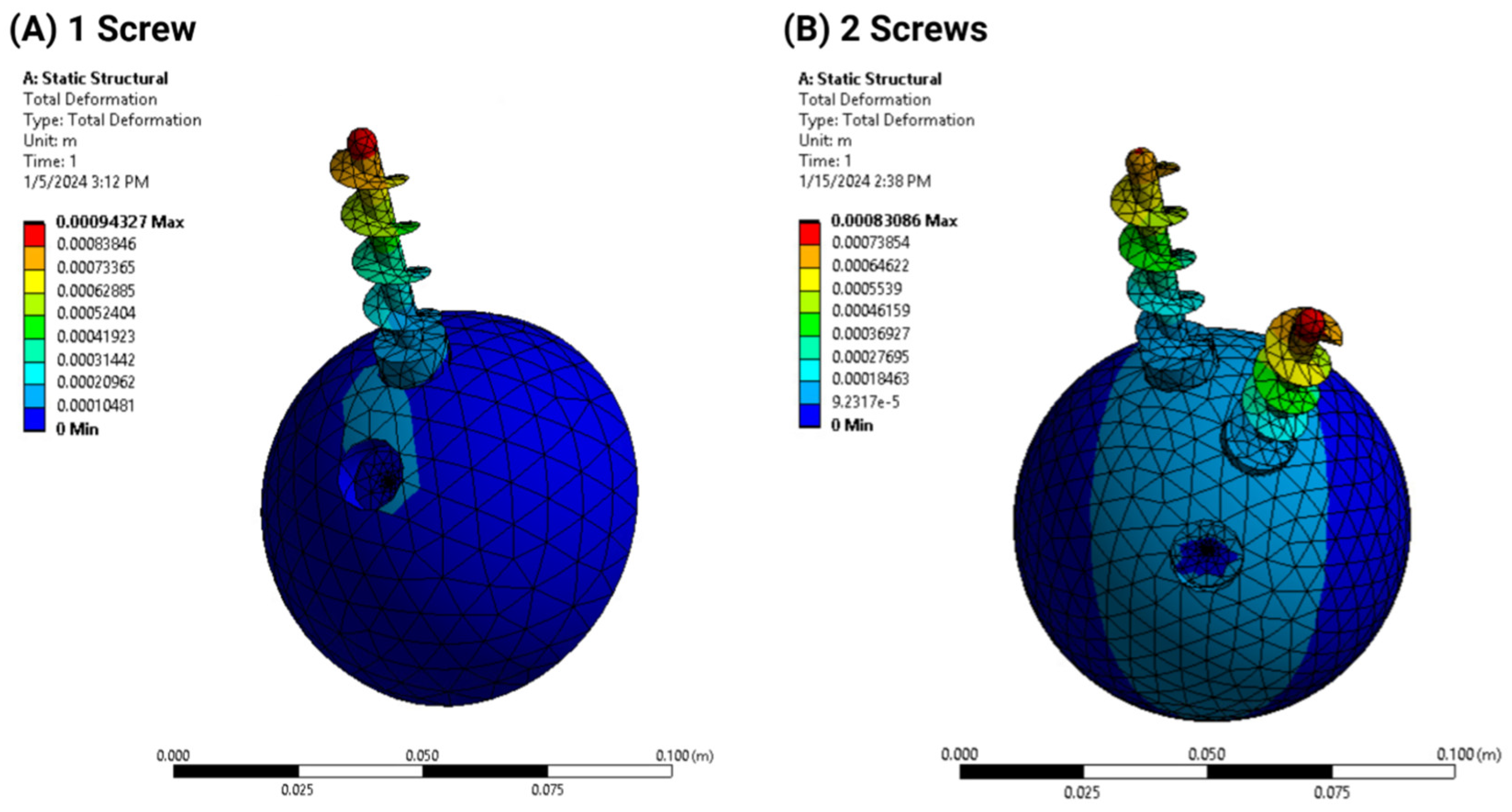
3.1. Finite Element Analysis
- Deformation distribution varied with screw configuration, with the 2-screw model exhibiting greater stability than the 1-screw model;
- Load simulations confirmed that additional screws reduced acetabular cup displacement but increased stress concentration in adjacent bone structures.
3.2. Design Optimization Outcomes
- Goodness of Fit: This figure illustrates the model’s predictive accuracy by comparing simulated values against experimental (reference) results. A high Goodness of Fit score indicates strong correlation and model reliability, ensuring that stress–strain distributions are accurately represented. Notably, the results indicate that higher accuracy is achieved when screw positioning is optimized, confirming the importance of precise placement.
- 3D Response Graph: This graph visualizes how different input parameters, such as screw position and material properties, influence key output variables, like stress and strain. Non-linear trends are highlighted, allowing for the identification of optimal configurations that minimize stress concentrations and maximize implant stability. The results show that improper screw angulation leads to uneven stress distribution, which can compromise implant integrity.
- Local Sensitivity Graph: This figure quantifies how small variations in design parameters affect the overall implant performance. By analyzing sensitivity across multiple variables, the graph helps determine which parameters have the most significant impact on stress distribution and fixation stability. The results emphasize that even minor deviations in bone density significantly impact screw fixation strength, reinforcing the need for patient-specific planning.
- Local Sensitivity Curves: These curves offer a detailed visualization of the sensitivity analysis results, illustrating how minor changes in specific input parameters influence the biomechanical behavior of the implant. This aids in refining implant design to enhance performance and reduce failure risks. The findings suggest that higher-grade titanium screws reduce peak stress concentrations, enhancing long-term stability.
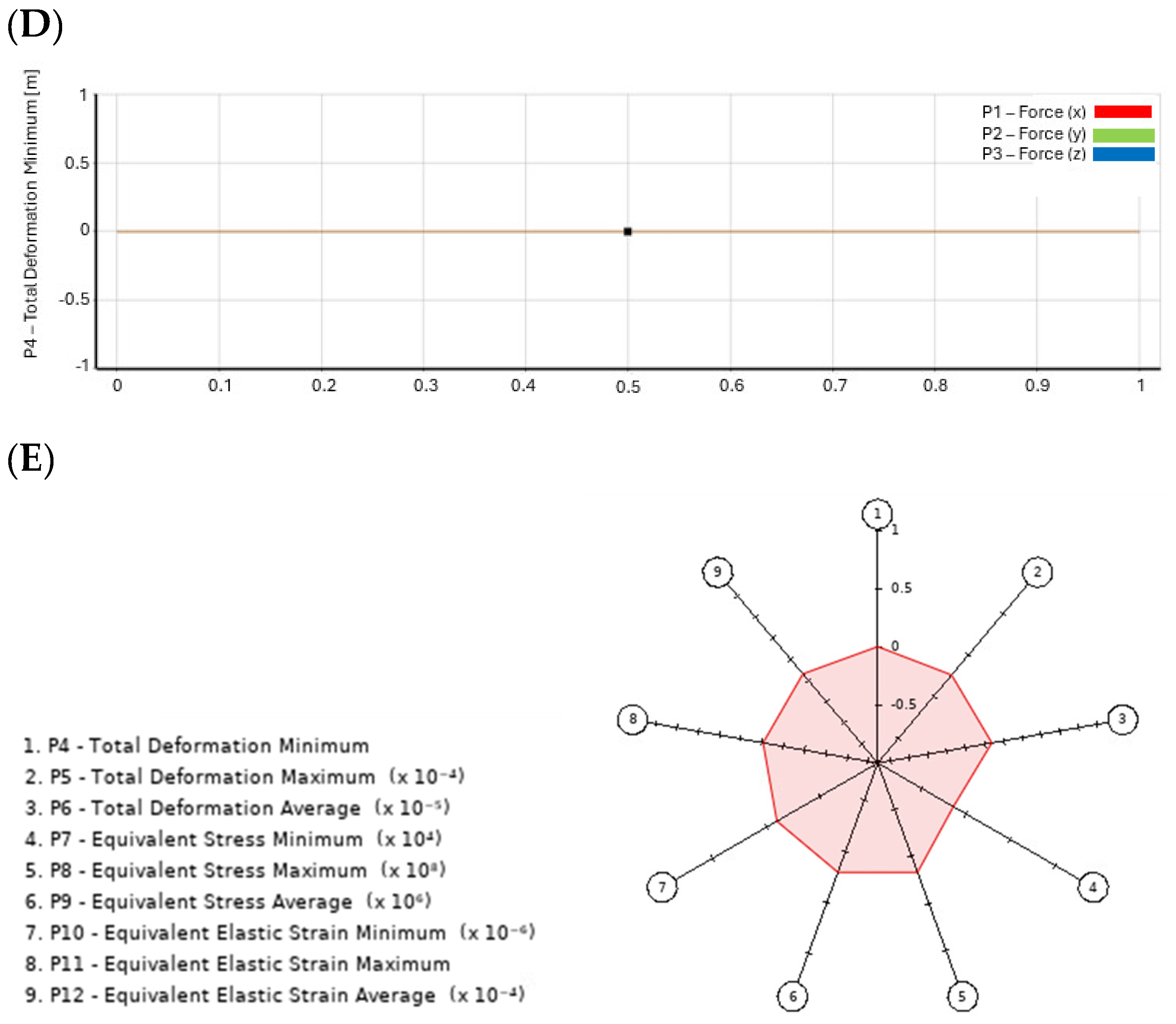
- Spider Chart (Radar Chart): The Radar Chart provides a comprehensive assessment of trade-offs between multiple design variables, such as implant orientation, bone quality, and screw fixation techniques. By mapping these interactions, the figure aids in selecting the most balanced and effective screw configuration for optimal implant performance. The results confirm that increasing screw length improves load distribution but may also elevate stress in adjacent bone structures, requiring a careful balance in design choices.

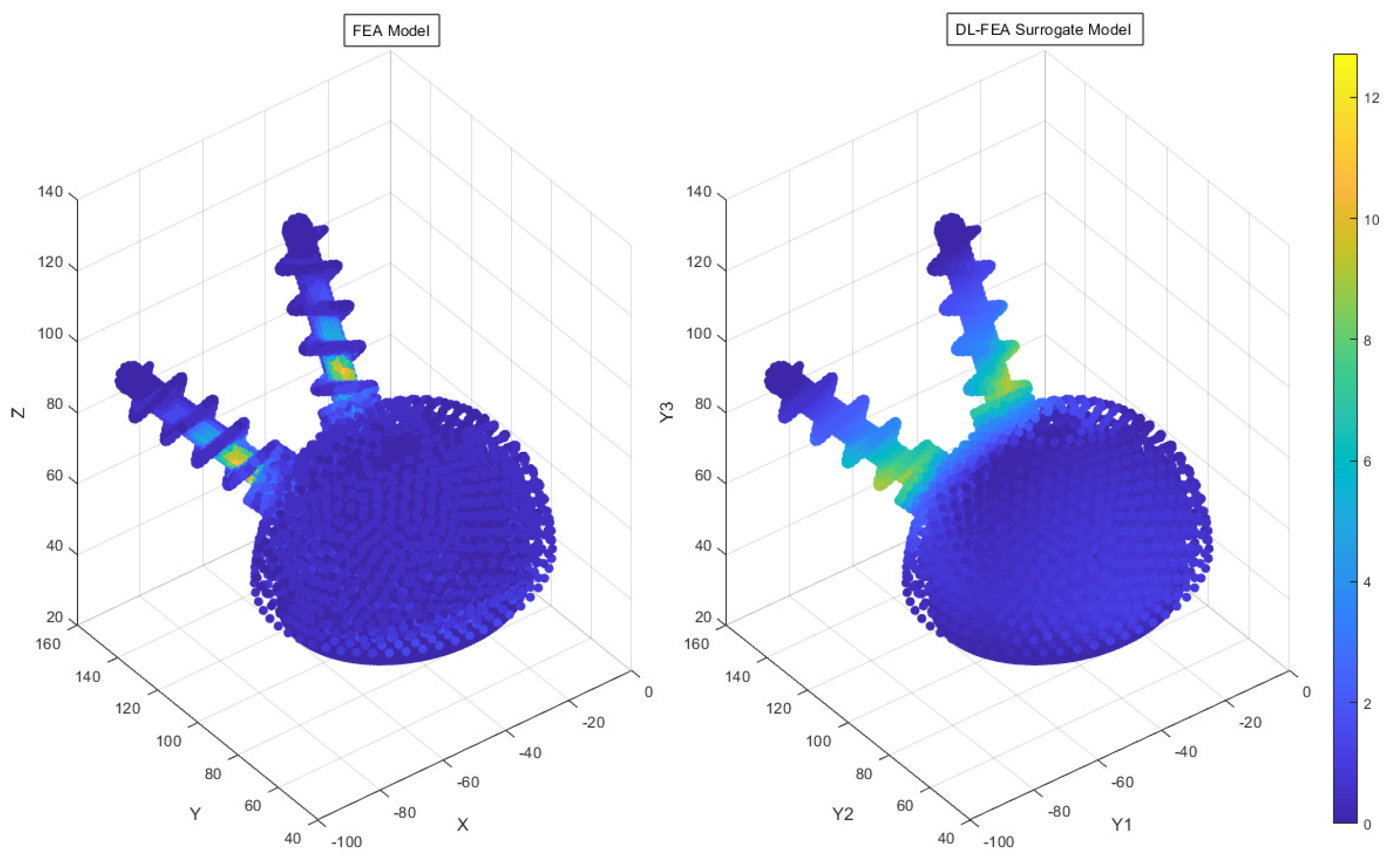
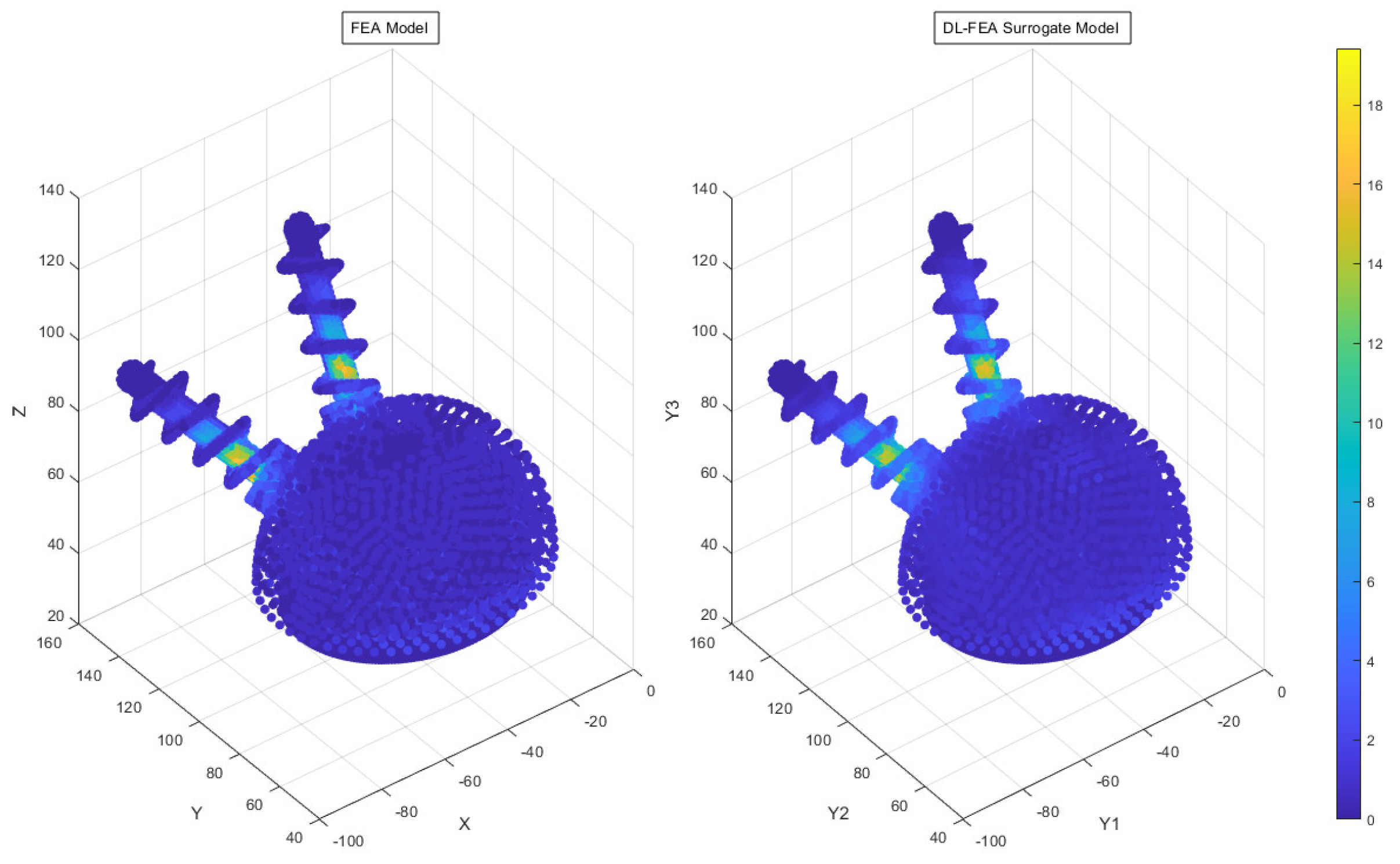
3.3. Deep Learning Model Analysis
3.4. Comparative Analysis Results
- Accuracy findings: The DL-FEA model demonstrated reasonable accuracy in replicating traditional FEA results, with an MSE of 24.06%. Minor deviations in high-stress regions indicate areas for future refinement.
- Computational efficiency gains: traditional FEA required extensive computation time for complex loading cases, whereas DL-FEA provided near-instantaneous predictions, highlighting its potential for real-time surgical planning.
- Empirical validation outcomes: the stress distribution patterns from DL-FEA closely aligned with empirical studies on acetabular cup fixation, supporting its reliability.
- Robustness and sensitivity insights: sensitivity analyses confirmed that DL-FEA maintained stability across varying input conditions, successfully adapting to changes in bone density and implant orientation, demonstrating its applicability for personalized implant optimization.
- Computational cost reduction: Traditional FEA requires extensive computation for complex loading scenarios, making real-time surgical planning impractical. In contrast, once trained, the DL-FEA model generates near-instantaneous predictions, eliminating the need for repeated full-scale simulations and significantly reducing processing time.
- Streamlined optimization process: Traditional FEA relies on manual parameter tuning and iterative analysis, making design optimization labor-intensive. DL-FEA automates this process using machine learning algorithms to predict optimal stress distributions, making data-driven optimization faster, and more efficient.
- Comparable predictive accuracy: While traditional FEA remains the gold standard for biomechanical modeling, the DL-FEA model demonstrated a reasonable MSE of 24.06%, effectively replicating deformation and stress–strain patterns. Future improvements, including expanding the dataset and refining neural network architectures, could enhance the accuracy further.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cieremans, D.; Shah, A.; Slover, J.; Schwarzkopf, R.; Meftah, M. Trends in Complications and Outcomes in Patients Aged 65 Years and Younger Undergoing Total Hip Arthroplasty: Data from the American Joint Replacement Registry. J. Am. Acad. Orthop. Surg. Glob. Res. Rev. 2023, 7, e22. [Google Scholar] [CrossRef] [PubMed]
- Kelmer, G.; Stone, A.H.; Turcotte, J.; King, P.J. Reasons for Revision: Primary Total Hip Arthroplasty Mechanisms of Failure. J. Am. Acad. Orthop. Surg. 2021, 29, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Angerame, M.R.; Fehring, T.K.; Masonis, J.L.; Mason, J.B.; Odum, S.M.; Springer, B.D. Early Failure of Primary Total Hip Arthroplasty: Is Surgical Approach a Risk Factor? J. Arthroplast. 2018, 33, 1780–1785. [Google Scholar] [CrossRef] [PubMed]
- Konow, T.; Baetz, J.; Melsheimer, O.; Grimberg, A.; Morlock, M. Factors Influencing Periprosthetic Femoral Fracture Risk. Bone Jt. 2021, 103, 650–658. [Google Scholar] [CrossRef]
- Zywiel, M.G.; Mustafa, L.H.; Bonutti, P.M.; Mont, M.A. Are Abductor Muscle Quality and Previous Revision Surgery Predictors of Constrained Liner Failure in Hip Arthroplasty? Int. Orthop. 2011, 35, 797–802. [Google Scholar] [CrossRef][Green Version]
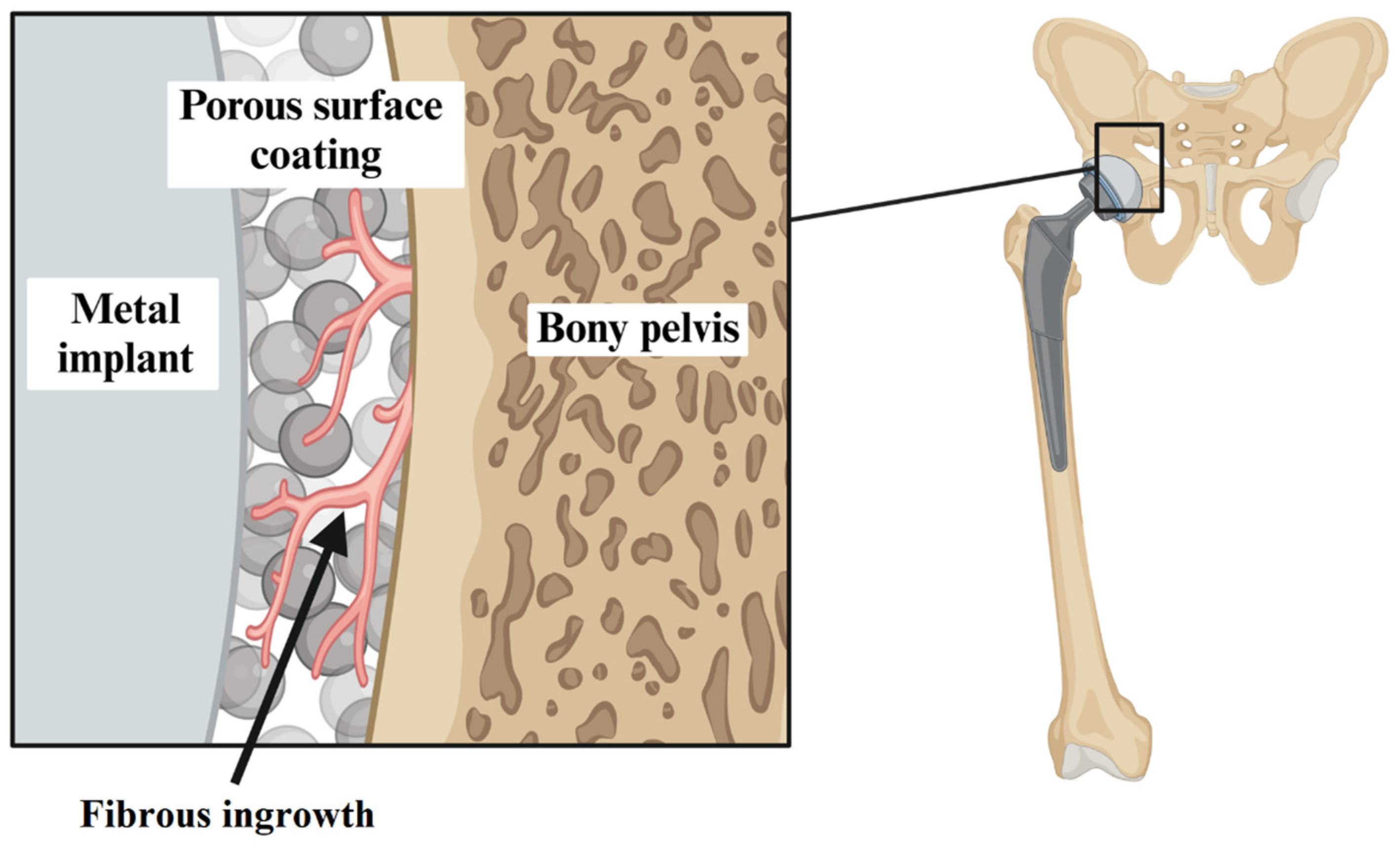
- Qin, Y.X.; McLeod, K.J.; Guilak, F.; Chiang, F.P.; Rubin, C.T. Correlation of Bony Ingrowth to the Distribution of Stress and Strain Parameters Surrounding a Porous-Coated Implant. J. Orthop. Res. 1996, 14, 862–870. [Google Scholar] [CrossRef]
- Nam, H.-J.; Lim, Y.-W.; Jo, W.-L.; Bahk, J.H.; Kwon, S.Y.; Park, H.C.; AlShammari, S.M. Is the Construct Stability of the Acetabular Cup Affected by the Acetabular Screw Configuration in Bone Defect Models? J. Orthop. Surg. Res. 2023, 18, 354. [Google Scholar] [CrossRef]
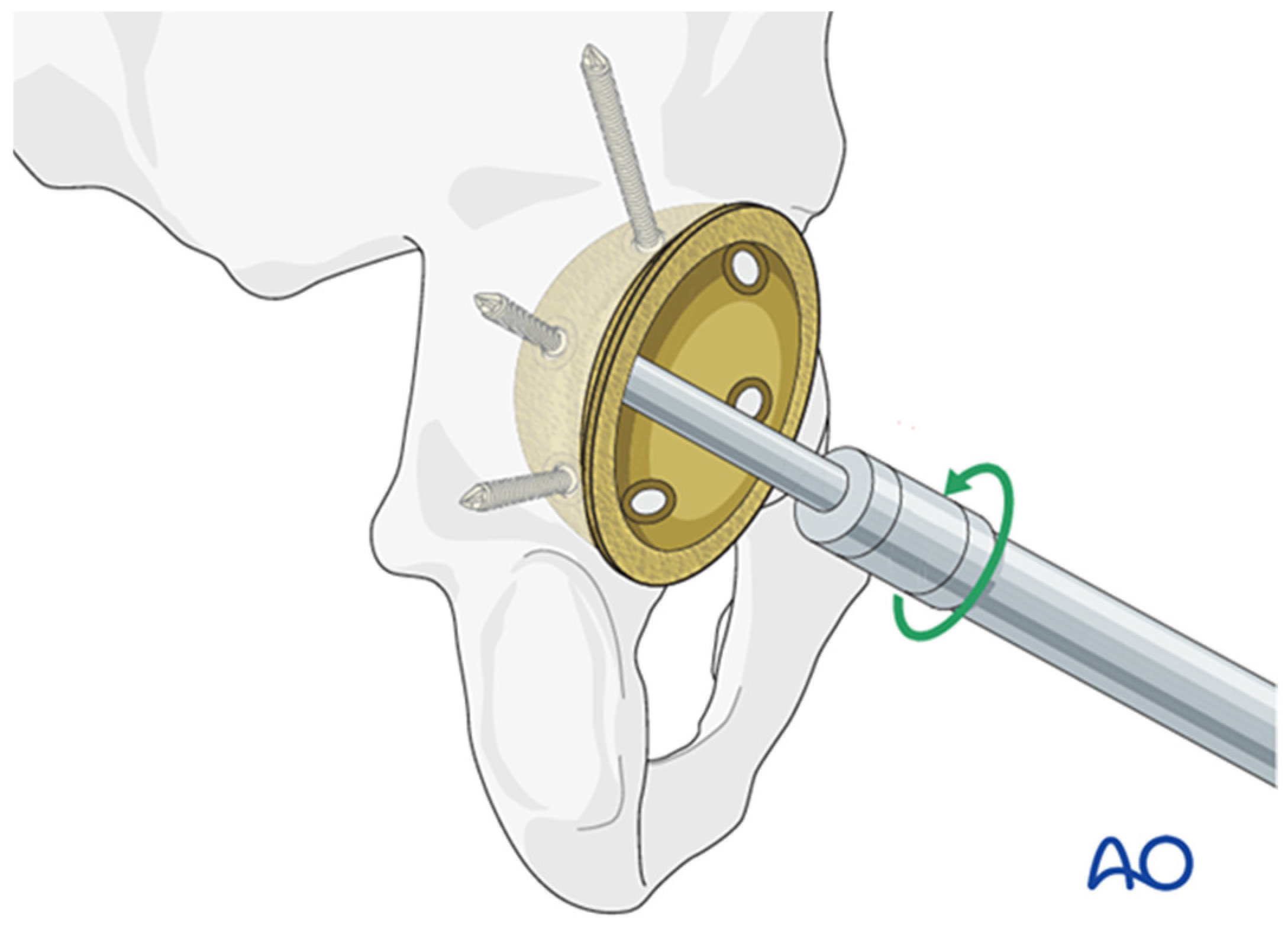
- AO Foundation; Total Hip Arthroplasty for Basicervical Femoral Neck Fractures. AO Surgery Reference: Davos, Switzerland, 2022. Available online: https://surgeryreference.aofoundation.org (accessed on 16 January 2025).
- Wasielewski, R.C.; Cooperstein, L.A.; Kruger, M.P.; Rubash, H.E. Acetabular Anatomy and the Transacetabular Fixation of Screws in Total Hip Arthroplasty. J. Bone Jt. Surg. Am. 1990, 72, 501–508. [Google Scholar] [CrossRef]
- Wasielewski, R.C.; Galat, D.D.; Sheridan, K.C.; Rubash, H.E. Acetabular Anatomy and Transacetabular Screw Fixation at the High Hip Center. Clin. Orthop. Relat. Res. 2005, 438, 171–176. [Google Scholar] [CrossRef]
- Ohashi, H.; Kikuchi, S.; Aota, S.; Hakozaki, M.; Konno, S. Surgical Anatomy of the Pelvic Vasculature, With Particular Reference to Acetabular Screw Fixation in Cementless Total Hip Arthroplasty in the Asian Population. J. Orthop. Surg. 2017, 25. [Google Scholar] [CrossRef]
- Meldrum, R.; Johansen, R.L. Safe Screw Placement in Acetabular Revision Surgery. J. Arthroplasty 2001, 16, 953–960. [Google Scholar] [CrossRef] [PubMed]
- Aguado-Maestro, I.; de Blas-Sanz, I.; Sanz-Peñas, A.E.; Campesino-Nieto, S.V.; Diez-Rodríguez, J.; Valle-López, S.; Espinel-Riol, A.; Fernández-Díez, D.; García-Alonso, M. Dual Mobility Cups as the Routine Choice in Total Hip Arthroplasty. Medicina 2022, 58, 528. [Google Scholar] [CrossRef] [PubMed]
- Davis, E.T.; Pagkalos, J.; Kopjar, B. Using an Asymmetric Crosslinked Polyethylene Liner in Primary Total Hip Arthroplasty Is Associated With a Lower Risk of Revision Surgery: An Analysis of the National Joint Registry. Bone Jt. J. 2021, 103, 1479–1487. [Google Scholar] [CrossRef]
- Fernandez, M.A.; Achten, J.; Parsons, N.; Griffin, X.L.; Png, M.-E.; Gould, J.; McGibbon, A.; Costa, M.L. Cemented or Uncemented Hemiarthroplasty for Intracapsular Hip Fracture. N. Engl. J. Med. 2022, 386, 521–530. [Google Scholar] [CrossRef]
- Lachiewicz, P.F.; Kleeman, L.T.; Seyler, T. Bearing Surfaces for Total Hip Arthroplasty. J. Am. Acad. Orthop. Surg. 2018, 26, 45–57. [Google Scholar] [CrossRef]
- Rogmark, C.; Nåtman, J.; Jobory, A.; Hailer, N.P.; Cnudde, P. The Association of Surgical Approach and Bearing Size and Type With Dislocation in Total Hip Arthroplasty for Acute Hip Fracture. Bone Jt. J. 2022, 104, 844–851. [Google Scholar] [CrossRef]
- Rogmark, C.; Nauclér, E. Dual Mobility Cups Do Not Reduce the Revision Risk for Patients With Acute Femoral Neck Fracture: A Matched Cohort Study From the Swedish Arthroplasty Register. Injury 2022, 53, 620–625. [Google Scholar] [CrossRef]
- Malahias, M.-A.; Ma, Q.-L.; Jang, S.J.; Loucas, M.; Gu, A.; Gkiatas, I.; Sedran, J.-C.; Nikolaou, V.S.; Sculco, P.K. Polyethylene Liner Cementation Into a Well-Fixed Metal Acetabular Shell for the Management of Periacetabular Osteolysis: A Systematic Review. Eur. J. Orthop. Surg. Traumatol. 2022, 32, 1459–1468. [Google Scholar] [CrossRef]
- Nebergall, A.K.; Rader, K.; Palm, H.; Malchau, H.; Greene, M.E. Precision of Radiostereometric Analysis (RSA) of Acetabular Cup Stability and Polyethylene Wear Improved by Adding Tantalum Beads to the Liner. Acta Orthop. 2015, 86, 563–568. [Google Scholar] [CrossRef]
- Tian, J.-L.; Sun, L.; Hu, R.-Y.; Han, W.; Tian, X.-B. Correlation of Cup Inclination Angle With Liner Wear for Metal-on-Polyethylene in Hip Primary Arthroplasty. Orthop. Surg. 2017, 9, 186–190. [Google Scholar] [CrossRef]
- Bahl, J.S.; Nelson, M.J.; Taylor, M.; Solomon, L.B.; Arnold, J.B.; Thewlis, D. Biomechanical Changes and Recovery of Gait Function After Total Hip Arthroplasty for Osteoarthritis: A Systematic Review and Meta-Analysis. Osteoarthr. Cartil. 2018, 26, 847–863. [Google Scholar] [CrossRef]
- Wang, K.; Kenanidis, E.; Miodownik, M.; Tsiridis, E.; Moazen, M. Periprosthetic Fracture Fixation of the Femur Following Total Hip Arthroplasty: A Review of Biomechanical Testing-Part II. Clin. Biomech. 2019, 61, 144–162. [Google Scholar] [CrossRef] [PubMed]
- Riglet, L.; Viste, A.; De Leissègues, T.; Naaim, A.; Liebgott, H.; Dumas, R.; Fessy, M.H.; Gras, L.L. Accuracy and Precision of the Measurement of Liner Orientation of Dual Mobility Cup Total Hip Arthroplasty Using Ultrasound Imaging. Med. Eng. Phys. 2022, 108, 103877. [Google Scholar] [CrossRef]
- Ko, S.; Pareek, A.; Ro, D.H.; Lu, Y.; Camp, C.L.; Martin, R.K.; Krych, A.J. Artificial Intelligence in Orthopedics: Three Strategies for Deep Learning With Orthopedic Specific Imaging. Knee Surg. Sports Traumatol. Arthrosc. 2022, 30, 758–761. [Google Scholar] [CrossRef] [PubMed]
- ASTM F2996-20; Standard Practice for Finite Element Analysis (FEA) of Non-Modular Metallic Orthopaedic Hip Femoral Stems. ASTM International: West Conshohocken, PA, USA, 2020.
- Zhu, Y.; Babazadeh-Naseri, A.; Dunbar, N.J.; Brake, M.R.W.; Zandiyeh, P.; Li, G.; Leardini, A.; Leardini, B.; Leardini, B.J. Finite Element Analysis of Screw Fixation Durability Under Multiple Boundary and Loading Conditions for a Custom Pelvic Implant. Med. Eng. Phys. 2023, 111, 103930. [Google Scholar] [CrossRef] [PubMed]
- Chethan, K.N.; Zuber, M.; Shenoy, S.; Kini, C.R. Static Structural Analysis of Different Stem Designs Used in Total Hip Arthroplasty Using Finite Element Method. Heliyon 2019, 5, e01767. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stroud, J.; Yan, E.T.; Anthony, J.; Walker, K.; Goh, C.-H. Optimizing Screw Fixation in Total Hip Arthroplasty: A Deep Learning and Finite Element Analysis Approach. Appl. Sci. 2025, 15, 3722. https://doi.org/10.3390/app15073722
Stroud J, Yan ET, Anthony J, Walker K, Goh C-H. Optimizing Screw Fixation in Total Hip Arthroplasty: A Deep Learning and Finite Element Analysis Approach. Applied Sciences. 2025; 15(7):3722. https://doi.org/10.3390/app15073722
Chicago/Turabian StyleStroud, Jacob, Emily T. Yan, Jacob Anthony, Kyle Walker, and Chung-Hyun Goh. 2025. "Optimizing Screw Fixation in Total Hip Arthroplasty: A Deep Learning and Finite Element Analysis Approach" Applied Sciences 15, no. 7: 3722. https://doi.org/10.3390/app15073722
APA StyleStroud, J., Yan, E. T., Anthony, J., Walker, K., & Goh, C.-H. (2025). Optimizing Screw Fixation in Total Hip Arthroplasty: A Deep Learning and Finite Element Analysis Approach. Applied Sciences, 15(7), 3722. https://doi.org/10.3390/app15073722






