Abstract
Addressing the limitations of restricted coding capacity and material dependency in acoustic identity tags for autonomous underwater vehicles (AUVs), this study introduces a novel passive acoustic identification tag (AID) design based on multilayered elastic cylindrical shells. By developing a Normal Mode Series (NMS) analytical model and validating it through finite element method (FEM) simulations, the work elucidates how material layering strategies regulate far-field target strength (TS) and establishes a time-domain multi-peak echo-based encoding framework. Results demonstrate that optimizing material impedance contrasts achieves 99% detection success at a 3 dB signal-to-noise ratio. Jaccard similarity analysis of 3570 material combinations reveals a system-wide average recognition error rate of 0.41%, confirming robust encoding reliability. The solution enables the combinatorial expansion of coding capacity with structural layers, yielding 210, 840, and 2520 unique codes for three-, four-, and five-layer configurations, respectively. These findings validate a scalable, hull-integrated acoustic identification system that overcomes material constraints while providing high-capacity encoding for compact AUVs, significantly advancing underwater acoustic tagging technologies through physics-driven design and systematic performance validation.
1. Introduction
With the advancement of materials science and computational theory, the use of Autonomous Underwater Vehicles (AUVs) in marine industries has significantly increased. Compared to manned/remotely operated underwater vehicles, AUVs have demonstrated superior reliability and cost-effectiveness in executing underwater missions [1]. To efficiently and stably accomplish complex tasks—such as pipeline inspections for oil and gas industries, oceanographic observations, bathymetric surveys, military applications, high-resolution seabed inspections, mapping, commercial explorations, and neutralization of seabed mining areas—in unknown underwater environments, formation control of AUVs has emerged as a critical research focus [2]. Concurrently, theories related to radio frequency, optical, and acoustic communication have been continuously developed to enhance data transmission capabilities between AUVs in underwater environments [3]. Among these, active and passive positioning between AUVs is regarded as a fundamental prerequisite for mission execution [4].
For AUV identification and localization, traditional transponder-based methods face limitations in deployment/maintenance costs and device power constraints. Optical approaches are restricted by critical factors such as lighting conditions, turbidity, and feature richness [5], with localization accuracy varying by up to an order of magnitude across different vision-based algorithms [6]. Meanwhile, sonar-based simultaneous localization and mapping (SLAM) techniques incur high computational costs and exhibit significant uncertainties under complex environmental conditions [7].
To address these challenges, a series of novel AUV underwater identification and localization methods have been continuously proposed. These include the establishment of underwater artificial landmarks detectable by cameras or optical sensors [8], though vision-based solutions are limited to short-range applications. In response, Satish et al. [9,10] introduced the concept of a passive Acoustic Identification Tag (AID). This tag reflects unique acoustic characteristics when interrogated by sonar pulses, enabling it to function as a low-maintenance, cost-effective navigation aid. Inspired by passive surface acoustic wave RFID tags [11], AID tags modulate parameters such as acoustic material type, arrangement, and thickness to generate distinctive acoustic signatures. Building on this concept, Bhardwaj et al. [12] developed an AID tag capable of infinite ultrasonic wireless power transfer and backscatter-based localization.
Concurrently, leveraging SonarBell Corporation’s research on polymer target acoustic scattering [13], Zhou et al. [14] experimentally validated the feasibility of passive acoustic markers utilizing Rayleigh wave resonance in biaxially oriented acrylic spheres. Satish et al. [15] further optimized the design of multilayered hemispherical shell AID tags. Following this methodology. Kepros and Chahal [16] created a PMUT-based ultrasonic tag with 136-day battery life (CR2032) for sensor data transmission in RF-limited/noisy environments, enabling low-power IoT solutions. Somaan et al. [17] investigated the application and optimization methods of this approach in turbid waters for navigation purposes; subsequently, in their field trials [18], the team further demonstrated the viability of concentric acrylic-based AID tags for precise AUV navigation and positioning. Ding Dong et al. [19] established the feasibility of time-domain echo coding using four-layer elastic spherical shells. Most recently, Zhou et al. [20] achieved a breakthrough by combining periodic rib-plate and helical groove structures with polymethyl methacrylate (PMMA) multi-sphere assemblies, successfully integrating time-frequency domain scattering features with geometric-elastic characteristics. This work verifies the practicality of acoustic coding and pioneers new approaches for intelligent underwater target recognition.
While the aforementioned studies on AID tags provide efficient and low-cost solutions, their limited information density and the size constraints of dual-sphere configurations (e.g., radius 0.05 m, spacing 0.25 m) [14] may render them unsuitable for AUVs. Furthermore, the multilayer shell design proposed by Satish et al. [15] necessitates precise control over layer thicknesses and material properties (e.g., impedance matching between acrylic and water). Nonuniform interlayer water gaps could lead to encoding distortions.
Current studies reveal that dual-sphere configurations suffer from low information density, while multilayer shells exhibit encoding distortion due to nonuniform water gaps, highlighting critical limitations in existing acoustic tagging systems. This paper proposes an AID tag design method for multilayer elastic cylindrical shell structures, integrable onto AUV hull surfaces, based on the Normal Mode Series (NMS) [21]. By developing an analytical model for acoustic scattering in multilayer shells and validating it via finite element method (FEM) simulations, we quantitatively analyze the impact of material stratification strategies on far-field Target Strength (TS). Additionally, a coding generation and recognition methodology is introduced, leveraging the specificity of time-domain echo characteristics. The contributions of this paper can be summarized as follows:
- (1)
- First theoretical framework linking layered cylindrical shell geometry to acoustic coding mechanisms.
- (2)
- Development of a hybrid NMS-FEM validation framework for systematic design optimization.
- (3)
- 99% detection success rate at 3 dB SNR via impedance contrast optimization.
- (4)
- Combinatorial encoding capacity scaling (210 codes for three layers, 2520 codes for five layers).
2. Materials and Methods
This study presents a comprehensive approach to address four critical challenges in acoustic identity tags (AUV-AID) for autonomous underwater vehicles: (1) overcoming the coding capacity limitations of traditional dual-sphere configurations and the multilayer shell distortion caused by nonuniform water gaps; (2) reducing material dependency resulting from strict impedance matching requirements; (3) achieving reliable recognition in challenging 3 dB SNR environments; and (4) validating scalable coding expansion through structural layering.
To achieve these objectives, we implement a closed-loop framework integrating theoretical modeling, numerical simulation, and systematic optimization. A novel Normal Mode Series (NMS) acoustic scattering model for multilayered elastic cylindrical shells is developed using displacement potential function theory and Navier–Cauchy equations, establishing layer-dependent matrix equations with verified boundary conditions. COMSOL finite element simulations confirm the theoretical-simulative consistency of far-field target strength measurements. Our methodology further generates time-domain echoes through Gaussian-windowed amplitude-modulated pulse excitation, extracting binary acoustic barcodes via inverse Fourier transform and matched filtering. For enhanced noise robustness, we implement a Jaccard similarity analysis combined with Bootstrap resampling, ultimately developing a TOP-K optimized Jaccard-cosine hybrid algorithm that achieves 99% recognition accuracy with <1.5 s processing latency.
2.1. Theoretical Foundation
In the cylindrical coordinate system, the elastodynamic behavior of an infinite multilayered elastic cylindrical shell under normally incident plane wave excitation is investigated using the displacement potential function method. Let the wave vector of the incident wave be . The -direction displacement in the elastic cylindrical structure can be fully characterized using two scalar potential functions (dilatational) and (shear), which satisfy the Navier–Cauchy equation:
where
- = Dilatational potential function.
- = Shear potential function.
- = Dilatational wavenumber.
- = Shear wavenumber.
- = Lamé constants of the material.
- = Angular frequency.
As depicted in Figure 1, a plane wave is incident on an infinitely long multilayered elastic cylindrical shell, inducing scattered waves.
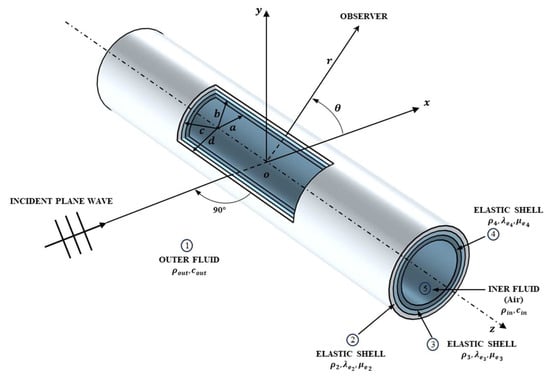
Figure 1.
Plane wave incident on an infinitely long multilayered elastic cylindrical shell.
The internal solutions within the elastic cylinder derived through the separation of variables method are expressed as follows:
where
- = Mode coefficients for layer .
- = Bessel and Neumann functions of order [21].
- = Cylindrical coordinates.
The displacements and stresses must satisfy the following function:
The exterior and interior acoustic fields of the cylinder can be expressed as follows:
By applying the continuity conditions for stress and displacement, we derive the system of equations for an infinitely long cylindrical shell with an exterior fluid medium and an interior air-filled cavity. The matrix dimensionality is dependent on the number of layers. For instance, a two-layer shell corresponds to a 6 × 6 matrix, three-layer to 10 × 10, four-layer to 14 × 14, and so forth. The solution to the system is given by , with matrix elements detailed in Appendix A.
When a plane wave is incident normally on an infinitely long cylindrical shell, the scattered sound pressure can be expressed as follows:
where
- = Scattering coefficients.
- = Hankel function of first kind.
- = Acoustic wavenumber in water.
- = Speed of sound in water.
Target Strength (TS) is defined as follows:
where
- = Scattered sound pressure.
- = Incident sound pressure.
- = Scattered pressure is projected to 1 m (the standard reference).
Similarly, the reflection coefficient and the average power reflection coefficient can be determined using the Normal Mode Series (NMS) method.
2.2. Numerical Verification
To validate the reliability of the NMS model, four representative material combinations from Table 1 (e.g., Al-AA, PMMA-PVC-PETG) were used to construct multilayer cylindrical shells with a radius of 0.25 m and a layer thickness gradient of 0.01 m (innermost structural steel layer: 0.002 m).

Table 1.
Properties of commonly used materials.
A finite element model of a multilayered elastic cylindrical shell was developed using COMSOL Multiphysics 6.2 software. Acoustic-structure interaction analysis was implemented through multiphysics coupling between the Acoustic Module and Structural Mechanics Module. The geometric modeling employed a 2D axisymmetric approximation to simulate an infinitely long cylindrical shell, with the outermost radius set at 0.25 m and uniform thickness of 0.01 m for each polymer layer. In the physical settings, the external water domain (density 1000 kg/m3, sound speed 1476 m/s) was connected with the internal air cavity through an acoustic-structure interaction interface. Material properties strictly followed Table 1 data, using frequency-independent isotropic parameters to define elastic layer characteristics (e.g., PMMA’s Young’s modulus 2.8 GPa, Poisson’s ratio 0.38). Meshing adopted the λ/10 accuracy criterion, as illustrated in Figure 2.
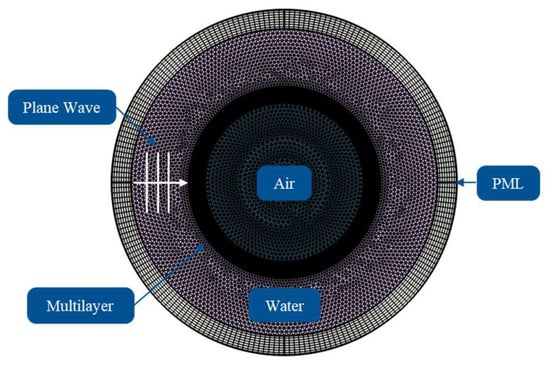
Figure 2.
Finite element model.
Computational results from both the Normal Mode Series (NMS) and Finite Element Method (FEM) for a cylindrical shell with radius , constructed using selected materials from Table 1, are shown in Figure 3.
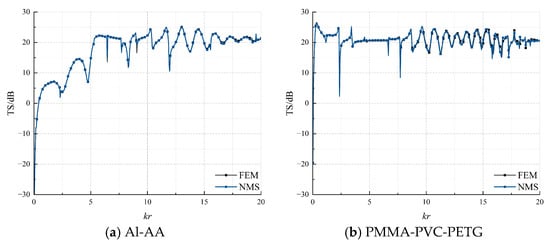
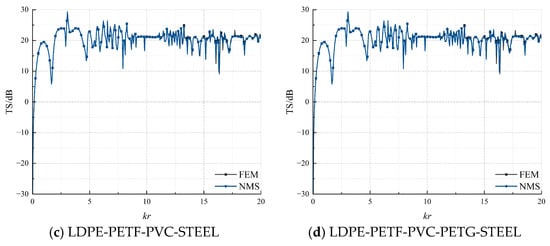
Figure 3.
Target Strength (TS) comparison between Normal Mode Series (NMS) analytical solutions and Finite Element Method (FEM) results for four multilayer cylindrical shells (radius r = 0.25 m reference distance 1000 m). Subfigures (a–d) correspond to material combinations Al-AA, PMMA-PVC-PETG, LDPE-PTFE-PVC-STEEL, and LDPE-PTFE-PVC-PETG-STEEL, respectively (the thickness of the steel is 0.002 m).
2.3. AlD Tag Generation Workflow
As shown in Figure 3, comparative analysis reveals that for multilayer shell structures of varying materials, the theoretical analytical solutions and numerical simulation results for far-field target strength (TS) exhibit remarkable consistency in spatial distribution characteristics across the reduced frequency range , where is the wavenumber and the shell radius.
Based on the frequency-domain indirect method [22], a Gaussian-windowed tone burst with a center frequency and fractional bandwidth was employed as the excitation signal. The frequency-domain backscattered sound pressure of the multilayer cylindrical shell was calculated, and the time-domain echo was obtained via inverse Fourier transform. The governing equations are as follows:
where represents the theoretical transfer function derived from the Normal Mode Series (NMS) scattering model.
The Gaussian-windowed tone burst is given by the following equation:
where
- = Bandwidth control parameter.
- = Time center of pulse.
- = Center frequency.
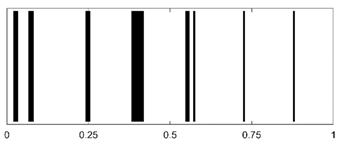
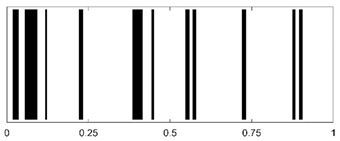
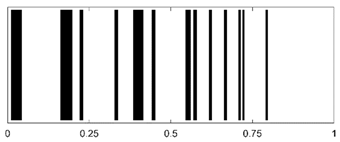
To extract the time-domain echo peak features from the acoustic backscatter signals of cylindrical shells under different stratification strategies, a matched filtering technique is employed by convolving the echo signal with the incident signal. Simultaneously, positional information of distinct peak points and peak interval sequence information are extracted, quantized, and encoded into a 1D barcode. The detailed workflow is illustrated in Figure 4.
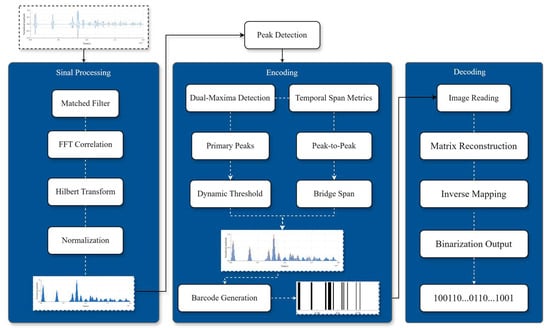
Figure 4.
Acoustic barcode generation workflow: (1) incident Gaussian-windowed tone burst (500 kHz, bandwidth 70%) excites the multilayered shell; (2) backscattered pressure is processed via inverse Fourier transform and matched filtering; (3) peak detection extracts time intervals between consecutive echoes; (4) quantization maps to binary sequences, forming unique AID tags.
For a three-layer cylindrical shell with an outermost radius of 0.25 m and a uniform shell thickness of 0.01 m per layer, optimized stratification strategies enable the generation of distinct time-domain echo characteristics. These features are encoded into corresponding AID tags, demonstrating unique acoustic fingerprints for material-layer configurations.
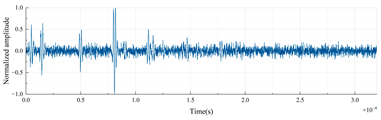
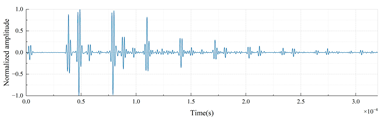
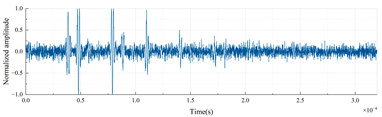
Wenz [23] systematically classified the ocean noise spectrum for the first time, delineating the frequency distributions of natural sources (wind, waves, marine life) and anthropogenic sources. High-frequency noise is predominantly thermal noise generated by molecular thermal motion (Brownian motion) in seawater, with noise level decreasing as frequency increases. To validate the effectiveness of AID tags, this study added Gaussian white noise (uniformly distributed across all frequencies, signal-to-noise ratio (SNR) = 3 dB) to the echo signals and performed the Shapiro–Wilk normality test [24]. The results confirmed that the added noise followed a normal distribution. The signal-to-noise ratio [25] (SNR) is defined as the ratio of signal power to noise power (in decibels, dB):
where denotes the signal power and represents the noise power.
3. Verifications and Results
The experimental environment configuration is shown in Table 2.

Table 2.
Experimental environment configuration.
3.1. Effectiveness of AID Tags
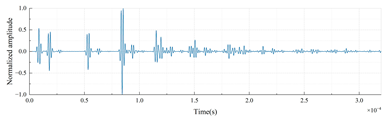
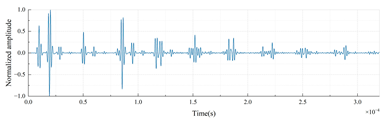
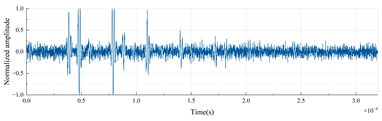
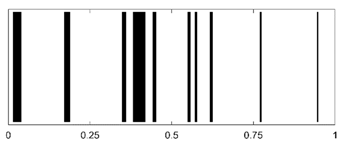
Time-domain echo signals and their corresponding AID tags for different material layer arrangements in a three-layer cylindrical shell (outer radius: 0.25 m, uniform layer thickness: 0.01 m) are shown in Table 3.

Table 3.
Time-domain echoes and corresponding AID tags for six three-layer polymer combinations (outer radius 0.25 m, layer thickness 0.01 m). Binary encoding based on peak intervals demonstrates unique signatures despite 3 dB Gaussian noise.
The barcodes in Table 3, when decoded, exist as 0–1 binary sequences at the host terminal. For binary existence-based set data, target recognition can be performed using the Mean Jaccard Index (MJI) [26], as defined in Equation (16). To enhance recognition accuracy, multiple sampling analyses were conducted, with the aggregated results presented in Table 4.
where

Table 4.
Mean Jaccard Index (MJI) Comparison: Noisy vs. Clean Data (SNR = 3 dB).
- = Binary code sets from clean/noisy signals.
- = Cardinality of set.
AUVs typically employ aluminum alloys or high-strength steel for structural frames and pressure hulls [27]. To further analyze the impact of metallic backplates on AID tag feature recognition, an additional thin metal layer (0.002 m) was introduced under the same conditions as Table 4 for MJI detection comparison. The results are presented in Table 5.

Table 5.
Detection robustness analysis with metallic backing plates (thickness 0.002 m). Structural steel and aluminum substrates maintain MJI > 97.5% across all configurations, confirming minimal acoustic coupling between AID tags and AUV hull materials.
For cylindrical shells internally filled with air, the addition of rigid internal structures has minimal impact on target feature recognition, as demonstrated in Table 4, where the average recognition rate remains largely unchanged.
To further investigate the diversity and effectiveness of AID tags, seven materials from Table 1 (excluding water, structural steel, and aluminum) were selected. The study systematically controls material permutation sequences and layer counts, with the specific combinatorial configurations quantified in Table 6.

Table 6.
Calculation content.
A Jaccard similarity coefficient comparison was conducted between a total of 3570 datasets and their corresponding counterparts with added Gaussian noise, with the results illustrated in Figure 5.
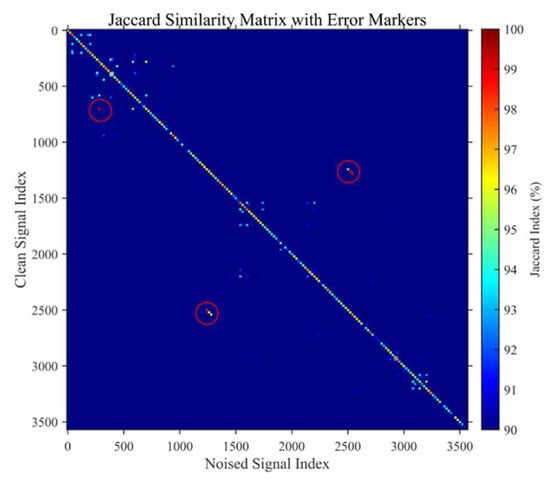
Figure 5.
Jaccard similarity coefficient heatmap of 3570 material combinations under 3 dB SNR (sampling interval = 20). Diagonal elements (blue) represent self-similarity between clean/noisy signals (<90%), while off-diagonal values (yellow-red) indicate cross-talk between distinct configurations. Circled red regions highlight interference from material pairs with low impedance (e.g., PMMA-PVC).
As illustrated in the heatmap in Figure 5, the red points within the circled area represent recognition errors caused by the co-arrangement of materials with similar impedance. Statistical analysis reveals that these errors are most significantly influenced by the distinct layered combinations of Acrylic Acid (AA), PMMA, and PVC. The average power reflection coefficients for these three materials under varying combinations are shown in Figure 6.
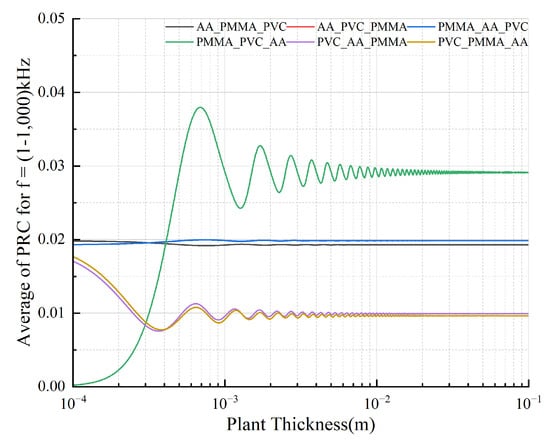
Figure 6.
Average broadband power reflection coefficients under different material arrangements.
As shown in Figure 7, when materials with low acoustic impedance differences are employed, the average power reflection coefficient remains below 0.05 at a thickness of 0.01 m. This diminishes the characteristic features of the target echo, necessitating the avoidance of layered configurations using materials with closely matched acoustic impedance.

Figure 7.
Jaccard similarity coefficient heatmap with a sampling interval of 10 (excluding interfering material arrangements; color mapping is a change from blue to cyan, from yellow to magenta, and then to red, and it is proportional to the magnitude of the values).
As delineated in Figure 7, the intervals 1–210, 211–1050, and 1051–3570 correspond to three-, four-, and five-layered media, respectively. A 95% confidence interval Bootstrap resampling analysis [22] was applied to calculate the Jaccard similarity coefficients between noise-containing and noise-free echo signals from identical materials in the diagonal regions of the heatmap. The analysis utilized a sample size matching the original dataset and 10,000 resamples, with results summarized in Table 7.

Table 7.
Bootstrap Resampling.
The global confidence interval for all combinations in Table 6 is [94.70%, 94.82%], confirming the statistical reliability of the system over a wide parameter range.
To further quantify the impact of the aforementioned material arrangements on the detection accuracy of AID tags, error rates with and without these arrangements were repeatedly calculated under a 3 dB SNR. Higher error rates indicate a stronger influence of material configurations on target recognition. The results are presented in Figure 8.
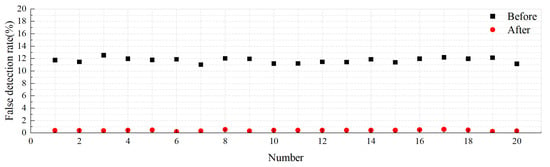
Figure 8.
Detection error rates for 3570 material combinations under 3 dB SNR: including interfering material pairs (e.g., PMMA-PVC) results in a 12 % error; after excluding low-contrast combinations, the error drops to . Error bars represent 95% confidence intervals from 10,000 Bootstrap resamples.
As shown in Figure 9, the detection error remains around 12% when using the aforementioned material combinations. In contrast, avoiding these materials significantly reduces the error rate, with an average detection error rate of merely 0.41%. Interfering material arrangements that disrupt target recognition are substantially minimized. Furthermore, systematic screening can exclude specific combinations to further reduce errors.
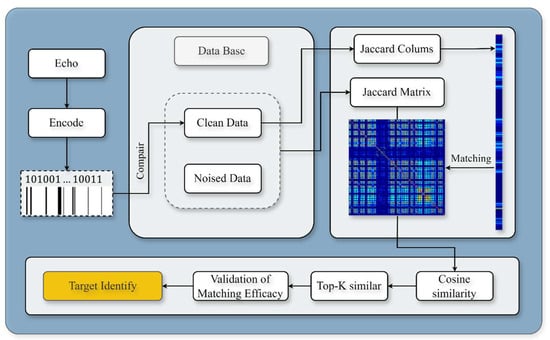
Figure 9.
Flowchart of the Target Recognition Methodology.
3.2. Target Recognition Methodology
Following the reduction in average detection error, the data stored in AID tags can be more effectively leveraged for target recognition. The proposed methodology for target recognition is described below, with its detailed workflow illustrated in Figure 9.
Upon acquiring the noise-containing time-domain echo signal, the corresponding AID tag can be generated. This tag is converted into its binarized form after host retrieval. The binarized data is then compared with its noise-free counterpart using the Jaccard similarity coefficient, yielding a column vector of Jaccard similarity coefficients. Subsequently, cosine similarity [28,29] is computed between this vector and the Jaccard matrix, as expressed in Equation (17). To further enhance recognition accuracy, the TOP-K query optimization method [30] is applied.
To validate recognition stability, a column vector of Jaccard similarity coefficients was compared with 20 additional Jaccard matrices under 3 dB SNR noise interference for similarity recognition trials. Validation shows that the computation time for the Jaccard column matrices referenced in Figure 9 is approximately 0.005 s. The full Jaccard matrix computation time remains below 0.5 s (matrices are precomputed and stored in the database, eliminating additional computational overhead). Finally, the processing time for column-to-matrix matching in target recognition is around 1.5 s. The calculation is carried out based on the matrix of the maximum dimension, which can be further reduced when matching with lower-dimensional matrices.
As demonstrated in Figure 10, the detection error rate exhibits a significant reduction with increasing matching dimensionality, with the overall detection success rate reaching 99%.
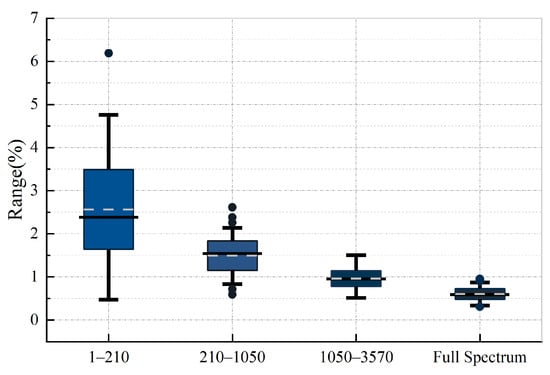
Figure 10.
Detection error rate variation with matrix dimensionality (boxplot, the grey dotted line represents the average value, the black solid line within the box is the median line, and the black dots are the outliers).
4. Conclusions
Unlike conventional dual-sphere tags, this work pioneers hull-integrated acoustic tags through scalable cylindrical geometry, where the acoustic encoding scheme based on multilayered elastic cylindrical shells outperforms existing methods (e.g., dual-sphere configurations and multilayered hemispherical shells) in coding capacity, environmental robustness, and noise tolerance. This study addresses the high-density identification requirements for autonomous underwater vehicles (AUVs) by proposing a passive acoustic identification tag (AID) design based on multilayered elastic cylindrical shell structures. Through theoretical modeling using the normal series method, finite element numerical validation, and large-scale material combination simulations, we elucidate the regulatory mechanisms of material layering strategies on far-field acoustic scattering characteristics and establish a time-frequency domain fusion encoding system with high robustness. The results demonstrate that the proposed scheme achieves competitive performance in encoding capacity and noise resistance, offering an innovative solution for underwater collaborative navigation. Key findings include the following.
By adjusting the material stacking sequence and impedance matching in multilayered elastic cylindrical shells, distinctive time-domain multi-peak echo features can be engineered. These features enable high-information-density encoding via peak interval sequences, while optimized impedance differences effectively suppress encoding distortion.
Under 3 dB SNR conditions, Jaccard similarity analysis and Bootstrap resampling quantify the influence of layering strategies on encoding uniqueness. Combined with rapid matching algorithms (single recognition cycle <1.5 s) and noise-resistant processing, the system achieves a 99% recognition success rate in complex acoustic environments.
Increasing the number of material layers significantly expands encoding combinations: three-, four-, and five-layer structures generate 210, 840, and 2520 unique codes, respectively (Table 4). This represents a substantial improvement over traditional dual-sphere tags, which offer only a limited number of combinations.
Author Contributions
Conceptualization, Z.P.; methodology, Z.D., S.X. and Z.P.; software, Z.D.; validation, Z.D.; formal analysis, Z.D.; investigation, Z.D. and S.X.; resources, Z.D. and Z.P.; data curation, Z.D.; writing—original draft preparation, Z.D.; writing—review and editing, Z.D., Z.P. and S.X.; visualization, Z.D. and Z.P.; supervision, Z.P. and S.X.; project administration, Z.P. and S.X.; funding acquisition, Z.P. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (52201397); Laboratory of Science and technology on integrated Logistics Support, National University of Defense Technology (WDZC20235250311); Open Fund of Ship Vibration and Noise Key Laboratory (6142204230709, 6142204240202), Natural Science Foundation of Hunan Provincial (2023JJ60544).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All evaluated data are presented in this paper in graphical form. Original data of this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The distribution of matrix elements of multilayered cylindrical shells follows certain rules. Taking the double-layer cylindrical shell as an example, the boundary conditions are introduced at the contact surface between the external fluid and the solid to solve for the following:
where correspond to the negatives of ,, respectively. Following this pattern, matrices for elastic media interactions in multilayered shells can be extended by successively stacking and arranging according to the established rules. Taking a two-layered cylindrical shell as an example, the internal acoustic field is expressed as follows:
For , simply replace and with and , where
References
- Wernli, R.L. AUV commercialization-who’s leading the pack? In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Conference Proceedings (Cat. No.00CH37158), Providence, RI, USA, 11–14 September 2000; Volume 1, pp. 391–395. [Google Scholar]
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Gussen, C.M.; Diniz, P.S.; Campos, M.L.; Martins, W.A.; Costa, F.M.; Gois, J.N. A survey of underwater wireless communication technologies. J. Commun. Inf. Sys. 2016, 31, 242–255. [Google Scholar] [CrossRef]
- Maurelli, F.; Krupiński, S.; Xiang, X.; Petillot, Y. AUV localisation: A review of passive and active techniques. Int. J. Intell. Robot. Appl. 2022, 6, 246–269. [Google Scholar] [CrossRef]
- González-García, J.; Gómez-Espinosa, A.; Cuan-Urquizo, E.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Escobedo Cabello, J.A. Autonomous underwater vehicles: Localization, navigation, and communication for collaborative missions. Appl. Sci. 2020, 10, 1256. [Google Scholar] [CrossRef]
- Qin, J.; Li, M.; Li, D.; Zhong, J.; Yang, K. A survey on visual navigation and positioning for autonomous UUVs. Remote Sens. 2022, 14, 3794. [Google Scholar] [CrossRef]
- Aulinas, J.; Petillot, Y.; Salvi, J.; Lladó, X. The SLAM problem: A survey. In Artificial Intelligence Research and Development, Proceedings of the 11th International Conference of the Catalan Association for Artificial Intelligence, CCIA 2008, Sant Martí d’Empúries, Spain, 22–24 October 2008; IOS Press: Amsterdam, The Netherlands, 2008; pp. 363–371. [Google Scholar]
- Jung, J.; Li, J.H.; Choi, H.T.; Myung, H. Localization of AUVs using visual information of underwater structures and artificial landmarks. Intell. Serv. Robot. 2017, 10, 67–76. [Google Scholar] [CrossRef]
- Satish, A.; Nichols, B.; Trivett, D.; Sabra, K.G. Passive underwater acoustic tags using layered media. J. Acoust. Soc. Am. 2019, 145, EL84–EL89. [Google Scholar] [CrossRef]
- Satish, A.; Trivett, D.; Sabra, K.G. Omnidirectional passive acoustic identification tags for underwater navigation. J. Acoust. Soc. Am. 2020, 147, EL517–EL522. [Google Scholar] [CrossRef]
- Jalal, A.S.A. Passive RFID Tags. Wulfenia J. 2015, 22, 415–435. [Google Scholar]
- Bhardwaj, A.; Allam, A.; Erturk, A.; Sabra, K.G. Ultrasound-Powered Wireless Underwater Acoustic Identification Tags for Backscatter Communication. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 71, 304–313. [Google Scholar] [CrossRef]
- Islas-Cital, A.; Atkins, P.; Gardner, S.; Tiltman, C. Performance of an enhanced passive sonar reflector SonarBell: A practical technology for underwater positioning. Underw. Technol. 2013, 31, 113–122. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, J.; Huang, J.; Wang, B. Passive underwater acoustic barcodes using Rayleigh wave resonance. J. Appl. Phys. 2022, 131, 124901. [Google Scholar] [CrossRef]
- Satish, A.; Sabra, K.G. Passive underwater acoustic identification tags using multi-layered shells. J. Acoust. Soc. Am. 2021, 149, 3387–3405. [Google Scholar] [PubMed]
- Kepros, E.; Chahal, P. Ultra Low Power Wireless Ultrasonic Sensor Tag with ID. IEEE Sens. J. 2025, 25, 8823–8827. [Google Scholar]
- Somaan, N.; Bhardwaj, A.; Sabra, K.G. Passive underwater Acoustic IDentification (AID) tags for enhancing Autonomous Underwater Vehicle (AUV) navigation during docking or homing operations. J. Acoust. Soc. Am. 2023, 153 (Suppl. S3), A345. [Google Scholar]
- Somaan, N.; Bhardwaj, A.; Sabra, K.G. Passive acoustic identification tags for marking underwater docking stations. JASA Express Lett. 2024, 4, 126001. [Google Scholar] [CrossRef]
- Ding, D.; Chen, C.X.; Kong, H.M.; Fan, J.; Peng, Z.L. Acoustic encoding of high-frequency time-domain echoes from layered elastic spherical shells in water. Appl. Acoust. 2023, 42, 781–791. [Google Scholar]
- Zhou, F.; Fan, J.; Wang, B.; Zhou, Y.; Huang, J. Acoustic barcode based on the acoustic scattering characteristics of underwater targets. Appl. Acoust. 2022, 189, 108607. [Google Scholar]
- Gaunaurd, G.C. Sonar cross section of a coated hollow cylinder in water. J. Acoust. Soc. Am. 1977, 61, 360–368. [Google Scholar] [CrossRef]
- Martins, N. A Time Frequency Approach to Blind Deconvolution in Multipath Underwater Channels. Master’s Thesis, Universidade do Algarve Faro, Portugal, 2001. [Google Scholar]
- Wenz, G.M. Acoustic ambient noise in the ocean: Spectra and sources. J. Acoust. Soc. Am. 1962, 34, 1936–1956. [Google Scholar]
- Royston, P. Approximating the Shapiro-Wilk W-test for non-normality. Stat. Comput. 1992, 2, 117–119. [Google Scholar] [CrossRef]
- Lucas, E.; Wang, Z. Performance prediction of underwater acoustic communications based on channel impulse responses. Appl. Sci. 2022, 12, 1086. [Google Scholar] [CrossRef]
- Bag, S.; Kumar, S.K.; Tiwari, M.K. An efficient recommendation generation using relevant Jaccard similarity. Inf. Sci. 2019, 483, 53–64. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Q.; He, X.; Wang, R.; Liu, Q. Preparation of highly dewetted porous steel for shallow water AUV based on laser ablation method. Appl. Surf. Sci. 2024, 652, 159261. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: Boca Raton, FL, USA, 1994. [Google Scholar]
- Huang, M.; Chen, D.; Feng, D. The Fruit Recognition and Evaluation Method Based on Multi-Model Collaboration. Appl. Sci. 2025, 15, 994. [Google Scholar] [CrossRef]
- Adomavicius, G.; Zhang, J. Classification, ranking, and top-K stability of recommendation algorithms. INFORMS J. Comput. 2016, 28, 129–147. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).