Effects of Structural Dynamic Characteristics on Soil–Structure Interaction (SSI) Analysis of High-Frequency-Dominant Seismic Excitation
Abstract
:1. Introduction
2. FE Modeling and SSI Analysis Method
2.1. Modeling of the Structure
2.2. Modeling of the Soil for SSI Analysis
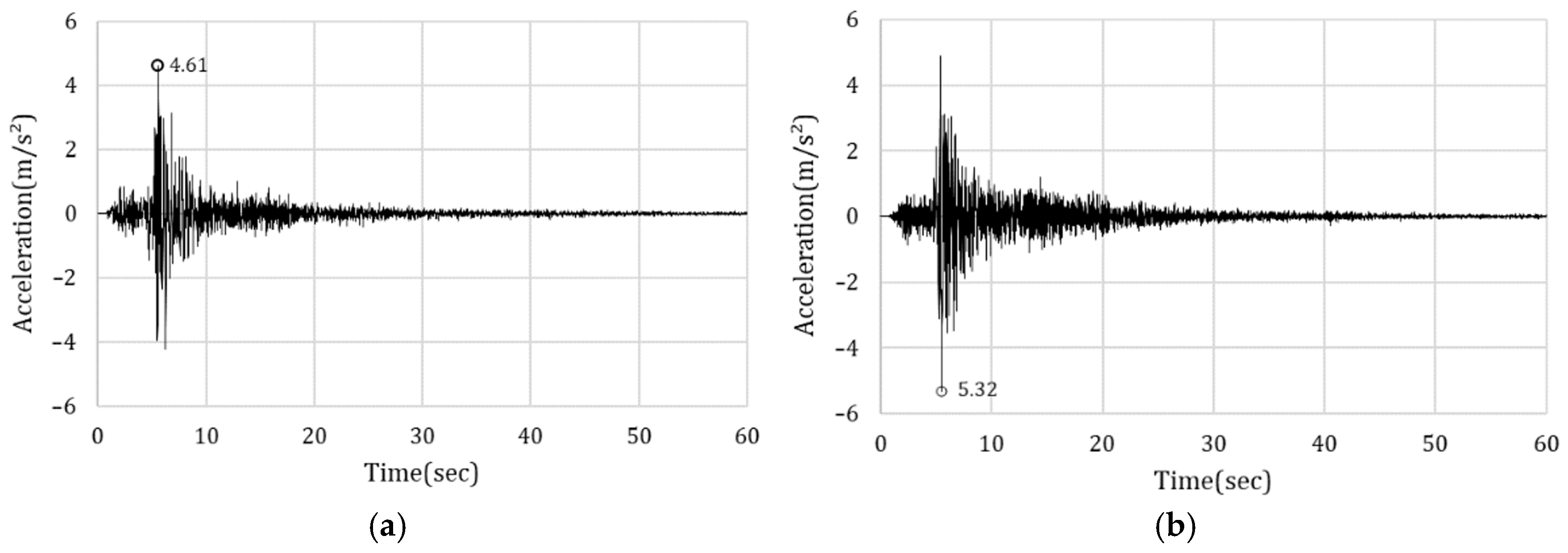
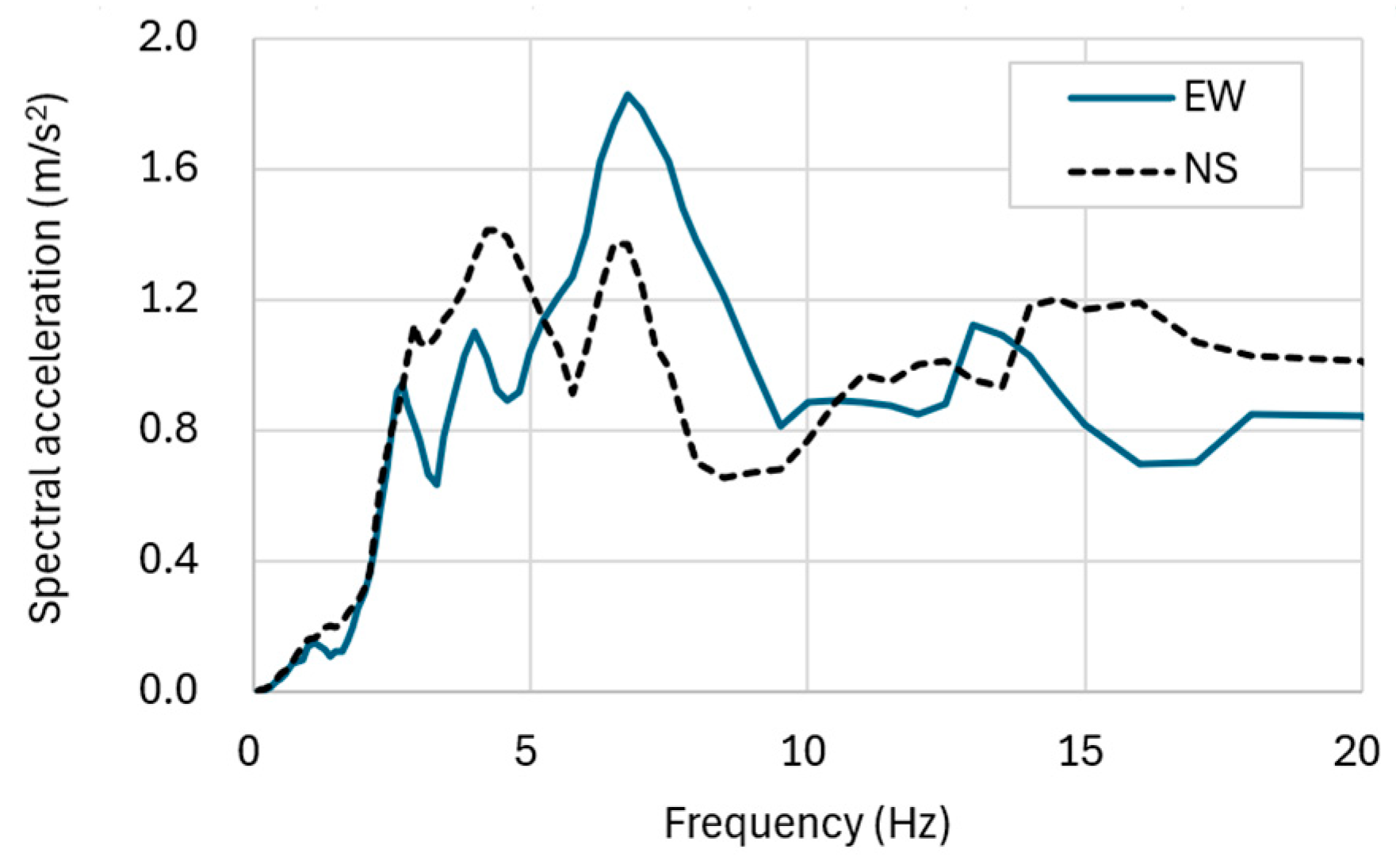
2.3. Characteristics of the Input Seismic Motion and SSI Analysis Procedure
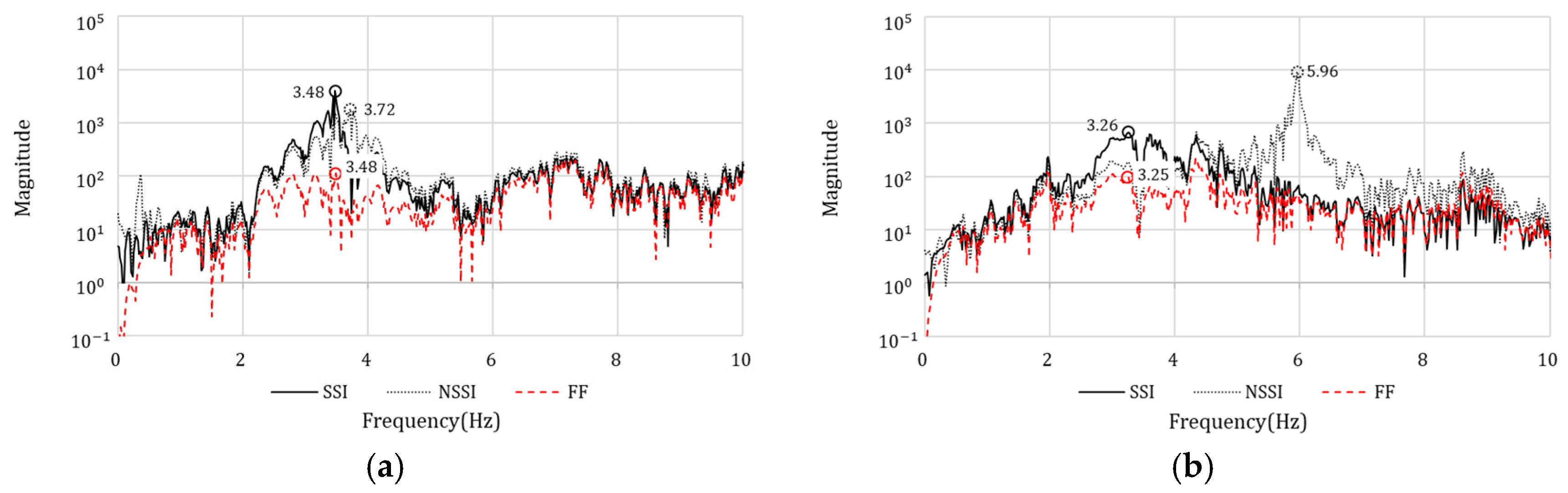
3. Analysis Results and Discussion
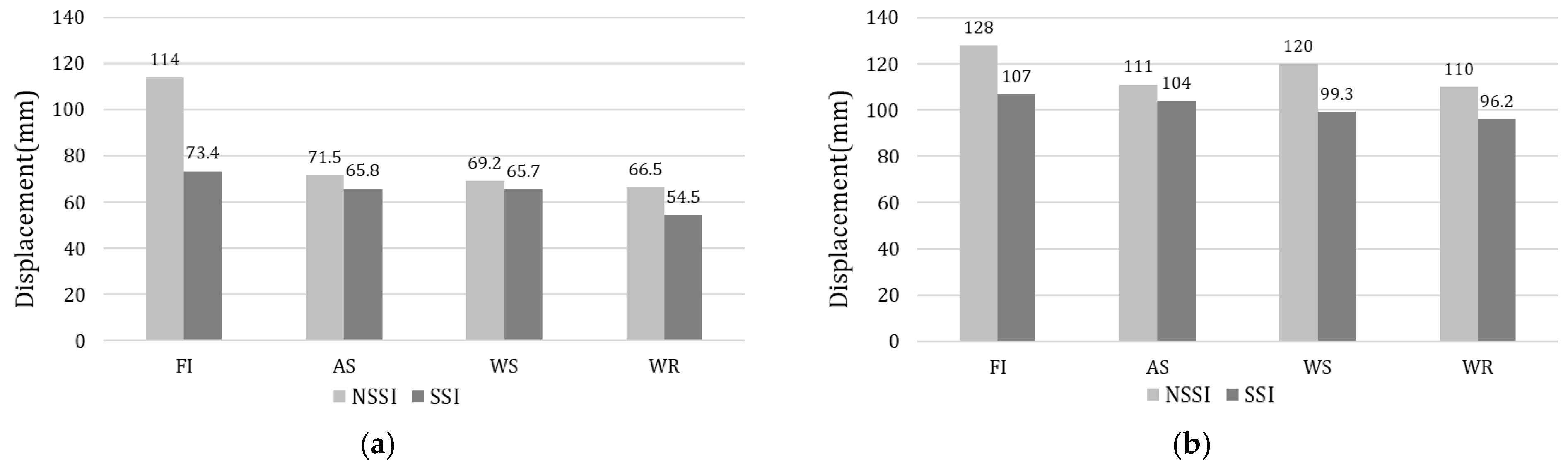
3.1. Effect of SSI on the Low-Frequency Structure
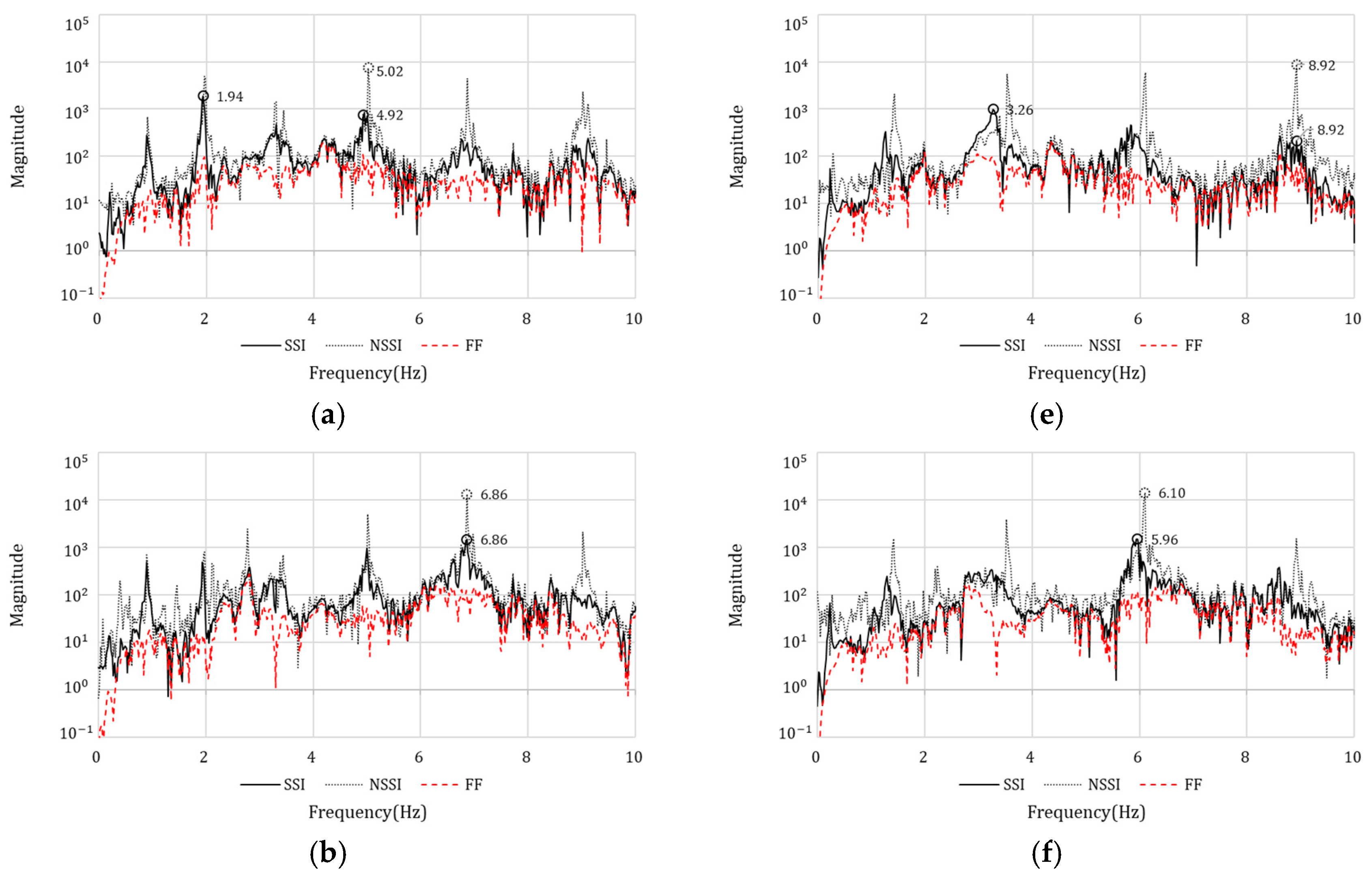
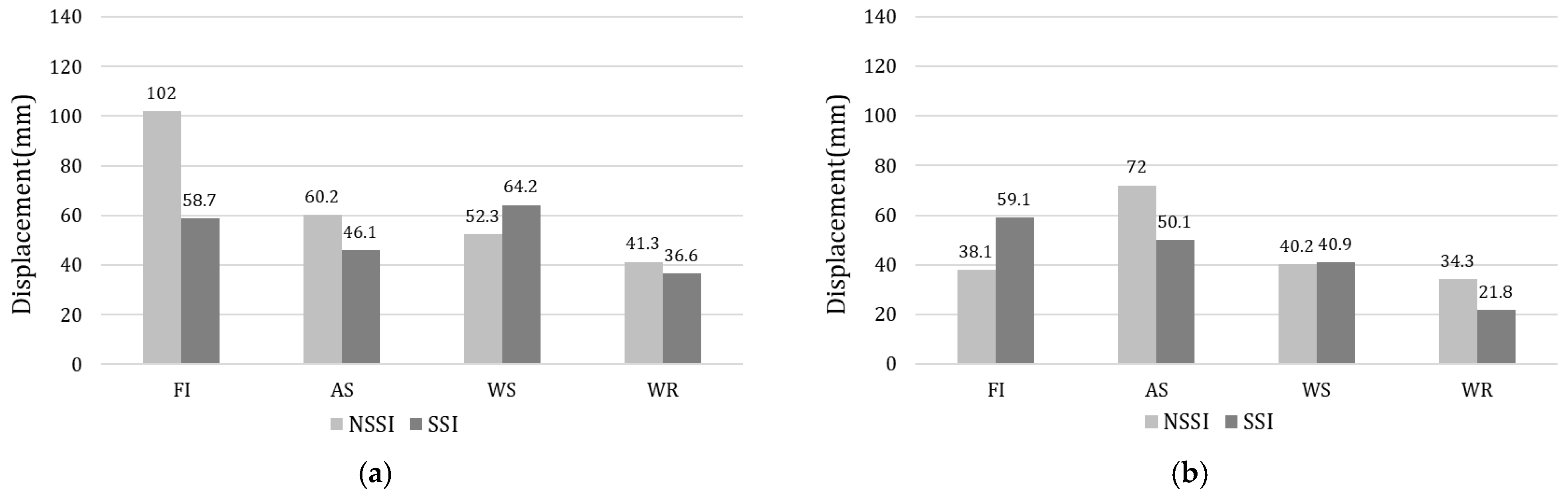
3.2. Comparative Analysis Between Low-Frequency and High-Frequency Structures
4. Conclusions
- In the analysis results of the low-frequency structure, it was found that the peak acceleration amplitude decreases when SSI is considered for all four soil types considered. This is known to be due to the change in support conditions and the energy dissipation effect of the ground;
- The maximum relative displacement of the low-frequency structure also decreased across all soil conditions when considering the SSI effect, with the most significant reduction observed on FI soil: 35.6% in the EW direction and 16.4% in the NS direction;
- The maximum relative displacement of the short-period structure also decreased generally when the SSI was considered but increased by 22.8% and 55.1% for the EW direction of WS soil and NS direction of FI soil, respectively. From these results, it is observed that a larger response can be obtained when SSI is considered. The reason for this result is that the natural frequencies of the structure calculated considering the stiffness of the ground are in the frequency region where the amplitude of the free-field response is larger than otherwise;
- For both low-frequency and high-frequency structures, considering the SSI results in additional damping as the energy dissipation of the ground is reflected in the analysis, which reduces the dynamic response. However, when SSI is considered, the support conditions of the structure change, resulting in the lower natural frequency of the structure and a change in the dynamic response. Therefore, depending on the overlap between the dominant frequency range of the input seismic wave and the natural frequency range of the structure, SSI consideration may be necessary for conservative design results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, Y.S. Structure-Soil Interaction and Earthquake Analysis; Goomi-Seogwan: Seoul, Republic of Korea, 2010. [Google Scholar]
- Kim, Y.S. SSI effects on the dynamic response of structures. J. Comput. Struct. Eng. Inst. Korea 1993, 6, 87–93. [Google Scholar]
- Kim, J.M. Soil-structure dynamic interaction. J. KSNVE 2002, 12, 316–321. [Google Scholar]
- KDS 41 17 00; Standard for Seismic Design of Buildings. Korean Design Standard. Ministry of Land, Infrastructure and Transport: Seoul, Republic of Korea, 2022. Available online: https://www.kcsc.re.kr (accessed on 6 September 2024).
- Bapir, B.; Abrahamczyk, L.; Wichtmann, T.; Prada-Sarmiento, L.F. Soil-structure interaction: A state-of-the-art review of modeling techniques and studies on seismic response of building structures. Front. Built Environ. 2023, 9, 1120351. [Google Scholar]
- Tadesse, Z.L.; Padavala, H.K.; Koteswara, V.R.P. Effect of subterranean levels on the dynamic response of RC-MRF buildings. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1273, 012014. [Google Scholar]
- Ansari, T.A.; Jamle, S. Performance-based analysis of RC buildings with underground storey considering soil-structure interaction. Int. J. Adv. Eng. Res. Sci. 2019, 6, 767–771. [Google Scholar] [CrossRef]
- Bhojegowda, V.T.; Subramanya, K.G. Soil structure interaction of framed structure supported on different types of foundation. Int. Res. J. Eng. Technol. 2015, 2, 651–660. [Google Scholar]
- Pulikanti, S.; Ramancharla, P.K. SSI analysis of framed structure supported on pile foundations-with and without interface elements. Front. Geotech. Eng. 2014, 1, 10–16. [Google Scholar]
- Alonge, J.L. Modeling the effects of soil-structure interaction on a tall building bearing on a mat foundation. Civ. Eng. Pract. 2005, 20, 51–68. [Google Scholar]
- Kim, J.W.; Kim, D.K.; Kim, H.S. Spectrum shape considering seismic characteristics in Korea. Proc. Annu. Conf. Archit. Inst. Korea 2019, 39, 414–417. [Google Scholar]
- Ahn, J.H. Analysis of lateral force resistance performance according to the core area ratio of tower-type flat slab system apartments. J. Archit. Inst. Korea 2012, 28, 65–72. [Google Scholar]
- Lee, E.H.; Kim, J.M.; Seo, C.G. Large-scale 3D SSI analysis using KIESSI-3D program. J. Comput. Struct. Eng. Inst. Korea 2013, 26, 439–445. [Google Scholar] [CrossRef]
- Jang, H.; Yoon, J.; Kim, Y.; Lee, J. SSI (Soil-Structure Interaction) analysis using simplified modeling of RC columns and PML element. J. Comput. Struct. Eng. Inst. Korea 2025, 38. in press. [Google Scholar]
- Zulkefli, Z.F.; Zawawi, M.H.; Hassan, N.H.; Zainol, M.R.R.M.A.; Abas, M.A.; Mazlan, A.Z.A. Calculating the moduli elasticity for reinforced concrete using new rule of mixtures approach for the dam structure. MATEC Web Conf. 2018, 217, 04003. [Google Scholar] [CrossRef]
- Sun, S.C.; Han, J.T.; Cho, W.J. Proposal of representative shear wave velocity for domestic geological layers through synthesis of in-situ seismic test data. Korean Soc. Eng. Geol. 2012, 22, 293–307. [Google Scholar]
- Kim, S.D.; Yoon, J.; Cho, W.; Lee, J. Evaluation of seismic performance and soil-structure interaction (SSI) for piloti-type buildings considering Korean geotechnical conditions. Adv. Civ. Eng. 2021, 2021, 7876389. [Google Scholar] [CrossRef]
- Jin, Y.; Jeong, S.; Moon, M.; Kim, D. Analysis of the dynamic behavior of multi-layered soil grounds. Appl. Sci. 2024, 14, 5256. [Google Scholar] [CrossRef]
- Katuwal, S.; Pandit, A.; Shilpakar, A. Soil deformation behavior and SSI study by varying Poisson’s ratio of granular soil. SSRN Electron. J. 2022, 12, 1302–1309. Available online: https://kcc.edu.np/wp-content/uploads/2022/11/Final_Manuscript.pdf (accessed on 18 March 2025).
- Basu, U. Explicit finite element perfectly matched layer for transient three-dimensional elastic waves. Int. J. Numer. Methods Eng. 2009, 77, 151–176. [Google Scholar] [CrossRef]
- Kim, J.M.; Lee, G.H.; Hong, K.Y.; Lee, E.H. Verification of linear FE model for nonlinear SSI analysis by boundary reaction method. J. Comput. Struct. Eng. Inst. Korea 2014, 27, 95–102. [Google Scholar]
- Genç, A.; Kuvat, A.; Sesli, H. A study on efficiency of perfectly matched layer (PML) for seismic soil-structure interaction. Bursa Uludağ Univ. J. Fac. Eng. 2022, 27, 467–486. [Google Scholar] [CrossRef]
- LSTC. LS-DYNA Keyword User’s Manual Volume II: Material Models; LSTC Co.: Livermore, CA, USA, 2024. [Google Scholar]
- NECIS (National Earthquake Comprehensive Information System). Korea Meteorological Administration. 2019. Available online: https://necis.kma.go.kr (accessed on 31 December 2024).
- Ha, J.G.; Jo, S.G.; Park, H.J.; Kim, D.S. Evaluation of Rocking Behaviors During Earthquake for the Shallow Foundation System on the Weathered Soil Using Dynamic Centrifuge Test. J. Earthq. Eng. Soc. Korea 2016, 20, 285–293. [Google Scholar] [CrossRef]
- Ko, K.W.; Ha, J.G.; Park, H.J.; Kim, D.S. Evaluation of Rocking Mechanism for Embedded Shallow Foundation via Horizontal Slow Cyclic Tests. J. Earthq. Eng. Soc. Korea 2016, 20, 413–425. [Google Scholar]
- Zhang, W.; Han, L.; Feng, L.; Ding, X.; Wang, L.; Chen, Z.; Liu, H.; Aljarmouzi, A.; Sun, W. Study on seismic behaviors of a double box utility tunnel with joint connections using shaking table model tests. Soil Dyn. Earthq. Eng. 2020, 136, 106118. [Google Scholar] [CrossRef]
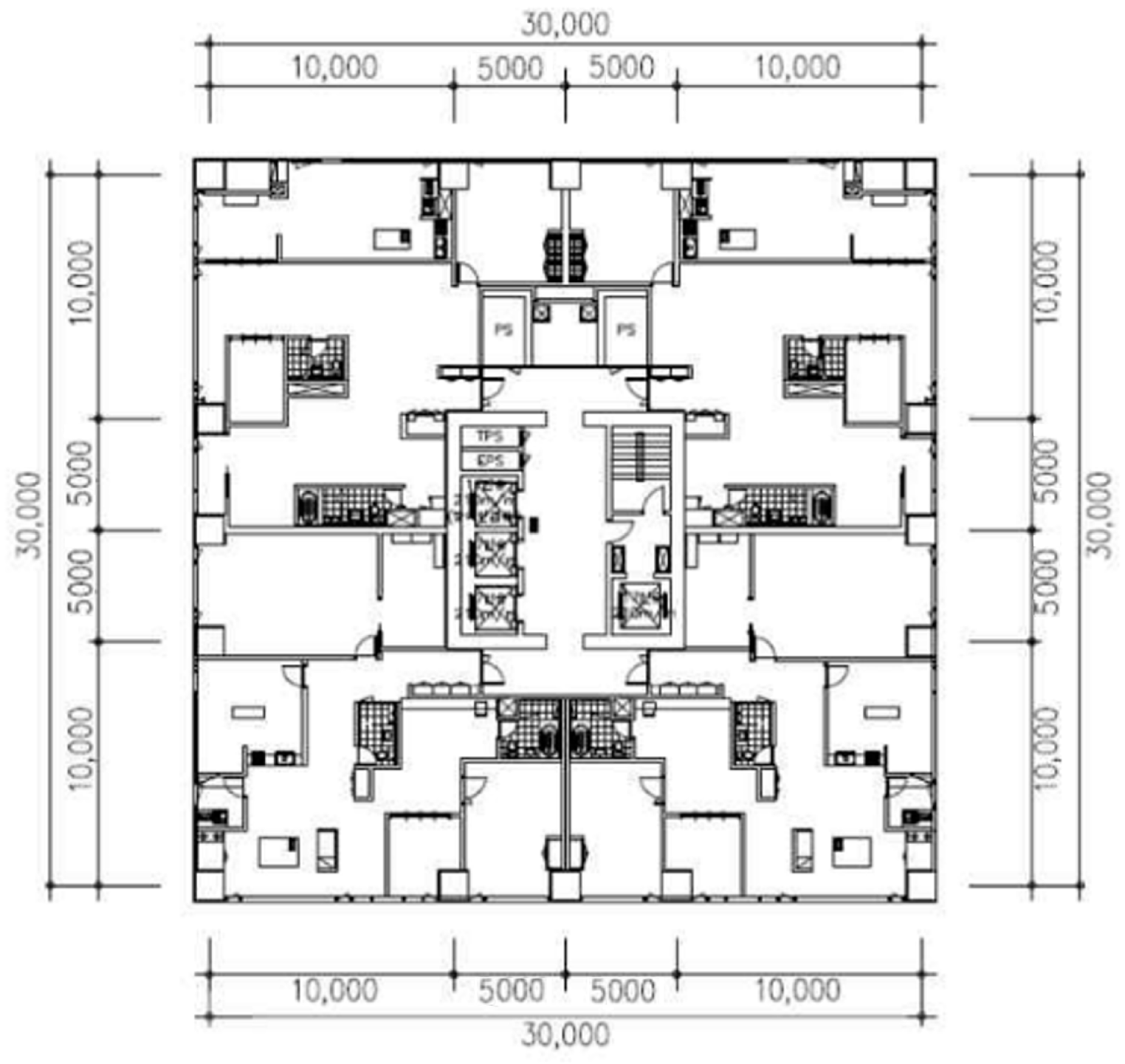
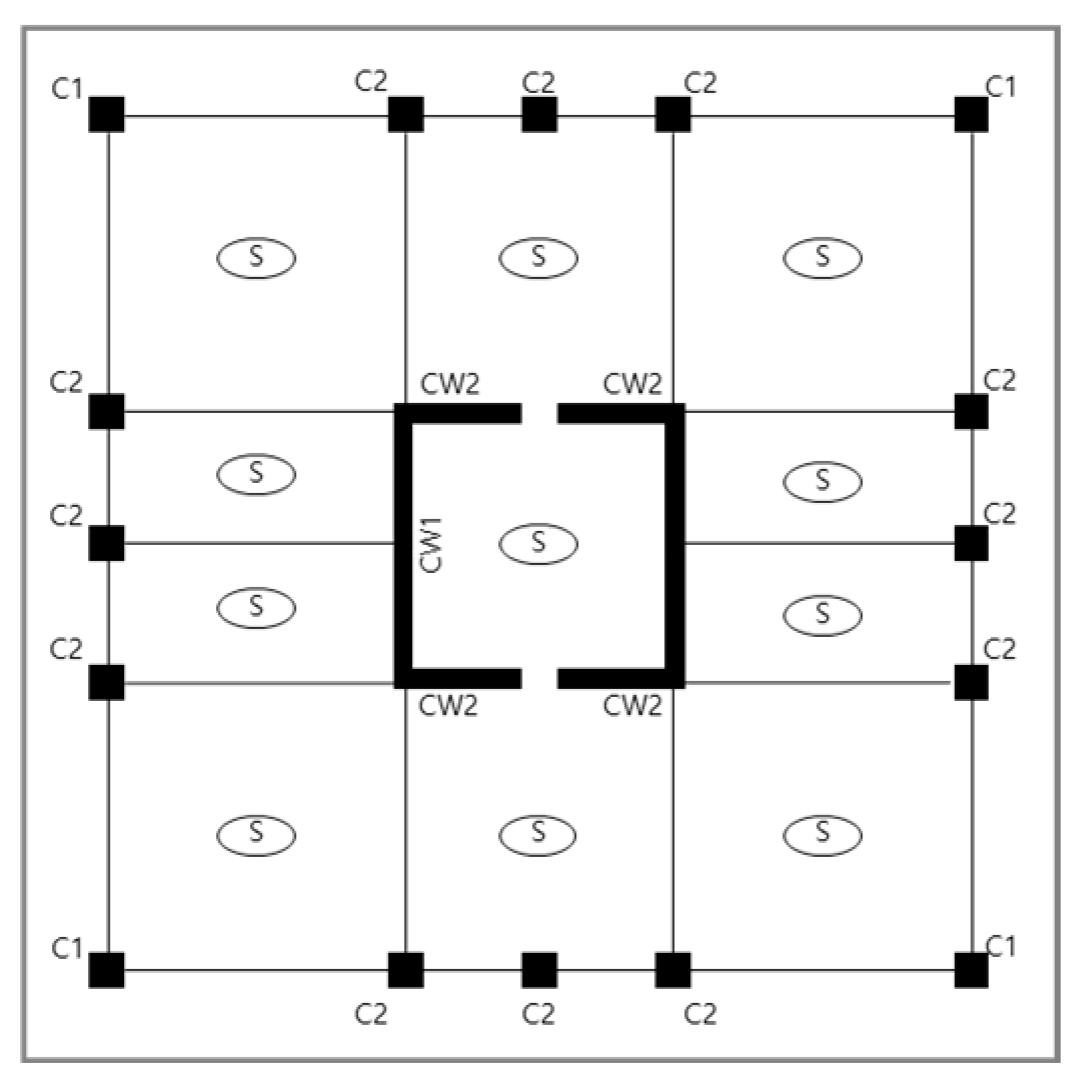

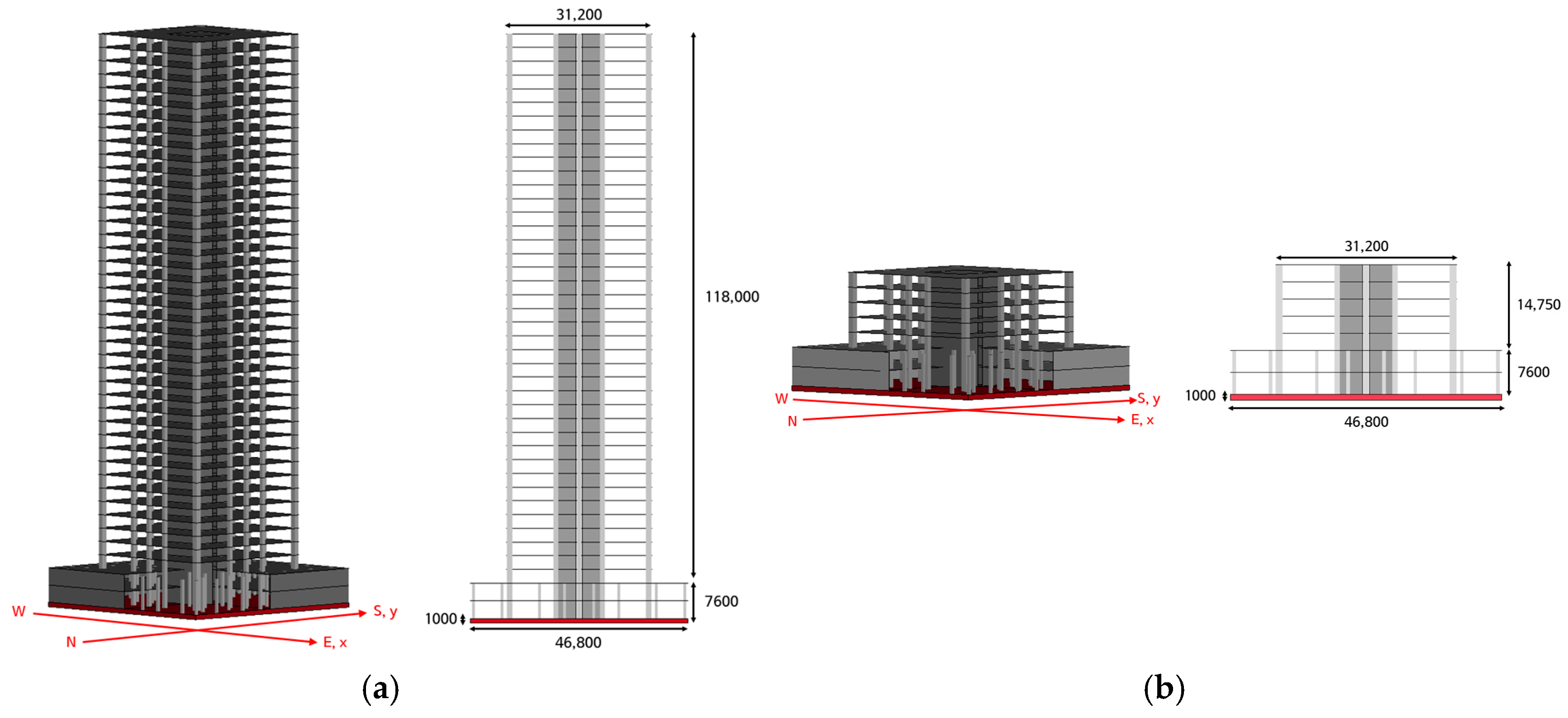


| Type | ID | Dimension (mm) | Strength of Concrete (MPa) | ||
|---|---|---|---|---|---|
| 1F–15F | 16F–30F | 31F–40F | |||
| Column | C1 | 1200 × 1200 | 50 | 40 | 30 |
| C2 | 900 × 900 | 50 | 40 | 30 | |
| Wall | CW1 | THK 600 | 50 | 40 | 30 |
| CW2 | THK 600 | 50 | 40 | 30 | |
| Slab | S | THK 250 | 40 | 30 | 24 |
| Type | ID | Dimension (mm) | Strength of Concrete (MPa) |
|---|---|---|---|
| B1–B2 | |||
| Column | C3 | 600 × 600 | 50 |
| Wall | BW | THK 450 | 50 |
| Slab | BS | THK 400 | 40 |
| ID | Floor | Unit Mass (t/mm3) | Elastic Modulus (GPa) | Yield Stress (MPa) | Tangent Modulus (GPa) |
|---|---|---|---|---|---|
| C1 | 1F–15F | 2.46 × 10−9 | 36.79 | 56.33 | 4.091 |
| 16F–30F | 34.44 | 45.45 | 4.091 | ||
| 31F–40F | 31.95 | 34.46 | 4.091 | ||
| C2 | 1F–15F | 2.46 × 10−9 | 36.49 | 56.10 | 3.942 |
| 16F–30F | 34.16 | 45.26 | 3.942 | ||
| 31F–40F | 31.67 | 34.30 | 3.942 | ||
| C3 | B1–B2 | 2.45 × 10−9 | 36.89 | 56.03 | 3.899 |
| Type | ID | Floor | Unit Mass (t/mm3) | Elastic Modulus (GPa) | Yield Stress (MPa) |
|---|---|---|---|---|---|
| Wall | CW | 1F–15F | 2.58 × 10−9 | 36.91 | 50 |
| 16F–30F | 34.66 | 40 | |||
| 31F–40F | 32.25 | 30 | |||
| BW | B1–B2 | 2.37 × 10−9 | 33.42 | 50 | |
| Slab | S | 1F–15F | 2.60 × 10−9 | 34.37 | 40 |
| 16F–30F | 31.90 | 30 | |||
| 31F–40F | 30.22 | 24 | |||
| BS | B1–B2 | 2.35 × 10−9 | 30.76 | 40 |
| Type | B (mm) | D (mm) | A (mm2) | Ix (mm4) | Iy (mm4) | J (mm4) | As (mm2) |
|---|---|---|---|---|---|---|---|
| C1 | 1200 | 1200 | 1.440 × 106 | 1.728 × 1011 | 1.728 × 1011 | 2.920 × 1011 | 1.200 × 106 |
| C2 | 900 | 900 | 8.100 × 105 | 5.468 × 1010 | 5.468 × 1010 | 9.240 × 1010 | 6.750 × 105 |
| C3 | 600 | 600 | 3.600 × 105 | 1.080 × 1010 | 1.080 × 1010 | 1.825 × 1010 | 3.000 × 105 |
| High-Rise Structure | Low-Rise Structure | ||
|---|---|---|---|
| Mode | 1st | 2nd | 1st |
| x-bending | 0.23 | 0.90 | 3.70 |
| y-bending | 0.27 | 1.40 | 5.94 |
| Soil Type | FI | AS | WS | WR |
|---|---|---|---|---|
| ) | 1.70 × 10−9 | 1.84 × 10−9 | 1.90 × 10−9 | 1.99 × 10−9 |
| ) | 16,670 | 18,000 | 18,640 | 19,510 |
| ) | 58.813 | 136.151 | 211.835 | 720.461 |
| ) | 158.796 | 353.993 | 550.772 | 1801.154 |
| ) | 176.440 | 294.994 | 458.976 | 1200.769 |
| ) | 0.35 | 0.30 | 0.30 | 0.25 |
| ) | 186 | 283 | 353 | 651 |
| ) | 387 | 529 | 660 | 1128 |
| ) (°) | 30 | 30 | 31 | 33 |
| ) | 0 | 0.01 | 0.02 | 0.10 |
| High-Rise Structure | Low-Rise Structure | |||
|---|---|---|---|---|
| Mode | Soil Type | 1st | 2nd | 1st |
| x-bending | FI | 0.20 | 0.88 | 1.97 |
| AS | 0.20 | 0.89 | 2.81 | |
| WS | 0.21 | 0.89 | 3.27 | |
| WR | 0.22 | 0.90 | 3.66 | |
| y-bending | FI | 0.21 | 1.24 | 3.25 |
| AS | 0.23 | 1.27 | 3.43 | |
| WS | 0.23 | 1.29 | 3.46 | |
| WR | 0.25 | 1.35 | 5.11 | |
| Mode | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| x-bending | 0.23 | 0.90 | 1.97 | 3.32 | 5.01 | 6.86 | 9.03 |
| y-bending | 0.27 | 1.40 | 3.50 | 6.07 | 8.86 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, H.; Yoon, J.; Cho, W.; Lee, J. Effects of Structural Dynamic Characteristics on Soil–Structure Interaction (SSI) Analysis of High-Frequency-Dominant Seismic Excitation. Appl. Sci. 2025, 15, 3679. https://doi.org/10.3390/app15073679
Jang H, Yoon J, Cho W, Lee J. Effects of Structural Dynamic Characteristics on Soil–Structure Interaction (SSI) Analysis of High-Frequency-Dominant Seismic Excitation. Applied Sciences. 2025; 15(7):3679. https://doi.org/10.3390/app15073679
Chicago/Turabian StyleJang, Huina, Jaeyong Yoon, Wanjei Cho, and Jungwhee Lee. 2025. "Effects of Structural Dynamic Characteristics on Soil–Structure Interaction (SSI) Analysis of High-Frequency-Dominant Seismic Excitation" Applied Sciences 15, no. 7: 3679. https://doi.org/10.3390/app15073679
APA StyleJang, H., Yoon, J., Cho, W., & Lee, J. (2025). Effects of Structural Dynamic Characteristics on Soil–Structure Interaction (SSI) Analysis of High-Frequency-Dominant Seismic Excitation. Applied Sciences, 15(7), 3679. https://doi.org/10.3390/app15073679







