Windage and Leakage Losses in Impeller Back Gap and Labyrinth Seal Cavities of Supercritical CO₂ Centrifugal Compressors

Abstract

The windage loss in impeller back gap and labyrinth seal cavities significantly impacts the aerodynamic performances of supercritical carbon dioxide (sCO₂) compressors. To accurately calculate windage loss, essential factors affecting the skin friction coefficients C_f,d (disk-type gap) and C_f,s (shaft-type gap), including Reynolds number Re, pressure ratio π, and radius ratio η, are investigated in this paper. The flow characteristics of the gap are analyzed and prediction models are proposed. The results indicate that both C_f,d and C_f,s decrease with increasing Re and grow with π and η, attributable to expanded high-vorticity regions caused by enhanced flow instability and larger vortices. The leakage flow rate m is unchanged for Re < 10⁶ since the fluid can flow into the impeller back gap, and slightly decreases for Re ≥ 10⁶ due to the centrifugal force and the inhibition effect of the vortices filling inlet regions. Moreover, the m grows with π and η due to a larger pressure difference and through-flow area. Maximal relative deviations of 6.23% and 6.83% can satisfy the requirements for calculating accurate windage loss in the impeller back gap and labyrinth seal cavities, which help the primary design of sCO₂ compressors.

1. Introduction

The supercritical CO₂ (sCO₂) Brayton cycle first proposed by Angelino and Feher [1,2] has, in recent years, been a research hotspot due to its higher efficiency than power cycles using conventional fluid as working fluid above 600 °C [3,4,5,6]. Additionally, a higher density of sCO₂ allows for compact power devices, all of which can be incorporated into a turbine-alternator-compressor (TAC) unit for the sCO₂ Brayton cycle of output power below 1 MW [7,8,9], reducing cycle costs and enabling modular construction technology [10].

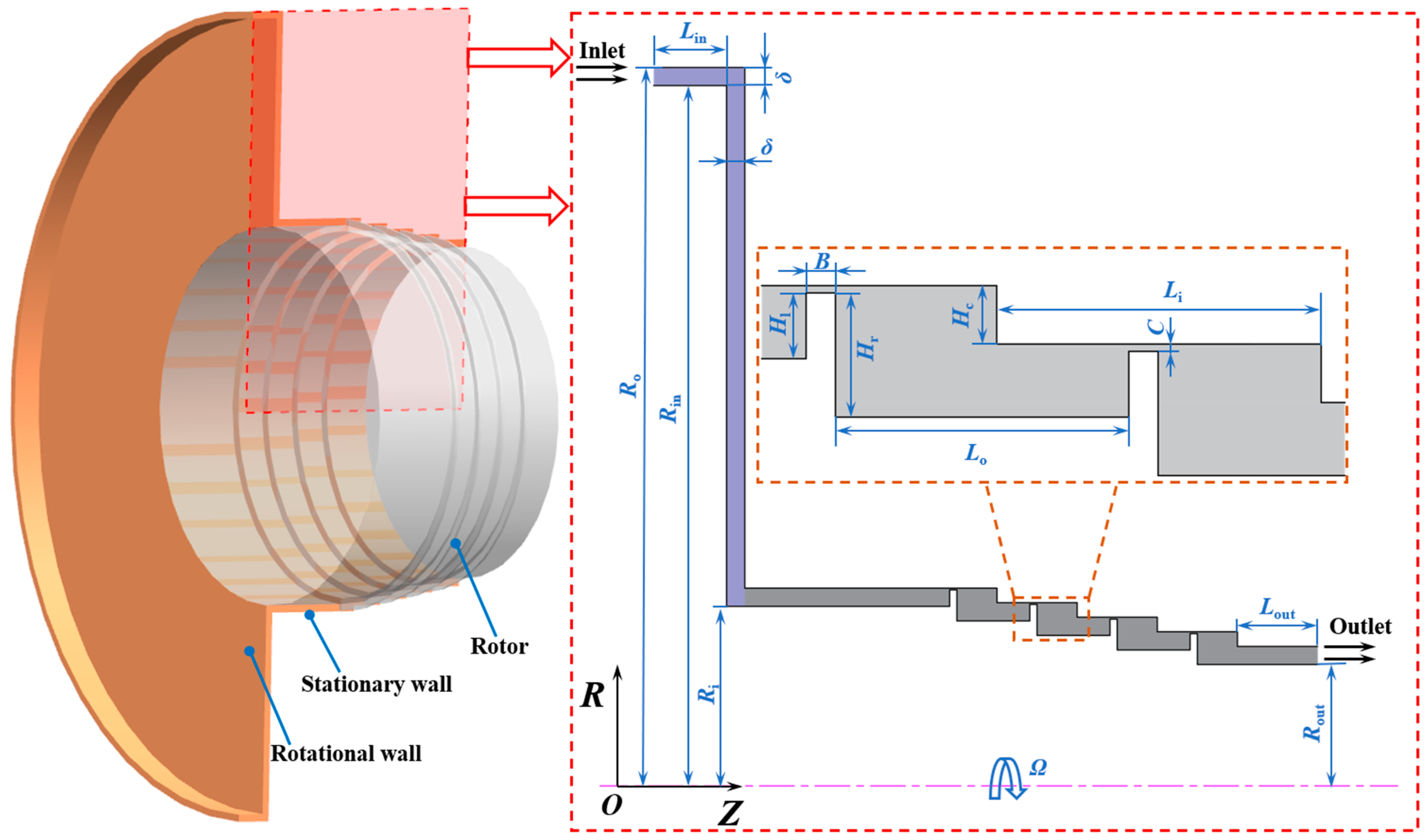
Figure 1 depicts the structure of a sCO₂ (TAC) unit, in which the fluid leakage from the compressor into the impeller back gap and labyrinth seal cavities can also be seen. According to Refs. [11,12,13], it is pointed out that the leakage flow in the gap and cavity generates windage losses due to friction when the rotor rotates and a cubic relationship between the windage losses and the rotational speed, indicating that the windage losses increase rapidly with the increase of rotational speed. Conboy found that the windage loss accounts for up to 37.5% of the total loss in a sCO₂ TAC unit because the rotational speed is undoubtedly higher for smaller power devices [14], reducing the output power and potentially leading to rotor overheating [15].

The research conducted thus far has revealed that the windage loss in the impeller back gap and labyrinth seal cavities, which corresponds to the blue and red regions in Figure 1, respectively, significantly impacts the aerodynamic performances of sCO₂ centrifugal compressors and even TAC units [16,17]. Thus, it is essential to research windage loss, flow, and the model of C_f in the regions. Moreover, the impeller back gap is considered a disk-type gap, commonly regard as a rotor-stator disk system [14]. The labyrinth seal is similar to the shaft-type gap, which can be assumed to be a concentric cylinder system [18]. In response to the difference in loss mechanisms in the two gap types, their windage losses need to be studied separately.

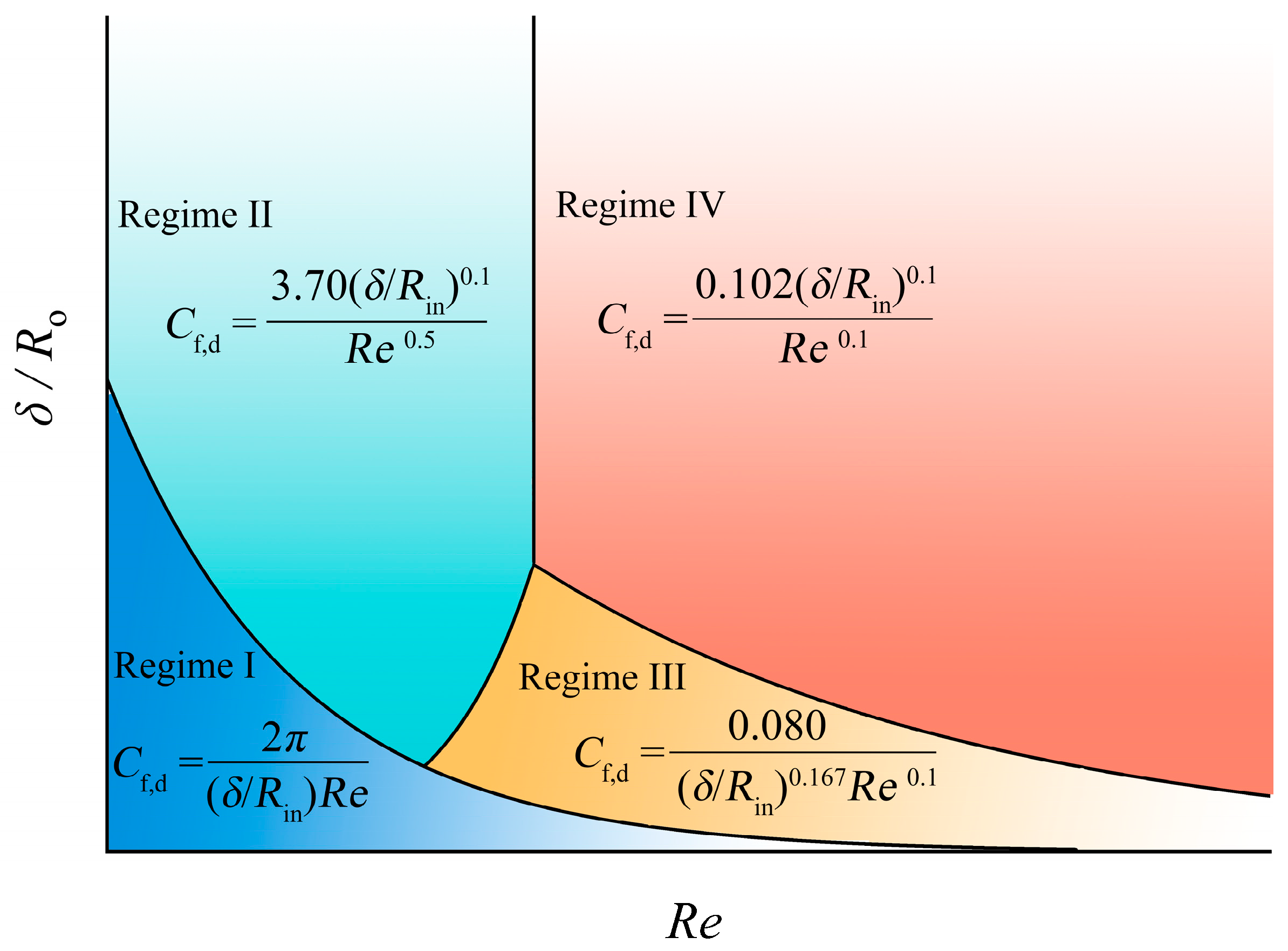
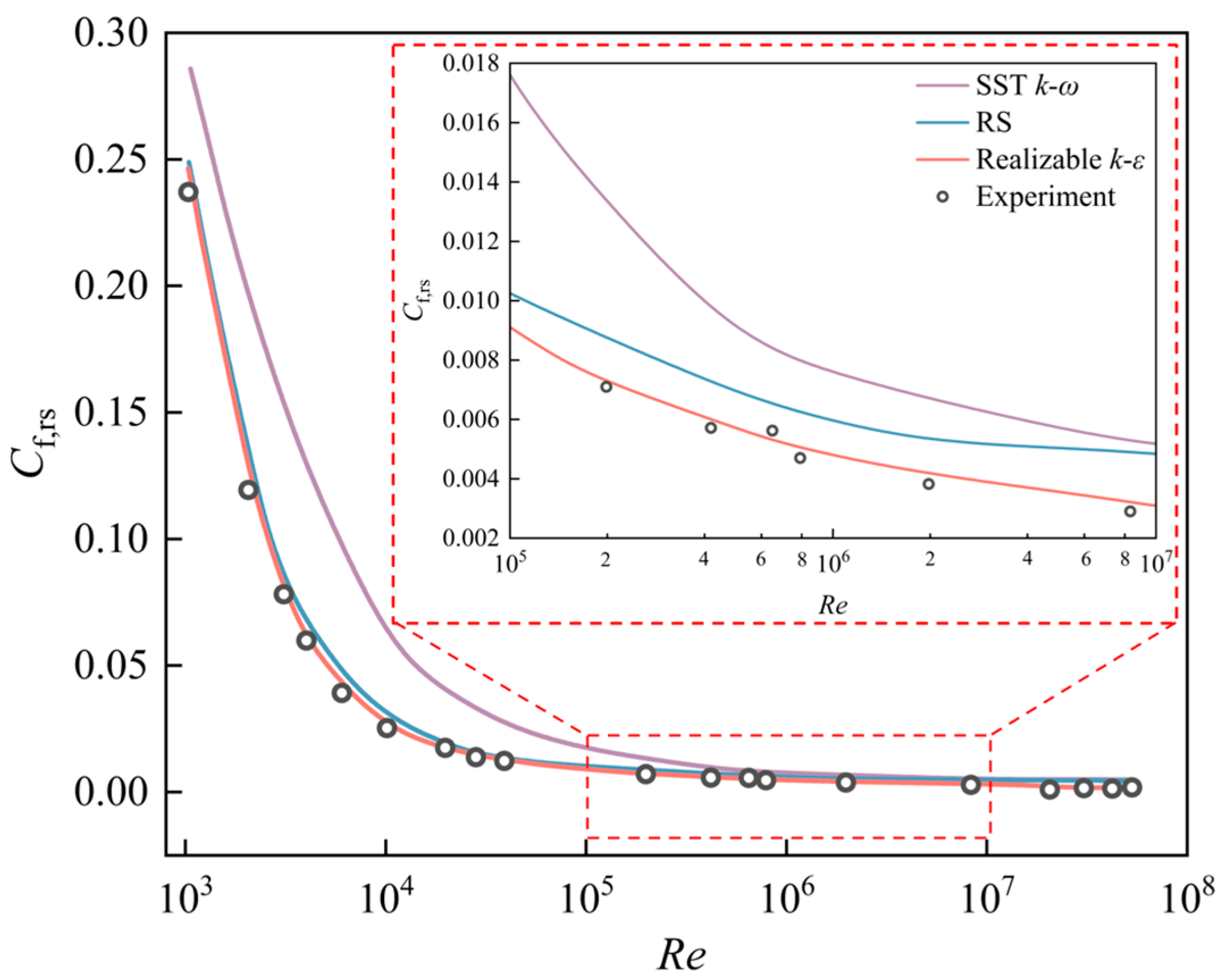
For disk-type gaps, Daily et al. first identified the four flow regimes in enclosed disk-type gaps under smooth wall conditions, based on Reynolds number Re and radius ratio δ/R_o, as highlighted in Figure 2 [19]. Models for calculating the skin friction coefficient C_f, a parameter that is influenced by several key variables related to windage loss, were proposed for each of the four regimes. Nowadays, the models have been widely used to predict disk-type windage loss [20]. However, Poullikkas et al. confirmed that the C_f grows with surface roughness, and they imply that Daily’s model is inapplicable to rough walls [21]. The evaluation of windage losses for disk-type gaps was conducted by Etemad et al., and the results show that windage loss is proportional to the square of throughflow and a dependency on throughflow direction [22]. In addition, further research on flow characteristics in disk-type gaps has revealed new insights. A variety of vortex structures, such as primary and secondary vortices and the vortex in turbulent boundary layers, were observed by Zhao et al. [23]. At higher Re, vortex cores are denser in the boundary layer and vortex intensity decreases, consistent with the conclusion that the streamline instability becomes dominant in the transition boundary layer [24]. Gu et al. developed a one-dimensional pressure model and a design tool for solving the flow in pump side chambers by investigating leakage and pressure distribution in disk-type gaps of centrifugal pumps with water as working fluid [25].

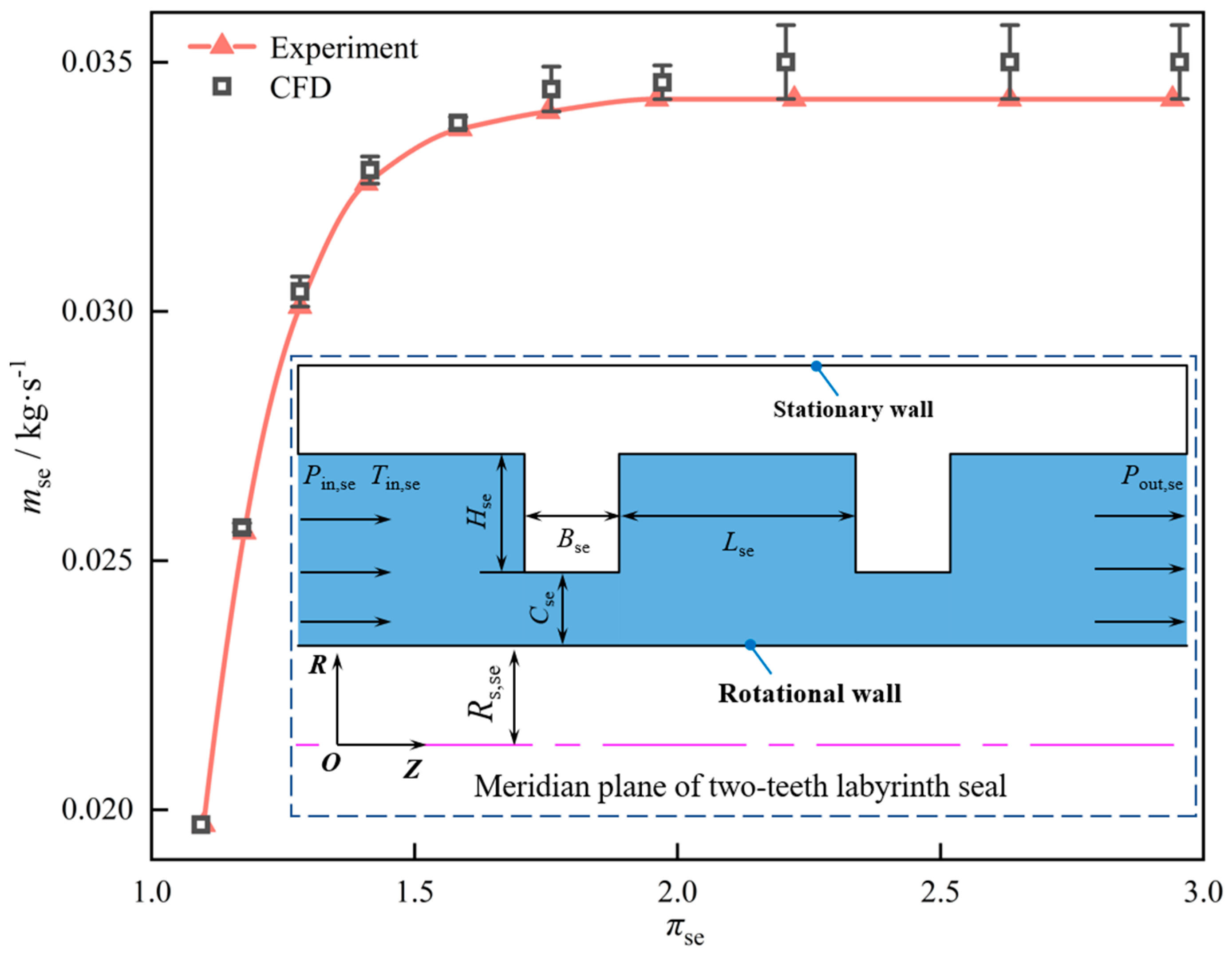
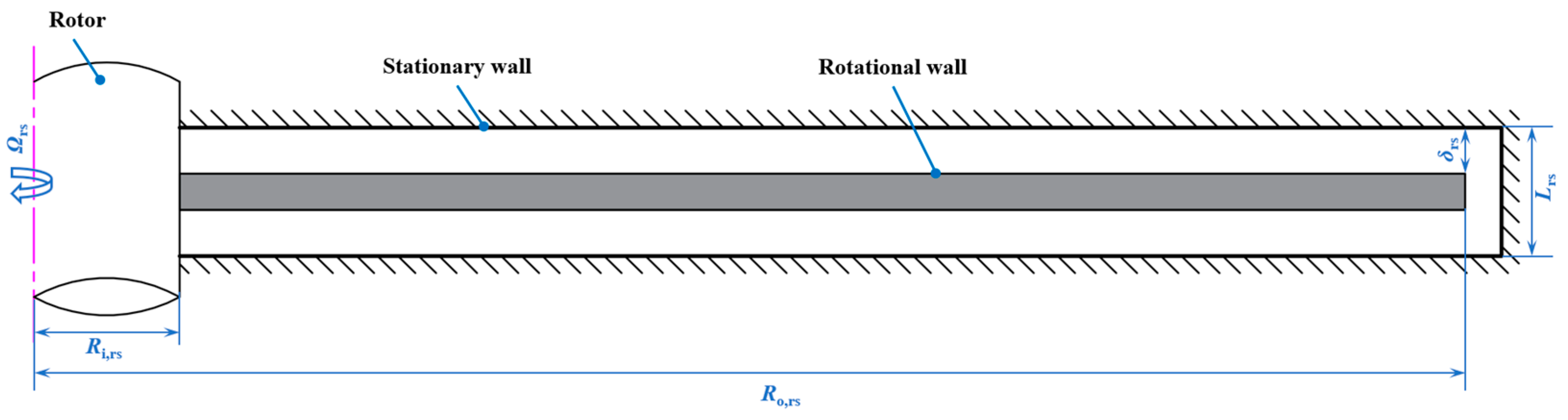
For shaft-type gaps, there has been extensive research on windage loss and flow in enclosed shaft-type gaps and labyrinth seals. Hu et al. initially validated Bilgen models and discovered that the Bilgen model is not applicable to predict C_f when Re falls between 7 × 10³ and 3 × 10⁴ or exceeds 3 × 10⁴, and an improved model of C_f incorporating CO₂ as working fluid was built based on numerical results [26]. Berghout et al. analyzed Taylor-Couette flow, which provides insight into the causes of windage loss [27,28,29]. Cao et al. reported that the leakage flow in labyrinth seal causes a drop of 1.1% in isentropic efficiency of the sCO₂ centrifugal compressor [30]. It reduces the diffuser inlet radial velocity, increases the flow angle, and reduces the pressure drop, particularly for high flow coefficients. Yuan et al. studied the impact of operating conditions on the performance of the labyrinth seal when sCO₂ flows through with the method of experiment investigation [31]. Guidotti et al. studied a compressor, including a cavity structure, both numerically and experimentally, and found that numerical simulations predicted the overall compressor performance and details of the flow characteristics very effectively [32]. The effect of leakage flow on the aerodynamic performance of centrifugal compressors was investigated using numerical methods by Mischo et al. The results show that the direction and location of leakage re-entry affect aerodynamic performance and efficiency [33].

Despite the continuous research on windage loss and C_f in enclosed disk-type and shaft-type gaps, little attention has been paid to windage loss and C_f models in open gaps. Leakage flow in open gaps complicates the formation of flow fields and windage losses compared to closed gaps. For example, different vortices will form in an open gap compared to a closed gap. Most of the current studies are focused on windage loss influencing factors [34], and have not modeled windage losses by combining the three key parameters of Re, π, and η. Furthermore, while the aerodynamic performance of compressors and leakage flow in labyrinth seals have been the focus of attention, less attention has been paid to windage losses in the impeller back gap and labyrinth seal cavities, and few studies have been conducted on the losses with the sCO₂ medium.

Therefore, the skin friction coefficients C_f,d and C_f,s are studied to predict windage loss in the impeller back gap and labyrinth seal cavities. Above all, the effects of Reynolds number Re of 10²~10⁸, pressure ratio π of 4.5~6.0 and radius ratio η of 0.018~0.054 are investigated. The three key parameters are intended to enable the exploration of the relationship between the role of physical properties and rotational speed, leakage flow rate, and geometric features on the skin friction coefficient. Subsequently, the action mechanisms are explored in the form of analyzing flow characteristics. Finally, the models of C_f, are proposed in different Re ranges, and the models are adapted to different key parameters. The conclusions of this paper help to use a more accurate form of predicting windage loss when designing sCO₂ compressors.

2. Windage Loss Model

2.1. Disk-Type Windage Loss

The calculation method for disk-type windage loss is presented by Theodorsen and Regier [35], and the torque on rotor in laminar flow can be expressed as Equation (1) [19]. The skin friction coefficient can be proposed and the windage loss model can be obtained using Equation (2):

$$Mr={\int }_{R_{\mathrm{i}}}^{R_{\mathrm{i}\mathrm{n}}}2\pi {\displaystyle \frac{\mu \Omega R^3}{\delta }}dR$$

(1)

$$W={\displaystyle \frac{1}{2}}{C}_{\mathrm{f},\mathrm{d}}\rho {\Omega }^3\left(R_{\mathrm{i}\mathrm{n}}^5-R_{\mathrm{i}}^5\right)$$

(2)

where C_f,d is called the skin friction coefficient of the disk-type gap, which is determined through simulations or experiments for turbulent flow. In this paper, the Reynolds number Re and radius ratio η are defined as follows:

$$Re={\displaystyle \frac{\rho R_{\mathrm{i}\mathrm{n}}\Omega \delta }{\mu }}$$

(3)

$$\eta ={\displaystyle \frac{\delta }{R_{\mathrm{i}\mathrm{n}}}}$$

(4)

In addition, pressure ratio π is expressed as:

$$\pi ={\displaystyle \frac{P_{\mathrm{i}\mathrm{n}}}{P_{\mathrm{o}\mathrm{u}\mathrm{t}}}}$$

(5)

2.2. Shaft-Type Windage Loss

Following the comprehensive derivations presented by Vrancik [36], Equation (6) is the viscous force on the rotor for laminar flow, and Equation (7) can be employed to estimate shaft-type windage loss:

$$F={\displaystyle \frac{2\pi \mu {L\Omega R}_{\mathrm{i}}^2}{\delta }}$$

(6)

$$W=\pi C_{\mathrm{f},\mathrm{s}}{\rho {\Omega }^{3}R}_{\mathrm{i}}^{4}L$$

(7)

where C_f,s is called the skin friction coefficient of the disk-type gap.

By conducting computational fluid dynamic (CFD) simulations and experiments to study windage loss W, it is feasible to obtain the corresponding torque T. Given the known rotational speed Ω, the windage loss can be expressed as follows:

$$W=T\Omega$$

(8)

Bringing Equation (8) into Equations (2) and (7), the C_f,d and C_f,s are expressed, respectively, as:

$$C_{\mathrm{f},\mathrm{d}}={\displaystyle \frac{2T}{\rho {\Omega }^2\left(R_{\mathrm{i}\mathrm{n}}^5-R_{\mathrm{i}}^5\right)}}$$

(9)

$$C_{\mathrm{f},\mathrm{s}}={\displaystyle \frac{T}{{\pi \rho {\Omega }^{2}R}_{\mathrm{i}}^{4}L}}$$

(10)

3. Geometry and Numerical Method

3.1. Geometry and Boundary Conditions

Figure 3 presents the gap model, which comprises the impeller back gap of a sCO₂ compressor, such as a disk-type gap, a labyrinth seal, and a shaft-type gap. For the computation domain, the inner radius of the impeller back gap R_i is fixed as 13.0 mm. The inner radius at inlet and outlet R_in and R_out, as well as the length of the outer walls at inlet and outlet L_in and L_out are constants and remain consistent with the investigations of Hu et al. [16]. The geometric parameters of the labyrinth seal remain unchanged due to the structural limitations of the rotor, with its dimensions detailed in

Table 1. Geometric parameters of the labyrinth seal.

Parameter	Value	Unit
Teeth number, N	3	-
Teeth width, B	0.20	mm
Clearance width, C	0.05	mm
Teeth height at left side, Hl	0.45	mm
Teeth height at right side, Hr	0.85	mm
Cavity height, Hc	0.40	mm
Cavity length of inner wall, Li	2.20	mm
Cavity length of outer wall, Lo	2.00	mm

.

Additionally, the gap width of the impeller back gap δ, which equals the difference between R_o and R_in, is variable. The values of R_o and η for different cases are listed in

Table 2. Dimensions of the outer radius R_o and radius ratio η.

Parameter	Case I	Case II	Case III	Unit
Outer radius of impeller back gap, Ro	27.8	28.3	28.8	mm
Radius ratio, η	0.018	0.036	0.054	-

in detail. The selection of geometric parameters is based on the compressor dimensions in the TAC unit. The main dimensions of compressors of similar power are basically within the range.

The physical properties of CO₂ in this study were obtained from the NIST database REFPROP (Gaithersburg, MD, USA), utilizing the equation of state proposed by Ref. [37]. At the inlet and outlet planes, pressure-type boundary conditions are specified, with the parameters listed in

Table 3. Parameters of boundary conditions.

Parameter	Value	Unit
Temperature at inlet, Tin	303.15	K
Pressure at compressor inlet, Pin	9~12	MPa
Pressure at outlet, Pout	2.0	MPa
Rotational speed, Ω	10−1~105	r/min
Reynolds number, Re	102~108	-
Pressure ratio, π	4.5~6.0	-

. Notably, the inlet pressure corresponds to that of the impeller outlet of sCO₂ compressors, and it can be adjusted according to the compressor operating under the off-design conditions. The inlet pressure is derived from the TAC unit and similarly powered compressors. However, the outlet pressure is 2 MPa, which depends on seal performance [30]. Additionally, the inner walls, rotating at a speed determined by the Reynolds number Re and stationary outer walls are adiabatic and non-slip. It is worth stating that for Re, the actual sCO₂ compressor operation will not be below 10⁵ except in the startup condition, and the large range of Re is chosen to make the C_f models more applicable.

3.2. Numerical Method

In this study, ANSYS (Canonsburg, PA, USA) Fluent 18.0 was utilized to perform CFD simulations, and the steady-state RANS equations were solved. Moreover, to conduct CFD simulations of turbulent flow in the impeller back gap and labyrinth seal cavities, solving the governing equations was implemented by the realizable k-ε turbulence model.

In this study, the finite volume approach with the SIMPLE algorithm was employed to discretize RANS equations, and the numerical integration was carried out using a pressure-based solver. The leakage flow rate m at inlet and outlet was monitored, and the CFD results were recognized as reliable when m tended to stabilize and fluctuate less than 1% with iterations. Additionally, the residual values were used to evaluate solution convergence.

3.3. Model Validation

3.3.1. Numerical Method Validation

In this paper, the experiment results of Yuan et al. [31] about the leakage flow rate m_se when sCO₂ passes through labyrinth seal are compared to CFD results to perform computational approach validation. The meridian plane of two-teeth labyrinth seal is shown in Figure 4, and its geometry dimensions and operating conditions are presented in

Table 4. Geometry dimensions and experimental conditions of two-teeth labyrinth seal.

Parameter	Value	Unit
Shaft radius, Rs,se	1.500	mm
Teeth number, Nse	2	-
Teeth height, Hse	0.775	mm
Teeth width, Bse	1.270	mm
Cavity length, Lse	1.270	mm
Clearance width, Cse	0.105	mm
Pressure at inlet, Pin,se	10	MPa
Temperature at inlet, Tin,se	320	K
Pressure at outlet, Pout,se	3.400~9.200	MPa
Pressure ratio, πse	1.086~2.941	-

. Furthermore, the realizable k-ε turbulence model with wall function was used in validation simulations.

Figure 4 describes the comparison between the CFD results and experimental data under the different pressure ratio π_se conditions. The deviations between them gradually increase with larger π_se, but they are still slight overall. Furthermore, the maximum relative deviation of 2.1% indicates that CFD results closely align with experimental results. These findings strongly suggest that the numerical method can effectively predict m_se of sCO₂ passing through the labyrinth seal.

3.3.2. Turbulence Model Validation

To simulate turbulent flow in the impeller back gap and labyrinth seal, it is crucial to select an appropriate turbulence model for CFD simulations. Three turbulence models, such as SST k-ω, realizable k-ε, and the Reynolds stress model (RSM), were employed to evaluate the reliability of simulations, and skin friction coefficient C_f,rs obtained from the experiment of the rotor-stator disk system [19] was used as the benchmark for validation. The rotor-stator disk system, which consists of stationary and rotational walls, is presented in Figure 5, and

Table 5. Dimensions of rotor-stator disk system.

Parameter	Value	Unit
Inner radius of gap, Ri,rs	25.40	mm
Outer radius of gap, Ro,rs	249.20	mm
Gap width, δrs	6.35	mm
Gap length, Lrs	19.05	mm

provides its dimensions. In the experiment, the working fluid was water, and the rotational speed was determined by Re, ranging from 10³ to 5.8 × 10⁷. Additionally, the structured mesh for the computational domain of the rotor-stator disk system was generated with the first cell height of 5.0 × 10⁻⁴ mm near walls, making the maximum Y⁺ satisfy the requirements of all turbulent models.

As depicted in Figure 6, the values of C_f,rs simulated using the three turbulence models were compared to experimental results under different Re conditions. It was observed that the downward trends of C_f,rs versus Re are similar across all turbulence models, and also agree with the experiment. However, at Re < 10⁵, CFD results adopting realizable k-ε and RSM models are closer to the experimental results than the SST k-ω model. Furthermore, the detailed comparison revealed that the realizable k-ε model provides more accurate results than the RS model for Re > 10⁵. The maximum relative deviations of RS and the realizable k-ε and models compared to experimental results are 6.20% and 4.02%, respectively. Meanwhile, the validation in the above section also demonstrated that the realizable k-ε model can predict the leakage flow rate of sCO₂ in the labyrinth seal. Therefore, it is applicable that the realizable k-ε model for CFD simulations be used.

3.4. Grid Independence Validation

Figure 7 presents the structured mesh, which is generated by ANSYS ICEM 18.0. It is noted that the mesh is denser near stationary and rotational walls compared to the center since the flow is complex in boundary layer. To satisfy the requirements of the turbulence model, the first cell height near walls is 5.0 × 10⁻⁷ m with a growth rate of 1.1, ensuring that Y⁺ is appropriately controlled.

The method recommended by Celik et al. [38] was used to perform grid independence validation with the three different grid numbers, consisting of 1.6 million, 3.2 million, and 6.4 million grids, to ensure that CFD simulations were independent of the number of grids. The non-dimensional velocity distributions under different axial position conditions for each mesh are shown in Figure 8a, where u denotes fluid velocity, V represents the linear velocity of rotor, and Z is the axial coordinate. It exhibits a negligible variation as the number of grids increases from 3.2 million to 6.4 million. Furthermore, the maximum relative deviation between their results is only 2.32%. Figure 8b describes the 3.2 million grid solution with a discretization error. The maximum relative deviation between the non-dimensional velocity and the extrapolated solution for 3.2 million grids is merely 1.66%, indicating that mesh refinement can enhance reliability in CFD results. Therefore, adopting the 3.2 million grids allows for the performance of CFD simulations in this study.

4. Results and Discussion

In this section, the influence rules of the Reynolds number Re of 10²~10⁸, pressure ratio π of 4.5~6.0, and radius ratio η of 0.018~0.054 on the skin friction coefficients C_f,d and C_f,s and the flow characteristics are analyzed, and the models of C_f in the impeller back gap and labyrinth seal cavities are proposed and validated.

4.1. Effects of Reynolds Number and Pressure Ratio

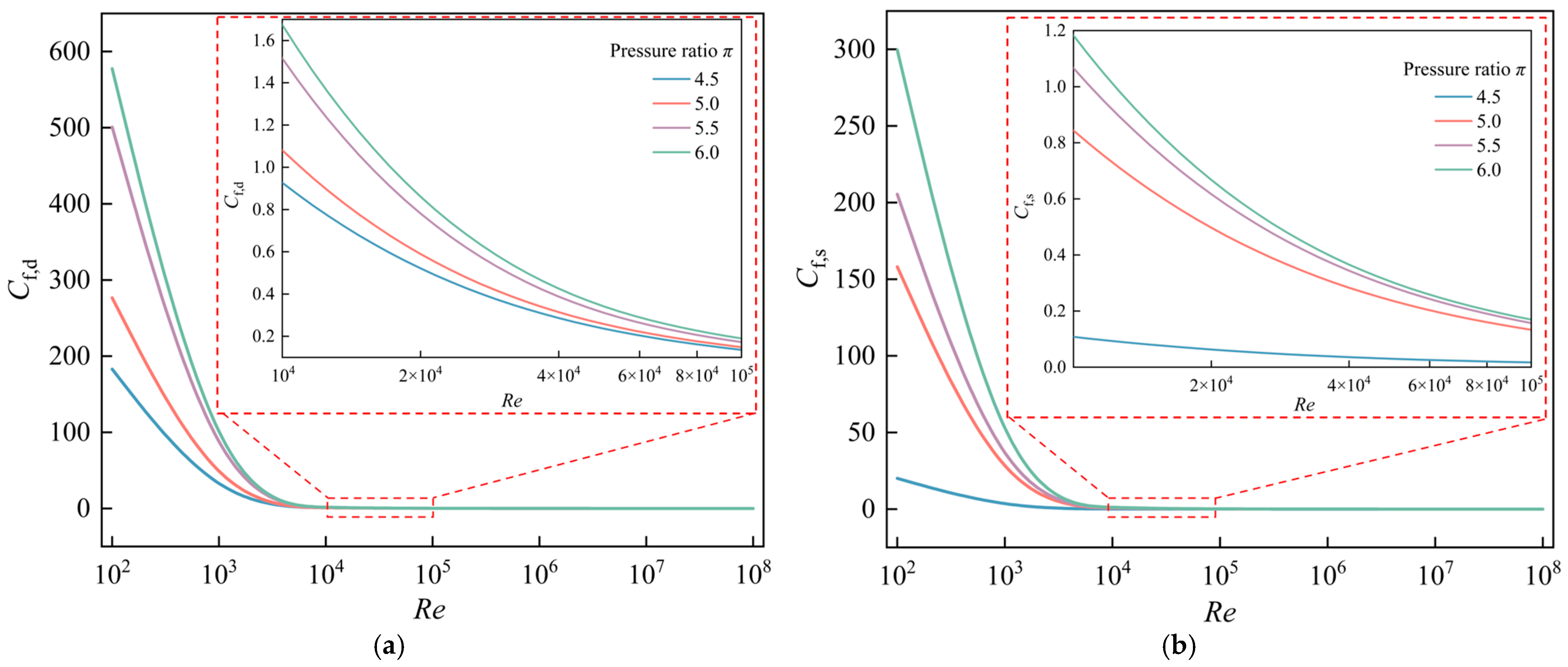
Figure 9 illustrates the behavior of C_f,d and C_f,s versus Re for Case I, with a different π ranging from 4.5 to 6.0, respectively. The results reveal that both C_f,d and C_f,s decrease with increasing Re, and the decreasing rate remains unchanged when Re ≤ 10³ and gradually decreases to 0 for Re ranging from 10⁴ to 10⁸. Consequently, C_f,d and C_f,s become independent of Re while Re exceeds 10⁵. Given the variability in the rates at which C_f,d and C_f,s decrease with respect to Re, the models of C_f,d and C_f,s in Section 4.4 need to be segmented, with Re being 10³ and 10⁵ as the demarcation point.

It is also observed that C_f,d and C_f,s increase with π from 4.5 to 6.0 under the conditions of the same Re since a larger π corresponds to a higher fluid density, and thus windage loss and C_f,d and C_f,s are larger as known from Equations (1) and (5). Moreover, the comparison between Figure 9a,b reveals that the C_f,d is larger than C_f,s, which is because disk-type windage loss is significantly greater than shaft-type.

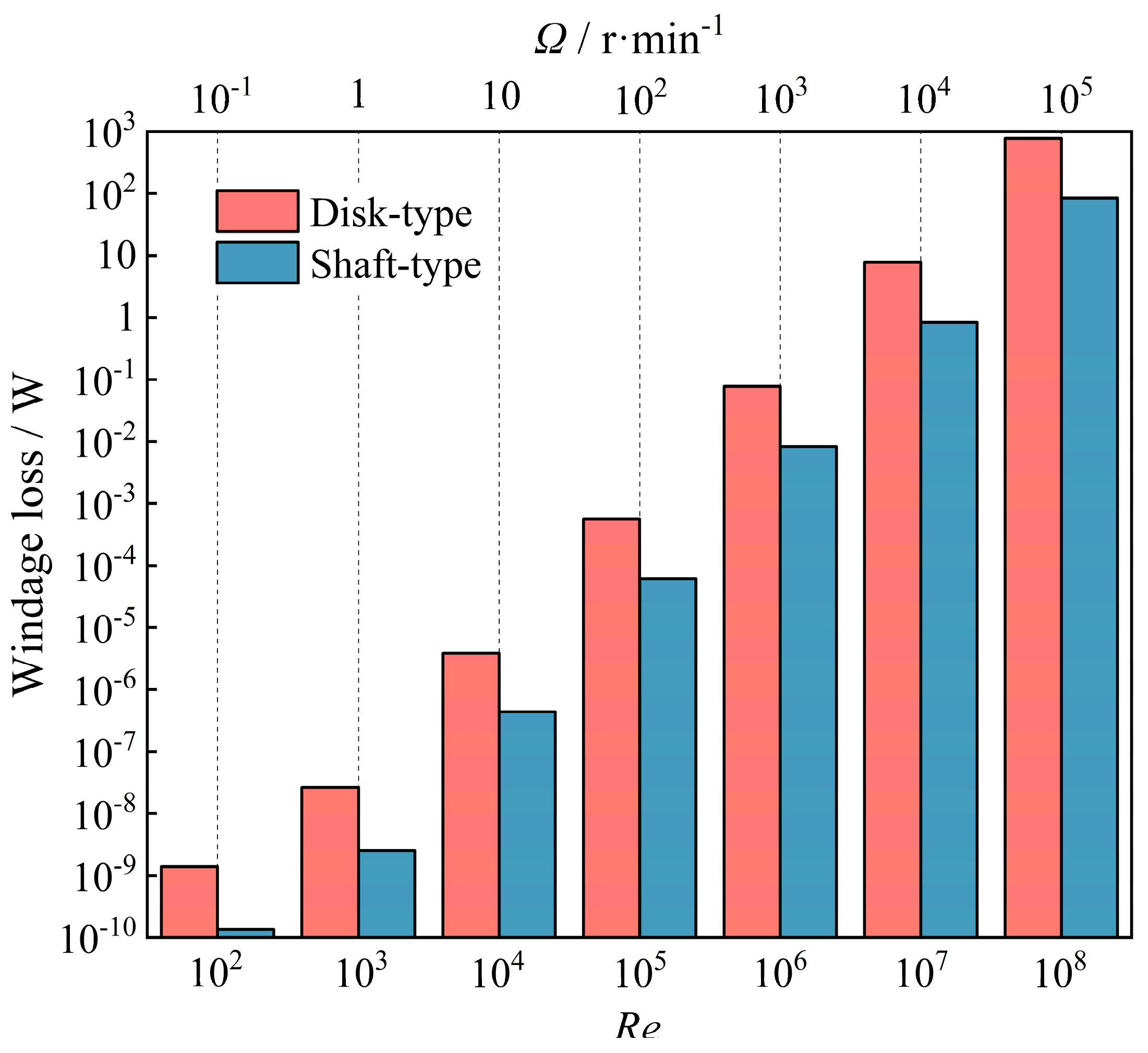
In Figure 10, disk-type and shaft-type windage losses for Re from 10² to 10⁸, corresponding to rotational speed Ω being 10⁻¹~10⁵ r/min under π = 4.5 conditions are presented. It is observed that windage losses rapidly increase with Re and are much larger in disk-type gaps than in shaft-type gaps. For example, at Re = 10⁶ and Ω = 10³ r/min, disk-type and shaft-type windage losses are 0.08 W and 0.008 W, and at Re = 10⁸ and Ω = 10⁵ r/min, they are 780 W and 84.250 W, respectively, which is basically consistent with the findings reported by Ponceta et al. [39].

This observation is because the impeller back gap is the primary region compared to the labyrinth seal, according to Figure 1 and Figure 3, leading to much larger disk-type windage loss than shaft-type, as confirmed in Figure 10, which further supports the previous conclusions that C_f,d is larger than C_f,s in Figure 9.

Figure 11 describes the proportion of disk-type and shaft-type windage losses. The proportion of shaft-type windage loss increases with Re, while it decreases with π. On the contrary, the proportion of disk-type windage loss exhibits the opposite trend to that of shaft-type, falling as Re increases and rising with π. Notably, the proportion of disk-type windage loss is consistently far larger than that of shaft-type loss under various Re and π conditions, with its minimum reaching 90%, which indicates that windage loss in the impeller back gap significantly contributes to total windage loss. Nonetheless, it is still necessary to consider the influences of shaft-type windage loss in the preliminary design and operation of sCO₂ compressors and TAC units.

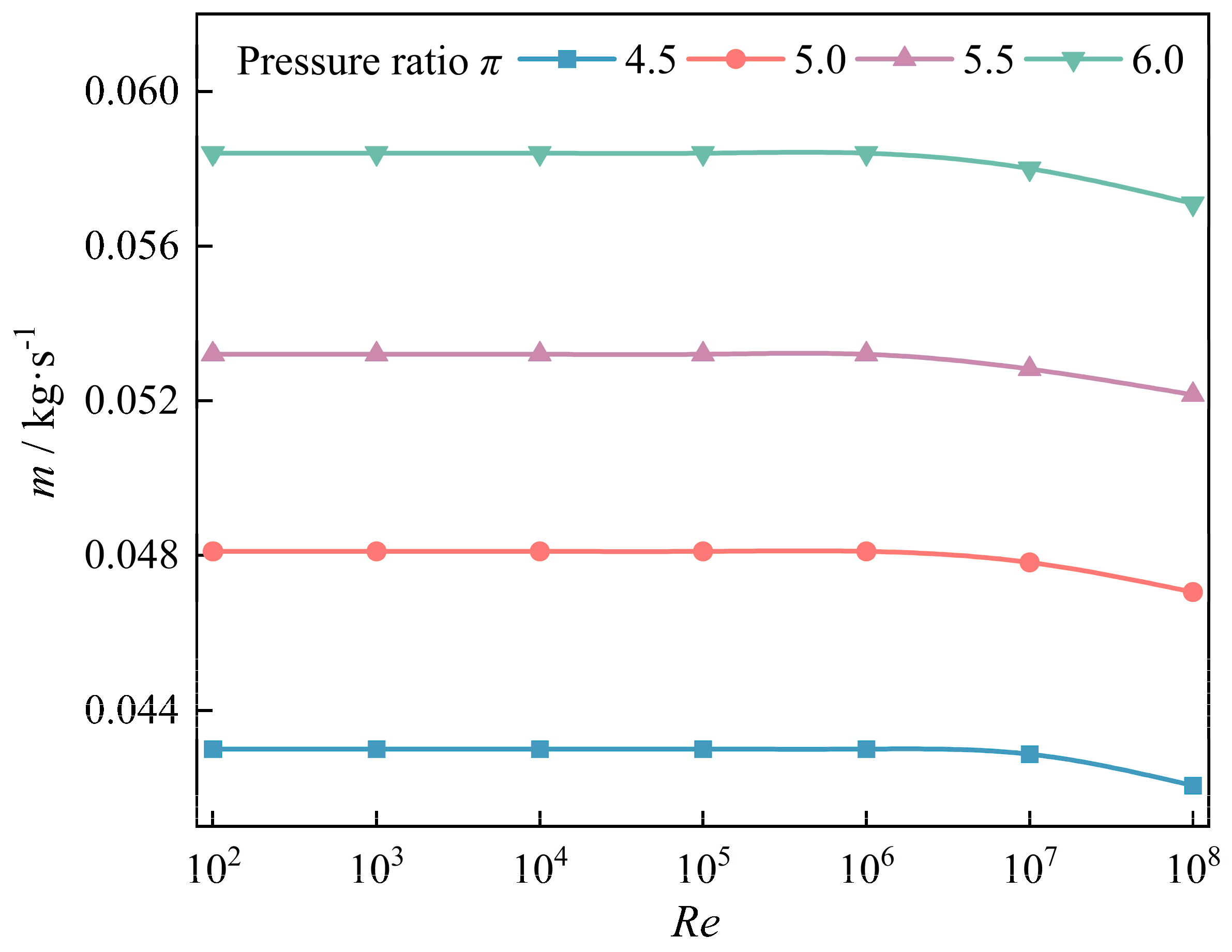
In order to evaluate the flow characteristics in the impeller back gap and labyrinth seal cavities, the leakage flow rate m is a crucial parameter. The m versus Re for π ranging from 4.5 to 6.0 is presented in Figure 12. As the velocity of fluid in gaps is higher as π increases, the m gradually grows when the area at the inlet and outlet is same. Moreover, with the increment of Re, the m is unchanged for Re < 10⁶ and decreases for Re ≥ 10⁶. It also was found that when Re ranges from 10² to 10⁶, the m is 0.0584 kg/s, and it drops to 0.0571 kg/s for Re = 10⁸ when π = 6.0. When the Reynolds number is high, on the one hand, due to the centrifugal force of the fluid slowing down the radial flow, and on the other hand, due to the complexity of turbulence, the vortex in the gap impedes the flow of the fluid along the pressure gradient. The vortices in computational domain are fewer, and the inhibition effect on leakage flow is small due to the significantly minor influences of the centrifugal force on fluid at a low Re, leading to unchanged m when Re < 10⁶. However, the number of vortices increases because of enhanced flow instability when the influences of centrifugal force are more primary than that of viscous force at high Re, which makes leakage flow in gap and labyrinth seal inhibited, thus causing m to decrease with increasing Re when Re ≥ 10⁶.

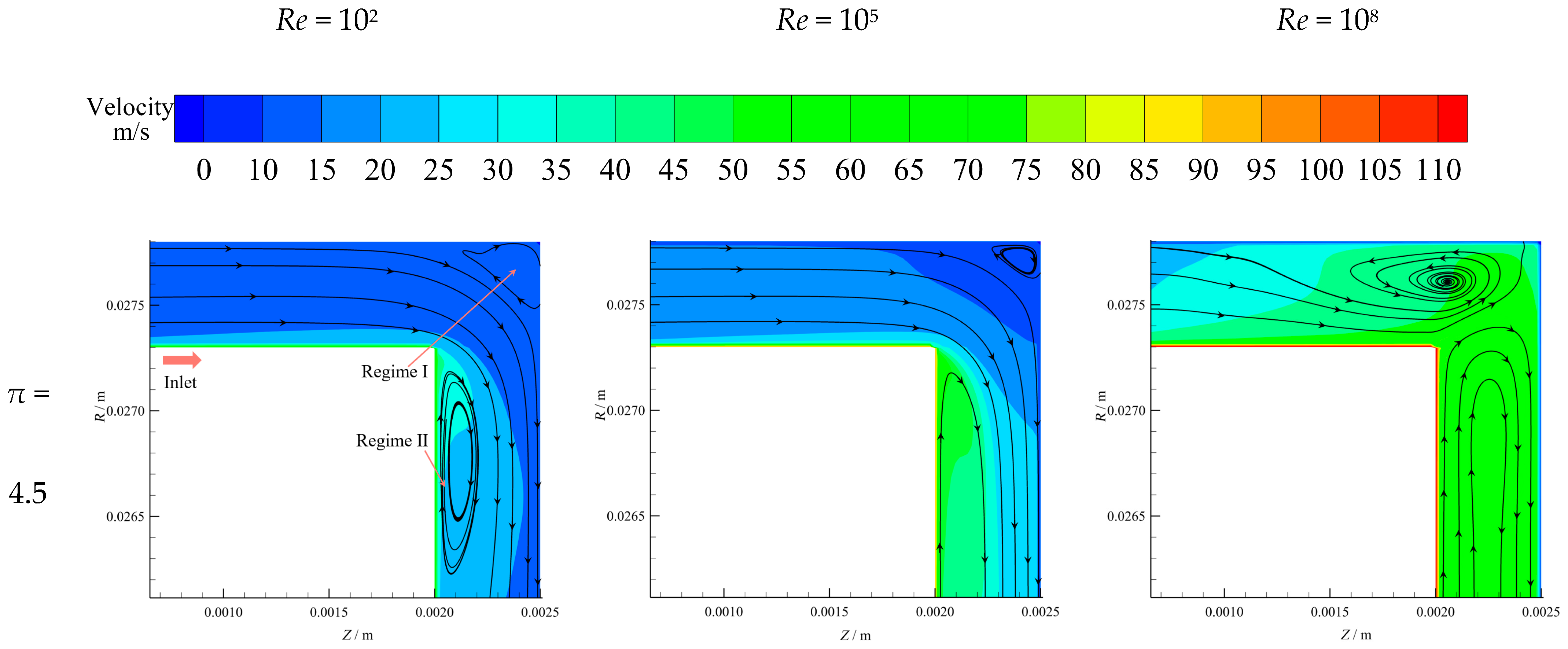
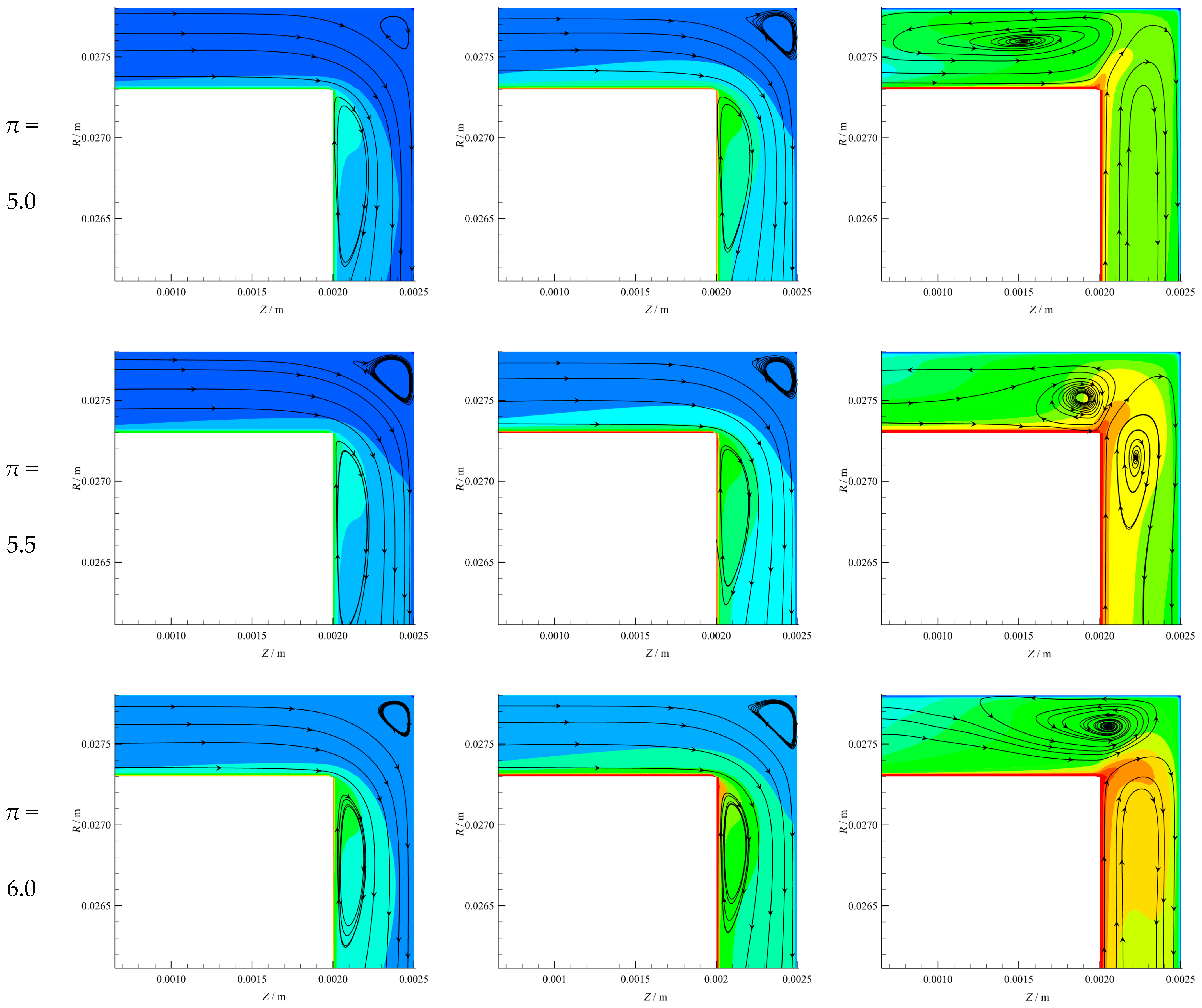
4.2. Flow Characteristic Analysis

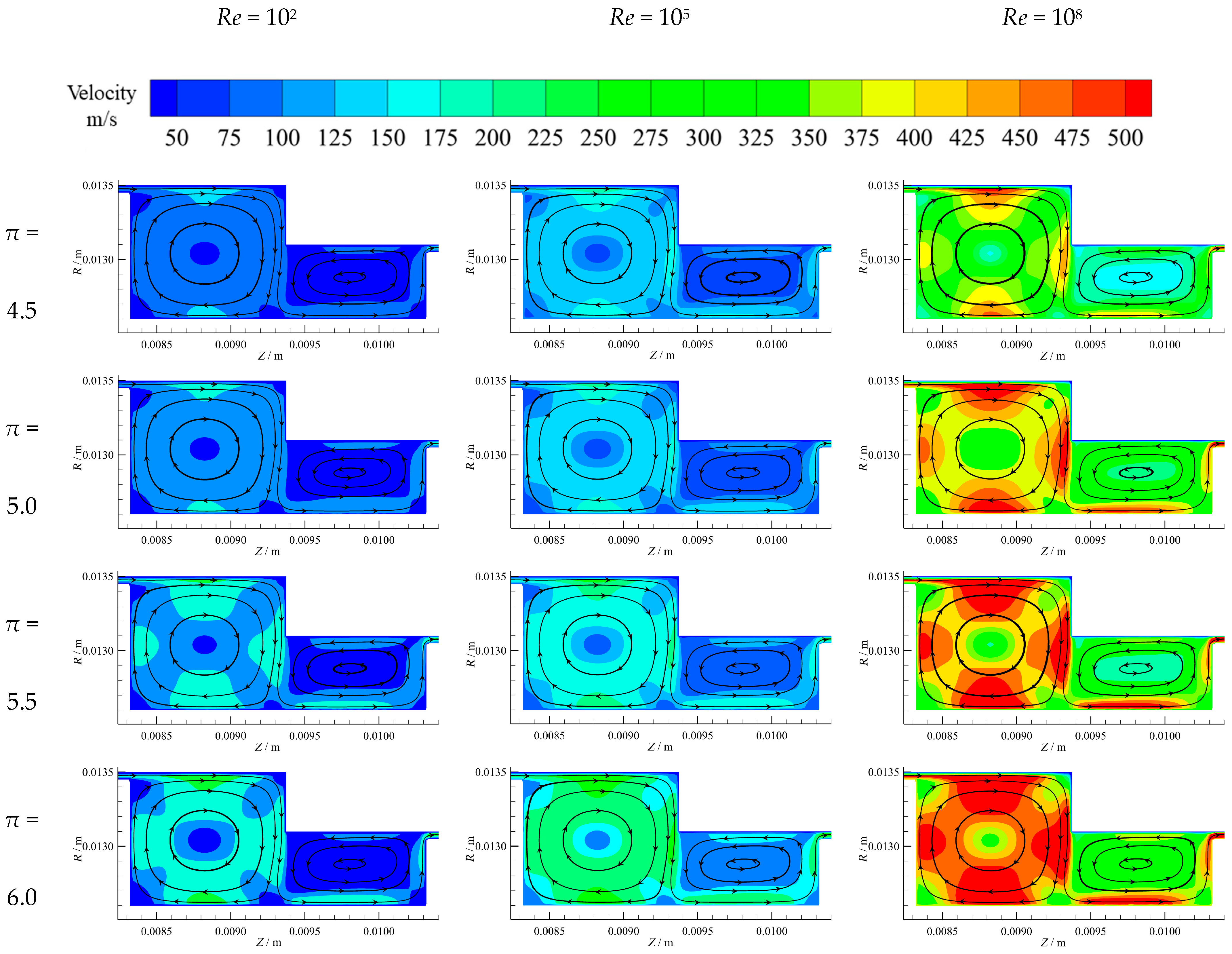
To analyze the influences of Re and π on C_f,s, C_f,d, and m from flow characteristics’ point of view, Figure 13 depicts the streamlines and velocity at the inlet regions for Case I, where Re = 10², 10⁵, and 10⁸ and π = 4.5, 5.0, 5.5, and 6.0. It can be seen that the streamlines exhibit similar flow patterns and indicate that fluid can flow smoothly into the impeller back gap as a whole when Re = 10² and 10⁵. However, there are a small number of vortices in the transition regions between the inlet and impeller back gap, such as Regime I near the stationary walls and Regime II near the rotational walls. The reason for this is that the velocity direction of fluid in transition regions suddenly changes, resulting in a dramatic decrease in the velocity magnitude and generation of vortices.

As Re increases, the centrifugal force becomes more prominent, leading to increased flow instability and the formation of vortices that fill the whole inlet region. As a result, the m decreases with increasing Re under Re ≥ 10⁶ conditions, as depicted in Figure 12. Furthermore, it is also worth noting that the size of the vortices in the impeller back gap, which makes disk-type windage loss generated, increases when the π rises from 4.5 to 6.0 under the same Re conditions. The vortex shape at the inlet of the disk-type gap changes when the Re increases. It shifts from being attached to the rotor wall (Regime II) to filling the entire inlet region. This is attributed to the fact that, at this point, the influence of leakage flow is weakened and the centrifugal force acts as the main role to enhance the vortex formation. The phenomenon can be attributed to the higher inlet velocity under a larger π, which leads to the larger decreasing rate of velocity when the fluid in Regime I and Regime II change velocity direction.

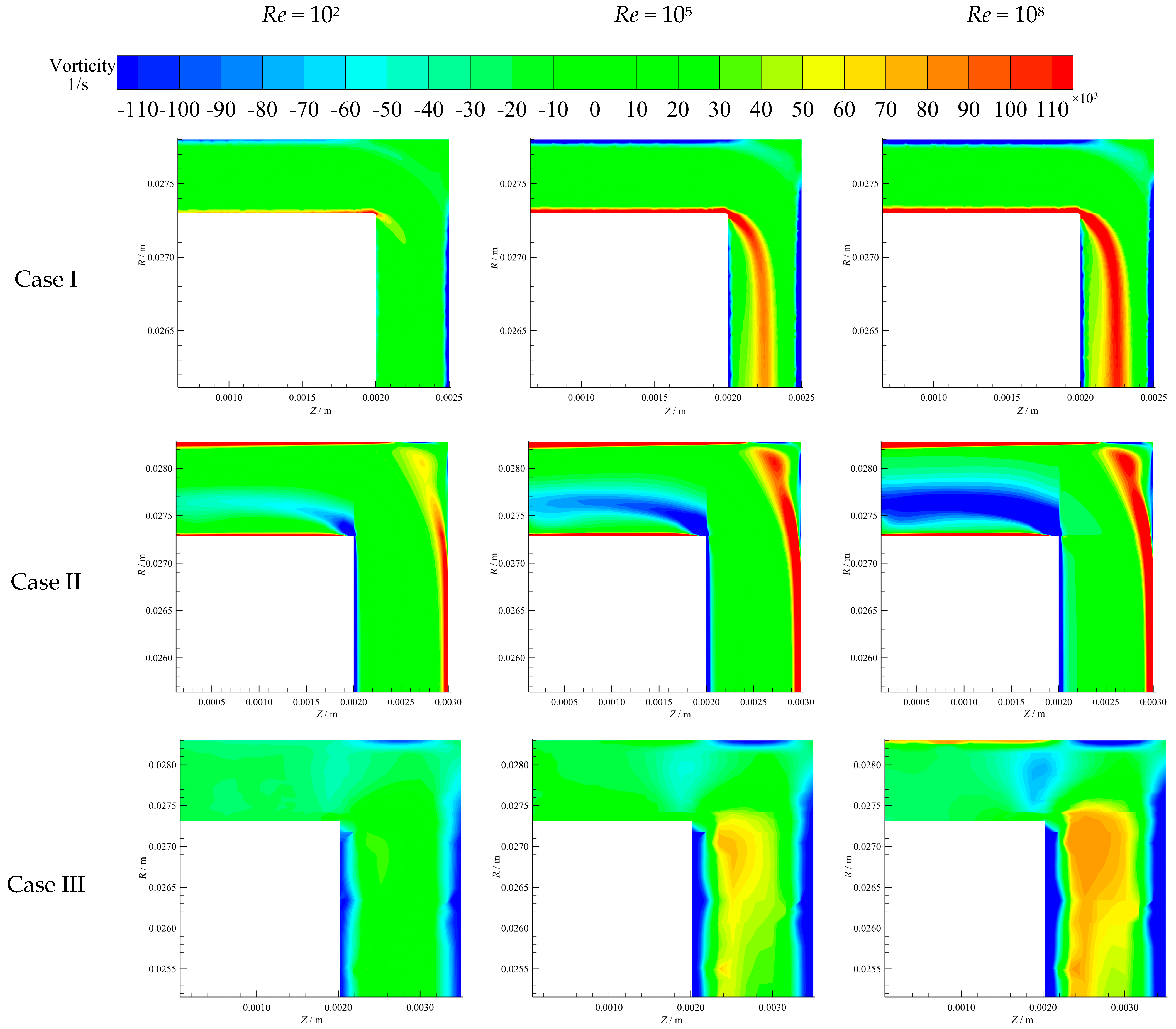
The contours reveal that the velocity increases with Re and π due to a larger centrifugal force that depends on Re and the pressure difference related to π. However, the velocity diversity under different Re conditions is more pronounced than that of different π, suggesting that the centrifugal force has a more significant influence on velocity distribution than the pressure difference because its variation is smaller. Additionally, the velocity gradually decreases from the rotational walls, where fluid velocity equals the linear velocity of the rotor, to the stationary walls, where the fluid velocity is 0 due to the non-slip wall. It is further observed that as Re and π rise, the high-velocity regions near the rotational walls expand, while the low-velocity regions near the stationary walls shrink. This trend indicates that the high-velocity regions become dominant for a larger Re and π.

In addition, the streamlines and velocity contours in the cavities of the seal for Case I, with a different Re of 10², 10⁵, and 10⁸ and a π of 4.5, 5.0, 5.5, and 6.0 are shown in Figure 14.

The velocity in the cavities is observed to be higher than that at inlet regions described in Figure 13, which is due to the dramatic decrease in the through-flow area when the fluid passes through the labyrinth seal. Similarly, the velocity increases with Re and π, and the effects of Re on velocity are still more prominent than π, as previously analyzed.

Moreover, it is worth noting that there are high-velocity regions near the rotational and stationary walls and low-velocity regions at the center of the cavities. As Re increases, the high-velocity regions grow, and the low-pressure regions decrease. On the other hand, with an increase in π, the high-velocity regions gradually intensify, but the low-pressure regions remain primarily unaffected, which suggests that the influences of centrifugal force are more primary than those of pressure difference. Regardless of the Re and π values, vortices are generated within the cavities due to the velocity gradient between the walls and center, as presented in the streamlines in Figure 14, which is a primary reason for windage loss. Nevertheless, as discussed in Section 4.3, the windage loss in the labyrinth seal is considerably lower than that occurring in the impeller back gap, which is attributed to the fewer number of teeth and cavities presented in Figure 14, resulting in the impeller back gap being the primary contributor to windage loss.

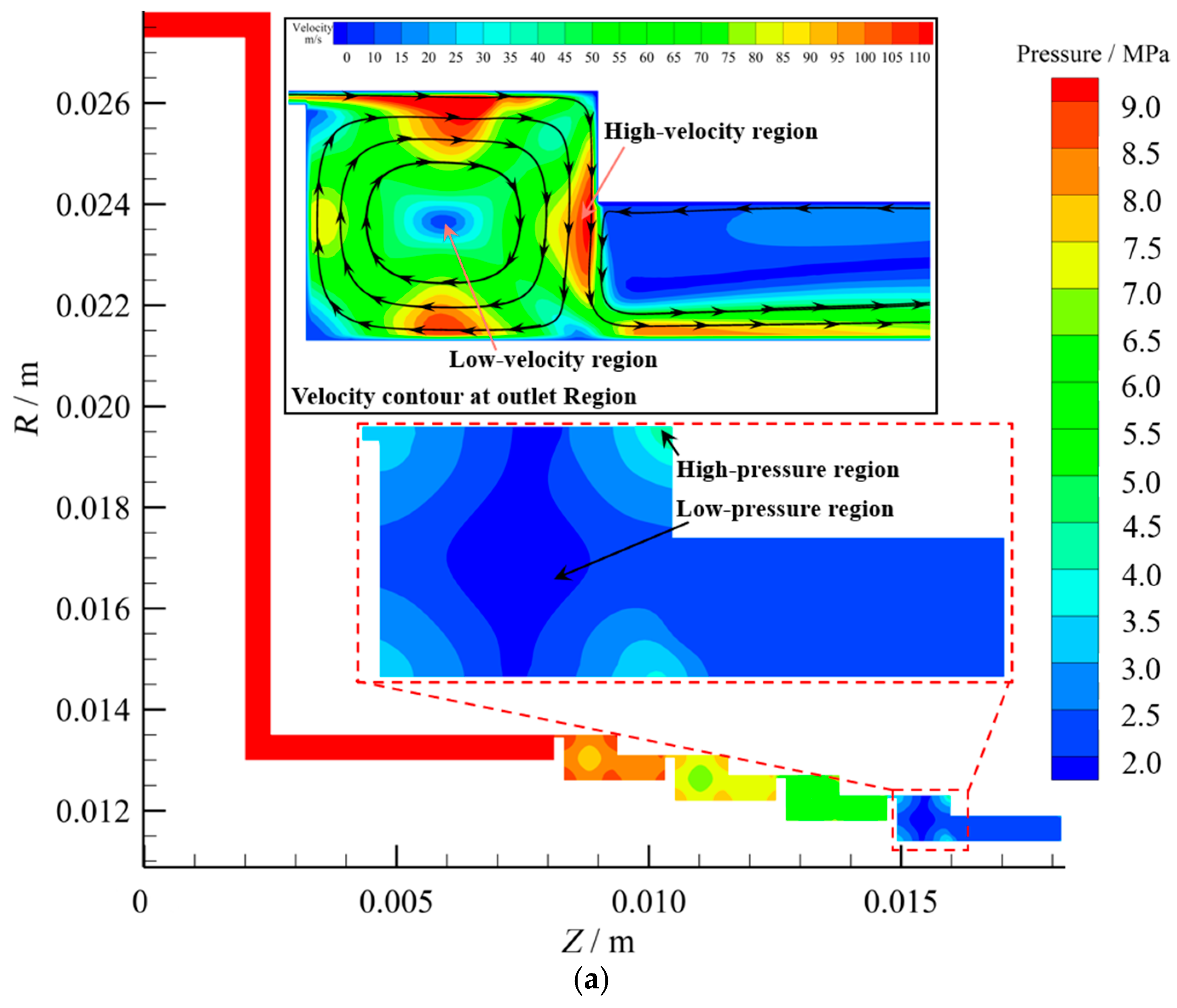
The pressure contour and streamlines at the outlet region for Case I when Re = 10⁴ and π = 4.5 is illustrated in Figure 15a. It is apparent that the pressure is unchanged in the impeller back gap and it gradually decreases from the inlet of the labyrinth seal to the outlet. This behavior indicates that the increase in velocity in the impeller back gap is relatively small compared to that in the labyrinth seal, which is similar to the conclusions drawn in Figure 13 and Figure 14.

At the outlet region, the pressure decreases to a minimum value of 2 MPa, which matches the boundary condition specified in Table 3. In the last cavity of the labyrinth seal, high-pressure regions near the walls and low-pressure regions at the center are observed, which is the opposite of the velocity contour presented in Figure 14. The reason for the discrepancy is the conservative conversion between pressure energy and kinetic energy. Furthermore, it is observed that the whole outlet region is filled with vortices because of the influences of shear stress generated by the rotational walls, which results in the leakage flow rate being inhibited. 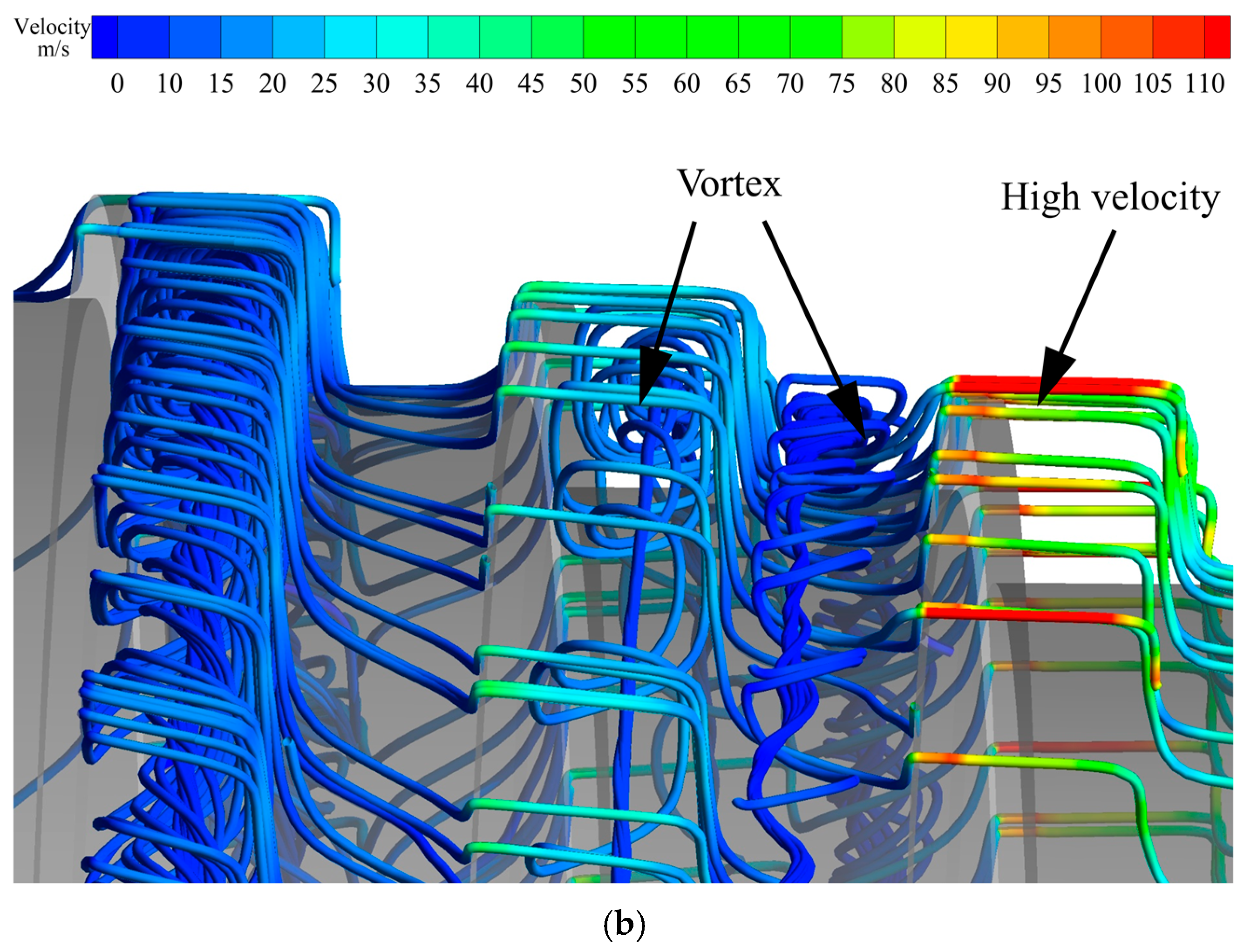Figure 15b illustrates the distribution of streamlines in the labyrinth seal. The vortices formed in the seal can be clearly visualized, consistent with those in Figure 14. And a high velocity region appears at the top. After the fluid passes through the seal, a large cavity is formed between the two seals, resulting in a sudden increase in fluid volume and the formation of a strong vortex. Pressure recovery in this area is limited.

4.3. Effects of Radius Ratio

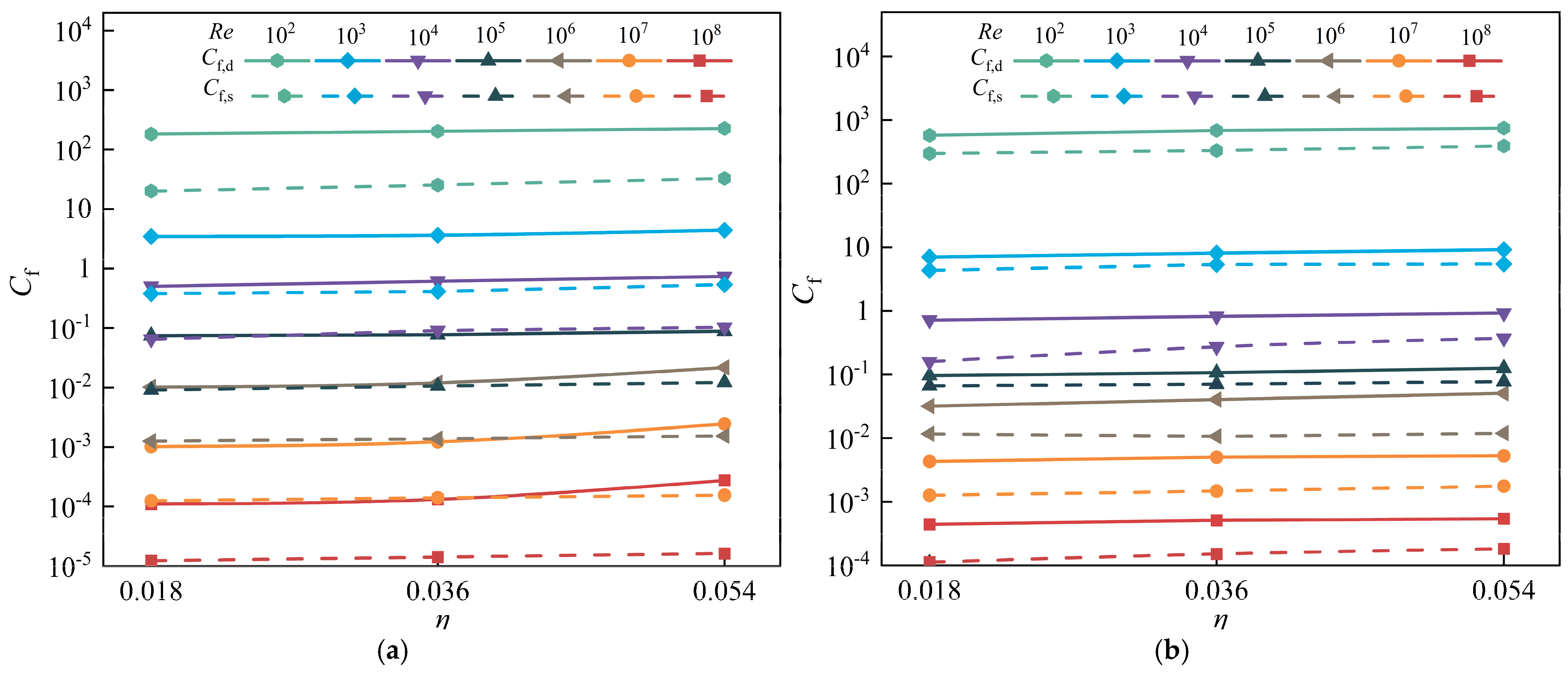
Figure 16 presents the variation of C_f,d and C_f,s with respect to the radius ratio η for Re ranging from 10² to 10⁸ when π is 4.5 and 6.0, respectively. It is found that both C_f,d and C_f,s slightly rise as η increases, regardless of whether the value of π is 4.5 or 6.0 under different Re conditions. This increase is attributed to the increased flow instability and vortex generation in gaps as the value of η becomes larger, resulting in larger disk-type and shaft-type windage losses. Further evidence supporting this conclusion will be provided later. In addition, C_f,d is a great deal larger than C_f,s for the same Re and π values, as well as C_f,d and C_f,s being larger at higher π values, which is consistent with the conclusions drawn from Figure 9. However, the impacts of η on C_f,d and C_f,s have a negligible effect relative to Re and π, since the growing rate in C_f,d and C_f,s with η is minimal.

The m versus η for Re =10² for π ranging from 4.5 to 6.0 is presented in Figure 17. When π = 4.5, the m increases from 0.0430 kg/s at η = 0.018 to 0.2145 kg/s at η = 0.054, and similarly to the conditions of π = 6.0, the m grows from 0.0584 kg/s at η = 0.018 to 0.3021 kg/s at η = 0.054 due to larger through-flow area. The rate of the increase in m is constant for different η, indicating that the influencing degree of different η on m is identical. Moreover, regardless of the values of η, the m grows when π grows from 4.5 to 6.0, which is consistent with the observations in Figure 12.

Moreover, Figure 18 depicts the vorticity at inlet regions with Re of 10², 10⁵, and 10⁸ and η of 0.018, 0.036, and 0.054 under π = 4.5 conditions in order to analyze the flow characteristics for different η. It is noted that the red and blue regions indicate the opposite rotational direction of the vortices, but both represent larger vorticity in all contours, and the green regions mean that the vorticity is 0. From all contours, it can be seen that the high-vorticity regions expand with increasing Re and η, which reveals that a larger Re, corresponding to larger centrifugal force, results in enhanced flow instability, and a larger η makes the size of vortices increases, which indicates that the effects of vortex dissipation is the main reason for an increase in C_f,d and C_f,s with η, as presented in Figure 16. Furthermore, it is observed that the vorticity in the vicinity of the walls is considerably higher than that at the center due to the effect of the boundary layer attached to the wall, as evident in all contours. As Re becomes larger, the boundary layer effect becomes more pronounced.

4.4. Models of Skin Friction Coefficients in Shaft-Type and Disk-Type Gaps

Based on the previous discussion presented in Section 4.1, Section 4.2 and Section 4.3, it is found that the windage loss and flow characteristics in the impeller back gap and labyrinth seal cavities are relatively essential, which indicates that they cannot be neglected during the primary design and operation of sCO₂ compressors. However, the lack of corresponding models of C_f,d and C_f,s makes it challenging to accurately predict windage loss. Therefore, it is significantly urgent to propose models of C_f,d and C_f,s based on previous CFD results.

The results in Figure 9 reveal that the decreasing rates of C_f,d and C_f,s vary for different Re ranges; hence, it is necessary to segment the models of C_f,d and C_f,s with an Re of 10³ and 10⁵ as the demarcation point. According to the previous analysis, the C_f is related to Re, π, and η. Thus, the models can be expressed as:

$$C_{\mathrm{f}}=af(Re,\pi ,\eta )$$

(11)

In addition, following the approach of Daily [19] and Bilgen and Boulos [27], the C_f is to be written as follows:

$$C_{\mathrm{f}}=a{Re}^b{\pi }^c{\eta }^d$$

(12)

Adopting the Least-Square Method, the models of C_f,d and C_f,s are listed in

Table 6. Models of C_f,d and C_f,s.

Models of Cf,d	Models of Cf,s	Range
$C_{\mathrm{f},\mathrm{d}}={\displaystyle \frac{3755{\pi }^{3.82}{\eta }^{0.01}}{{Re}^{1.88}}}$	$C_{\mathrm{f},\mathrm{s}}={\displaystyle \frac{109.4{\pi }^{5.19}{\eta }^{0.06}}{{Re}^{1.79}}}$	${10}^2\le Re<{10}^3$
$C_{\mathrm{f},\mathrm{d}}={\displaystyle \frac{163.0{\pi }^{1.32}{\eta }^{0.02}}{{Re}^{0.85}}}$	$C_{\mathrm{f},\mathrm{s}}={\displaystyle \frac{4.542{\pi }^{3.62}{\eta }^{0.06}}{{Re}^{0.90}}}$	${10}^3\le Re<{10}^5$
$C_{\mathrm{f},\mathrm{d}}={\displaystyle \frac{0.1937{\pi }^{5.32}{\eta }^{0.02}}{{Re}^{0.86}}}$	$C_{\mathrm{f},\mathrm{s}}={\displaystyle \frac{0.368{\pi }^{3.25}{\eta }^{0.03}}{{Re}^{0.67}}}$	${10}^5\le Re\le {10}^8$

. It needs to be noted that the models are only applicable to the conditions where Re is 10²~10⁸, π ranges from 4.5 to 6.0, and η is 0.018~0.054.

According to the Least-Square Method, the higher fitting accuracy for the models is indicated by SSE and R² values approaching 0 and 1, respectively. In this paper, the maximum SSE and minimal R² are 5.62 × 10⁻⁷ and 0.940 for models of C_f,d, and 2.43 × 10⁻⁶ and 0.917 for models of C_f,s, demonstrating that the fitting accuracy of models is remarkably high.

CFD simulations are used to calculate the values of C_f,d and C_f,s for the different Re in the impeller back gap, based on the dimensions and boundary conditions presented in

Table 7. Parameters of validated geometry.

Parameter	Value	Unit
Gap width, δ	0.50	mm
Temperature at inlet, Tin	303.15	K
Pressure at inlet, Pin	9	MPa
Pressure at outlet, Pout	2	MPa
Reynolds number, Re	102~108	-
Radius ratio, η	0.038	-
Pressure ratio, π	4.5	-

, which are applicable to the sCO₂ compressor designed by Cao et al. [30] to assess the reliability of models. It needs to be pointed out that the dimensions of the labyrinth seal are consistent with those listed in Table 1.

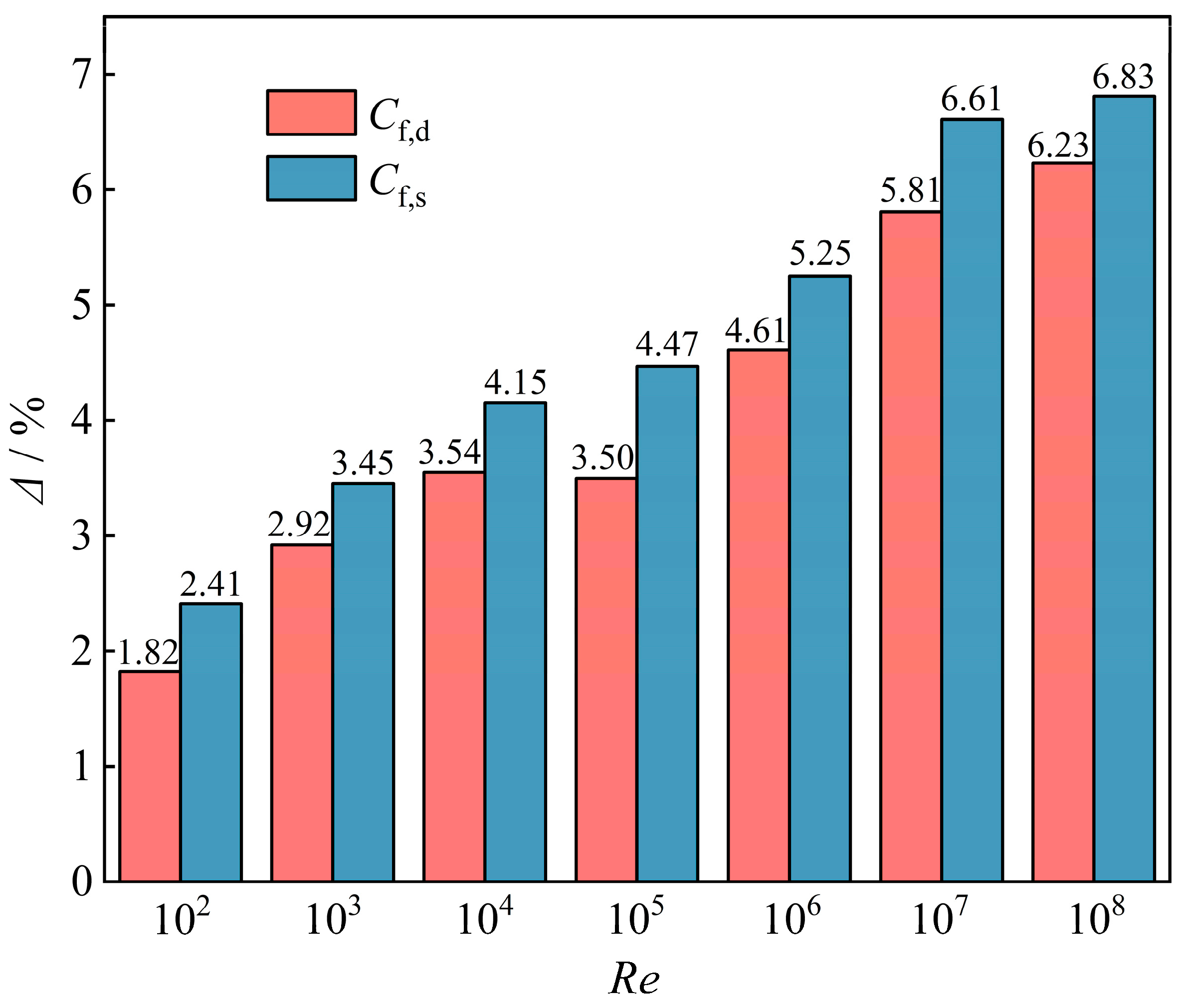
To quantitatively assess the predictive accuracy of the models, the relative deviation Δ is defined, and Figure 19 illustrates the relative deviations Δ of C_f,d and C_f,s for Re ranging from 10² to 10⁸.

$$\Delta ={\displaystyle \frac{C_{\mathrm{f},\mathrm{m}}-C_{\mathrm{f},\mathrm{n}}}{C_{\mathrm{f},\mathrm{n}}}}\times 100\%$$

(13)

It is noteworthy that the Δ is small, with maximum values of 6.23% and 6.83% for C_f,d and C_f,s. These results demonstrate the excellent agreement between the predicted values and CFD simulations, indicating that the proposed models can predict windage loss in the impeller back gap and labyrinth seal cavities.

The design of the sCO₂ compressor in engineering practice can refer to the windage loss models in Table 6 and Equations (2) and (7). In order to reduce windage losses and increase the compressor efficiency, the following suggestions are given. Firstly, the rotational speed and windage loss present a cubic relationship; it is very effective to reduce the rotational speed in a reasonable range. Secondly, reduce the radius ratio under the condition of axial-thrust compliance. Finally, increase the sealing outlet pressure to reduce the pressure ratio, which can effectively reduce the windage loss.

5. Conclusions

The windage loss in the impeller back gap and labyrinth seal cavities significantly impacts the aerodynamic performances of supercritical CO₂ (sCO₂) compressors. To accurately calculate windage loss, essential factors affecting the skin friction coefficients C_f,d (for the disk-type gap) and C_f,s (for the shaft-type gap), including the Reynolds number Re, pressure ratio π, and radius ratio η, are investigated in this paper. The flow characteristics of the gap are analyzed and prediction models are proposed, respectively. The conclusions help to use a more accurate form of predicting windage loss when designing sCO₂ compressors. The main conclusions are as follows:

(1)

The slope of skin friction coefficients (C_f,d and C_f,s) varies abruptly for the Reynolds number (Re) from 10³ to 10⁴, which is the transition zone from laminar to turbulent flow. Moreover, the disk-type gap exhibits higher windage losses compared to the shaft-type gap, with impeller back gap losses exceeding 90% of total windage losses. Furthermore, the pressure ratio’s influence on leakage flow diminishes beyond Re ≥ 10⁶, attributable to emerging flow instability effects;

(2)

As Re increases beyond 10⁶, centrifugal dominance causes the vortices to fully occupy the inlet region, reducing mass flow rate (m). Rotational speed and pressure ratio (π) jointly enhance inlet velocity, though Re exhibits a stronger correlation. The cavity velocities surpass the inlet values due to the labyrinth seal-induced flow area contraction, showing positive correlation with both Re and π;

(3)

The radius ratio (η) exhibits negligible influence on skin friction coefficients C_f,d and C_f,s compared to Re and π. While η equivalently affects mass flow rate across tested ranges, increasing Re and η synergistically expands high-vorticity zones. The instability of the flow causes C_f,d and C_f,s to increase with η. The vorticity near the wall is the principal source of windage loss, which is due to the flow instability of the boundary layers;

(4)

The models of C_f,d and C_f,s for the impeller back gaps and labyrinth seal cavities are proposed and validated across Re regimes (10²~10⁸). With maximal relative deviations 6.23% and 6.83%, the models demonstrate engineering-grade accuracy for aerodynamic loss prediction in sCO₂ compressors. Incorporating the Reynolds number, pressure ratio, and radius ratio, these correlations enable the pre-optimization of parameter combinations during preliminary design phases, achieving reduction through parameter selection.