Effect of Tendon Profile Layout on Flexural Strength of Unbonded Post-Tensioned Prestressed Concrete Bridge I-Girder
Abstract
1. Introduction
- Increasing the load resistance.
- Increasing the bending moment capacity.
- Better deflection control.
- Increasing the stiffness of prestressed concrete I-bridge girders.
- Decreases in construction costs.
2. Experimental Program
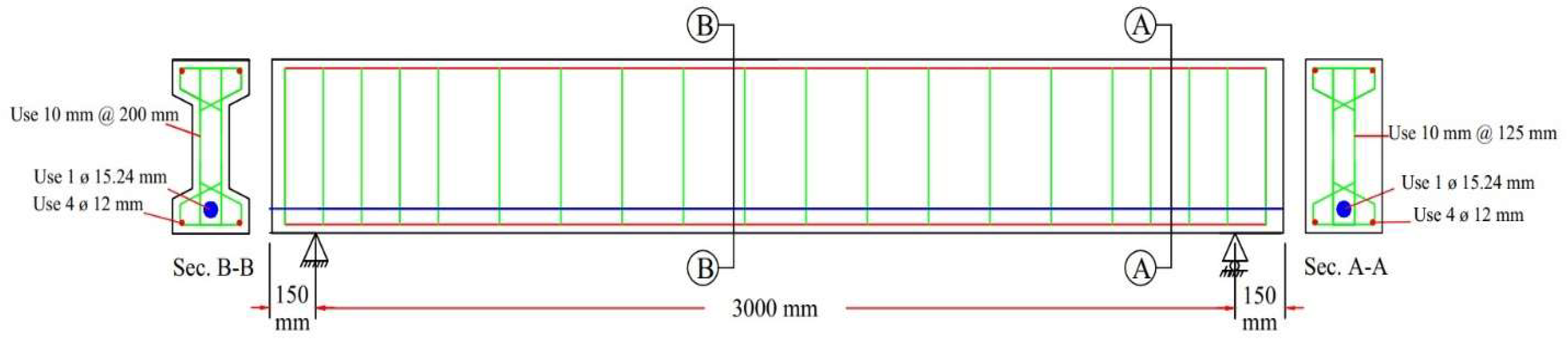
2.1. Size and Shape of the Test Specimens
2.2. Prestressing and Reinforcement Detail
2.3. Concrete Mix Specification
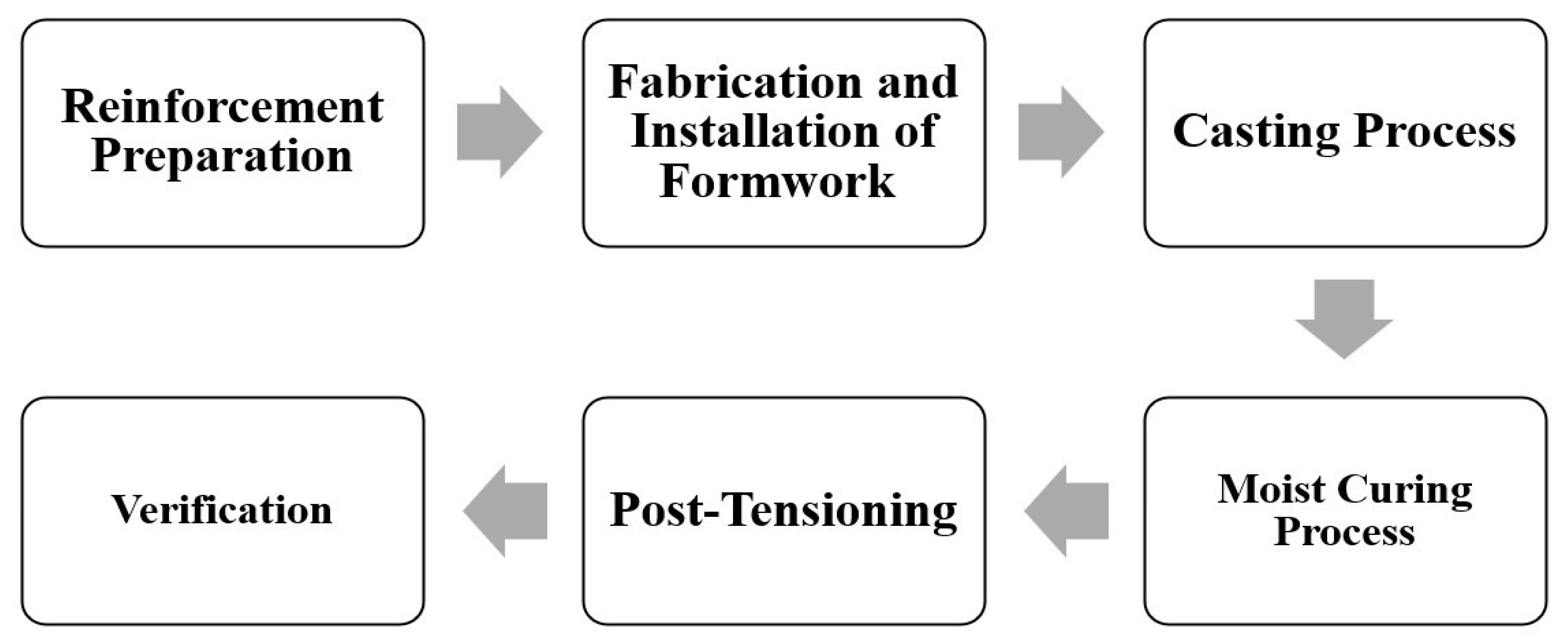
2.4. Preparation of the Test Specimens
2.5. Experimental Variables
2.6. Test Setup and Instrumentation
2.7. Experimental Procedure
- Connect the load cell and LVDTs to the data logger to obtain real-time measurements of the specimens’ load and displacement as the applied load increases, as shown in Figure 9a.
- Link the data logger to the computer. The computerized data acquisition system will automatically record and store the data.
- Loosen the load adjustment control wheel to prevent the sudden application of load to the specimen.
- After placing the specimen properly on the testing rig, slowly and steadily tighten the load adjustment control wheel to apply the load.
- The load control method was employed during the test, with the load applied at an average rate of 90 kN/min during the linear elastic stage. As cracks developed and the concrete began to exhibit plastic behavior, the digital load indicator no longer displayed a constant loading rate.
- For safety reasons, the test was terminated when the load remained constant or slightly decreased while the displacement significantly increased. On average, the tests took about 16 min from the beginning of the loading process until termination.
- While holding the load adjustment control wheel, highlight and mark each crack with a line.
- Finally, loosen the load adjustment control wheel before turning off the machine and disconnecting it from the computer.
3. Experimental Section
3.1. Tested Specimens
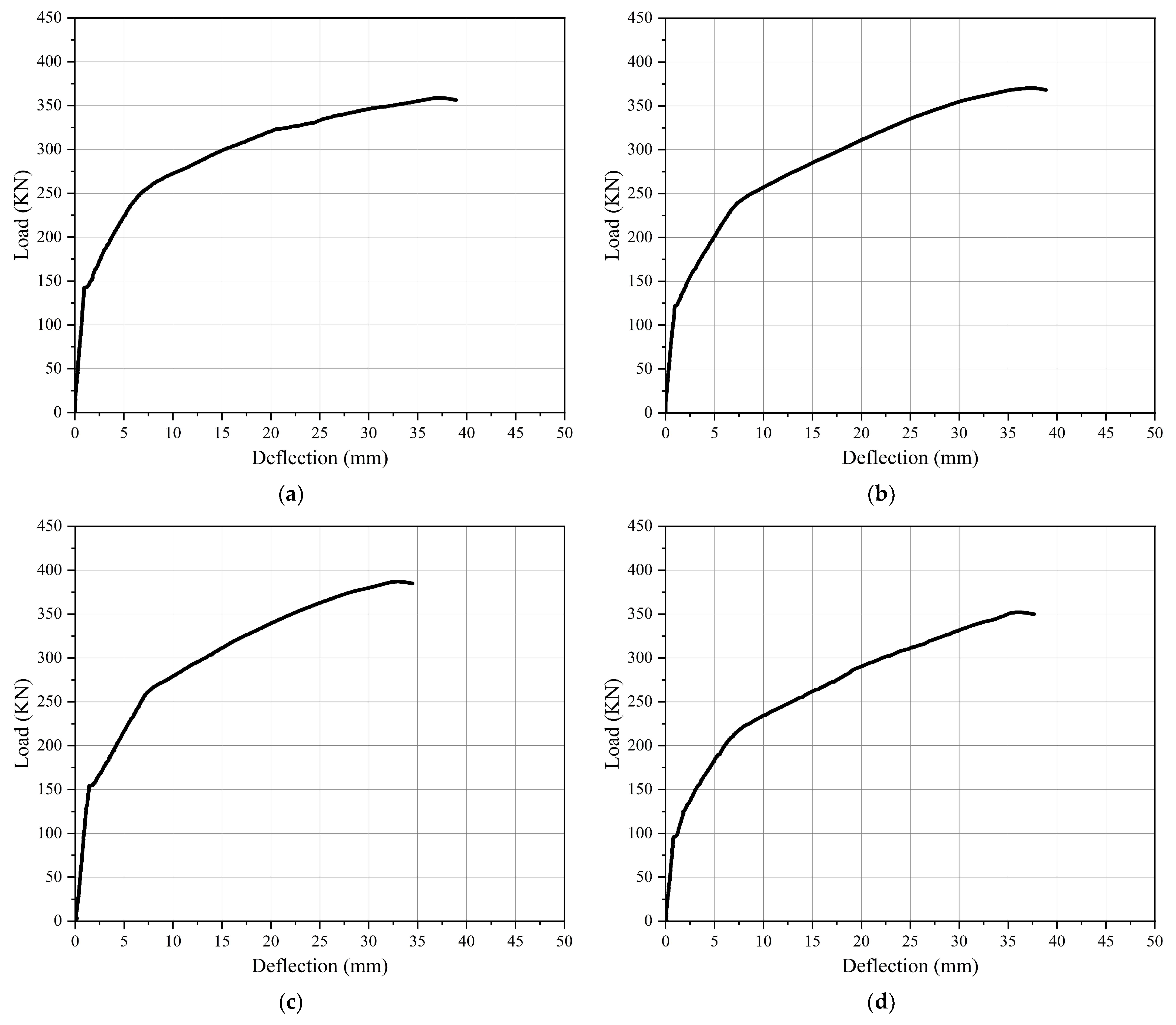
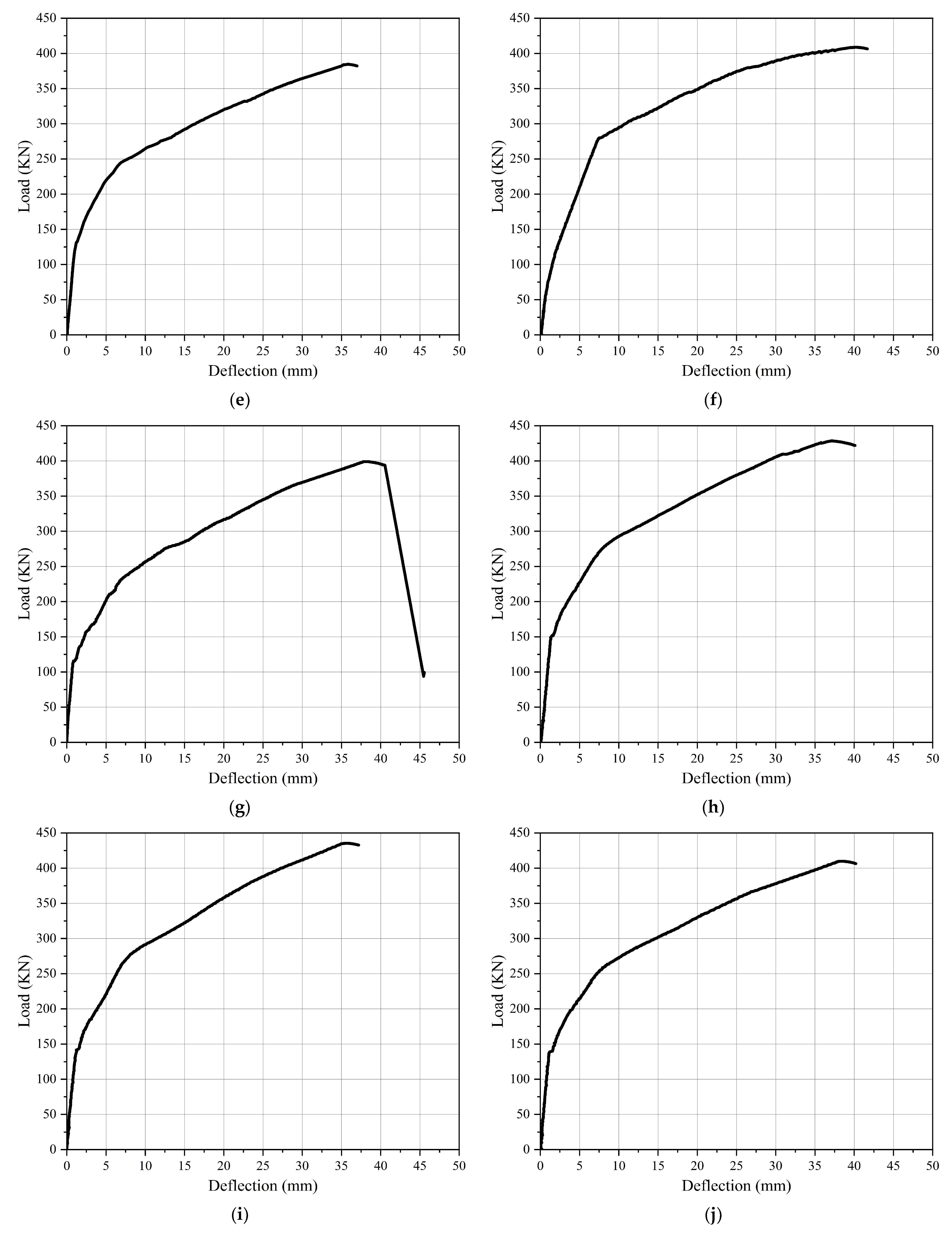
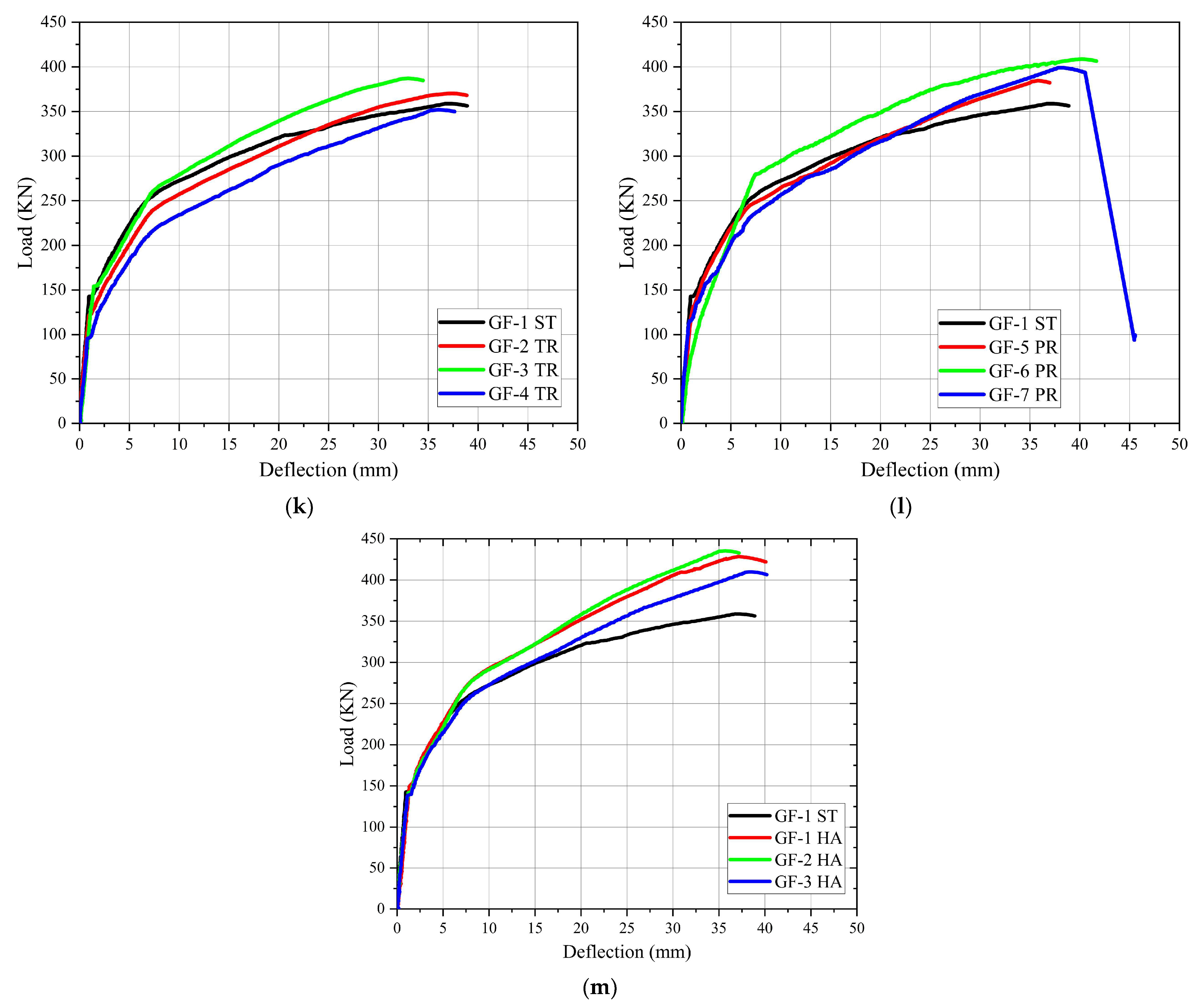
3.2. Load–Deflection Curves
3.3. Crack Patterns and Mode of Failure
4. Conclusions
- The flexural destruction of unbonded prestressed concrete bridge I-girders experienced elastic, elastic–plastic, and ductility (plastic) stages similar to those of bonded prestressed concrete bridge I-girders. However, unbonded prestressed concrete bridge I-girders present superior ductility and deformation-recovery ability after unloading.
- The tendon profile layout has a significant influence on the destruction process in unbonded prestress concrete bridge I-girders.
- The experimental results showed that the flexural behavior of the tested specimens is divided into three stages: the elastic stage, the elastic–plastic stage, and the plastic (ductility) stage. All specimens exhibited flexural failure.
- The ultimate load of the specimens using a trapezoidal tendon profile showed a maximum increase of 28.02 kN with an increasing rate of 7.81% for specimen GF-3 TR if we compare it to the control beam.
- The ultimate load of the specimens using a parabolic tendon profile had a maximum increased load of 49.6 kN with an increasing rate of 13.83% for specimen GF-6 PR if we compare it to the control beam.
- The ultimate load of the specimens using a harped tendon profile had a maximum increased load of 75.3 kN with an increasing rate of 20.99% for specimen GF-2 HA if we compare it to the control beam.
- For the specimens using a trapezoidal tendon profile, specimen GF-3 TR had a minimum vertical deflection of 32.36 mm, which was less than the control beam by 4.44 mm, with a decreasing rate of 12.07% from the control beam.
- For specimens with a parabolic tendon profile, specimen GF-5 PR had a minimum vertical deflection of 35.22 mm, which was lower than the control beam by 1.58 mm, with a decreasing rate of 4.29% from the control beam.
- For the specimens with a harped tendon profile, specimen GF-2 HA had a minimum vertical deflection of 35 mm, which was less than the control beam by 1.80 mm, with a decreasing rate of 4.89% from the control beam.
- Each tendon profile shape (trapezoidal, parabolic, harped) with eccentricity at the end (ee) = 0 had a maximum ultimate load capacity. It can be concluded that specimen GF-2 HA with a harped tendon profile had the maximum ultimate load capacity compared to all other specimens. Also, it can be concluded that specimen GF-3 TR with a trapezoidal tendon profile had minimum deflection compared to all other specimens, which agrees with the results of the finite element analysis by Ansys 14.0 and Sap2000 version 14 software, completed by Dixit and Naser [27,28], and it has the highest (Pcr/Pu) ratio compared to all other specimens. These enhancements in specimen stiffness, ultimate load capacities, and deflections are because of the effect of the tendon profile layout on the flexural capacity of girders.
- The experimental results of the tests on girders with optimized tendon profiles illustrated remarkable improvements in performance. These girders carried higher loads with less deflection than the control beam. The efficiency of prestressing forces throughout the girder length makes the girders with optimized tendon configurations more performant. These improvements allow for a more even distribution of the induced stresses to the concrete member, engaging with more of the cross-section for load carrying. This uniform stress distribution enhances the ductility of the girder and, hence, the service life of the structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nilson, A.H. Design of Prestressed Concrete, 2nd ed.; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Naser, A.F.; Zonglin, W. Strengthening of Jiamusi Pre-Stressed Concrete Highway Bridge by Using External Post-Tensioning Technology in China. J. Eng. Appl. Sci. 2010, 5, 60–69. [Google Scholar]
- Naser, A.F.; Zonglin, W. Finite Element and Experimental Analysis and Evaluation of Static and Dynamic Responses of Oblique Pre-Stressed Concrete Box Girder Bridge. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3642–3657. [Google Scholar] [CrossRef]
- Abdullah, A.B.M.; Rice, J.A.; Hamilton, H.R.; Consolazio, G.R. Damage Identification in Unbonded Tendons for Post-Tensioned Bridges. In Proceedings of the International Conference on Advances in Experimental Structural Engineering, Champaign, IL, USA, 1–2 August 2015; p. 8. [Google Scholar]
- Corven, J.; Natio, C.; Pessiki, S. Designing and Detailing Post-Tensioned Bridges to Accommodate Nondestructive Evaluation; Office of Bridges and Structures: Hong Kong, China, 2018.
- Nusrath, F.R.; Satheesh, V.S.; Manigandan, M.; Suresh, B.S. An Overview on Tendon Layout for Prestressed Concrete Beams. IJISET-Int. J. Innov. Sci. Eng. Technol. 2015, 2, 944. [Google Scholar]
- Lim, S.S.; Wong, J.Y.; Yip, C.C.; Pang, J.W. Flexural Strength Test on New Profiled Composite Slab System. Case Stud. Constr. Mater. 2021, 15, e00638. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, G.; Song, C.; Li, X.; Hou, Y. Flexural Behavior of Unbonded Prestressed Concrete Bridge Girders. Adv. Civ. Eng. 2021, 2021, 6642513. [Google Scholar] [CrossRef]
- Moreira, L.S.; Sousa, J.B.M.; Parente, E. Nonlinear Finite Element Simulation of Unbonded Prestressed Concrete Beams. Eng. Struct. 2018, 170, 167–177. [Google Scholar] [CrossRef]
- Páez, P.M.; Sensale, B. Improved Prediction of Long-Term Prestress Loss in Unbonded Prestressed Concrete Members. Eng. Struct. 2018, 174, 111–125. [Google Scholar] [CrossRef]
- ACI 318-19 Building Code Requirements for Structural Concrete (ACI 318-19) Commentary on Building Code Requirements for Structural Concrete (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019.
- AASHTO. AASHTO LRFD Bridge Design Specifications: SI Unit, 4th ed.; AASHTO: Washington, DC, USA, 2007. [Google Scholar]
- Kim, M.S.; Lee, Y.H. Flexural Behavior of Posttensioned Concrete Beams with Unbonded High-Strength Strands. Adv. Mater. Sci. Eng. 2020, 2020, 5317456. [Google Scholar] [CrossRef]
- Najem, R.M. Optimum Tendon Placement for Post Tensioned S.S. Beam with Variable Eccentricity. Tikrit J. Eng. Sci. 2018, 25, 27–35. [Google Scholar] [CrossRef]
- Park, H.; Jeong, S.; Lee, S.C.; Cho, J.Y. Flexural Behavior of Post-Tensioned Prestressed Concrete Girders with High-Strength Strands. Eng. Struct. 2016, 112, 90–99. [Google Scholar] [CrossRef]
- Dogu, M.; Menkulasi, F. A Flexural Design Methodology for UHPC Beams Posttensioned with Unbonded Tendons. Eng. Struct. 2020, 207, 110193. [Google Scholar] [CrossRef]
- Oukaili, N.; Peera, I. Behavioral Nonlinear Modeling of Prestressed Concrete Flexural Members with Internally Unbonded Steel Strands. Results Eng. 2022, 14, 100411. [Google Scholar] [CrossRef]
- Vichare, A.M.; Barbudhe, P.S.; Rele, R. Effective Positioning of Cable Profiles in Prestressed: I Girders. J. Emerg. Technol. Innov. Res. 2024, 11, 447–460. [Google Scholar]
- Aravinthan, T.; Witchukreangkrai, E.; Mutsuyoshi, H. Flexural Behavior of Two-Span Continuous Prestressed Concrete Girders with Highly Eccentric External Tendons. Aci. Struct. J. 2005, 102, 402–411. [Google Scholar] [CrossRef]
- Ibrahim, R.K.; Lateef, A.M. Flexural Behavior of Corroded One-Way Slabs Strengthened with CFRP in Two Different Techniques. Innov. Infrastruct. Solut. 2024, 9, 353. [Google Scholar] [CrossRef]
- Khdie, M.K.; Qziz, O.Q. ZANCO Journal of Pure and Applied Sciences The Flexural Behavior of UHP Pre-Stressed Concrete Beams. Zanco J. Pure Appl. Sci. 2016, 28, 29–36. [Google Scholar]
- Burhan, M. A Finite Element Model for the Study of The Creep and Shrinkage Effects in the Partially Prestressed Continuous Composite Beams. Tikrit J. Eng. Sci. 2005, 12, 77–100. [Google Scholar] [CrossRef]
- Ng, P.L.; Kwan, A.K.H. Practical Determination of Prestress Tendon Profile by Load-Balancing Method. Hkie Trans. Hong Kong Inst. Eng. 2006, 13, 27–35. [Google Scholar] [CrossRef]
- Khan, A.A.; Pathak, K.K.; Dindorkar, N. Cable Layout Design of One Way Prestressed Slabs Using Fem. J. Eng. Sci. Manag. Educ. 2010, 2, 34–41. [Google Scholar]
- Jagarapu, D.C.K.; Venkat, L. Genetic Algorithm Based Optimum Design of Prestressed Concrete Beam. Int. J. Comput. Civ. Struct. Eng. 2013, 3, 644–654. [Google Scholar]
- Colajanni, P.; Recupero, A.; Spinella, N. Design Procedure for Prestressed Concrete Beams. Comput. Concr. 2014, 13, 235–253. [Google Scholar] [CrossRef]
- Dixit, A.S.; Khurd, V.G. Effect of Prestressing Force, Cable Profile and Eccentricity on Post Tensioned Beam. Int. Res. J. Eng. Technol. 2017, 4, 626–632. [Google Scholar]
- Naser, A.F. Optimum Design of Vertical Steel Tendons Profile Layout of Post-Tensioning Concrete Bridges: Fem Static Analysis. Arpn J. Eng. Appl. Sci. 2018, 13, 9244–9256. [Google Scholar]
- Mohammed, A.H.; Abdul-Razzaq, K.S.; Mohammedali, T.K.; Nassani, K.D.E.; Hussein, A.K. Finite Element Modeling of Post-Tensioned Two-Way Concrete Slabs under Flexural Loading. Civ. Eng. J. 2018, 4, 1–10. [Google Scholar] [CrossRef]
- Yakov, Z.; Amir, O. Layout Optimization of Post-Tensioned Cables in Concrete Slabs. Struct. Multidiscip. Optim. 2021, 63, 1951–1974. [Google Scholar] [CrossRef]
- Xu, G.; Zeng, M.; Su, Q. Layout and Optimization of the External Prestressing Tendons of Hybrid Beam Rigid Frame Bridges. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 719, pp. 1–10. [Google Scholar]
- Rani, U.M. Effect of Tendon Profile on Deflections in Prestressed Concrete Beams Using C Programme. Int. J. Comput. Sci. Eng. 2021, 8, 6–8. [Google Scholar] [CrossRef]
- Mohamed, G.A.; Eisa, A.S.; Purcz, P.; Ručinský, R.; El-Feky, M.H. Effect of External Tendon Profile on Improving Structural Performance of RC Beams. Buildings 2022, 12, 789. [Google Scholar] [CrossRef]
- Nawy, E.G. Prestressed Concrete: A Fundamental Approach, 5th ed.; Person Education: London, UK, 2010; ISBN 0136081509. [Google Scholar]
- Nilson, A.H.; Darwin, D.; Dolan, C.W. Design of Concrete Structures, 14th ed.; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-007-131139-7. [Google Scholar]
- ASTM A416/A416M-24; Standard Specification for Low-Relaxation Seven-Wire Steel Strand for Prestressed Concrete (ASTM A416/A416M-24). ASTM International: West Conshohocken, PA, USA, 2024; Volume 01.04.
- ACI Committee 211. Selecting Proportions for Normal-Density and High-Density Concrete-Guide Inch-Pound Units Selecting Proportions for Normal-Density and High-Density Concrete-Guide (ACI Committee 211); American Concrete Institute: Farmington Hills, MI, USA, 2022. [Google Scholar]
- Hassan, O.S. Concrete Job Mix Formula for (Precast-Prestressed Girder Plant); Kirkuk Limited Company for Concrete Girder: Kirkuk, Iraq, 2023. [Google Scholar]
- ASTM C496/C496M-17; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens (ASTM C496/C496M-17). ASTM International: West Conshohocken, PA, USA, 2017; Volume 04.02.
- ASTM C78/C78M-18; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression (ASTM C78/C78M-18). ASTM International: West Conshohocken, PA, USA, 2018; Volume 04.02.
- ASTM C469/C469M-14; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression (ASTM C469/C469M-14). ASTM International: West Conshohocken, PA, USA, 2014; Volume 04.02.










| Type | Diameter (mm) | Area (mm2) | Yield Stress (MPa) | Ultimate Strength (MPa) | Maximum Elongation (%) | Modulus of Elasticity (MPa) |
|---|---|---|---|---|---|---|
| Strand | 15.26 | 140.54 | - | 2018 | 4.28 | 196,370 |
| Deformed bar | 11.74 | 108.28 | 595 | 673 | 20 | 200,000 |
| Deformed bar | 9.857 | 76.31 | 610 | 696 | 21 | 200,000 |
| Cement (g) | Water (L) | Additive (L) | Fine Aggregate (kg) | Coarse Aggregate (kg) | W/C | Slump (mm) | Maximum Aggregate Size (mm) |
|---|---|---|---|---|---|---|---|
| 425 | 160 | 4 | 880 | 910 | 0.38 | 150–180 | 19 |
| Specimen Name | Tendon Profile Name | Tendon Profile Layout, Units in (mm) |
|---|---|---|
| GF-1 ST Control Beam | Straight Tendon Profile With e = 180 mm | 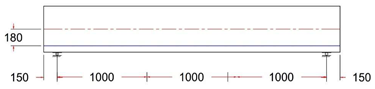 |
| GF-2 TR | Trapezoidal Tendon Profile With ee = +80 mm | 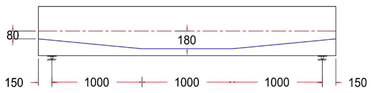 |
| GF-3 TR | Trapezoidal Tendon Profile With ee = 0 mm | 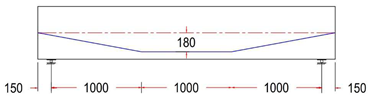 |
| GF-4 TR | Trapezoidal Tendon Profile With ee = −80 mm | 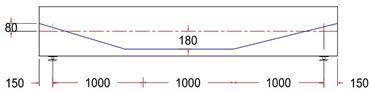 |
| GF-5 PR | Parabolic Tendon Profile With ee = +80 mm | 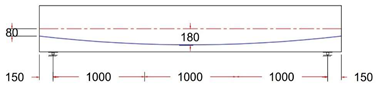 |
| GF-6 PR | Parabolic Tendon Profile With ee = 0 mm |  |
| GF-7 PR | Parabolic Tendon Profile With ee = −80 mm |  |
| GF-1 HA | Harped Tendon Profile With ee = +80 mm | 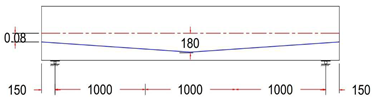 |
| GF-2 HA | Harped Tendon Profile With ee = 0 mm | 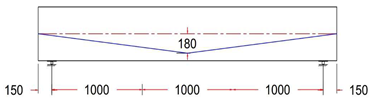 |
| GF-3 HA | Harped Tendon Profile With ee = −80 mm | 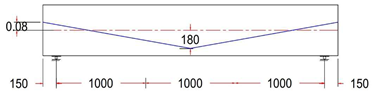 |
| Specimen Name | First Crack Load (kN) | First Crack Deflection (mm) | Ultimate Load (kN) | Ultimate Load Deflection (mm) | Pcr/Pu % | Failure Mode |
|---|---|---|---|---|---|---|
| PCR | ∆CR | Pu | ∆u | |||
| GF-1 ST | 142.60 | 0.95 | 358.70 | 36.80 | 39.75% | Flexural a,b |
| GF-2 TR | 122.02 | 0.96 | 371.63 | 36.76 | 32.83% | Flexural a,b |
| GF-3 TR | 154.12 | 1.42 | 386.72 | 32.36 | 39.85% | Flexural a,b |
| GF-4 TR | 95.80 | 0.79 | 351.27 | 35.24 | 27.27% | Flexural a,b |
| GF-5 PR | 131.72 | 1.16 | 383.75 | 35.22 | 34.32% | Flexural a,b |
| GF-6 PR | 120.07 | 2 | 408.30 | 39.56 | 29.41% | Flexural a,b |
| GF-7 PR | 119.1 | 0.85 | 398.98 | 37.83 | 29.85% | Flexural a,b |
| GF-1 HA | 150.45 | 1.52 | 426 | 35.74 | 35.32% | Flexural a,b |
| GF-2 HA | 151.03 | 1.20 | 434.00 | 35.00 | 34.80% | Flexural a,b |
| GF-3 HA | 139.02 | 1.20 | 409.00 | 37.90 | 33.99% | Flexural a,b |
| Compared Specimen | Increase in Ultimate Load | Decrease in Ultimate Load | Increase In Ultimate Load Deflection | Decrease In Ultimate Load Deflection | ||||
|---|---|---|---|---|---|---|---|---|
| (KN) | % | (KN) | % | (mm) | % | (mm) | % | |
| GF-1 ST and GF-2 TR | 12.93 | 3.60% | - | - | - | - | 0.04 | 0.11% |
| GF-1 ST and GF-3 TR | 28.02 | 7.81% | - | - | - | - | 4.44 | 12.07% |
| GF-1 ST and GF-4 TR | - | 7.43 | 2.07% | - | - | 1.56 | 4.24% | |
| GF-1 ST and GF-5 PR | 25.05 | 6.98% | - | - | - | - | 1.58 | 4.29% |
| GF-1 ST and GF-6 PR | 49.6 | 13.83% | - | - | 2.76 | 7.50% | - | |
| GF-1 ST and GF-7 PR | 40.28 | 11.23% | - | - | 1.03 | 2.80% | - | |
| GF-1 ST and GF-1 HA | 67.3 | 18.76% | - | - | - | - | 1.06 | 2.88% |
| GF-1 ST and GF-2 HA | 75.3 | 20.99% | - | - | - | - | 1.8 | 4.89% |
| GF-1 ST and GF-3 HA | 50.3 | 14.02% | - | - | 1.1 | 3% | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasib, S.I.; Lateef, A.M.; Aziz, O.Q. Effect of Tendon Profile Layout on Flexural Strength of Unbonded Post-Tensioned Prestressed Concrete Bridge I-Girder. Appl. Sci. 2025, 15, 3669. https://doi.org/10.3390/app15073669
Hasib SI, Lateef AM, Aziz OQ. Effect of Tendon Profile Layout on Flexural Strength of Unbonded Post-Tensioned Prestressed Concrete Bridge I-Girder. Applied Sciences. 2025; 15(7):3669. https://doi.org/10.3390/app15073669
Chicago/Turabian StyleHasib, Swar I., Assim M. Lateef, and Omar Q. Aziz. 2025. "Effect of Tendon Profile Layout on Flexural Strength of Unbonded Post-Tensioned Prestressed Concrete Bridge I-Girder" Applied Sciences 15, no. 7: 3669. https://doi.org/10.3390/app15073669
APA StyleHasib, S. I., Lateef, A. M., & Aziz, O. Q. (2025). Effect of Tendon Profile Layout on Flexural Strength of Unbonded Post-Tensioned Prestressed Concrete Bridge I-Girder. Applied Sciences, 15(7), 3669. https://doi.org/10.3390/app15073669






