GC4MRec: Generative-Contrastive for Multimodal Recommendation
Abstract
1. Introduction
- A novel multimodal learning paradigm employing enhanced self-supervised learning is introduced to uncover latent user preferences and enable effective multimodal fusion.
- Latent user preferences are captured more effectively via a dual spatio-temporal cross-residual module, which integrates information from both the original and enhanced graph at various temporal stages.
- A metadata-aware fusion method provides a flexible mechanism for fusing multimodal data.
- Experimental validation is performed on several public datasets.
2. Related Work
2.1. Multimodal Recommendation
2.2. Contrastive Learning
2.3. Generative Models in Recommendation
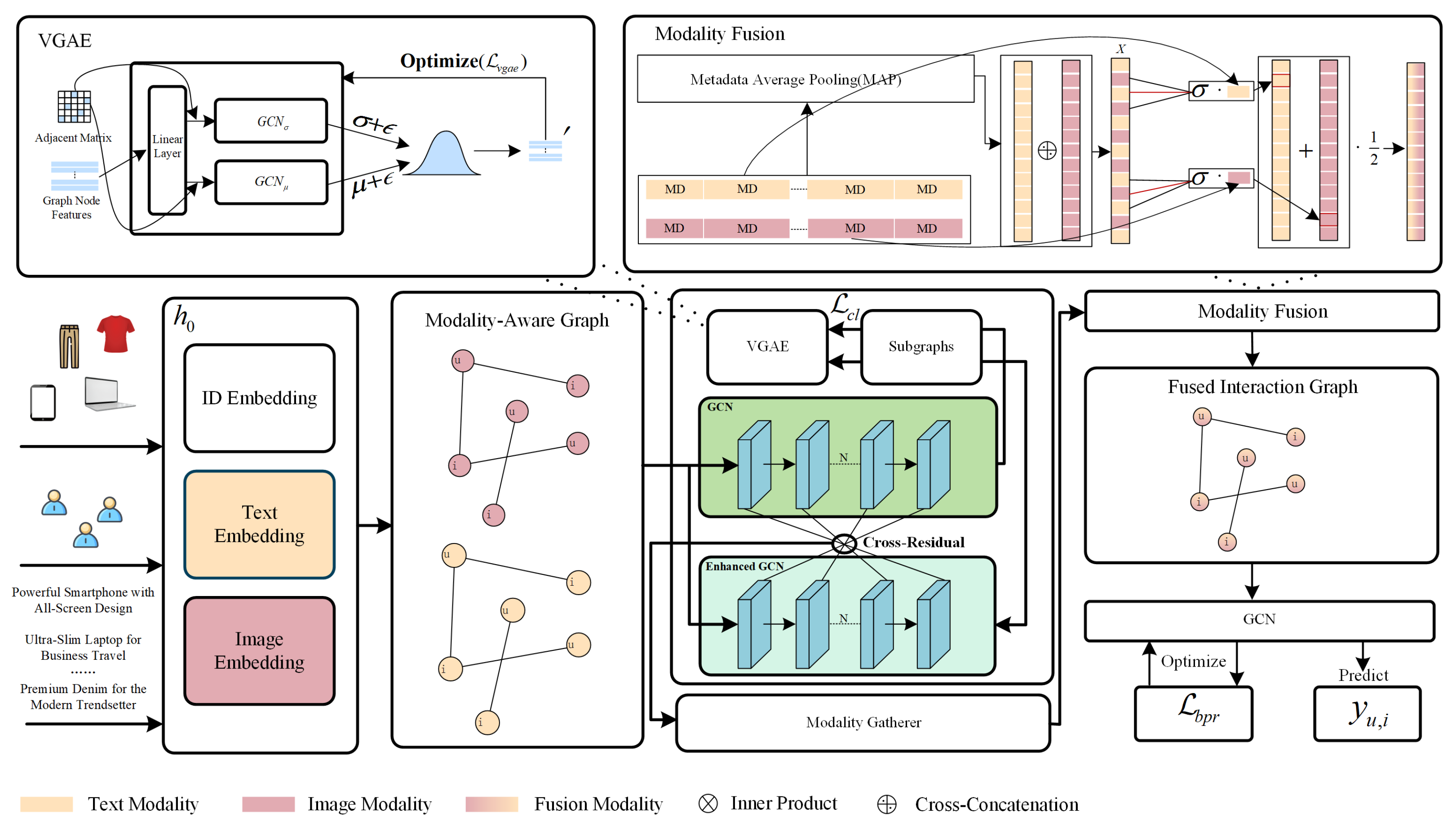
3. Methodology
3.1. Preliminaries
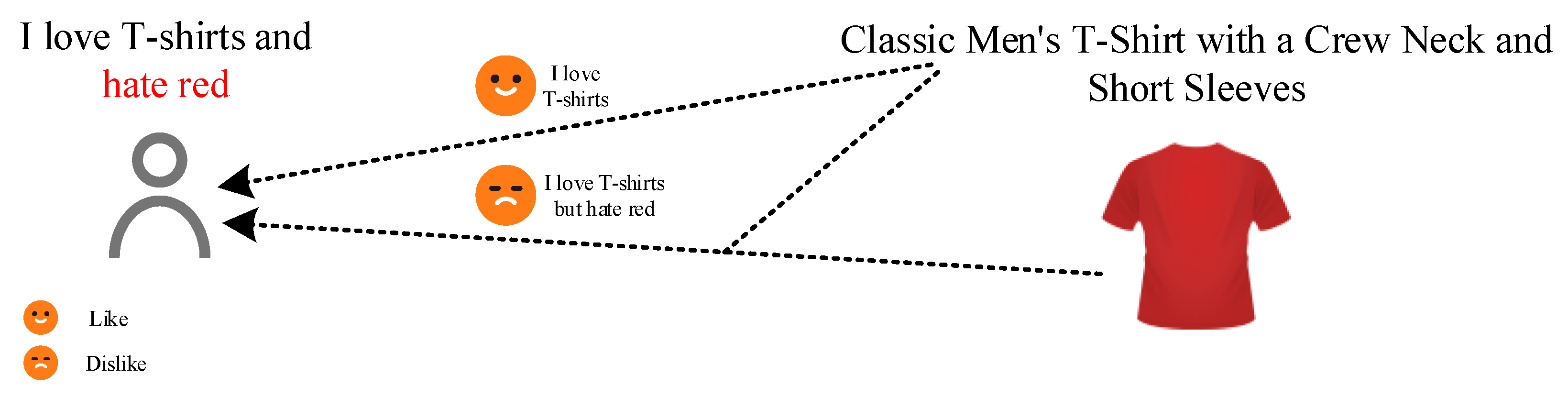
3.2. Graph Information Enhancement
3.2.1. Modality-Aware Subgraph Generation
3.2.2. Graph Reconstruction with Resample
3.2.3. Optimization
3.3. Graph Contrastive Learning
3.4. Dual Spatio-Temporal Cross-Residual Module
3.5. Multimodal Fusion
3.5.1. Metadata and Meta-Preference Modeling
3.5.2. Channel Cross-Fusion Convolution (CCFC)
3.6. Prediction and Optimization
4. Experiment
4.1. Experimental Settings
4.1.1. Datasets
4.1.2. Baselines
4.1.3. Evaluation Protocols
4.1.4. Implementation Details
4.2. Performance Comparison
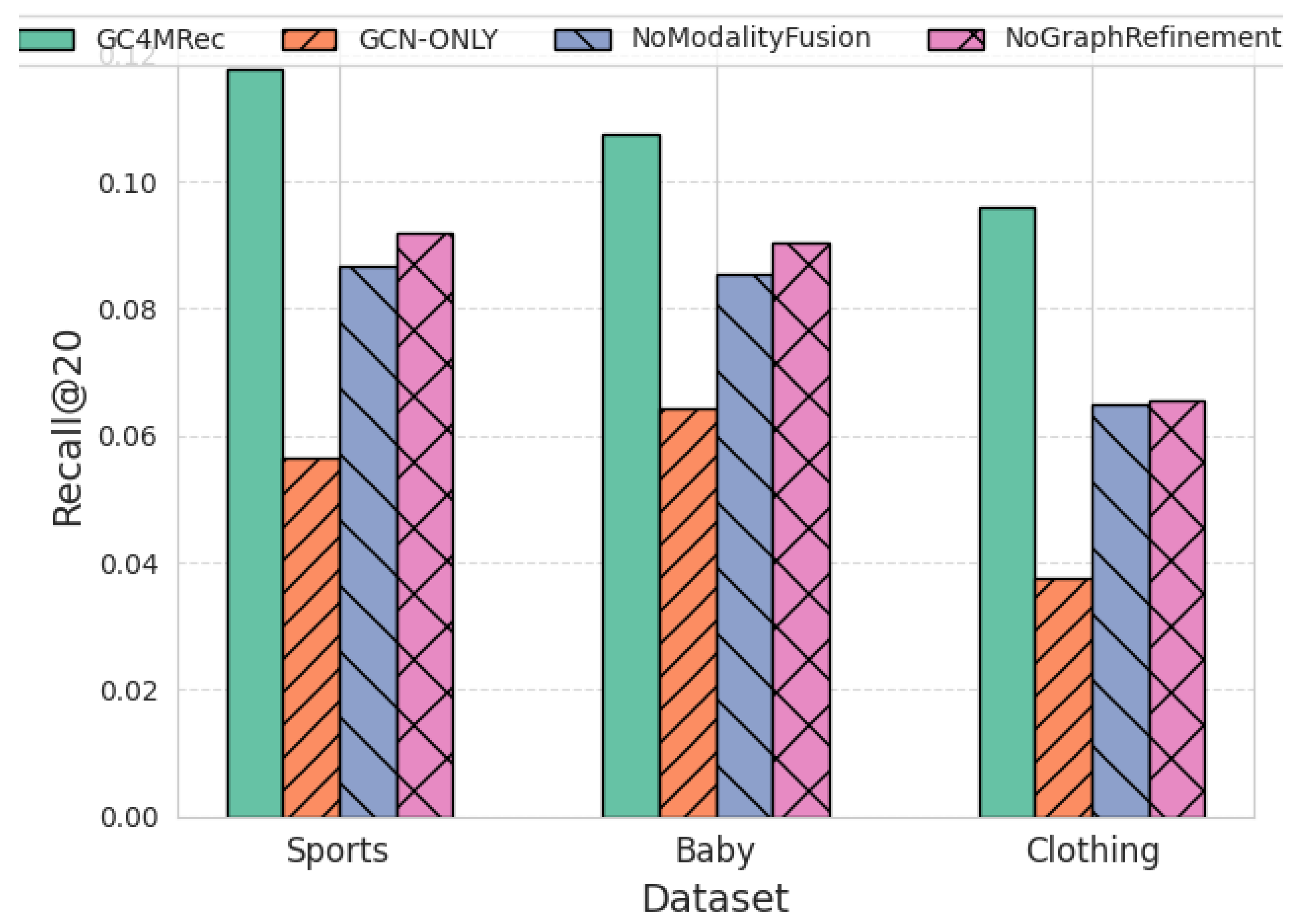
4.3. Ablation Study
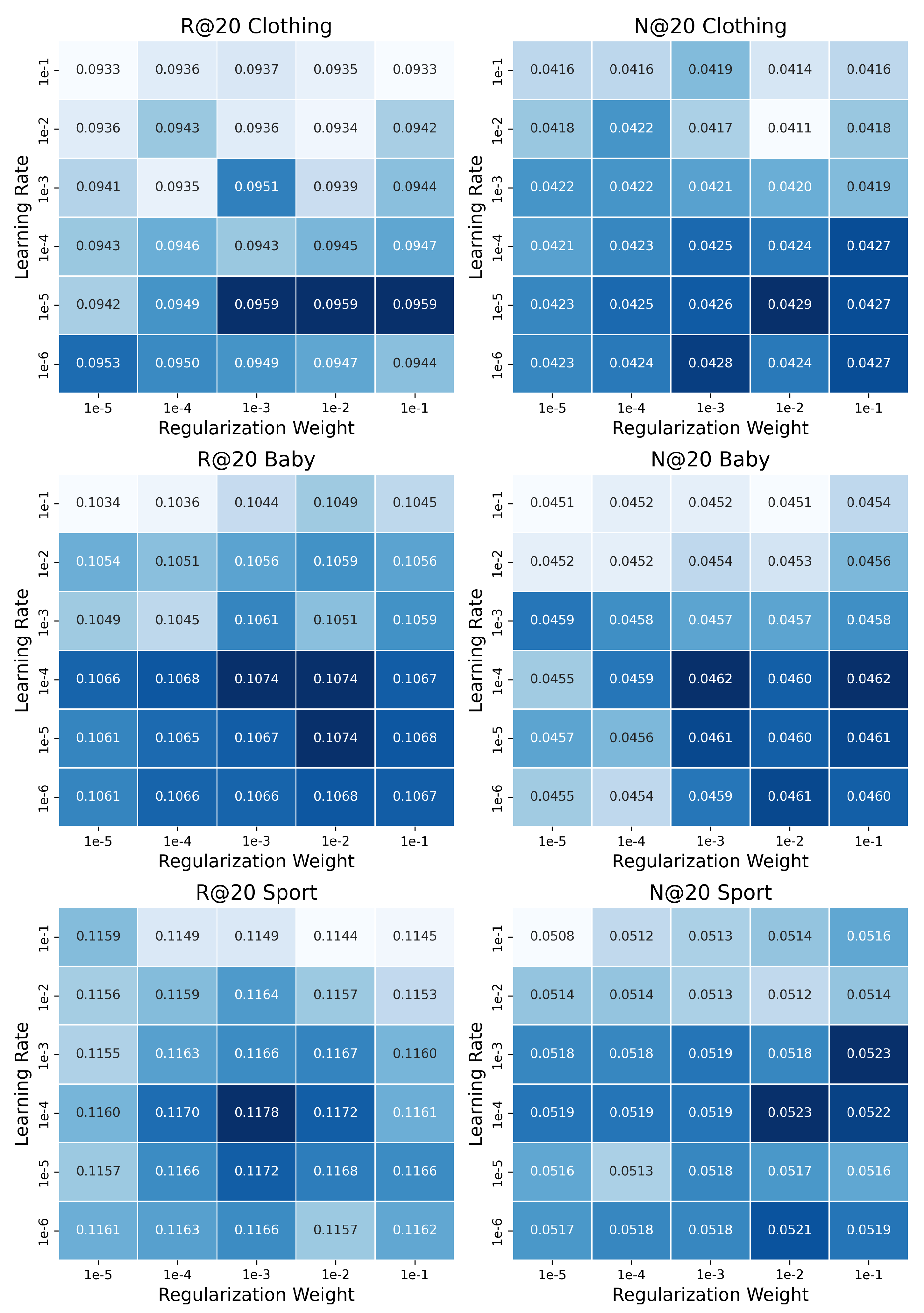
4.4. Hyperparameter Combination Effectiveness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lops, P.; de Gemmis, M.; Semeraro, G. Content-based Recommender Systems: State of the Art and Trends. In Recommender Systems Handbook; Spring: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Mooney, R.J.; Roy, L. Content-based book recommending using learning for text categorization. In Proceedings of the Fifth ACM Conference on Digital Libraries, ACM, San Antonio, TX, USA, 2–7 June 2000; DL00. pp. 195–204. [Google Scholar] [CrossRef]
- Koren, Y.; Rendle, S.; Bell, R. Advances in collaborative filtering. In Recommender Systems Handbook; Spring: Berlin/Heidelberg, Germany, 2021; pp. 91–142. [Google Scholar] [CrossRef]
- Goldberg, D.; Nichols, D.; Oki, B.M.; Terry, D. Using collaborative filtering to weave an information tapestry. Commun. ACM 1992, 35, 61–70. [Google Scholar] [CrossRef]
- Breese, J.S.; Heckerman, D.; Kadie, C. Empirical analysis of predictive algorithms for collaborative filtering. arXiv 2013, arXiv:1301.7363. [Google Scholar]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th international conference on World Wide Web, Hong Kong, China, 1–5 May 2001; pp. 285–295. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 639–648. [Google Scholar] [CrossRef]
- Liu, F.; Cheng, Z.; Zhu, L.; Gao, Z.; Nie, L. Interest-aware message-passing GCN for recommendation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 12–16 April 2021; pp. 1296–1305. [Google Scholar] [CrossRef]
- Peng, S.; Sugiyama, K.; Mine, T. SVD-GCN: A simplified graph convolution paradigm for recommendation. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 1625–1634. [Google Scholar] [CrossRef]
- Wu, L.; Sun, P.; Hong, R.; Fu, Y.; Wang, X.; Wang, M. Socialgcn: An efficient graph convolutional network based model for social recommendation. arXiv 2018, arXiv:1811.02815. [Google Scholar]
- Wei, Y.; Wang, X.; Nie, L.; He, X.; Hong, R.; Chua, T.S. MMGCN: Multi-modal graph convolution network for personalized recommendation of micro-video. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 1437–1445. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Liu, Q.; Wu, S.; Wang, S.; Wang, L. Mining latent structures for multimedia recommendation. In Proceedings of the 29th ACM International Conference on Multimedia, Online, 20–24 October 2021; pp. 3872–3880. [Google Scholar] [CrossRef]
- Zhou, X.; Miao, C. Disentangled graph variational auto-encoder for multimodal recommendation with interpretability. IEEE Trans. Multimed. 2024, 26, 7543–7554. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, X.; Zhang, L.; Shen, Z. Enhancing dyadic relations with homogeneous graphs for multimodal recommendation. In ECAI 2023; IOS Press: Amsterdam, The Netherlands, 2023; pp. 3123–3130. [Google Scholar] [CrossRef]
- Liu, K.; Xue, F.; Guo, D.; Sun, P.; Qian, S.; Hong, R. Multimodal graph contrastive learning for multimedia-based recommendation. IEEE Trans. Multimed. 2023, 25, 9343–9355. [Google Scholar] [CrossRef]
- Zhou, B.; Liang, Y. UPGCN: User Perception-Guided Graph Convolutional Network for Multimodal Recommendation. Appl. Sci. 2024, 14, 10187. [Google Scholar] [CrossRef]
- Cui, X.; Qu, X.; Li, D.; Yang, Y.; Li, Y.; Zhang, X. Mkgcn: Multi-modal knowledge graph convolutional network for music recommender systems. Electronics 2023, 12, 2688. [Google Scholar] [CrossRef]
- Zhou, X.; Shen, Z. A tale of two graphs: Freezing and denoising graph structures for multimodal recommendation. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October– 3 November 2023; pp. 935–943. [Google Scholar] [CrossRef]
- Li, X.; Wang, N.; Zeng, J.; Li, J. Time-frequency sensitive prompt tuning framework for session-based recommendation. Expert Syst. Appl. 2025, 270, 126501. [Google Scholar] [CrossRef]
- Wang, X.; Yue, H.; Guo, L.; Guo, F.; He, C.; Han, X. User identification network with contrastive clustering for shared-account recommendation. Inf. Process. Manag. 2025, 62, 104055. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, S.; Huang, J.; Wang, D. Hierarchical Self-Supervised Learning for Knowledge-Aware Recommendation. Appl. Sci. 2024, 14, 9394. [Google Scholar] [CrossRef]
- Ma, J.; Wan, Y.; Ma, Z. Memory-Based Learning and Fusion Attention for Few-Shot Food Image Generation Method. Appl. Sci. 2024, 14, 8347. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- He, R.; McAuley, J. VBPR: Visual bayesian personalized ranking from implicit feedback. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar] [CrossRef]
- Liu, F.; Cheng, Z.; Sun, C.; Wang, Y.; Nie, L.; Kankanhalli, M. User diverse preference modeling by multimodal attentive metric learning. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 1526–1534. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; He, X.; Nie, L.; Liu, W.; Chua, T.S. Attentive collaborative filtering: Multimedia recommendation with item-and component-level attention. In Proceedings of the 40th International ACM SIGIR conference on Research and Development in Information Retrieval, Shinjuku, Tokyo, Japan, 7–11 August 2017; pp. 335–344. [Google Scholar]
- Tao, Z.; Wei, Y.; Wang, X.; He, X.; Huang, X.; Chua, T.S. Mgat: Multimodal graph attention network for recommendation. Inf. Process. Manag. 2020, 57, 102277. [Google Scholar] [CrossRef]
- Wei, W.; Huang, C.; Xia, L.; Zhang, C. Multi-modal self-supervised learning for recommendation. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April– 4 May 2023; pp. 790–800. [Google Scholar] [CrossRef]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8748–8763. Available online: https://proceedings.mlr.press/v139/radford21a (accessed on 19 January 2025).
- Wu, J.; Wang, X.; Feng, F.; He, X.; Chen, L.; Lian, J.; Xie, X. Self-supervised graph learning for recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 726–735. [Google Scholar] [CrossRef]
- Xie, X.; Sun, F.; Liu, Z.; Wu, S.; Gao, J.; Zhang, J.; Ding, B.; Cui, B. Contrastive learning for sequential recommendation. In Proceedings of the 2022 IEEE 38th International Conference on Data Engineering (ICDE), IEEE, Virtual Event, 9–12 May 2022; pp. 1259–1273. [Google Scholar] [CrossRef]
- Xia, X.; Yin, H.; Yu, J.; Wang, Q.; Cui, L.; Zhang, X. Self-supervised hypergraph convolutional networks for session-based recommendation. In Proceedings of the AAAI conference on artificial intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 4503–4511. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, L.; Hong, R.; Zhang, K.; Wang, M. Enhanced graph learning for collaborative filtering via mutual information maximization. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 71–80. [Google Scholar] [CrossRef]
- Lin, Z.; Tian, C.; Hou, Y.; Zhao, W.X. Improving graph collaborative filtering with neighborhood-enriched contrastive learning. In Proceedings of the ACM Web Conference 2022, Virtual Event, 25–29 April 2022; pp. 2320–2329. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, J.; Wang, Z.; Wang, X.; Yuan, Y.; He, X. Generate What You Prefer: Reshaping Sequential Recommendation via Guided Diffusion. Adv. Neural Inf. Process. Syst. 2024, 36, 24247–24261. [Google Scholar]
- Xie, Z.; Liu, C.; Zhang, Y.; Lu, H.; Wang, D.; Ding, Y. Adversarial and contrastive variational autoencoder for sequential recommendation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 449–459. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, L.; Guo, Q.; Hong, L.; Li, J. Collaborative large language model for recommender systems. In Proceedings of the ACM on Web Conference 2024, Singapore, 13–17 May 2024; pp. 3162–3172. [Google Scholar] [CrossRef]
- Sun, F.; Liu, J.; Wu, J.; Pei, C.; Lin, X.; Ou, W.; Jiang, P. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1441–1450. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, P.; Fang, J.; Qu, J.; Liu, G.; Zhuang, F.; Sheng, V.S.; Zhou, X. Meta-optimized joint generative and contrastive learning for sequential recommendation. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), IEEE, Utrecht, The Netherlands, 13–17 May 2024; pp. 705–718. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11531–11539. [Google Scholar] [CrossRef]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. arXiv 2012, arXiv:1205.2618. [Google Scholar]
- Tao, Z.; Liu, X.; Xia, Y.; Wang, X.; Yang, L.; Huang, X.; Chua, T.S. Self-supervised learning for multimedia recommendation. IEEE Trans. Multimed. 2022, 25, 5107–5116. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://proceedings.neurips.cc/paper/2019/hash/bdbca288fee7f92f2bfa9f7012727740-Abstract.html (accessed on 19 January 2025).
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]


| Dataset 1 | # Users | # Items | # Interactions | Density |
|---|---|---|---|---|
| Clothing | 39,387 | 23,033 | 237,488 | 0.00026 |
| Sports | 35,598 | 18,357 | 256,308 | 0.00039 |
| Baby | 19,445 | 7050 | 139,110 | 0.00101 |
| R@10 Ranking | R@20 Ranking | ||||||
|---|---|---|---|---|---|---|---|
| Model | Sports | Baby | Clothing | Model | Sports | Baby | Clothing |
| GC4MRec (Ours) | 0.0784 | 0.0677 | 0.0645 | GC4MRec (Ours) | 0.1178 | 0.1074 | 0.0959 |
| DGVAE | 0.0753 4.12% | 0.0636 6.45% | 0.0619 4.20% | DGVAE | 0.1127 4.53% | 0.1009 6.44% | 0.0917 4.58% |
| FREEDOM | 0.0717 9.34% | 0.0627 7.97% | 0.0629 2.54% | FREEDOM | 0.1089 8.17% | 0.0992 8.27% | 0.0941 1.91% |
| SLMRec | 0.0671 16.84% | 0.0504 34.33% | 0.0447 44.30% | SLMRec | 0.0998 18.04% | 0.0768 39.84% | 0.0662 44.86% |
| MMSSL | 0.0652 20.25% | 0.0620 9.19% | 0.0492 31.10% | MMSSL | 0.0981 20.08% | 0.0969 10.84% | 0.0783 22.48% |
| LATTICE | 0.0588 33.33% | 0.0528 28.22% | 0.0483 33.54% | LATTICE | 0.0926 27.21% | 0.0842 27.55% | 0.0726 32.09% |
| VBPR | 0.0542 44.65% | 0.0450 50.44% | 0.0277 132.85% | VBPR | 0.0849 38.75% | 0.0668 60.78% | 0.0405 136.79% |
| LightGCN | 0.0527 48.77% | 0.0503 34.59% | 0.0371 73.85% | LightGCN | 0.0832 41.59% | 0.0766 40.21% | 0.0547 75.32% |
| MMGCN | 0.0401 95.51% | 0.0390 73.59% | 0.0220 193.18% | MMGCN | 0.0632 86.39% | 0.0624 72.12% | 0.0347 176.37% |
| MF-BPR | 0.0451 73.84% | 0.0346 95.66% | 0.0177 264.41% | MF-BPR | 0.0662 77.95% | 0.0566 89.75% | 0.0252 280.56% |
| N@10 Ranking | N@20 Ranking | ||||||
| Model | Sports | Baby | Clothing | Model | Sports | Baby | Clothing |
| GC4MRec (Ours) | 0.0421 | 0.0360 | 0.0349 | GC4MRec (Ours) | 0.0523 | 0.0462 | 0.0429 |
| DGVAE | 0.0410 2.68% | 0.0340 5.88% | 0.0336 3.87% | DGVAE | 0.0506 3.36% | 0.0436 5.96% | 0.0412 4.13% |
| FREEDOM | 0.0385 9.35% | 0.0330 9.09% | 0.0341 2.35% | FREEDOM | 0.0481 8.73% | 0.0424 8.96% | 0.0420 2.14% |
| MMSSL | 0.0369 14.09% | 0.0333 8.11% | 0.0271 28.78% | MMSSL | 0.0462 13.20% | 0.0427 8.20% | 0.0345 24.35% |
| SLMRec | 0.0354 18.93% | 0.0299 20.40% | 0.0231 51.08% | SLMRec | 0.0445 17.53% | 0.0367 25.89% | 0.0299 43.48% |
| LATTICE | 0.0311 35.37% | 0.0281 28.11% | 0.0251 39.04% | LATTICE | 0.0399 31.08% | 0.0352 31.25% | 0.0311 37.94% |
| VBPR | 0.0310 35.81% | 0.0236 52.54% | 0.0155 125.16% | VBPR | 0.0401 30.42% | 0.0299 54.52% | 0.0189 126.98% |
| LightGCN | 0.0291 44.67% | 0.0250 44.00% | 0.0192 81.77% | LightGCN | 0.0354 47.74% | 0.0335 37.91% | 0.0248 72.98% |
| MMGCN | 0.0189 122.75% | 0.0207 73.91% | 0.0115 203.48% | MMGCN | 0.0244 114.34% | 0.0284 62.68% | 0.0153 180.39% |
| MF-BPR | 0.0244 72.54% | 0.0205 75.61% | 0.0100 249.00% | MF-BPR | 0.0301 73.75% | 0.0250 84.80% | 0.0119 260.50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, Y.; Wang, H.; Li, J. GC4MRec: Generative-Contrastive for Multimodal Recommendation. Appl. Sci. 2025, 15, 3666. https://doi.org/10.3390/app15073666
Wang L, Li Y, Wang H, Li J. GC4MRec: Generative-Contrastive for Multimodal Recommendation. Applied Sciences. 2025; 15(7):3666. https://doi.org/10.3390/app15073666
Chicago/Turabian StyleWang, Lei, Yingjie Li, Heran Wang, and Jun Li. 2025. "GC4MRec: Generative-Contrastive for Multimodal Recommendation" Applied Sciences 15, no. 7: 3666. https://doi.org/10.3390/app15073666
APA StyleWang, L., Li, Y., Wang, H., & Li, J. (2025). GC4MRec: Generative-Contrastive for Multimodal Recommendation. Applied Sciences, 15(7), 3666. https://doi.org/10.3390/app15073666






