Numerical Simulation of Flexural Deformation Through an Integrated Cosserat Expanded Constitutive Model and the Drucker–Prager Criterion
Abstract
1. Introduction
- The alternating layered medium is composed of a medium bonding different mechanical properties, and the bonding properties of the interface of every layered medium is good. There is no sliding, opening or embedding between them.
- When subjected to deformations of stretching and bending, four side faces of the block element maintain the plane (Plane Section Assumption).
- The material strain is very small (Small Deformation Assumption).
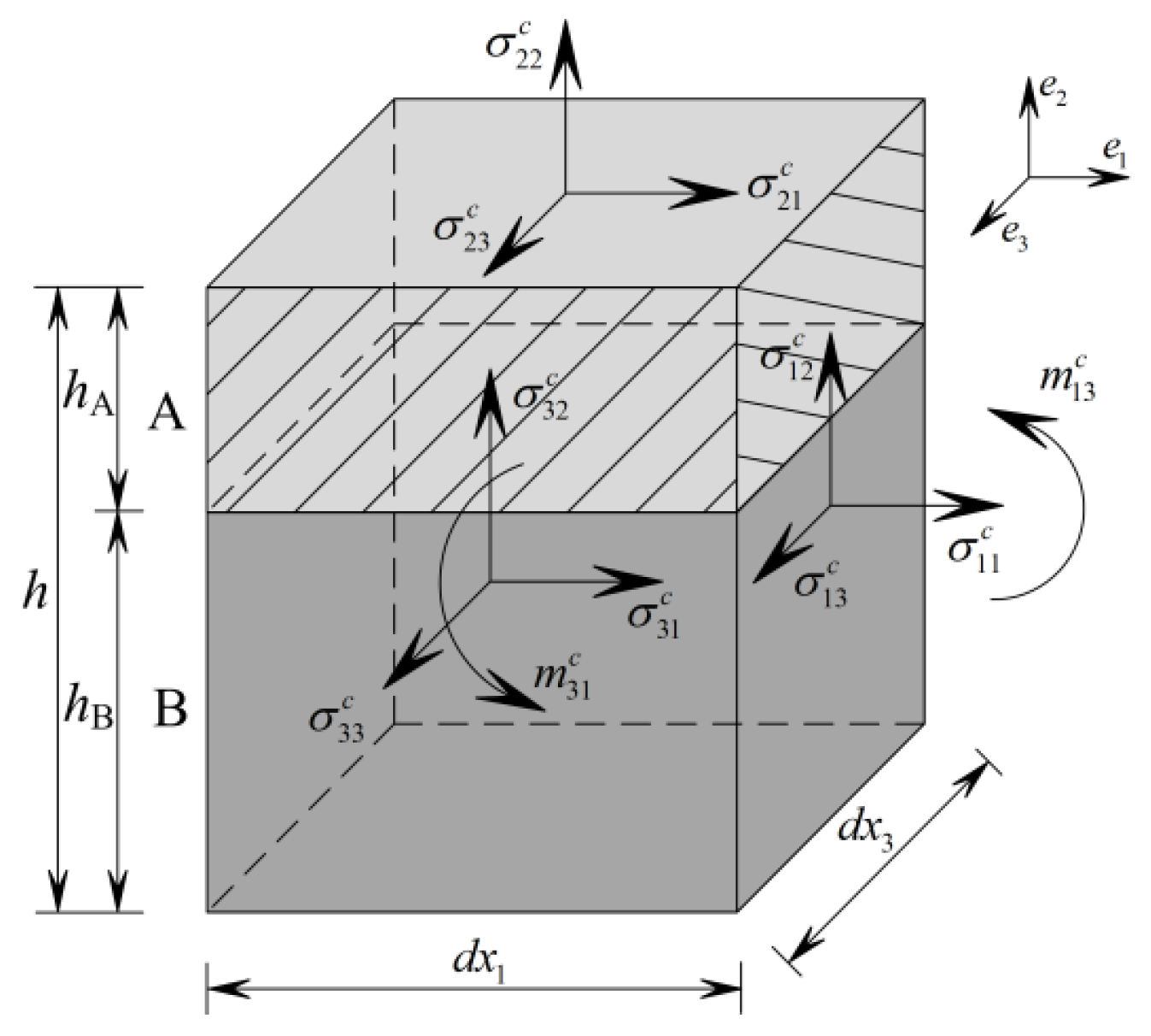
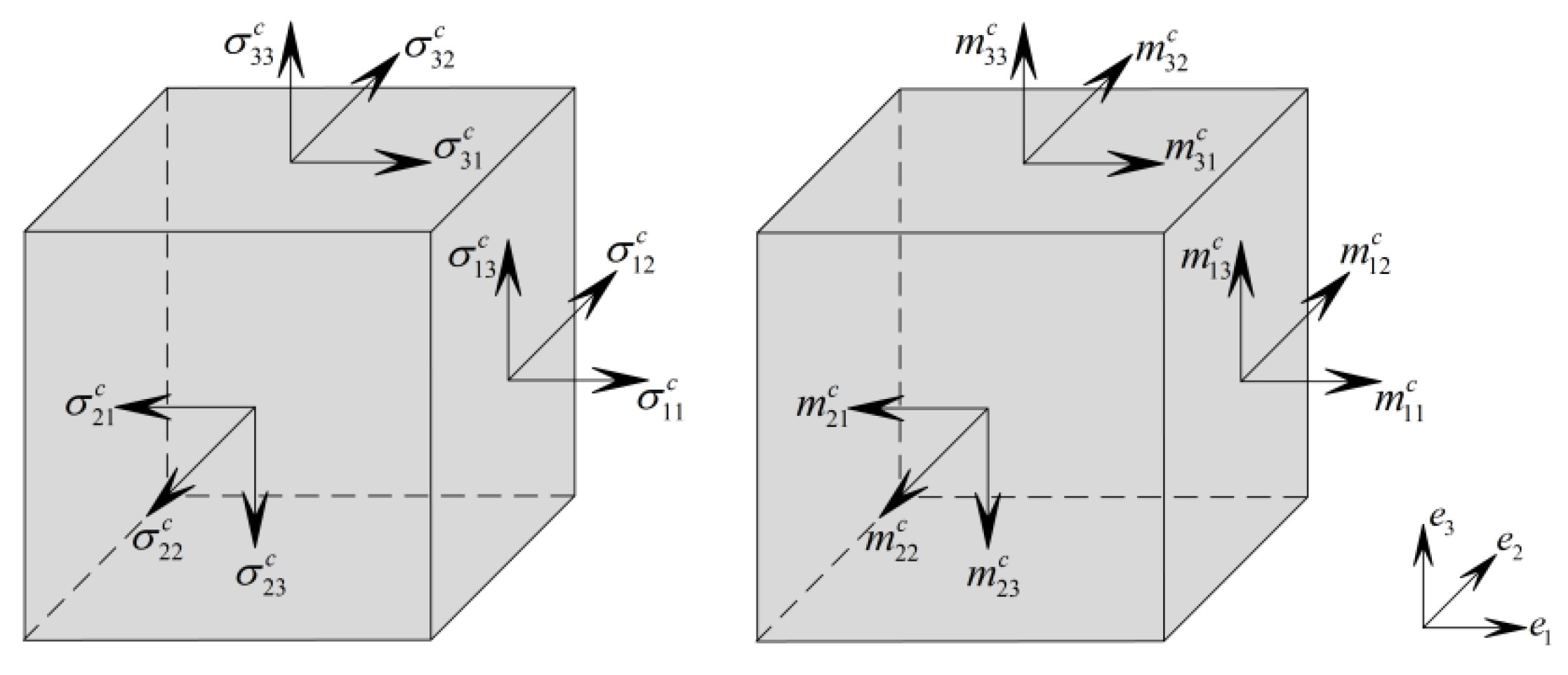
2. Basics of the Cosserat Continuum Theory
3. Finite Element Expressions
4. Three-Dimensional Cosserat Constitutive Equations
5. Modified Yield Criteria in Cosserat Medium Theory
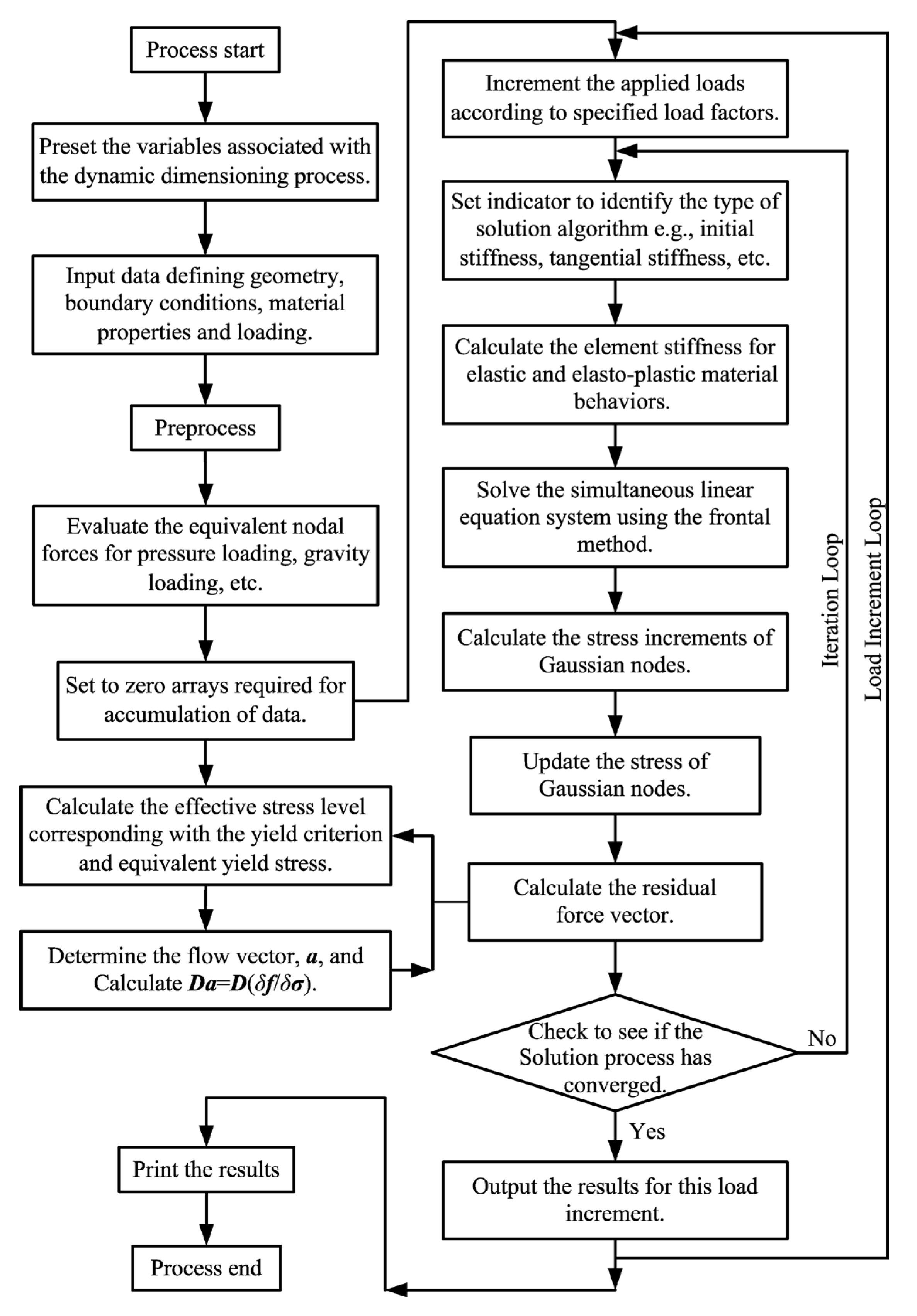
6. The Elasto-Plastic Cos-FEA Using MATLAB
7. Numerical Examples
7.1. Layered Cantilever Plate Subjected to a Transverse Shear Traction Force
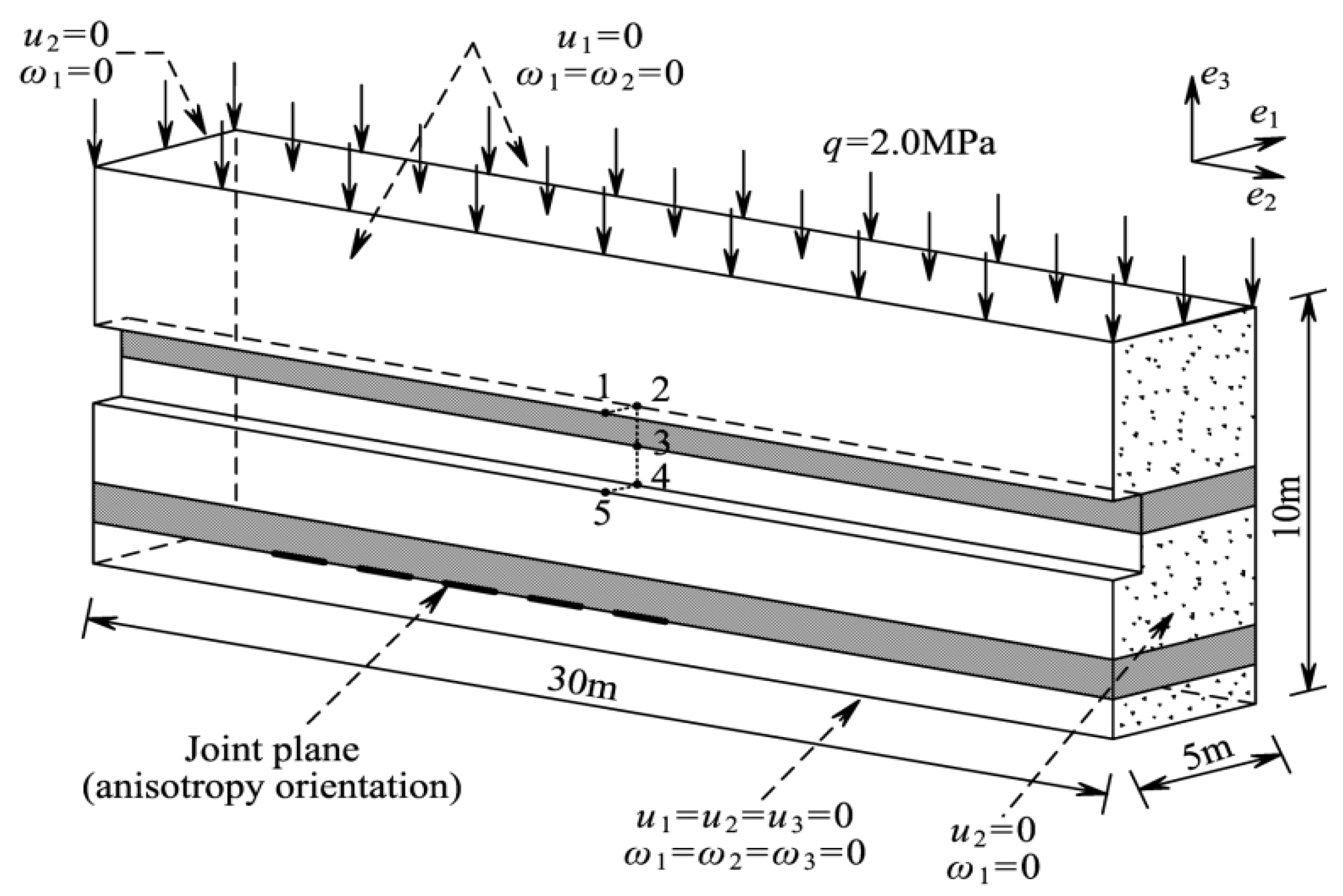
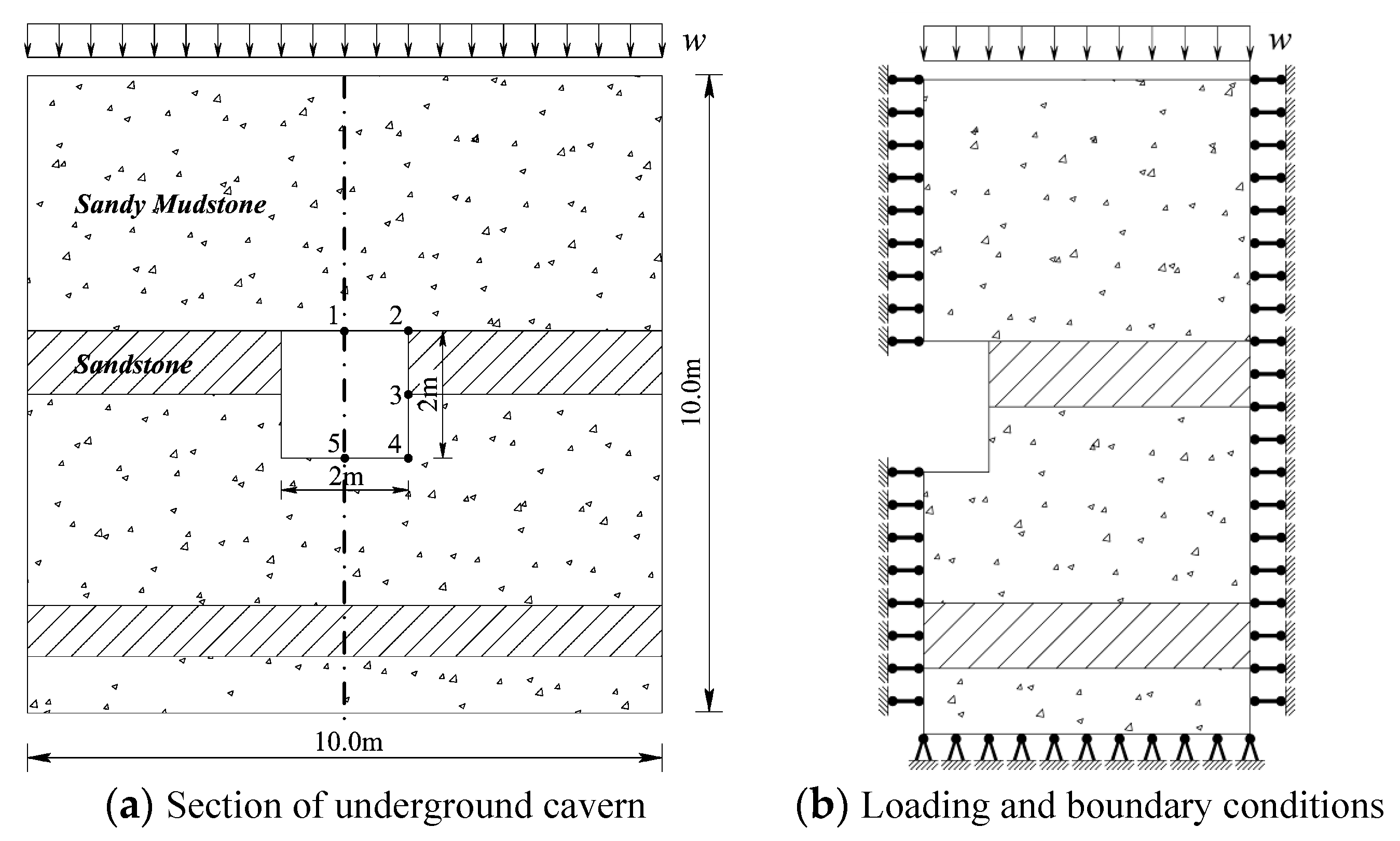
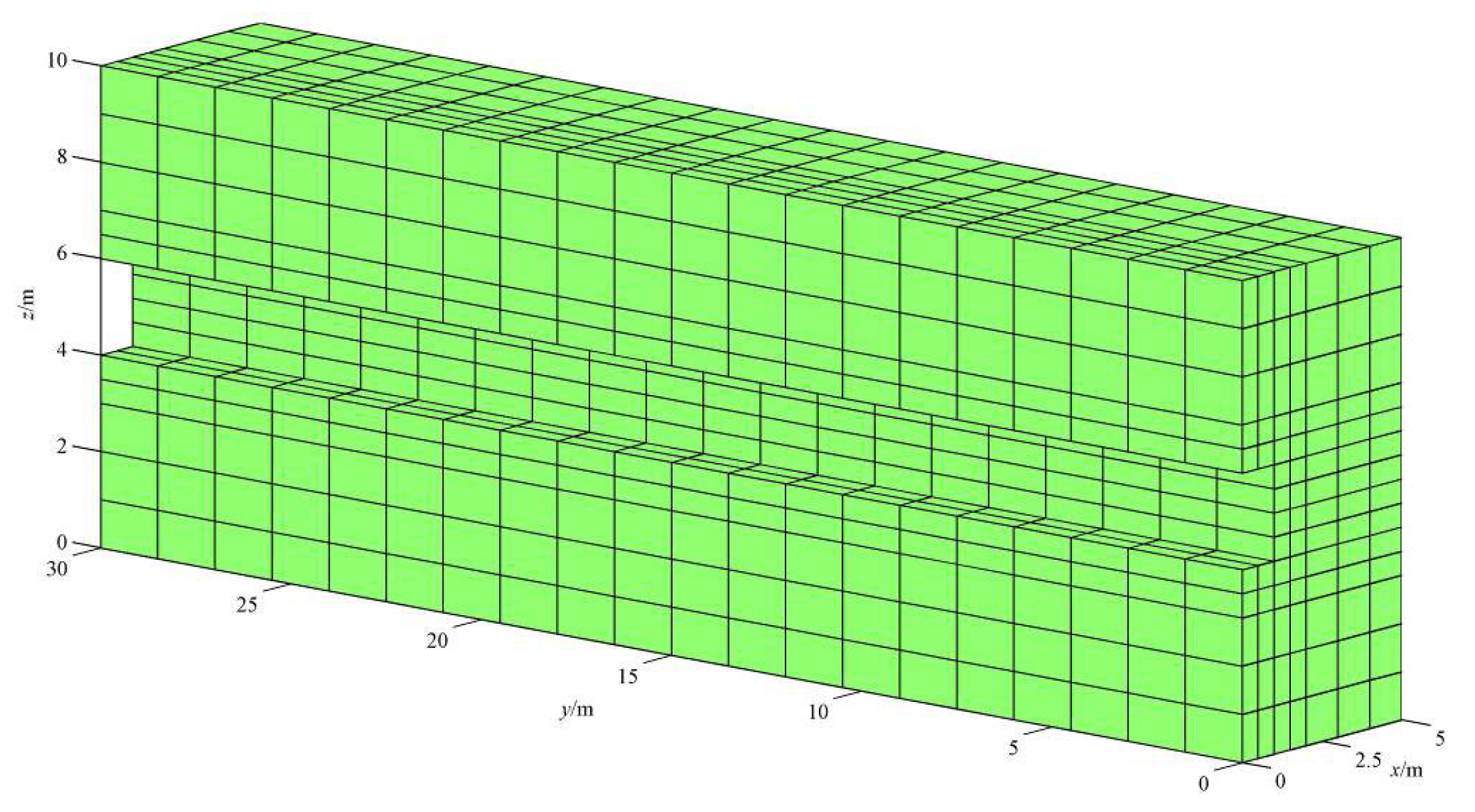
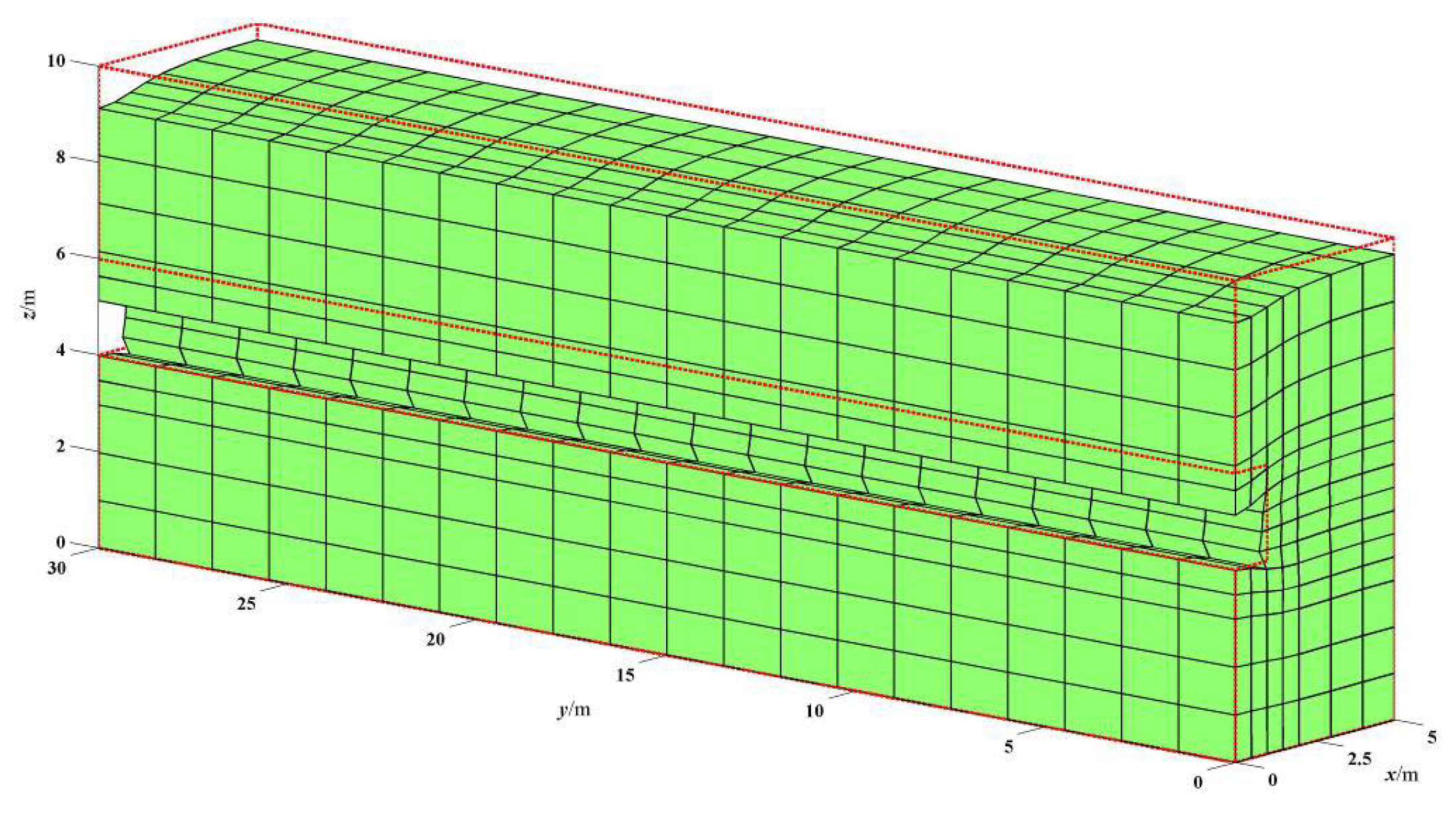
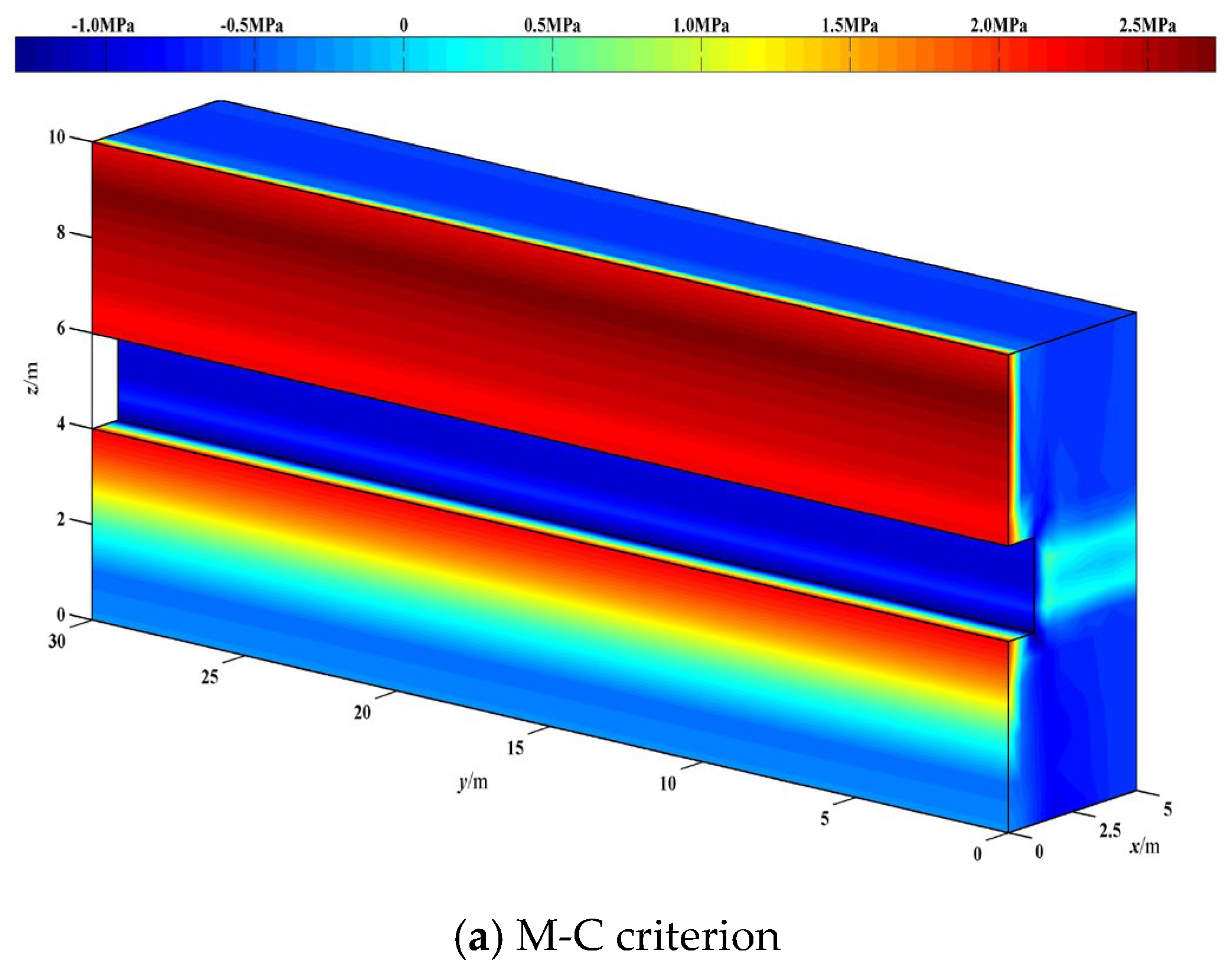
7.2. 3D Analysis of an Excavation in Layered Rock
8. Conclusions
- (1)
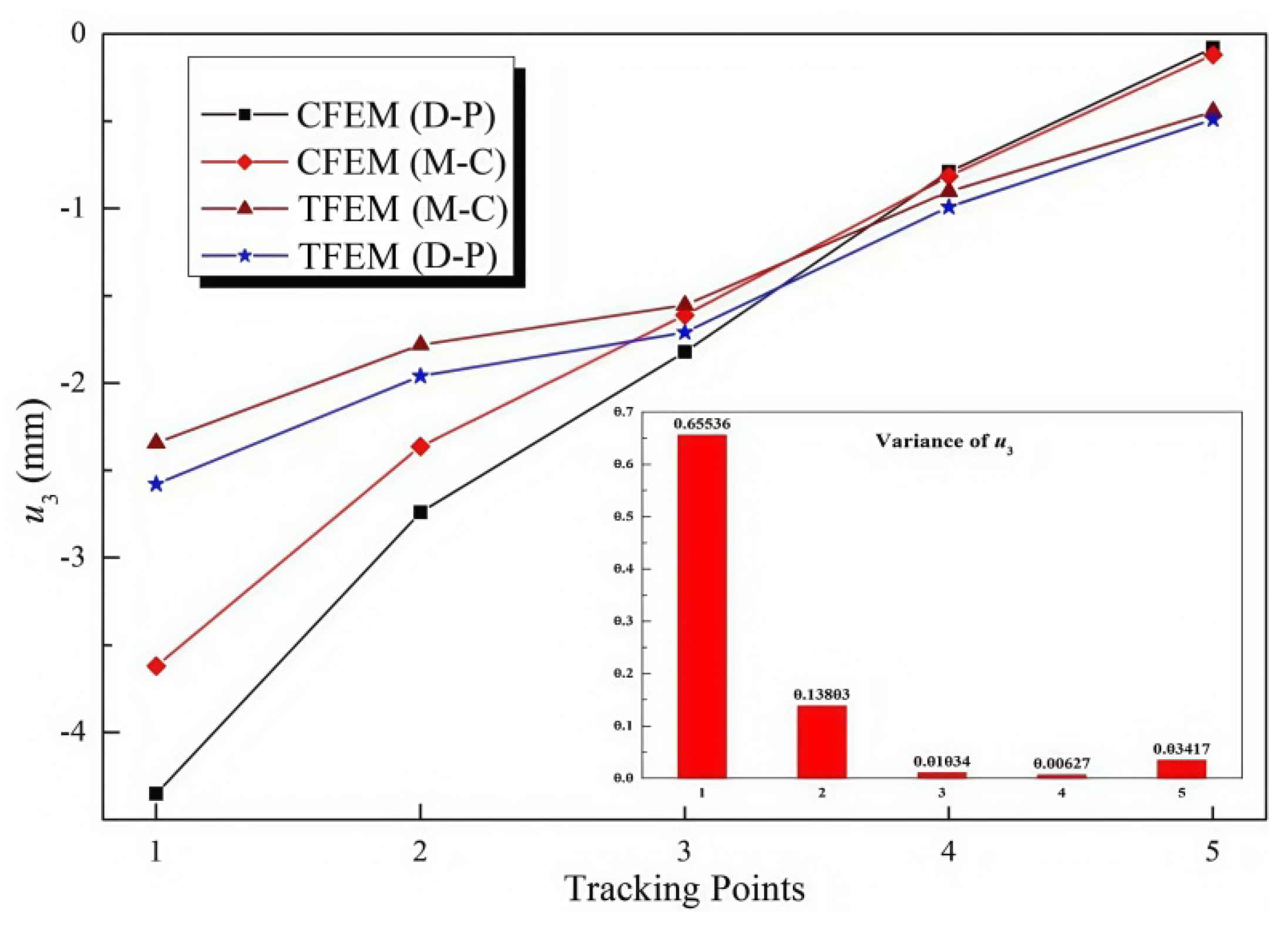
- The numerical simulation examples showed that based on M-C and D-P criteria, the Cos-FEA was effective in analyzing the flexural deformation of an underground cave in an alternating rock mass. The vertical displacement (u3) value of the top cavern calculated using the D-P criterion was found to be higher than that of the modified M-C method. However, horizontal displacements of the former were lower than the latter.
- (2)
- Under the same calculation capacity, the D-P criterion-based Cos-FEA was observed to have a higher convergence speed and a lower number of iterations when compared with that based on the M-C criterion.
- (3)
- Since the M-C hexagonal yield surface is not smooth but has corners, these corners of the hexagon can cause numerical difficulty in its application to the asymmetric Cosserat constitutive relationship. However, the D-P criterion can be viewed as a smooth approximation of the M-C criterion to avoid such difficulty, and the D-P criterion can be made to match the M-C criterion by adjusting the size of the cone. Meanwhile, the M-C criterion does not take into account the influence of the intermediate principal stress on strength, but the D-P criterion is able to reflect the combined effect of the three principal stresses. Thus, the D-P criterion-based Cos-FEA is observed to have a higher convergence speed and stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cosserat, E.; Cosserat, F. Théorie des Corps Déformables; A. Herman et Fils: Paris, France, 1909. [Google Scholar]
- Marin, M.; Seadawy, A.; Vlase, S.; Chirila, A. On mixed problem in thermoelasticity of type III for Cosserat media. J. Taibah Univ. Sci. 2022, 16, 1264–1274. [Google Scholar] [CrossRef]
- Alavi, S.; Ganghoffer, J.; Sadighi, M.; Nasimsobhan, M.; Akbarzadeh, A. Continualization method of lattice materials and analysis of size effects revisited based on Cosserat models. Int. J. Solids Struct. 2022, 254, 111894. [Google Scholar] [CrossRef]
- Surówka, P.; Souslov, A.; Jülicher, F.; Banerjee, D. Odd Cosserat elasticity in active materials. Phys. Rev. E 2023, 108, 064609. [Google Scholar] [PubMed]
- Tummers, M.; Lebastard, V.; Boyer, F.; Troccaz, J.; Rosa, B.; Chikhaoui, M.T. Cosserat rod modeling of continuum robots from newtonian and lagrangian perspectives. IEEE Trans. Robot. 2023, 39, 2360–2378. [Google Scholar]
- Marin, M.; Carrera, E.; Othman, M.I.A.; Abbas, I. A variational approach of the boundary value problem for elastic Cosserat bodies. Mech. Adv. Mater. Struct. 2024, 31, 58–63. [Google Scholar]
- Ghiba, I.-D.; Rizzi, G.; Madeo, A.; Neff, P. Cosserat micropolar elasticity: Classical Eringen vs. dislocation form. J. Mech. Mater. Struct. 2023, 18, 93–123. [Google Scholar]
- Song, X.; Pashazad, H. Computational Cosserat periporomechanics for strain localization and cracking in deformable porous media. Int. J. Solids Struct. 2024, 288, 112593. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Mühlhaus, H.B.; Dyskin, A.V. A numerical study of flexural buckling of foliated rock slopes. Int. J. Numer. Anal. Methods Geomech. 2001, 30, 871–884. [Google Scholar]
- Mühlhaus, H. Continuum models for layered and blocky rock. Compr. Rock Eng. 2014, 2, 209–231. [Google Scholar]
- She, C.; Xiong, W.; Chen, S. Elasto-visco plastic Cosserat theory of layered rock mass and its application in engineering. J. Hydraul. Eng. 1996, 4, 10–17. [Google Scholar]
- Li, Y.P.; Yang, C.H. Three-dimensional expanded Cosserat medium constitutive model for laminated salt rock. Rock Soil Mech. 2006, 27, 509–513. [Google Scholar]
- Marin, M.; Fudulu, I.M.; Vlase, S. On some qualitative results in thermodynamics of Cosserat bodies. Bound. Value Probl. 2022, 2022, 69. [Google Scholar]
- Li, H.; Xun, L.; Zheng, G.; Renda, F. Discrete cosserat static model-based control of soft manipulator. IEEE Robot. Autom. Lett. 2023, 8, 1739–1746. [Google Scholar]
- Nebel, L.J.; Sander, O.; Bîrsan, M.; Neff, P. A geometrically nonlinear Cosserat shell model for orientable and non-orientable surfaces: Discretization with geometric finite elements. Comput. Methods Appl. Mech. Eng. 2023, 416, 116309. [Google Scholar]
- Yu, F.; Huang, G.; Li, W.; Ni, H.; Huang, B.; Li, J.; Duan, J. Modeling lateral vibration of bottom hole assembly using Cosserat theory and laboratory experiment verification. Geoenergy Sci. Eng. 2023, 222, 211359. [Google Scholar]
- Boyer, F.; Lebastard, V.; Candelier, F.; Renda, F.; Alamir, M. Statics and dynamics of continuum robots based on Cosserat rods and optimal control theories. IEEE Trans. Robot. 2022, 39, 1544–1562. [Google Scholar]
- Tuan, L.T.; Dung, N.T.; Van Thom, D.; Van Minh, P.; Zenkour, A.M. Propagation of non-stationary kinematic disturbances from a spherical cavity in the pseudo-elastic cosserat medium. Eur. Phys. J. Plus 2021, 136, 1–16. [Google Scholar]
- Tang, H.; Wei, W.; Liu, F.; Chen, G. Elastoplastic Cosserat continuum model considering strength anisotropy and its application to the analysis of slope stability. Comput. Geotech. 2020, 117, 103235. [Google Scholar]
- Tang, H.; Wei, W.; Song, X.; Liu, F. An anisotropic elastoplastic Cosserat continuum model for shear failure in stratified geomaterials. Eng. Geol. 2021, 293, 106304. [Google Scholar]
- Reda, H.; Alavi, S.; Nasimsobhan, M.; Ganghoffer, J. Homogenization towards chiral Cosserat continua and applications to enhanced Timoshenko beam theories. Mech. Mater. 2021, 155, 103728. [Google Scholar]
- Armanini, C.; Hussain, I.; Iqbal, M.Z.; Gan, D.; Prattichizzo, D.; Renda, F. Discrete cosserat approach for closed-chain soft robots: Application to the fin-ray finger. IEEE Trans. Robot. 2021, 37, 2083–2098. [Google Scholar] [CrossRef]
- Ghiba, I.D.; Bîrsan, M.; Lewintan, P.; Neff, P. The isotropic Cosserat shell model including terms up to O (h 5). Part I: Derivation in matrix notation. J. Elast. 2020, 142, 201–262. [Google Scholar] [CrossRef]
- Colatosti, M.; Fantuzzi, N.; Trovalusci, P.; Masiani, R. New insights on homogenization for hexagonal-shaped composites as Cosserat continua. Meccanica 2022, 57, 885–904. [Google Scholar] [CrossRef]
- Shirani, M.; Steigmann, D.J. A Cosserat model of elastic solids reinforced by a family of curved and twisted fibers. Symmetry 2020, 12, 1133. [Google Scholar] [CrossRef]
- Giorgio, I.; De Angelo, M.; Turco, E.; Misra, A. A Biot–Cosserat two-dimensional elastic nonlinear model for a micromorphic medium. Contin. Mech. Thermodyn. 2020, 32, 1357–1369. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Tang, H.; Liu, J.; Zhuo, Y. Scaled boundary polygon formula for Cosserat continuum and its verification. Eng. Anal. Bound. Elem. 2021, 126, 136–150. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Trovalusci, P.; Luciano, R. Material symmetries in homogenized hexagonal-shaped composites as Cosserat continua. Symmetry 2020, 12, 441. [Google Scholar] [CrossRef]
- Russo, R.; Forest, S.; Girot Mata, F.A. Thermomechanics of Cosserat medium: Modeling adiabatic shear bands in metals. Contin. Mech. Thermodyn. 2020, 35, 919–938. [Google Scholar] [CrossRef]
- Orekhov, A.L.; Simaan, N. Solving cosserat rod models via collocation and the magnus expansion. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 8653–8660. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]




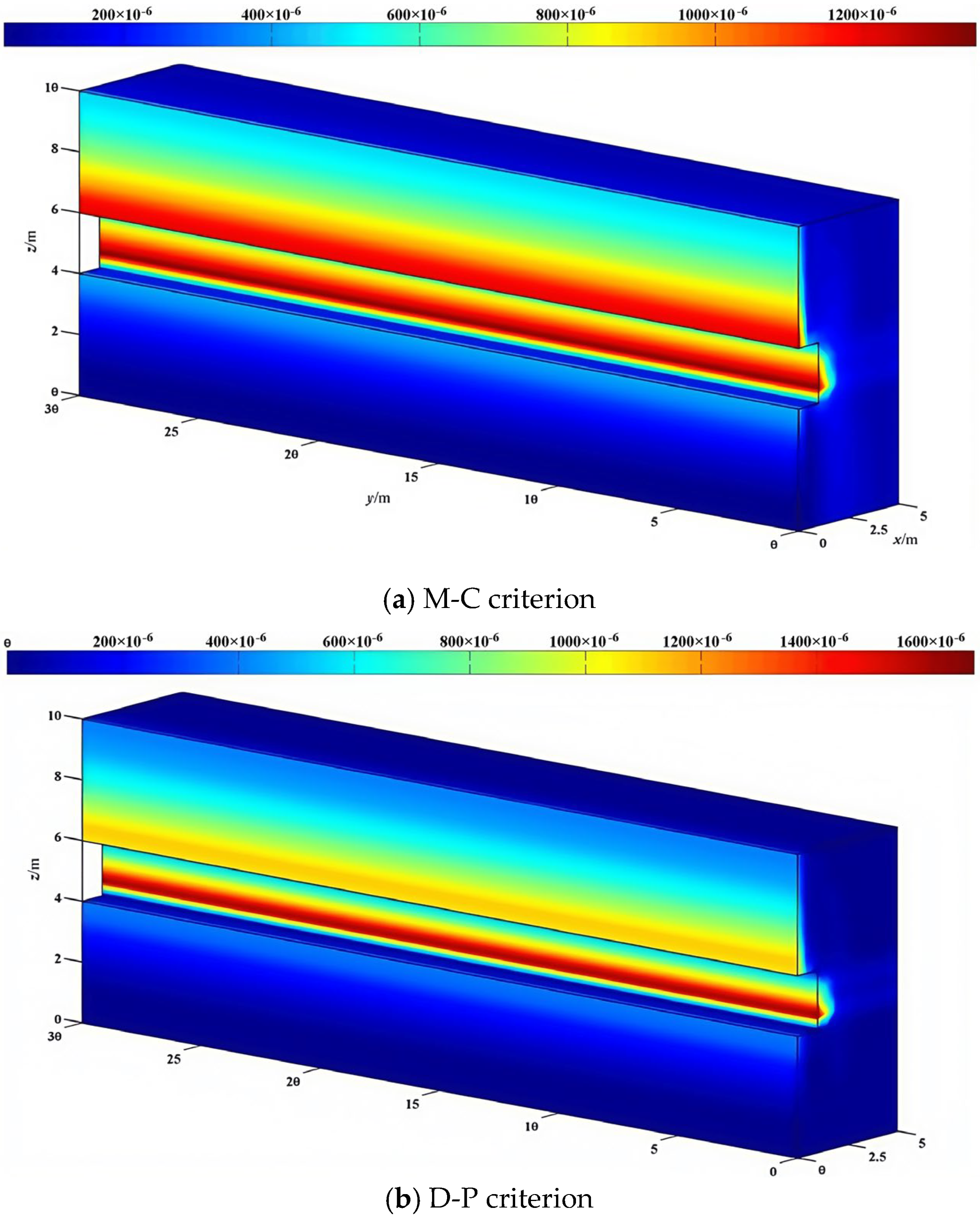
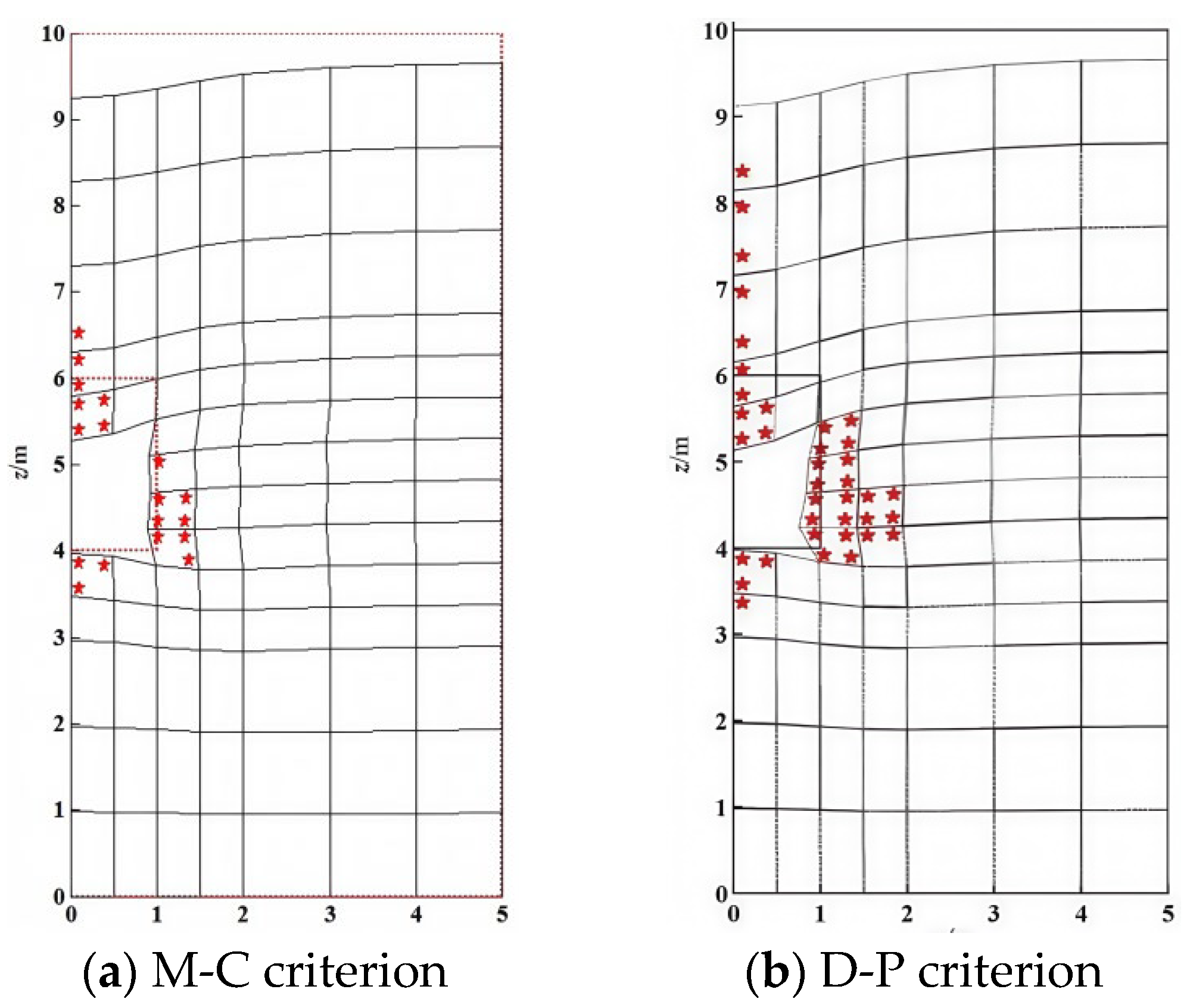

| Yield Criterion | Mohr–Coulomb | Drucker–Prager |
|---|---|---|
| c1 | α | |
| c2 | 1 | |
| c3 | 0 |
| Timoshenko Solution (mm) | Cosserat FEM of Solution (mm) | Traditional FEM of Solution (mm) |
|---|---|---|
| 2.854 | 2.794 | 2.524 |
| Name | Sandstone | Sandy Mudstone | |
|---|---|---|---|
| Parameters | |||
| Volume concentration (n)/% | 25.0 | 75.0 | |
| Volume density (k)/kN·m−3 | 24.9 | 25.8 | |
| Elastic modulus (E)/GPa | 21.78 | 5.15 | |
| Internal friction angle (γ)/° | 26.0 | 34.0 | |
| Cohesive strength (σc)/MPa | 1.40 | 0.75 | |
| Poisson’s ratio (μ) | 0.23 | 0.31 | |
| Tracking Points (Coordinate) | D-P | M-C | ||||
|---|---|---|---|---|---|---|
| u1/mm | u3/mm | ω2/mrad | u1/mm | u3/mm | ω2/mrad | |
| 1 (0, 15, 6) | 0.000 | −4.350 | 0.000 | 0.000 | −3.619 | 0.000 |
| 2 (1, 15, 6) | −0.174 | −2.740 | −1.806 | −0.090 | −2.361 | −1.485 |
| 3 (1, 15, 5) | −0.822 | −1.820 | −0.462 | −0.360 | −1.609 | −0.370 |
| 4 (1, 15, 4) | −0.105 | −0.790 | 0.829 | −0.101 | −0.814 | 0.810 |
| 5 (0, 15, 4) | 0.000 | −0.080 | 0.000 | 0.000 | −0.120 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, N.; Zhang, J.; Jia, Z.; Jiang, X.; Gong, X. Numerical Simulation of Flexural Deformation Through an Integrated Cosserat Expanded Constitutive Model and the Drucker–Prager Criterion. Appl. Sci. 2025, 15, 3604. https://doi.org/10.3390/app15073604
Bai N, Zhang J, Jia Z, Jiang X, Gong X. Numerical Simulation of Flexural Deformation Through an Integrated Cosserat Expanded Constitutive Model and the Drucker–Prager Criterion. Applied Sciences. 2025; 15(7):3604. https://doi.org/10.3390/app15073604
Chicago/Turabian StyleBai, Naining, Jiancheng Zhang, Zikang Jia, Xueguo Jiang, and Xinping Gong. 2025. "Numerical Simulation of Flexural Deformation Through an Integrated Cosserat Expanded Constitutive Model and the Drucker–Prager Criterion" Applied Sciences 15, no. 7: 3604. https://doi.org/10.3390/app15073604
APA StyleBai, N., Zhang, J., Jia, Z., Jiang, X., & Gong, X. (2025). Numerical Simulation of Flexural Deformation Through an Integrated Cosserat Expanded Constitutive Model and the Drucker–Prager Criterion. Applied Sciences, 15(7), 3604. https://doi.org/10.3390/app15073604





