PerMSCA-YOLO: A Perceptual Multi-Scale Convolutional Attention Enhanced YOLOv8 Model for Rail Defect Detection
Abstract
1. Introduction
- A lightweight FasterNet backbone network is introduced, reducing the model’s parameter count and computational load through operations like grouped and depthwise convolutions, while achieving real-time detection without compromising feature representational power.
- A multi-scale convolutional attention module (MSCAM) is integrated into the feature extraction phase, combining large receptive fields with channel and spatial attention mechanisms to enhance the recognition ability for defects of varying sizes, particularly small targets and narrow cracks.
- To address common challenges such as complex textures and noise on track surfaces, perceptual loss is incorporated into the YOLOv8 loss function, aligning detection targets in the deep feature space to further improve the model’s robustness in capturing and distinguishing fine defects.
2. Related Work
2.1. Traditional Methods
2.2. Computer Vision Methods
2.3. Deep Learning Methods
3. Methodology
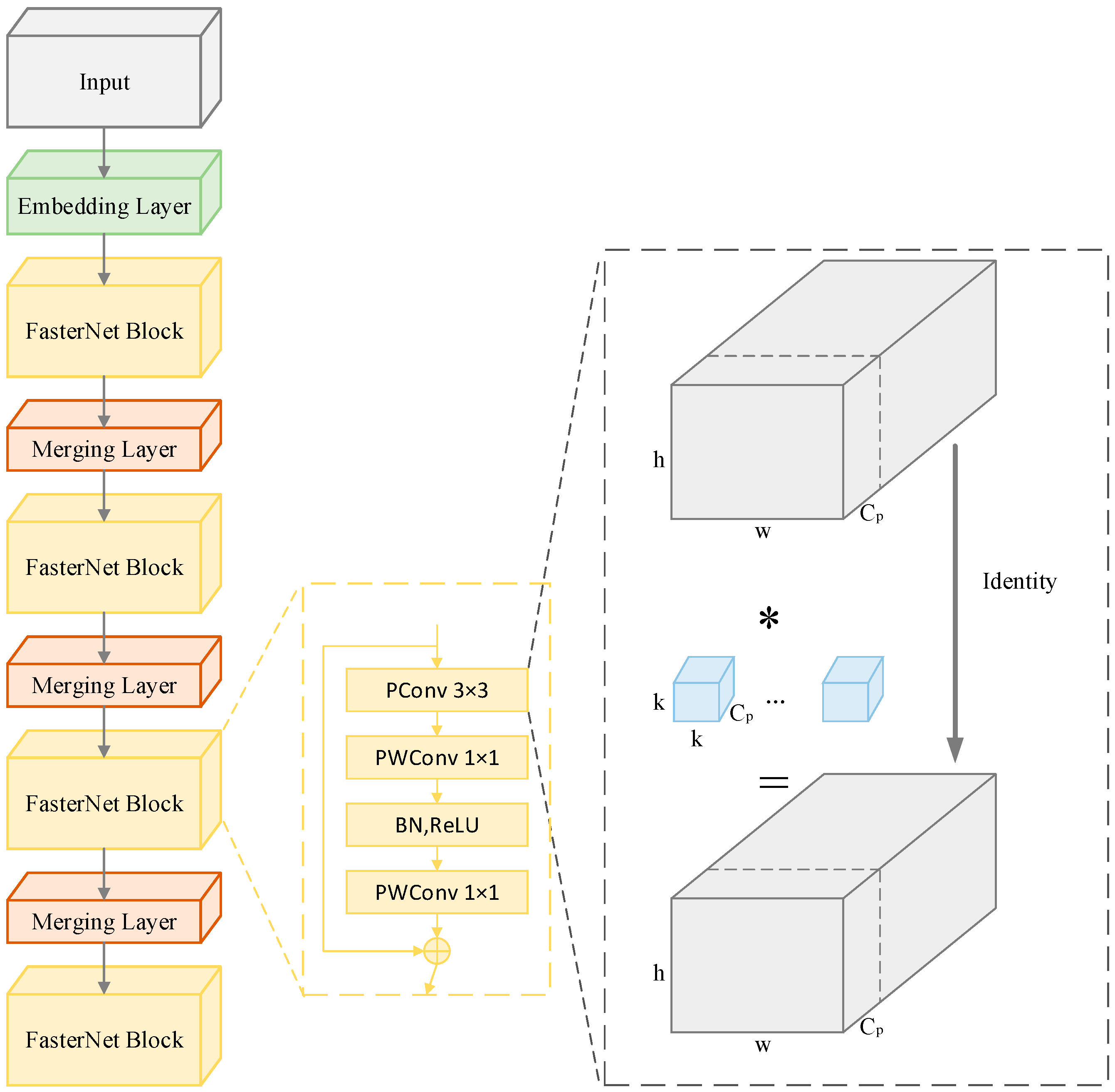
3.1. Overall Architecture of PerMSCA-YOLO
3.2. FasterNet Backbone
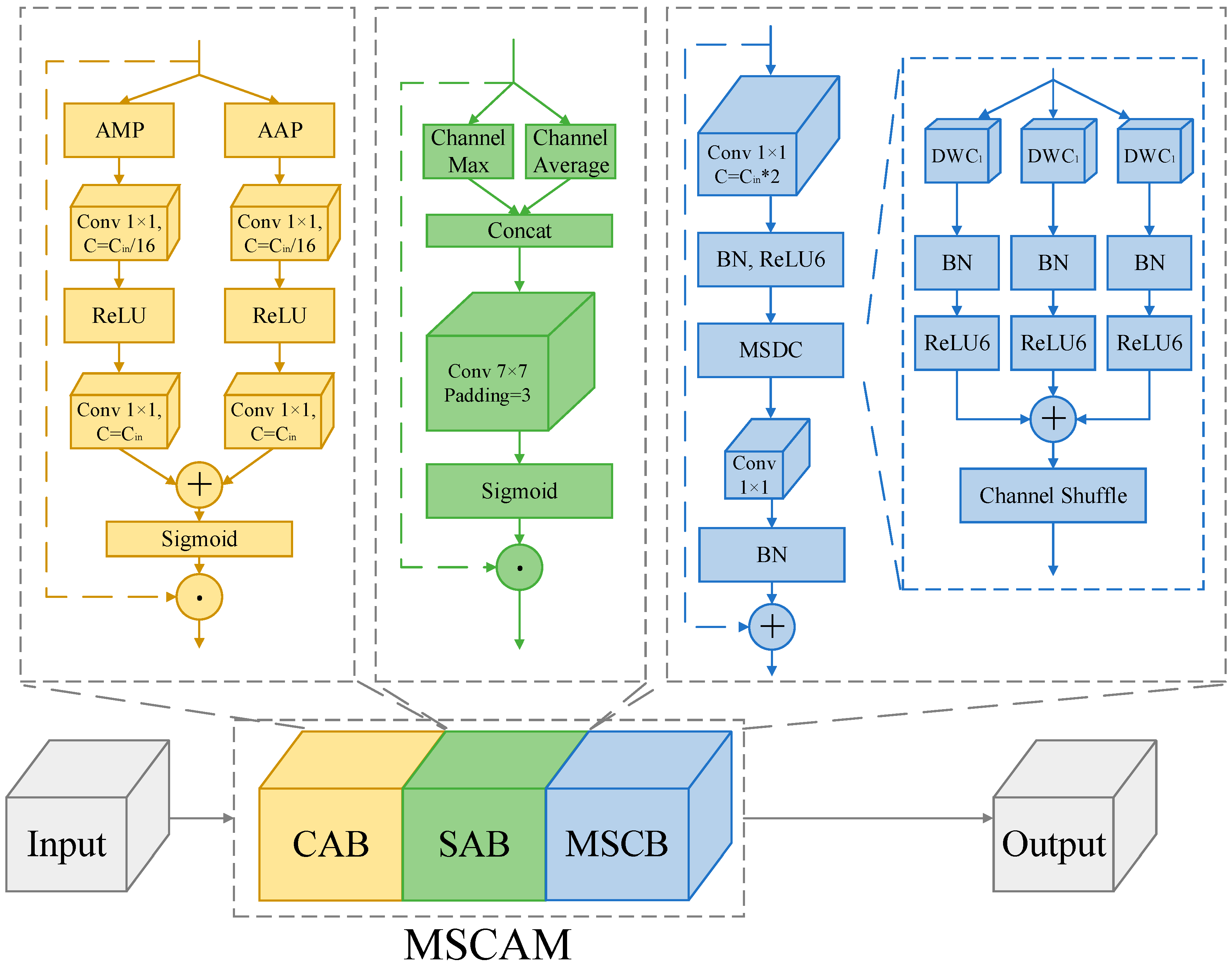
3.3. Multi-Scale Convolutional Attention Module
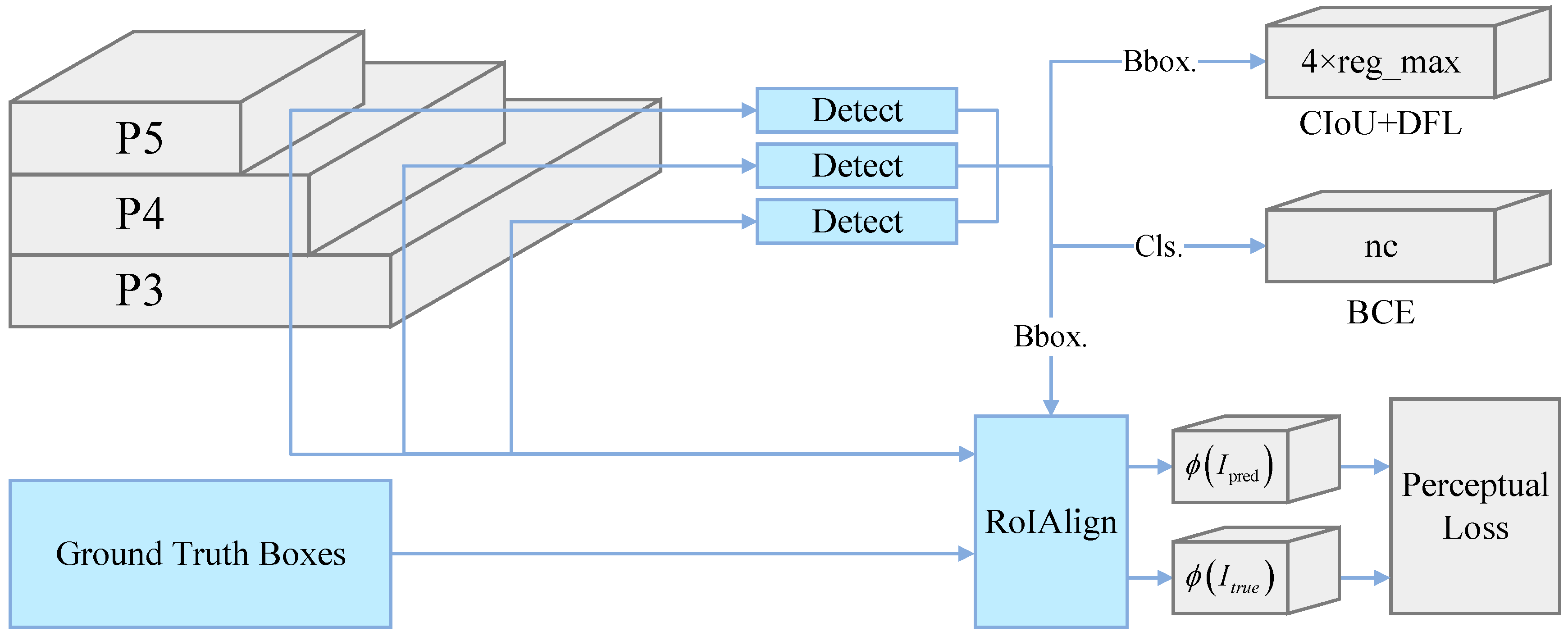
3.4. Loss Function Design
4. Experiments
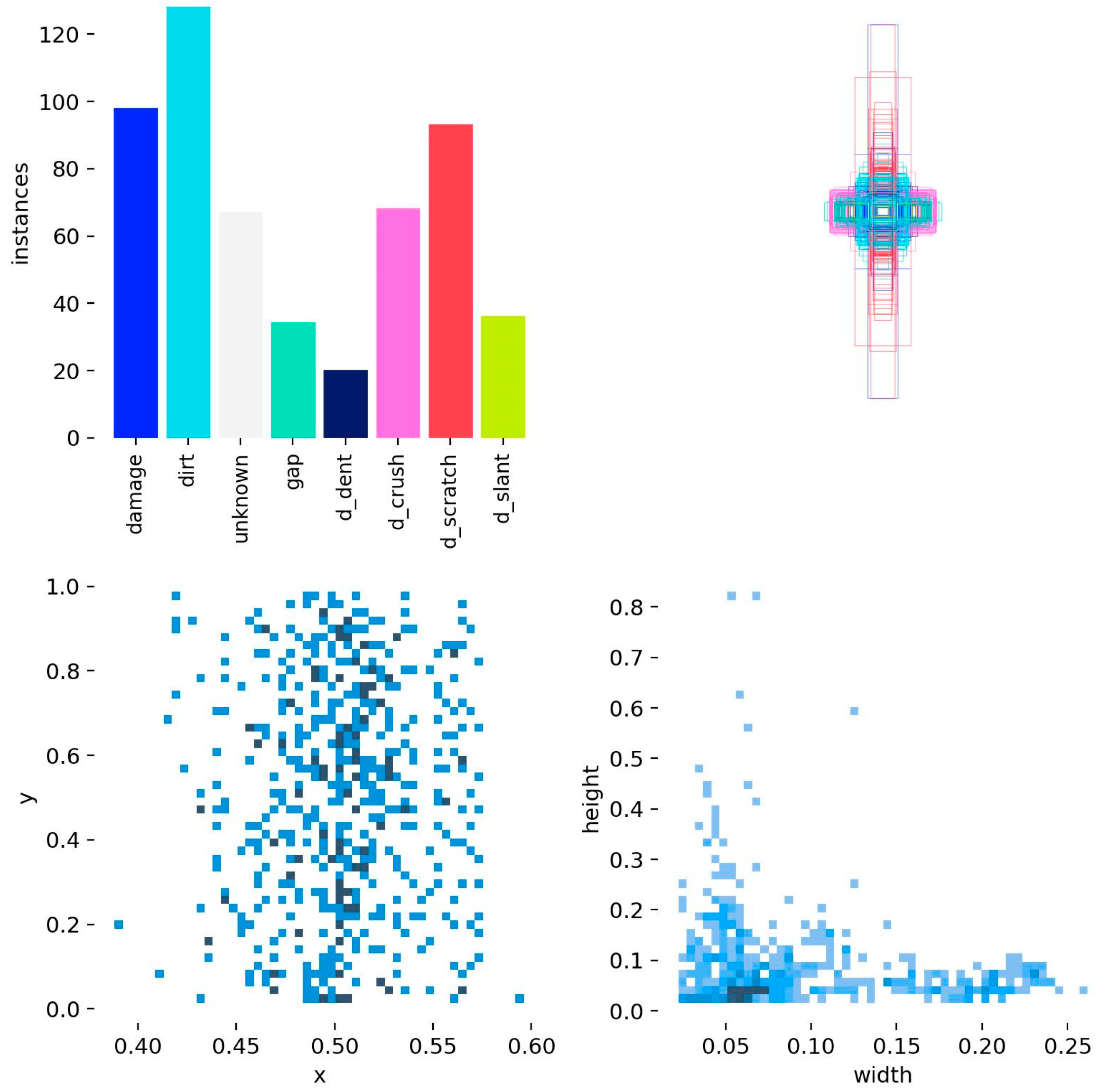
4.1. Experimental Setup and Dataset
4.2. Ablation Experiments
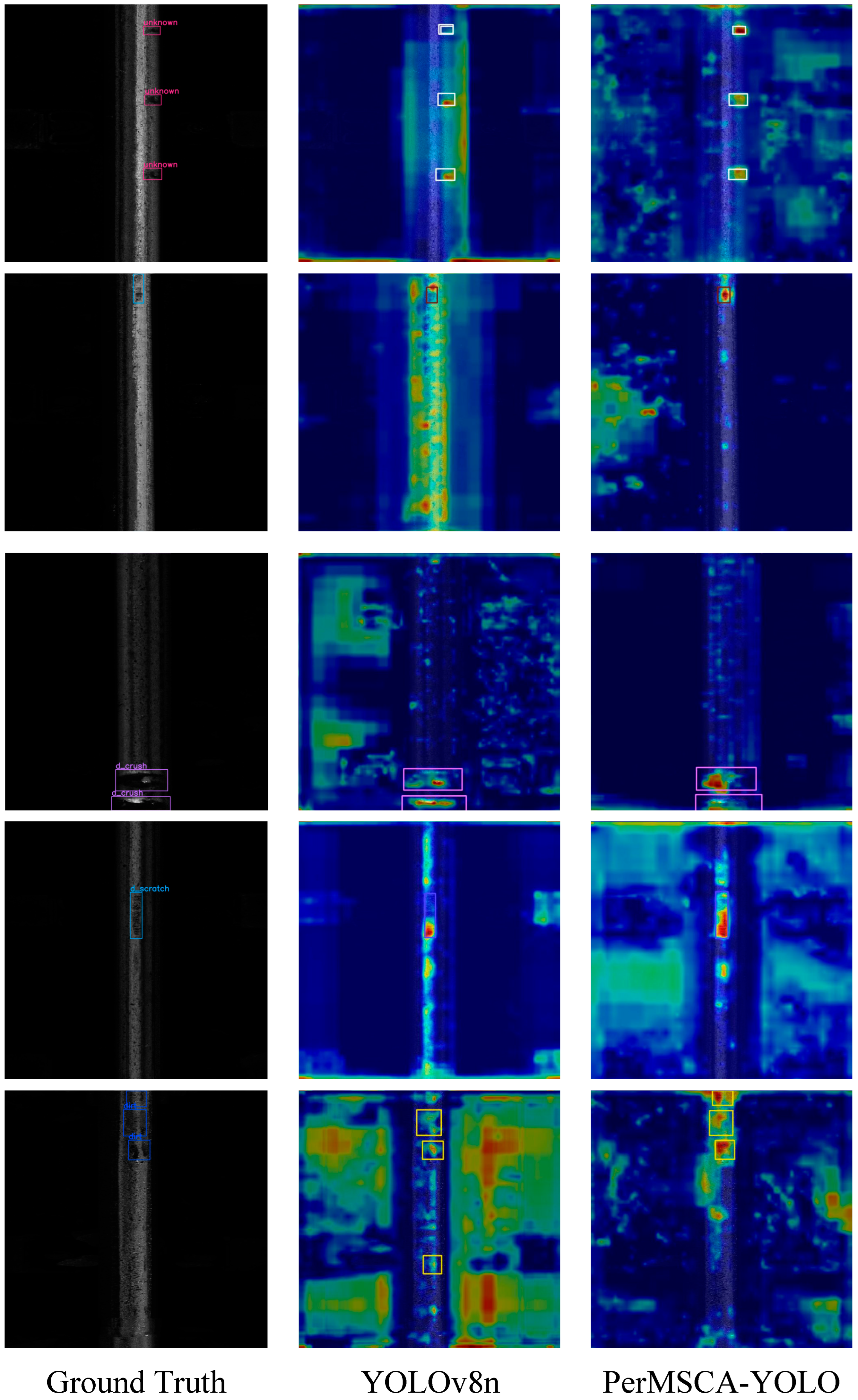
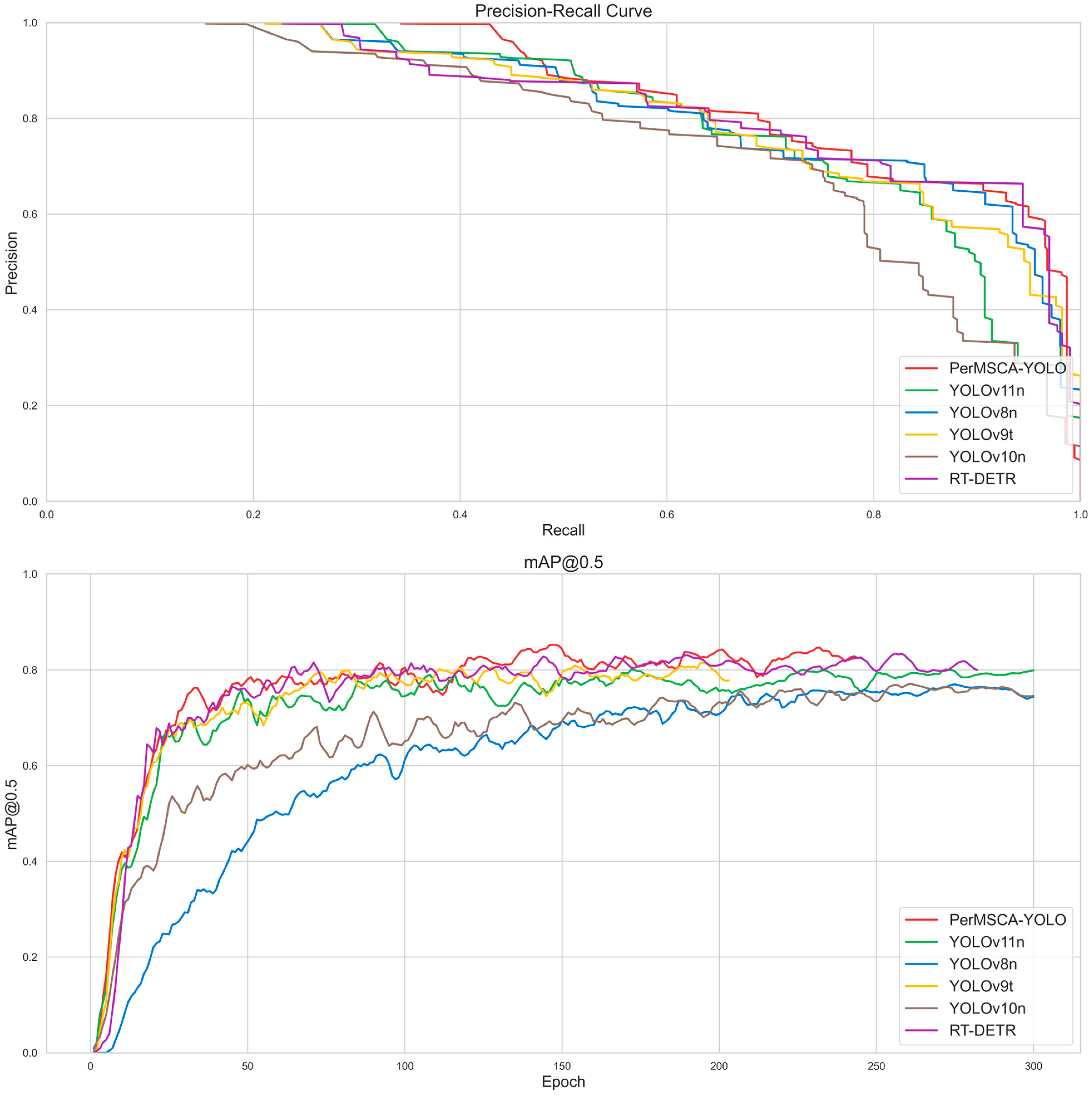
4.3. Comparative Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oh, K.; Yoo, M.; Jin, N.; Ko, J.; Seo, J.; Joo, H.; Ko, M. A review of deep learning applications for railway safety. Appl. Sci. 2022, 12, 10572. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Yi, D.; Yu, X.; Sha, X.; Li, L.; Sun, H.; Zhan, Z.; Li, W.J. A review on rail defect detection systems based on wireless sensors. Sensors 2022, 22, 6409. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Akbar, M.F.; Jawad, G.N.; Mohamed, M.F.P.; Ab Wahab, M.N. Nondestructive testing technologies for rail inspection: A review. Coatings 2022, 12, 1790. [Google Scholar] [CrossRef]
- Feng, J.H.; Yuan, H.; Hu, Y.Q.; Lin, J.; Liu, S.W.; Luo, X. Research on deep learning method for rail surface defect detection. IET Electr. Syst. Transp. 2020, 10, 436–442. [Google Scholar]
- Faghih-Roohi, S.; Hajizadeh, S.; Núñez, A.; Babuska, R.; De Schutter, B. Deep convolutional neural networks for detection of rail surface defects. In Proceedings of the 2016 International joint conference on neural networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2584–2589. [Google Scholar]
- Gibert, X.; Patel, V.M.; Chellappa, R. Deep multitask learning for railway track inspection. IEEE Trans. Intell. Transp. Syst. 2016, 18, 153–164. [Google Scholar]
- García, D.F.; Usamentiaga, R. Rail surface inspection system using differential topographic images. IEEE Trans. Ind. Appl. 2021, 57, 2994–3003. [Google Scholar]
- Tomita, K.; Chew, M.Y.L. A review of infrared thermography for delamination detection on infrastructures and buildings. Sensors 2022, 22, 423. [Google Scholar] [CrossRef]
- Alvarenga, T.A.; Carvalho, A.L.; Honorio, L.M.; Cerqueira, A.S.; Filho, L.M.A.; Nobrega, R.A. Detection and classification system for rail surface defects based on Eddy current. Sensors 2021, 21, 7937. [Google Scholar] [CrossRef]
- Park, J.W.; Lee, T.G.; Back, I.C.; Park, S.J.; Seo, J.M.; Choi, W.J.; Kwon, S.G. Rail surface defect detection and analysis using multi-channel eddy current method based algorithm for defect evaluation. J. Nondestruct. Eval. 2021, 40, 83. [Google Scholar]
- Abbas, M.; Shafiee, M. Structural health monitoring (SHM) and determination of surface defects in large metallic structures using ultrasonic guided waves. Sensors 2018, 18, 3958. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, X.; Luo, L.; Pan, Y.; Qiu, C. Simulation of laser ultrasonics for detection of surface-connected rail defects. J. Nondestruct. Eval. 2017, 36, 70. [Google Scholar]
- Yuan, F.; Yu, Y.; Liu, B.; Li, L. Investigation on optimal detection position of DC electromagnetic NDT in crack characterization for high-speed rail track. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- De Melo, A.L.O.; Kaewunruen, S.; Papaelias, M.; Bernucci, L.L.B.; Motta, R. Methods to monitor and evaluate the deterioration of track and its components in a railway in-service: A systemic review. Front. Built Environ. 2020, 6, 118. [Google Scholar]
- Yu, H.; Li, Q.; Tan, Y.; Gan, J.; Wang, J.; Geng, Y.-A.; Jia, L. A coarse-to-fine model for rail surface defect detection. IEEE Trans. Instrum. Meas. 2018, 68, 656–666. [Google Scholar]
- Gan, J.; Li, Q.; Wang, J.; Yu, H. A hierarchical extractor-based visual rail surface inspection system. IEEE Sens. J. 2017, 17, 7935–7944. [Google Scholar]
- Zhang, H.; Jin, X.; Wu, Q.M.J.; Wang, Y.; He, Z.; Yang, Y. Automatic visual detection system of railway surface defects with curvature filter and improved Gaussian mixture model. IEEE Trans. Instrum. Meas. 2018, 67, 1593–1608. [Google Scholar] [CrossRef]
- Wu, Y.; Qin, Y.; Wang, Z.; Jia, L. A UAV-based visual inspection method for rail surface defects. Appl. Sci. 2018, 8, 1028. [Google Scholar] [CrossRef]
- Cao, X.; Xie, W.; Ahmed, S.M.; Li, C.R. Defect detection method for rail surface based on line-structured light. Measurement 2020, 159, 107771. [Google Scholar]
- Nieniewski, M. Morphological detection and extraction of rail surface defects. IEEE Trans. Instrum. Meas. 2020, 69, 6870–6879. [Google Scholar]
- Ni, X.; Liu, H.; Ma, Z.; Wang, C.; Liu, J. Detection for rail surface defects via partitioned edge feature. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5806–5822. [Google Scholar]
- Mandriota, C.; Nitti, M.; Ancona, N.; Stella, E.; Distante, A. Filter-based feature selection for rail defect detection. Mach. Vis. Appl. 2004, 15, 179–185. [Google Scholar]
- Deutschl, E.; Gasser, C.; Niel, A.; Werschonig, J. Defect detection on rail surfaces by a vision based system. In Proceedings of the IEEE Intelligent Vehicles Symposium 2004, Parma, Italy, 14–17 June 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 507–511. [Google Scholar]
- Resendiz, E.; Hart, J.M.; Ahuja, N. Automated visual inspection of railroad tracks. IEEE Trans. Intell. Transp. Syst. 2013, 14, 751–760. [Google Scholar] [CrossRef]
- Masci, J.; Meier, U.; Ciresan, D.; Schmidhuber, J.; Fricout, G. Steel defect classification with max-pooling convolutional neural networks. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Zheng, D.; Li, L.; Zheng, S.; Chai, X.; Zhao, S.; Tong, Q.; Wang, J.; Guo, L. A defect detection method for rail surface and fasteners based on deep convolutional neural network. Comput. Intell. Neurosci. 2021, 2021, 2565500. [Google Scholar] [PubMed]
- Bai, T.; Gao, J.; Yang, J.; Yao, D. A study on railway surface defects detection based on machine vision. Entropy 2021, 23, 1437. [Google Scholar] [CrossRef] [PubMed]
- Bai, T.; Yang, J.; Xu, G.; Yao, D. An optimized railway fastener detection method based on modified Faster R-CNN. Measurement 2021, 182, 109742. [Google Scholar]
- Wang, Y.; Zhang, K.; Wang, L.; Wu, L. An improved YOLOv8 algorithm for rail surface defect detection. IEEE Access 2024, 12, 44984–44997. [Google Scholar]
- Teng, S.; Liu, Z.; Chen, G.; Cheng, L. Concrete crack detection based on well-known feature extractor model and the YOLO_v2 network. Appl. Sci. 2021, 11, 813. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, X.; Zhou, X.; Qian, S.; Yu, J. Defect detection for metal base of TO-Can packaged laser diode based on improved YOLO algorithm. Electronics 2022, 11, 1561. [Google Scholar] [CrossRef]
- Hu, J.; Qiao, P.; Lv, H.; Yang, L.; Ouyang, A.; He, Y.; Liu, Y. High speed railway fastener defect detection by using improved YoLoX-Nano Model. Sensors 2022, 22, 8399. [Google Scholar] [CrossRef]
- Giben, X.; Patel, V.M.; Chellappa, R. Material classification and semantic segmentation of railway track images with deep convolutional neural networks. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 621–625. [Google Scholar]
- Wei, X.; Wei, D.; Suo, D.; Jia, L.; Li, Y. Multi-target defect identification for railway track line based on image processing and improved YOLOv3 model. IEEE Access 2020, 8, 61973–61988. [Google Scholar]
- Hao, S.; An, B.; Ma, X.; Sun, X.; He, T.; Sun, S. PKAMNet: A transmission line insulator parallel-gap fault detection network based on prior knowledge transfer and attention mechanism. IEEE Trans. Power Deliv. 2023, 38, 3387–3397. [Google Scholar]
- Zhang, C.; Xu, D.; Zhang, L.; Deng, W. Rail surface defect detection based on image enhancement and improved YOLOX. Electronics 2023, 12, 2672. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Wan, Z. Rail surface defect detection based on improved Mask R-CNN. Comput. Electr. Eng. 2022, 102, 108269. [Google Scholar]
- Zhang, B.; Fang, S.; Li, Z. Research on Surface Defect Detection of Rare-Earth Magnetic Materials Based on Improved SSD. Complexity 2021, 2021, 4795396. [Google Scholar]
- Wang, J.; Li, Q.; Gan, J.; Yu, H.; Yang, X. Surface defect detection via entity sparsity pursuit with intrinsic priors. IEEE Trans. Ind. Inform. 2019, 16, 141–150. [Google Scholar]
- Niu, M.; Song, K.; Huang, L.; Wang, Q.; Yan, Y.; Meng, Q. Unsupervised saliency detection of rail surface defects using stereoscopic images. IEEE Trans. Ind. Inform. 2020, 17, 2271–2281. [Google Scholar]
- Zhang, D.; Song, K.; Wang, Q.; He, Y.; Wen, X.; Yan, Y. Two deep learning networks for rail surface defect inspection of limited samples with line-level label. IEEE Trans. Ind. Inform. 2020, 17, 6731–6741. [Google Scholar]
- Sohan, M.; Ram, T.S.; Reddy, C.V.R. A review on yolov8 and its advancements. In Proceedings of the International Conference on Data Intelligence and Cognitive Informatics, Tirunelveli, India, 18–20 November 2024; Springer: Singapore, 2024; pp. 529–545. [Google Scholar]
- Li, H.; Wang, F.; Liu, J.; Song, H.; Hou, Z.; Dai, P. Ensemble model for rail surface defects detection. PLoS ONE 2022, 17, e0268518. [Google Scholar]
- Arain, A.; Mehran, S.; Shaikh, M.Z.; Kumar, D.; Chowdhry, B.S.; Hussain, T. Railway track surface faults dataset. Data Brief 2024, 52, 110050. [Google Scholar]
- Ozdemir, R.; Koc, M. On the enhancement of semi-supervised deep learning-based railway defect detection using pseudo-labels. Expert Syst. Appl. 2024, 251, 124105. [Google Scholar]
- Rodríguez-Abreo, O.; Quiroz-Juárez, M.A.; Macías-Socarras, I.; Rodríguez-Reséndiz, J.; Camacho-Pérez, J.M.; Carcedo-Rodríguez, G.; Camacho-Pérez, E. Automatic Detection of Railway Faults Using Neural Networks: A Comparative Study of Transfer Learning Models and YOLOv11. Infrastructures 2024, 10, 3. [Google Scholar] [CrossRef]






| Environment | Parameters | Value |
|---|---|---|
| Hardware | CPU | AMD R9 9900X |
| GPU | NVIDIA RTX 4090 | |
| Memory | DDR5 6000 MHz 64 G | |
| Software | Operating system | Windows 10 |
| Development language | Python 3.9 | |
| Deep learning framework | Pytorch 2.6.0 | |
| Computing platform | CUDA 12.7 + cuDNN 9.5.1 |
| Parameters | Value |
|---|---|
| Epoch | 300 |
| Batch size | 16 |
| Workers | 8 |
| Lr0 | 0.01 |
| Lrf | 0.01 |
| Momentum | 0.937 |
| Weight decay | 0.0005 |
| Warmup epochs | 3.0 |
| Warmup momentum | 0.8 |
| Warmup bias lr | 0.1 |
| Optimizer | SGD |
| Data augmentation | Mosaic, Close mosaic = 10 |
| Baseline | FasterNet | MSCAM | Perceptual Loss | mAP@0.5 | F1 | FPS |
|---|---|---|---|---|---|---|
| YOLOv8n | 0.831 | 0.75 (conf = 0.449) | 134 | |||
| √ | 0.822 | 0.78 (conf = 0.596) | 185 | |||
| √ | 0.847 | 0.80 (conf = 0.556) | 112 | |||
| √ | 0.842 | 0.77 (conf = 0.660) | 135 | |||
| √ | √ | 0.839 | 0.76 (conf = 0.532) | 164 | ||
| √ | √ | 0.834 | 0.75 (conf = 0.517) | 181 | ||
| √ | √ | 0.861 | 0.79 (conf = 0.487) | 109 | ||
| √ | √ | √ | 0.856 | 0.79 (conf = 0.462) | 142 |
| Model | mAP@0.5 | F1 | FPS |
|---|---|---|---|
| YOLOv8n | 0.831 | 0.75 (conf = 0.449) | 134 |
| YOLOv9t | 0.824 | 0.76 (conf = 0.575) | 133 |
| YOLOv10n | 0.774 | 0.71 (conf = 0.298) | 187 |
| YOLOv11n | 0.813 | 0.75 (conf = 0.582) | 155 |
| RT-DETR | 0.838 | 0.82 (conf = 0.778) | 61 |
| PerMSCA-YOLO | 0.856 | 0.79 (conf = 0.462) | 142 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, R.; Luan, F.; Zhang, H. PerMSCA-YOLO: A Perceptual Multi-Scale Convolutional Attention Enhanced YOLOv8 Model for Rail Defect Detection. Appl. Sci. 2025, 15, 3588. https://doi.org/10.3390/app15073588
Zhang J, Zhang R, Luan F, Zhang H. PerMSCA-YOLO: A Perceptual Multi-Scale Convolutional Attention Enhanced YOLOv8 Model for Rail Defect Detection. Applied Sciences. 2025; 15(7):3588. https://doi.org/10.3390/app15073588
Chicago/Turabian StyleZhang, Jialiang, Ruiqi Zhang, Fengkai Luan, and Hu Zhang. 2025. "PerMSCA-YOLO: A Perceptual Multi-Scale Convolutional Attention Enhanced YOLOv8 Model for Rail Defect Detection" Applied Sciences 15, no. 7: 3588. https://doi.org/10.3390/app15073588
APA StyleZhang, J., Zhang, R., Luan, F., & Zhang, H. (2025). PerMSCA-YOLO: A Perceptual Multi-Scale Convolutional Attention Enhanced YOLOv8 Model for Rail Defect Detection. Applied Sciences, 15(7), 3588. https://doi.org/10.3390/app15073588






