Weighting Optimization for Fuel Cell Hybrid Vehicles: Lifetime-Conscious Component Sizing and Energy Management
Abstract
Featured Application
Abstract
1. Introduction
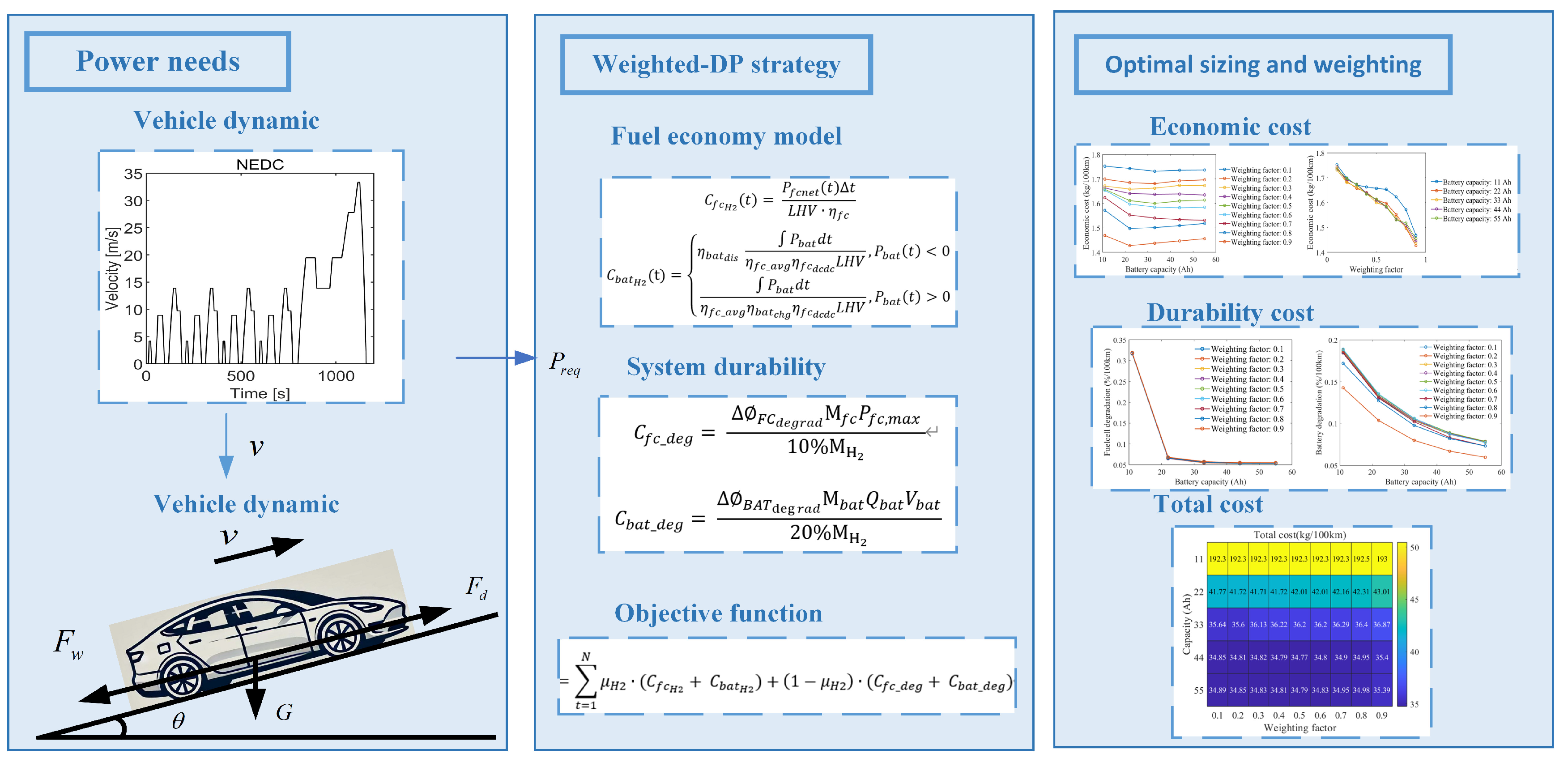
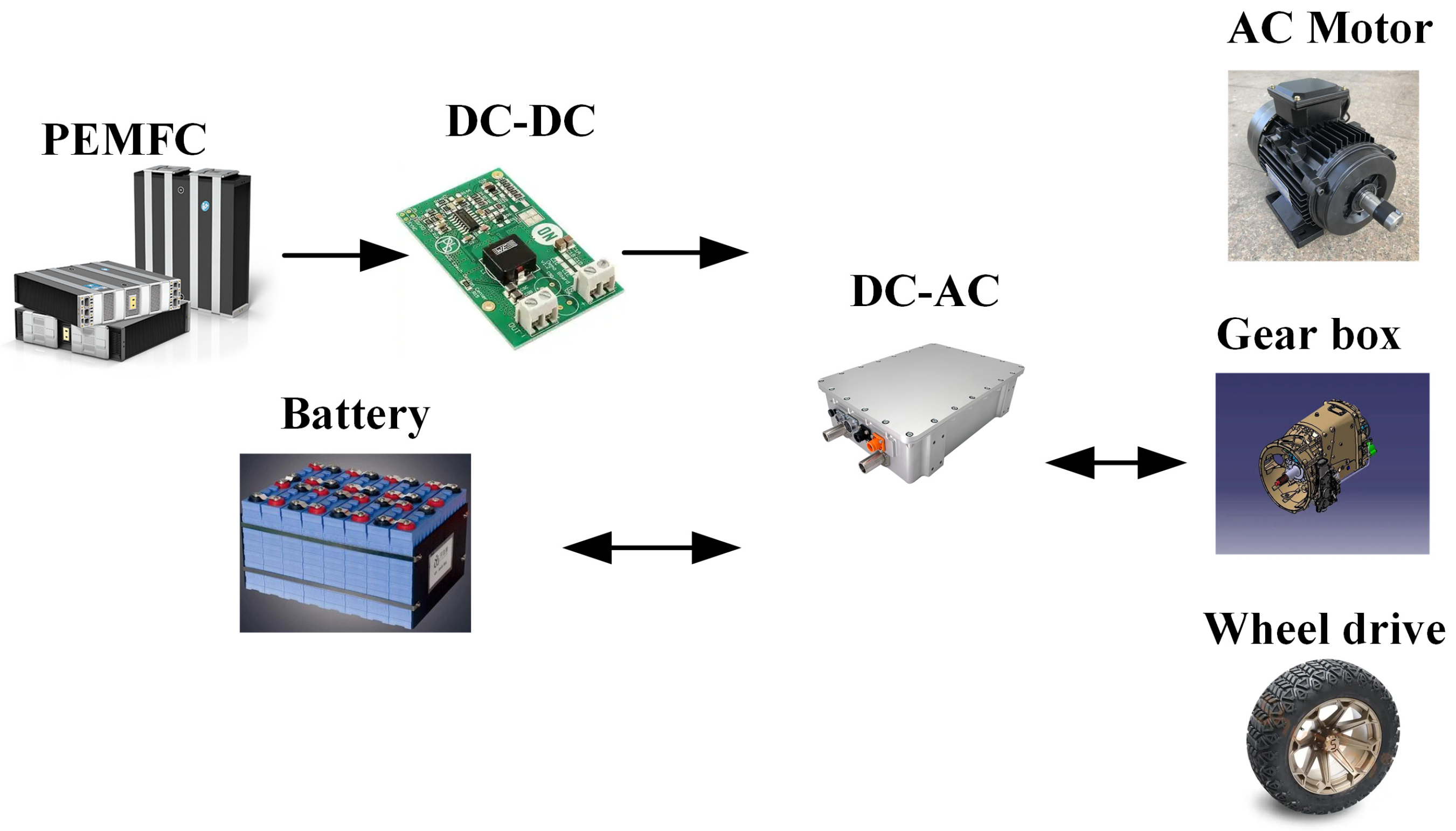
2. System Model Description
2.1. Vehicle Longitudinal Dynamic Model
2.2. Fuel Economy Model
2.3. System Durability Model
2.4. Equivalent Degradation Model
2.5. Dynamic Programming
3. Power Sizing and Energy Management Strategy
3.1. Component Sizing Problem
3.2. Optimization Problem Formulation
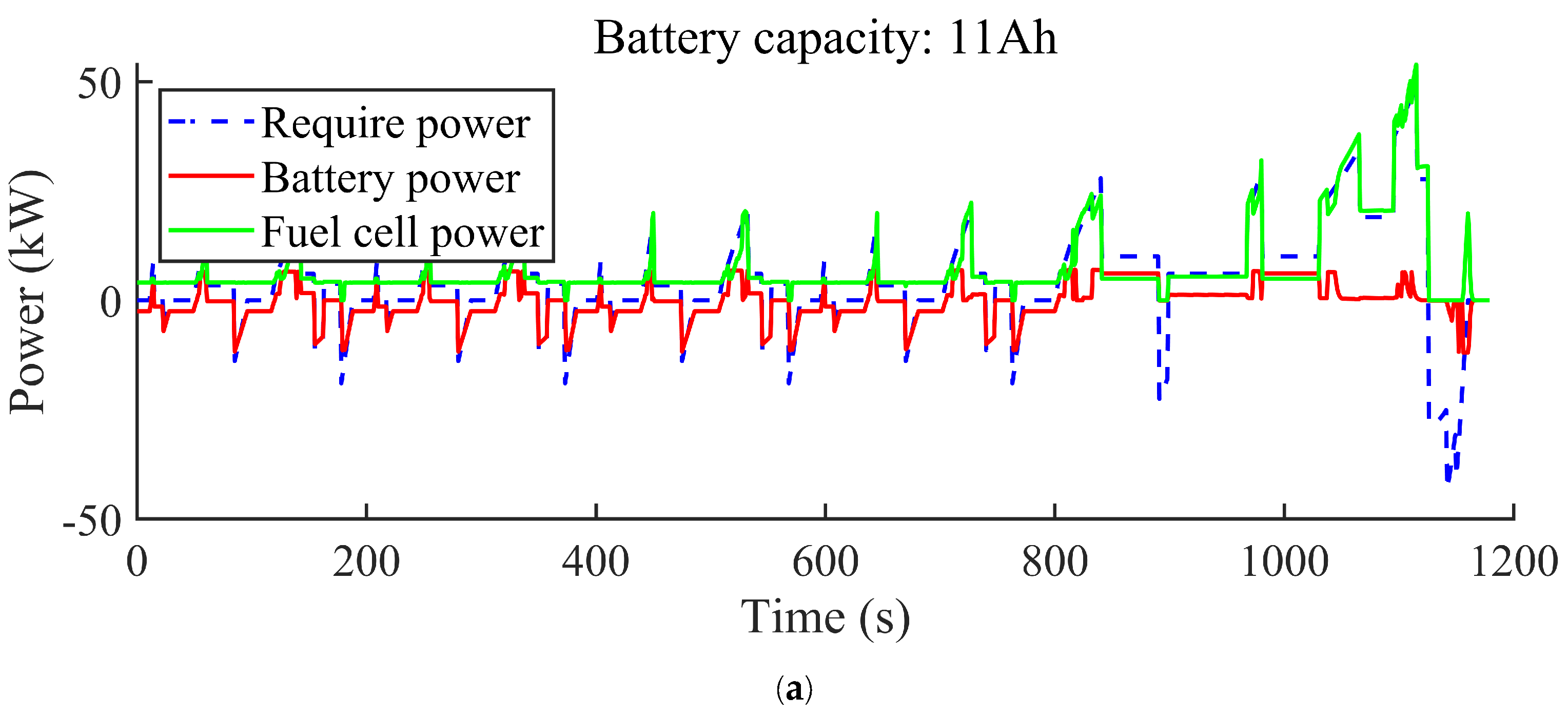
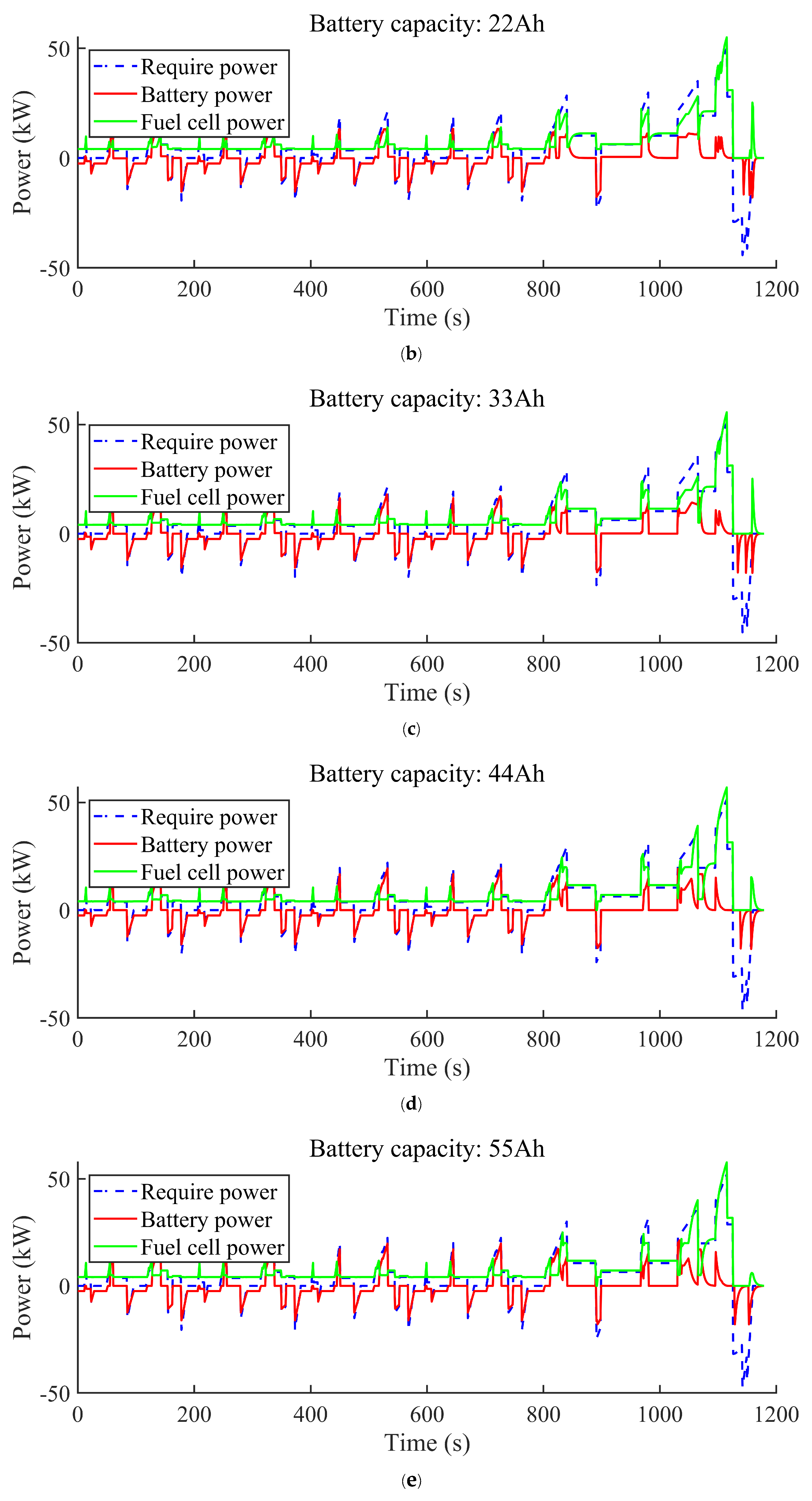
4. Results and Discussion
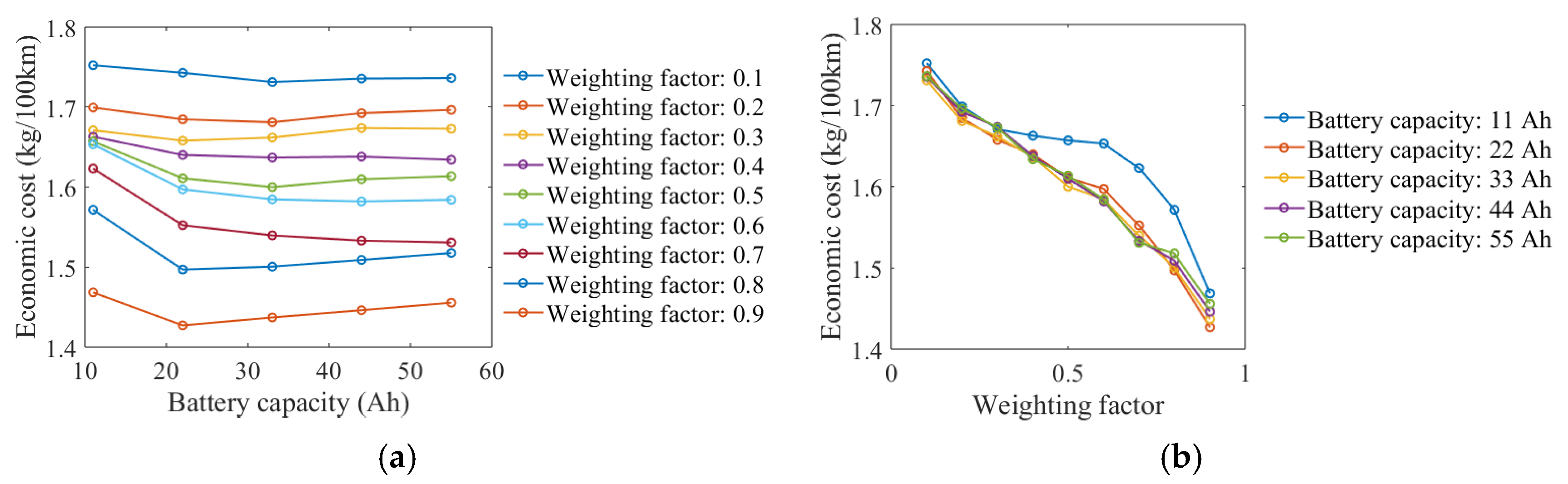
4.1. Fuel Economic
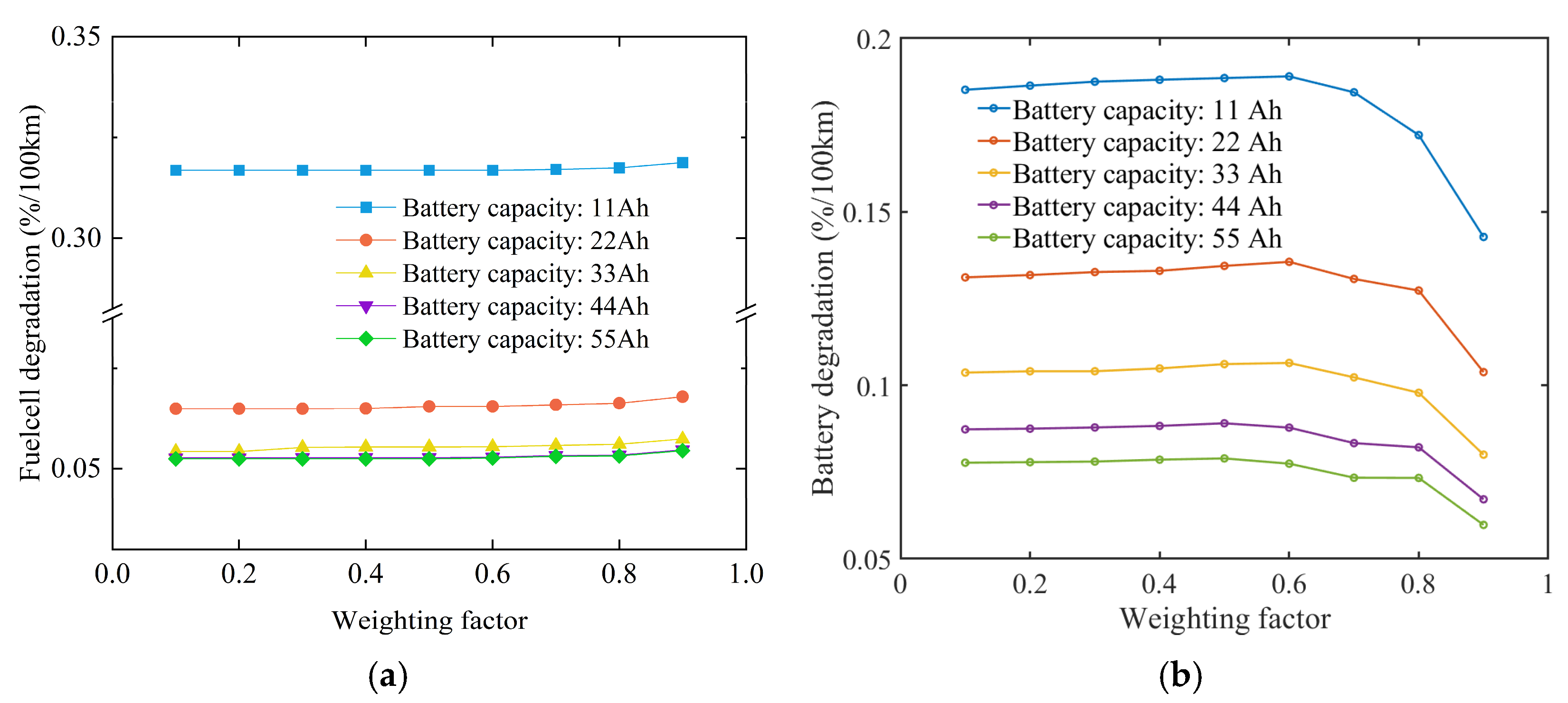
4.2. System Durability Cost
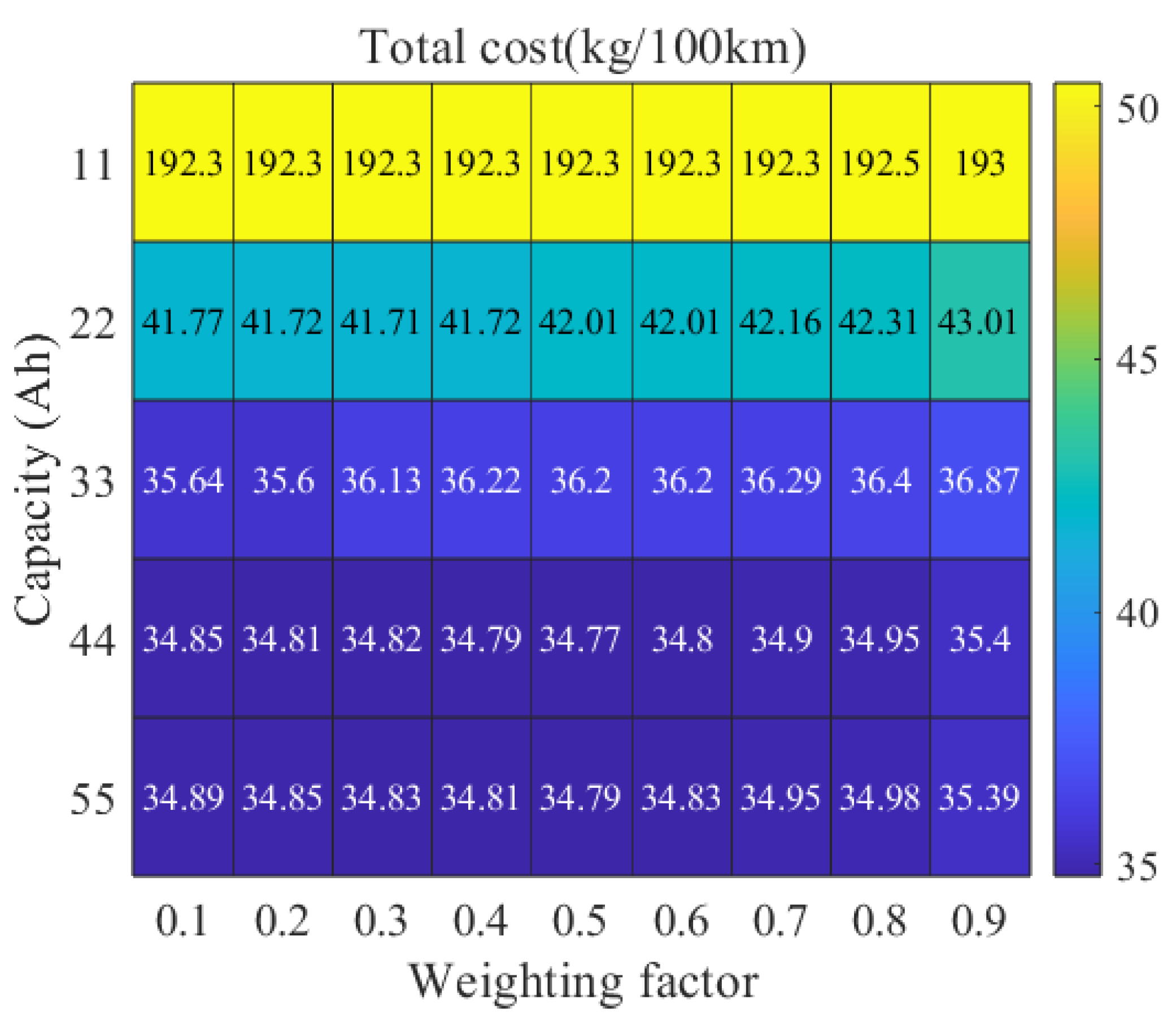
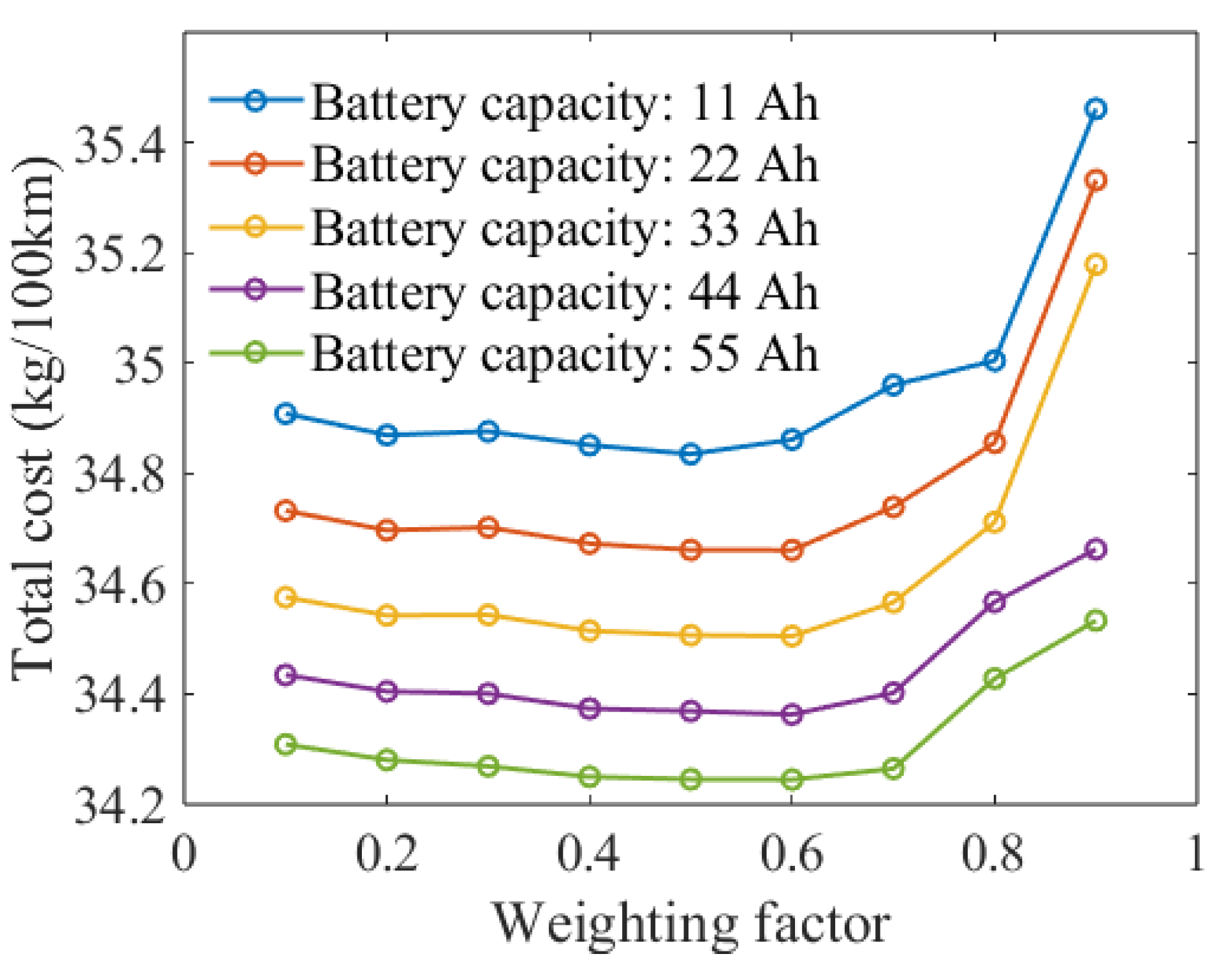
4.3. Total Cost
4.4. Price Impact
5. Conclusions
- (1)
- Based on the NEDC, a battery capacity of approximately 44 Ah, a maximum fuel cell power of 80 kW, and a weighting factor of 0.5 achieve an optimal balance between fuel economy and system durability in light-duty fuel cell passenger vehicles. Total costs are reduced by 1% compared to selecting the optimal system durability using the Pareto frontier.
- (2)
- Increasing the battery capacity can effectively reduce the total operational costs of FCHVs by minimizing per kilometer battery degradation and providing sufficient dynamic power. However, once the battery capacity reaches a level sufficient to deliver optimal dynamic power, further increases in capacity lead to a higher price and weight, thereby raising the total costs.
- (3)
- The weighting factor significantly influences the trade-off between fuel economy and system durability costs by altering energy distribution strategies. As the weighting factor increases, fuel economy costs decrease while durability costs rise, and vice versa. This effect differs fundamentally from that of changing the battery capacity. At present, fuel economy and system durability are equally important considerations. However, as power source prices decrease in the future, system durability may become less critical for fuel cell hybrid systems, with fuel economy optimization emerging as the primary focus.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ah-throughput [Ah] | |
| Battery degradation coefficient [-] | |
| Equivalent hydrogen consumption [kg] | |
| Drag coefficient [-] | |
| Current flux [C] | |
| Activation energy [J/mol] | |
| Frontal area of the vehicle [m2] | |
| Gravitational acceleration [m/s2] | |
| Current [A] | |
| J | Total cost [kg] |
| Fuel cell degradation coefficients [%/h] | |
| Cost at time T [-] | |
| Lower heating value | |
| Mass [kg] | |
| Price [$] | |
| Power [kW] | |
| Capacity (Ah) | |
| Gas constant [J/(kg·K)] | |
| Resistance [Ω] | |
| Time [s] | |
| Temperature [K] | |
| Voltage [V] | |
| Velocity [m/s] | |
| Power law factor [-] | |
| Subscripts | |
| Vehicle | |
| Basic | |
| Drag | |
| Fuel cell | |
| Battery | |
| Require | |
| Gearbox | |
| Motor | |
| DC–AC converter | |
| DC–DC converter | |
| Optimal | |
| Open-circuit voltage | |
| Average | |
| Discharge | |
| Charge | |
| Greek symbols | |
| Penalty coefficient [-] | |
| Specific energy of the battery [] | |
| Power-to-weight ratio of the fuel cell [] | |
| Discretization step [s] | |
| Road grade [-] | |
| Rolling resistance coefficient [-] | |
| Efficiency [-] | |
| Degradation [%] | |
| Air density [] | |
| Abbreviations | |
| ADVISOR | Advanced Vehicle Simulator |
| CDCS | Charge–Depletion–Charge–Sustain |
| DP | Dynamic Programming |
| ECMS | Equivalent Consumption Minimization Strategy |
| EMS | Energy Management Strategy |
| FCHV | Fuel Cell Hybrid Vehicle |
| FCREx | Range-Extender Fuel Cell Vehicle |
| FCS | Fuel Cell Stack |
| H2 | Hydrogen |
| NEDC | New European Driving Cycle |
| PEMFC | Proton Exchange Membrane Fuel Cells |
| PMP | Pontryagin’s Minimum Principle |
| SQP | Sequential Quadratic Programming |
| SOC | State of Charge |
References
- Aminudin, M.; Kamarudin, S.; Lim, B.; Majilan, E.; Masdar, M.; Shaari, N. An overview: Current progress on hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2023, 48, 4371–4388. [Google Scholar]
- Desantes, J.; Molina, S.; Novella, R.; Lopez-Juarez, M. Comparative global warming impact and NOX emissions of conventional and hydrogen automotive propulsion systems. Energy Convers. Manag. 2020, 221, 113137. [Google Scholar]
- Li, D.; Leung, M.F.; Tang, J.; Wang, Y.; Hu, J.; Wang, S. Generative Self-Supervised Learning for Cyberattack-Resilient EV Charging Demand Forecasting. IEEE Trans. Intell. Transp. Syst. 2025, 1–10. [Google Scholar] [CrossRef]
- Desantes, J.; Novella, R.; Pla, B.; Lopez-Juarez, M. A modeling framework for predicting the effect of the operating conditions and component sizing on fuel cell degradation and performance for automotive applications. Appl. Energy 2022, 317, 119137. [Google Scholar] [CrossRef]
- Lü, X.; Qu, Y.; Wang, Y.; Qin, C.; Liu, G. A comprehensive review on hybrid power system for PEMFC-HEV: Issues and strategies. Energy Convers. Manag. 2018, 171, 1273–1291. [Google Scholar]
- Wang, S.; Jiang, S.P. Prospects of fuel cell technologies. Natl. Sci. Rev. 2017, 4, 163–166. [Google Scholar]
- Alpaslan, E.; Karaoğlan, M.U.; Colpan, C.O. Investigation of drive cycle simulation performance for electric, hybrid, and fuel cell powertrains of a small-sized vehicle. Int. J. Hydrogen Energy 2023, 48, 39497–39513. [Google Scholar]
- Yuan, H.-B.; Zou, W.-J.; Jung, S.; Kim, Y.-B. Optimized rule-based energy management for a polymer electrolyte membrane fuel cell/battery hybrid power system using a genetic algorithm. Int. J. Hydrogen Energy 2022, 47, 7932–7948. [Google Scholar]
- Li, Q.; Meng, X.; Gao, F.; Zhang, G.; Chen, W. Approximate Cost-Optimal Energy Management of Hydrogen Electric Multiple Unit Trains Using Double Q-Learning Algorithm. IEEE Trans. Ind. Electron. 2022, 69, 9099–9110. [Google Scholar]
- Gao, D.; Jin, Z.; Lu, Q. Energy management strategy based on fuzzy logic for a fuel cell hybrid bus. J. Power Sources 2008, 185, 311–317. [Google Scholar]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A wavelet-fuzzy logic based energy management strategy for a fuel cell/battery/ultra-capacitor hybrid vehicular power system. J. Power Sources 2009, 194, 369–380. [Google Scholar]
- Teng, Y.-T.; Wang, F.-C. Cost Analyses and Optimization of a PEMFC Electric Vehicle Model. In Proceedings of the 2016 IEEE/SICE International Symposium on System Integration (SII), Sapporo, Japan, 13–15 December 2016; pp. 887–892. [Google Scholar]
- Jalil, N.; Kheir, N.A.; Salman, M. A rule-based energy management strategy for a series hybrid vehicle. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 6 June 1997. [Google Scholar]
- Zhang, Y.; Zhang, C.; Fan, R.; Huang, S.; Yang, Y.; Xu, Q. Twin delayed deep deterministic policy gradient-based deep reinforcement learning for energy management of fuel cell vehicle integrating durability information of powertrain. Energy Convers. Manag. 2022, 274, 116454. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K. Health-conscious deep reinforcement learning energy management for fuel cell buses integrating environmental and look-ahead road information. Energy 2024, 290, 130146. [Google Scholar]
- Song, K.; Huang, X.; Xu, H.; Sun, H.; Chen, Y.; Huang, D. Model predictive control energy management strategy integrating long short-term memory and dynamic programming for fuel cell vehicles. Int. J. Hydrogen Energy 2024, 56, 1235–1248. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F.; Lu, L.; Hua, J. Application of Pontryagin’s Minimal Principle to the energy management strategy of plugin fuel cell electric vehicles. Int. J. Hydrogen Energy 2013, 38, 10104–10115. [Google Scholar]
- Wu, X.; Hu, X.; Yin, X.; Li, L.; Zeng, Z.; Pickert, V. Convex programming energy management and components sizing of a plug-in fuel cell urban logistics vehicle. J. Power Sources 2019, 423, 358–366. [Google Scholar]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F. Dynamic Programming Algorithm for minimizing operating cost of a PEM fuel cell vehicle. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1490–1495. [Google Scholar]
- Kim, M.-J.; Peng, H. Power management and design optimization of fuel cell/battery hybrid vehicles. J. Power Sources 2007, 165, 819–832. [Google Scholar]
- Dominguez, R.; Solano, J.; Jacome, A. Sizing of Fuel Cell—Ultracapacitors Hybrid Electric Vehicles Based on the Energy Management Strategy. In Proceedings of the 2018 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 27–30 August 2018. [Google Scholar]
- Hu, Z.; Li, J.; Xu, L.; Song, Z.; Fang, C.; Ouyang, M.; Dou, G.; Kou, G. Multi-objective energy management optimization and parameter sizing for proton exchange membrane hybrid fuel cell vehicles. Energy Convers. Manag. 2016, 129, 108–121. [Google Scholar]
- Chen, J.; He, H.; Wang, Y.X.; Quan, S.; Zhang, Z.; Wei, Z.; Han, R. Research on energy management strategy for fuel cell hybrid electric vehicles based on improved dynamic programming and air supply optimization. Energy 2024, 300, 131567. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F.; Lu, L.; Hua, J. Optimal sizing of plug-in fuel cell electric vehicles using models of vehicle performance and system cost. Appl. Energy 2013, 103, 477–487. [Google Scholar]
- Molina, S.; Novella, R.; Pla, B.; Lopez-Juarez, M. Optimization and sizing of a fuel cell range extender vehicle for passenger car applications in driving cycle conditions. Appl. Energy 2021, 285, 116469. [Google Scholar] [CrossRef]
- Feroldi, D.; Carignano, M. Sizing for fuel cell/supercapacitor hybrid vehicles based on stochastic driving cycles. Appl. Energy 2016, 183, 645–658. [Google Scholar] [CrossRef]
- KoteswaraRao, K.V.; Srinivasulu, G.N.; Rahul, J.R.; Velisala, V. Optimal component sizing and performance of Fuel Cell—Battery powered vehicle over world harmonized and new european driving cycles. Energy Convers. Manag. 2024, 300, 117992. [Google Scholar] [CrossRef]
- Tazelaar, E.; Shen, Y.; Veenhuizen, P.; Hofman, T.; Bosch, P.v.D. Sizing Stack and Battery of a Fuel Cell Hybrid Distribution Truck. Oil Gas Sci. Technol.-Rev. D Ifp Energ. Nouv. 2012, 67, 563–573. [Google Scholar] [CrossRef]
- Hu, X.; Murgovski, N.; Johannesson, L.M.; Egardt, B. Optimal dimensioning and power management of a fuel cell/battery hybrid bus via convex programming. IEEE-ASME Trans. Mechatron. 2015, 20, 457–468. [Google Scholar] [CrossRef]
- Han, J.; Kokkolaras, M.; Papalambros, P.Y. Optimal Design of Hybrid Fuel Cell Vehicles. J. Fuel Cell Sci. Technol. 2008, 5, 041014. [Google Scholar] [CrossRef]
- Xu, L.; Mueller, C.D.; Li, J.; Ouyang, M.; Hu, Z. Multi-objective component sizing based on optimal energy management strategy of fuel cell electric vehicles. Appl. Energy 2015, 157, 664–674. [Google Scholar] [CrossRef]
- Pei, P.; Chang, Q.; Tang, T. A quick evaluating method for automotive fuel cell lifetime. Int. J. Hydrogen Energy 2008, 33, 3829–3836. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Kittner, N.; Lill, F.; Kammen, D.M. Energy storage deployment and innovation for the clean energy transition. Nat. Energy 2017, 2, 17125. [Google Scholar] [CrossRef]
- Fuel Cell System Cost-2016, DOE Hydrogen and Fuel Cells Program Record; Rec. No. 16020; U.S. Department of Energy: Washington, DC, USA, 2016.



| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Mass | 1848 | kg | |
| Coefficient of friction | 0.015 | - | |
| Drag coefficient | 0.3 | - | |
| Air density | 1.025 | ||
| Frontal area | 2.79 | m2 | |
| Power-to-weight ratio of the fuel cell | 0.157 | ||
| Specific energy of the battery | 70 | ||
| Transmission efficiency | 0.95 | - | |
| Motor efficiency | 0.95 | - | |
| DC–AC converter efficiency | 0.95 | - | |
| Fuel cell DC–DC converter efficiency | 0.95 | - | |
| Brake energy recovery rate | 0.6 | - |
| Coefficient | Values (Unit) | Definitions |
|---|---|---|
| 0.00126 (%/h) | Output power less than 5% of max power | |
| 0.00196 (%/cycle) | One full start–stop | |
| 0.0000593 (%/h) | Absolute value of load variations rate is larger than 10% of max power per second | |
| 0.00147 (%/h) | Higher than 90% of maximal power | |
| 1.47 | - |
| Parameters | Value | Unit |
|---|---|---|
| 147 | ||
| 411 | ||
| 5.88 |
| Parameter | Value | Unit |
|---|---|---|
| 180 | ||
| 80 | ||
| 6.5 | % |
| Method | Economic Cost (kg/100 km) | Fuel Cell Degradation (%/100 km) | Battery Degradation (%/100 km) | Total Cost (kg/100 km) | Battery Capacity (Ah) |
|---|---|---|---|---|---|
| Weighting factor | 1.5679 | 0.0527 | 0.0877 | 34.7721 | 44 |
| Fuel economy only | 1.2668 | 0.9916 | 0.089 | 597.0159 | 22 |
| System durability only | 1.8122 | 0.0526 | 0.0869 | 34.9211 | 44 |
| Pareto for economic | 1.5534 | 0.0553 | 0.1047 | 36.2042 | 33 |
| Pareto for durability | 1.5739 | 0.0526 | 0.0765 | 34.7932 | 55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Shu, C.; Dong, H.; Tang, Y.; Feng, J.; Yuan, H.; Bai, S.; Zhu, S.; Li, G. Weighting Optimization for Fuel Cell Hybrid Vehicles: Lifetime-Conscious Component Sizing and Energy Management. Appl. Sci. 2025, 15, 3586. https://doi.org/10.3390/app15073586
Xiao X, Shu C, Dong H, Tang Y, Feng J, Yuan H, Bai S, Zhu S, Li G. Weighting Optimization for Fuel Cell Hybrid Vehicles: Lifetime-Conscious Component Sizing and Energy Management. Applied Sciences. 2025; 15(7):3586. https://doi.org/10.3390/app15073586
Chicago/Turabian StyleXiao, Xuanyu, Chen Shu, Huaiwei Dong, Yujun Tang, Jinfeng Feng, Hao Yuan, Shuzhan Bai, Sipeng Zhu, and Guoxiang Li. 2025. "Weighting Optimization for Fuel Cell Hybrid Vehicles: Lifetime-Conscious Component Sizing and Energy Management" Applied Sciences 15, no. 7: 3586. https://doi.org/10.3390/app15073586
APA StyleXiao, X., Shu, C., Dong, H., Tang, Y., Feng, J., Yuan, H., Bai, S., Zhu, S., & Li, G. (2025). Weighting Optimization for Fuel Cell Hybrid Vehicles: Lifetime-Conscious Component Sizing and Energy Management. Applied Sciences, 15(7), 3586. https://doi.org/10.3390/app15073586








